Abstract
Nonorthogonal polynomials have many useful properties like being used as a basis for spectral methods, being generated in an easy way, having exponential rates of convergence, having fewer terms and reducing computational errors in comparison with some others, and producing most important basic polynomials. In this regard, this paper deals with a new indirect numerical method to solve fractional optimal control problems based on the generalized Lucas polynomials. Through the way, the left and right Caputo fractional derivatives operational matrices for these polynomials are derived. Based on the Pontryagin maximum principle, the necessary optimality conditions for this problem reduce into a two-point boundary value problem. The main and efficient characteristic behind the proposed method is to convert the problem under consideration into a system of algebraic equations which reduces many computational costs and CPU time. To demonstrate the efficiency, applicability, and simplicity of the proposed method, several examples are solved, and the obtained results are compared with those obtained with other methods.
Similar content being viewed by others
1 Introduction and background
Fractional optimal control problems (FOCPs) are indeed generalizations of classical optimal control problems (OCPs) in which either the dynamic constraints or the performance index or both include at least one fractional derivative term. In recent years, this kind of problems has received much attention, since many real-world phenomena can be demonstrated or modeled by fractional differential equations (FDEs) much better than by integer order ones. There is a growing body of literature recognizing the importance of FOCPs, like [1–4]. It should be also emphasized that obtaining exact analytical solutions for nonlinear FOCPs is difficult, and in most cases impossible. Therefore, there exists a critical need to introduce numerical methods to solve these problems.
In spite of the fact that a number of numerical methods have been extensively used for solving FOCPs, considerable attention is still directed to finding some alternative and new methods. It should be remarked that numerical methods for solving FOCPs may be classified into two main categories: indirect and direct methods. The indirect methods are generally based upon the generalization of Pontryagin maximum principle (PMP) for FOCPs and usually need the numerical solution of two-point boundary value problem resulting from the related necessary optimality conditions. Nevertheless, the direct methods are based upon discretization-then-optimization of the main FOCPs. For indirect numerical methods, Agrawal in [5, 6], with dependence on Riemann–Liouville and Caputo operators, introduced a general formulation and solution method for FOCPs. Sweilam et al. in [7] studied two distinct numerical methods based on Chebyshev polynomials for solving FOCP in the sense of Caputo. Pooseh et al. in [8] achieved the necessary optimality conditions for FOCPs with free terminal time. Moreover, one can refer to Legendre spectral collocation method [9], Bessel collocation method [10], Jacobi spectral collocation method [11], fractional Chebyshev pseudospectral method [12], Legendre wavelet collocation method [13], variational iterative method [14], and predictor–corrector method [15]. For direct numerical methods, one can address Legendre orthogonal polynomials [16], Bernoulli polynomials [17], shifted Legendre orthogonal polynomials [18], wavelets methods [19, 20], Boubaker polynomials [21], shifted Chebyshev schemes [22], Hermite polynomials [23], Bernoulli wavelet basis [24], fractional-order Dickson functions [25], generalized shifted Legendre polynomials [26], and generalized Bernoulli polynomials [27].
The above literature review indicates that many researchers have widely used orthogonal basis functions to obtain approximate solutions of FOCPs, but little attention has been directed toward nonorthogonal polynomials such as Fibonacci and Lucas polynomials. The main two advantages of Lucas polynomials in comparison with shifted Legendre and shifted Chebyshev polynomials to approximate an arbitrary function defined in \([0, 1]\) are as follows:
-
The Lucas polynomials have fewer terms than shifted Legendre and shifted Chebyshev polynomials; for example, the sixth Lucas polynomial has four terms, whereas the sixth shifted Legendre and shifted Chebyshev polynomials have seven terms, and this difference will increase by increasing the degree of polynomials. Therefore, Lucas polynomials take less CPU time as compared to shifted Legendre and shifted Chebyshev polynomials to approximate an arbitrary function.
-
The coefficients of the individual terms in Lucas polynomials are smaller than the corresponding ones in shifted Legendre and shifted Chebyshev polynomials. Due to the fact that computational errors in the product are related to the coefficients of individual terms, using Lucas polynomials reduces computational errors.
Recently, by regarding the advantages of Lucas polynomials, attention to these polynomials in the literature has grown. The authors in [28, 29] established numerical algorithms based on Lucas polynomials and generalized Lucas polynomials (GLPs) to solve multiterm fractional differential equations. In [30] the GLPs are utilized to obtain numerical solution of fractional initial value problems. Oruç provided numerical solutions for nonlinear sinh-Gordon and generalized Benjamin–Bona–Mahony–Burgers equations based on a hybridization method of Fibonacci and Lucas polynomials [31, 32]. Dehestani et al. solved variable-order fractional reaction-diffusion and sub-diffusion equations using Lucas multiwavelet functions [33]. The authors in [34] applied Lucas wavelets for solving fractional Fredholm–Volterra integro-differential equations. In [35], a numerical optimization method based on fractional Lucas functions is developed for evaluating the approximate solution of the multidimensional fractional differential equations. Kumar et al. used normalized Lucas wavelets to solve Lane–Emden and pantograph equations [36]. Ali et al. [37] numerically solved multidimensional Burgers-type equations using Lucas polynomials. Furthermore, the authors in [38] investigated the GLPs to solve certain types of fractional pantograph differential equations numerically.
Up to now, great attention has been paid to numerical solutions of fractional differential equations taking Lucas polynomials as basis functions. This gives us a strong motivation to test their ability to solve FOCPs and introduce an efficient numerical method. The principal aim of this research is to construct an indirect numerical method for solving FOCPs using the GLPs in which high accuracy of the obtained approximate solution is one of the remarkable features of the method. To this end, first, we establish the necessary optimality conditions for FOCPs and obtain the operational matrices. Then, we use the necessary optimality conditions, the spectral collocation method, and operational matrices based on the GLPs to reduce the given problem into a nonlinear (or linear) system of algebraic equations that can be simply solved through the Newton iterative technique. Numerical test examples are also given to illustrate the accuracy and simplicity of the proposed method.
This article is organized in the following way. Some preliminaries of fractional calculus are presented in Sect. 2. The problem formulation and also the necessary optimality conditions are introduced in Sect. 3. Section 4 is devoted to introducing the GLPs and some of their properties. In Sect. 5, the GLPs operational matrices of the integer and Caputo fractional derivatives are determined. The proposed scheme is described in Sect. 6 to solve the given FOCP, and numerical examples are considered to show the efficiency of the new approach in Sect. 7. Finally, the conclusions and remarks are given in Sect. 8.
2 Some basic preliminaries of fractional calculus
In this section, we remind some notations and definitions for Caputo fractional derivatives, Riemann–Liouville fractional derivatives, and integrals. These concepts are common in fractional differential equations references and are used frequently (see for instance [39, 40]).
Definition 2.1
Assume that \(\mathcal{G}:[0,T]\to \mathbb{R} \) is a function and \(\alpha >0 \) is the order of derivative or integral. For \(\tau \in [0,T]\), we define
-
The left-side and right-side Caputo fractional derivatives by
$$ {}^{C}_{0}{D}_{\tau}^{\alpha}\mathcal{G}(\tau )= \frac{1}{\Gamma (p-\alpha )} \int _{0}^{\tau }(\tau -s)^{p-\alpha -1} \mathcal{G}^{(p)}(s)\,ds $$(2.1)and
$$ {}^{C}_{\tau}{D}_{T}^{\alpha}\mathcal{G}(\tau )= \frac{(-1)^{p}}{\Gamma (p-\alpha )}\biggl( \int _{\tau}^{T} (s-\tau )^{p- \alpha -1} \mathcal{G}^{(p)}(s)\,ds\biggr), $$(2.2)respectively;
-
The left-side and right-side Riemann–Liouville fractional derivatives by
$$ {}_{0}{D}_{\tau}^{\alpha}\mathcal{G}( \tau )= \frac{1}{\Gamma (p-\alpha )} \frac{d^{p}}{d\tau ^{p}}\biggl( \int _{0}^{ \tau }(\tau -s)^{p-\alpha -1} \mathcal{G}(s)\,ds\biggr) $$(2.3)and
$$ {}_{\tau}{D}_{T}^{\alpha}\mathcal{G}(\tau )= \frac{(-1)^{p}}{\Gamma (p-\alpha )} \frac{d^{p}}{d\tau ^{p}}\biggl( \int _{ \tau}^{T} (s-\tau )^{p-\alpha -1} \mathcal{G}(s)\,ds\biggr), $$(2.4)respectively;
-
The left-side and right-side Riemann–Liouville fractional integrals by
$$ {}_{0}{I}_{\tau}^{\alpha}\mathcal{G}( \tau )= \frac{1}{\Gamma (\alpha )} \int _{0}^{\tau }(\tau -s)^{\alpha -1} \mathcal{G}(s)\,ds $$(2.5)and
$$ {}_{\tau}{I}_{T}^{\alpha}\mathcal{G}(\tau )= \frac{1}{\Gamma (\alpha )} \int _{\tau}^{T} (s-\tau )^{\alpha -1} \mathcal{G}(s)\,ds, $$(2.6)respectively;
where \(\Gamma (.) \) denotes the gamma function and \(p=[\alpha ]+1 \) (\([\alpha ]\) is the integer part of α).
The Caputo and Riemann–Liouville fractional derivatives are linked with each other as follows:
and
As a consequence, if \(\mathcal{G} \) and \(\mathcal{G}^{(k)}\), \(k=1,2,\ldots p-1\), vanish at \(\tau =0 \), then
and if they vanish at \(\tau =T \), then
Caputo fractional derivatives of the power functions are yielded in the following forms:
and
where \(\lfloor \alpha \rfloor \) and \(\lceil \alpha \rceil \) are the largest integer less than or equal to α and the smallest integer greater than or equal to α, respectively. Also \(\mathbb{N} _{0}=\{0,1,2,\ldots \} \) and \(\mathbb{N}=\{1,2,3,\ldots \} \).
Theorem 2.2
Let \(\alpha \in (0,1) \) and \(f,g:[0,T] \to R \) be two functions of class \(C^{1} \). Then the formula for fractional integration by parts is derived as follows [41]:
3 Necessary optimality conditions for FOCPs
In this study, we consider a class of FOCPs in the sense of Caputo as follows:
where \(0<\alpha \leq 1 \), \(\mathfrak{V} \in R^{n} \), \(\mathfrak{W} \in R^{s} \), \(\mathcal{F}:R \times R^{n} \times R^{s} \to R \), and \(\mathcal{G}:R \times R^{n} \times R^{s} \to R^{n} \). The scalar function \(\mathcal{F} \) and the vector function \(\mathcal{G} \) are generically nonlinear and supposed to be differentiable functions; also \(\mathfrak{V}(\tau ) \) and \(\mathfrak{W}(\tau ) \) are the state and the control variables, respectively. Obviously, when \(\alpha =1 \), this problem is transformed to the standard OCPs.
In 2014, a general formulation of FOCPs in the sense of Caputo was presented by Pooseh et al. In order to obtain the necessary optimality conditions for problem (3.1), we follow the method of [8]. First, the Hamiltonian scalar function is defined as
where \(\lambda (\tau )\) is a Lagrange multiplier. Then the necessary optimality conditions for problem (3.1) are determined by the following theorem [8].
Theorem 3.1
If \((\mathfrak{V}(\tau ),\mathfrak{W}(\tau )) \) is a minimizer of (3.1), then there exists a co-state vector \(\lambda (\tau ) \) for which the triple \((\mathfrak{V}(\tau ),\mathfrak{W}(\tau ),\lambda (\tau )) \) satisfies the following relations:
for all \(\tau \in [0,T]\), where \(\mathcal{H} \) is described by (3.2).
4 The generalized Lucas polynomials and their properties
Lucas polynomials \(L_{n}(\tau ) \) of degree n defined over \([0,1]\), originally studied by Bicknell in 1970, can be generated through the following recurrence relation [42]:
Also, the Binet form of the Lucas polynomials is given by [42]
Moreover, these polynomials can be represented by the following explicit form as well [29]:
It has been shown that these polynomials satisfy the following properties:
-
\(L_{n}(\tau )=\mathtt{F}_{n+1}(\tau )+\mathtt{F}_{n-1}(\tau )\),
-
\(\tau L_{n}(\tau )=\mathtt{F}_{n+2}(\tau )-\mathtt{F}_{n-2}(\tau )\),
-
\(L_{-n}(\tau )=(-1)^{n}L_{n}(\tau )\),
-
\(\frac{dL_{n}(\tau )}{d\tau}=\frac{n}{\tau ^{2}+4}(\tau L_{n}(\tau )+2L_{n-1}( \tau ))\),
-
\(L_{n}(0)=1+(-1)^{n}\),
-
\(L_{n}(1)=\mathcal{L}_{n}\),
where \(\mathtt{F}_{n}(\tau )\) is the Fibonacci polynomials of order n and \(\mathcal{L}_{n}\) is the Lucas number [42].
Besides, if a and b are nonzero real constants, the sequence of generalized Lucas polynomials (GLPs) defined over \([0,1]\) is given by the following recurrence relation [29]:
In this regard, the first few GLPs \(\mu _{j}^{a,b}(\tau ) \) can be computed as follows:
It is also shown that the GLPs can be described with two equivalent forms [29]
and
where
The Binet form for these polynomials is [29]
It is worthy to mention here that from the GLPs for special values of a and b, we can extract some of the well-known polynomials; some specific cases of these values are shown in Table 1 [29].
Any continuous function \(W(\tau ) \) defined over \([0 , 1 ] \) can be expanded in terms of the GLPs in the following form [29]:
By truncating the infinite series in equation (4.7), it can be written as follows:
where
and
Now, the following two theorems state the convergence and error estimate of the generalized Lucas expansion.
Theorem 4.1
Suppose that \(h(\tau )\) is defined over \([0,1]\) and \(\vert h^{(j)}(0) \vert \leq K^{j}\), \(j \geq 0\), where K is a positive constant. Also, suppose that \(h(\tau )\) has the expansion \(h(\tau )=\sum_{j=0}^{\infty}c_{j} \mu _{j}^{a,b}(\tau ) \); then it holds that
-
1.
\(\vert c_{j} \vert \leq \frac{ \vert a \vert ^{-j} K^{j} \cosh (2 \vert a \vert ^{-1} b^{\frac{1}{2}} K)}{j!} \);
-
2.
The series converges absolutely.
Proof
The proof is given in [29]. □
Theorem 4.2
If \(h(\tau )\) satisfies the assumptions stated in Theorem 4.1and \(e_{N}(\tau )= \sum_{j=N+1}^{\infty}c_{j} \mu _{j}^{a,b}(\tau ) \), then the global error estimate is given as follows:
Proof
The proof is given in [29]. □
5 Operational matrices of the GLPs
This section is devoted to deriving operational matrices of derivatives for the GLPs. Based on the GLPs vector \(\Phi (\tau ) \) mentioned in equation (4.10), we can determine the operational matrix of integer derivative as follows [29, 30]:
where \(\mathcal{S}^{(1)}=(\mathcal{S}_{ij}^{(1)}) \) is the \((N+1)\times (N+1) \) operational matrix of the first derivative; then, the elements of this matrix can be obtained explicitly in the following form:
where
Equation (5.1) enables one to obtain \(\frac{d^{i} \Phi (\tau )}{d\tau ^{i}} \) for \(i\geq 1\) as
Now, we elicit the left Caputo fractional derivative operational matrix of the GLPs of order α, which generalizes the integer differentiation operator matrix. This matrix will be derived in the next theorem [29, 30].
Theorem 5.1
Let \(\Phi (\tau ) \) be the GLPs vector defined in equation (4.10); then, for any \(\alpha >0\), we have
where \(\mathcal{S}^{(\alpha )} \) is the \((N+1)\times (N+1) \) lower triangular generalized Lucas operational matrix of order α for the left Caputo fractional derivative. This matrix is obtained explicitly in the form
where
also, \(\xi _{i} \) and \(\delta _{j} \) are given in equations (4.6) and (5.2).
Moreover, we can express the right Caputo fractional derivative operational matrix of order α of the GLPs vector \(\Phi (\tau ) \) in the following form:
which is constructed with the help of the following lemmas.
Lemma 5.2
Let \(\Phi (\tau )\) and \(T_{N}(\tau )=[1,\tau ,\ldots ,\tau ^{N}] ^{T}\) be the vectors of generalized Lucas and Taylor polynomials, respectively; then \(\Phi (\tau )=AT_{N}(\tau ) \), where \(A=(a_{i+1,j+1})_{i,j=0}^{N}\) is a lower triangular \((N+1)\times (N+1)\) matrix, and
where \(\xi _{i} \) is mentioned in equation (4.6).
Proof
Regarding the definition expressed in (4.5), we have
where
So, the desired result is obtained. □
Lemma 5.3
Suppose that \(\Phi (\tau )\) and \(T_{N}(\tau ) \) are defined in Lemma 5.2. Then there is a lower triangular matrix L such that \(T_{N}(l-\tau )=LT_{N}(\tau ) \), where \(T_{N}(l-\tau )=[1,l-\tau ,\ldots ,(l-\tau )^{N}]^{T}\), and the entries of the matrix L are given in the form
Moreover, we can conclude that \(\Phi (\tau )=AL^{-1}T_{N}(l-\tau ) \).
Proof
Using the binomial expansion of \((l-\tau )^{i}\), we have
So, we get the following relation:
where
Now, using Lemma 5.2 and relation (5.8), we obtain \(\Phi (\tau )=AL^{-1}T_{N}(l-\tau ) \), which completes the proof. □
Note: As a consequence of Lemma 5.3, we have
Now, by taking the right Caputo fractional derivative operator of the vector \(T_{N}(l-\tau ) \) and using (2.12), we obtain
Furthermore, it can be written as follows:
Therefore, substituting (5.11) into (5.10) yields that
Indeed equation (5.12) determines an easy way for calculating the right Caputo fractional derivative operational matrix of the GLPs vector \(\Phi (\tau ) \).
6 Description of the proposed method
Herein, we will concentrate on the numerical solution of the FOCP defined in (3.1) by applying the operational matrices for the GLPs and the spectral collocation technique. To do this, first, the necessary optimality conditions for the problem are attained from Theorem 3.1 as
It should be mentioned that, in practice, we compute an expression for \(\mathfrak{W}(\tau ) \) in terms of \(\mathfrak{V}(\tau ) \) and \(\lambda (\tau ) \) from the condition given in (6.3) in a very straightforward manner. Also, we can replace \({}_{\tau}{\mathfrak{D}}_{T}^{\alpha}\lambda (\tau ) \) with \({}^{C}_{\tau}{\mathfrak{D}}_{T}^{\alpha}\lambda (\tau ) \) by using (2.10). Thus, we can rewrite the above-mentioned system in the following form:
where \(\mathcal{M}(\tau ,\mathfrak{V}(\tau ),\lambda (\tau )) \) and \(\mathcal{W}(\tau ,\mathfrak{V}(\tau ),\lambda (\tau )) \) are known functions. Now, we can approximate \(\mathfrak{V}(\tau ) \) and \(\lambda (\tau ) \) as
where
are unknown vectors which should be determined. By virtue of Sect. 5, the functions \({}^{C}_{0}{\mathfrak{D}}_{\tau}^{\alpha}\mathfrak{V}(\tau ) \) and \({}^{C}_{\tau}{\mathfrak{D}}_{T}^{\alpha}\lambda (\tau ) \) can be approximated in the following manner:
In addition, the boundary conditions expressed in (6.4) yield
Substituting (6.7) and (6.8) into (6.5) and (6.6), the residuals of these equations can be computed as follows:
The application of the spectral collocation technique is based on forcing the residuals to vanish at selected collocation nodes. There are even some other selections for choosing these nodes; one can use the following collocation nodes as well:
where \(t_{j}\), \(j=0,1,\ldots ,N \), are the shifted Chebyshev–Gauss–Lobatto points in the interval \([0,T] \). We should construct the associated system of \((2N+2) \) algebraic equations since \((2N+2) \) unknown coefficients \(\mathfrak{V}_{j} \) and \(\lambda _{j} \) (\(j=0,1,\ldots ,N\)) exist. For this purpose, the first equation of (6.10) is collocated at the nodes \(t_{i}\), \(i=1,\ldots ,N \), and the second equation of (6.10) is collocated at the nodes \(t_{k}\), \(k=0,1,\ldots ,N-1 \), as follows:
Hence, the above-mentioned system contains 2N algebraic equations. Now, equations given in (6.12) together with the boundary conditions (6.9) form a nonlinear (or linear) system of algebraic equations in the unknown coefficients \(\mathfrak{V}_{j} \) and \(\lambda _{j} \) (\(j=0,1,\ldots ,N\)) that has \((2N+2) \) equations and \((2N+2) \) unknowns. We can utilize the Newton iterative technique for solving this system; then, by determining \(\mathfrak{V}_{j} \) and \(\lambda _{j} \) (\(j=0,1,\ldots ,N\)), the desired approximate solutions can be calculated from (6.7).
7 Numerical experiments
In this section, we introduce some examples to test the performance and efficiency of the proposed method. These examples are selected from the literature for their importance and repetition. They also cover a variety of FOCPs. In Examples 1, 2, 3, and 5, we consider a linear time-invariant system with a quadratic performance index. Example 5 is a practical example with engineering applications. Moreover, a nonlinear time-varying system with a quadratic performance index is presented in Example 4. For these examples, the exact solutions when \(\alpha =1\) are known, and we can compare them with the approximate solutions obtained by the proposed method. The numerical simulations are implemented by MAPLE 18 with Digits = 20. All computations are performed on a Core i5 PC Laptop with 6 GB of RAM and 1.80 GHz of CPU to show no limitation on memory usage. In the following examples, the parameter N denotes the number of the GLPs.
Example 1
Consider the following FOCP:
subject to
The exact solution to this problem when \(\alpha =1\) is as follows:
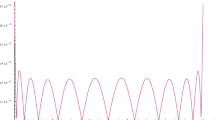
where \(\theta =- \frac {\cosh (\sqrt{2})+\sqrt{2}\sinh (\sqrt{2})}{\sqrt{2}\cosh (\sqrt{2})+\sinh (\sqrt{2})}\). The minimum value of the performance index \(\mathfrak{J}\) when \(\alpha =1\) is \(\mathfrak{J}^{*} = 0.1929092980932\). In Fig. 1, the approximate values and the absolute errors of \(\mathfrak{J}\) for some values of N when \(\alpha =1\) are plotted. Figures 2 and 3 compare the exact solutions and the approximate solutions of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) for various values of α and \(N=8\), respectively. Tables 2 and 3 show a comparison between the approximate solutions obtained by our method for various values of α at some values of τ and the exact solutions. In addition, the CPU time for various values of α is included in Table 2. From these results, it is clear that the approximate solutions at \(\alpha =1\) are in very good agreement with the corresponding exact solutions. Furthermore, as α approaches 1, the approximate solutions of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) converge to the exact solutions. The approximate values of \(\mathfrak{J}\) at \(\alpha =0.8\), 0.9, and 1 for the proposed and several numerical methods are included in Table 4. We compare the approximate values of \(\mathfrak{J}\) and the CPU time obtained using the methods in [44, 45] and the proposed method in Table 5. From this table, it is clear that our method requires significantly less CPU time. In Table 5, \(M_{1}\), \(M_{2}\), and \(N_{1}\) are the order of Bernoulli polynomials, Taylor polynomials, and block-pulse functions, respectively. The absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) when \(\alpha =1\) and \(N=4\), 6, 8, and 10 are shown in Figs. 4 and 5. These figures also illustrate the fast convergence rate of the proposed method since the errors decay rapidly by increasing the number of the GLPs. Moreover, Table 6 reports the maximum absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) and the absolute errors of \(\mathfrak{J}\) given by the proposed method in comparison to the methods in [18, 23] at \(\alpha =1\) and \(N=4\), 6, 8, and 10. The obtained results show that the errors, specially to control variable \(\mathfrak{W}(\tau )\), are better for the proposed method than those obtained in [18, 23]. From these tables and figures, it can be seen that the state and the control variables are accurately approximated by our method.
Graphs of the approximate values and the absolute errors of \(\mathfrak{J}\) when \(\alpha =1\) for some values of N in Example 1
Graphs of the exact and numerical solutions of \(\mathfrak{V}(\tau )\) for various values of α in Example 1
Graphs of the exact and numerical solutions of \(\mathfrak{W}(\tau )\) for \(\alpha =1\) in Example 1
Graphs of the absolute errors of \(\mathfrak{V}(\tau )\) when \(\alpha =1\) for some values of N in Example 1
Graphs of the absolute errors of \(\mathfrak{W}(\tau )\) when \(\alpha =1\) for some values of N in Example 1
Example 2
Consider the following FOCP:
subject to
For any value of \(\alpha > 0 \), the exact solution to this problem is
The minimum value of the performance index \(\mathfrak{J}\) when \(\alpha =1\) is \(\mathfrak{J}^{*} = 0\). Figure 6 compares the exact solutions and the approximate solutions of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) for \(N=8\) and \(\alpha =0.5\), 0.7, 0.9, and 1, respectively. In Fig. 7, we plot the state variable \(\mathfrak{V}(\tau )\) and the control variable \(\mathfrak{W}(\tau )\) for \(\alpha =0.5\) and some values of N along with the exact solutions. The absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) for various values of α are listed in Tables 7 and 8. In addition, the CPU time and the absolute errors of \(\mathfrak{J}\) for various values of α are included in these tables, respectively. From these results, it is worthwhile to note that the approximate solutions obtained by the proposed method completely coincide with the exact solutions.
Graphs of the exact and numerical solutions for various values of α in Example 2
Graphs of the exact and numerical solutions when \(\alpha =0.5\) for some values of N in Example 2
Example 3
Consider the following FOCP:
subject to
We obtain the exact solution to this problem when \(\alpha =1\) as follows:
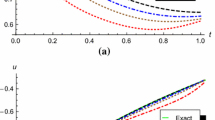
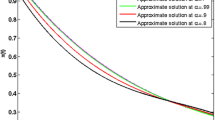
where \(\theta _{1}= \frac {e^{-2}\sqrt{2}+5e^{\sqrt{2}}-e^{-2}}{2(e^{-\sqrt{2}}\sqrt{2}+e^{\sqrt{2}}\sqrt{2}-e^{-\sqrt{2}}+e^{\sqrt{2}})}\) and \(\theta _{2}= \frac {e^{-2}\sqrt{2}-5e^{-\sqrt{2}}+e^{-2}}{2(e^{-\sqrt{2}}\sqrt{2}+e^{\sqrt{2}}\sqrt{2}-e^{-\sqrt{2}}+e^{\sqrt{2}})}\). The minimum value of the performance index \(\mathfrak{J}\) when \(\alpha =1\) is \(\mathfrak{J}^{*} =0.4319872403\). Figure 8 compares the exact solutions and the approximate solutions of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) for various values of α and \(N=8\), respectively. From this figure, it is clear that the approximate solutions when \(\alpha =1\) are in very good agreement with the corresponding exact solutions. Furthermore, as α approaches 1, the approximate solutions of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) converge to the exact solutions. Table 9 reports the absolute errors of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) obtained by the proposed method in comparison to the method in [25] at \(\alpha =1\) and \(N=5\) and 8. The yielded results show that the approximate solutions are more accurate for the proposed method than the method in [25]. Moreover, the absolute errors of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) for \(N=11\) and \(\alpha =1\) are shown in Fig. 9. These results also illustrate the fast convergence rate of the proposed method since the errors decay rapidly by increasing the number of the GLPs. The approximate values of \(\mathfrak{J}\) at \(\alpha =0.5\), 0.8, 0.9, 0.99, and 1 for the proposed method and the methods in [25] are included in Table 10. In addition, the CPU time for various values of α is included in Table 10. From these tables and figures, it can be seen that the state and the control variables are accurately approximated by the proposed method.
Graphs of the exact and numerical solutions for various values of α in Example 3
Graphs of the absolute errors when \(\alpha =1\) and \(N=12\) in Example 3
Example 4
Consider the following FOCP:
subject to
The exact solution to this problem when \(\alpha =1\) is as follows:
The minimum value of the performance index \(\mathfrak{J}\) when \(\alpha =1\) is \(\mathfrak{J}^{*} = 0\). Figure 10 compares the exact solutions and the approximate solutions of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) for various values of α and \(N=6\), respectively. From this figure, it is clear that the approximate solutions for the case of \(\alpha =1\) are in very good agreement with the corresponding exact solutions. Furthermore, as α approaches 1, the approximate solutions of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) converge to the exact solutions. The absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) at \(\alpha =1\) and \(N=5\) are shown in Fig. 11. Moreover, Table 11 reports the absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) obtained by our method in comparison to the method in [48] at \(\alpha =1\) and \(N=5\). Table 12 lists the maximum absolute errors of \(\mathfrak{V}(\tau )\) and \(\mathfrak{W}(\tau )\) and the absolute errors of \(\mathfrak{J}\) given by the proposed method in comparison to the method in [49] at \(\alpha =1\) and \(N=6\). The obtained results show that the errors, specially to \(\mathfrak{W}(\tau )\), are better for the proposed method than those obtained in [48, 49]. From these tables and figures, it can be seen that the state and the control variables are accurately approximated by the proposed method.
Graphs of exact and numerical solutions for various values of α in Example 4
Graphs of the absolute errors when \(\alpha =1\) and \(N=5\) in Example 4
Example 5
Consider the vibration of a mass-spring-damper system subjected to an external force. In particular, we aim to examine the step forcing functions, impulses, and response to harmonic excitations. Mostly, motors, rotating machinery, and so on lead to periodic motions of structures to induce vibrations into other mechanical devices and structures nearby [50]. Here, the action of an actuator force caused the control force \(F(\tau ) = b\mathfrak{W}(\tau )\), where b is a constant. On summing the forces, the equation for the forced vibration of the system in Fig. 12 becomes
where m, c, and k are constants. We remind that the mass-spring-damper system can be used to model the response of most dynamic systems as well as study the elasticity and mechanical behavior of nonlinear and viscoelastic material. Based on the number and arrangement (parallel or series combination) of the elements of this system (i.e. mass, spring, or damper), the mass-spring-damper systems have various practical applications, including but not limited to suspension systems of vehicles, vibrations of building on viscoelastic-like foundations, simulation of the motion of tendons and muscle deformations, and computer animations. With the specific application of the linear regulator problem in vibration suppression, extracted from [23], we find the following FOCP:
subject to
Choosing \(c=2\) and \(a=b=m=k=1\), we obtain the exact solution when \(\alpha =1\) as follows:
The minimum value of the performance index \(\mathfrak{J}\) when \(\alpha =1\) is \(\mathfrak{J}^{*} =0.6631296243\). In Fig. 13, the approximate values and the absolute errors of \(\mathfrak{J}\) for some values of N when \(\alpha =1\) are plotted. Figure 14 compares the exact solutions and the approximate solutions of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) for various values of α at \(N=8\), respectively. In Table 13, the absolute errors of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) for \(N=4\) and 10 at \(\alpha =1\) along with the CPU time are listed. Moreover, the absolute errors of \(\mathfrak{V}_{1}(\tau )\), \(\mathfrak{V}_{2}(\tau )\), and \(\mathfrak{W}(\tau )\) when \(\alpha =1\) and \(N=11\) are shown in Fig. 15. These results also illustrate the fast convergence rate of the proposed method since the errors decay rapidly by increasing the number of the GLPs.
Graphs of the approximate values and absolute errors of \(\mathfrak{J}\) when \(\alpha =1\) for some values of N in Example 5
Graphs of the exact and numerical solutions for various values of α in Example 5
Graphs of the absolute errors when \(\alpha =1\) and \(N=11\) in Example 5
8 Conclusions and remarks
In this paper, we established an accurate and efficient new scheme to solve a class of FOCPs. By applying the GLPs, determining the operational matrices of fractional derivatives and the necessary optimality conditions, we reduced the main problem to the simple problem of solving a system of algebraic equations. The proposed scheme is illustrated in some test examples, and the results demonstrate that our scheme is perfectly valid. It is also shown that the new scheme is quite reliable, simple, and reasonably accurate to solve FOCPs. As further research works, we will use the proposed scheme for delay FOCPs. Moreover, the new method has the ability to be applied for solving variable order FOCPs in new research.
Availability of data and materials
Data sharing is not applicable to this study.
References
Bushnaq, S., Saeed, T., Torres, D.F.M., Zeb, A.: Control of COVID-19 dynamics through a fractional-order model. Alex. Eng. J. 60(4), 3587–3592 (2021)
Dong, N.P., Long, H.V., Khastan, A.: Optimal control of a fractional order model for granular SEIR epidemic with uncertainty. Commun. Nonlinear Sci. Numer. Simul. 88, 1–39 (2020)
Naik, P.A., Zu, J., Owolabi, K.M.: Global dynamics of a fractional order model for the transmission of HIV epidemic with optimal control. Chaos Solitons Fractals 138, 1–24 (2020)
Shi, R., Li, Y., Wang, C.: Stability analysis and optimal control of a fractional-order model for African swine fever. Virus Res. 288, 1–24 (2020)
Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38(1), 323–337 (2004)
Agrawal, O.P.: A formulation and numerical scheme for fractional optimal control problems. J. Vib. Control 14(9–10), 1291–1299 (2008)
Sweilam, N.H., Al-Ajami, T.M., Hoppe, R.H.W.: Numerical solution of some types of fractional optimal control problems. Sci. World J. 2013, Article ID 306237 (2013)
Pooseh, S., Almeida, R., Torres, D.F.M.: Fractional order optimal control problems with free terminal time. J. Ind. Manag. Optim. 10(2), 363–381 (2014)
Sweilam, N.H., Al-Ajami, T.M.: Legendre spectral-collocation method for solving some types of fractional optimal control problems. J. Adv. Res. 6(3), 393–403 (2015)
Tohidi, E., Saberi Nik, H.: A Bessel collocation method for solving fractional optimal control problems. Appl. Math. Model. 39(2), 455–465 (2015)
Yang, Y., Zhang, J., Liu, H., Vasilev, A.O.: An indirect convergent Jacobi spectral collocation method for fractional optimal control problems. Math. Methods Appl. Sci. 44(4), 2806–2824 (2021)
Habibli, M., Noori Skandari, M.H.: Fractional Chebyshev pseudospectral method for fractional optimal control problems. Optim. Control Appl. Methods 40(3), 558–572 (2019)
Kumar, N., Mehra, M.: Legendre wavelet collocation method for fractional optimal control problems with fractional Bolza cost. Numer. Methods Partial Differ. Equ. 37(2), 1693–1724 (2021)
Alizadeh, A., Effati, S.: An iterative approach for solving fractional optimal control problems. J. Vib. Control 24(1), 18–36 (2018)
Jajarmi, A., Baleanu, D.: On the fractional optimal control problems with a general derivative operator. Asian J. Control 23(2), 1062–1071 (2021)
Lotfi, A., Yousefi, S.A., Dehghan, M.: Numerical solution of a class of fractional optimal control problems via the Legendre orthonormal basis combined with the operational matrix and the Gauss quadrature rule. J. Comput. Appl. Math. 250, 143–160 (2013)
Keshavarz, E., Ordokhani, Y., Razzaghi, M.: A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control 22(18), 3889–3903 (2016)
Ezz-Eldien, S.S., Doha, E.H., Baleanu, D., Bhrawy, A.H.: A numerical approach based on Legendre orthonormal polynomials for numerical solutions of fractional optimal control problems. J. Vib. Control 23(1), 16–30 (2017)
Heydari, M.H., Hooshmandasl, M.R., Maalek Ghaini, F.M., Cattani, C.: Wavelets method for solving fractional optimal control problems. Appl. Math. Comput. 286, 139–154 (2016)
Sahu, P.K., Saha Ray, S.: Comparison on wavelets techniques for solving fractional optimal control problems. J. Vib. Control 24(6), 1185–1201 (2018)
Rabiei, K., Ordokhani, Y., Babolian, E.: The Boubaker polynomials and their application to solve fractional optimal control problems. Nonlinear Dyn. 88(2), 1013–1026 (2017)
Abdelhakem, M., Moussa, H., Baleanu, D., El-Kady, M.: Shifted Chebyshev schemes for solving fractional optimal control problems. J. Vib. Control 25(15), 2143–2150 (2019)
Yari, A.: Numerical solution for fractional optimal control problems by Hermite polynomials. J. Vib. Control 27(5–6), 698–716 (2021)
Barikbin, Z., Keshavarz, E.: Solving fractional optimal control problems by new Bernoulli wavelets operational matrices. Optim. Control Appl. Methods 41(4), 1188–1210 (2020)
Dehestani, H., Ordokhani, Y.: A spectral framework for the solution of fractional optimal control and variational problems involving Mittag-Leffler nonsingular kernel. J. Vib. Control 28(3–4), 260–275 (2022)
Hassani, H., Tenreiro Machado, J.A., Mehrabi, S.: An optimization technique for solving a class of nonlinear fractional optimal control problems: application in cancer treatment. Appl. Math. Model. 93, 868–884 (2021)
Hassani, H., Tenreiro Machado, J.A., Hosseini Asl, M.K., Dahaghin, M.S.: Numerical solution of nonlinear fractional optimal control problems using generalized Bernoulli polynomials. Optim. Control Appl. Methods 42(4), 1045–1063 (2021)
Abd-Elhameed, W.M., Youssri, Y.H.: Spectral solutions for fractional differential equations via a novel Lucas operational matrix of fractional derivatives. Rom. J. Phys. 61(5–6), 795–813 (2016)
Abd-Elhameed, W.M., Youssri, Y.H.: Generalized Lucas polynomial sequence approach for fractional differential equations. Nonlinear Dyn. 89(2), 1341–1355 (2017)
Mokhtar, M.M., Mohamed, A.S.: Lucas polynomials semi-analytic solution for fractional multi-term initial value problems. Adv. Differ. Equ. 2019(1), 1 (2019)
Oruç, Ö.: A new algorithm based on Lucas polynomials for approximate solution of 1D and 2D nonlinear generalized Benjamin–Bona–Mahony–Burgers equation. Comput. Math. Appl. 74(12), 3042–3057 (2017)
Oruç, Ö.: A new numerical treatment based on Lucas polynomials for 1D and 2D sinh-Gordon equation. Commun. Nonlinear Sci. Numer. Simul. 57, 14–25 (2018)
Dehestani, H., Ordokhani, Y., Razzaghi, M.: A novel direct method based on the Lucas multiwavelet functions for variable-order fractional reaction-diffusion and subdiffusion equations. Numer. Linear Algebra Appl. 28(2), e2346 (2021)
Dehestani, H., Ordokhani, Y., Razzaghi, M.: Combination of Lucas wavelets with Legendre–Gauss quadrature for fractional Fredholm–Volterra integro-differential equations. J. Comput. Appl. Math. 382, 113070 (2021)
Dehestani, H., Ordokhani, Y., Razzaghi, M.: Fractional Lucas optimization method for evaluating the approximate solution of the multi-dimensional fractional differential equations. Eng. Comput. 38, 481–495 (2022)
Kumar, R., Koundal, R., Srivastava, K., Baleanu, D.: Normalized Lucas wavelets: an application to Lane-Emden and pantograph differential equations. Eur. Phys. J. Plus 135(11), 1–24 (2020)
Ali, I., Haq, S., Nisar, K.S., Baleanu, D.: An efficient numerical scheme based on Lucas polynomials for the study of multidimensional Burgers-type equations. Adv. Differ. Equ. 2021(1), 1 (2021)
Youssri, Y.H., Abd-Elhameed, W.M., Mohamed, A.S., Sayed, S.M.: Generalized Lucas polynomial sequence treatment of fractional pantograph differential equation. Int. J. Appl. Comput. Math. 7(2), 1–16 (2021)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)
Podlubny, I.: Fractional Differential Equations, vol. 198. Elsevier, Amsterdam (1999)
Agrawal, O.P.: Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A, Math. Theor. 40(24), 6287–6303 (2007)
Koshy, T.: Fibonacci and Lucas Numbers with Applications, vol. 2. Wiley, New York (2019)
Agrawal, O.P.: General formulation for the numerical solution of optimal control problems. Int. J. Control 50(2), 627–638 (1989)
Mashayekhi, S., Razzaghi, M.: An approximate method for solving fractional optimal control problems by hybrid functions. J. Vib. Control 24(9), 1621–1631 (2018)
Yonthanthum, W., Rattana, A., Razzaghi, M.: An approximate method for solving fractional optimal control problems by the hybrid of block-pulse functions and Taylor polynomials. Optim. Control Appl. Methods 39(2), 873–887 (2018)
Akbarian, T., Keyanpour, M.: A new approach to the numerical solution of fractional order optimal control problems. Appl. Appl. Math. 8(2), 523–534 (2013)
Singha, N., Nahak, C.: An efficient approximation technique for solving a class of fractional optimal control problems. J. Optim. Theory Appl. 174(3), 785–802 (2017)
Dehestani, H., Ordokhani, Y., Razzaghi, M.: Fractional-order Bessel wavelet functions for solving variable order fractional optimal control problems with estimation error. Int. J. Syst. Sci. 51(6), 1032–1052 (2020)
Heydari, M.H., Avazzadeh, Z.: A new wavelet method for variable-order fractional optimal control problems. Asian J. Control 20(5), 1804–1817 (2018)
Inman, D.J.: Vibration with Control. Wiley, New York (2017)
Acknowledgements
Not available.
Funding
The financial assistance is not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karami, S., Fakharzadeh Jahromi, A. & Heydari, M.H. A computational method based on the generalized Lucas polynomials for fractional optimal control problems. Adv Cont Discr Mod 2022, 64 (2022). https://doi.org/10.1186/s13662-022-03737-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-022-03737-1