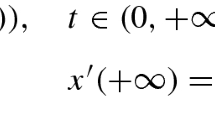Abstract
By defining the Banach spaces endowed with the appropriate norm, constructing a suitable projection scheme, and using the coincidence degree theory due to Mawhin, we study the existence of solutions for functional boundary value problems at resonance on the half-line with \(\operatorname{dim}\operatorname{Ker}L = 1\). And an example is given to show that our result here is valid.
Similar content being viewed by others
1 Introduction
In this article, we discuss the following functional boundary-value problems at resonance on the half-line with \(\operatorname{dim}\operatorname{Ker}L = 1\):
where \(n\geq 3\), \(\Gamma _{1},\Gamma _{2}:C^{n-1}[0,+\infty )\rightarrow \mathbb{R}\) are two linear bounded functionals with resonance condition \(\Gamma _{1}(1)\Gamma _{2}(x^{n-2})-\Gamma _{2}(1)\Gamma _{1}(x^{n-2})=0\).
In the last few years, considerable motivation has been provided to the subject of differential equations on the finite interval with specific boundary conditions and resonance scenarios (see [1–6] and the references cited therein). Very recently, the attention has shifted to problems on the infinite interval with linear functional conditions. There are a few papers to investigate the functional boundary value problems on the finite interval (see [7–11]). For example, in [8], Kosmatov and Jiang investigated second order functional problems with resonance of dimension one
which improves the results of [6] and [7] in that respect as well and generalizes a number of recent works about two-point, three-point, multi-point, and integral boundary value problems. In addition, it clearly can also be used for higher order problems with functional conditions.
Higher order boundary value problems for ordinary differential equations arise naturally in technical applications [12–23]. For example, in [22], the authors discussed some higher order boundary value problems at resonance with integral boundary conditions:
As far as we know, this is the first paper to study the higher order functional boundary value problems at resonance on the half-line.
2 Preliminaries
We give some theoretical foundations which will be used in what follows.
Definition 2.1
Let X, Y be real Banach spaces, \(L:\operatorname{dom} L\subset X\rightarrow Y\) be a linear operator. L is said to be the Fredholm operator of index zero provided that:
-
(i)
ImL is a closed subset of Y;
-
(ii)
\(\operatorname{dim}\operatorname{Ker} L = \operatorname{codim}\operatorname{Im}L<+\infty \).
Let \(P:X\rightarrow X\), \(Q:Y\rightarrow Y\) be continuous projectors such that \(\operatorname{Im}P=\operatorname{Ker}L\), \(\operatorname{Ker}Q=\operatorname{Im}L\), \(X=\operatorname{Ker}L\oplus \operatorname{Ker}P\), and \(Y=\operatorname{Im}L\oplus \operatorname{Im}Q\). It follows that \(L|_{\operatorname{dom}L\cap \operatorname{Ker}P}:\operatorname{dom}L\cap \operatorname{Ker}P\rightarrow \operatorname{Im}L\) is reversible. We denote the inverse of the mapping \(L|_{\operatorname{dom}L\cap \operatorname{Ker}P} \) by \(K_{P}\). Let Ω be an open bounded subset of X such that \(\operatorname{dom}L\cap \Omega \neq \emptyset \). The mapping \(N:X\rightarrow Y\) will be called L-compact on Ω̅ if \(QN(\overline{\Omega })\) is bounded and \(K_{P}(I-Q)N:\overline{\Omega }\rightarrow X\) is compact.
Theorem 2.2
(see [24] Mawhin continuation theorem)
Let \(L:\operatorname{dom}L \subset X\rightarrow Y\) be a Fredholm operator of index zero and \(N:X\rightarrow Y\) be L-compact on Ω̅. Assume that the following conditions are satisfied:
-
(i)
\(Lx \neq \lambda Nx\) for every \((x,\lambda )\in [(\operatorname{dom} L\setminus \operatorname{Ker} L) \cap \partial \Omega ]\times (0,1)\);
-
(ii)
\(Nx \notin \operatorname{Im} L\) for every \(x\in \operatorname{Ker} L \cap \partial \Omega \);
-
(iii)
\(\operatorname{deg}(QN|_{\operatorname{Ker} L}, \Omega \cap \operatorname{Ker} L, 0) \neq 0\), where \(Q: Y\rightarrow Y\) is a continuous projection such that \(\operatorname{Im} L= \operatorname{Ker} Q\).
Then the equation \(Lx=Nx\) has at least one solution in \(\operatorname{dom} L \cap \overline{\Omega }\).
Lemma 2.3
(see [25])
Assume that \(V\subset X\) (X appearing in this article) is bounded. V is compact if \(\{\frac{\varphi (x)}{e^{x}}:\varphi \in V\}\) is equicontinuous on \([0,T]\), \(\forall T<\infty \), and equiconvergent at infinity.
In this paper, we will always suppose that the following condition holds:
- \((H_{1})\):
-
Let \(f:[0,+\infty )\times \mathbb{R}^{n}\rightarrow \mathbb{R}\) be continuous. For any constant \(r>0\), there exists \(h_{r}(x)\in L[0,+\infty )\) such that \(|f(x,e^{x}y_{1},e^{x}y_{2},\ldots ,e^{x}y_{n})|\leq h_{r}(x)\), \(x\in [0,+ \infty )\), \(|y_{i}|\leq r\), \(i=1,2,\ldots ,n\).
3 Main results
Let \(X=\{\varphi :\varphi \in C^{n-1}[0,+\infty ), \sup_{x\in [0,+ \infty )}\frac{|\varphi ^{(j)}(x)|}{e^{x}}<\infty ,\varphi ^{(i)}(0)=0,i=1,2, \ldots ,n-3,j=0,1,2,\ldots ,n-1\}\) with the norm \(\|\varphi \|= \max \{\|\frac{\varphi ^{(i)}}{e^{x}}\|_{\infty }, i=0,1,2, \ldots ,n-1\}\), where \(\|\varphi \|_{\infty }=\sup_{t\in [0,+\infty )}|\varphi (x)|\), and \(Y=L[0,+\infty )\) with the norm \(\|u\|_{1}=\int _{0}^{+\infty }|u(x)|\,dx\).
It is easy to prove that \((X,\|\cdot \|)\) and \((Y,\|\cdot \|_{1})\) are Banach spaces.
We define an operator L as follows:
with \(\operatorname{dom} L=\{\varphi \in X:\varphi ^{(n)}(x)\in Y,\varphi ^{(n-1)}(+ \infty )=0,\Gamma _{1}(\varphi (x))=0,\Gamma _{2}(\varphi (x))=0\}\).
An operator \(N:X\rightarrow Y\) is defined as follows:
So, problem (1.1) becomes \(L\varphi =N\varphi \).
For convenience, we denote
- \((H_{2})\):
-
The linear functionals \(\Gamma _{1},\Gamma _{2}:X\rightarrow \mathbb{R}\) satisfy \(\Gamma _{2}(1)=b\), \(\Gamma _{2}(x^{n-2})=a\), \(\Gamma _{1}(1)=\alpha b\), \(\Gamma _{1}(x^{n-2})=\alpha a\), \((\Gamma _{1}-\alpha \Gamma _{2})(x^{n}e^{-x}) \neq 0\), where \(a^{2}+b^{2}\neq 0\), \(\alpha ,a,b\in \mathbb{R}\).
- \((H_{3})\):
-
The functionals \(\Gamma _{1},\Gamma _{2}:X\rightarrow \mathbb{R}\) are linear continuous with the respective norms \(\beta _{1}\), \(\beta _{2}\), that is, \(|\Gamma _{i}(\varphi )|\leq \beta _{i}\|\varphi \|\), \(i=1,2\).
Lemma 3.1
There must exist \(g\in Y\) such that
where
Proof
Since we just need to find a specific g satisfying the equation, in particular, let \(\mathbf{x}=x^{n}e^{-x}\in X\), \(h(x)=(x^{n}e^{-x})^{(n)}\in Y\), \(x\in [0,+ \infty )\), we have
Now, considering condition \((H_{2})\), take
thus,
□
Lemma 3.2
L is a Fredholm operator of index zero.
Proof
From \(\varphi ^{(n)}(x)=u(x)\) and \(\varphi ^{(i)}(0)=0\), \(1\leq i\leq n-3\), we have
Now we will give KerL and ImL.
Taking \(\varphi \in \operatorname{dom}L\) with \(L\varphi =0\), we obtain \(\varphi (x)=\varphi (0)+\frac{\varphi ^{(n-1)}(0)}{(n-1)!}x^{n-1} + \frac{\varphi ^{(n-2)}(0)}{(n-2)!}x^{n-2}\). This, together with \(\varphi ^{(n-1)}(+\infty )=0\), \(\Gamma _{1}(\varphi (x))=0\) and \(\Gamma _{2}(\varphi (x))=0\), implies that
Based on condition \((H_{2})\), we have
So,
In order to prove
To see this, let us suppose that \(u\in \operatorname{Im}L\), then there exists \(\varphi \in \operatorname{dom}L\) such that \(u=L\varphi \in Y\). From (3.1) and \(\varphi ^{(n-1)}(+\infty )=0\), we have
It follows from \(\Gamma _{1}(\varphi (x))=0\), \(\Gamma _{2}(\varphi (x))=0\), and \((H_{2})\) that
That is,
If \(u\in \{ u\in Y:(\Gamma _{1}-\alpha \Gamma _{2}) (\int _{0}^{\infty }k(x,y)u(y)\,dy )=0 \} \), take
In view of \((H_{2})\), it is easy to deduce that \(L\varphi =\varphi ^{(n)}(x)=u(x)\), \(\varphi ^{(i)}(0)=0\), \(1\leq i\leq n-3\), \(\varphi ^{(n-1)}(+\infty )=0\), and \(\Gamma _{i}(\varphi (x))=0\), \(i=1,2\). That is, \(u\in \operatorname{Im}L\), i.e.,
Combining the above, we obtain (3.3).
Define \(Q:Y\rightarrow Y\) by
where \(g(x)\) is introduced in Lemma 3.1.
Clearly, \(\operatorname{Ker}Q=\operatorname{Im}L\), \(\operatorname{Im}Q=\{u|u=cg(x),x\geq 0,c\in \mathbb{R}\}\), and \(Q:Y\rightarrow Y\) is a linear projector. In fact, for \(u\in Y\), we have
For \(u\in Y\), we have \(u=(u-Qu)+Qu\), \(Qu\in \operatorname{Im}Q\), \((I-Q)u\in \operatorname{Ker}Q= \operatorname{Im}L\). So, we obtain \(Y=\operatorname{Im}Q+\operatorname{Im}L\). Take \(u_{0}\in \operatorname{Im}Q\) means that \(u_{0}\) can be written \(u_{0}=cg(x)\), \(c\in \mathbb{R}\). At the same time, by \(u_{0}\in \operatorname{Im}L\) and Lemma 3.1, we get \(c=0\). This implies that \(u_{0}=0\). Thus, \(Y=\operatorname{Im}Q\oplus \operatorname{Im}L\) and \(\operatorname{dim}\operatorname{Ker}L=\operatorname{codim}\operatorname{Im}L<+\infty \). Observing that ImL is a closed subspace of Y; L is a Fredholm operator of index zero. □
Define \(P:X\rightarrow X\) as
Clearly, \(P:X\rightarrow X\) is a linear continuous projector and \(\operatorname{Im}P=\{u|u(x)=c(a-bx^{n-2}),x\geq 0,c\in \mathbb{R}\}= \operatorname{Ker}L\). Thus, \(X=\operatorname{Im}P\oplus \operatorname{Ker}P=\operatorname{Ker}L\oplus \operatorname{Ker}P\).
Define \(K_{P}:\operatorname{Im}L\rightarrow \operatorname{dom}L\cap \operatorname{Ker}P\) by
By simple calculations, for \(\varphi \in \operatorname{dom}L\cap \operatorname{Ker}P\),
and \((L_{P}K_{P})u=u\), \(\forall u\in \operatorname{Im}L\). So, \(K_{P}=(L_{P})^{-1}\), where \(L_{P}=L|_{\operatorname{dom}L\cap \operatorname{Ker}P}:\operatorname{dom}L \cap \operatorname{Ker}P\rightarrow \operatorname{Im}L\).
Define the linear isomorphism \(J: \operatorname{Ker}L\rightarrow \operatorname{Im}Q\) as \(J(c(a-bx^{n-2}))=cg(x)\), \(c\in \mathbb{R}\), where \(g(x)\) is also introduced in Lemma 3.1.
The next lemma provides norm estimates needed for the following result.
Lemma 3.3
For \(u\in Y\), \(\|K_{P}u\|\leq B\|u\|_{1}\), where
Proof
Observe that due to \(|\Gamma _{2}(\varphi (x))|\leq \beta _{2}\|\varphi \|\),
Then
□
Lemma 3.4
N is L-compact on Ω̅ if \(\operatorname{dom}L\cap \overline{\Omega }\neq \emptyset \), where Ω is a bounded open subset of X.
Proof
For convenience, denote \(M_{r}:=\int _{0}^{+\infty }|h_{r}(y)|\,dy\).
We will prove that \(QN:X\rightarrow Y \) is continuous and bounded.
Since \(\Omega \subset X\) is bounded, for \(\varphi \in \overline{\Omega }\), there exists a constant \(r>0\) such that \(\|\varphi \|< r\).
It is not difficult to verify that \(\sup_{x\in [0,+\infty )} \frac{|(\int _{0}^{+\infty }k(x,y)N\varphi (y)\,dy)^{(i)}|}{e^{x}}\leq \int _{0}^{+\infty }|N\varphi (y)|\,dy\), \(i=0,1,2,\ldots ,n-1\).
By condition \((H_{1})\), we have
So, \(QN:X\rightarrow Y\) is bounded. By \((H_{1})\) and the Lebesgue dominated convergence theorem, we see that \(QN:X\rightarrow Y\) is continuous.
Now, we will prove that \(K_{P}(I-Q)N:\overline{\Omega }\rightarrow X\) is compact.
Similarly, \(\{ \frac{ \vert (K_{P}(I-Q)N\varphi )^{(i)} \vert }{e^{x}}<+\infty : \varphi \in \overline{\Omega },i=2,3,\ldots ,n-1 \}\), i.e., \(K_{P}(I-Q)N: \overline{\Omega }\rightarrow X\) is bounded.
Secondly, for \(\varphi \in \overline{\Omega }\), \(0< x_{1}< x_{2}< T<+\infty \),
where
Define \(F_{1}(x)=\int _{0}^{+\infty }k(x,y)(I-Q)N\varphi (y)\,dy\), \(x\in (0,T)\), \(T< \infty \). Obviously,
By the uniform continuity of \(\{ \frac{{x}^{n-j}}{e^{x}},j=1,2,3,\ldots ,n \} \) in \([0,T]\) and the absolute continuity of the integral, we see that \(\{\frac{(K_{P}(I-Q)N\varphi )^{(i)}}{e^{x}}:\varphi \in \overline{\Omega },i=0,1,\ldots ,n-1 \} \) is equicontinuous on \([0,T]\), \(\forall T<\infty \). Thirdly, for \(\varepsilon >0\), there exists a constant \(T_{1}>0\) such that if \(x>T_{1}\), then
For \(\varepsilon >0\), there exists a constant \(T_{2}>0\) such that if \(x>T_{2}\), then
Take \(\widetilde{T}=\max \{T_{1},T_{2}\}\), for \(\varphi \in \overline{\Omega }\), \(\widetilde{T}\leq x_{1}< x_{2}\), we have
For \(\varepsilon >0\), there exists a constant \(T_{3}>0\) such that if \(x>T_{3}\), then
For \(\varepsilon >0\), there exists a constant \(T_{4}>0\) such that if \(x>T_{4}\), then
Take \(T^{*}=\max \{T_{3},T_{4}\}\), for \(\varphi \in \overline{\Omega }\), \(T^{*}\leq x_{1}< x_{2}\), we have
For the above two arguments, take \(T=\max \{\widetilde{T},T^{*}\}\), we hold that \(\{(K_{P}(I-Q)N\varphi )^{(i)}:\varphi \in \overline{\Omega },i=0,1 \}\) is equiconvergent for any \(x_{1},x_{2}\geq T\). Similarly, \(\{(K_{P}(I-Q)N\varphi )^{(i)}:\varphi \in \overline{\Omega },i=2,3,\ldots ,n-1 \}\) is also equiconvergent at infinity. Therefore, by the Ascoli–Arzela theorem, \(K_{P}(I-Q)N:\overline{\Omega }\rightarrow X\) is compact and \(QN(\overline{\Omega })\) is bounded, i.e., N is L-compact. □
Theorem 3.5
Assume that \((H_{1})\)–\((H_{3})\) with \(b\neq 0\) and the following conditions hold:
- \((H_{4})\):
-
There exist functions \(r, q_{i}\in L[0,+\infty )\) with \((\|K_{P}\|+\frac{|a|+|b|}{|b|(n-2)!} ) \sum_{i=1}^{n} \|q_{i}\|_{1}<1\) such that
$$\bigl\vert f(x,y_{1},y_{2},\ldots ,y_{n}) \bigr\vert \leq \sum_{i=1}^{n}q_{i}(x)e^{-x} \vert y_{i} \vert +r(x), $$where \(x\in [0,+\infty )\), \(y_{i}\in \mathbb{R}\).
- \((H_{5})\):
-
There exists a constant \(M>0\) such that if \(|\varphi ^{(n-2)}(x)|>M\) for all \(x\in [0,+\infty )\), then
$$(\Gamma _{1}-\alpha \Gamma _{2}) \biggl( \int _{0}^{+\infty }k(x,y) f\bigl(y,\varphi (y), \varphi '(y),\varphi ''(y),\ldots ,\varphi ^{(n-1)}(y)\bigr)\,dy \biggr) \neq 0. $$ - \((H_{6})\):
-
There is a constant \(a_{0}>0\) such that if \(|c|>a_{0}\) either
$$\begin{aligned} c\Gamma \biggl( \int _{0}^{+\infty }k(x,y)N\bigl(c\bigl(a-by^{n-2} \bigr)\bigr)\,dy \biggr)< 0 \end{aligned}$$(3.5)or
$$\begin{aligned} c\Gamma \biggl( \int _{0}^{+\infty }k(x,y)N\bigl(c\bigl(a-by^{n-2} \bigr)\bigr)\,dy \biggr)>0. \end{aligned}$$(3.6)
Then boundary value problem (1.1) has at least one solution.
The following results will play a very important role in our subsequent analysis.
Lemma 3.6
The set
is bounded if \((H_{1})\)–\((H_{5})\) are satisfied.
Proof
Take \(\varphi \in \Omega _{1}\), then \(N\varphi \in \operatorname{Im}L\), thus we have
This, together with \((H_{5})\), means that there exists \(x_{0}\in [0,\infty )\) such that \(|\varphi ^{(n-2)}(x_{0})|\leq M\).
Since \(\varphi ^{(n-1)}(x)=-\int _{x}^{+\infty }\varphi ^{(n)}(y)\,dy+\varphi ^{(n-1)}(+ \infty )\) and \(\varphi ^{(n-2)}(x)=\int _{x_{0}}^{x}\varphi ^{(n-1)}(y)\,dy+\varphi ^{(n-2)}(x_{0})\), we get \(|\varphi ^{(n-1)}(x)|\leq \|N\varphi \|_{1}\) and
Write \(\varphi (x)=\varphi _{1}(x)+\varphi _{2}(x)\), where \(\varphi _{1}(x)=(I-P)\varphi (x)\in \operatorname{dom}L\cap \operatorname{Ker}P\) and \(\varphi _{2}(x)=P\varphi (x)\in \operatorname{Im} P\). Then since \(\varphi _{1}(x)=(I-P)\varphi (x)\in \operatorname{dom}L\cap \operatorname{Ker}P\), we have
As is the proof of Lemma 3.3,
Now, \(\varphi _{2}(x)=P\varphi (x)=c(\varphi )(a-bx^{n-2})\), where
is introduced for the sake of brevity. Hence
by (3.8). That is,
Thus,
By (3.9) and (3.10), \(\|\varphi \|\leq \|\varphi _{1}\|+\|\varphi _{2}\|\leq C_{1}\|N \varphi \|_{1}+C_{2}\), where
Finally, it follows from \((H_{4})\) that
Therefore, \(\Omega _{1}\) is bounded. □
Lemma 3.7
The set
is bounded if \((H_{1})\)–\((H_{3})\), \((H_{6})\) hold.
Proof
Let \(\varphi \in \Omega _{2}\), then \(\varphi (x)\equiv c(a-bx^{n-2})\), and \(N\varphi \in \operatorname{Im}L\). So, we can get
According to \((H_{6})\), we have \(|c|\leq a_{0}\), i.e., \(\|\varphi \| \leq a_{0}(|a|+|b|(n-2)!)\). The proof of Lemma 3.7 is completed. □
Lemma 3.8
The set
is bounded if conditions \((H_{1})\)–\((H_{3})\), \((H_{6})\) are satisfied, where \(J: \operatorname{Ker}L\rightarrow \operatorname{Im}Q\) is a linear isomorphism given by \(J(c(a-bx^{n-2}))=cg(x)\), \(c\in \mathbb{R}\) and
Proof
Suppose that \(\varphi \in \Omega _{3}\), we have \(\varphi (x)=c(a-bx^{n-2})\) and
If \(\lambda =0\), by \((H_{6})\), we have \(|c|\leq a_{0}\). If \(\lambda =1\), then \(c=0\). If \(\lambda \in (0,1)\), we suppose \(|c|> a_{0}\), then
which contradicts \(\lambda c^{2}>0\). So, Lemma 3.8 holds. □
Theorem 3.5 can be proved next.
Proof of Theorem 3.5
Let Ω be a bounded open subset of X such that \(\{0\}\cup \bigcup_{j=1}^{3} \overline{\Omega }_{j} \subset \Omega \). From Lemma 3.4, we know that N is L-compact on Ω̅. In view of Lemmas 3.6 and 3.7, we can get:
-
(i)
\(L\varphi \neq \lambda N\varphi \) for every \((\varphi ,\lambda )\in [(\operatorname{dom} L\setminus \operatorname{Ker} L) \cap \partial \Omega ]\times (0,1)\);
-
(ii)
\(N\varphi \notin \operatorname{Im} L\) for every \(\varphi \in \operatorname{Ker} L \cap \partial \Omega \).
At last, we will prove that (iii) of Theorem 2.2 is satisfied.
Let \(H (\varphi ,\lambda )=\lambda J\varphi +\alpha (1-\lambda )QN \varphi \). Noting \(\Omega _{3}\subset \Omega \), we know \(H (\varphi ,\lambda )\neq 0\) for every \(\varphi \in \partial \Omega \cap \operatorname{Ker} L\). Thus, by the homotopic property of degree, we have
By Theorem 2.2, the functional boundary value problem (1.1) has at least one solution in X. The proof of Theorem 3.5 is completed. □
Example
Let us consider the following boundary value problem at resonance:
where
Corresponding to problem (1.1), we have that \(n=3\), \(\Gamma _{1}(1)=1\), \(\Gamma _{1}(x)=2\), \(\Gamma _{2}(1)=2\), \(\Gamma _{2}(x)=4\). By simple calculation, we obtain \(\alpha =\frac{1}{2}\), \(a=4\), \(b=2\), and \(\operatorname{Ker} L=\{c(2-x),c\in \mathbb{R}\}\). It is not difficult to verify that \((\Gamma _{1}-\alpha \Gamma _{2}) (x^{3}e^{-x} )=\frac{3}{e}\neq 0\), \((\Gamma _{1}-\alpha \Gamma _{2}) (\int _{0}^{+\infty }k(x,y)g(y)\,dy )=1\), where \(g(y)=\frac{2e^{1-y}}{6-7e}\). Moreover,
that is, \(\beta _{2}=4\), and \(\|K_{p}\|=(1+\frac{|a|+|b|}{a^{2}+b^{2}}\beta _{2})= \frac{11}{5}\).
Take \(h_{r}(x)=2e^{-17x}+e^{-x}+re^{-16x}\), \(q_{i}(x)=e^{-16x}\), \(i=1, 2,3\), \(r(x)=e^{-x}\); moreover, \((\|K_{P}\|+\frac{|a|+|b|}{|b|})\sum_{i=1}^{n}\|q_{i}\|_{1}= \frac{39}{40}<1\). Obviously, \((H_{1})\) and \((H_{4})\) are satisfied.
When \(A>0\) is fixed, we take \(M=3e^{17A}>0\). If \(\varphi '(x)>M\), then \(f(x,\varphi (x),\varphi '(x),\varphi ''(x))>Me^{-17A}-2>0\), \(x\in [0,A]\), \(f(x,\varphi (x),\varphi '(x),\varphi ''(x))>0\), \(x\in [A,+\infty )\), i.e., \(f(x,\varphi (x),\varphi '(x),\varphi ''(x))>0\), \(x\in [0,+\infty )\).
If \(\varphi '(x)<-M\), then \(f(x,\varphi (x),\varphi '(x),\varphi ''(x))<3-Me^{-A}<0\), \(x\in [0,A]\), \(f(x,\varphi (x),\varphi '(x), \varphi ''(x))<0\), \(x\in [A,+\infty )\), i.e., \(f(x,\varphi (x),\varphi '(x),\varphi ''(x))<0\), \(x\in [0,+\infty )\).
For convenience, we denote \(F(x)=N\varphi (x)\). Hence
provided \(\varphi (x)\in \operatorname{dom} L\setminus \operatorname{Ker} L\) satisfies \(|\varphi '(x)|>M\). This means that condition \((H_{5})\) is satisfied.
Finally, take \(\varphi \in \operatorname{Ker} L\) and \(\varphi (x)=c(2-x)\); similarly, one can choose \(a_{0}=2e^{17A}>0\) such that
provided \(|c|>a_{0}\).
Since if \(A\geq 1\), \(cN(c(2-y))=ce^{-17y}\sin (c(2-y))+e^{-17y}(-c^{2})+ce^{-y}\leq 2|c|-c^{2}e^{-17}=|c|(2-|c|e^{-17})<0\), \(y\in [0,1]\), \(cN(c(2-y))\leq |c|e^{-17}-c^{2}e^{-17}+|c|e^{-1}<0\), \(y\in [1,A]\), and \(cN(c(2-y))<0\), \(y\in [A,+\infty )\).
Similarly, if \(A<1\), \(cN(c(2-y))<|c|(2-|c|e^{-17})<0\), \(y\in [0,A]\), and \(cN(c(2-y))<0\), \(y\in [A,+\infty )\).
So, condition \((H_{6})\) holds. It follows from Theorem 3.5 that there must be at least one solution in X.
4 Conclusion
In this paper, we study the subject of differential equations on the infinite interval with functional boundary conditions at resonance. As far as we know, the resonance problem is a difficult subject in the boundary value problem. Therefore, it is more meaningful to study the high order resonance problem with functional conditions, and it is more difficult and practical to solve this problem in infinite intervals. In the last section, we use an example to illustrate the theoretical result we give.
References
Ma, R.: Existence results of a m-point boundary value problem at resonance. J. Math. Anal. Appl. 294, 147–157 (2004)
Feng, W., Webb, J.R.L.: Solvability of m-point boundary value problems with nonlinear growth. J. Math. Anal. Appl. 212, 467–480 (1997)
Lin, X., Du, Z., Ge, W.: Solvability of multipoint boundary value problems at resonance for higher-order ordinary differential equations. Comput. Math. Appl. 49(1), 1–11 (2005)
Lian, H., Pang, H., Ge, W.: Solvability for second-order three-point boundary value problems at resonance on a half-line. J. Math. Anal. Appl. 337, 1171–1181 (2008)
Djafri, S., Moussaoui, T., O’Regan, D.: Existence of solutions for a nonlocal boundary value problem at resonance on the half-line. Differ. Equ. Dyn. Syst. (2019). https://doi.org/10.1007/s12591-019-00490-y
Cui, Y.: Solvability of second-order boundary-value problems at resonance involving integral conditions. Electron. J. Differ. Equ. 2012, 45, 1–9 (2012)
Zhao, Z., Liang, J.: Existence of solutions to functional boundary value problem of second- order nonlinear differential equation. J. Math. Anal. Appl. 373, 614–634 (2011)
Kosmatov, N., Jiang, W.: Second-order functional problems with a resonance of dimension one. Differ. Equ. Appl. 8(3), 349–365 (2016)
Kosmatov, N., Jiang, W.: Resonant functional problems of fractional order. Chaos Solitons Fractals 91, 573–579 (2016)
Jiang, W., Sun, B.: Existence of solutions for functional boundary value problems of second-order nonlinear differential equations system at resonance. Adv. Differ. Equ. 2017, 269 (2017)
Du, Z.: Solvability of functional differential equations with multi-point boundary value problems at resonance. Comput. Math. Appl. 55(11), 2653–2661 (2008)
Coyle, J., Eloe, P.W.: Bifurcation from infinity and higher order ordinary differential equations. J. Math. Anal. Appl. 195, 32–43 (1995)
Eloe, P.W., Henderson, J.: Singular nonlinear \((n-k, k)\) conjugate boundary value problems. J. Differ. Equ. 133, 136–151 (1997)
Agarwal, R.P., O’Regan, D.: Multiplicity results for singular conjugate, focal, and (N,P) problems. J. Differ. Equ. 170 142–156 (2001)
Gupta, C.P.: Existence and uniqueness results for some fourth order fully quasilinear boundary value problem. Appl. Anal. 36, 15–169 (1990)
Guendouz, C., Haddouchi, F., Benaicha, S.: Existence of positive solutions for a nonlinear third-order integral boundary value problem. Ann. Acad. Rom. Sci. Ser. Math. Appl. 10(2), 314–328 (2018)
Zhang, S.: Multiple solutions of Navier boundary value problem for fourth-order elliptic equation with variable exponents. J. Shandong Univ. Nat. Sci. 53(2), 32–37 (2018)
Zhang, X., Zhong, Q.: Uniqueness of solution for higher-order fractional differential equations with conjugate type integral conditions. Fract. Calc. Appl. Anal. 20(6), 1471–1484 (2018)
Wang, S., Li, Y.: Solvability of nonlinear second-order boundary value problems with nonlinearities which cross the resonance points. J. Shandong Univ. Nat. Sci. 53(6), 53–56 (2018)
Liu, Y., Ge, W.: Solvability of nonlocal boundary value problems for ordinary differential equations of higher order. Nonlinear Anal. 57, 435–458 (2004)
Liu, B., Li, J., Liu, L.: Existence and uniqueness for an m-point boundary value problem at resonance on infinite intervals. Comput. Math. Appl. 64(6), 1677–1690 (2012)
Iyase, S.A., Adeleke, O.J.: On some higher order boundary value problems at resonance with integral boundary conditions. Arab J. Math. Sci. 24(2), 225–234 (2018)
Sun, Q., Cui, Y.: Solvability of \((k, n-k)\) conjugate boundary value problems with integral boundary conditions at resonance. J. Funct. Spaces 2016, Article ID 3454879 (2016)
Mawhin, J.: Topological Degree Methods in Nonlinear Boundary Value Problems. NSFCBMS Regional Conference Series in Mathematics. Am. Math. Soc., Providence (1979)
Kosmatov, N.: Multi-point boundary value problems on an unbounded domain at resonance. Nonlinear Anal. 68, 2158–2171 (2008)
Acknowledgements
The authors would like to thank the handling editors for the help in the processing of the paper.
Availability of data and materials
Data sharing not applicable to this paper as no datasets were generated or analyzed during the current study.
Funding
This work was supported by the Natural Science Foundation of China (11775169), the Natural Science Foundation of Hebei Province (A2018208171).
Author information
Authors and Affiliations
Contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
All analyses were based on previous published studies, thus no ethical approval and patient consent are required.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Written informed consent for publication was obtained from all participants.
Additional information
Abbreviations
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, B., Jiang, W. Existence of solutions for functional boundary value problems at resonance on the half-line. Bound Value Probl 2020, 163 (2020). https://doi.org/10.1186/s13661-020-01459-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-020-01459-5