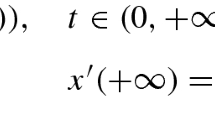The existence of positive solutions for multi-point boundary value problem at resonance on the half-line

Abstract

We establish new results on the existence of positive solutions for the multi-point boundary value problem at resonance on the half-line. Our results are based on the Leggett-Williams norm-type theorem due to O’Regan and Zima, which requires appropriate Banach spaces and proper operators. An example is given to illustrate the main results.

1 Introduction

In this paper, we will discuss the existence of positive solutions for the multi-point boundary value problem

$$ \textstyle\begin{cases} u''(t)+f (t,u(t) )=0,\quad t\in[0,+\infty),\\ u(0)=0,\qquad u'(+\infty)=\sum_{i=1}^{m-1}\alpha_{i}u'(\xi_{i}), \end{cases} $$

(1.1)

where $f \in C([0,+\infty)\times\mathbf{R}\rightarrow\mathbf {R})$, $f(t,0)$ is not always equal to 0, $t\in[0,+\infty)$, $\alpha _{i}>0$, $\sum_{i=1}^{m-1}\alpha_{i}=1$, $i=1,2,\ldots,m-1$, $0= \xi _{1}<\cdots<\xi_{m-1}<\infty$.

Boundary value problems of differential equations are applied to more and more disciplines, and the existence of one or multiple positive solutions for multi-point BVPs has been attracting more and more authors, for details see [1–16]. Generally speaking, the boundary value problems of differential equations can be roughly divided into two parts. One is boundary value problems on the finite interval; Infante and Zima [17] obtained the existence of positive solutions for the problem

$$\textstyle\begin{cases} x''(t)+f(t,x(t))=0,\quad t\in(0,1),\\ x'(0)=0, \qquad x(1)=\sum_{i=1}^{m-2}\alpha_{i}x(\eta_{i}), \end{cases} $$

with $0< \eta_{1}<\eta_{2}<\cdots<\eta_{m-2}<1$, $\alpha_{i}>0$, $\sum_{i=1}^{m-2}\alpha_{i}=1$. The other is boundary value problems on the infinite interval, for details see [18–22]; [20] obtained the existence of positive solutions for the problem

$$\textstyle\begin{cases} x{''}(t)=f(t,x(t),x'(t)),\quad t\in(0,+\infty),\\ x(0)=x(\eta),\qquad \lim_{t\rightarrow+\infty}x'(t)=0, \end{cases} $$

and

$$\textstyle\begin{cases} x{''}(t)=f(t,x(t),x'(t))+e(t), \quad t\in(0,+\infty),\\ x(0)=x(\eta),\qquad \lim_{t\rightarrow+\infty}x'(t)=0, \end{cases} $$

where $f:[0,+\infty)\times\mathbf{R}^{2}\rightarrow\mathbf {R}$, $e:[0,+\infty)\rightarrow\mathbf{R}$ are continuous and $\eta\in (0,+\infty)$.

To the best of our knowledge, only few authors studied the existence of positive solutions for boundary value problems at resonance on the half-line. In [21], the authors dealt with the second order boundary value problem with integral boundary conditions on a half-line

$$\textstyle\begin{cases} (p(t)x'(t))'+g(t)f(t,x(t))=0, \quad \mbox{a.e. in } (0,+\infty),\\ x(0)=\int_{0}^{+\infty}x(s)g(s)\,ds, \qquad \lim_{t\rightarrow+\infty}p(t)x'(t)=p(0)x'(0). \end{cases} $$

In [22], the authors investigated the existence of positive solutions for the two-point problem at resonance on the half line,

$$\textstyle\begin{cases} D_{0^{+}}^{\alpha}u(t)=f(t,u(t)), \quad t\in[0,+\infty),\\ u(0)=u'(0)=u{''}(0)=0, \qquad D_{0^{+}}^{\alpha-1}u(0)=\lim_{t\rightarrow+\infty}D_{0^{+}}^{\alpha-1}u(t), \end{cases} $$

where $D_{0^{+}}^{\alpha}$ is the standard Riemann-Liouville fractional derivative.

Inspired by the works above, we will study the existence of positive solutions for the problem (1.1).

Define 1.1

We call u is a positive solution of the boundary value problem (1.1), if $u\geq0$, $u\neq0$, and satisfies the problem (1.1).

2 Preliminaries

Let us recall some standard facts and the Leggett-Williams norm-type theorem due to O’Regan and Zima.

Let X, Y be real Banach spaces. A linear mapping $L:\operatorname {dom}L\subset X\rightarrow Y$ is called a Fredholm operator of index zero if ImL is closed and $\dim \operatorname {Ker}L=\operatorname {codim}\operatorname {Im}L< \infty$, which implies that there exist continuous projectors $P:X\rightarrow X$ and $Q:Y\rightarrow Y$ such that $\operatorname {Im}P= \operatorname {Ker}L$ and $\operatorname {Ker}Q= \operatorname {Im}L$. Moreover, since $\dim \operatorname {Im}Q=\operatorname {codim}\operatorname {Im}L$, there exists an isomorphism $J:\operatorname {Im}Q\rightarrow \operatorname {Ker}L$. Denote by $L_{P}$ the restriction of L to $\operatorname {Ker}P \cap \operatorname {dom}L\rightarrow \operatorname {Im}L$ and its inverse by $K_{P}$. So $K_{P}:\operatorname {Im}L\rightarrow \operatorname {Ker}P\cap \operatorname {dom}L$ and the coincidence equation $Lx=Nx$ is equivalent to $x=(P+JQN)x+K_{P}(I-Q)Nx$.

A nonempty convex closed set $C\subset X$ is said to be a cone provided that

• (i) $\lambda x \in C$, for $x\in C$, $\lambda\geq0$;

• (ii) $x, -x\in C$ implies $x=0$.

Note that every cone $C\subset X$ induces a partial order in X by $x\preceq y$ if and only if $y-x\in C$.

Let $\gamma:X\rightarrow C$ be a retraction, i.e. γ is a continuous mapping such that $\gamma(x)=x$, $x\in C$.

Let $\Psi:=P+JQN+K_{P}(I-Q)N$ and $\Psi_{\gamma}:=\Psi\circ\gamma$.

Theorem 2.1

([12])

Let C be a cone in X and $\Omega _{1}$, $\Omega_{2}$ be open bounded subsets of X with $\overline{\Omega}_{1}\subset\Omega_{2}$ and $C\cap(\overline{\Omega}_{2}\setminus\Omega_{1})\neq\emptyset$. Assume that $L:\operatorname {dom}L\subset X\rightarrow Y$ is a Fredholm operator of index zero and the following conditions are satisfied.

• (C1) $QN:X\rightarrow Y$ is continuous and bounded and $K_{P}(I-Q)N:X\rightarrow X$ is compact on every bounded subset of X;

• (C2) $Lx\neq\lambda Nx$ for all $x\in C\cap\partial\Omega _{2}\cap \operatorname {dom}L$ and $\lambda\in(0,1)$;

• (C3) γ maps subsets of $\overline{\Omega}_{2}$ into bounded subsets of C;

• (C4) $d_{B}([I-(P+JQN)\gamma]\mid_{\operatorname {Ker}L},\operatorname {Ker}L\cap\Omega _{2},0)\neq0$, where $d_{B}$ stands for the Brouwer degree;

• (C5) there exists $u_{0}\in C\backslash\{0\}$ such that $\Vert x\Vert \leq\sigma(u_{0})\Vert \Psi x\Vert$ for $x \in C(u_{0})\cap\partial\Omega _{1}$, where $C(u_{0})=\{ x\in C:\mu u_{0}\preceq x\textit{ for some }\mu> 0\}$ and $\sigma(u_{0})$ is such that $\Vert x+u_{0}\Vert \geq\sigma(u_{0})\Vert x\Vert$ for every $x\in C$;

• (C6) $(P+JQN)\gamma(\partial\Omega_{2})\subset C$;

• (C7) $\Psi_{\gamma}(\overline{\Omega}_{2}\backslash\Omega _{1})\subset C$.

Then the equation $Lx=Nx$ has a solution in the set $C\cap(\overline {\Omega}_{2}\backslash\Omega_{1})$.

Lemma 2.1

([23])

Assume that $V\subset X$ is bounded. V is compact if $\{ \frac{u(t)}{1+t}:u\in V \}$ is equicontinuous on $[0,T]$, $\forall T<\infty$, and equiconvergent at infinity.

In this paper, we will always suppose that the following condition holds.

(A₁) $f:[0,+\infty)\times\textbf{R}\rightarrow\textbf{R}$ is continuous and $f(t,0)$ is not always equal to 0. For any $r>0$, there exists $h_{r}(t)\in L[0,+\infty)$, $h_{r}(t)>0$ satisfying $\vert f(t,(1+t)u)\vert \leq h_{r}(t)$, $t\in[0,+\infty)$, $\vert u\vert \leq r$, $\alpha_{i}>0$, $\sum_{i=1}^{m-1}\alpha_{i}=1$.

3 Main result

Let

$$X= \biggl\{ u: u\in C[0,+\infty), u(0)=0, \sup_{t\in[0,+\infty)} \frac{\vert u(t)\vert }{1+t}< \infty \biggr\} , $$

with the norm $\Vert u\Vert =\sup_{t\in[0,+\infty)}\frac{\vert u(t)\vert }{1+t}$, and

$$Y= \Bigl\{ y:y\in C[0,+\infty)\cap L[0,+\infty), \sup_{t\in[0,+\infty)} \bigl\vert y(t)\bigr\vert < +\infty \Bigr\} , $$

with the norm $\Vert y\Vert _{1}=\int_{0}^{+\infty} \vert y(t)\vert \,dt+\sup_{t\in [0,+\infty)}\vert y(t)\vert$.

It is easy to prove that $(X, \Vert \cdot \Vert )$ and $(Y, \Vert \cdot \Vert _{1})$ are Banach spaces.

Define $L:\operatorname {dom}L\subset X\rightarrow Y$ and $N:X\rightarrow Y$ as follows:

$$(Lu) (t)=-u{''}(t),\qquad (Nu) (t)=f\bigl(t,u(t) \bigr),\qquad u(t)\in X, t\in[0,+\infty), $$

where

$$\operatorname {dom}L= \Biggl\{ u(t)\in X| u{''}(t)\in Y, u'(+\infty)=\sum_{i=1}^{m-1} \alpha _{i}u'(\xi_{i}) \Biggr\} . $$

Then the boundary value problem (1.1) can be written

$$(Lu) (t)=(Nu) (t),\quad u(t)\in \operatorname {dom}L. $$

For convenience, denote the function $G(t,s)$ as follows:

$$G(t,s)=\textstyle\begin{cases} 0, & t=0,\\ \frac{(1-\sum_{i=k}^{m-1}\alpha_{i})(\frac {3}{2}t+e^{-t}-1)}{t\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}-\frac {t-s}{t}+e^{-s},& s\leq t, \xi_{k-1}\leq s < \xi_{k}, k=2,\ldots,m-1,\\ \frac{(1-\sum_{i=k}^{m-1}\alpha_{i})(\frac {3}{2}t+e^{-t}-1)}{t\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}+e^{-s}, & 0< t< s, \xi_{k-1}\leq s < \xi_{k}, k=2,\ldots,m-1,\\ \frac{\frac{3}{2}t+e^{-t}-1}{t\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}-\frac{t-s}{t}+e^{-s}, & \xi_{m-1}\leq s\leq t,\\ \frac{\frac{3}{2}t+e^{-t}-1}{t\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}+e^{-s}, & 0< t< s, \xi_{m-1}\leq s. \end{cases} $$

Clearly, $G(t,s)\leq\frac{3}{2\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}+1$, for $t,s\in[0,+\infty)$.

Lemma 3.1

L is a Fredholm operator of index zero.

Proof

It is easy to get

$$ \operatorname {Ker}L=\bigl\{ u\in \operatorname {dom}L| u(t)=ct,t\geq0, c\in\mathbf{R}\bigr\} , $$

(3.1)

and

$$ \operatorname {Im}L= \Biggl\{ y\in Y \Big| \sum_{i=1}^{m-1} \alpha_{i} \int_{\xi_{i}}^{+\infty }y(s)\,ds=0 \Biggr\} . $$

(3.2)

Define $Q:Y\rightarrow Y$ by

$$ (Qy) (t)=\frac{e^{-t}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi _{i}}}\sum_{i=1}^{m-1} \alpha_{i} \int_{\xi_{i}}^{+\infty }y(s)\,ds,\quad y\in Y. $$

(3.3)

Clearly, $\operatorname {Ker}Q=\operatorname {Im}L$, $\operatorname {Im}Q=\{y\mid y=ce^{-t},t\geq0, c\in\textbf{R}\}$, and $Q:Y\rightarrow Y$ is a linear projector. In fact, for $y(t)\in Y$, we have

$$\bigl(Q^{2}y\bigr) (t)=\bigl(Q(Qy)\bigr) (t)=Q\bigl(e^{-t} \bigr)\frac{1}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}\sum_{i=1}^{m-1} \alpha_{i} \int_{\xi _{i}}^{+\infty}y(s)\,ds=(Qy) (t). $$

For $y\in Y$, we have $y=(y-Qy)+Qy$, $Qy\in \operatorname {Im}Q$, $(I-Q)y\in \operatorname {Ker}Q=\operatorname {Im}L$. So we obtain $Y=\operatorname {Im}Q+\operatorname {Im}L$. Take $y_{0}\in \operatorname {Im}Q\cap \operatorname {Im}L$. $y_{0}\in \operatorname {Im}Q$ means that $y_{0}$ can be written $y_{0}=ce^{-t}$, $c\in\textbf{R}$. At the same time, by $y_{0}\in \operatorname {Im}L$ and (3.2), we get

$$\sum_{i=1}^{m-1}\alpha_{i} \int_{\xi_{i}}^{+\infty}ce^{-s}\,ds=0, $$

i.e. $c=0$. This implies that $y_{0}=0$. Thus, $Y=\operatorname {Im}Q\oplus \operatorname {Im}L$ and $\dim \operatorname {Ker}L=\operatorname {codim}\operatorname {Im}L=1<+\infty$. Observing that ImL is closed in Y, L is a Fredholm operator of index zero. □

Define $P:X\rightarrow X$ as

$$ (Pu) (t)=t \int_{0}^{+\infty}e^{-t}u(t)\,dt,\quad u(t)\in X. $$

(3.4)

Clearly, $P:X\rightarrow X$ is a linear continuous projector and

$$\operatorname {Im}P=\bigl\{ u\mid u(t)=ct, t\geq0, c\in\textbf{R}\bigr\} =\operatorname {Ker}L. $$

Thus, $X=\operatorname {Im}P\oplus \operatorname {Ker}P=\operatorname {Ker}L\oplus \operatorname {Ker}P$.

Define $K_{P}:\operatorname {Im}L\rightarrow \operatorname {Ker}P\cap \operatorname {dom}L$ by

$$ (K_{P}y) (t)=- \int_{0}^{t}(t-s)y(s)\,ds+t \int_{0}^{+\infty }e^{-s}y(s)\,ds,\quad y\in \operatorname {Im}L. $$

(3.5)

By simple calculations, we have $(K_{P}L_{P})u=u$, $\forall u\in \operatorname {dom}L\cap \operatorname {Ker}P$, and $(L_{P}K_{P})y=y$, $\forall y\in \operatorname {Im}L$. So $K_{P}=(L_{P})^{-1}$, where $L_{P}=L\mid_{\operatorname {dom}L\cap \operatorname {Ker}P}:\operatorname {dom}L\cap \operatorname {Ker}P\rightarrow \operatorname {Im}L$.

Define the linear isomorphism $J:\operatorname {Im}Q\rightarrow \operatorname {Ker}L$ as

$$J\bigl(ce^{-t}\bigr)=ct, \quad t\geq0, c\in\textbf{R}. $$

Thus, $JQN+K_{P}(I-Q)N:X\rightarrow X$ is given by

$$ \bigl[JQN+K_{P}(I-Q)N\bigr]u(t)=t \int_{0}^{+\infty}G(t,s)f\bigl(s,u(s)\bigr)\,ds. $$

(3.6)

Lemma 3.2

$QN:X\rightarrow Y$ is continuous and bounded and $K_{P}(I-Q)N:\overline{\Omega}\rightarrow X$ is compact, where $\Omega\subset X$ is bounded.

Proof

For convenience, denote $M_{r}:=\frac{\int_{0}^{+\infty}h_{r}(\tau)\,d\tau}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}$.

We will prove that $QN:X\rightarrow Y$ is continuous and bounded.

Since $\Omega\subset X$ is bounded, for $u\in\overline{\Omega}$, there exists a constant $r>0$, such that $\Vert u\Vert < r$. By the condition (A₁), we have

$$\begin{aligned} \Vert QNu\Vert _{1}={}& \int_{0}^{+\infty} \Biggl\vert \frac{e^{-s}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int _{\xi_{i}}^{+\infty}f\bigl(\tau, u(\tau)\bigr)\,d\tau \Biggr\vert \,ds \\ &{}+\sup_{t\in [0,+\infty)} \Biggl\vert \frac{e^{-t}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi _{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int_{\xi_{i}}^{+\infty}f\bigl(\tau , u(\tau)\bigr)\,d\tau \Biggr\vert \\ \leq{}& \int_{0}^{+\infty}\frac{e^{-s}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha _{i} \int_{\xi_{i}}^{+\infty} \bigl\vert f\bigl(\tau, u(\tau)\bigr) \bigr\vert \,d\tau \,ds \\ &{}+\sup_{t\in[0,+\infty)}\frac{e^{-t}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int _{\xi_{i}}^{+\infty} \bigl\vert f\bigl(\tau, u(\tau) \bigr) \bigr\vert \,d\tau \\ \leq{}&\frac{\int_{0}^{+\infty}h_{r}(\tau)\,d\tau }{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}} +\frac{\int_{0}^{+\infty}h_{r}(\tau)\,d\tau}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}=2M_{r}. \end{aligned}$$

So $QN:X\rightarrow Y$ is bounded. By (A₁) and the Lebesgue dominated convergence theorem, we see that $QN:X\rightarrow Y$ is continuous.

Now, we will prove that $K_{P}(I-Q)N:\overline{\Omega}\rightarrow X$ is compact.

First of all, by the condition (A₁) and $u\in\overline{\Omega}$, we have

$$\begin{aligned} &\biggl\vert \frac{K_{P}(I-Q)Nu(t)}{1+t}\biggr\vert \\ &\quad =\biggl\vert - \int_{0}^{t}\frac {t-s}{1+t}(I-Q)Nu(s)\,ds+ \frac{t}{1+t} \int_{0}^{+\infty }e^{-s}(I-Q)Nu(s)\,ds\biggr\vert \\ &\quad \leq \int_{0}^{t}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds+ \int _{0}^{+\infty}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds \\ &\quad \leq2 \int_{0}^{+\infty}\bigl\vert Nu(s)\bigr\vert \,ds+2 \int_{0}^{+\infty}\bigl\vert QNu(s)\bigr\vert \,ds \\ &\quad \leq2 \int_{0}^{\infty}h_{r}(s) \,ds+2M_{r}\leq 4M_{r}< +\infty, \end{aligned}$$

i.e. $K_{P}(I-Q)N:\overline{\Omega}\rightarrow X$ is bounded.

Second, for $u\in\overline{\Omega}$, $0< t_{1}< t_{2}< T<\infty$,

$$\begin{aligned} &\biggl\vert \frac{K_{P}(I-Q)Nu(t_{2})}{1+t_{2}}-\frac {K_{P}(I-Q)Nu(t_{1})}{1+t_{1}}\biggr\vert \\ &\quad = \biggl\vert - \int_{0}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}(I-Q)Nu(s)\,ds+ \frac{t_{2}}{1+t_{2}} \int_{0}^{+\infty }e^{-s}(I-Q)Nu(s)\,ds \\ &\qquad {} - \biggl(- \int_{0}^{t_{1}}\frac {t_{1}-s}{1+t_{1}}(I-Q)Nu(s)\,ds+ \frac{t_{1}}{1+t_{1}} \int_{0}^{+\infty }e^{-s}(I-Q)Nu(s)\,ds \biggr) \biggr\vert \\ &\quad \leq \int_{0}^{t_{1}}\biggl\vert \frac{t_{2}-s}{1+t_{2}}- \frac {t_{1}-s}{1+t_{1}}\biggr\vert \bigl\vert (I-Q)Nu(s)\bigr\vert \,ds+ \int_{t_{1}}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds \\ &\qquad {}+\biggl\vert \frac{t_{2}}{1+t_{2}}-\frac {t_{1}}{1+t_{1}}\biggr\vert \int_{0}^{+\infty}e^{-s}\bigl\vert (I-Q)Nu(s) \bigr\vert \,ds \\ &\quad \leq \int_{0}^{t_{1}}\biggl\vert \frac{t_{2}-s}{1+t_{2}}- \frac {t_{1}-s}{1+t_{1}}\biggr\vert h_{r}(s)\,ds+ \int_{0}^{t_{1}}\biggl\vert \frac {t_{2}-s}{1+t_{2}}- \frac{t_{1}-s}{1+t_{1}}\biggr\vert \bigl\vert QNu(s)\bigr\vert \,ds \\ &\qquad {}+ \int_{t_{1}}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}h_{r}(s) \,ds+ \int_{t_{1}}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}\bigl\vert QNu(s) \bigr\vert \,ds \\ &\qquad {}+\biggl\vert \frac{t_{2}}{1+t_{2}}-\frac {t_{1}}{1+t_{1}}\biggr\vert \int_{0}^{+\infty}h_{r}(s)\,ds+\biggl\vert \frac {t_{2}}{1+t_{2}}-\frac{t_{1}}{1+t_{1}}\biggr\vert \int_{0}^{+\infty}\bigl\vert QNu(s)\bigr\vert \,ds \\ &\quad \leq \int_{0}^{t_{1}}\biggl\vert \frac {t_{2}-s}{1+t_{2}}- \frac{t_{1}-s}{1+t_{1}}\biggr\vert h_{r}(s)\,ds+M_{r} \int _{0}^{t_{1}}\biggl\vert \frac{t_{2}-s}{1+t_{2}}- \frac{t_{1}-s}{1+t_{1}}\biggr\vert e^{-s}\,ds \\ &\qquad {}+ \int_{t_{1}}^{t_{2}}h_{r}(s) \,ds+M_{r} \int _{t_{1}}^{t_{2}}e^{-s}\,ds+2\biggl\vert \frac{t_{2}}{1+t_{2}}-\frac {t_{1}}{1+t_{1}}\biggr\vert M_{r}. \end{aligned}$$

By the uniform continuity of $\frac{t-s}{1+t}$ in $[0,T]\times[0,T]$ and $\frac{t}{1+t}$ in $[0,T]$, and the absolute continuity of the integral, we see that $K_{P}(I-Q)N:\overline {\Omega}\rightarrow X$ is equicontinuous on $[0,T]$, $\forall T>0$.

Third, for $\varepsilon>0$, there exists a constant $l>0$, such that

$$\int_{l}^{+\infty}h_{r}(s)\,ds< \frac{\varepsilon}{12}, \qquad \int_{l}^{+\infty }e^{-s}\,ds< \frac{\varepsilon}{12M_{r}}. $$

Since $\lim_{t\rightarrow+\infty}\frac{t-l}{1+t}=1$, $\lim_{t\rightarrow+\infty}\frac{t}{1+t}=1$, there exists a constant $T>l$ such that

$$\biggl\vert 1-\frac{t-l}{1+t}\biggr\vert < \frac{\varepsilon}{12M_{r}},\qquad \biggl\vert 1-\frac{t}{1+t}\biggr\vert < \frac{\varepsilon}{12M_{r}} ,\quad t\geq T. $$

For $u\in\overline{\Omega}$, $T\leq t_{1}< t_{2}$, we have

$$\begin{aligned} &\biggl\vert \frac{K_{P}(I-Q)Nu(t_{2})}{1+t_{2}}-\frac {K_{P}(I-Q)Nu(t_{1})}{1+t_{1}}\biggr\vert \\ &\quad = \biggl\vert - \int_{0}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}(I-Q)Nu(s)\,ds+ \frac{t_{2}}{1+t_{2}} \int_{0}^{+\infty }e^{-s}(I-Q)Nu(s)\,ds \\ &\qquad {}- \biggl(- \int_{0}^{t_{1}}\frac {t_{1}-s}{1+t_{1}}(I-Q)Nu(s)\,ds+ \frac{t_{1}}{1+t_{1}} \int_{0}^{+\infty }e^{-s}(I-Q)Nu(s)\,ds \biggr) \biggr\vert \\ &\quad \leq \int_{0}^{l}\biggl\vert \frac{t_{2}-s}{1+t_{2}}- \frac {t_{1}-s}{1+t_{1}}\biggr\vert \bigl\vert (I-Q)Nu(s)\bigr\vert \,ds+ \int_{l}^{t_{2}}\frac {t_{2}-s}{1+t_{2}}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds \\ &\qquad {}+ \int_{l}^{t_{1}}\frac {t_{1}-s}{1+t_{1}}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds+\biggl\vert \frac{t_{2}}{1+t_{2}}-\frac {t_{1}}{1+t_{1}} \biggr\vert \int_{0}^{+\infty}e^{-s}\bigl\vert (I-Q)Nu(s) \bigr\vert \,ds \\ &\quad \leq \biggl[ \biggl(1-\frac{t_{2}-l}{1+t_{2}} \biggr)+ \biggl(1- \frac{t_{1}-l}{1+t_{1}} \biggr) \biggr] \int_{0}^{+\infty }\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds+2 \int_{l}^{+\infty}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds \\ &\qquad {} + \biggl[ \biggl(1-\frac{t_{2}}{1+t_{2}} \biggr)+ \biggl(1- \frac {t_{1}}{1+t_{1}} \biggr) \biggr] \int_{0}^{+\infty}\bigl\vert (I-Q)Nu(s)\bigr\vert \,ds \\ &\quad \leq \biggl[ \biggl(1-\frac{t_{2}-l}{1+t_{2}} \biggr)+ \biggl(1- \frac{t_{1}-l}{1+t_{1}} \biggr) \biggr]2M_{r}+2 \int_{l}^{+\infty }h_{r}(s) \,ds+2M_{r} \int_{l}^{+\infty}e^{-s}\,ds \\ &\qquad {} + \biggl[ \biggl(1-\frac{t_{2}}{1+t_{2}} \biggr)+ \biggl(1- \frac {t_{1}}{1+t_{1}} \biggr) \biggr]2M_{r}< \varepsilon. \end{aligned}$$

Thus, $K_{P}(I-Q)N:\overline{\Omega}\rightarrow X$ is equiconvergent at infinity.

By Lemma 2.1, we see that $K_{P}(I-Q)N:\overline{\Omega}\rightarrow X$ is compact. □

Theorem 3.1

Assume that (A₁) and the following conditions hold.

(A₂) For $u\geq0$, there exist three nonnegative functions $\mu (t)$, $\beta_{i}(t)$, $i=1,2$, such that

$$-\mu(t)ue^{-t}\leq f(t,u)\leq-\beta_{1}(t)ue^{-t}+ \beta _{2}(t), \qquad G(t,s)f(s,u)\geq-e^{-s}u,\quad t,s\in[0,+\infty), $$

where $\mu(t)ue^{-t}, \beta_{2}(t), \beta_{1}(t)ue^{-t}\in L[0,+\infty )$, $\inf_{t\in[0,+\infty)}\beta_{1}(t) :=\beta_{0}>0$ and $\mu(t)$ satisfying

• (i) $\sup_{t\in[0,+\infty)}\mu(t):=\mu _{1}<\frac{2\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi _{i}}}{3+2\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}$,

• (ii) there exists $t_{0}\in[0,+\infty)$, such that $d_{0}:=\frac {t_{0}}{1+t_{0}}\int_{0}^{+\infty}[1-G(t_{0},s)\mu (s)](1+s)e^{-s}\,ds>1$, $G(t_{0},s)\geq0$.

(A₃) There exists $R>\frac{\mu_{1}+\alpha_{1}\beta_{0}+1}{\alpha_{1}\beta _{0}}\int_{0}^{\infty}\beta_{2}(s)\,ds$, such that $f(t,Rt)<0$, $t\in[0,+\infty)$.

Then the problem (1.1) has at least one positive solution.

Proof

Take a cone

$$C=\bigl\{ u(t)\in X|u(t)\geq0, t\in[0,+\infty)\bigr\} . $$

Set

$$\Omega_{1}= \biggl\{ u\in X\Big|\frac{1}{d_{0}}\Vert u\Vert < \frac{\vert u(t)\vert }{1+t}< r< R, t\in[0,+\infty) \biggr\} , \qquad \Omega_{2}= \bigl\{ u\in X\mid \Vert u\Vert < R\bigr\} , $$

where $d_{0}$ is given by the condition (A₂) and $R>\frac{\mu_{1}+\alpha_{1}\beta_{0}+1}{\alpha_{1}\beta _{0}}\int_{0}^{\infty}\beta_{2}(s)\,ds$. Clearly, $\Omega_{1}$, $\Omega_{2}$ are open and bounded sets of X, $\overline{\Omega}_{1}= \{u\in X |\frac{1}{d_{0}}\Vert u\Vert \leq\frac{\vert u(t)\vert }{1+t}\leq r< R \}\subset\Omega_{2}$, and ${C\cap(\overline{\Omega}_{2}\setminus\Omega_{1})\neq\emptyset}$.

In view of Lemmas 3.1 and 3.2, L is a Fredholm operator of index zero and the condition (C1) of Theorem 2.1 is fulfilled.

Suppose that there exist $u_{1}(t)\in C\cap\partial\Omega_{2}\cap \operatorname {dom}L$ and $\lambda_{0}\in(0,1)$ such that $Lu_{1}=\lambda_{0}Nu_{1}$, i.e. $u_{1}''(t)+\lambda_{0} f(t,u_{1}(t))=0$. By $u_{1}(t)\in \operatorname {dom}L$, we have

$$\begin{aligned}& u_{1}'(+\infty)-\sum_{i=1}^{m-1} \alpha_{i}u_{1}'(\xi _{i})=0, \\& \quad \textit{i.e. } {-}\lambda_{0} \int_{0}^{+\infty }f\bigl(s,u_{1}(s)\bigr)\,ds+ \sum_{i=1}^{m-1}\alpha_{i} \lambda_{0} \int _{0}^{\xi_{i}}f\bigl(s,u_{1}(s)\bigr) \,ds=0. \end{aligned}$$

It follows from (A₂) that

$$0= \sum_{i=1}^{m-1}\alpha_{i} \int_{\xi_{i}}^{+\infty }f\bigl(s,u_{1}(s)\bigr)\,ds \leq\sum_{i=1}^{m-1}\alpha_{i} \int_{\xi _{i}}^{+\infty}\bigl[-\beta_{1}(s)u_{1}(s)e^{-s}+ \beta_{2}(s)\bigr]\,ds. $$

So

$$ \alpha_{1} \int_{0}^{+\infty}\beta_{1}(s)u_{1}(s)e^{-s} \,ds\leq \int _{0}^{+\infty}\beta_{2}(s)\,ds. $$

(3.7)

Considering (A₂), (3.7), and

$$\begin{aligned} u_{1}(t)&=(I-P)u_{1}(t)+Pu_{1}(t)=K_{P}L(I-P)u_{1}(t)+Pu_{1}(t)=K_{P}Lu_{1}(t)+Pu_{1}(t) \\ &=-\lambda_{0} \int _{0}^{t}(t-s)f\bigl(s,u_{1}(s) \bigr)\,ds+\lambda_{0}t \int_{0}^{+\infty }e^{-s}f\bigl(s,u_{1}(s) \bigr)\,ds+t \int_{0}^{+\infty}e^{-s}u_{1}(s)\,ds, \end{aligned}$$

we obtain

$$\begin{aligned} &\frac{u_{1}(t)}{1+t}=-\frac{\lambda_{0}}{1+t} \int _{0}^{t}(t-s)f\bigl(s,u_{1}(s) \bigr)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}=}{}+\frac{\lambda_{0}t}{1+t} \int_{0}^{+\infty }e^{-s}f\bigl(s,u_{1}(s) \bigr)\,ds+\frac{t}{1+t} \int_{0}^{+\infty}e^{-s}u_{1}(s)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\leq\lambda_{0} \int_{0}^{t}\frac{(t-s)}{1+t}\mu (s)u_{1}(s)e^{-s}\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}=}{}+\frac{\lambda_{0}t}{1+t} \int_{0}^{+\infty }e^{-s}\bigl[- \beta_{1}(s)u_{1}(s)e^{-s}+\beta_{2}(s) \bigr]\,ds+\frac{t}{1+t} \int _{0}^{+\infty}e^{-s}u_{1}(s)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\leq \int_{0}^{t}\frac{\beta_{1}(s)e^{-s}\mu (s)u_{1}(s)}{\beta_{1}(s)}\,ds+ \int_{0}^{+\infty}\beta_{2}(s)\,ds+ \int _{0}^{+\infty}\frac{\beta_{1}(s)e^{-s}u_{1}(s)}{\beta_{1}(s)}\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\leq\frac{\mu_{1}+\alpha_{1}\beta_{0}+1}{\alpha _{1}\beta_{0}} \int_{0}^{+\infty}\beta_{2}(s)\,ds< R, \\ &\frac{u_{1}(t)}{1+t}=-\frac{\lambda_{0}}{1+t} \int _{0}^{t}(t-s)f\bigl(s,u_{1}(s) \bigr)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}=}{}+\frac{\lambda_{0}t}{1+t} \int_{0}^{+\infty }e^{-s}f\bigl(s,u_{1}(s) \bigr)\,ds+\frac{t}{1+t} \int_{0}^{+\infty}e^{-s}u_{1}(s)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\geq\lambda_{0} \int_{0}^{t}\frac{t-s}{1+t}\bigl[\beta _{1}(s)u_{1}(s)e^{-s}-\beta_{2}(s) \bigr]\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}=}{}+\frac{\lambda_{0}t}{1+t} \int _{0}^{+\infty}e^{-s}\bigl[- \mu(s)u_{1}(s)e^{-s}\bigr]\,ds+\frac{t}{1+t} \int _{0}^{+\infty}e^{-s}u_{1}(s)\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\geq- \int_{0}^{t}\beta_{2}(s)\,ds- \int_{0}^{+\infty}\frac {\beta_{1}(s)\mu(s)e^{-s}u_{1}(s)}{\beta_{1}(s)}\,ds \\ &\hphantom{\frac{u_{1}(t)}{1+t}}\geq-\frac{\alpha_{1}\beta_{0}+\mu_{1}}{\alpha_{1}\beta _{0}} \int_{0}^{+\infty}\beta_{2}(s)\,ds>-R. \end{aligned}$$

These contradict $u_{1}(t)\in C\cap\partial\Omega_{2}\cap \operatorname {dom}L$. So (C2) is satisfied.

Let $(\gamma u)(t)=\vert u(t)\vert$, $u(t)\in X$. Then $\gamma:X\rightarrow C$ is a retraction and maps subsets of $\overline{\Omega}_{2}$ into bounded subsets of C, i.e. (C3) holds.

Let $u(t)\in \operatorname {Ker}L\cap\partial\Omega_{2}$, then $u(t)=ct$, $t\geq0$. Define

$$\begin{aligned} H(ct,\lambda)&= \bigl[I-\lambda(P+JQN)\gamma \bigr](ct) \\ &= ct-\lambda t \int_{0}^{+\infty}e^{-t}\vert c\vert t\,dt- \frac{\lambda t}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum_{i=1}^{m-1} \alpha_{i} \int _{\xi_{i}}^{+\infty}f\bigl(t,\vert c\vert t\bigr)\,dt, \end{aligned}$$

where $c\in\{-R,R\}$ and $\lambda\in[0,1]$. Suppose $H(ct,\lambda )=0$, by (A₂), we obtain

$$\begin{aligned} c&=\lambda \Biggl(\vert c\vert +\frac{1}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int_{\xi _{i}}^{+\infty}f\bigl(t,\vert c\vert t\bigr)\,dt \Biggr) \\ &\geq\lambda \vert c\vert \Biggl(1-\frac{1}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int _{\xi_{i}}^{+\infty}\mu(t)te^{-t}\,dt \Biggr) \\ & \geq\lambda \vert c\vert \Biggl(1-\frac{\mu_{1}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum _{i=1}^{m-1}\alpha_{i} \int _{0}^{+\infty}te^{-t}\,dt \Biggr)\\ &=\lambda \vert c\vert \biggl(1-\frac{\mu _{1}}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}} \biggr)\geq0. \end{aligned}$$

Hence $H(ct,\lambda)= 0$ implies $c\geq0$. Furthermore, if $H(Rt,\lambda)=0$, we have

$$R(1-\lambda)=\frac{\lambda}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}} \sum_{i=1}^{m-1} \alpha_{i} \int_{\xi _{i}}^{+\infty}f(t,Rt)\,dt\geq0, $$

which is a contradiction to the condition (A₃).

Thus, $H(u,\lambda)\neq0$, for $u\in \operatorname {Ker}L\cap\partial\Omega_{2}$, and $\lambda\in[0,1]$. Therefore

$$\begin{aligned} &d_{B}\bigl(\bigl[I-(P+JQN)\gamma\bigr]\mid_{\operatorname {Ker}L}, \operatorname {Ker}L \cap\Omega_{2}, 0\bigr) \\ &\quad =d_{B}\bigl(H(\cdot,1), \operatorname {Ker}L\cap\Omega_{2}, 0 \bigr) \\ &\quad =d_{B}\bigl(H(\cdot,0), \operatorname {Ker}L\cap\Omega_{2}, 0 \bigr)=d_{B}(I, \operatorname {Ker}L\cap\Omega _{2}, 0)=1\neq0. \end{aligned}$$

Thus, (C4) holds.

Let $u_{0}(t)=t$, $t \in[0,+\infty)$, then $u_{0}\in C\setminus\{0\}$, $C(u_{0})=\{u\in C| u(t)\geq\mu t \mbox{ for some } \mu>0, t \in[0,+\infty )\}$, and we take $\sigma(u_{0})=1$. Let $u \in C(u_{0})\cap\partial \Omega_{1}$, we have $\frac{1}{d_{0}}\Vert u\Vert \leq\frac{\vert u(t)\vert }{1+t}\leq r$, $t \in[0,+\infty)$.

For $u\in C(u_{0})\cap\partial\Omega_{1}$, by (A₂), we get

$$\begin{aligned} \frac{\Psi u(t_{0})}{1+t_{0}}&=\frac{t_{0}}{1+t_{0}} \int_{0}^{+\infty}e^{-s}u(s)\,ds+ \frac {t_{0}}{1+t_{0}} \int_{0}^{+\infty}G(t_{0},s)f\bigl(s,u(s)\bigr) \,ds \\ & \geq\frac{t_{0}}{1+t_{0}} \int_{0}^{+\infty} \bigl(e^{-s}u(s)-G(t_{0},s) \mu(s)u(s)e^{-s} \bigr)\,ds \\ & =\frac{t_{0}}{1+t_{0}} \int_{0}^{+\infty }\bigl[1-G(t_{0},s)\mu(s) \bigr](1+s)e^{-s}\frac{u(s)}{1+s}\,ds \\ & \geq\frac{t_{0}}{1+t_{0}} \int_{0}^{+\infty }\bigl[1-G(t_{0},s)\mu(s) \bigr](1+s)e^{-s}\,ds\frac{1}{d_{0}}\Vert u\Vert =\Vert u \Vert . \end{aligned}$$

Thus, $\Vert u\Vert \leq\sigma(u_{0})\Vert \Psi u\Vert$, for $u\in C(u_{0})\cap\partial \Omega_{1}$. So (C5) holds.

For $u(t)\in\partial\Omega_{2}$, $t\in[0,+\infty)$, by the condition (A₂), we have

$$\begin{aligned} (P+JQN)\gamma(u)&=t \int_{0}^{+\infty}e^{-s}\bigl\vert u(s)\bigr\vert \,ds+\frac{t}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi_{i}}}\sum_{i=1}^{m-1} \alpha_{i} \int _{\xi_{i}}^{+\infty}f\bigl(s,\bigl\vert u(s)\bigr\vert \bigr)\,ds \\ & \geq t \int_{0}^{+\infty}e^{-s}\bigl\vert u(s)\bigr\vert \,ds-\frac{t}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}}\sum_{i=1}^{m-1} \alpha_{i} \int_{\xi _{i}}^{+\infty}\mu(s)\bigl\vert u(s)\bigr\vert e^{-s}\,ds \\ &\geq t \int_{0}^{+\infty}e^{-s}\bigl\vert u(s)\bigr\vert \,ds-\frac{t}{\sum_{i=1}^{m-1}\alpha _{i}e^{-\xi_{i}}} \int_{0}^{+\infty}\mu(s)\bigl\vert u(s)\bigr\vert e^{-s}\,ds \\ &= t \int_{0}^{+\infty }e^{-s}\bigl\vert u(s)\bigr\vert \biggl(1-\frac{\mu(s)}{\sum_{i=1}^{m-1}\alpha_{i}e^{-\xi _{i}}}\biggr)\,ds\geq0, \end{aligned}$$

which means that $(P+JQN)\gamma(\partial\Omega_{2})\subset C$. Hence, (C6) holds.

For $u(t)\in\overline{\Omega}_{2}\setminus\Omega_{1}$, $t\in[0,+\infty)$, by the condition (A₂), we have

$$\begin{aligned} (\Psi_{\gamma}u) (t)&=t \int_{0}^{+\infty}e^{-s}\bigl\vert u(s)\bigr\vert \,ds+t \int_{0}^{+\infty }G(t,s)f\bigl(s,\bigl\vert u(s)\bigr\vert \bigr)\,ds \\ &\geq t \int_{0}^{+\infty}e^{-s}\bigl\vert u(s)\bigr\vert \,ds-t \int_{0}^{+\infty }e^{-s}\bigl\vert u(s)\bigr\vert \,ds \\ &=0. \end{aligned}$$

So $\Psi_{\gamma}(\overline{\Omega}_{2}\setminus\Omega_{1})\subset C$, i.e. (C7) is satisfied.

By Theorem 2.1, we confirm that the equation $Lu=Nu$ has a positive solution u, i.e. the problem (1.1) has at least one positive solution. □

4 Examples

Let us consider the following boundary value problem:

$$ \textstyle\begin{cases} u''(t)+te^{-t}-\frac{1}{90}u(t)e^{-t}=0,\quad t\in[0,+\infty),\\ u(0)=0,\qquad u'(+\infty)=0.68u'(0)+0.018u'(0.5)+0.302u'(0.95). \end{cases} $$

(4.1)

Here, $f(t,u(t))=te^{-t}-\frac{1}{90}u(t)e^{-t}$, $\alpha _{1}=0.68$, $\alpha_{2}=0.018$, $\alpha_{3}=0.302$, $\xi_{1}=0$, $\xi _{2}=0.5$, $\xi_{3}=0.95$. Take $h_{r}(t)=te^{-t}+\frac{r}{90}(1+t)e^{-t}$, $\mu (t)=\frac{1}{80}$, $\beta_{1}(t)=\frac{1}{100}$, $\beta_{2}(t)=te^{-t}$, $t\in[0,+\infty)$, $t_{0}=1.05$, $R=160$, $r=150$.

Obviously, $\vert f(t,(1+t)u)\vert \leq h_{r}(t)$, $t\in[0,+\infty)$, $r>0$, $\vert u\vert < r$. By our calculations, we can get $0.0029\leq G(t,s)\leq2.8571$ and

$$\begin{aligned}& -\mu(t)ue^{-t}\leq f(t,u)\leq-\beta_{1}(t)ue^{-t}+ \beta_{2}(t), \\& G(t,s)f(s,u)> -e^{-s}u, \quad u\geq 0, t\in[0,+\infty), \end{aligned}$$

$\mu_{1}=\sup_{t\in[0,+\infty)}\mu(t)=\frac {1}{80}$, $\beta_{0}=\inf_{t\in[0,+\infty)}\beta_{1}(t)=\frac {1}{100}$, $\beta_{2}(t)\in L[0,+\infty)$; $f(t,Rt)<0$, $t\in[0,+\infty)$. By simple calculations, we can get that $0.348< G(1.05,s)<1.478$, so

$$G(1.05,s)>0,\quad d_{0}:=\frac{1.05}{1+1.05} \int_{0}^{+\infty}\bigl[1-G(1.05,s)\mu (s) \bigr](1+s)e^{-s}\,ds\geq1.005>1. $$

So the conditions (A₁)-(A₃) hold. By Theorem 3.1, we can conclude that the problem (4.1) has at least one positive solution.