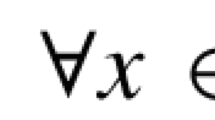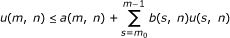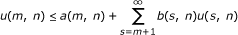1. Introduction

Finite difference inequalities in one or two independent variables which provide explicit bounds play a fundamental role in the study of boundedness, uniqueness, and continuous dependence on initial data of solutions of difference equations. Many difference inequalities have been established (for example, see [1–11] and the references therein). In the research of difference inequalities, generalization of known inequalities has been paid much attention by many authors. Here we list some recent results in the literature.

In [[12], Theorems 2.6-2.8], Pachpatte presents the following six discrete inequalities, based on which some new bounds on unknown functions are established.

Preprint submitted to Advances in Difference Equations June 16, 2011

where u, a, b, c are nonnegative functions defined on m ∈ ℕ0, n ∈ ℕ0, and L : ℕ0 × ℕ0 × ℝ+ → ℝ+ satisfies 0 ≤ L(m, n, u) - L(m, n, v) ≤ M(m, n, v)(u - v) for u ≥ v ≥ 0, where M : ℕ0 × ℕ0 × ℝ+ → ℝ+.

Recently, in [[13], Theorems 1-6], Meng and Li present the following inequalities with more general forms.

where p ≥ 1 is a constant, u, a, b, c, e are nonnegative functions defined on m ∈ ℕ0, n ∈ ℕ0, and L is defined the same as in (a 5)-a(6).

As one can see, (b 1)-(b 2) are generalizations of (a 1)-(a 2), while (b 4)-(b 6) are generalizations of (a 4)-(a 6).

More recently, Meng and Ji [[14], Theorems 3, 4, 7, 8] extended (b 1)-(b 4) to the following inequalities.

where p, q, r are constants with p ≥ q, p ≥ r, p ≠ 0, and u, a, b, c, d, e are nonnegative functions defined on m ∈ ℕ0, n ∈ ℕ0.

The presented inequalities above have proved to be very useful in the study of quantitative as well as qualitative properties of solutions of certain difference equations.

Motivated by the work mentioned above, in this paper, we will establish some more generalized finite difference inequalities, which provide new bounds for unknown functions lying in these inequalities. We will illustrate the usefulness of the established results by applying them to study the boundedness, uniqueness, and continuous dependence on initial data of solutions of certain difference equations.

Throughout this paper, ℝ denotes the set of real numbers and ℝ+ = [0, ∞), and ℤ denotes the set of integers, while ℕ0 denotes the set of nonnegative integers. I := [m 0, ∞] ∩ ℤ and are two fixed lattices of integral points in ℝ, where m 0, n 0 ∈ ℤ. Let . We denote the set of all ℝ-valued functions on Ω by ℘(Ω), and denote the set of all ℝ+-valued functions on Ω by ℘+(Ω). The partial difference operators Δ1 and Δ2 on u ∈ ℘(Ω) are defined as Δ1 u(m, n) = u(m +1, n) - u(m, n), Δ2 u(m, n) = u(m, n + 1) - u(m, n).

2. Main results

Lemma 2.1. [[15]] Assume that a ≥ 0, p ≥ q ≥ 0, and p ≠ 0, then for any K > 0

Lemma 2.2. Let u(m, n), a(m, n), b(m, n) are nonnegative functions defined on Ω with a(m, n) not equivalent to zero.

  1. (1)

    Assume that a(m, n) is nondecreasing in the first variable. If

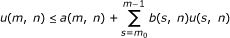
for (m, n) ∈ Ω, then

  1. (2)

    Assume that a(m, n) is decreasing in the first variable. If

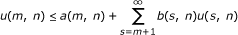
for (m, n) ∈ Ω, then

Remark 1. Lemma 2.2 is a direct variation of [[12], Lemma 2.5].

Theorem 2.1. Suppose u, a, b, f, g, h, w ∈ ℘+ (Ω), and b, f, g, h, w are nondecreasing in the first variable, while decreasing in the second variable. α : I → I is nondecreasing with α (m) ≤ m for ∀m ∈ I, while is nondecreasing with β(n) ≥ n for . p, q, r, l are constants with p ≥ q, p ≥ r, p ≥ l, p ≠ 0.

If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

(1)

then we have

(2)

provided H(m.n) > 0, where K > 0 is a constant, and

(3)

Proof. Let .

Then we have

(4)

Furthermore, if given (X, Y ) ∈ Ω, and (m, n) ∈ ([m 0, X]×[Y, ∞]) ∩ Ω, then using (4) and Lemma 2.1 we have

(5)

where H, , , are defined in (3).

Let the right side of (5) be v(m, n). Then

(6)

and

Considering v(m, n) ≥ v(m, n + 1), we have

(7)

Setting n = t in (7), and a summary with respect to t from n to r - 1 yields

(8)

Letting r → ∞ in (8), using v(m, ∞) = H(X, Y ) we obtain

which is followed by

(9)

Setting m = s in (9), and a multiple with respect to s from m 0 to m - 1 yields

(10)

Considering v(m 0, n) = H(X, Y ), and then combining (4), (6) and (10) we obtain

(11)

Setting m = X, n = Y in (11), and considering (X, Y ) ∈ Ω is selected arbitrarily, then after substituting X, Y with m, n we obtain the desired inequality.

Remark 2. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α (m) = m, β(n) = n, and omit the conditions "b, f, g, h, w are nondecreasing in the first variable, while decreasing in the second variable" in Theorem 2.1, which is unnecessary for the proof since α(m) = m, β(n) = n, then Theorem 2.1 reduces to [[14], Theorem 3]. Furthermore, if g(m, n) ≡ 0, q = 1, p ≥ 1, then Theorem 2.1 reduces to [[13], Theorem 1].

Following a similar process as the proof of Theorem 2.1, we have the following three theorems.

Theorem 2.2. Suppose u, a, b, f, g, h, w ∈ ℘ + (Ω), and b, f, g, h, w are decreasing both in the first variable and the second variable. α : I → I is nondecreasing with α(m) ≥ m for ∀m ∈ I, while is nondecreasing with β(n) ≥ n for . p, q, r, l are defined as in Theorem 2.1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then we have

provided H(m.n) > 0, where , , are defined as in Theorem 2.1, and

Remark 3. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "b, f, g, h, w are decreasing both in the first variable and the second variable" in Theorem 2.2, which are unnecessary for the proof since α(m) = m, β(n) = n, then Theorem 2.2 reduces to [[14], Theorem 4]. Furthermore, if g(m, n) ≡ 0, q = 1, p ≥ 1, then Theorem 2.2 reduces to [[13], Theorem 2].

Theorem 2.3. Suppose u, a, b, f, g, h, w ∈ ℘ + (Ω), and b, f, g, h, w are nondecreasing both in the first variable and the second variable. α : I → I is nondecreasing with α(m) ≤ m for ∀m ∈ I, while is nondecreasing with β(n) ≤ n for . p, q, r, l are defined as in Theorem 2.1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then we have

provided H(m.n) > 0, where , , are defined as in Theorem 2.1, and

Theorem 2.4. Suppose u, a, b, f, g, h, w ∈ ℘+ (Ω), and b, f, g, h, w are decreasing in the first variable, while nondecreasing in the second variable. α : I → I is nondecreasing with α(m) ≥ m for ∀m ∈ I, while is nondecreasing with β(n) ≤ n for . p, q, r, l are defined as in Theorem 2.1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then we have

provided H(m.n) > 0, where , , are defined as in Theorem 2.1, and

Next we will study the following difference inequality:

(12)

where u, a, b, f, g, h, w ∈ ℘+(Ω) with a(m, n) not equivalent to zero, and f, g, h, w are nondecreasing in the first variable, while decreasing in the second variable, a is nondecreasing in the first variable, and b is decreasing in the second variable, α, β, p, q, r, l are defined as in Theorem 2.1.

Theorem 2.5. If for (m, n) ∈ Ω, u(m, n) satisfies (12), then we have

(13)

provided , where K > 0 is a constant, and

(14)

Proof: Denote , and v(m, n) = a(m, n) + z(m, n). Then v(m, n) is nondecreasing in the first variable, and

(15)

By Lemma 2.2 we obtain

(16)

where J(m, n) is defined in (14). Furthermore, using Lemma 2.1 we have

(17)

where , , , are defined in (14).

Obviously, , , are nondecreasing in the first variable, while decreasing in the second variable. Following in a same manner as the proof of Theorem 2.1 we obtain

(18)

Combining (16) and (18) we obtain the desired result.

Remark 4. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "f, g, h, w are nondecreasing in the first variable, while decreasing in the second variable" and "b is decreasing in the second variable" in Theorem 2.5, then Theorem 2.5 reduces to [[14], Theorem 7]. Furthermore, if g(m, n) ≡ 0, q = 1, p ≥ 1, then Theorem 2.5 reduces to [[13], Theorem 3].

Following a almost same process as the proof of Theorem 2.5, we have the following two theorems.

Theorem 2.6. Suppose u, a, b, f, g, h, w ∈ ℘+ (Ω) with a(m, n) not equivalent to zero, and f, g, h, w are decreasing both in the first variable and the second variable, a is decreasing in the first variable, and b is decreasing in the second variable, α, β are defined as in Theorem 2.2, and p, q, r l are defined as in Theorem 2.1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then we have

provided , where

Theorem 2.7. Suppose u, a, b, f, g, h, w ∈ ℘+ (Ω) with a(m, n) not equivalent to zero, and f, g, h, w are decreasing both in the first variable and the second variable, a is nondecreasing in the first variable, and b is decreasing in the second variable, α, β are defined as in Theorem 2.2, and p, q, r, l are defined as in Theorem 2.1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then we have

provided , where K > 0 is a constant, and

and , , , J(m, n) are defined as in Theorem 2.5.

Remark 5. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "f, g, h, w are decreasing both in the first variable and the second variable" and "b is decreasing in the second variable" in Theorem 2.6, then Theorem 2.6 reduces to [[14], Theorem 8]. Furthermore, if g(m, n) ≡ 0, q = 1, p ≥ 1, then Theorem 2.6 reduces to [[13], Theorem 4].

Remark 6. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "f, g, h, w are decreasing both in the first variable and the second variable" and "b is decreasing in the second variable" in Theorem 2.7, then Theorem 2.7 reduces to [[12], Theorem 2.7(q1)].

In the following, we will study the difference inequality with the following form

(19)

where u, a, b, w ∈ ℘+(Ω) with a(m, n) not equivalent to zero, and w is nondecreasing in the first variable, while decreasing in the second variable, a is nondecreasing in the first variable, and b is decreasing in the second variable, α, β are defined as in Theorem 2.1, L : Ω × ℝ+ → ℝ+ satisfies 0 ≤ L(m, n, u) - L(m, n, v) ≤ M(m, n, v)(u - v) for u ≥ v ≥ 0, where M : Ω × ℝ+ → ℝ+. p, l are defined as in Theorem 2.1 with p ≥ 1.

Theorem 2.8. If for (m, n) ∈ Ω, u(m, n) satisfies (19), then

(20)

provided that , and is nondecreasing in the first variable and decreasing in the second variable, where K > 0 is a constant, and

(21)

Proof: Denote , and v(m, n) = a(m, n) + z(m, n). Then v(m, n) is nondecreasing in the first variable, and

(22)

By Lemma 2.2 we obtain

(23)

where J(m, n) is defined in (21). Furthermore,

(24)

where , , are defined in (21).

Then following in a same manner as the proof of Theorem 2.1 we obtain

(25)

The desired inequality can be deduced by the combination of (23) and (25).

Theorem 2.9. Suppose u, a, b, w ∈ ℘+(Ω) with a(m, n) not equivalent to zero, and w is decreasing both in the first variable and the second variable, a is decreasing in the first variable, and b is decreasing in the second variable, α, β are defined as in Theorem 2.2, and L is defined as in Theorem 2.8. p, l are defined as in Theorem 2.1 with p ≥ 1. If for (m, n) ∈ Ω, u(m, n) satisfies the following inequality

then

provided that , and is decreasing both in the first variable and the second variable, where

The proof for Theorem 2.8 is similar to Theorem 2.7, and we omit it here.

Remark 7. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "w is nondecreasing in the first variable, while decreasing in the second variable", " is nondecreasing in the first variable and decreasing in the second variable", and "b is decreasing in the second variable" in Theorem 2.8, then Theorem 2.8 reduces to [[13], Theorem 5].

Remark 8. If we take Ω = ℕ0 × ℕ0, w(m, n) ≡ 0, α(m) = m, β(n) = n, and omit the conditions "w is decreasing both in the first variable and the second variable", " is decreasing both in the first variable and the second variable" and "b is decreasing in the second variable" in Theorem 2.9, then Theorem 2.9 reduces to [[13], Theorem 6].

3. Applications

In this section, we will present some applications for the established results above, and show they are useful in the study of boundedness, uniqueness, continuous dependence of solutions of certain difference equations.

Example 1. Consider the following difference equation

(26)

with the initial condition

(27)

where p ≥ 1 is an odd number, u ∈ ℘ (Ω), F 1, F 2 : Ω × ℝ → ℝ.

Theorem 3.1. Suppose u(m, n) is a solution of (26) and (27). If |f(m) + g(n) - C| ≤ σ, |F 1(m, n, u)| ≤ f 1(m, n)|u|, and |F 2(m, n, u)| ≤ f 2(m, n)|u|, where f 1, f 2 ∈ ℘+(Ω), then we have

(28)

where K > 0 is a constant, and

(29)

Proof. The equivalent form of (26) and (27) is denoted by

(30)

Then we have

(31)

We note that it is unnecessary for f 1, f 2 being nondecreasing or decreasing since α(m) = m, β(n) = n here, and a suitable application of Theorem 2.1 to (31) yields the desired result.

The following theorem deals with the uniqueness of solutions of (26) and (27).

Theorem 3.2. Suppose |F i (m, n, u) - F i (m, n, v)| ≤ f i (m, n)|u p - v p |, i = 1, 2, where f i ∈ ℘+(Ω), i = 1, 2, then (26) and (27) has at most one solution.

Proof. Suppose u 1(m, n), u 2(m, n) are two solutions of (26) and (27). Then

(32)

Treat as one variable, and a suitable application of Theorem 2.1 to (32) yields , which implies . Since p is an odd number, then we have u 1(m, n) ≡ u 2(m, n), and the proof is complete.

The following theorem deals with the continuous dependence of the solution of (26) and (27) on the functions F 1, F 2 and the initial value f (m), g(n).

Theorem 3.3. Assume , i = 1,2, where f i ∈ ℘+(Ω), i = 1, 2, , where ε > 0 is a constant, and furthermore, assume , is the solution of the following difference equation

(33)

with the initial condition

(34)

where , : Ω × ℝ → ℝ, then

(35)

provided that G(m, n) ≤ K, where

Proof. The equivalent form of (33) and (34) is denoted by

(36)

Then from (30) and (36) we have

(37)

Then a suitable application of Theorem 2.1 to (37) yields the desired result.

Example 2. Consider the following difference equation

(38)

where u, a, b ∈ ℘(Ω) with a(m, n) not equivalent to zero, p ≥ 1 is an odd number, F 1, F 2 : Ω × ℝ → ℝ.

Theorem 3.4. Suppose u(m, n) is a solution of (38). If |F 1(m, n, u)| ≤ L(m, n, u), |F 2(m, n, u)| ≤ w(m, n)|u| l, where L is defined as in Theorem 2.8, and w ∈ ℘+(Ω), l ≥ 0, p ≥ l, then we have

(39)

where

(40)

Proof. From (38) we have

(41)

Then a suitable application of Theorem 2.9 (with α(m) = m, β(n) = n) to (41) yields the desired result.

Similar to Theorems 3.2 and 3.3, we also have the following two theorems dealing with the uniqueness and continuous dependence of the solution of (38) on the functions a, b, F 1, F 2.

Theorem 3.5. Suppose |F i (m, n, u) - F i (m, n, v)| ≤ f i (m, n)|u p - v p |, i = 1, 2, where f i ∈ ℘+(Ω), i = 1, 2, then (38) has at most one solution.

Theorem 3.6. Assume , i = 1, 2, where f i ∈ ℘+(Ω), i = 1, 2, , and furthermore, assume , is the solution of the following difference equation

(42)

where , : Ω × ℝ → ℝ, then

provided that , where

and

The proof for Theorems 3.5-3.6 is similar to Theorems 3.2-3.3, in which Theorem 2.6 is used. Due to the limited space, we omit it here.

4. Conclusions

In this paper, some new finite difference inequalities in two independent variables are established, which can be used as a handy tool in the study of boundedness, uniqueness, continuous dependence on initial data of solutions of certain difference equations. The established inequalities generalize some existing results in the literature.

6. Authors'contributions

QF carried out the main part of this article. All authors read and approved the final manuscript.