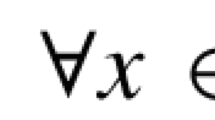Abstract
In this paper we study the existence and the multiplicity of solutions for an impulsive boundary value problem for fourth-order differential equations. The notions of classical and weak solutions are introduced. Then the existence of at least one and infinitely many nonzero solutions is proved, using the minimization, the mountain-pass, and Clarke’s theorems.
MSC: 34B15, 34B37, 58E30.
Similar content being viewed by others
1 Introduction
The theory of impulsive boundary value problems (IBVPs) became an important area of studies in recent years. IBVPs appear in mathematical models of processes with sudden changes in their states. Such processes arise in population dynamics, optimal control, pharmacology, industrial robotics, etc. For an introduction to theory of IBVPs one is referred to [1]. Some classical tools used in the study of impulsive differential equations are topological methods as fixed point theorems, monotone iterations, upper and lower solutions (see [2–4]). Recently, some authors have studied the existence of solutions of IBVPs using variational methods. The pioneering work in this direction is the paper of Nieto and O’Regan [5], where the second-order impulsive problem
(with ) is studied, using the minimization and the mountain-pass theorem. We mention also other papers for second-order impulsive equations as [6, 7]. In several recent papers [8–10], fourth-order impulsive problems are considered via variational methods.
In this paper, we consider the boundary value problem for fourth-order differential equation with impulsive effects
Here, , the limits and exist and , .
We look for solutions in the classical sense, as given in the next definition.
Definition 1 A function and , is said to be a classical solution of the problem (P), if u satisfies the equation a.e. on , the limits and exist and satisfy the impulsive conditions , , , and boundary conditions .
Moreover, we introduce, for every , the following real functions:
To deduce the existence of solutions, we assume the following conditions:
(H1) The constant a is positive, b and c are continuous functions on and there exist positive constants , , , and such that and . The functions , , , are continuous functions.
(H2) There exist such that functions , , , satisfy the conditions
A simple example of functions fulfilling the last condition is given by
where and , , are positive constants.
Note that (2) implies that there exist positive constants , such that
In the next section we will prove the following existence result for .
Theorem 2 Suppose that and conditions (H1) and (H2) hold. Then the problem (P) has at least one nonzero classical solution.
Having in mind the case , we introduce the following condition:
(H3) There exist positive constants , , such that the functions , , defined in (3), satisfy the conditions
A simple example of this new situation is given by the functions and .
The result to be proven is the following.
Theorem 3 Suppose that , the functions , , , are odd and conditions (H1) and (H3) hold. Then the problem (P) has infinitely many nonzero classical solutions.
If we consider the problem
we introduce the following condition.
(H2′) There exist and positive constants , such that functions , , and , , satisfy the conditions
A simple example now is , .
The obtained result is the following.
Theorem 4 Suppose that and conditions (H1) and (H2′) hold. If , the problem (P1) has only the zero solution. If , the problem (P1) has at least one nonzero classical solution.
The proofs of the main results are given in Section 3.
2 Preliminaries
Denote by for , the Lebesgue space of p-integrable functions over the interval , endowed with the usual norm , and by and the corresponding norms in and ,
Denote by and the Sobolev spaces
and
Let be the Hilbert space endowed with the usual scalar product
and the corresponding norm.
By assumption (H1) an equivalent scalar product and norm in X are given by
and
It is well known (see [[9], Lemma 2.2], [11]) that the following Poincaré and imbedding inequalities hold for all :
where M is a positive constant depending on T, a and .
We have the following compactness embedding, which can be proved in the standard way.
Proposition 5 The inclusion is compact.
We define the functional , as follows:
By assumption (H1), we find that is continuously differentiable and, for , the following identity holds:
In the sequel we introduce the concept of a weak solution of our problem.
Definition 6 A function is said to be a weak solution of the problem (P), if for every , the following identity holds:
As a consequence, the critical points of ϕ are the weak solutions of the problem (P). Let us see that they are, actually, strong solutions too.
Lemma 7 If u is a weak solution of (P) then is classical solution of (P).
Proof Let be a weak solution of (P), i.e. (11) holds for any . For a fixed we take a test function , such that for . We have by (11)
This means that for every
and satisfies the equation
By a standard regularity argument (see [9, 11]) the weak derivative and therefore the limits and exist.
We have for
Summing the last identities for we obtain
Therefore, by (11) and (12), we have
Now, take a test function , , such that
Then we obtain and . Similarly, we prove that , which shows that u is a classical solution of the problem (P). The lemma is proved. □
In the proofs of the theorems, we will use three critical point theorems which are the main tools to obtain weak solutions of the considered problems.
To this end, we introduce classical notations and results. Let E be a reflexive real Banach space. Recall that a functional is lower semi-continuous (resp. weakly lower semi-continuous (w.l.s.c.)) if (resp. ) in E implies (see [12], pp.3-5).
We have the following well-known minimization result.
Theorem 8 Let I be a weakly lower semi-continuous operator that has a bounded minimizing sequence on a reflexive real Banach space E. Then I has a minimum . If is a differentiable functional, is a critical point of I.
Note that a functional is w.l.s.c. on I if , is convex and continuous and is sequentially weakly continuous (i.e. in E implies ) (see [13], pp.301-303). The existence of a bounded minimizing sequence appears, when the functional I is coercive, i.e. as .
Next, recall the notion of the Palais-Smale (PS) condition, the mountain-pass theorem and Clarke’s theorem.
We say that I satisfies condition (PS) if any sequence for which is bounded and as possesses a convergent subsequence.
Theorem 9 ([[14], p.4])
Let E be a real Banach space and satisfying condition (PS). Suppose and
-
(i)
there are constants such that if ,
-
(ii)
there is an , such that .
Then I possesses a critical value . Moreover, c can be characterized as where .
Theorem 10 ([[14], p.53])
Let E be a real Banach space and with I even, bounded from below, and satisfying condition (PS). Suppose that , there is a set such that K is homeomorphic to by an odd map, and .
Then I possesses, at least, m distinct pairs of critical points.
3 Proofs of main results
This section is devoted to the proof of the three theorems enunciated in the introduction of this work.
First consider the case for which we prove that the functional ϕ satisfies the Palais-Smale condition.
Lemma 11 Suppose that and conditions (H1) and (H2) hold. Then the functional satisfies condition (PS).
Proof Let and be such that
Then we have
and
for all sufficiently large k, . Taking in (15), we have for
In particular,
Adding the last inequality with (14), by assumption (H2), we obtain
which implies that is a bounded sequence in X.
Then, by the compact inclusion , it follows that, up to a subsequence, weakly in X and strongly in . As a consequence, from the inequality
it follows that
and
Then by (16) it follows that
i.e., strongly in X, which completes the proof. □
Now, we are in a position to prove the main results of this paper.
Proof of Theorem 2 We find by (H1) and (8) that the following inequalities are valid for every :
It is evident that this last expression is strictly positive when , with ρ small enough. Next, let and , with . Then, by (H2) and (3), we have
where .
Since , we conclude that for sufficiently large λ. According to the mountain-pass Theorem 9, together with Lemmas 11 and 7, we deduce that there exists a nonzero classical solution of the problem (P). □
Now consider the case . In the next result we prove that the Palais-Smale condition is also valid.
Lemma 12 Suppose that and conditions (H1) and (H3) hold. Then the functional is bounded from below and satisfies condition (PS).
Proof By , conditions (H1), (H3), and inequality (8), it follows that the functional ϕ is bounded from below:
Further, if is a (PS) sequence, by (17) it follows that is a bounded sequence in X. Then, as in Lemma 11, we conclude that has a convergent subsequence. □
Now we are in a position to prove the next existence result for the problem (P).
Proof of Theorem 3 By assumption, we know that and are odd functions. So are are even functions and the functional ϕ is even. By Lemma 12 we know that ϕ is bounded from below and satisfies condition (PS). Let , be a natural number and define, for any fixed, the set
is homeomorphic to by the odd mapping defined as
Moreover, for , the following inequalities hold:
Clearly is a subset of the m-dimensional subspace
and there exist positive constants and , such that
where is the induced norm of on .
Arguing as in [[15], pp.16-18], one can prove that there exists , such that
Denote
By (H3) we see that for every , , the following inequalities are fulfilled:
and
Denote . Then by (18)-(21) we have
where .
By the last inequality, it follows that if . Then, by (18), choosing
we obtain for any .
By Clarke’s Theorem 10, there exist at least m pairs of different critical points of the functional ϕ. Since m is arbitrary, there exist infinitely many solutions of the problem (P), which concludes the proof. □
Concerning the problem (P1), one can introduce similarly the notions of classical and weak solutions. In this case it is not difficult to verify that the weak solutions are critical points of the functional defined as
Proof of Theorem 4 By the Poincaré inequalities (7) we find that is an equivalent norm to in X and the functional is convex.
Since the functional
is sequentially weakly continuous, from the fact that the inclusion is compact, we deduce that the functional is weakly lower semi-continuous.
Next, let us see that is bounded from below:
where
Then, by Theorem 8, there exists a minimizer of , which is a critical point of .
Let u be a weak solution of (P1), i.e., a critical point of . Then
If then . Suppose that u is a nonzero solution and . By (H2′), (7), and (24) it follows that
which is a contradiction. Then, for , the problem (P1) has only the zero solution.
Suppose now that .
Take , . Then
where . For it follows that . Then, since , by (25) it follows that for sufficiently small . In consequence we show that . So we ensure the existence of a nonzero minimizer of , which completes the proof of Theorem 4. □
References
Samoilenko AM, Perestyuk NA: Impulsive Differential Equations. World Scientific, Singapore; 1995.
Agarwal RP, O’Regan D: Multiple nonnegative solutions for second order impulsive differential equations. Appl. Math. Comput. 2000, 114: 51-59. 10.1016/S0096-3003(99)00074-0
Georgescu P, Moroşanu G: Pest regulation by means of impulsive controls. Appl. Math. Comput. 2007, 190: 790-803. 10.1016/j.amc.2007.01.079
Franco D, Nieto JJ: Maximum principle for periodic impulsive first order problems. J. Comput. Appl. Math. 1998, 88: 149-159. 10.1016/S0377-0427(97)00212-4
Nieto J, O’Regan D: Variational approach to impulsive differential equations. Nonlinear Anal., Real World Appl. 2009, 10: 680-690. 10.1016/j.nonrwa.2007.10.022
Bonanno G, Di Bella B, Henderson J: Existence of solutions to second-order boundary-value problems with small perturbations of impulses. Electron. J. Differ. Equ. 2013., 2013: Article ID 126
Xiao J, Nieto JJ: Variational approach to some damped Dirichlet nonlinear impulsive differential equations. J. Franklin Inst. 2011, 348: 369-377. 10.1016/j.jfranklin.2010.12.003
Afrouzi G, Hadjian A, Radulescu V: Variational approach to fourth-order impulsive differential equations with two control parameters. Results Math. 2013. 10.1007/s00025-013-0351-5
Sun J, Chen H, Yang L: Variational methods to fourth-order impulsive differential equations. J. Appl. Math. Comput. 2011, 35: 323-340. 10.1007/s12190-009-0359-x
Xie J, Luo Z: Solutions to a boundary value problem of a fourth-order impulsive differential equation. Bound. Value Probl. 2013., 2013: Article ID 154. http://www.boundaryvalueproblems.com/content/2013/1/154
Tersian S, Chaparova J: Periodic and homoclinic solutions of extended Fisher-Kolmogorov equations. J. Math. Anal. Appl. 2001, 260: 490-506. 10.1006/jmaa.2001.7470
Mawhin J, Willem M: Critical Point Theory and Hamiltonian Systems. Springer, New York; 1989.
Berger M: Nonlinearity and Functional Analysis. Academic Press, New York; 1977.
Rabinowitz P CBMS Reg. Conf. 65. In Minimax Methods in Critical Point Theory with Applications to Differential Equations. Am. Math. Soc., Providence; 1986.
Chen J, Tang XH: Existence and multiplicity of solutions for some fractional boundary value problem via critical point theory. Abstr. Appl. Anal. 2012., 2012: Article ID 648635 10.1155/2012/648-635
Acknowledgements
The authors are thankful to the anonymous referees for the careful reading of the manuscript and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cabada, A., Tersian, S. Existence and multiplicity of solutions to boundary value problems for fourth-order impulsive differential equations. Bound Value Probl 2014, 105 (2014). https://doi.org/10.1186/1687-2770-2014-105
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2014-105