Abstract
By constructing a suitable Lyapunov functional and using some inequalities, we investigate the existence, uniqueness and global exponential stability of periodic solutions for a class of generalized cellular neural networks with impulses and time-varying delays. Finally, an illustrative example and simulations are given to show the effectiveness of the main results.
Similar content being viewed by others
1 Introduction
The dynamics of cellular neural networks has been deeply investigated due to its applicability in solving image processing, signal processing and pattern recognition problems [1, 2]. Recently, the study of the existence and exponential stability of periodic solutions for neural networks has received much attention and many known results have been obtained [3–27]. For example, authors [11] considered the following neural networks with delays:
when , are constants, a set of easily verifiable sufficient conditions guaranteeing the existence and globally exponential stability of one periodic solution was derived.
However, in practice, impulsive effects are inevitably encountered in implementation of networks, which can also be found in information science, electronics, automatic control systems and so on (see [12, 13, 17–19, 21, 22, 24–27]). Thus it is necessary to study the impulsive case of system (1).
Motivated by the discussion, in this paper, by employing some inequalities and constructing a suitable Lyapunov functional, we aim to investigate the existence and exponential stability of a periodic solution for a class of nonautonomous neural networks with impulses and time-varying delays as follows:
where , n corresponds to the number of units in the neural networks. corresponds to the state variable at time t, is the activation of the neurons. is the external bias at time t. , corresponds to the transmission delay respectively, , , , . The fixed moments of time satisfy , . , and exists. represents impulsive perturbations of the i th unit at , .
By appropriately choosing coefficients, system (2) contains many models as its special cases, which were studied in [6, 8, 12, 24, 25, 27] respectively.
Throughout this paper, for , , , , , , , , , are all continuous ω-periodic functions and . Further, we suppose that:
(H1) There exist positive constants and such that
(H2) There exists a constant such that for .
(H3) There exists a positive integer q such that , .
For convenience, we introduce the following notations:
This paper is organized as follows. In Section 2, preliminaries are introduced. In Section 3, by constructing a suitable Lyapunov functional, the criteria ensuring global exponential stability of a periodic solution for system (2) are established. In Section 4, an example and simulations are shown to illustrate the validity of the main results. Finally, we conclude this paper with a brief discussion in Section 5.
2 Preliminaries
Firstly, we introduce some definitions and lemmas. Let be the space of n-dimensional real column vectors, and PC = { is continuous for , , exists for , }.
A function is called a solution of (2) with the initial condition given by
if satisfies (2) and (3), where . We denote a solution through ϕ by or , for all , . Obviously, any solution of (2) is continuous at and right-hand continuous at , . In addition, we define , where and is a constant.
Definition 1 System (2) is said to be globally exponentially stable if for any two solutions and , there exist some constants and such that
for all .
Definition 2 Let be a continuous function, then the Dini right derivative of is defined as
From Definition 2, we can easily obtain the following lemma.
Lemma 1 [12]
Let be a continuous function on R. If is differentiable at , then
Next, we introduce two important inequalities which play a key role in obtaining the main results.
Lemma 2 (Beckenbach and Bellman) [12, 28]
For , , , the following inequality holds:
where are some constants and , .
Lemma 3 (Halanay inequality) [12, 24]
Assume that p, q are constants satisfying . is a continuous nonnegative function on satisfying for all , where . Then, for all , we have
where λ is the unique positive root of the equation .
3 Main results
In this section, we construct a suitable Lyapunov functional to study the existence and global exponential stability of periodic solutions of system (2).
Theorem 1 Suppose that (H1)-(H3) hold. Further,
(H4) There exist , , , , , and (, ) such that , , where
(H5) There is such that , , , λ is the unique positive solution of the equation .
Then system (2) has a unique ω-periodic solution which is globally exponentially stable.
Proof Let and be two solutions of (2) through ϕ and ψ, respectively, where , then we have
Let . Consider the following Lyapunov functional:
Calculating the Dini upper right derivative of along the solution of (2) at a continuous point and applying Lemma 2, we have
For any , by (H4) and Lemma 3, we have
i.e.,
Also, it follows from (H2) that
Therefore, from (6) and (7), for any , we have
Similar to (6), for all , we can derive that
Again by (H2), then
Thus, for any ,
By mathematical induction, for all , we have
According to (H5), for all , hence
Therefore,
i.e.,
where , . This implies that system (2) is globally exponentially stable.
Next, we prove the existence of a periodic solution of (2). Define a Poincáre mapping as follows:
By the periodicity of (2), we can derive that for any integer . From the above conclusion, we can choose a positive integer m such that . According to the periodicity of and , we have
Then operator is a construction mapping in . Obviously, is a Banach space. By virtue of the Banach fixed point theorem, has a unique fixed point . On the other hand, , then is also a fixed point of . By the uniqueness of fixed point, we obtain that . Therefore, system (2) has a unique ω-periodic solution which is globally exponentially stable. The proof is complete. □
If there is no impulse, system (2) reduces to (1) studied in [11]. From the proof of Theorem 1, we have the following corollary.
Corollary 1 Suppose that (H1)-(H4) hold. Then system (1) has a unique ω-periodic solution which is globally exponentially stable.
Remark 1 In [11], by using the Mawhin continuation theorem and constructing Lyapunov functionals, the authors studied the existence and stability of system (1), where the delays are constant. However, in this paper, for time-varying delays, by employing many different analysis techniques from [11], we establish the criteria ensuring the existence and exponential stability of a periodic solution of (1). Furthermore, if we take , , , , , then condition (H4) is transformed into (H4)′ as follows:
which is just the corresponding condition in [11]. One can derive the same results as [11]. That is, the criteria in [11] are the special case of Theorem 1. Therefore, we extend and improve the earlier results in this sense.
If , then system (2) is transformed into the following model studied in [12].
Using a similar proof as above, one can obtain the main result of [12]. It is omitted here.
If , then (2) is transformed into the following model:
Similarly, we can obtain the sufficient conditions of the existence and exponential stability of a periodic solution to system (10), we omit it.
If one takes , , , , , then (H4) is reduced to
The following corollary can be derived.
Corollary 2 Suppose that (H1)-(H3), (H4)∗, (H5) hold, then system (10) has a unique exponentially stable ω-periodic solution.
Remark 2 Corollary 2 is just the result of [27]. In [27], the impulses are required to be linear functions. However, without the above restrictions, we also establish the criteria ensuring the existence of an ω-periodic solution which is exponentially stable. Thus we extend and generalize the earlier results.
In addition, if , (2) reduces to the model studied in [8]. Similar results can be derived. In [8], the delay functions are required to be differential, but we do not need the restriction here.
On the other hand, in real world, by appropriately choosing parameters r, m, , , , , , one can see that many known assumptions can be included as special cases of (H4), hence the discussion is interesting and valuable.
4 An illustrative example and simulations
In this section, we give an example and simulations to show the validity of the main results.
Example Let
where
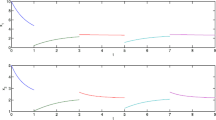
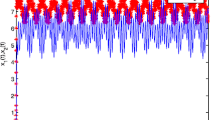
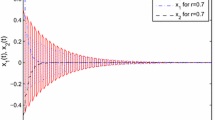
Take , , , . It is easy to verify that conditions of Theorem (1) hold. Therefore, by Theorem 1, system (11) has a unique π-periodic solution, which is globally exponentially stable. By numerical analysis, the conclusion can be showed clearly, see Figure 1.
5 Conclusion
In this paper, by using the Halanay inequality and constructing Lyapunov functions, we address the existence and exponential stability of periodic solutions for a class of generalized cellular neural networks with impulses and time-varying delays. Easily verifiable sufficient conditions are obtained. The main results extend and improve some previously known results [8, 11, 12, 27]. The criteria possess many adjustable parameters which provide flexibility for the design and analysis of a dynamical system. It is interesting and valuable.
References
Chua LO, Yang L: Cellular neural networks: theory and applications. IEEE Trans. Circuits Syst. 1988, 35: 1257-1290.
Venetianlr PL, Roska T: Image compression by cellular networks. IEEE Trans. Circuits Syst. I 1998, 45: 205-215.
Sun CY, Feng CB: Exponential periodicity and stability of delayed neural networks. Math. Comput. Simul. 2004, 66: 469-478.
Xu BJ, Liu XZ, Liao XX: Global exponential stability of high order Hopfield type neural networks. Appl. Math. Comput. 2006, 174: 98-116.
Xu BJ, Liu XZ, Liao XX: Global asymptotic stability of high-order Hopfield type neural networks with time delays. Comput. Math. Appl. 2003, 45: 1729-1737.
Cao JD: New results concerning exponential stability and periodic solutions of delayed cellular neural networks. Phys. Lett. A 2003, 307: 136-147.
Cao JD, Wang J: Absolute exponential stability of recurrent neural networks with Lipschitz-continuous activation functions and time delays. Neural Netw. 2004, 17: 379-390.
Jiang HJ, Cao JD: Global exponential stability of periodic neural networks with time-varying delays. Neurocomputing 2006, 70: 343-350.
Jiang HJ, Teng ZD: Global exponential stability of cellular neural networks with time-varying coefficient and delays. Neural Netw. 2004, 17: 1415-1425.
Jiang HJ, Li ZM, Teng ZD: Boundedness and stability for nonautonomous cellular neural networks with delay. Phys. Lett. A 2003, 306: 313-325.
Xiang H, Yan KM, Wang BY: Existence and global exponential stability of periodic solution for delayed high-order Hopfield-type neural networks. Phys. Lett. A 2006, 352: 341-349.
Gu HB, Jiang HJ, Teng ZD: Stability and periodicity in high-order neural networks with impulsive effects. Nonlinear Anal. 2007. 10.1016/j.na.2007.03.024
Wang H, Liao XF, Li CD: Existence and exponential stability of periodic solution of BAM neural networks with impulse and time-varying delay. Chaos Solitons Fractals 2007, 33: 1028-1039.
Zhao HY, Wang GL: Delay-independent exponential stability of recurrent neural networks. Phys. Lett. A 2004, 333: 399-407.
Huang LH, Huang CX, Liu BW: Dynamics of a class of cellular neural networks with time-varying delays. Phys. Lett. A 2005, 345: 330-344.
Zhou J, Liu Z, Chen G: Dynamics of periodic delayed neural networks. Neural Netw. 2004, 17: 87-101.
Shao YF: Exponential stability of periodic neural networks with impulsive effects and time-varying delays. Appl. Math. Comput. 2011, 217: 6893-6899.
Li YK, Hua YC, Fei Y: Global exponential stability of delayed Cohen-Grossberg BAM neural networks with impulses on time scales. J. Inequal. Appl. 2009. 10.1155/2009/491268
Yang XF, Liao XF, Evans DJ, Tang YY: Existence and stability of periodic solution in impulsive Hopfield neural networks with finite distributed delays. Phys. Lett. A 2005, 343: 108-116.
Liao XF, Liu Q, Zhang W: Delay-dependent asymptotic stability for neural networks with distributed delays. Nonlinear Anal., Real World Appl. 2006, 7: 1178-1192.
Li YK: Global exponential stability of BAM neural networks with delays and impulses. Chaos Solitons Fractals 2005, 24: 279-285.
Li YK, Xing WY, Lu LH: Existence and global exponential stability of periodic solution of a class of neural networks with impulses. Chaos Solitons Fractals 2006, 27: 437-445.
Li YK, Liu P: Existence and stability of positive periodic solution for BAM neural networks with delays. Math. Comput. Model. 2004, 40: 757-770.
Yang YQ, Cao JD: Stability and periodicity in delayed cellular neural networks with impulsive effects. Nonlinear Anal., Real World Appl. 2007, 8: 362-374.
Gui ZJ, Ge WG: Periodic solutions of nonautonomous cellular neural networks with impulses. Chaos Solitons Fractals 2007, 32: 1760-1771.
Shao YF, Dai BX: The existence of exponential periodic attractor of impulsive BAM neural network with time-varying coefficients and distributed delays. Neurocomputing 2010, 73: 3123-3131.
Gui ZJ, Ge WG: Existence and uniqueness of periodic solutions of nonautonomous cellular neural networks with impulses. Phys. Lett. A 2006, 354: 84-94.
Beckenbach EF, Bellman R: Inequalities. Springer, Berlin; 1965.
Acknowledgements
This paper is supported by National Natural Science Foundation of P.R. China (11161015, 11361012, 11161011), Natural Science Foundation of Guangxi (2013GXNSFAA019003, 2013GXNSFDA019001), and partially supported by National High Technology Research and Development Program 863 of P.R. China.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Shao, Y., Zhang, Q. Stability and periodicity for impulsive neural networks with delays. Adv Differ Equ 2013, 352 (2013). https://doi.org/10.1186/1687-1847-2013-352
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-352