1 Introduction

During the past decades, high-order cellular neural networks (HCNNs) have been extensively investigated due to their immense potential of application perspective in various fields such as signal and image processing, pattern recognition, optimization, and many other subjects. Many results on the problem of global stability of equilibrium points and periodic solutions of HCNNs have been reported (see [1–9]). In applied sciences, the existence of anti-periodic solutions plays a key role in characterizing the behavior of nonlinear differential equations [10–13]. In recent years, there have been some papers which deal with the problem of existence and stability of anti-periodic solutions. For example, Gong [14] investigated the existence and exponential stability of anti-periodic solutions for a class of Cohen-Grossberg neural networks; Peng and Huang [15] studied the anti-periodic solutions for shunting inhibitory cellular neural networks with continuously distributed delays, Zhang [16] focused on the existence and exponential stability of anti-periodic solutions for HCNNs with time-varying leakage delays. For details, we refer readers to [15, 17–35]. We know that many evolutionary processes exhibit impulsive effects [33, 36–43]. Thus, it is worthwhile to investigate the existence and stability of anti-periodic solutions for HCNNs with impulses. To the best of our knowledge, very few scholars have considered the problem of anti-periodic solutions for such impulsive systems. In this paper, we study the anti-periodic solution of the following high-order cellular neural network with mixed delays and impulses modeled by

$$ \left \{ \textstyle\begin{array}{l} \dot{x}_{i}(t)=-b_{i}(t)x_{i}(t)+\sum_{j=1}^{n}c_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t)))\\ \hphantom{\dot{x}_{i}(t)=}{}+\sum_{j=1}^{n}d_{ij}(t)\int_{0}^{\sigma}k_{ij}(s)g_{j}(x_{j}(t-s))\,ds\\ \hphantom{\dot{x}_{i}(t)=}{} +\sum_{j=1}^{n}\sum_{l=1}^{n}e_{ijl}(t)g_{j}(x_{j}(t-\alpha_{jl}(t)))g_{l}(x_{l}(t-\beta _{jl}(t)))+I_{i}(t),\quad t\neq{t_{k}},\\ {x_{i}}(t_{k}^{+})=(1+\gamma_{ik})x_{i}(t_{k}),\quad k=1,2,\dots, \end{array} \right .$$
(1.1)

where \(i=1, 2, \dots, n\), \(x_{i}(t)\) denotes the state of the ith unit, \(b_{i}(t)>0\) denotes the passive decay, \(c_{ij}\), \(d_{ij}\), \(e_{ijl}\) are the synaptic connections strengths, \(\tau_{ij}(t)\geq0\), \(\alpha_{jl}(t)\geq0\) and \(\beta_{jl}(t)\geq0\) correspond to the delays, \(I_{i}(t)\) stands for the external inputs, \(g_{j}\) is the activation function of signal transmission, the delay kernels \(k_{ij}\) is a real-valued negative continuous function defined on \(R^{+}:=[0,\infty)\), \(t_{k}\) is the impulsive moment, and \(\gamma_{ik}\) characterizes the impulsive jump at time \(t_{k}\) for the ith unit.

For convenience, we introduce some notations as follows.

$$\begin{aligned}& \overline{c}_{ij}=\sup_{t\in{R}}\bigl|c_{ij}(t)\bigr|, \qquad \overline{d}_{ij}=\sup_{t\in{R}}\bigl|d_{ij}(t)\bigr|, \qquad\overline{e}_{ijl}=\sup_{t\in{R}}\bigl|e_{ijl}(t)\bigr|, \qquad\overline{I}_{i}=\sup_{t\in{R}}\bigl|I_{i}(t)\bigr|, \\& \underline{b}_{i}=\inf_{t\in{R}}\bigl|b_{i}(t)\bigr|,\qquad \tau=\sup_{t\in{R}}\max_{1\leq {i,j,l}\leq{n}}\bigl\{ \tau_{ij}(t),\alpha_{jl}(t),\beta_{jl}(t),\sigma \bigr\} . \end{aligned}$$

Throughout this paper, we assume that

(H1) For \(i,j,l=1,2,\dots,n\), \(b_{i}, c_{ij}, d_{ij}, e_{ijl}, I_{i}(t), g_{j}: R\rightarrow{R}\), \(k_{ij}: R^{+}\rightarrow{R^{+}}\), \(\alpha_{jl},\beta_{jl}: R\rightarrow{R^{+}}\) are continuous functions, and there exists a constant \(T>0\) such that

$$\begin{aligned}& b_{i}(t+T)=b_{i}(t),\qquad I_{i}(t+T)=-I_{i}(t), \qquad\tau_{ij}(t+T)=\tau_{ij}(t),\qquad \alpha _{jl}(t+T)=\alpha_{jl}(t), \\& c_{ij}(t+T)g_{j}(u)=-c_{ij}(t)g_{j}(-u), \qquad d_{ij}(t+T)g_{j}(u)=-d_{ij}(t)g_{j}(-u), \\& \beta_{jl}(t+T)=\beta _{jl}(t),\qquad e_{ijl}(t+T)g_{j}(u)g_{l}(u)=-e_{ijl}(t)g_{j}(-u)g_{l}(-u). \end{aligned}$$

(H2) The sequence of times \(\{t_{k}\}\) (\(k\in{N}\)) satisfies \(t_{k}< t_{k+1}\) and \(\lim_{k\rightarrow{+\infty}}t_{k}=+\infty\), and \(\gamma_{ik}\) satisfies \(-2\leq\gamma_{ik}\leq0\) for \(i\in\{1,2,\dots,n\}\) and \(k\in{N}\).

(H3) There exists \(q\in{N}\) such that \(\gamma_{i(k+q)}=\gamma_{ik}\), \(t_{k+q}=t_{k}+T\), \(k\in{N}\).

(H4) For each \(j\in\{1,2,\dots,n\}\), the activation function \(g_{j}: R\rightarrow{R}\) is continuous, and there exist nonnegative constants \(L_{g}^{j}\) and \(M_{g}\) such that, for all \(u,v\in{R}\),

$$g_{j}(0)=0,\qquad \bigl|g_{j}(u)\bigr|\leq{M_{g}},\qquad \bigl|g_{j}(u)-g_{j}(v)\bigr|\leq{L_{g}^{j}}|u-v| \quad\mbox{for all } u,v\in{R}. $$

(H5) There exist constants \(\eta>0\), \(\lambda>0\), \(i=1, 2, \dots, n\), such that

$$\begin{aligned}& (\lambda-\underline{b}_{i})+\sum_{j=1}^{n} \overline {c}_{ij}L_{g}^{j}e^{\lambda\tau}+\sum _{j=1}^{n}|\overline{d}_{ij}|\int _{0}^{\sigma}\bigl|k_{ij}(s)\bigr|L_{g}^{j}e^{\lambda{s}} \,ds \\& \quad{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl} \bigl(M_{g}L_{g}^{l}e^{\lambda \tau}+M_{g}L_{g}^{j}e^{\lambda\tau} \bigr)< -\eta< 0. \end{aligned}$$

(H6) For \(i=1,2,\ldots,n\), the following condition holds:

$$\left \{ \textstyle\begin{array}{@{}l} -b_{i}+\sum_{j=1}^{n}\bar{c}_{ij}L_{g}^{j}+\sum_{j=1}^{n}L_{g}^{j}\bar {d}_{ij}\int_{0}^{\sigma}|k_{ij}(s)|\,ds< 0,\\ (-b_{i}+\sum_{j=1}^{n}\bar{c}_{ij}L_{g}^{j}+\sum_{j=1}^{n}L_{g}^{j}\bar {d}_{ij}\int_{0}^{\sigma}|k_{ij}(s)|\,ds )^{2}-4\bar{I}_{i}\sum_{j=1}^{n}\sum_{l=1}^{n}\bar{e}_{ijl}L_{g}^{j}L_{g}^{l}>0. \end{array} \right . $$

Let \(x=(x_{1},x_{2},\dots,x_{n})^{T}\in{R^{n}}\), in which `T’ denotes the transposition. We define \(|x|=(|x_{1}|,|x_{2}|,\dots,|x_{n}|)^{T}\) and \(\|x\|=\max_{1\leq{i}\leq{n}}|x_{i}|\). Obviously, the solution \(x(t)=(x_{1}(t),x_{2}(t), \dots,x_{n}(t))^{T}\) of (1.1) has components \(x_{i}(t)\) piece-wise continuous on \((-\tau,+\infty)\), \(x(t)\) is differentiable on the open intervals \((t_{k-1},t_{k})\) and \(x(t_{k}^{+})\) exists.

Definition 1.1

Let \(u(t):R\rightarrow{R}\) be a piece-wise continuous function having a countable number of discontinuous \(\{t_{k}\}|_{k=1}^{+\infty}\) of the first kind. It is said to be T-anti-periodic on R if

$$\left \{ \begin{array}{@{}l} u(t+T)=-u(t), \quad t\neq{t_{k}},\\ u((t_{k}+T)^{+})=-u(t_{k}^{+}), \quad k=1,2,\dots. \end{array} \right . $$

Definition 1.2

Let \(x^{*}(t)= (x^{*}_{1}(t), x^{*}_{2}(t),\dots, x^{*}_{n}(t) )^{T} \) be an anti-periodic solution of (1.1) with initial value \(\varphi^{*}=(\varphi^{*}_{1}(t), \varphi^{*}_{2}(t), \dots, \varphi^{*}_{n}(t))^{T} \). If there exist constants \(\lambda>0\) and \(M >1\) such that for every solution \(x(t)=(x_{1}(t), x_{2}(t),\dots,x_{n}(t))^{T} \) of (1.1) with an initial value \(\varphi=(\varphi_{1}(t), \varphi_{2}(t), \dots, \varphi_{n}(t))^{T}\),

$$\bigl|x_{i}(t)-x^{*}_{i}(t)\bigr|\leq M \bigl\| \varphi- \varphi^{*}\bigr\| e^{-\lambda t} \quad\mbox{for all } t>0, i=1, 2, \dots, n, $$

where

$$\bigl\| \varphi-\varphi^{*}\bigr\| =\sup_{-\tau\leq s\leq0} \max _{1\leq i\leq n}\bigl|\varphi_{i}(s)-\varphi_{i}^{*}(s)\bigr|. $$

Then \(x^{*}(t)\) is said to be globally exponentially stable.

The purpose of this paper is to present sufficient conditions of existence and exponential stability of anti-periodic solution of system (1.1). Not only can our results be applied directly to many concrete examples of cellular neural networks, but they also extend, to a certain extent, the results in some previously known ones. In addition, an example with its numerical simulations is presented to illustrate the effectiveness of our main results.

The rest of this paper is organized as follows. In the next section, we give some preliminary results. In Section 3, we derive the existence of T-anti-periodic solution, which is globally exponential stable. In Section 4, we present an example to illustrate the effectiveness of our main results.

2 Preliminary results

In this section, we present two important lemmas which are used to prove our main results in Section 3.

Lemma 2.1

Let (H1)-(H6) hold. Suppose that \({x}(t)= ({x}_{1}(t), {x}_{2}(t),\dots, {x}_{n}(t))^{T} \) is a solution of (1.1) with initial conditions

$$ {x}_{i}(s)={\varphi}_{i}(s), \quad\bigl|{ \varphi}_{i}(s)\bigr|< \delta, s\in[-\tau,0], i=1,2,\dots,n. $$
(2.1)

Then

$$ \bigl|{x}_{i}(t)\bigr|< \delta\quad \textit{and}\quad \bigl|{x}_{i} \bigl(t_{k}^{+}\bigr)\bigr|< \delta\quad \textit{for all } t\geq0, i=1,2, \dots,n, $$
(2.2)

where δ satisfies

$$\begin{aligned} -\underline{b}_{i}\delta+\sum _{j=1}^{n}\overline {c}_{ij}L_{g}^{j} \delta+\sum_{j=1}^{n}L_{g}^{j} \overline{d}_{ij}\delta\int_{0}^{\sigma}\bigl|k_{ij}(s)\bigr| \,ds+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl}L_{g}^{j}L_{g}^{l} \delta ^{2}+\overline{I}_{i}< 0. \end{aligned}$$
(2.3)

Proof

For any given initial condition, hypothesis (H4) guarantees the existence and uniqueness of \(x(t)\), the solution to (1.1) in \([-\tau, +\infty)\). Consider the following polynomial \(ax^{2}+bx+c\), where a, b, c are all real numbers. If \(a<0\) and \(b^{2}-4ac<0\), then \(ax^{2}+bx+c>0\). In view of (H6), we know that there exists a positive constant δ which satisfies (2.3). By way of contradiction, we assume that (2.2) does not hold. Notice that \({x}_{i}(t_{k}^{+})=(1+\gamma_{ik}){x}_{i}(t_{k})\) and by assumption (H2), \(-2\leq\gamma_{ik}\leq0\), then \(|{x}_{i}(t_{k}^{+})|=|(1+\gamma_{ik})||{x}_{i}(t_{k})|\leq|{x}_{i}(t_{k})|\). Then, if \(|{x}_{i}(t_{k}^{+})|\geq\delta\), then \(|{x}_{i}(t_{k})|\geq\delta\). Thus we may assume that there must exist \(i\in\{1,2,\dots,n \}\) and \(\widetilde{t}\in(t_{k},t_{k+1}]\) such that

$$ \bigl|{x}_{i}(\widetilde{t})\bigr| =\delta \quad\mbox{and}\quad \bigl|{x}_{j}(\widetilde{t})\bigr| < \delta \quad\mbox{for all } t\in(-\tau, \widetilde{t}), j=1,2,\dots,n. $$
(2.4)

By directly computing the upper left derivative of \(|{x}_{i}(t)|\), together with assumptions (2.3), (H4) and (2.4), we deduce that

$$\begin{aligned} 0 \leq& D^{+}\bigl(\bigl|{x}_{i}(\widetilde{t})\bigr|\bigr) \\ \leq& -b_{i}(t)\bigl|x_{i}(\widetilde{t})\bigr|+ \Biggl|\sum _{j=1}^{n}c_{ij}(\widetilde {t})g_{j}\bigl(x_{j}\bigl(\widetilde{t}-\tau_{ij}( \widetilde{t})\bigr)\bigr)+\sum_{j=1}^{n}d_{ij}( \widetilde{t})\int_{0}^{\sigma}k_{ij}(s)g_{j} \bigl(x_{j}(\widetilde {t}-s)\bigr)\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}e_{ijl}(\widetilde{t})g_{j} \bigl(x_{j}\bigl(\widetilde {t}-\alpha_{jl}(\widetilde{t}) \bigr)\bigr)g_{l}\bigl(x_{l}\bigl(\widetilde{t}-\beta _{jl}(\widetilde{t})\bigr)\bigr)+I_{i}(\widetilde{t}) \Biggr| \\ \leq& -b_{i}(t)\bigl|x_{i}(\widetilde{t})\bigr|+\sum _{j=1}^{n}\bigl|c_{ij}(\widetilde {t})\bigr|\bigl|g_{j}\bigl(x_{j}\bigl(\widetilde{t}- \tau_{ij}(\widetilde{t})\bigr)\bigr)\bigr|+\sum_{j=1}^{n}\bigl|d_{ij}( \widetilde{t})\bigr|\int_{0}^{\sigma }\bigl|k_{ij}(s)\bigr|\bigl|g_{j} \bigl(x_{j}(\widetilde{t}-s)\bigr)\bigr|\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(\widetilde{t})\bigr|\bigl|g_{j} \bigl(x_{j}\bigl(\widetilde {t}-\alpha_{jl}(\widetilde{t}) \bigr)\bigr)\bigr|\bigl|g_{l}\bigl(x_{l}\bigl(\widetilde{t}-\beta _{jl}(\widetilde{t})\bigr)\bigr)\bigr|+\bigl|I_{i}(\widetilde{t})\bigr| \\ \leq& -b_{i}(t)\bigl|x_{i}(\widetilde{t})\bigr|+\sum _{j=1}^{n}\overline {c}_{ij}L_{g}^{j}\bigl|x_{j} \bigl(\widetilde{t}-\tau_{ij}(\widetilde{t})\bigr)\bigr|+\sum _{j=1}^{n}L_{g}^{j} \overline{d}_{ij}\int_{0}^{\sigma}\bigl|k_{ij}(s)\bigr|\bigl|x_{j}( \widetilde {t}-s)\bigr|\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl}L_{g}^{j}L_{g}^{l}\bigl|x_{j} \bigl(\widetilde {t}-\alpha_{jl}(\widetilde{t})\bigr)\bigr|\bigl|x_{l} \bigl(\widetilde{t}-\beta_{jl}(\widetilde {t})\bigr)\bigr|+ \overline{I}_{i} \\ \leq& -\underline{b}_{i}\delta+\sum_{j=1}^{n} \overline{c}_{ij}L_{g}^{j}\delta+\sum _{j=1}^{n}L_{g}^{j} \overline{d}_{ij}\delta\int_{0}^{\sigma }\bigl|k_{ij}(s)\bigr|\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl}L_{g}^{j}L_{g}^{l} \delta ^{2}+\overline{I}_{i}< 0, \end{aligned}$$
(2.5)

which is a contradiction and implies that (2.2) holds. This completes the proof. □

Lemma 2.2

Suppose that (H1)-(H6) hold. Let \(x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\dots, x^{*}_{n}(t))^{T} \) be the solution of (1.1) with initial value \(\varphi^{*}=(\varphi^{*}_{1}(t), \varphi^{*}_{2}(t), \dots, \varphi^{*}_{n}(t))^{T} \), and \(x(t)=(x_{1}(t), x_{2}(t), \dots,x_{n}(t))^{T} \) be the solution of (1.1) with initial value \(\varphi=(\varphi_{1}(t), \varphi_{2}(t), \dots, \varphi _{n}(t))^{T}\). Then there exist constants \(\lambda>0\) and \(M>1\) such that

$$\bigl|x_{i}(t)-x^{*}_{i}(t)\bigr|\leq M \bigl\| \varphi- \varphi^{*}\bigr\| e^{-\lambda t}\quad\textit{for all } t>0, i=1, 2, \dots, n. $$

Proof

Let \(y(t)=\{y_{ j}(t) \}=\{x_{ j}(t)-x^{\ast}_{ j}(t) \}=x(t)-x^{*}(t)\). Then

$$\begin{aligned}& \begin{aligned}[b] y_{i}^{\prime}(t) ={}& {-}b_{i}(t) \bigl[x_{i}(t)-x_{i}^{*}(t)\bigr]+\sum _{j=1}^{n}c_{ij}(t)\bigl[g_{j} \bigl(x_{j}\bigl(t-\tau_{ij}(t)\bigr)\bigr)-g_{j} \bigl(x_{j}^{*}\bigl(t-\tau _{ij}(t)\bigr)\bigr)\bigr]\\ &{}+\sum_{j=1}^{n}d_{ij}(t)\int _{0}^{\sigma }k_{ij}(s)\bigl[g_{j} \bigl(x_{j}(t-s)\bigr)-g_{j}\bigl(x_{j}^{*}(t-s)\bigr) \bigr]\,ds\\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}e_{ijl}(t)\bigl[g_{j} \bigl(x_{j}\bigl(t-\alpha _{jl}(t)\bigr)\bigr)g_{l} \bigl(x_{l}\bigl(t-\beta_{jl}(t)\bigr)\bigr)\\ &{}-g_{j}\bigl(x_{j}^{*}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta _{jl}(t)\bigr) \bigr)\bigr]+I_{i}(t)\\ ={}& {-}b_{i}(t)\bigl[x_{i}(t)-x_{i}^{*}(t)\bigr]+ \sum_{j=1}^{n}c_{ij}(t) \bigl[g_{j}\bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr)-g_{j}\bigl(x_{j}^{*}\bigl(t-\tau_{ij}(t)\bigr) \bigr)\bigr]\\ &{} +\sum_{j=1}^{n}d_{ij}(t)\int _{0}^{\sigma }k_{ij}(s)\bigl[g_{j} \bigl(x_{j}(t-s)\bigr)-g_{j}\bigl(x_{j}^{*}(t-s)\bigr) \bigr]\,ds\\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}e_{ijl}(t)\bigl[g_{j} \bigl(x_{j}\bigl(t-\alpha _{jl}(t)\bigr)\bigr)g_{l} \bigl(x_{l}\bigl(t-\beta_{jl}(t)\bigr)\bigr)\\ &{}-g_{j}\bigl(x_{j}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr)\\ &{}+g_{j}\bigl(x_{j}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr)\\ &{}-g_{j}\bigl(x_{j}^{*}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr)\bigr],\quad t\neq {t_{k}}, \end{aligned} \end{aligned}$$
(2.6)
$$\begin{aligned}& y_{i}\bigl(t_{k}^{+}\bigr)=(1+ \gamma_{ik})y_{i}(t_{k}), \quad k=1,2,\dots, \end{aligned}$$
(2.7)

where \(i=1, 2, \dots, n\). Next, define a Lyapunov functional as

$$ V_{i }(t) =\bigl|y_{i }(t)\bigr|e^{\lambda t},\quad i=1, 2, \dots, n. $$
(2.8)

It follows from (2.6), (2.7) and (2.8) that

$$\begin{aligned} D^{+}\bigl(V_{i }(t)\bigr) \leq& D^{+} \bigl(\bigl|y_{i}(t)\bigr|\bigr)e^{\lambda t}+\lambda\bigl|y_{i}(t)\bigr|e^{\lambda t} \\ \leq& \bigl(\lambda-b_{i}(t)\bigr)\bigl|y_{i}(t)\bigr|e^{\lambda t}+ \Biggl[\sum_{j=1}^{n}\bigl|c_{ij}(t)\bigr|\bigl|g_{j} \bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr)\bigr)-g_{j} \bigl(x_{j}^{*}\bigl(t-\tau_{ij}(t)\bigr)\bigr)\bigr| \\ &{}+\sum_{j=1}^{n}\bigl|d_{ij}(t)\bigr|\int _{0}^{\sigma }\bigl|k_{ij}(s)\bigr|\bigl|g_{j} \bigl(x_{j}(t-s)\bigr)-g_{j}\bigl(x_{j}^{*}(t-s) \bigr)\bigr|\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(t)\bigr|\bigl|g_{j} \bigl(x_{j}\bigl(t-\alpha _{jl}(t)\bigr)\bigr)g_{l} \bigl(x_{l}\bigl(t-\beta_{jl}(t)\bigr)\bigr) \\ &-g_{j}\bigl(x_{j}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr)\bigr| \\ &{}+\bigl|g_{j}\bigl(x_{j}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr) \\ &-g_{j}\bigl(x_{j}^{*}\bigl(t-\alpha_{jl}(t)\bigr) \bigr)g_{l}\bigl(x_{l}^{*}\bigl(t-\beta_{jl}(t)\bigr) \bigr)\bigr| \Biggr]e^{\lambda t} \\ \leq& \bigl(\lambda-b_{i}(t)\bigr)\bigl|y_{i}(t)\bigr|e^{\lambda t}+ \Biggl\{ \sum_{j=1}^{n}\bigl|c_{ij}(t)\bigr|L_{g}^{j}\bigl|y_{j}(x_{j} \bigl(t-\tau_{ij}(t)\bigr)\bigr| \\ &{}+\sum_{j=1}^{n}\bigl|d_{ij}(t)\bigr|\int _{0}^{\sigma }\bigl|k_{ij}(s)\bigr|L_{g}^{j}\bigl|y_{j}(t-s)\bigr| \,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(t)\bigr| \bigl[M_{g}L_{g}^{l}\bigl|y_{l} \bigl(t-\beta _{jl}(t)\bigr)\bigr| \\ &{}+M_{g}L_{g}^{j}\bigl|y_{j} \bigl(t-\alpha_{jl}(t)\bigr)\bigr| \bigr] \Biggr\} e^{\lambda t},\quad t \neq{t_{k}}, \end{aligned}$$
(2.9)

and

$$ V_{i}\bigl(t_{k}^{+} \bigr)=\bigl|y_{i}\bigl(t_{k}^{+}\bigr)\bigr|e^{\lambda t_{k}}=\bigl|x_{i} \bigl(t_{k}^{+}\bigr)-x_{i}^{*}\bigl(t_{k}^{+} \bigr)\bigr|e^{\lambda t_{k}}=|1+\gamma_{ik}|\bigl|y_{i}(t_{k})\bigr|e^{\lambda t_{k}}, $$
(2.10)

where \(i=1, 2, \dots,n\). Let \(M>1\) denote an arbitrary real number and set

$$\bigl\| \varphi-\varphi^{*}\bigr\| =\sup_{-\tau\leq s\leq0}\max _{1\leq j\leq n } \bigl|\varphi_{ j}(s)-\varphi_{j}^{*}(s)\bigr|>0,\quad j=1, 2, \dots, n. $$

Then, by (2.8), we have

$$V_{i }(t) =\bigl|y_{i }(t)\bigr|e^{\lambda t}< M\bigl\| \varphi- \varphi^{*}\bigr\| \quad\mbox{for all } t\in[-\tau, 0], i=1, 2, \dots, n. $$

Thus we can claim that

$$ V_{i }(t) =\bigl|y_{i }(t)\bigr|e^{\lambda t}< M\bigl\| \varphi-\varphi^{*}\bigr\| \quad \mbox{for all } t\in[-\tau, t_{1}], i=1, 2, \dots, n. $$
(2.11)

Otherwise, there must exist \(i \in\{ 1, 2, \dots, n \}\) and \(\sigma\in(-\tau, t_{1}]\) such that

$$ V_{i}(\sigma)=M\bigl\| \varphi-\varphi^{*}\bigr\| ,\qquad V_{j}(t)< M\bigl\| \varphi-\varphi^{*}\bigr\| \quad\mbox{for all } t\in[- \tau, \sigma), j=1, 2, \dots, n. $$
(2.12)

Combining (2.9), (2.10) with (2.12), we obtain

$$\begin{aligned} 0 \leq& D^{+}\bigl(V_{i }(\sigma)-M\bigl\| \varphi- \varphi^{*}\bigr\| \bigr) \\ =& D^{+}\bigl(V_{i }(\sigma)\bigr) \\ \leq& \bigl(\lambda-b_{i}(\sigma)\bigr)\bigl|y_{i}( \sigma)\bigr|e^{\lambda \sigma}+ \Biggl\{ \sum_{j=1}^{n}\bigl|c_{ij}( \sigma)\bigr|L_{g}^{j}\bigl|y_{j}(x_{j}\bigl(\sigma- \tau _{ij}(\sigma)\bigr)\bigr| \\ &{}+\sum_{j=1}^{n}\bigl|d_{ij}( \sigma)\bigr|\int_{0}^{\sigma }\bigl|k_{ij}(s)\bigr|L_{g}^{j}\bigl|y_{j}( \sigma-s)\bigr|\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(\sigma)\bigr| \bigl[M_{g}L_{g}^{l}\bigl|y_{l}\bigl(\sigma- \beta _{jl}(\sigma)\bigr)\bigr|+M_{g}L_{g}^{j}\bigl|y_{j} \bigl(\sigma-\alpha_{jl}(\sigma)\bigr)\bigr|\bigr] \Biggr\} e^{\lambda \sigma} \\ = &\bigl(\lambda-b_{i}(\sigma)\bigr)\bigl|y_{i}( \sigma)\bigr|e^{\lambda \sigma}+\sum_{j=1}^{n}\bigl|c_{ij}( \sigma)\bigr|L_{g}^{j}\bigl|y_{j}(x_{j}\bigl(\sigma- \tau _{ij}(\sigma)\bigr)\bigr|e^{\lambda(\sigma-\tau_{ij}(\sigma))}e^{\lambda\tau _{ij}(\sigma)} \\ &{}+\sum_{j=1}^{n}\bigl|d_{ij}( \sigma)\bigr|\int_{0}^{\sigma }\bigl|k_{ij}(s)\bigr|L_{g}^{j}\bigl|y_{j}( \sigma-s)\bigr|e^{\lambda(\sigma-s)}e^{\lambda {s}}\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(\sigma)\bigr| \bigl[M_{g}L_{g}^{l}\bigl|y_{l}\bigl(\sigma - \beta_{jl}(\sigma)\bigr)\bigr|e^{\lambda(\sigma-\beta_{jl}(\sigma))}e^{\lambda \beta_{jl}(\sigma)} \\ &{}+M_{g}L_{g}^{j}\bigl|y_{j}\bigl( \sigma-\alpha_{jl}(\sigma)\bigr)\bigr|e^{\lambda(\sigma -\alpha_{jl}(\sigma))}e^{\lambda\alpha_{jl}(\sigma)} \bigr] \\ \leq&\bigl(\lambda-b_{i}(\sigma)\bigr)M\bigl\| \varphi- \varphi^{*}\bigr\| +\sum_{j=1}^{n}\bigl|c_{ij}( \sigma)\bigr|L_{g}^{j}M\bigl\| \varphi-\varphi^{*} \bigr\| e^{\lambda\tau _{ij}(\sigma)} \\ &{}+\sum_{j=1}^{n}\bigl|d_{ij}( \sigma)\bigr|\int_{0}^{\sigma}\bigl|k_{ij}(s)\bigr|L_{g}^{j}M \bigl\| \varphi-\varphi^{*}\bigr\| e^{\lambda{s}}\,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(\sigma)\bigr| \bigl[M_{g}L_{g}^{l}M\bigl\| \varphi - \varphi^{*}\bigr\| e^{\lambda\beta_{jl}(\sigma)}+M_{g}L_{g}^{j}M \bigl\| \varphi-\varphi ^{*}\bigr\| e^{\lambda\alpha_{jl}(\sigma)} \bigr] \\ = & \Biggl[\bigl(\lambda-b_{i}(\sigma)\bigr)+\sum _{j=1}^{n}\bigl|c_{ij}(\sigma )\bigr|L_{g}^{j}e^{\lambda\tau_{ij}(\sigma)}+\sum _{j=1}^{n}\bigl|d_{ij}(\sigma)\bigr|\int _{0}^{\sigma}\bigl|k_{ij}(s)\bigr|L_{g}^{j}e^{\lambda{s}} \,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\bigl|e_{ijl}(\sigma)\bigr| \bigl(M_{g}L_{g}^{l}e^{\lambda\beta_{jl}(\sigma)}+M_{g}L_{g}^{j}Me^{\lambda\alpha _{jl}(\sigma)} \bigr) \Biggr]M\bigl\| \varphi-\varphi^{*}\bigr\| \\ \leq& \Biggl[(\lambda-\underline{b}_{i})+\sum _{j=1}^{n}\overline {c}_{ij}L_{g}^{j}e^{\lambda\tau}+ \sum_{j=1}^{n}|\overline{d}_{ij}| \int_{0}^{\sigma}\bigl|k_{ij}(s)\bigr|L_{g}^{j}e^{\lambda{s}} \,ds \\ &{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl} \bigl(M_{g}L_{g}^{l}e^{\lambda\tau}+M_{g}L_{g}^{j}e^{\lambda\tau} \bigr) \Biggr]M\bigl\| \varphi -\varphi^{*}\bigr\| . \end{aligned}$$
(2.13)

Then

$$\begin{aligned} &(\lambda-\underline{b}_{i})+\sum_{j=1}^{n} \overline {c}_{ij}L_{g}^{j}e^{\lambda\tau}+\sum _{j=1}^{n}|\overline{d}_{ij}|\int _{0}^{\sigma}\bigl|k_{ij}(s)\bigr|L_{g}^{j}e^{\lambda{s}} \,ds\\ &\quad{}+\sum_{j=1}^{n}\sum _{l=1}^{n}\overline{e}_{ijl} \bigl(M_{g}L_{g}^{l}e^{\lambda \tau}+M_{g}L_{g}^{j}e^{\lambda\tau} \bigr)>0, \end{aligned}$$

which contradicts (H5). Then (2.11) holds. In view of (2.11), we know that

$$V_{i}(t_{1})=\bigl|y_{i}(t_{1})\bigr|e^{\lambda t_{1}}< M \bigl\| \varphi-\varphi^{*}\bigr\| ,\quad i=1,2,\dots $$

and

$$V_{i}\bigl(t_{1}^{+}\bigr)=|1+ \gamma_{i1}|\bigl|y_{i}(t_{1})\bigr|e^{\lambda t_{1}} \leq\bigl|y_{i}(t_{1})\bigr|e^{\lambda t_{1}}. $$

Then

$$ V_{i}\bigl(t_{1}^{+}\bigr)< M\bigl\| \varphi-\varphi^{*}\bigr\| . $$
(2.14)

Thus, for \(t\in[t_{1},t_{2}]\), we can repeat the above procedure and obtain

$$V_{i}(t)=\bigl|y_{i}(t)\bigr|e^{\lambda t}< M\bigl\| \varphi- \varphi^{*}\bigr\| \quad\mbox{for all } t\in[t_{1},t_{2}],i=1,2, \dots. $$

Similarly, we have

$$V_{i}(t)=\bigl|y_{i}(t)\bigr|e^{\lambda t}< M\bigl\| \varphi- \varphi^{*}\bigr\| \quad\mbox{for all } t>0,i=1,2,\dots. $$

Namely,

$$\bigl|x_{i}(t)-x_{i}^{*}(t)\bigr|=\bigl|y_{i}(t)\bigr|< M\bigl\| \varphi- \varphi^{*}\bigr\| \quad\mbox{for all } t>0,i=1,2,\dots. $$

This completes the proof. □

Remark 2.1

If \(x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\dots,x^{*}_{n}(t))^{T} \) is a T-anti-periodic solution of (1.1), it follows from Lemma 2.2 and Definition 1.2 that \(x^{*}(t)\) is globally exponentially stable.

3 Main result

In this section,we present our main result that there exists the exponentially stable anti-periodic solution of (1.1).

Theorem 3.1

Assume that (H1)-(H6) are satisfied. Then (1.1) has exactly one T-anti-periodic solution \(x^{*}(t)\). Moreover, this solution is globally exponentially stable.

Proof

Let \(v(t)= (v_{1}(t), v_{2}(t),\dots, v_{n}(t))^{T} \) be a solution of (1.1) with initial conditions

$$ v_{i}(s)=\varphi^{v}_{i}(s),\quad \bigl| \varphi^{v}_{i}(s)\bigr|< \delta, s\in (-\tau, 0], i=1,2,\dots,n. $$
(3.1)

Thus, according to Lemma 2.1, the solution \(v(t)\) is bounded and

$$ \bigl|v_{i}(t)\bigr|< \delta \quad\mbox{for all } t\in{R}, i=1,2, \dots,n. $$
(3.2)

For \(p\in N\), if \(t\notin{t_{k}}\), then \(t + (p+1)T\notin\{t_{k}\}\); if \(t\in{t_{k}}\), then \(t + (p+1)T\in\{t_{k}\}\). From (1.1), we obtain

$$\begin{aligned} &\bigl((-1)^{p+1}v_{i} \bigl(t + (p+1)T \bigr)\bigr)' \\ &\quad=(-1)^{p+1} \Biggl\{ -b_{i}\bigl(t + (p+1)T \bigr)v_{i}\bigl(t + (k+1)T\bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}\bigl(t + (p+1)T\bigr)g_{j}\bigl(v_{j}\bigl(t + (p+1)T- \tau_{ij}\bigl(t + (p+1)T\bigr)\bigr)\bigr) \\ &\qquad{}+\sum_{j=1}^{n}d_{ij}\bigl(t + (p+1)T\bigr)\int_{0}^{\sigma}k_{ij}(s)g_{j} \bigl(v_{j}\bigl(t +(p+1)T-s\bigr)\bigr)\,ds \\ &\qquad{}+\sum_{j=1}^{n}\sum _{l=1}^{n}e_{ijl}\bigl(t +(p+1)T \bigr)g_{j}\bigl(v_{j}\bigl(t + (p+1)T-\alpha _{jl} \bigl(t + (p+1)T\bigr)\bigr)\bigr) \\ &\qquad{}\times{g_{l}}\bigl(v_{l}\bigl(t + (p+1)T- \beta_{jl}\bigl(t + (p+1)T\bigr)\bigr)\bigr)+I_{i}\bigl(t + (p+1)T\bigr) \Biggr\} \\ &\quad=-b_{i}(t) (-1)^{p+1}v_{i}\bigl(t +(p+1)T \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(t)g_{j} \bigl((-1)^{p+1}v_{j}\bigl(t +(p+1)T-\tau _{ij}(t) \bigr)\bigr) \\ &\qquad{}+\sum_{j=1}^{n}d_{ij}(t)\int _{0}^{\sigma}k_{ij}(s)g_{j} \bigl((-1)^{p+1}v_{j}\bigl(t +(p+1)T-s\bigr)\bigr)\,ds \\ &\qquad{}+\sum_{j=1}^{n}\sum _{l=1}^{n}e_{ijl}(t)g_{j} \bigl((-1)^{p+1}v_{j}\bigl(t + (p+1)T-\alpha_{jl}(t) \bigr)\bigr) \\ &\qquad{}\times{g_{l}}\bigl((-1)^{p+1}v_{l}\bigl(t +(p+1)T-\beta_{jl}(t)\bigr)\bigr)+I_{i}(t),\quad t \neq{t_{k}} \end{aligned}$$
(3.3)

and

$$\begin{aligned} (-1)^{p+1}v_{i}\bigl(\bigl(t_{k}+(p+1)T \bigr)^{+}\bigr) =& (-1)^{p+1}\bigl(1+\gamma_{i(k+(p+1)q)}v_{i} \bigl(t_{k}+(p+1)T\bigr)\bigr) \\ =&(-1)^{p+1}(1+\gamma_{ik})v_{i} \bigl(t_{k}+(p+1)T\bigr) \\ =&(1+\gamma_{ik}) \bigl((-1)^{p+1}v_{i} \bigl(t_{k}+(p+1)T\bigr)\bigr), \quad k=1,2,\dots, \end{aligned}$$
(3.4)

where \(i=1, 2, \dots,n\). Thus \((-1)^{p+1} v(t +(p+1)T)\) are solutions of (1.1) on \(R^{+}\) for any natural number p. Then, from Lemma 2.2, there exists a constant \(M>1\) such that

$$\begin{aligned} &\bigl|(-1)^{p+1}v_{i} \bigl(t + (p+1)T \bigr)-(-1)^{k} v_{i}(t + pT)\bigr| \\ &\quad\leq M e^{-\lambda(t + pT)}\sup_{-\tau\leq s\leq0}\max_{1\leq i\leq n}\bigl|v_{i} \bigl(s + (p+1) T\bigr)+ v_{i} (s+pT)\bigr| \\ &\quad\leq 2e^{-\lambda(t + pT)} M\delta, \end{aligned}$$
(3.5)

and

$$\begin{aligned} &\bigl|(-1)^{p+1}v_{i} \bigl( \bigl(t_{k} + (p+1)T\bigr)^{+}\bigr)-(-1)^{p} v_{i}\bigl((t_{k} + pT)^{+}\bigr)\bigr| \\ &\quad= \bigl|x_{i}\bigl(\bigl(t_{k}+(p+1)T\bigr)^{+} \bigr)+x_{i}\bigl((t_{k}+pT)^{+}\bigr)\bigr| \\ &\quad=|1+\gamma_{ik}|\bigl|x_{i}\bigl(t_{k}+(p+1)T \bigr)+x_{i}(t_{k}+pT)\bigr| \leq2M\delta{e^{-\lambda(pT+t_{k})}}, \end{aligned}$$
(3.6)

where \(k\in{N}\), \(i=1,2,\dots,n\). Thus, for any natural number m, we have

$$\begin{aligned} &(-1)^{m+1} v_{i} \bigl(t + (m+1)T\bigr) \\ &\quad = v_{i} (t ) +\sum_{k=0}^{m} \bigl[(-1)^{k+1} v _{i}\bigl(t + (k+1)T\bigr)-(-1)^{k} v_{i} (t + kT)\bigr],\quad t\neq{t_{k}}. \end{aligned}$$
(3.7)

Hence

$$\begin{aligned} &\bigl|(-1)^{m+1} v_{i} \bigl(t + (m+1)T\bigr)\bigr| \\ &\quad\leq \bigl| v_{i} (t )\bigr| +\sum_{k=0}^{m}\bigl| (-1)^{k+1} v _{i}\bigl(t + (k+1)T\bigr)-(-1)^{k} v_{i} (t + kT)\bigr|,\quad t\neq{t_{k}}, \end{aligned}$$
(3.8)

and

$$\begin{aligned} \bigl|(-1)^{m+1} v_{i} \bigl(\bigl(t_{k} + (m+1)T\bigr)^{+}\bigr)\bigr|&=\bigl|(1+\gamma_{ik}) (-1)^{m+1}v_{i}\bigl(t_{k}+(m+1)T\bigr)\bigr| \\ &\leq \bigl|(-1)^{m+1}v_{i}\bigl(t_{k}+(m+1)T\bigr)\bigr|, \end{aligned}$$
(3.9)

where \(i =1,2,\dots,n\). It follows from (3.5)-(3.9) that \((-1)^{m+1}v_{i}(t+(m+1)T)\) is a fundamental sequence on any compact set of \({R}^{+}\). Obviously, \(\{(-1)^{m} v (t + mT)\}\) uniformly converges to a piece-wise continuous function \(x^{*}(t)=(x^{*}_{1}(t), x^{*}_{2}(t),\dots,x^{*}_{n}(t))^{T}\) on any compact set of \({R}^{+}\).

Now we show that \(x^{*}(t)\) is T-anti-periodic solution of (1.1). Firstly, \(x^{*}(t)\) is T-anti-periodic, since

$$\begin{aligned} x^{*}(t+T) =&\lim_{m\to\infty}(-1)^{m } v (t +T+ mT) \\ =&-\lim_{(m+1)\to\infty}(-1)^{m+1 } v \bigl(t +(m +1)T \bigr)=-x^{*}(t ),\quad t\neq{t_{k}}, \end{aligned}$$
(3.10)

and

$$\begin{aligned} x^{*}\bigl((t+T)^{+}\bigr) =&\lim _{m\to\infty}(-1)^{m } v \bigl((t +T+ mT)^{+}\bigr) \\ =&-\lim_{(m+1)\to\infty}(-1)^{m+1 } v \bigl(\bigl(t +(m +1)T \bigr)^{+}\bigr)=-x^{*}(t_{k})^{+}. \end{aligned}$$
(3.11)

In the sequel, we prove that \(x^{*}(t)\) is a solution of (1.1). Noting that the right-hand side of (1.1) is piece-wise continuous, (3.3) and (3.4) imply that \(\{((-1)^{m+1} v (t +(m+1)T))'\}\) uniformly converges to a piece-wise continuous function on any compact subset of \({R}^{+}\). Thus, letting \(m \to\infty\) on both sides of (3.3) and (3.4), we can easily obtain

$$ \left \{ \textstyle\begin{array}{@{}l} \dot{x}_{i}^{*}(t)=-b_{i}(t)x_{i}^{*}(t)+\sum_{j=1}^{n}c_{ij}(t) g_{j}(x_{j}^{*}(t-\tau_{ij}(t)))\\ \hphantom{\dot{x}_{i}^{*}(t)=}{}+\sum_{j=1}^{n}d_{ij}(t) \int_{0}^{\sigma}k_{ij}(s)g_{j}(x_{j}^{*}(t-s))\,ds\\ \hphantom{\dot{x}_{i}^{*}(t)=}{} +\sum_{j=1}^{n}\sum_{l=1}^{n}e_{ijl}(t) g_{j}(x_{j}^{*}(t-\alpha_{jl}(t)))g_{l}(x_{l}^{*}(t-\beta _{jl}(t)))+I_{i}(t),\quad t\neq{t_{k}},\\ {x_{i}}^{*}(t_{k}^{+})=(1+\gamma_{ik})x_{i}^{*}(t_{k}),\quad k=1,2,\dots, \end{array} \right .$$
(3.12)

where \(i=1,2,\dots,n\). Therefore, \(x^{*}(t)\) is a solution of (1.1). Finally, by applying Lemma 2.2, it is easy to check that \(x^{*}(t)\) is globally exponentially stable. The proof of Theorem 3.1 is completed. □

Remark 3.1

In [10–12, 14, 15, 20–24, 44], although authors consider the existence and exponential stability of anti-periodic solutions of neural networks, they do not consider the impulsive case. In this paper, we consider the high-order cellular neural networks with impulses. The obtained results show that impulses play a certain role in the existence and exponential stability of anti-periodic solutions of cellular neural networks. If the \(\gamma_{ik}=0 \) (i.e., there is no impulse), then Theorem 3.1 is still valid if we delete the condition on the impulse. All the results in [10–12, 14, 15, 20–24, 44] cannot be applicable to system (1.1) to obtain the existence and exponential stability of anti-periodic solutions. This implies that the results of this paper are essentially new. Our results complement the previous work.

4 An example

In this section, we give an example to illustrate our main results obtained in previous sections. Consider the high-order cellular neural network with delays and impulses

$$\begin{aligned}& \begin{aligned}[b] \dot{x}_{1}(t)={}& {-}x_{1}(t)+ \frac{1}{12}g_{1}\bigl(x_{1}\bigl(t-\sin^{2}t \bigr)\bigr) +\frac{1}{14}g_{2}\bigl(x_{2}\bigl(t-7 \sin^{2}t\bigr)\bigr) \\ &{}+\frac{1}{36}|\sin t|\int_{0}^{20} e^{-s}g_{1}\bigl(x_{1}(t-s)\bigr)\,ds + \frac{1}{20}|\cos{t}|\int_{0}^{20} e^{-s}g_{2}\bigl(x_{2}(t-s)\bigr)\,ds \\ &{}+\frac{1}{80}\sin{t}g_{1}\bigl(x_{1}\bigl(t-3 \sin^{2}t\bigr)\bigr)g_{2}\bigl(x_{2}\bigl(t-2 \sin^{2}t\bigr)\bigr)+2\sin {t}, \end{aligned}\\& \begin{aligned}[b] \dot{x}_{2}(t) ={}& {-}x_{2}(t)+\frac{1}{16}g_{1}\bigl(x_{1} \bigl(t-\cos^{2}t\bigr)\bigr) +\frac{1}{16}g_{2}\bigl(x_{2} \bigl(t-4\sin^{2}t\bigr)\bigr) \\ &{}+\frac{1}{20}|\cos t|\int_{0}^{20} e^{-s}g_{1}\bigl(x_{1}(t-s)\bigr)\,ds + \frac{1}{20}|\sin{t}|\int_{0}^{20} e^{-s}g_{2}\bigl(x_{2}(t-s)\bigr)\,ds \\ &{}+\frac{1}{15}\sin{t}g_{1}\bigl(x_{1}\bigl(t- \sin^{2}t\bigr)\bigr)g_{2}\bigl(x_{2}\bigl(t-2 \sin^{2}t\bigr)\bigr)+\sin {t},\quad t\neq{t_{k}}, \end{aligned}\\& \begin{aligned} &{x_{1}}\bigl(t_{k}^{+}\bigr)=0.4x_{1}(t_{k}),\quad k=1,2,\dots,\\ &{x_{2}}\bigl(t_{k}^{+}\bigr)=0.4x_{2}(t_{k}),\quad k=1,2, \dots, \end{aligned} \end{aligned}$$
(4.1)

where \(g_{1}(u)=g_{2}(u)=\frac{1}{2}(|u+1|-|u-1|)\) and

$$\begin{aligned}& \begin{bmatrix} c_{11}(t) & c_{12}(t) \\ c_{21}(t) & c_{22}(t) \end{bmatrix} = \begin{bmatrix} \frac{1}{11} & \frac{1}{14} \\ \frac{1}{16} & \frac{1}{16} \end{bmatrix},\quad \begin{bmatrix} k_{11}(s) & k_{12}(s) \\ k_{21}(s) & k_{22}(s) \end{bmatrix} = \begin{bmatrix} e^{-s} & e^{-s} \\ e^{-s} & e^{-s} \end{bmatrix}, \\& \begin{bmatrix} \tau_{11}(t) & \tau_{12}(t) \\ \tau_{21}(t) & \tau_{22}(t) \end{bmatrix} = \begin{bmatrix} \sin^{2}t & 7\sin^{2}t \\ \cos^{2}t & 4\sin^{2}t \end{bmatrix},\quad \begin{bmatrix} d_{11}(t) & d_{12}(t) \\ d_{21}(t) & d_{22}(t) \end{bmatrix} = \begin{bmatrix} \frac{1}{36}|\sin t| & \frac{1}{20}|\cos t| \\ \frac{1}{20}|\cos t| & \frac{1}{20}|\sin t| \end{bmatrix}, \\& \begin{bmatrix} u_{1l}(t) & u_{2l}(t) \\ v_{1l}(t) & v_{2l}(t) \end{bmatrix} = \begin{bmatrix} 3\sin^{2}t & \sin^{2}t \\ 2\sin^{2}t & 2\sin^{2}t \end{bmatrix}, \quad \begin{bmatrix} e_{11l}(t) & e_{12l}(t) \\ e_{21l}(t) & e_{22l}(t) \end{bmatrix}= \begin{bmatrix} \frac{1}{80}\sin t & \frac{1}{80}\sin t \\ \frac{1}{15}\sin t & \frac{1}{15}\sin t \end{bmatrix},\\& \begin{bmatrix} b_{1}(t) & b_{2}(t) \\ I_{1}(t) & I_{2}(t) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 2\sin t & \sin t \end{bmatrix}, \end{aligned}$$

where \(l=1,2\). By a simple calculation, we get

$$\begin{aligned}& \underline{b}_{i}=L_{i}^{g}=M_{g}=1\quad(i=1,2),\qquad \overline{c}_{11}=\frac{1}{11},\qquad \overline{c}_{12}= \frac{1}{14},\qquad\overline{c}_{21}=\frac{1}{16},\qquad\overline {c}_{22}=\frac{1}{16}, \\& \overline{d}_{11}=\frac{1}{36},\qquad \overline{d}_{12}= \frac{1}{20},\qquad\overline{d}_{21}=\frac{1}{20},\qquad\overline {d}_{22}=\frac{1}{20},\\& \overline{e}_{1jl}= \frac{1}{80}, \qquad\overline{e}_{2jl}=\frac{1}{15}\quad(j,l=1,2), \\& \overline{\tau}_{11}=1,\qquad\overline{\tau}_{12}=7,\qquad\overline{\tau }_{21}=1,\qquad\overline{\tau}_{22}=4,\qquad \overline{I}_{1}=2,\qquad \overline{I}_{2}=1. \end{aligned}$$

Let \(\eta=0.2\), \(\lambda=0.001\). Then

$$\begin{aligned} &(\lambda-\underline{b}_{i})+\sum_{j=1}^{2} \overline {c}_{ij}L_{g}^{j}e^{\lambda\tau}+\sum _{j=1}^{2}|\overline{d}_{ij}|\int _{0}^{\sigma}\bigl|k_{ij}(s)\bigl|L_{g}^{j}e^{\lambda{s}} \,ds\\ &\qquad{}+\sum_{j=1}^{2}\sum _{l=1}^{2}\overline{e}_{ijl} \bigl(M_{g}L_{g}^{l}e^{\lambda \tau}+M_{g}L_{g}^{j}e^{\lambda\tau} \bigr)\\ & \quad\leq(0.001-1)+ \biggl(\frac{1}{11}+\frac{1}{14}+\frac{1}{16}+ \frac {1}{16} \biggr)e^{0.007}+ \biggl(\frac{1}{11}+ \frac{1}{36}+\frac {3}{20} \biggr)\\ &\qquad{}+ \biggl(\frac{1}{80}+\frac{1}{80}+\frac{1}{15}+ \frac{1}{15} \biggr)\times2\times{e^{0.001}}=-0.2149< -0.2< 0 \end{aligned}$$

and

$$\begin{aligned}& \begin{aligned}[b] &{-}b_{i}+\sum_{j=1}^{2} \bar{c}_{ij}L_{g}^{j}+\sum _{j=1}^{2}L_{g}^{j} \bar{d}_{ij}\int_{0}^{\sigma}\bigl|k_{ij}(s)\bigl| \,ds\\ &\quad< -1+\frac{1}{11}+\frac{1}{14}+\frac{1}{16}\times \frac{1}{36} +\frac{1}{10}\times\frac{1}{20}=-0.8309< 0, \end{aligned}\\& \begin{aligned}[b] &\Biggl(-b_{i}+\sum_{j=1}^{2} \bar{c}_{ij}L_{g}^{j}+\sum _{j=1}^{2}L_{g}^{j}\bar {d}_{ij}\int_{0}^{\sigma}\bigl|k_{ij}(s)\bigr| \,ds \Biggr)^{2} -4\bar{I}_{i}\sum _{j=1}^{2}\sum_{l=1}^{2} \bar{e}_{ijl}L_{g}^{j}L_{g}^{l}\\ &\quad< \biggl(-1+\frac{1}{11}+\frac{1}{14}+\frac{1}{16}\times \frac{1}{36} +\frac{1}{10}\times\frac{1}{20} \biggr)^{2}-4 \times \biggl(\frac{1}{40}+\frac {1}{10} \biggr)=0.14>0, \end{aligned} \end{aligned}$$

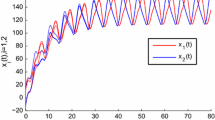
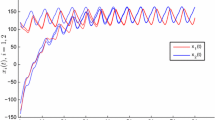
which implies that system (4.1) satisfies all the conditions in Theorem 3.1. Thus, (4.1) has exactly one π-anti-periodic solution. Moreover, this solution is globally exponentially stable. The results are shown in Figure 1.

Figure 1
figure 1

Times series of \(\pmb{x_{1}(t)}\) and \(\pmb{x_{2}(t)}\) of system ( 4.1 ).

Full size image