Investigation of Weight Effects on the Critical Speed of Inclined Turbocharger Rotor System

Abstract

Turbochargers have been widely used in various base conditions, such as horizontal, vertical, or inclined. The prediction of the dynamics is of utmost importance to inclined turbocharger designers. In this paper, the effect of weight on the critical speed of an inclined turbocharger rotor coupled with floating ring bearings is investigated. The inclined turbocharger rotor is modeled by lumped mass model. The nonlinear floating ring bearing model is derived using Capone’s model. Then the nonlinear dynamic model of the turbocharger rotor system is obtained. The balance position of the turbocharger rotor system is obtained by solving the nonlinear static equation. Linear system of the turbocharger rotor system is derived based on the balance position, and the critical speed is obtained by solving an eigenvalue problem. Three vibration modes, i.e. conical whirl, cylindrical whirl, and bending are obtained. Increasing the inclined angle would decrease the critical speed. Increasing the inclined angle would decrease the critical speed. Among the three vibration modes, the critical speed of cylindrical whirl furnishes the highest decrease while the critical speed of bending attains the lowest decrease. The vertical turbocharger rotor has a more wide operating speed range than the horizontal turbocharger rotor.

1 Introduction

Turbochargers are a special class of turbomachinery used to increase engine power by providing compressed air for combustion. In order to meet the demand for high power production, the operating speed of turbochargers has been increased to an extremely high range. Under such circumstances, the dynamics of the turbocharger rotor system accordingly becomes inevitably challenging in the stages of product design and fault diagnosis.

Rotor dynamics of turbochargers have been studied widely. Pettinato and DeChoudhury [1] analytically and experimentally studied the critical speed and failure mechanisms for redesign a high-speed turbocharger. Chen [2] discussed the critical speed of larger turbochargers with various bearing designs. Ying et al. [3] investigated the effect of foundation excitation on the dynamical behavior of a turbocharger.

Traditionally, the turbocharger rotor-bearing unit includes two fluid lubricated floating ring bearings as well as a single overhung rotor with the compressor and turbine disks at the two ends. Measurements and simulations show that rotors supported in full-floating ring bearings exhibit diverse nonlinear oscillation effects [4,5,6], which originate in the high nonlinearities introduced by the floating ring bearings. Nonlinear rotor dynamics have been studied widely by different methods [7,8,9]. Krik et al. [10] studied the linear stability threshold speeds and the nonlinear transient response of the automotive turbocharger with varying bearing designs and properties. Schilder et al. [11] investigated the quasi-periodic oscillations of a finite beam-element turbocharger model with nonlinear oil-film forces. Schweizer [12, 13] examined the oil whirl, oil whip, whirl/whip synchronization, and the total instability of turbocharger rotors supported in full-floating ring bearings. Bonello [14] analyzed the nonlinear dynamic behavior of a turbocharger on floating ring bearings by transient modal analysis. Tian et al. [15, 16] investigated the dynamic response and synchronous and sub-synchronous vibrations of turbocharger rotor systems supported on floating ring bearings. Koutsovasilis et al. [17] applied a methodology to quantify the sub-synchronous vibrations of a turbocharger with full-floating ring bearings. Liang et al. [18] developed a method to control the magnitude and frequency of nonlinear whirl motion of turbocharger rotor using the outer clearance of semi-floating ring bearing. Smolik et al. [19] studied the effects of radial bearing clearances on the amplitudes of the sub-synchronous response of the turbocharger rotor. Zhang et al. [20] studied the impact of the reduced load capacities and bearing torques caused by circumferential or/and axial grooves in full-floating-ring bearings on the nonlinear oscillations of turbocharger rotors. Singh and Gupta [21] studied the effect of rotating unbalance and engine excitations on the nonlinear dynamic response of turbocharger flexible rotor system supported on floating ring bearings.

Turbochargers have been widely used in various base conditions, such as horizontal, vertical, or inclined. The vertical and inclined rotors have been studied by several scholars. Shi et al. [22] comprehensively studied the nonlinear dynamics of a vertical rotor-bearing system based on the bifurcation diagrams, waterfall diagrams, rotor center orbits, Poincare maps, and frequency spectrums. Luneno et al. [23] gave a good agreement between the simulation and experimental results of a vertical rotor bearings system. Cha and Glavatskih [24] investigated the nonlinear dynamic behavior of vertical and horizontal rotors in compliant liner tilting pad journal bearings. Nishimura et al. [25] demonstrated the nonlinear steady-state vibration of the self-excited vibration of a vertical rotating shaft with journal bearing. Shi et al. [26] studied the influence of pivot design on nonlinear dynamic characteristics of a vertical and horizontal rotor. Liu et al. [27, 28] applied numerical and experimental methods to study the periodic solution and stability of the inclined rotor journal bearing system. Capone’s short bearing model was employed to describe the journal bearing support properties. Xu et al. [29] investigated the vibration characteristics of an eccentric rotor with both the axially inclined angle and the orientation angle. So far, no previous work has been done on the critical speed of inclined turbocharger rotor coupled with nonlinear floating ring bearings.

Hence, the purpose of this work is to investigate the effect of weight on the critical speed of an inclined turbocharger rotor coupled with two nonlinear floating ring bearings. Based on the lumped mass model and Capone’s model, the inclined turbocharger rotor is modeled as a nonlinear dynamic system. The linear system of the turbocharger rotor system is derived using Taylor’s series expansion. Then the critical speed is obtained by solving an eigenvalue problem. The influence of inclined angle on the critical speed of an inclined turbocharger rotor system is investigated in detail.

2 Dynamic Model of an Inclined Turbocharger Rotor System

2.1 Turbocharger Rotor Modeling

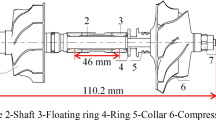
The structure of an inclined turbocharger rotor system is depicted in Fig. 1, where the left end is a compressor wheel, and the right end is a turbine wheel. The inclined angle θ is defined as the intersection angle of the rotor axis line and horizontal plane. When θ = 0, the turbocharger rotor is horizontal. When θ = 90°, the turbocharger rotor is vertical. The shaft is supported by two floating ring bearings. The inclined turbocharger rotor is simplified to four mass nodes connected by three massless beam sections. Meanwhile, the moment of inertia of the beam elements was also concentrated on the corresponding mass nodes. m_i is the mass of the ith disk, d_i and l_i are the diameter and the length of the ith shaft section, respectively. The X and Y directions are set in the disc plane, and Z direction is along with the shaft axis.

Fig. 1

The turbocharger rotor-bearing model

Following the way described in Ref. [3], the governing equations of motion for turbocharger rotor system are formulated as

$$ m_{1} \ddot{X}_{1} + \frac{{12EI_{1} }}{{l_{1}^{3} }}X_{1} + \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{y1} - \frac{{12EI_{1} }}{{l_{1}^{3} }}X_{2} + \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{y2} = m_{1} e_{1} \omega^{2} \cos \omega t $$

(1)

$$ J_{a1} \ddot{\varphi }_{y1} - \omega J_{p1} \dot{\varphi }_{x1} + \frac{{6EI_{1} }}{{l_{1}^{2} }}X_{1} + \frac{{4EI_{1} }}{{l_{1} }}\varphi_{y1} - \frac{{6EI_{1} }}{{l_{1}^{2} }}X_{2} + \frac{{2EI_{1} }}{{l_{1} }}\varphi_{y2} = 0 $$

(2)

$$ \begin{aligned} & m_{2} \ddot{X}_{2} - \frac{{12EI_{1} }}{{l_{1}^{3} }}X_{1} - \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{y1} + \left( {\frac{{12EI_{1} }}{{l_{1}^{3} }} + \frac{{12EI_{2} }}{{l_{2}^{3} }}} \right)X_{2} + \left( { - \frac{{6EI_{1} }}{{l_{1}^{2} }} + \frac{{6EI_{2} }}{{l_{2}^{2} }}} \right)\varphi_{y2} \\ & \quad - \frac{{12EI_{2} }}{{l_{2}^{3} }}X_{3} + \frac{{6EI_{2} }}{{l_{2}^{2} }}\varphi_{y3} = - F_{x,2}^{in} \\ \end{aligned} $$

(3)

$$ \begin{aligned} & J_{a2} \ddot{\varphi }_{y2} - \omega J_{p2} \dot{\varphi }_{x2} + \frac{{6EI_{1} }}{{l_{1}^{2} }}X_{1} + \frac{{2EI_{1} }}{{l_{1} }}\varphi_{y1} + \left( { - \frac{{6EI_{1} }}{{l_{1}^{2} }} + \frac{{6EI_{2} }}{{l_{2}^{2} }}} \right)X_{2} + \left( {\frac{{4EI_{1} }}{{l_{1} }} + \frac{{4EI_{2} }}{{l_{2} }}} \right)\varphi_{y2} \\ & \quad - \frac{{6EI_{2} }}{{l_{2}^{2} }}X_{3} + \frac{{2EI_{2} }}{{l_{2} }}\varphi_{y3} = 0 \\ \end{aligned} $$

(4)

$$ \begin{aligned} & m_{3} \ddot{X}_{3} - \frac{{12EI_{2} }}{{l_{2}^{3} }}X_{2} - \frac{{6EI_{2} }}{{l_{2}^{2} }}\varphi_{y2} + \left( {\frac{{12EI_{2} }}{{l_{2}^{3} }} + \frac{{12EI_{3} }}{{l_{3}^{3} }}} \right)X_{3} + \left( { - \frac{{6EI_{2} }}{{l_{2}^{2} }} + \frac{{6EI_{3} }}{{l_{3}^{2} }}} \right)\varphi_{y3} \\ & \quad - \frac{{12EI_{3} }}{{l_{3}^{3} }}X_{4} + \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{y4} = - F_{x,3}^{in} \\ \end{aligned} $$

(5)

$$ \begin{aligned} & J_{a3} \ddot{\varphi }_{y3} - \omega J_{p3} \dot{\varphi }_{x3} + \frac{{6EI_{2} }}{{l_{2}^{2} }}X_{2} + \frac{{2EI_{2} }}{{l_{2} }}\varphi_{y2} + \left( { - \frac{{6EI_{2} }}{{l_{2}^{2} }} + \frac{{6EI_{3} }}{{l_{3}^{2} }}} \right)X_{3} + \left( {\frac{{4EI_{2} }}{{l_{2} }} + \frac{{4EI_{3} }}{{l_{3} }}} \right)\varphi_{y3} \\ & \quad - \frac{{6EI_{3} }}{{l_{3}^{2} }}X_{4} + \frac{{2EI_{3} }}{{l_{3} }}\varphi_{y4} = 0 \\ \end{aligned} $$

(6)

$$ m_{4} \ddot{X}_{4} - \frac{{12EI_{3} }}{{l_{3}^{3} }}X_{3} - \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{y3} + \frac{{12EI_{3} }}{{l_{3}^{3} }}X_{4} - \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{y4} = m_{4} e_{4} \omega^{2} \cos \omega t $$

(7)

$$ J_{a4} \ddot{\varphi }_{y4} - \omega J_{p4} \dot{\varphi }_{x4} + \frac{{6EI_{3} }}{{l_{3}^{2} }}X_{3} + \frac{{2EI_{3} }}{{l_{3} }}\varphi_{y3} - \frac{{6EI_{3} }}{{l_{3}^{2} }}X_{4} + \frac{{4EI_{3} }}{{l_{3} }}\varphi_{y4} = 0 $$

(8)

$$ m_{1} \ddot{Y}_{1} + \frac{{12EI_{1} }}{{l_{1}^{3} }}Y_{1} - \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{x1} - \frac{{12EI_{1} }}{{l_{1}^{3} }}Y_{2} - \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{x2} = m_{1} e_{1} \omega^{2} \sin \omega t - m_{1} g\cos \theta $$

(9)

$$ J_{a1} \ddot{\varphi }_{x1} + \omega J_{p1} \dot{\varphi }_{y1} - \frac{{6EI_{1} }}{{l_{1}^{2} }}Y_{1} + \frac{{4EI_{1} }}{{l_{1} }}\varphi_{x1} + \frac{{6EI_{1} }}{{l_{1}^{2} }}Y_{2} + \frac{{2EI_{1} }}{{l_{1} }}\varphi_{x2} = 0 $$

(10)

$$ \begin{aligned} & m_{2} \ddot{Y}_{2} - \frac{{12EI_{1} }}{{l_{1}^{3} }}Y_{1} + \frac{{6EI_{1} }}{{l_{1}^{2} }}\varphi_{x1} + \left( {\frac{{12EI_{1} }}{{l_{1}^{3} }} + \frac{{12EI_{2} }}{{l_{2}^{3} }}} \right)Y_{2} + \left( {\frac{{6EI_{1} }}{{l_{1}^{2} }} - \frac{{6EI_{2} }}{{l_{2}^{2} }}} \right)\varphi_{x2} \\ & \quad - \,\frac{{12EI_{2} }}{{l_{2}^{3} }}Y_{3} - \frac{{6EI_{2} }}{{l_{2}^{2} }}\varphi_{y3} = - m_{2} g\cos \theta - F_{y,2}^{in} \\ \end{aligned} $$

(11)

$$ \begin{aligned} & J_{a2} \ddot{\varphi }_{x2} + \omega J_{p2} \dot{\varphi }_{y2} - \frac{{6EI_{1} }}{{l_{1}^{2} }}Y_{1} + \frac{{2EI_{1} }}{{l_{1} }}\varphi_{x1} + \left( {\frac{{6EI_{1} }}{{l_{1}^{2} }} - \frac{{6EI_{2} }}{{l_{2}^{2} }}} \right)Y_{2} + \left( {\frac{{4EI_{1} }}{{l_{1} }} + \frac{{4EI_{2} }}{{l_{2} }}} \right)\varphi_{x2} \\ & \quad + \frac{{6EI_{2} }}{{l_{2}^{2} }}Y_{3} + \frac{{2EI_{2} }}{{l_{2} }}\varphi_{x3} = 0 \\ \end{aligned} $$

(12)

$$ \begin{aligned} & m_{3} \ddot{Y}_{3} - \frac{{12EI_{2} }}{{l_{2}^{3} }}Y_{2} + \frac{{6EI_{2} }}{{l_{2}^{2} }}\varphi_{x2} + \left( {\frac{{12EI_{2} }}{{l_{2}^{3} }} + \frac{{12EI_{3} }}{{l_{3}^{3} }}} \right)Y_{3} + \left( {\frac{{6EI_{2} }}{{l_{2}^{2} }} - \frac{{6EI_{3} }}{{l_{3}^{2} }}} \right)\varphi_{x3} \\ & \quad - \,\frac{{12EI_{3} }}{{l_{3}^{3} }}Y_{4} - \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{x4} = - m_{3} g\cos \theta - F_{y,3}^{in} \\ \end{aligned} $$

(13)

$$ \begin{aligned} & J_{a3} \ddot{\varphi }_{x3} + \omega J_{p3} \dot{\varphi }_{y3} - \frac{{6EI_{2} }}{{l_{2}^{2} }}Y_{2} + \frac{{2EI_{2} }}{{l_{2} }}\varphi_{y2} + \left( {\frac{{6EI_{2} }}{{l_{2}^{2} }} - \frac{{6EI_{3} }}{{l_{3}^{2} }}} \right)Y_{3} + \left( {\frac{{4EI_{2} }}{{l_{2} }} + \frac{{4EI_{3} }}{{l_{3} }}} \right)\varphi_{x3} \\ & \quad + \frac{{6EI_{3} }}{{l_{3}^{2} }}Y_{4} + \frac{{2EI_{3} }}{{l_{3} }}\varphi_{x4} = 0 \\ \end{aligned} $$

(14)

$$ m_{4} \ddot{Y}_{4} - \frac{{12EI_{3} }}{{l_{3}^{3} }}Y_{3} + \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{x3} + \frac{{12EI_{3} }}{{l_{3}^{3} }}Y_{4} + \frac{{6EI_{3} }}{{l_{3}^{2} }}\varphi_{x4} = m_{4} e_{4} \omega^{2} \sin \omega t - m_{4} g\cos \theta $$

(15)

$$ J_{a4} \ddot{\varphi }_{x4} + \omega J_{p4} \dot{\varphi }_{y4} - \frac{{6EI_{3} }}{{l_{3}^{2} }}Y_{3} + \frac{{2EI_{3} }}{{l_{3} }}\varphi_{x3} + \frac{{6EI_{3} }}{{l_{3}^{2} }}Y_{4} + \frac{{4EI_{3} }}{{l_{3} }}\varphi_{x4} = 0 $$

(16)

where X_i is the displacement of the ith disk along the X axis, Y_i is the displacement of the ith disk along the Y axis, φ_xi is the angular displacement of the ith disk around the X axis, φ_yi is the angular displacement of the ith disk around the Y axis, J_ai is the transverse moment of inertia of the ith disk, J_pi is the polar moment of inertia of the ith disk, e_i is the eccentricity of the ith disk, I_i is the moment of inertia of the ith shaft, $F_{x,2}^{in}$ and $F_{x,3}^{in}$ are the inner oil film force along the X axis under the second and third mass nodes, $F_{y,2}^{in}$ and $F_{y,3}^{in}$ are the inner oil film force along the Y axis under the second and third mass nodes, E is the modulus of elasticity of the shaft, ω is the rotational speed of the turbocharger rotor, g is the acceleration of gravity and t is time.

2.2 Floating Ring Bearing Modeling

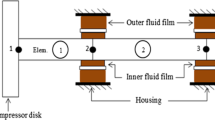
There are two fluid films (i.e. inner and outer) in a floating ring bearing, as shown in Fig. 2. The inner fluid film is formed between the journal and the floating ring, whereas the outer film is between the floating ring and bearing housing. The fixed right-hand frame of reference coordinates O_bXY is given where O_b denotes the bearing origin. The nonlinear floating ring bearings model developed in this paper is derived in dimensional form using Capone’s model [15, 16]. The Reynolds equations for the inner and outer oil films can be written as follows:

$$ \begin{gathered} \frac{{1}}{{R_{i}^{2} }}\frac{\partial }{\partial \alpha }\left( {\frac{{h_{in}^{3} }}{{12\mu_{in} }}\frac{{\partial p_{in} }}{\partial \alpha }} \right) + \frac{\partial }{{\partial Z_{in} }}\left( {\frac{{h_{in}^{3} }}{{12\mu_{in} }}\frac{{\partial p_{in} }}{{\partial Z_{in} }}} \right) = \frac{{\omega + \omega_{r} }}{2}\frac{{\partial h_{in} }}{\partial \alpha } + \frac{{\partial h_{in} }}{\partial t} \hfill \\ \frac{{1}}{{R_{r}^{2} }}\frac{\partial }{\partial \beta }\left( {\frac{{h_{out}^{3} }}{{12\mu_{out} }}\frac{{\partial p_{out} }}{\partial \beta }} \right) + \frac{\partial }{{\partial Z_{out} }}\left( {\frac{{h_{out}^{3} }}{{12\mu_{out} }}\frac{{\partial p_{out} }}{{\partial Z_{out} }}} \right) = \frac{{\omega_{r} }}{2}\frac{{\partial h_{out} }}{\partial \beta } + \frac{{\partial h_{out} }}{\partial t} \hfill \\ \end{gathered} $$

(17)

where the subscripts in and out identify the parameters of the inner oil film and outer oil film, respectively. R_i and R_r correspond to the journal radius and floating ring outer radius, respectively. α and β are the circumferential position of the inner and outer oil films, respectively. p is the oil film pressure, h is the oil film thicknesses, Z is the oil film thicknesses and μ denotes the lubricating oil viscosity, and ω_r is the rotational speed of the floating ring.

Fig. 2

Floating ring bearing middle plane and reference frame

According to Fig. 2, we have

$$ \begin{gathered} h_{in} (\alpha ,t) = C_{in} - x_{i} \cos \alpha - y_{i} \sin \alpha \hfill \\ h_{out} (\beta ,t) = C_{out} - X_{r} \cos \beta - Y_{r} \sin \beta \hfill \\ \end{gathered} $$

(18)

$$ \begin{gathered} \frac{{\partial h_{in} }}{\partial t} = - \dot{x}_{i} \cos \alpha - \dot{y}_{i} \sin \alpha \hfill \\ \frac{{\partial h_{out} }}{\partial t} = - \dot{X}_{r} \cos \beta - \dot{Y}_{r} \sin \beta \hfill \\ \end{gathered} $$

(19)

$$ \begin{gathered} x_{i} = X_{i} - X_{r} \hfill \\ y_{i} = Y_{i} - Y_{r} \hfill \\ \end{gathered} $$

(20)

where C_in and C_out are the radial average clearance of inner and outer oil films, (X_i, Y_i) is the displacement of journal center O_i of the ith disk, (X_r, Y_r) is the displacement of floating ring center O_r, (x_i, y_i) is the displacement of journal center O_i relative to floating ring center O_r.

Applying infinite short bearing approximation theory, Eq. (17) can be rewritten.

$$ \begin{gathered} \frac{\partial }{{\partial Z_{in} }}\left( {\frac{{h_{in}^{3} }}{{12\mu_{in} }}\frac{{\partial p_{in} }}{{\partial Z_{in} }}} \right) = \frac{{\omega + \omega_{r} }}{2}\frac{{\partial h_{in} }}{\partial \alpha } + \frac{{\partial h_{in} }}{\partial t} \hfill \\ \frac{\partial }{{\partial Z_{out} }}\left( {\frac{{h_{out}^{3} }}{{12\mu_{out} }}\frac{{\partial p_{out} }}{{\partial Z_{out} }}} \right) = \frac{{\omega_{r} }}{2}\frac{{\partial h_{out} }}{\partial \beta } + \frac{{\partial h_{out} }}{\partial t} \hfill \\ \end{gathered} $$

(21)

Substituting Eqs. (18)–(20) into Eq. (21), and integrating the Reynolds equations twice, the expression for pressure distribution is obtained as follows

$$ \begin{gathered} p_{in} = \frac{{3\mu_{in} }}{{h_{in}^{3} }}\left( {Z_{in}^{2} - \frac{1}{4}L_{in}^{2} } \right)\left\{ {\left[ {(\omega + \omega_{r} )x_{i} - 2\dot{y}_{i} } \right]\sin \alpha - \left[ {(\omega + \omega_{r} )y_{i} + 2\dot{x}_{i} } \right]\cos \alpha } \right\} \hfill \\ p_{out} = \frac{{3\mu_{out} }}{{h_{out}^{3} }}\left( {Z_{out}^{2} - \frac{1}{4}L_{out}^{2} } \right)\left[ {(\omega_{r} X_{r} - 2\dot{Y}_{r} )\sin \beta - (\omega_{r} Y_{r} + 2\dot{X}_{r} )\cos \beta } \right] \hfill \\ \end{gathered} $$

(22)

The boundary conditions of inner and outer oil films are given as

$$ \begin{array}{*{20}c} {p_{in} (\alpha_{0} ) = 0,} & {\left. {\frac{{\partial p_{in} }}{\partial \alpha }} \right|_{{\alpha = \alpha_{0} }} > 0} \\ {p_{out} (\beta_{0} ) = 0,} & {\left. {\frac{{\partial p_{out} }}{\partial \beta }} \right|_{{\beta = \beta_{0} }} > 0} \\ \end{array} $$

(23)

Based on Eq. (22) and Eq. (23), one has

$$ \begin{gathered} \alpha_{0} = \arctan \frac{{(\omega + \omega_{r} )y_{i} + 2\dot{x}_{i} }}{{(\omega + \omega_{r} )x_{i} - 2\dot{y}_{i} }} \hfill \\ \beta_{0} = \arctan \frac{{\omega_{r} Y_{r} + 2\dot{X}_{r} }}{{\omega_{r} X_{r} - 2\dot{Y}_{r} }} \hfill \\ \end{gathered} $$

(24)

Thus, the oil force of the inner oil film is

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {F_{x,i}^{in} } \\ {F_{y,i}^{in} } \\ \end{array} } \right\} & = \int_{{\alpha_{0} }}^{{\pi + \alpha_{0} }} {\int_{{ - \frac{1}{2}L_{in} }}^{{\frac{1}{2}L_{in} }} {p_{in} R_{i} \,\left\{ {\begin{array}{*{20}c} {\cos \alpha } \\ {\sin \alpha } \\ \end{array} } \right\}} } \,\,dZ_{in} d\alpha \\ & = - \frac{1}{2}\mu_{in} R_{i} L_{in}^{3} A_{i} \,\int_{{\alpha_{0} }}^{{\pi + \alpha_{0} }} {\frac{{\cos \alpha_{0} \sin \alpha - \sin \alpha_{0} \cos \alpha }}{{h_{in}^{3} }}\,\left\{ {\begin{array}{*{20}c} {\cos \alpha } \\ {\sin \alpha } \\ \end{array} } \right\}\,d\alpha } \\ & = - \frac{1}{4}\mu_{in} R_{i} L_{in}^{3} A_{i} \left( {\cos \alpha_{0} \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} G_{1} }}{{\partial x_{i} \partial y_{i} }}} \\ {\frac{{\partial^{2} G_{1} }}{{\partial y_{i}^{2} }}} \\ \end{array} } \right\} - \sin \alpha_{0} \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} G_{1} }}{{\partial x_{i}^{2} }}} \\ {\frac{{\partial^{2} G_{1} }}{{\partial x_{i} \partial y_{i} }}} \\ \end{array} } \right\}} \right) \\ \end{aligned} $$

(25)

where

$$ A_{i} = \sqrt {\left( {(\omega + \omega_{r} )x_{i} - 2\dot{y}_{i} } \right)^{2} + \left( {(\omega + \omega_{r} )y_{i} + 2\dot{x}_{i} } \right)^{2} } $$

(26)

$$ G_{1} = \int_{{\alpha_{0} }}^{{\pi + \alpha_{0} }} {\frac{1}{{h_{in} }}\,d\alpha } = \frac{2}{{\sqrt {C_{in}^{2} - x_{i}^{2} - y_{i}^{2} } }}\left[ {\frac{\pi }{2} + \arctan \left( {\frac{{y_{i} \cos \alpha_{0} - x_{i} \sin \alpha_{0} }}{{\sqrt {C_{in}^{2} - x_{i}^{2} - y_{i}^{2} } }}} \right)} \right] $$

(27)

From Eq. (27), yields

$$ \frac{{\partial^{2} G_{1} }}{{\partial x_{i}^{2} }} = \frac{{G_{1} }}{{N_{i,1} }} + \frac{{3x_{i}^{2} G_{1} }}{{N_{i,1}^{2} }} + \frac{{2N_{i,5} }}{{N_{i,1} N_{i,4} }} + \frac{{6x_{i}^{2} N_{i,2} }}{{N_{i,1}^{2} N_{i,4} }} - \frac{{2N_{i,3} \sin 2\alpha_{0} }}{{N_{i,4}^{2} }} + \frac{{4x_{i} N_{i,2} N_{i,3} \cos \alpha_{0} }}{{N_{i,1} N_{i,4}^{2} }} $$

(28)

$$ \frac{{\partial^{2} G_{1} }}{{\partial x_{i} \partial y_{i} }} = \frac{{3x_{i} y_{i} G_{1} }}{{N_{i,1}^{2} }} + \frac{{4x_{i} \cos \alpha_{0} }}{{N_{i,1} N_{i,4} }} + \frac{{6x_{i} y_{i} N_{i,2} }}{{N_{i,1}^{2} N_{i,4} }} - \frac{{4N_{i,3} \sin^{2} \alpha_{0} }}{{N_{i,4}^{2} }} + \frac{{4x_{i} N_{i,2} N_{i,3} \sin \alpha_{0} }}{{N_{i,1} N_{i,4}^{2} }} $$

(29)

$$ \frac{{\partial^{2} G_{1} }}{{\partial y_{i}^{2} }} = \frac{{G_{1} }}{{N_{i,1} }} + \frac{{3y_{i}^{2} G_{1} }}{{N_{i,1}^{2} }} + \frac{{2N_{i,6} }}{{N_{i,1} N_{i,4} }} + \frac{{6y_{i}^{2} N_{i,2} }}{{N_{i,1}^{2} N_{i,4} }} + \frac{{2N_{i,3} \sin 2\alpha_{0} }}{{N_{i,4}^{2} }} + \frac{{4y_{i} N_{i,2} N_{i,3} \sin \alpha_{0} }}{{N_{i,1} N_{i,4}^{2} }} $$

(30)

where $N_{i,1} = C_{in}^{2} - x_{i}^{2} - y_{i}^{2}$, $N_{i,2} = y_{i} \cos \alpha_{0} - x_{i} \sin \alpha_{0}$, $N_{i,3} = x_{i} \cos \alpha_{0} + y_{i} \sin \alpha_{0}$, $N_{i,4} = N_{i,1} + N_{i,2}^{2}$, $N_{i,5} = y_{i} \cos \alpha_{0} - 3x_{i} \sin \alpha_{0}$, $N_{i,6} = 3y_{i} \cos \alpha_{0} - x_{i} \sin \alpha_{0}$.

The oil force of the outer oil film is

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {F_{x,i}^{out} } \\ {F_{y,i}^{out} } \\ \end{array} } \right\} & = \int_{{\beta_{0} }}^{{\pi + \beta_{0} }} {\int_{{ - \frac{1}{2}L_{out} }}^{{\frac{1}{2}L_{out} }} {p_{out} R_{r} \left\{ {\begin{array}{*{20}c} {\cos \beta } \\ {\sin \beta } \\ \end{array} } \right\}} } dZ_{out} d\beta \\ & = - \frac{1}{2}\mu_{out} R_{r} L_{out}^{3} A_{r} \int_{{\beta_{0} }}^{{\pi + \beta_{0} }} {\frac{{\cos \beta_{0} \sin \beta - \sin \beta_{0} \cos \beta }}{{h_{out}^{3} }}\left\{ {\begin{array}{*{20}c} {\cos \beta } \\ {\sin \beta } \\ \end{array} } \right\}} d\beta \\ & = - \frac{1}{4}\mu_{out} R_{r} L_{out}^{3} A_{r} \left( {\cos \beta_{0} \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} G_{2} }}{{\partial X_{r} \partial Y_{r} }}} \\ {\frac{{\partial^{2} G_{2} }}{{\partial Y_{r}^{2} }}} \\ \end{array} } \right\} - \sin \beta_{0} \left\{ {\begin{array}{*{20}c} {\frac{{\partial^{2} G_{2} }}{{\partial X_{r}^{2} }}} \\ {\frac{{\partial^{2} G_{2} }}{{\partial X_{r} \partial Y_{r} }}} \\ \end{array} } \right\}} \right) \\ \end{aligned} $$

(31)

where

$$ A_{r} = \sqrt {(\omega_{r} X_{r} - 2\dot{Y}_{r} )^{2} + (\omega_{r} Y_{r} + 2\dot{X}_{r} )^{2} } $$

(32)

$$ G_{2} = \int_{{\beta_{0} }}^{{\pi + \beta_{0} }} {\frac{1}{{h_{out} }}} d\beta = \frac{2}{{\sqrt {C_{out}^{2} - X_{r}^{2} - Y_{r}^{2} } }}\left[ {\frac{\pi }{2} + \arctan \left( {\frac{{Y_{r} \cos \beta_{0} - X_{r} \sin \beta_{0} }}{{\sqrt {C_{out}^{2} - X_{r}^{2} - Y_{r}^{2} } }}} \right)} \right] $$

(33)

From Eq. (33), yields

$$ \frac{{\partial^{2} G_{2} }}{{\partial X_{r}^{2} }} = \frac{{G_{2} }}{{N_{r,1} }} + \frac{{3X_{r}^{2} G_{2} }}{{N_{r,1}^{2} }} + \frac{{2N_{r,5} }}{{N_{r,1} N_{r,4} }} + \frac{{6X_{r}^{2} N_{r,2} }}{{N_{r,1}^{2} N_{r,4} }} - \frac{{2N_{r,3} \sin 2\beta_{0} }}{{N_{r,4}^{2} }} + \frac{{4X_{r} N_{r,2} N_{r,3} \cos \beta_{0} }}{{N_{r,1} N_{r,4}^{2} }} $$

(34)

$$ \frac{{\partial^{2} G_{2} }}{{\partial X_{r} \partial Y_{r} }} = \frac{{3X_{r} Y_{r} G_{2} }}{{N_{r,1}^{2} }} + \frac{{4X_{r} \cos \beta_{0} }}{{N_{r,1} N_{r,4} }} + \frac{{6X_{r} Y_{r} N_{r,2} }}{{N_{r,1}^{2} N_{r,4} }} - \frac{{4N_{r,3} \sin^{2} \beta_{0} }}{{N_{r,4}^{2} }} + \frac{{4X_{r} N_{r,2} N_{r,3} \sin \beta_{0} }}{{N_{r,1} N_{r,4}^{2} }} $$

(35)

$$ \frac{{\partial^{2} G_{2} }}{{\partial Y_{r}^{2} }} = \frac{{G_{2} }}{{N_{r,1} }} + \frac{{3Y_{r}^{2} G_{2} }}{{N_{r,1}^{2} }} + \frac{{2N_{r,6} }}{{N_{r,1} N_{r,4} }} + \frac{{6Y_{r}^{2} N_{r,2} }}{{N_{r,1}^{2} N_{r,4} }} + \frac{{2N_{r,3} \sin 2\beta_{0} }}{{N_{r,4}^{2} }} + \frac{{4Y_{r} N_{r,2} N_{r,3} \sin \beta_{0} }}{{N_{r,1} N_{r,4}^{2} }} $$

(36)

where $N_{r,1} = C_{out}^{2} - X_{r}^{2} - Y_{r}^{2}$, $N_{r,2} = Y_{r} \cos \beta_{0} - X_{r} \sin \beta_{0}$, $N_{r,3} = X_{r} \cos \beta_{0} + Y_{r} \sin \beta_{0}$, $N_{r,4} = N_{r,1} + N_{r,2}^{2}$, $N_{r,5} = Y_{r} \cos \beta_{0} - 3X_{r} \sin \beta_{0}$, $N_{r,6} = 3Y_{r} \cos \beta_{0} - X_{r} \sin \beta_{0}$.

The floating ring is subjected to both the inner oil force and the outer oil force. The first floating ring bearing is located on disk 2. The second floating ring bearing is located on disk 3. The equations of the motion for the two floating rings can be given as

$$ \begin{gathered} m_{r} \ddot{X}_{{r{1}}} = F_{{x,{2}}}^{out} - F_{{x,{2}}}^{in} \hfill \\ m_{r} \ddot{Y}_{{r{1}}} = F_{{y,{2}}}^{out} - F_{{y,{2}}}^{in} - m_{r} g\cos \theta \hfill \\ \end{gathered} $$

(37)

$$ \begin{gathered} m_{r} \ddot{X}_{{r{2}}} = F_{{x,{3}}}^{out} - F_{{x,{3}}}^{in} \hfill \\ m_{r} \ddot{Y}_{{r{2}}} = F_{{y,{3}}}^{out} - F_{{y,{3}}}^{in} - m_{r} g\cos \theta \hfill \\ \end{gathered} $$

(38)

where m_r is the mass of floating ring.

The floating ring rotational speed ω_r largely determines the steady-state and dynamic force response of a floating ring bearing. An overly simplified analysis based on the short-length bearing model and nearly centered operation predicts a ring speed ratio equal to [30]

$$ \frac{{\omega_{r} }}{\omega } = \frac{1}{{1 + \mu_{out} L_{out} R_{r}^{3} C_{in} /(\mu_{in} L_{in} R_{r0}^{3} C_{out} )}} $$

(39)

2.3 Nonlinear Dynamics of Turbocharger Rotor System

The governing differential equation of turbocharger rotor Eqs. (1)–(16) and floating ring bearings Eqs. (37)-(38) are combined to form the equation of system for the turbocharger system. The combined equation in matrix form is shown as:

$$ {\mathbf{M}}\ddot{q} + \omega {\mathbf{G}}\dot{\user2{q}} + {\mathbf{K}}{\varvec{q}} = - {\varvec{F}}_{oil} + {\varvec{F}}_{ub} + {\varvec{F}}_{g} $$

(40)

where M is the mass matrix, G is the gyroscopic matrix and of the rotor-FRB system, K is the stiffness matrix, F_oil is the oil force vector of floating ring bearing, F_ub is the unbalance force vector, F_g is the gravitational force vector. The expression of these matries and vectors are:${\varvec{q}} = \left\{ {\begin{array}{*{20}c} {\varvec{X}} & {\varvec{Y}} & {{\varvec{X}}_{r} } & {{\varvec{Y}}_{r} } \\ \end{array} } \right\}^{T}$, ${\varvec{X}} = \left\{ {\begin{array}{*{20}l} {X_{1} } \hfill & {\varphi_{y1} } \hfill & {X_{2} } \hfill & {\varphi_{y2} } \hfill & {X_{3} } \hfill & {\varphi_{y3} } \hfill & {X_{4} } \hfill & {\varphi_{y4} } \hfill \\ \end{array} } \right\}$, ${\varvec{Y}} = \left\{ {\begin{array}{*{20}l} {Y_{1} } \hfill & {\varphi_{x1} } \hfill & {Y_{2} } \hfill & {\varphi_{x2} } \hfill & {Y_{3} } \hfill & {\varphi_{x3} } \hfill & {Y_{4} } \hfill & {\varphi_{x4} } \hfill \\ \end{array} } \right\}$, ${\varvec{X}}_{r} = \left\{ {\begin{array}{*{20}c} {X_{r1} } & {X_{r2} } \\ \end{array} } \right\}$, ${\varvec{Y}}_{r} = \left\{ {\begin{array}{*{20}c} {Y_{r1} } & {Y_{r2} } \\ \end{array} } \right\}$, ${\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{x} } & {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{M}}_{y} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{M}}_{r} } \\ \end{array} } \right]$, ${\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{G}}_{x} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{G}}_{y} } & {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{0}}_{{{4} \times {4}}} } \\ \end{array} } \right]$, ${\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{x} } & {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{0}}_{8 \times 8} } & {{\mathbf{K}}_{y} } & {{\mathbf{0}}_{{8 \times {4}}} } \\ {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{0}}_{{{4} \times 8}} } & {{\mathbf{0}}_{{{4} \times {4}}} } \\ \end{array} } \right]$, ${\mathbf{M}}_{x} = {\mathbf{M}}_{y} = {\text{diag}}\left\{ {\begin{array}{*{20}c} {m_{1} } & {J_{a1} } & {m_{2} } & {J_{a2} } & {m_{3} } & {J_{a3} } & {m_{4} } & {J_{a4} } \\ \end{array} } \right\}$, ${\mathbf{M}}_{r} = {\text{diag}}\left\{ {\begin{array}{*{20}c} {m_{r} } & {m_{r} } & {m_{r} } & {m_{r} } \\ \end{array} } \right\}$, ${\mathbf{G}}_{x} = - {\mathbf{G}}_{y} = {\text{diag}}\left\{ {\begin{array}{*{20}c} 0 & { - J_{p1} } & 0 & { - J_{p2} } & 0 & { - J_{p3} } & 0 & { - J_{p4} } \\ \end{array} } \right\}$, ${\mathbf{K}}_{x} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{x11} } & {{\mathbf{K}}_{x12} } \\ {{\mathbf{K}}_{x21} } & {{\mathbf{K}}_{x22} } \\ \end{array} } \right]$, ${\mathbf{K}}_{x11} = \left[ {\begin{array}{*{20}c} {\frac{{12EI_{1} }}{{l_{1}^{3} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }}} & { - \frac{{12EI_{1} }}{{l_{1}^{3} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }}} \\ {\frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{4EI_{1} }}{{l_{1} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{2EI_{1} }}{{l_{1} }}} \\ { - \frac{{12EI_{1} }}{{l_{1}^{3} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{12EI_{1} }}{{l_{1}^{3} }} + \frac{{12EI_{2} }}{{l_{2}^{3} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }} + \frac{{6EI_{2} }}{{l_{2}^{2} }}} \\ {\frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{2EI_{1} }}{{l_{1} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }} + \frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{4EI_{1} }}{{l_{1} }} + \frac{{4EI_{2} }}{{l_{2} }}} \\ \end{array} } \right]$, ${\mathbf{K}}_{x12} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ { - \frac{{12EI_{2} }}{{l_{2}^{3} }}} & {\frac{{6EI_{2} }}{{l_{2}^{2} }}} & 0 & 0 \\ { - \frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{2EI_{2} }}{{l_{2} }}} & 0 & 0 \\ \end{array} } \right]$, ${\mathbf{K}}_{x21} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{12EI_{2} }}{{l_{2}^{3} }}} & { - \frac{{6EI_{2} }}{{l_{2}^{2} }}} \\ 0 & 0 & {\frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{2EI_{2} }}{{l_{2} }}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]$, ${\mathbf{K}}_{x22} = \left[ {\begin{array}{*{20}c} {\frac{{12EI_{2} }}{{l_{2}^{3} }} + \frac{{12EI_{3} }}{{l_{3}^{3} }}} & { - \frac{{6EI_{2} }}{{l_{2}^{2} }} + \frac{{6EI_{3} }}{{l_{3}^{2} }}} & { - \frac{{12EI_{3} }}{{l_{3}^{3} }}} & {\frac{{6EI_{3} }}{{l_{3}^{2} }}} \\ { - \frac{{6EI_{2} }}{{l_{2}^{2} }} + \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{4EI_{2} }}{{l_{2} }} + \frac{{4EI_{3} }}{{l_{3} }}} & { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{2EI_{3} }}{{l_{3} }}} \\ { - \frac{{12EI_{3} }}{{l_{3}^{3} }}} & { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{12EI_{3} }}{{l_{3}^{3} }}} & { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} \\ {\frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{2EI_{3} }}{{l_{3} }}} & { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{{4}EI_{3} }}{{l_{3} }}} \\ \end{array} } \right]$, ${\mathbf{K}}_{y} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{y11} } & {{\mathbf{K}}_{y12} } \\ {{\mathbf{K}}_{y21} } & {{\mathbf{K}}_{y22} } \\ \end{array} } \right]$, ${\mathbf{K}}_{y11} = \left[ {\begin{array}{*{20}c} {\frac{{12EI_{1} }}{{l_{1}^{3} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} & { - \frac{{12EI_{1} }}{{l_{1}^{3} }}} & { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} \\ { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{4EI_{1} }}{{l_{1} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{2EI_{1} }}{{l_{1} }}} \\ { - \frac{{12EI_{1} }}{{l_{1}^{3} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{12EI_{1} }}{{l_{1}^{3} }} + \frac{{12EI_{2} }}{{l_{2}^{3} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }} - \frac{{6EI_{2} }}{{l_{2}^{2} }}} \\ { - \frac{{6EI_{1} }}{{l_{1}^{2} }}} & {\frac{{2EI_{1} }}{{l_{1} }}} & {\frac{{6EI_{1} }}{{l_{1}^{2} }} - \frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{4EI_{1} }}{{l_{1} }} + \frac{{4EI_{2} }}{{l_{2} }}} \\ \end{array} } \right]$, ${\mathbf{K}}_{y12} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ { - \frac{{12EI_{2} }}{{l_{2}^{3} }}} & { - \frac{{6EI_{2} }}{{l_{2}^{2} }}} & 0 & 0 \\ {\frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{2EI_{2} }}{{l_{2} }}} & 0 & 0 \\ \end{array} } \right]$, ${\mathbf{K}}_{y21} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{{12EI_{2} }}{{l_{2}^{3} }}} & {\frac{{6EI_{2} }}{{l_{2}^{2} }}} \\ 0 & 0 & { - \frac{{6EI_{2} }}{{l_{2}^{2} }}} & {\frac{{2EI_{2} }}{{l_{2} }}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]$, ${\mathbf{K}}_{y22} = \left[ {\begin{array}{*{20}c} {\frac{{12EI_{2} }}{{l_{2}^{3} }} + \frac{{12EI_{3} }}{{l_{3}^{3} }}} & {\frac{{6EI_{2} }}{{l_{2}^{2} }} - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & { - \frac{{12EI_{3} }}{{l_{3}^{3} }}} & { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} \\ {\frac{{6EI_{2} }}{{l_{2}^{2} }} - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{4EI_{2} }}{{l_{2} }} + \frac{{4EI_{3} }}{{l_{3} }}} & {\frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{2EI_{3} }}{{l_{3} }}} \\ { - \frac{{12EI_{3} }}{{l_{3}^{3} }}} & {\frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{12EI_{3} }}{{l_{3}^{3} }}} & {\frac{{6EI_{3} }}{{l_{3}^{2} }}} \\ { - \frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{2EI_{3} }}{{l_{3} }}} & {\frac{{6EI_{3} }}{{l_{3}^{2} }}} & {\frac{{4EI_{3} }}{{l_{3} }}} \\ \end{array} } \right]$, ${\varvec{F}}_{oil} = \left\{ {\begin{array}{*{20}c} {{\varvec{F}}_{o,x} } & {{\varvec{F}}_{o,y} } & {{\varvec{F}}_{o,r} } \\ \end{array} } \right\}^{T}$, ${\varvec{F}}_{o,x} = \left\{ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {F_{x,2}^{in} } \hfill & 0 \hfill & {F_{x,3}^{in} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right\}$, ${\varvec{F}}_{o,y} = \left\{ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {F_{y,2}^{in} } \hfill & 0 \hfill & {F_{y,3}^{in} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right\}$, ${\varvec{F}}_{o,r} = \left\{ {\begin{array}{*{20}c} {F_{x,2}^{out} - F_{x,2}^{in} } & {F_{x,3}^{out} - F_{x,3}^{in} } & {F_{y,2}^{out} - F_{y,2}^{in} } & {F_{y,3}^{out} - F_{y,3}^{in} } \\ \end{array} } \right\}$, ${\varvec{F}}_{ub} = \left\{ {\begin{array}{*{20}c} {{\varvec{F}}_{ub,x} } & {{\varvec{F}}_{ub,y} } & {{\varvec{F}}_{ub,r} } \\ \end{array} } \right\}^{T}$, ${\varvec{F}}_{ub,x} = \left\{ {\begin{array}{*{20}c} {m_{1} e_{1} \omega^{2} \cos \omega t} & 0 & 0 & 0 & 0 & 0 & {m_{4} e_{4} \omega^{2} \cos \omega t} & 0 \\ \end{array} } \right\}$, ${\varvec{F}}_{ub,y} = \left\{ {\begin{array}{*{20}c} {m_{1} e_{1} \omega^{2} \sin \omega t} & 0 & 0 & 0 & 0 & 0 & {m_{4} e_{4} \omega^{2} \sin \omega t} & 0 \\ \end{array} } \right\}$, ${\varvec{F}}_{ub,r} = {\mathbf{0}}_{{1 \times {4}}}$, ${\varvec{F}}_{g} = \left\{ {\begin{array}{*{20}c} {{\varvec{F}}_{g,x} } & {{\varvec{F}}_{g,y} } & {{\varvec{F}}_{g,r} } \\ \end{array} } \right\}^{T}$, ${\varvec{F}}_{g,x} = {\mathbf{0}}_{1 \times 8}$, ${\varvec{F}}_{g,y} = \left\{ {\begin{array}{*{20}l} { - m_{1} g\cos \theta } \hfill & 0 \hfill & { - m_{2} g\cos \theta } \hfill & 0 \hfill & { - m_{3} g\cos \theta } \hfill & 0 \hfill & { - m_{4} g\cos \theta } \hfill & 0 \hfill \\ \end{array} } \right\}$, ${\varvec{F}}_{g,r} = \left\{ {\begin{array}{*{20}c} {0} & {0} & { - m_{r} g\cos \theta } & { - m_{r} g\cos \theta } \\ \end{array} } \right\}$.

3 The Critical Speed of Nonlinear Turbocharger Rotor System

From Eq. (40), the static displacement of the turbocharger rotor system due to gravity can be obtained by solving the following equation.

$$ Kq_{0} = - F_{oil} (q_{0} ) + F_{g} $$

(41)

where F_oil is a nonlinear function for q₀, and q₀ is the static balance position.

Substituting ${\varvec{q}} = \overline{\user2{q}}(t) + {\varvec{q}}_{0}$ into Eq. (40), yields

$$ M\ddot{\overline{q}} + \omega G\dot{\overline{q}} + K\overline{q} + Kq_{0} = - F_{oil} + F_{ub} + F_{g} $$

(42)

The Taylor expansion of nonlinear oil force F_oil in q₀ is

$$ F_{oil} = F_{oil} (q_{0} ) + K_{oil} \overline{q} + N_{2} (\overline{q}^{2} ) + N_{3} (\overline{q}^{3} ) + \cdots $$

(43)

where

$$ K_{oil} = \frac{{\partial F_{oil} (q_{0} )}}{\partial q} $$

(44)

Substituting Eq. (41) and Eq. (43) into Eq. (42) and neglecting the nonlinear terms, one has

$$ M\ddot{\overline{q}} + \omega G\dot{\overline{q}} + (K + K_{oil} )\overline{q} = F_{ub} $$

(45)

The solution of Eq. (45) is

$$ \overline{\user2{q}} = {\varvec{u}}e^{\lambda t} $$

(46)

The frequency of the turbocharger rotor system can be obtained by solving the following eigenvalue problem.

$$ (\lambda^{2} {\mathbf{M}} + \lambda \omega {\mathbf{G}} + {\mathbf{K}} + {\mathbf{K}}_{oil} ){\varvec{u}} = {\mathbf{0}} $$

(47)

One can also solve the following generalized eigenvalue problem.

$$ \left( {\lambda {\mathbf{P}} + {\mathbf{Q}}} \right)\left\{ {\begin{array}{*{20}c} {\varvec{u}} \\ {\lambda {\varvec{u}}} \\ \end{array} } \right\} = {\mathbf{0}} $$

(48)

where

$$ {\mathbf{P}} = \left[ {\begin{array}{*{20}c} {\omega {\mathbf{G}}} & {\mathbf{M}} \\ {\mathbf{M}} & {\mathbf{0}} \\ \end{array} } \right] $$

(49)

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}} + {\mathbf{K}}_{oil} } & {\mathbf{0}} \\ {\mathbf{0}} & { - {\mathbf{M}}} \\ \end{array} } \right] $$

(50)

The eigenvalues of Eq. (48) are image, i.e., λ = iω_n. The positive ω_n means a forward mode (precession motions in the same sense of rotation as the own rotation of the shaft) and the negative ω_n means a backward mode. The evolution of ω_n as a function of the rotational speed of the rotor gives a Campbell diagram in the rotating frame. The critical speeds of the turbocharger rotor system are the intersection of the line ω_n = ω and the different order frequency curves in the Campbell diagram.

4 Results and Discussions

The turbocharger rotor-floating ring bearing system is a highly nonlinear system. However, the linear behavior of the system is still important to understand the nonlinear responses of this system. In this section, the critical speed of an inclined turbocharger rotor system is investigated. The main parameters are given in Table 1.

Table 1 Parameters of the rotor and floating ring

From Eq. (41), the static balance position q₀ is determined by the gravitational force vector. It means q₀ is affected by the inclined angle θ. Moreover, K_oil is determined by q₀. From Eq. (47), we can conclude that the natural frequency of the linear system of turbocharger rotor system is affected by θ. The natural frequencies of the linear system of turbocharger rotor system under five inclined angle θ, i.e. 0°, 30°, 45°, 60°, and 90°, are studied in the following.

When θ = 0°, the Campbell diagram of the turbocharger rotor system is shown in Fig. 3. The forward mode is indicated by solid line, while the backward mode is marked by dash line. The dash-dot line means ω_n = ω. The intersection of dash-dot line and solid line is the critical speed of forward mode. The intersection of dash-dot line and dash line is the critical speed of backward mode.

Fig. 3

The Campbell diagram of turbocharger rotor system with θ = 0°

In order to reveal the mode shape of the turbocharger rotor system, the first six rotor mode shapes when the rotating speed is 100000 r/min are given in Fig. 4. What can be appreciated is that the first four modes are rigid modes, the fifth and sixth modes are bending modes. The first mode is a conical whirl backward mode. The second mode is a conical whirl forward mode. The third mode is a cylindrical whirl backward mode. The fourth mode is a cylindrical whirl forward mode. The fifth mode is a bending backward mode. The sixth mode is a bending forward mode.

Fig. 4

Mode shapes of turbocharger rotor system with ω = 100,000 r/min and θ = 0°

From Fig. 3, we can see that the critical speed of the conical whirl backward mode is 12768 r/min. The critical speed of the conical whirl forward mode is 15497 r/min. The critical speed of the cylindrical whirl backward mode is 40504 r/min. The critical speed of the cylindrical whirl forward mode is 40594 r/min. The critical speed of the bending backward mode is 138142 r/min. The critical speed of the bending forward mode is 202203 r/min.

The Campbell diagram of the turbocharger rotor system when the inclined angle θ is 30° is presented in Fig. 5. It shows that the critical speeds of all the modes are decreased. The critical speed of the conical whirl backward mode is 11959 r/min. The critical speed of the conical whirl forward mode is 14535 r/min. The critical speed of the cylindrical whirl backward mode is 38310 r/min. The critical speed of the cylindrical whirl forward mode is 38419 r/min. The critical speed of the bending backward mode is 138076 r/min. The critical speed of the bending forward mode is 202089 r/min.

Fig. 5

The Campbell diagram of turbocharger rotor system with θ = 30°

When the inclined angle θ is increased to 45° the Campbell diagram of the turbocharger rotor system is plotted in Fig. 6. The critical speeds of all the modes are further decreased. The critical speed of the conical whirl backward mode is 10915 r/min. The critical speed of the conical whirl forward mode is 13306 r/min. The critical speed of the cylindrical whirl backward mode is 35527 r/min. The critical speed of the cylindrical whirl forward mode is 35664 r/min. The critical speed of the bending backward mode is 137997 r/min. The critical speed of the bending forward mode is 201953 r/min.

Fig. 6

The Campbell diagram of turbocharger rotor system with θ = 45°

When the inclined angle θ is increased to 60° the Campbell diagram of the turbocharger rotor system is given in Fig. 7. The critical speeds of all the modes are also decreased. The critical speed of the conical whirl backward mode is 9374 r/min. The critical speed of the conical whirl forward mode is 11481 r/min. The critical speed of the cylindrical whirl backward mode is 31553 r/min. The critical speed of the cylindrical whirl forward mode is 31740 r/min. The critical speed of the bending backward mode is 137893 r/min. The critical speed of the bending forward mode is 201777 r/min.

Fig. 7

The Campbell diagram of turbocharger rotor system with θ = 60°

When the turbocharger rotor is vertical, i.e. θ = 90°, the Campbell diagram of the turbocharger rotor system is revealed in Fig. 8. The critical speeds of all the modes are decreased greatly. The critical speed of the conical whirl backward mode is 2724 r/min. The critical speed of the conical whirl forward mode is 3863 r/min. The critical speed of the cylindrical whirl backward mode is 20047 r/min. The critical speed of the cylindrical whirl forward mode is 20408 r/min. The critical speed of the bending backward mode is 137640 r/min. The critical speed of the bending forward mode is 201355 r/min.

Fig. 8

The Campbell diagram of turbocharger rotor system with θ = 90°

Table 2 and Fig. 9 show the critical speed of the turbocharger rotor system under different inclined angle θ. It clearly shows that the critical speed of the turbocharger rotor system is decreased as the inclined angle θ increases.

Table 2 The critical speed of turbocharger rotor system with different inclined angle

Fig. 9

The critical speed of turbocharger rotor system with different inclined angle

Figure 10 depicts the decrease of the critical speed versus inclined angle. One can see that the critical speed decreases of backward and forward with the same vibration mode are almost the same. Moreover, among the three vibration modes, i.e. conical whirl, cylindrical whirl, and bending, the critical speed of cylindrical whirl furnishes the highest decrease while the critical speed of bending attains the lowest decrease. In order to avoid resonance, the rotating speed of the turbocharger rotor should be far from the critical speed. Actually, the turbocharger rotor is operating in a quite wide speed range which is between the critical speed of cylindrical whirl mode and the critical speed of bending mode. More important the operating speed range is enlarged when the inclined angle of the turbocharger rotor is increased from 0 to 90°. It means the vertical turbocharger rotor has a more wide operating speed range than the horizontal turbocharger rotor.

Fig. 10

The decrease of critical speed of turbocharger rotor system with different inclined angle

5 Conclusions

In order to reveal the influence of weight on the critical speed of an inclined turbocharger rotor coupled with floating ring bearings, the nonlinear dynamic model of the turbocharger rotor system is derived using the lumped mass model and the Capone’s model. The critical speed of the linear system of the turbocharger rotor system is calculated. Three vibration modes, i.e. conical whirl, cylindrical whirl, and bending are obtained. Increasing the inclined angle would decrease the critical speed. Among the three vibration modes, the critical speed of cylindrical whirl furnishes the highest decrease while the critical speed of bending attains the lowest decrease. The vertical turbocharger rotor has a more wide operating speed range than the horizontal turbocharger rotor.