1 Introduction

The Philippine Sea plate moves northwestward with a speed of about 8 cm/year (Yu et al. 1997) to collide the Eurasian plate in Taiwan (e.g., Hsu 1971; Tsai et al. 1977; Wu 1978). The collision boundary is almost along the eastern coastal line of Taiwan. The collision yields high seismicity in the region (Hsu 1961; Wang et al. 1983; Wang 1988a, 1998; Wang and Shin 1998). The Hualien area is located around the northern segment of the collision boundary. Historically, many large earthquake sequences, for example, the 1951 sequence (e.g., Chen et al. 2007; Lee et al. 2008), the 1986 sequence (Chen and Wang 1986, 1988; Liaw et al. 1986; Wang, 1988b, 1998; Yeh et al. 1990), the 2002 sequence (e.g., Chen et al. 2004), and the 2018 sequence (e.g., Hwang et al. 2018; Kou-Chen et al. 2018; Wu et al. 2019), occurred in the area. The 1951 earthquake sequence and the 2018 earthquake caused serious damage in the area. Hence, the studies of earthquakes in the area are important and significant for both scientific interest and social needs.

The Central Weather Bureau reported the occurrence of an earthquake swarm with the largest event of local magnitude ML = 6.2 in Hualien, Taiwan, during April 7–August 31, 2021. The events are located at an area from 23°47′ N to 24°04′ N and from 121°25′ E to 121°42′ E. The focal depths, H, of the events were mainly in the range 0–25 km. Since an earthquake swarm does not often happen in the area, it is significant to investigate its characteristics.

There are numerous scaling laws, for example, the frequency-magnitude law (Gutenberg and Richter 1944), scaling laws of earthquake faults (see Wang 2018), and scaling law of earthquake source spectra (see Wang 2019), to describe self-similarity or scale-invariance of earthquakes and faults. In 1950’s, a mathematician Benoit B. Mandelbrot proposed the concept of fractal geometry with fractal dimension to describe the self-similar or scale-invariant natural phenomena (see Mandelbrot 1983). His concept has deeply influenced the Euclidean geometry. Mandelbrot (1989) measured fractal dimensions for geophysical problems. Fractal geometry has been widely applied to describe earthquake phenomena, including the spatial distributions of earthquakes (e.g., Hirata 1989; Turcotte 1989; Hirabayashi et al. 1992; Wang and Lin 1993; Wang and Lee 1995, 1996; Wang and Shen 1999; Wang et al. 2014; Fan and Lin 2017; Sri Lakshmi and Banerjee 2019; Hui et al. 2020), the time sequences of earthquakes (e.g., Smalley et al. 1987; Hirata 1989; Kagan and Jackson 1991; Ogata and Abe, 1991; Papadopoulos and Dedousis 1992; Koyama et al. 1995; Wang 1996; Wang and Lee 1995; Tang et al. 2012; Wang et al. 2014; Hui et al. 2020), the fault activities (e.g., Aviles et al. 1987; Okubo and Aki 1987; Lee 1995; Chang et al. 2007; Zhao et al. 2011; Ni et al. 2017), and the preseismic electromagnetic (EM) signals (e.g., Gotoh et al. 2003; Kiyashchenko et al. 2004; Ida et al. 2012; Smirnova et al. 2012). The studies made by Tang et al. (2012), Hui et al. (2020), Gotoh et al. (2003), Kiyashchenko et al. (2004), Ida et al. (2012), and Smirnova et al. (2012) are concerning the preseismic seismicity and EM signals for predicting an impending earthquake. These studies are useful for the estimates of seismic hazard.

For a fractal set of objects, the Hausdorff–Besicovitch dimension is not exactly equal to the Euclidean or topological dimension (Mandelbrot 1983). Mandelbrot (1983) defined the fractal dimension to represent a fractal set. Since the Hausdorff–Besicovitch’s definition is not convenient for measuring the fractal dimension of a set of objects in the real world, several different fractal dimensions have been defined (e.g., Grassberger and Procaccia 1983; Takayasu 1990). Four commonly-used dimensions are the similarity dimension DS, the capacity dimension DCA, the information dimension DI, and the correlation dimension DC. Their definitions can see Takayasu (1990). In general, the relationship among the four dimensions is DS = DCA ≥ DI ≥ DC. The equality DS = DCA = DI = DC holds only for homogeneous fractal sets. Most sets of natural objects are not perfectly self-similar and indeed multifractal, thus leading to DS = DCA > DI > DC. This indicates that a single fractal dimension is not good enough to characterize the fractal properties of natural objects. Therefore, fractality of objects has been extended from a single fractal dimension to the multifractal (or generalized fractal) dimension, Dq (Grassberger 1983; Hentshe and Procaccia 1983). Wang and Lee (1995) assumed that it is more complete to represent multifractality of a set of objects by using a Dq–q relation than by only taking the above-mentioned four fractal dimensions.

In this study, we will explore the self-similarity of the 2021 Haulien earthquake swarm by measuring the multifractal dimensions of ML ≥ 3 events with H ≤ 25 km for both the spatial distributions and time sequence. In the space domain, both the epicentral and hypocentral distances are taken into account.

2 Data

Since 1991, the Central Weather Bureau (CWB) has upgraded her old seismic network, by adding many new stations. This new network is named the CWB Seismic Network (CWBSN). In 1992 the Taiwan Telemetered Seismographics Network (TTSN), that was originally operated by the Institute of Earth Sciences, Academia Sinica (Wang 1989), was merged into the CWBSN. The earthquake magnitude of the earthquake catalogue has been unified to be the local magnitude (Shin 1992) that is denoted as ML. A detailed description about the CWBSN can be found in Shin (1992) and Shin and Chang (2005). The CWBSN is now composed of 72 stations, each equipped with three-component digital velocity seismometers, and many accelerations and broadband seismometers. The seismograms are recorded in both high- and low-gain forms. This network provides high-quality digital earthquake data to the seismological community. The data used in this study are directly retrieved from the CWB data base.

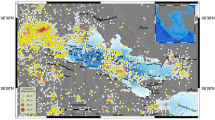
The earthquake epicenters of the swarm are plotted in Fig. 1. The location uncertainty of epicenter is about 2 km and the depth uncertainty is about 5 km (Shin and Chang 2005). The earthquakes with ML ≤ 6.2 occurred in an area from 23°47′ N to 24°04′ N and from 121°25′ E to 121°42′ E. We have to consider the size of the study area. The length of one degree of latitude slightly varies with latitude, while that of longitude remarkably varies with latitude (see Karney 2012). The lengths of one degree of latitude and one degree of longitude may be calculated from https://www.nhc.noaa.gov/gccalc.shtml which is the website of the National Hurricane Center, National Oceanic and Atmospheric Administration, USA. For the study area, the average lengths are ~ 31.13 km along the latitude, i.e., the NS direction, and ~ 28.62 km along the longitude, i.e., the EW direction. Hence, the study area is 31.13 × 28.62 km2 = 890.99 km2. The figure exhibits that most of the events are located at the Longitudinal Valley, some at the Costal Range, and some offshore. Figure 2a shows the depth distribution of number of events in a 5-km range along a selected longitude. The focal depths of the events were mainly in the range 0–25 km: a few events in the depth range 0–5 km and most of the events in the depth range 5–10 km. Wang et al. (1994) reported that inland earthquakes in Taiwan are located mainly in the depth range 0–12 km and the number of events remarkably decrease with increasing depth. The crust-upper mantle boundary with vp = 7.5 km/s in the Taiwan region is mainly in the range 35–45 km as inferred by several authors (e.g., Rau and Wu 1995; Ma et al. 1996; Kim et al. 2005). Hence, an average depth of 40 km is taken as a boundary to classify the events: a crustal event with H ≤ 40 km and an upper-mantle or subduction-zone event with H > 40 km. Hence, most of the events of the earthquake swarm are crustal earthquakes. Figure 2 also shows that there are three events with H > 25.0 km. Their epicenters that are all offshore are displayed by solid circles in Fig. 1.

Fig. 1
figure 1

Epicenters of ML ≥ 3 events with H ≤ 25 km of the 2021 earthquake swarm in Hualien, Taiwan. Different sizes of circles represent the magnitudes of earthquakes. The black solid circles denote the epicenters of three events with H > 25 km

Full size image
Fig. 2
figure 2

a for the depth distribution of number of ML ≥ 3 earthquakes in a depth unit of 5 km; and b for time sequences of magnitudes of ML ≥ 3 earthquakes with H ≤ 25 km. A vertical dashed line at H = 40 km in a is used to distinguish the crustal and mantle earthquakes

Full size image

Figure 2b shows the time sequence of earthquake magnitudes for ML ≥ 3 events with H ≤ 25 km. Clearly, the time sequence is not uniform. The frequency of events is high in some short time intervals and low in others. The largest inter-event time is 8.742 days and the shortest one is smaller than 1 day.

3 Multi-fractal dimension

3.1 Spatial distributions of earthquakes

The multifractal or generalized fractal dimension, Dq, in the space domain is defined by the following expression (Grassberger 1983; Hentschel and Procaccia 1983):

$$D_{q} = {\text{lim}}[{\text{log}}\left( {\Sigma p_{i}^{q} } \right)/{\text{log}}(\delta)]/\left( {q - {1}} \right)$$
(1)

where the parameter q can be any real number in the range from − ∞ to ∞ and pi is the probability that an event falls into a box with a length δ. Dq at large, positive q shows the fractal property of dense regions with large pi; while Dq at large, negative q displays that of thin regions with small pi. Dq for negative q may be larger than the spatial (or topological) dimension, d (d = 2 for the 2D space and d = 3 for 3D space), in Euclidean geometry. There is no geometric sense for Dq > d (Mandelbrot, 1989). For a set of objects, the value of Dq at small q shows the fractal property of its coarse structure and that at large q exhibits the fractal property of its fine structure. For q ≥ 0, the largest Dq is D0 and Dq decreases with increasing q. If two sets of objects have the same Dq–q relations, they are considered to be statistically similar. Note that D0, D1, and D2 are equivalent to the capacity dimension DCA, information dimension DI, and correlation dimension DC, respectively.

The probability pi may be estimated by the box-counting method from the observed data. Since such a method requires a large number of data, it is not so useful in practice. Kurths and Herzel (1987) suggested a correlation integral method as described below. A local density function nj(r) is defined by the following expression:

$$n_{j} \left( r \right) = \Sigma_{k} Q\left( {r - |{\mathbf{r}}_{j} - {\mathbf{r}}_{k} |} \right)/\left( {{\text{N}} - {1}} \right)$$
(2)

where the value of Θ(s) is 1 if s ≥ 0 and 0 if s < 0. In Eq. (2), rj and rk are the position vectors of events j and k, respectively, and thus |rj − rk| is the distance between the two events. A vector ri is denoted by < xi, yi, zi > where xi, yi, and zi are the latitude multiplied by 111 km, the longitude multiplied by 111 km, and the focal depth (in km), respectively. The value of 111 km is almost the length of 1° along both latitude and longitude on the ground surface (Oncel et al. 1995). Hence, a generalized correlation integral Cq(r) for the distance between two events is defined by

$$C_{q} \left( r \right) = \left[ {\Sigma n_{j}^{{q - }{1}} \left( r \right)} \right]^{{{1}/(q - {1})}} .$$
(3)

Cq(r) is considered to be related to r in the following power-law function with the scaling exponent Dq:

$${\text{C}}_{{\text{q}}} \left( {\text{r}} \right)\sim r^{Dq} .$$
(4)

There are two kinds of distance. The first one is the epicentral distance:

$$r_{jk} = \left| {{\mathbf{r}}_{j} - {\mathbf{r}}_{k} } \right| = \left[ {\left( {x_{j} - x_{k} } \right)^{{2}} + \left( {y_{j} - y_{k} } \right)^{{2}} } \right]^{{{1}/{2}}} .$$
(5)

This gives the so-called 2D measure. The second one is the hypocentral distance:

$$r_{jk} = \left| {{\mathbf{r}}_{j} - {\mathbf{r}}_{k} } \right| = \left[ {\left( {x_{j} - x_{k} } \right)^{{2}} + \left( {y_{j} - y_{k} } \right)^{{2}} + \left( {z_{j} - z_{k} } \right)^{{2}} } \right]^{{{1}/{2}}} .$$
(6)

This gives the so-called 3D measure.

When the study area is large, Hirata (1989) considered the spherical effect for rjk from the formula: rjk = cos−1[cosθjcosθk + sinθjsinθkcos(ϕj − ϕk)] where θi and ϕi are, respectively, the co-latitude and longitude of event i on the spherical surface. Some authors (e.g.,Oncel et al. 1995; Telesca et al. 2001; Marquez-Ramirez et al. 2012) used this formula to calculate the distance between two events for large study areas. However, since the area of this study is small (< 1° along both the latitude and the longitude), it is not necessary to consider the spherical effect. Hence, our calculations for rjk are merely based on Eqs. (5) and (6).

3.2 Time sequence of earthquakes

In order to study multifractal behavior of time sequence of earthquakes, Wang and Lee (1995) replaced the two spatial quantities by a time interval t and an inter-event time |ti–tk|, respectively. Hence, a generalized correlation integral Cq(t) for the time sequence is

$$C_{q} \left( t \right) = \left[ {\Sigma n_{j}^{q - 1} \left( t \right)} \right]^{1/(q - 1)} .$$
(7)

Cq(t) is considered to be related to t in the following power-law function with the scaling exponent Dq:

$$C_{q} \left( t \right)\sim t^{Dq} .$$
(8)

In the followings, first the values of Cq(r) and Cq(t) will be calculated from the data. Secondly, the log–log plots of Cq(r) versus r and those of Cq(t) versus t at different q’s will be first constructed. Finally, the value of Dq is evaluated from the slope of the linear portion of data points. In this study, only the values of Dq at positive q = 2, 3, …, 15, are calculated because we are only interested in the fractal properties of denser areas and time intervals.

4 Results

4.1 Spatial distributions of earthquakes

The value of Cq(r) are calculated from the spatial distributions of earthquakes of the 2021 Hualien swarm. The log–log plots of Cq(r) versus r at q = 2, 3, …, 15 are displayed in Fig. 3 for the 2D measure and in Fig. 4 for the 3D measure. In the two figures, the value of q increases from bottom to top. Since the uncertainty of epicenter is 2 km and the uncertainty of focal depth is about 5 km as mentioned above, the smallest distance, rl, is taken to be the average of the two values, i.e., 3.5 km, thus giving log(rl) = 0.54. In the following, we take log(ro) = 0.5. Since the lengths along the EW and along the NS direction are 31.13 km and 28.62 km, respectively, as mentioned above and the deepest focal depth is 25.0 km, the longest distance, rc, is (31.132 + 28.622)1/2 km = 42.29 km for the 2D measure and (31.132 + 28.622 + 25.02)1/2 km = 49.12 km for the 3D measure. This gives log(rc) = 1.63 for the 2D measure and log(rc) = 1.69 for the 3D measure. Li et al. (1994) suggested that the upper bound of the linear portion, rc, should be 30% or 50% of the largest distance between two events to avoid the possible existence of roll-over. According to their criterion, the value of rc of this study must be shorter than 12.69 km or 21.15 km for the 2D measure and 14.74 km or 24.56 km for the 3D measure. Nevertheless, rc is here still taken to be 50.7 km, i.e., log(50.7) = 1.71, for both 2D and 3D measures for the purpose of examining the possible existence of ‘roll-over’ which means that the deflection of data points from the regression line more or less in a shape of part of a circle. Hence, the data points are plotted in the range 0.5 ≤ log(r) ≤ 1.71. The regression line is inferred from the data in the range 0.5 ≤ log(r) ≤ 1.3. In Fig. 3, a vertical dashed line denotes log(ru) = 1.3. The degree of scattering of data points is higher in Fig. 4 than in Fig. 3.

Fig. 3
figure 3

The log–log plot of Cq(r) versus r at q = 2, 3, …, 15 (from bottom to top) for ML ≥ 3 events under 2D measure. The solid lines represent the regression lines inferred from the data points with 0.5 ≤ log(r) ≤ 1.5. A vertical dotted line denotes the upper bound of log(r), i.e., log(ru) = 1.3, for conducting linear regression

Full size image
Fig. 4
figure 4

The log–log plot of Cq(r) versus r at q = 2, 3, …, 15 (from bottom to top) for ML ≥ 3 events under 3D measure

Full size image

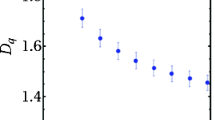
In Fig. 3 for the 2D measure, the data points are well distributed around a linear trend when 0.5 ≤ log(r) ≤ log(ru) where ru is the upper bound distance, and the data points are roll-over when log(r) > log(ru). The value of log(ru) is 1.5 and thus ru = 101.5 km = 31.6 km, which is 74.72% of rc = 42.29 km, for the 2D measure. The percentage for the 2D measure is 24.72% higher than the upper bound by Li et al. (1994). However, Fig. 5 displays that for 3D measure a linear pattern of log–log plot of Cq(r) versus r at each q, especially at larger q, appears only in a narrow range of log(r). Hence, we do not measure the values of Dq for the 3D measure. The least-squared method is applied to infer a linear regression equation to fit the linear portion of data points. Dq is just the slope value of the linear equation. For the 2D measure, the values of Dq at q = 2, 3, …, 15 and their standard deviations are listed in Table 1. The obtained Dq–q relations are shown in Fig. 5 with solid circles. Clearly, Dq decreases with increasing q.

Fig. 5
figure 5

The plot of Dq versus q: solid cycles for 2D measure of epicentral distribution and solid squares for the time sequence of events

Full size image
Table 1 The values of Dq with standard errors at q = 2, 3, …, 15 for the spatial distribution of events under 2D measure and those for the time sequence of events
Full size table

4.2 Time sequence of earthquakes

For the multifractal measures in the time domain, the maximum inter-event time is 8.792 days. The generalized correlation integral functions Cq(t) versus inter-event time t in days between two events at q = 2, 3, …, 15 are calculated from the data. The log–log plot of Cq(t) versus t are displayed in Fig. 6, in which the value of q increases from bottom to top. The data points are plotted in the range 0.5 ≤ log(t) ≤ 2.15. The upper bound time interval is tc = 102.15 days = 140 days that is almost equal to the time period of the swarm, i.e., 139.779 days. Obviously, the data points are linearly well distributed only in a range 0.5 ≤ log(t) ≤ log(tu) where log(tu) = 1.0 and thus tu = 101.0 days = 10 days. In Fig. 6, a vertical dotted line denotes log(tu) = 1.0. The regression line is plotted in the range 0.5 ≤ log(t) ≤ 1.0. When log(t) > 1.0, the pattern of data points shows ‘roll-over.’ Hence, the values of Dq that are evaluated from the data points are listed in Table 1. The Dq–q relation is shown in Fig. 5 with solid squares. Clearly, Dq decreases with increasing q. From Table 1, the evaluated values of Dq for the two cases are considered to be acceptable because the deviations of Dq at all q’s are lower than 0.014.

Fig. 6
figure 6

The log–log plots of Cq(t) versus t at q = 2, 3, …, 15 (from bottom to top) for ML ≥ 3 events. The solid lines represent the regression lines inferred from the data points with 0.5 ≤ log(t) ≤ 1.0. A vertical dotted line denotes the upper bound of log(t), i.e., log(tu) = 1.0, for conducting linear regression

Full size image

5 Discussion

5.1 Spatial distributions of earthquakes

For the epicentral distributions of earthquakes, the log–log plots of Cq(r) versus r are displayed in Fig. 3 for the 2D measure. There is a linear pattern when 0.5 ≤ log(r) ≤ 1.3 in Fig. 3. Results clearly suggest that the epicentral distribution of ML ≥ 3 events of the Hualien swarm is multifractal. In advance, the linear pattern of data points does not appear in the whole range of log(r) or r. This means that the finite size effect of the study area might influence multifractality. The finite size effect is also reported by Wang et al. (2014). The value of log(ru) of the linear portion is 1.3 or ru = ~ 20.0 km. The lengths along the latitude and longitude are 31.13 km and 28.62 km, respectively. This gives the longest length of the 2D structure to be rc = 42.29 km. Figure 1 shows that the epicenters are distributed almost in the entire study area along the longitude and latitude. Hence, for the 2D measure ru is shorter than rc and comparable to the length either along the latitude or along the longitude. Figure 3 also show that the pattern of data points is roll-over when log(r) > 1.3 because the values of log[Cq(r)] for log(r) > 1.3 are smaller than those calculated from the linear regression equation done from the data points with 0.5 ≤ log(r) ≤ 1.3. Table 1 demonstrates that the values of Dq for the 2D measure have the largest one of 1.107 and much smaller than 2 that is the spatial dimension in Euclidean geometry. This reflects the existence of many large voids in the 2D space of the study area (see Fig. 1). This makes the multifractal dimensions be much smaller than the space dimension, i.e., d = 2.

For the hypocentral distribution of earthquakes, the log–log plots of Cq(r) versus r are displayed in Fig. 4 for the 3D measure. The linear pattern only appears in a narrow range of log(r). Results clearly suggest that the hypocentral distribution of ML ≥ 3 events of the Hualien swarm is not multifractal. The upper bound of log(ru) for the linear pattern of data points is ~ 1.0, thus giving ru = 10 km. This reflects the finite size effect of the study area on multifractality. Since the deepest focal depth in use is 25 km, the longest length of the 3D structure is rc = 50.7 km. Nevertheless, Fig. 2a shows that most of the events in study are located within a focal depth range 0–10 km, thus leading to ru = 10 km. Clearly, for the 3D measure ru is much shorter than rc and mainly controlled by the focal depth of 10 km within which most of the events are located. Figure 2a displays that there are several tens of events with 10 km ≤ H ≤ 25 km. The depth range 10 − 25 km is longer than that 0 − 10 km. Hence, the spatial structure of the hypocentral distribution for the 3D measure is very sparse because there are many voids within the structure, especially in the depth range 10 − 25 km. This makes the log–log plots of Cq(r) versus r be very scattering, especially for log(r) > 1.0, thus being unable to lead to a wide enough range of log(r) for the linear pattern of data points. Hence, we cannot estimate the value of Dq for the 3D measure.

Wang and Lin (1993) and Wang and Lee (1996) measured the multifractal dimensions for the earthquakes with MD ≥ 1 (MD = the duration magnitude) in west Taiwan. They divided the study area into the north and south zone. They obtained that all Dq’s are smaller than 2 and the values of Dq (= 1.4–1.6) in the south zone with ru = 40 km are larger than those (= 1.0–1.3) in the north zone with ru = 25 km. The values of ru = 40 and 25 km are almost the smallest widths of epicentral distributions of the north and south zones, respectively. Considering 2D measure, the values of Dq of the 2021 Hualien earthquake swarm are smaller than those measured by Wang and Lee (1996) for earthquakes in the north and south zones in west Taiwan. The lower-bound magnitude was 1 for the earthquakes used by Wang and Lee (1996) and is 3 for the events of this study. This suggests that when more events with smaller magnitudes are taken into account, the values of Dq should be larger because of a decrease in spatial voids. For both 2D and 3D measures, Wang et al. (2014) measured the values of Dq from the ML ≥ 3 shallow earthquakes with H ≤ 40 km in the Taipei Metropolitan Area (TMA) during 1973–2010. In their study, the linear portion of the log–log plot of Cq(r) versus r appears in between log(rl) and log(ru). For the 2D and 3D measures, the value of log(rl) is 0.3 that is similar to the value of this study. The values of log(ru) are 1.7 and 1.4, respectively, for the 2D and 3D measures. For the 2D measure, their value is larger than that of this study. Their values of Dq are smaller than the spatial dimensions 2 and 3, respectively, for the 2D and 3D measures. Their values of Dq for 2D measures are similar to those of this study, thus suggesting similar 2D fractal structures in the two areas.

5.2 Time sequence of earthquakes

For the time sequence, the log–log plots of Cq(t) versus t as displayed in Fig. 6 for 0.5 ≤ log(t) ≤ 2.15. Clearly, the log–log plot shows a linear relationship in a large range of 0.5 ≤ log(t) ≤ 1.0 in which the value of Dq are evaluated. This suggests that the time sequence of ML ≥ 3 earthquakes of the swarm is multifractal. The values of Dq are all smaller than 0.475 and much smaller than 1. Table 1 and Fig. 5 with solid squares exhibit that as q > 10, the values of Dq are very similar for different q’s. The upper bound time for the linear portion is log(tu) = 1.0 or tu = 10 days. This value is only slightly larger than the maximum inter-event time of 8.792 days of the time sequence. This suggests that the maximum inter-event time is a factor in controlling whether or not a time sequence is multifractal.

Kagan and Jackson (1991) stated that the 1D process is Poissonian if the correlation dimension (i.e., D2) is 1, that is the standard time dimension, over the whole time period from zero to infinity. For global seismicity, they found that the mainshocks of earthquake sequences are specified with long-term, weak clustering and governed by a power-law temporal distribution. The correlation dimension of time sequences of those mainshocks is 0.8–0.9. This suggests that the mainshock occurrence is almost a stationary Poisson process. Wang (1996) measured the values of Dq for 44 Ms ≥ 7 earthquakes of Taiwan from 1900 to 1994 (Wang and Kuo 1995). Only the values of Dq for q < 7 were measured because the log–log plot of Cq(t) versus t is linearly well distributed for q < 7. This indicates that Ms ≥ 7 earthquakes in Taiwan shows multifractality only for the coarse structures of time sequence. In addition, the earthquake sequence shows a somewhat strong Poisson process because of D2 = 0.72. Smalley et al. (1987) measured the values D2 for the seismicity of the New Hebrides between mid-1978 and mid-1984. The measured values are D2 = 0.126–0.255. This makes them to assume that the earthquake occurrences significantly deviate from random or Poisson behavior. In comparison with previous three studies, the component of Poisson processes is weak in the time sequence of the 2021 Hualien earthquake swarm because of D2 = 0.475.

6 Conclusions

An earthquake swarm occurred in the Hualien area (from 23°47′ N to 24°04′ N and from 121°25′ E to 121°42′ E) during April 7–August 31, 2021. From the ML ≥ 3 events with H ≤ 25 km, the values of Cq(r) are calculated for the spatial distributions of both epicenters (2D measure) and hypocenters (3D measure) based on the distance between two events, r, and those of Cq(t) for the time sequence using the inter-event time between two events, t. The values of Dq are measured from the linear portions of the log–log plots of Cq(r) versus r and Cq(t) versus t. In the space domain, the maximum epicentral and hypocentral distance are 42.29 km and 49.12 km, respectively. The degree of scattering of data points is much higher for the 3D measure than for the 2D measure. For the 2D measure, there is a linear pattern in the range log(ro) ≤ log(r) ≤ log(ru) and roll-over when log(r) > log(ru) on the log–log plot. The values of log(ro) and log(ru) are, respectively, 0.5 and 1.3. The values of Dq are all smaller than 2 that is the spatial dimension in Euclidean geometry and monotonically decreases with increasing q. This indicates that the epicentral distribution of ML ≥ 3 earthquakes of the swarm shows multifractality when the epicentral distances are shorter than ru = 20.0 km, which is shorter than the length of the study area along either the latitude or the longitude. On the other hand, there is only a narrow linear pattern of data points on the log–log plot under the 3D measure for the hypocentral distribution. This means that the hypocentral distribution of ML ≥ 3 earthquakes of the swarm is not multifractal. In the time domain, the maximum inter-event time is 8.792 days. The log–log plot of Cq(t) versus t does show a linear pattern in a range of 0.5 ≤ log(t) ≤ 1.0, thus suggesting multifractality of the time sequence of ML ≥ 3 events of the swarm when the inter-event intervals are shorter than 8.792 days.