1 Introduction

Earthquakes are classic examples of complex phenomena that exhibit scale-invariance and fractality in their collective properties. These properties are revealed both in nature and laboratory experiments where the spatial, temporal and size distributions of earthquakes or laboratory acoustic emissions display structures that are invarient in scale (e.g., Sammonds et al., 1992; Main, 1996; Turcotte, 1997). The emergence of these properties is indicative of complexity and nonlinear dynamics in the earthquake generation process (Kagan, 1994), such that concepts like fractals and multifractals are becoming increasingly fundamental for understanding geophysical processes and estimating seismic hazard more efficiently. The general objective of this kind of analysis is to characterize the structure of the earthquake activity in a seismic region and evaluate qualitatively and, if possible, quantitatively its dynamical evolution. Following this approach, the fractal dimension has been used to characterize the degree of clustering in seismic sequences and laboratory acoustic emissions (Kagan and Knopoff, 1980; Smalley et al., 1987; Hirata et al., 1987; Hirata, 1989) and to map the dynamical evolution of the states in the seismogenic system (Singh et al., 2008).

In nature, though, most fractals in complex dynamical systems are known to be heterogeneous (Mandelbrot, 1989). Since earthquakes are the result of complex interactions operating in different scales, it is reasonable to expect the need for multifractal concepts to describe seismicity. In particular, properties like non-stationarity and intermittency are common in earthquake sequences such that the clustering degree varies with time. These variations can be identified by multifractal approaches that can enlighten the local fluctuations in the scaling properties of seismicity and then provide an appropriate tool for mapping the dynamical changes that take place in the physical process of seismogenesis (Geilikman et al., 1990; Godano et al., 1997). This ability has been in fact used in various studies in the detection of possible temporal changes in the multifractal dimension prior to large earthquakes (Hirabayashi et al., 1992; Nakaya and Hashimoto, 2002; Kiyashchenko et al., 2003).

Earthquake temporal clustering is revealed in aftershock sequences, where the Omori’s scaling relation states that the aftershock production rate decays as a power law with time (Omori, 1894; Utsu et al., 1995). Short-term and long-term clustering has also been exhibited in various earthquake sequences (Kagan and Jackson, 1991) and recently in the West Corinth rift, where the presence of scaling and two power law regions in short and long time intervals has been shown (Michas et al., 2013). These properties are indicative of non-stationary temporal clustering, multifractality and long-term memory in the earthquake generation process (e.g., Livina et al., 2005). The multifractal structure of interevent time series has been exhibited in various earthquake sequences (Godano and Caruso, 1995; Godano et al., 1997; Enescu et al., 2006; Telesca and Lapenna, 2006) and in the West Corinth rift (Telesca et al., 2002). These properties have led recently to the consideration of non-extensive statistical mechanics as an appropriate framework for studying the collective properties of earthquake time series based on the principle of entropy (e.g., Tsallis, 2009; Vallianatos et al., 2012; Papadakis et al., 2013; Michas et al., 2013).

In this work we study the earthquake time series of the recent activity in one of the most seismically active areas in Europe, the Corinth rift. The earthquake activity in the Corinth rift is typically characterized by fluctuating behavior, where periods of low to moderate activity are interspersed by sudden seismic bursts, which are related to frequent earthquake swarms and the occurrence of stronger events, followed by aftershock sequences. This intermittent behavior constitutes the multifractal approach as an appropriate tool to study the local fluctuations, the degree of clustering, and the dynamic variability of the seismotectonic activity in this region.

2 2008–2013 Earthquake Activity in the Corinth Rift

The area of Greece represents the most seismically active area in Europe due to its location on a tectonically active plate boundary in the convergence of the Eurasian and African lithospheric plates (Fig. 1) (e.g., Le Pichon and Angelier, 1979). In the back-arc region significant extension is taking place in the Aegean (e.g., Mercier et al., 1989; Le Pichon et al., 1995) that is accommodated across a series of extending grabens, such as the North Aegean trough, the Euboea graben, and the Corinth rift. In the latter area, a rapid continental extension of the order of 1.5 to 1 cm/year is taking place in the west and east part, respectively, (Briole et al., 2000) that classifies Corinth rift among the fastest extending continental rifts of the world. Deformation is accommodated by a S-dipping and N-dipping active normal fault system at the north and south margin of the rift respectively of an en echelon E-W system, creating an asymmetric tectonic graben (e.g., Armijo et al., 1996).

The high earthquake activity of the area is revealed from both historic and instrumental records, where several earthquakes of magnitude greater than 6 have occurred in the past (Ambraseys and Jackson, 1990, 1997; Latoussakis et al., 1991; Drakatos and Latoussakis, 1996; Papazachos and Papazachou, 1997; Papadopoulos et al., 2000). The last major earthquake was the 1995 Aigion earthquake (M s  = 6.2) that occurred in the west part of the rift (Bernard et al., 1997) and since then the activity is dominated by low to intermediate size earthquakes and frequent earthquake swarms. In January 2010 an M w  = 5.1 earthquake, followed four days later by another strong event (M w  = 5.1) and numerous aftershocks, occurred in the west part of the rift near the city of Efpalion (Fig. 1), ending a 15-year period of relative seismic quiescence in the area (Karakostas et al., 2012; Sokos et al., 2012; Ganas et al., 2013).

Fig. 1
figure 1

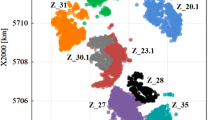
The 2008–2013 earthquake activity in the Corinth rift for M L  ≥ 2. Solid black lines represent faults in the broader area. Inset map of the broader area of Greece and the main tectonic features (SHSZ South Hellenic Subduction Zone, NHSZ North Hellenic Subduction Zone, KT Kephalonia Transform Fault). The rectangle marks the area of study

Full size image

In this work we study the 2008–2013 earthquake activity in the Corinth rift, as has been recorded by the Hellenic Unified Seismological Network (HUSN) (http://www.gein.noa.gr/en/networks/husn). HUSN started operating in 2007 as a nationwide unified network, linking the main seismological networks that operate in Greece and providing a better monitoring coverage for the wider area. Evaluation of the seismic network through simulations indicated that the magnitude of completeness (M c ) of HUSN catalog is approximately equal to 2 in most parts of continental Greece, with minimum 1.6 in the West Corinth rift (D’Alessandro et al., 2011). The spatiotemporal evolution of the completeness magnitude (M c ) of HUSN catalog has also been studied in a recently published work (Mignan and Chouliaras, 2014). In this work, and by using the Bayesian magnitude of completeness (BMC) method (Mignan et al., 2011), it was shown that M c varies between 2 and 2.5 for 2008–2011 in the area of Corinth rift, while an upgrade of the magnitude determination software in 2011 resulted in the improvement of the catalog’s quality by shifting M c one magnitude unit lower, being around 1.5 for the area of central Greece.

The catalogue used in this study was extracted from the database of HUSN, available at (http://bbnet.gein.noa.gr/HL/). In Fig. 1 the crustal earthquake activity (depth ≤30 km) of magnitude M L  ≥ 2 that corresponds to 8,320 events is shown. As can be seen from the seismicity map (Fig. 1), the majority of earthquakes are occurring offshore and in the west part of the rift, while two other clusters can be recognized in the central offshore part and in the northeastern end of the rift. This image of the earthquake activity is consistent with geodetic surveys that indicate that high strain rates are currently accommodated offshore (Briole et al., 2000). In the northwestern part of the rift, the 2010 Efpalion earthquakes are highlighted as the largest earthquakes during this period (Fig. 1). The Efpalion earthquake sequence is also apparent in Fig. 2 where the seismicity rate and the magnitude rate per day are plotted. After the occurrence of the first event on 18 January 2010 there is a sudden increase in the seismicity rate due to the production of numerous aftershocks. Then the seismicity rate continues to fluctuate till the beginning of 2011 where a period of low earthquake activity and a rather constant seismicity rate per day initiates in the rift (Fig. 2a). This period lasts for more than 2 years where an increase in the seismicity rate is observed due to the occurrence of two earthquake swarms during 22/5/13–26/6/13 that both lasted approximately two weeks. The first one occurred near the city of Aigion and the second one at the northeastern end of the rift near Kapareli that was the epicentral area of the third strong earthquake (M s  = 6.4) of the 1981 earthquake sequence (Jackson et al., 1982).

Fig. 2
figure 2

a Seismicity rate per day and b magnitude (M L ) rate per day

Full size image

3 Multifractal Analysis

While several methods have been used in the literature to perform multifractal analysis in non-stationary fluctuating signals, the two most widely used are the wavelet transform modulus maxima method (WTMM) (Muzy et al., 1991) and the multifractal detrended fluctuating analysis (MF-DFA) (Kantelhardt et al., 2002). The main advantage of these two methods is that they can eliminate polynomial trends from the signal and avoid artifacts due to non-stationarity. Although both methods can reliably estimate the multifractal structure of the analyzed signal, MF-DFA is preferred due to its simpler implementation and computational effort. MF-DFA also seems to perform slightly better than WTMM for short series (Kantelhardt et al., 2002), and it is recommended in the majority of situations in which the fractal character of the signal is unknown a priori (Oświecimka et al., 2006).

Multifractal detrended fluctuation analysis (MF-DFA) consists of the following steps. Let’s consider a fluctuating signal u(i) of total length N (i = 1,…,N) and of compact support, where u(i) = 0 has an insignificant fraction in the series. The signal is first shifted by the average ‹u› and integrated,

$$y(k) = \sum\limits_{i = 1}^{k} {[u(i) - {\langle }u{\rangle }]} ,$$
(1)

with k = 1,2,…,N. Then the integrated signal y(k) is divided into non-overlapping segments of equal size n resulting in N n  = (N/n) segments. Since the length N of the signal is not always a multiple of the segments size n, a short part at the end of the integrated signal y(k) is not included in the analysis. In order not to disregard this part, the procedure is repeated starting from the end of y(k), resulting in this way into 2N n total segments (Kantelhardt et al., 2001). In each of the 2N n segments, the integrated signal y(ν) (ν = 1,2,…2N n ) is fitted to a polynomial function y n (ν) that represents the local trend. For different orders l of the polynomial function, different trends can be removed from the signal. Thus, the polynomial trend is linear when l = 1, quadratic when l = 2, and cubic when l = 3. Then the integrated signal y(ν) is “detrended” by subtracting the local trend y n (ν) in each window, and the root mean-square fluctuation F(n, ν) is calculated,

$$F(n,\nu ) = \sqrt {\frac{1}{{2N_{n} }}\sum\limits_{\nu = 1}^{{2N_{n} }} {\left[ {y(\nu) - y_{n} (\nu)} \right]}^{2} }.$$
(2)

Then, the qth order fluctuation function is obtained after averaging over all segments,

$$F_{q} (n) = \left\{ {\frac{1}{{2N_{n} }}\sum\limits_{\nu = 1}^{{2N_{n} }} {[F^{2} (n,\nu )]^{q/2} } } \right\}^{1/q} ,$$
(3)

where the index variable q can take any real value. The standard detrended fluctuation analysis (DFA) corresponds to q = 2. The previous steps have to be repeated for various time scales n to obtain the relationship between the generalized q dependent fluctuation functions F q (n) and the time scales n. Then, the scaling behavior of the fluctuation functions can be determined by analyzing the plots of F q (n) and n for each value of q. If the series u(i) are long-range power law correlated, F q (n) will increase as a power law for the various values of n,

$$F_{q} (n)\sim n^{h(q)}.$$
(4)

For a stationary series, h(2) is identical to the Hurst exponent H (Hurst, 1951; Feder, 1988). Thus, h(q) may be called the generalized Hurst exponent or alternatively the q-order Hurst exponent. In the limit q → 0, the value of h(0) cannot be determined directly from Eq. (3) due to the diverging exponent and a logarithmic averaging procedure is employed,

$$F_{0} (n) \equiv \exp \left\{ {\frac{1}{{4N_{n} }}\sum\limits_{\nu = 1}^{{2N_{n} }} {1{\text{n[}}F^{2} (n,\nu ) ]} } \right\}.$$
(5)

For multifractal series, the exponent h(q) will depend on the various values of q. In this case small and large fluctuations scale differently. For positive values of q, the segments ν with large variance F 2(n, ν) will dominate the average F q (n) and h(q) will describe the scaling behavior of the segments ν with large fluctuations. For negative values of q, h(q) will describe the scaling behavior of the segments ν with small fluctuations, as the segments ν with small variance F 2(n, ν) will dominate the average F q (n) (Kantelhardt et al., 2002). On the other hand, if the series is monofractal, the scaling behavior of the variances F 2(n, ν) is similar for all segments ν and h(q) will be independent of q.

The q-order Hurst exponents h(q) is only one of various types of scaling exponents that are used to characterize the multifractal structure of a signal. In fact, it has been shown (Kantelhardt et al., 2002) that the multifractal scaling exponents h(q) defined in Eq. (4) can be directly related to the q-order mass exponents τ(q) that correspond to the multifractal formalism based on the standard partition function as,

$$\tau (q) = qh(q) - 1.$$
(6)

Typically, for random and monofractal series the mass exponent τ(q) has a linear dependency on q, while for multifractal series this linearity breaks.

Another way to characterize multifractal series is the singularity spectrum f(a) that can be directly obtained from the mass exponents τ(q) by using the Legendre transform (Feder, 1988):

$$\alpha = \frac{{{\text{d}}\tau }}{{{\text{d}}q}}.$$
(7)

Then the singularity spectrum f(a) can be obtained as

$$f(\alpha ) = q\alpha - \tau (q),$$
(8)

where a is the singularity strength or Hölder exponent and f(a) indicates the dimension of the subset of the series that has the same singularity strength a. In a monofractal series the singularity strength is the same in the entire range of the set so that the singularity spectrum collapses into a single point. The singularity spectrum f(a) and the generalized Hurst exponents h(q) can be considered as fundamental characteristics of a multifractal set.

4 Results

We applied MF-DFA in the interevent time series, i.e., the series of the time intervals between the successive earthquake events, defined as τ = τ (i + 1) − τ (i) (i = 1, 2,…, N – 1, where N is the total length). We performed the analysis for earthquakes with magnitude M ≥ M th = 2.6, considering that the selection of this threshold magnitude (M th) insures magnitude completeness for the studied area and the considered period (see discussion in Sect. 2). The interevent time series of total length N = 5,233 was initially divided into non-overlapping segments of minimum size n = 10 events up to the maximum size of N/4. Figure 3 shows the logarithm of the fluctuation functions F q (n) versus the logarithm of the segment size n that resulted from the analysis for q \(\in\) [−5, 5] and step size 0.2. Generally F q (n) grows as a power-law with n, indicating the presence of scaling. After performing the analysis for various orders l of the “detrending” polynomial function y n (ν), a second order (l = 2) polynomial function was considered sufficient to remove any possible trends from the series. For the segments of size greater than 285 events, considerable fluctuations in F q (n) for q < −2 are appearing due to the small number of segments that are formed in greater sizes (Fig. 3). These fluctuations can influence the least square fitting procedure for the low values of q. Thus, we restricted the fitting procedure up to the segment size n of 285 events (Fig. 3). For the various values of q, the fluctuation curves have different slopes in the range 0.623–1.073 for q = 5 and q = −5, respectively, indicating that small and large fluctuations scale differently. The entire range of the generalized Hurst exponents h(q) is shown in Fig. 4. The exponents h(q) are decreasing monotonically with increasing q that is typical for multifractal sets.

Fig. 3
figure 3

The logarithm of the fluctuation function F q (n) versus the logarithm of the segment size n for various values of q in the interval [−5, 5] and step size 0.2. A second order polynomial (l = 2) was used for detrending the interevent time series

Full size image
Fig. 4
figure 4

The spectrum of the generalized Hurst exponents h(q) for various values of q \(\in\) [−5, 5] and step size 0.2. The corresponding confidence intervals are plotted as error bars. The q-dependence of h(q) is typical for multifractal sets. The mean h(q) that resulted from ten randomly shuffled copies of the original interevent time series is also plotted

Full size image

Another way to identify multifractality in a series is the mass exponent τ(q) that can be estimated directly from Eq. (6). Figure 5 shows that the mass exponent τ(q) grows nonlinearly with q, exhibiting different behavior for q < 0 and q > 0 as can be expected for a multifractal set. Then, by using the Legendre transform (Eq. 7), we estimated the singularity spectrum f(a) from Eq. (8) for the various Hölder exponents a. The singularity spectrum f(a) indicates the fractal dimensions of the subsets that have the same singularity strength a and gives information about the relative importance of each fractal dimension. The singularity strength a can be considered as a local measure of self-similarity in a time series or equivalently as a global indicator of the local differentiability in the time series. Figure 6 shows the singularity spectrum f(a) for the various Hölder exponents a. The spectrum is wide, indicating once again multifractality in the interevent time series. Additionally, the width W of the spectrum that can be estimated as W = a max − a min and in our case is W = 0.6, is a measure of how wide the range of fractal dimensions in the series is. It can be then considered as a measure of the degree of multifractality.

Fig. 5
figure 5

The mass exponent τ(q) versus q. For the original interevent time series τ(q) is nonlinear indicating multifractality. The mean τ(q) that resulted from ten randomly shuffled copies of the original interevent time series is also presented

Full size image
Fig. 6
figure 6

The singularity spectrum f(a) versus the Hölder exponent a. The original interevent time series exhibit a wide spectrum indicating multifractality. The mean spectrum of the randomly shuffled series exhibits a less wide spectrum indicating weaker multifractality

Full size image

In order to evaluate the effect of the threshold magnitude M th on the observed multifractality, we performed the analysis for various M th in the range 2–2.8 and present the results in Fig. 7, where the spectrum’s width W versus M th is plotted. In Fig. 7, we can observe that the selection of M th in the range 2–2.6 and the possible incompleteness of the catalog in the lower magnitudes does not affect the results of the analysis, while for greater M th a wider spectrum is observed, indicating a wider range of fractal dimensions.

Fig. 7
figure 7

Singularity spectrum’s width W for various threshold magnitudes M th

Full size image

Next we look into the origin of multifractality in the interevent time series. While different long-term correlations for small and large fluctuations in the earthquake time series are most likely the cause of the observed multifractality, a broad probability distribution can also engender multifractality (Kantelhardt et al., 2002). The simplest way to distinguish the type of multifractality in the series is by analyzing the corresponding randomly shuffled series. By randomly shuffling the series, any correlations due to the order of the successive earthquakes are destroyed, while the probability distribution remains unchanged. Hence, the shuffled series will exhibit non-multifractal scaling and a random behavior (h shuf(q) = 0.5) in the case of long-term correlations. In the other hand, the generalized Hurst exponents will not be affected by the shuffling procedure (h(q) = h shuf(q)) if multifractality appears due to a broad probability distribution. In the case where both types of multifractality are present in the time series, then the randomly shuffled series will exhibit a weaker multifractality than the original.

We performed this analysis by applying MF-DFA in ten randomly shuffled copies of the original interevent time series. Then we averaged the resulted values to obtain the mean h(q), τ(q), α and f(α) for the ten randomly shuffled copies, which are shown in Figs. 4, 5, and 6, respectively, along with the results of the analysis on the original series. In Fig. 4 we can see that the shuffling procedure affects the values of the generalized Hurst exponents h(q), which are reduced to the range of values between 0.73 and 0.43 for q = −5 and q = 5, respectively, exhibiting weaker multifractality than the original series. The corresponding DFA scaling exponent h(2) is approximately equal to 0.5, indicating random behavior. Although the fluctuations of h(q) around the value of 0.5 indicate the loss of long-term correlations in the shuffled series, a q-dependence of h(q) still appears. This can also be observed in the plot of the mass exponents τ(q) (Fig. 5), where τ(q) is not linear with q and is made more apparent in the singularity spectrum f(α) (Fig. 6). Although is less wide than the spectrum of the original series, its width is still significant. Then the contribution of a broad probability distribution in the observed multifractality in the time series cannot be excluded. It has been in fact shown that the probability distribution of the interevent times in the West Corinth rift for the period 2001–2008 exhibits both short-term and long-term clustering effects and the presence of scaling at short time and long time intervals (Michas et al., 2013). This is a property shared by the dataset that we consider in the present study that covers the broader area of the Corinth rift (work under preparation).

The multifractal analysis described previously gives us important insights about the time dynamics of the earthquake activity during the considered period, but it does not give us any information about the dynamical changes that may occur in the evolution of the earthquake activity. In order to perform such an analysis, we apply MF-DFA at different time intervals by using a sliding temporal window F that depends on the width w and the sliding factor Δ (Gamero et al., 1997). In each temporal window the set of interevent times τ is defined according to:

$$F_{m} = \{ \tau_{j} ,j = 1 + m\varDelta , \ldots ,w + m\varDelta \} ,m = 0,1,2, \ldots ,M,$$

where m controls the time displacement of the sliding window. The width of w = 103 and the sliding factor of Δ = 10 events was used, resulting in 99 % overlapping between the successive windows. This choice of w and Δ assures that in each time window there is a sufficient number of data to perform the analysis and a good smoothing and resolution among the estimated values and the time. Then, in each time window, we apply MF-DFA on the interevent time series as previously and estimate the width W of the singularity spectrum f(α) as a measure of the degree of multifractality in each time period. The estimated value was then associated with the time of the last earthquake in each window. The results of this analysis are presented in Fig. 8. The degree of multifractality exhibits strong variations in time that are associated with the range of fractal dimensions present in each time period. In particular, these variations are more intense during 2009–2011, where the seismicity rate exhibits sharp increases (Fig. 2a). The most abrupt change in the multifractal behavior of the series occurs during the aftershock sequence that followed the 18/1/2010 Efpalion earthquake. During this period, when the aftershock sequence dominates the earthquake activity in the rift, the degree of clustering increases and the time dynamics are more homogeneous, resulting in a loss of multifractality and into a tendency towards monofractality. Telesca and Lapenna (2006) have observed a similar behavior in central Italy, where a loss of multifractality in the interevent time series occurred during the aftershock sequence that followed a strong event (M D  = 5.8) on September 26, 1997. During the period of 2011–2013, where the earthquake activity is relatively low (Fig. 2a), the degree of multifractality is nearly constant and the width of the singularity spectrum takes values around 1.5–2. In periods where both low and increased earthquake activity are incorporated in the dataset, the spectrum is “richer” in structure, with a wider range of fractal dimensions. We can observe this effect in the beginning of 2011 and immediately after the occurrence of the 18/1/10 Efpalion earthquake, where a sharp increase of W is observed, before the interevent times of the aftershock activity starting to dominate the series, causing the sharp decrease of W.

Fig. 8
figure 8

The width (W) of the singularity spectrum f(a) as a measure of multifractality in time for a window of 1,000 events sliding in time every ten events

Full size image

5 Discussion and Conclusions

In the present work we studied the structure and the clustering properties of the 2008–2013 earthquake time series in the Corinth rift by using multifractal detrended fluctuation analysis (MF-DFA), which is a suitable method to study the clustering variability of non-stationary fluctuating signals. The multifractal analysis showed that small time and large time intervals scale differently, indicating a multifractal structure in the interevent time series and a heterogeneous degree of clustering. These results imply non-Poissonian temporal evolution of the earthquake activity in the Corinth rift. The presence of a broad probability distribution on the other hand, can enhance multifractality in the analyzed series. To distinguish this effect, we analyzed the randomly shuffled series, which showed the loss of correlations and a weaker multifractality than the original series, indicating that the observed multifractality is mainly due to different scaling of the subsets and to a lower extent due to a broad probability distribution.

The analysis of the singularity spectrum’s width as a degree of multifractality in time exhibited high variability over a large range of scales for the different time periods. The large oscillations are related to variations between high and low earthquake activity, indicating an internal instability in the geodynamic behavior of the system. The most prominent effect is the loss of multifractality after the Efpalion earthquake due to greater homogeneity in the time series of the aftershock sequence that followed the main event. Coulomb stress analysis of the Efpalion earthquake showed static stress triggering of the second strong event four days later (Karakostas et al., 2012; Ganas et al., 2013), while the spatiotemporal analysis of the entire aftershock sequence indicated a slow stress diffusion process as the most possible mechanism for the slow migration of the aftershock zone after the occurrence of the second strong event (Michas et al., 2014). This particular process corresponds to a slow subdiffusive process, in accordance with anomalous stress diffusion in earthquake triggering on a global scale (Huc and Main, 2003) and aftershocks diffusion in California (Helmstetter et al., 2003). Diffusion is known to generate hierarchical clustering in very short times and small spatial scales (e.g., Godano et al., 1997). In this process, the influence of small earthquakes on local stress changes and stress diffusion cannot be considered negligible (Helmstetter et al., 2005), especially when the spatial clustering is strong like in the Corinth rift. In addition, high pore fluid pressures can reduce the effective normal stress in fault zones and trigger earthquakes. This is a mechanism that might be quite important in the seismogenic process in the Corinth rift, especially during sudden earthquake swarms (Bourouis and Cornet, 2009; Pacchiani and Lyon-Caen, 2010). In a critically stressed crust, these processes can influence substantially the geodynamic behavior of the system and mark the critical transitions that occur between periods of high and low earthquake activity.

Concluding, the dynamic multifractality in earthquake time series in the Corinth rift indicated strong clustering variability that is inherently related to the seismotectonic complexity in this region, where pore pressure induced seismicity and anomalous stress diffusion can be important factors in the seismogenic process.