Influence of induced magnetic field and surface roughness of Casson nanofluid flow over an exponentially stretching sheet

Abstract

In the present analysis, we have discussed the mixed convective of flow over an exponential sheet in presence of induced magnetic field and surface roughness. The effects of hall current and chemical reaction on flow are also considered. The non-Newtonian model behavior is characterized by Casson nanofluid. The similarity transformations are employed for the transformation of partial differential equations into non-dimensional form and obtained equations are solved by employing the Differential transformation method (DTM). Further, the importance of various parameters on various profiles and gradients are explored graphically with some suitable discussion. At the wall, the small ($\alpha$) and frequency ($n$) parameters influence on gradients are illustrated.

1 Introduction

A generalized word for the small irregularities in the surface texture of different materials that are frequently created during production is surface roughness. This inquiry is especially important because of how surface roughness affects the rates of heat and mass transfer between both the fluid and the surrounding surface. Several scientific and technological fields use surface roughness, including heat transfer devices, electronic cooling methods, and heat transfer exchangers [1,2,3]. Numerous researchers have conducted extensive research on the influence of roughnesson flows closer to the surface. By examining the changes in heat transfer rates, Smith and Epstein [4] and Kemeny and Cyphers [5] have conducted research on rough surfaces. Surface roughness has been examined by Owen and Thompson [6] using horseshoe-shaped vortices. Furthermore, Dipprey and Sabersky [7] examined how transverse slots affected the flow of fluid. How unnatural roughness influence on heat and motion transfer changes has been studied by Savage and Myers [8]. Townes and Sabersky [9] and Dawson and Trass [10], respectively, explored how surface roughness affected turbulent flow and mass transfer rates. Kandlikar et al. [11] continued the investigation on surface roughness, and their analysis was primarily oriented on fluid flow over small diameter tubes. AbuNada et al. [12] and Sheremet et al. [13] have recently investigated the role of wavy surfaces in improving the efficiency of different transport rates. Additionally, Salimpour et al. [14] focused on the impacts of surface roughness in their study on nanofluid pool boiling.

Keller and Magyari [15] were the first to propose the concept of fluid flow over an exponential sheet. They gave information about the properties of mass and heat transportation as well as numerical solutions over an exponentially sheet. The concept of boundary layer flow caused by exponential sheet is an important consideration in industries and engineering fields such as plastic paper manufacturing, and thinning and annealing of copper wire. The stretched velocity is not always linear, meaning that the stretching fluid’s velocity may be nonlinear or exponential. Srinivasacharya and Jagadeeshwar [16] have investigated the flow with hall current effect over an exponentially sheet. The influence of hall currents over an exponential sheet has been studied by Sarojamma et al. [17]. Recently, Asjad et al. [18], Muhammad et al. [19] and Prasannakumara [20] have analyzed the effects of chemical reaction on MHD nanofluid flow due to exponential sheet and the effects of Hall current on nanofluid flow over an exponentially sheet respectively.

When working fluid’s magnetic Reynolds number is so small, significance of the induced magnetic field is typically ignored in technical and industrial uses. When the magnetic Reynolds number $\ge 1,$ the impact of the induced magnetic field is actually most noticeable. The investigation of the induced magnetic field becomes important because of its numerous applications in science and the real world, including the production of glass, nuclear reactors, MHD energy generation systems, and so on. The impact of an induced magnetic field on the flow and heat transfer has received very little consideration to date. For instance, Kumari et al. [21] studied the MHD flow and heat transfer under the influence of an induced magnetic field. Recent investigations on induced magnetic field with various geometries are made by Amir Abbas et al. [22], Sahoo and Nandkeolyar [23], and Singh and Vishwanath [24].

The normal conductivity of the magnetic field is deduced to the free spiraling of electrons and ions around the magnetic lines force before colliding when the fluid is an ionised gas and the applied magnetic field is large. At this moment, the magnetic and electric fields both generate a current in a normal path. This process is called Hall effect. In a rarefied medium or a strong magnetic field, the impact of Hall current cannot be disregarded. The analysis of flows involving Hall current has significant industrial uses in a variety of geophysical and astrophysical situations as well as in a number of engineering challenges, including those involving Hall accelerators, Hall effect sensors. It is crucial to examine how Hall current affects fluid flow in the context of these uses. The first person to describe the Hall Effect on two parallel plates in a magnetic field was Sato [25]. Recent studies on Hall Effect are [26,27,28].

Due to the wide range of applications, the phenomenon of non-Newtonian fluids is receiving a significant amount of attention. One of the most important models that demonstrates the properties of yield stresses among all non-Newtonian liquid models is Casson’s fluid flow model, which was first proposed for the flow of non-Newtonian liquids in 1995.The mixing of the solid and liquid phases is the foundation of the Casson liquid model and it behaves like a solid when yield stresses dominate shear stresses. On the other hand, it begins to move when the yield stresses are lower than the shear stresses. Honey, hot sauce, and blood are a few examples of Casson liquids. This flow model finds use in the treatment of cancer. Nandkeolyar and Prashu [29] have investigated the flow of a Casson fluid. Reddy Konda et al. [30] have studied the mixed convection flow of Casson nanofluid on a nonlinear sheet. Whereas, Prabhakar et al. [31] have discussed the chemical reaction on Casson nanofluid over an exponentially sheet. Numerical solutions of the Casson nanofluid on sheet with porous medium are discussed by Ahmed et al. [32]. Very recently, Suresh Kumar et al. [33] and Sinha et al. [34] investigated the MHD Casson nanofluid flow with various effects.

The net influence of all the previously mentioned factors have not even been tried to be taken into account in any of the above mentioned analyses. The investigation’s main originality and area of interest is how exponential stretching sheets are affected by the Casson nanofluid mixed convective flow under the influence of surface roughness, induced magnetic field, hall current, and chemical reaction. The production of polymer sheets is relevant to the current mathematical modelling. Additionally, these sheets that emerge from the slit during manufacture might not be completely smooth and might have some surface roughness. Such roughness is thought to be modelled by a sine wave form in terms of $\alpha$ and $n$. Thus, the results of the current analysis are of interest to the design engineers in the polymer industries and assist them by providing the design parameters to control the heat and mass transport rates that decide the ultimate quality of the manufactured product. Here, Differential Transform Method (DTM) is used in the present paper to solve the equations. Without the requirement for an initial guess or discretization, DTM is employed to solve nonlinear ODE problems directly and is undisturbed by discretization defects [35,36,37]. The influences of relevant parameters on various profiles are provided with appropriate explanation.

2 Mathematical formulation

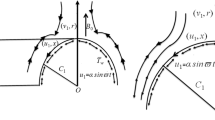
The surface roughness of Casson nanofluid flow over an exponentially stretching sheet with induced magnetic acting along the vertical channel is shown in Fig. 1.

Fig. 1

Schematic diagram of physical problem

The governing equations are given below [19, 24, 28, 30]:

The equation for continuity:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0, $$

(1)

$$ \frac{{\partial H_{1} }}{\partial x} + \frac{{\partial H_{2} }}{\partial y} = 0, $$

(2)

$$ u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \upsilon \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + g^{*} \beta_{T} \left( {T - T_{\infty } } \right) + g^{*} \beta_{C} \left( {C - C_{\infty } } \right) - \frac{{\sigma B^{2} }}{{\rho \left( {1 + m^{2} } \right)}}\left( {u + mw} \right) + \frac{\mu }{4\pi \rho }\left[ {H_{1} \frac{{\partial H_{1} }}{\partial x} + H_{2} \frac{{\partial H_{2} }}{\partial y}} \right], $$

(3)

$$ u\frac{\partial w}{{\partial x}} + v\frac{\partial w}{{\partial y}} = \upsilon \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\sigma B^{2} }}{{\rho \left( {1 + m^{2} } \right)}}\left( {mu - w} \right) + \frac{\mu }{4\pi p}\left[ {H_{1} \frac{{\partial H_{1} }}{\partial x} + H_{2} \frac{{\partial H_{2} }}{\partial y}} \right], $$

(4)

$$ u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha^{^{\prime\prime}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{B} \frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} } \right], $$

(5)

$$ u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \left( {C - C_{\infty } } \right)K_{r} , $$

(6)

$$ u\frac{{\partial H_{1} }}{\partial x} + v\frac{{\partial H_{1} }}{\partial y} = \mu_{e} \frac{{\partial^{2} H_{1} }}{{\partial y^{2} }} + H_{1} \left( {\frac{\partial u}{{\partial x}} + \frac{\partial w}{{\partial x}}} \right) + H_{2} \left( {\frac{\partial u}{{\partial y}} + \frac{\partial w}{{\partial y}}} \right). $$

(7)

The boundary conditions are given below [15,16,17, 19, 24]:

$$ u = U_{w} = U_{0} e^{\frac{x}{L}} \left[ {1 + \alpha Sin\left( \frac{nx}{L} \right)} \right],\,\,v = 0,\,\,w = 0,\,\,H_{1} = 0,\,\,\frac{{\partial H_{1} }}{\partial y} = H_{2} = 0,\,\,C = C_{w} ,\,\,T = T_{w} \,\,{\text{at}}\,\,y = 0, $$

(8)

$$ u \to 0,\,\,w \to 0,\,\,T \to T_{\infty } ,\,\,C \to C_{\infty } ,\,\,H_{1} \to H_{\infty } \,\,{\text{as}}\,\,y \to \infty . $$

(9)

$$ H_{\infty } = H_{0} e^{\frac{x}{L}} $$

Similarity transformations are:

$$ \left. \begin{gathered} u = U_{0} \exp \left( \frac{x}{L} \right)f{^\prime} \left( \eta \right),\,\,v = - \sqrt {\frac{{\upsilon U_{0} }}{2L}} e^{\frac{x}{2L}} \left[ {f\left( \eta \right) + \eta f{^\prime} \left( \eta \right)} \right],\,\,T = T_{\infty } + T_{0} e^{\frac{2x}{L}} \theta \left( \eta \right),\,\,C = C_{\infty } + C_{0} e^{\frac{2x}{L}} \phi \left( \eta \right),\,\, \hfill \\ H_{1} = H_{0} e^{\frac{x}{L}} h{^\prime} \left( \eta \right),\,\,H_{2} = - \sqrt {\frac{\upsilon }{{2U_{0} L}}H_{0} } e^{\frac{x}{2L}} \left[ {h\left( \eta \right) + \eta h{^\prime} \left( \eta \right)} \right],\,\,\eta = y\sqrt {\frac{{U_{0} }}{2\upsilon L}} e^{\frac{x}{2L}} ,\,\,\,\xi = \frac{x}{L},\,\,\,\psi = \sqrt {2\upsilon U_{0} L} e^{\frac{x}{2L}} f\left( \eta \right), \hfill \\ w = U_{0} e^{\frac{x}{L}} g\left( \eta \right),\,\,B = B_{0} e^{\frac{x}{2L}} . \hfill \\ \end{gathered} \right\}\, $$

(10)

where $\psi (x,y)$ is:

$$ u = \frac{\partial \psi }{{\partial y}},\,\,\,\,v = - \frac{\partial \psi }{{\partial x}}\,\, $$

(11)

$$ \left( {1 + \frac{1}{\beta }} \right)f^{\prime \prime \prime } - 2\left( {f^{\prime } } \right)^{2} + ff^{\prime \prime } - \frac{{2{\mkern 1mu} Ha}}{{\left( {1 + m^{2} } \right)}}\left( {f^{\prime } + mg} \right) + 2\lambda \left( {\theta + {\text{N}}\phi } \right) + 2M\left[ {\left( {h^{\prime } } \right)^{2} - \frac{1}{2}hh^{\prime } } \right] = 0, $$

(12)

$$ \left( {1 + \beta } \right)g^{^{\prime\prime}} - 2f{\prime} g + fg{\prime} + \frac{2\,Ha}{{\left( {1 + m^{2} } \right)}}\left( {mf{\prime} - g} \right) + 2M\left[ {\left( {h{\prime} } \right)^{2} - \frac{1}{2}hh{\prime} } \right] = 0, $$

(13)

$$ \theta^{^{\prime\prime}} + \Pr \left( {f\theta{\prime} - 4f{\prime} \theta + Nb\theta{\prime} \phi{\prime} + Nt\left( {\theta{\prime} } \right)^{2} } \right) = 0, $$

(14)

$$ \phi^{^{\prime\prime}} + Sc\left( {f\phi{\prime} - 4f{\prime} \phi - 2\phi \chi } \right) + \frac{Nt}{{Nb}}\theta^{^{\prime\prime}} = 0, $$

(15)

$$ \gamma h^{\prime \prime \prime } - hf^{\prime \prime } + fh^{\prime \prime } - hg^{\prime } + 2h^{\prime } g = 0. $$

(16)

Simultaneous boundary conditions are

$$ \left. \begin{gathered} f{\prime} \left( \eta \right) = 1 + \alpha Sin\left( {n\xi } \right),\,\,f = 0,\,\,g = 0,\,\,h{\prime} = 0,\,\,h = 0,\,\,\theta = 1,\,\,\phi = 1\,\,\,{\text{at}}\,\,\eta = 0, \hfill \\ f{\prime} \to 0,\,\,g \to 0,\,\,\,h{\prime} \to 1,\,\,\theta \to 0,\,\,\phi \to 0\,\,\,{\text{as}}\,\,\eta \to \infty . \hfill \\ \end{gathered} \right\}\,\, $$

(17)

The parameters are defined as:

$$ \left. \begin{gathered} Gr = \frac{{g^{*} \beta_{T} T_{0} L^{3} }}{{\upsilon^{2} \,}},\,\,{\rm N} = \frac{{\beta_{C} C_{0} }}{{\,\beta_{T} T_{0} \,}},\,\,\lambda = \frac{{g^{*} \beta_{T} T_{0} L}}{{U_{0}^{2} \,}},{\text{Re}} = \frac{{U_{0} L}}{\upsilon },\,\,Ha = \frac{{\sigma B_{0}^{2} L}}{{\rho U_{0} }},\,\,M = \frac{{\mu H_{0}^{2} }}{{4\pi pU_{0}^{2} }}, \hfill \\ \Pr = \frac{\upsilon }{{\alpha^{^{\prime\prime}} }},\,\,Nb = \frac{{\tau D_{B} C_{0} }}{\upsilon }e^{\frac{2x}{L}} ,\,\,Nt = \frac{{\tau D_{T} T_{0} }}{{T_{\infty } \upsilon }}e^{\frac{2x}{L}} ,\,\,Sc = \,\frac{\upsilon }{{D_{B} }},\,\,\gamma = \frac{{\mu_{e} }}{\upsilon }\,\,,\chi = \frac{{K_{0} L}}{{U_{0} }}. \hfill \\ \end{gathered} \right\}\,\, $$

(18)

3 Method of solution

The reduced governing Eqs. (12)–(16) with (17) are solved by employing DTM method. By employing DTM, we can find the solution of the Eqs. (12)–(16) with (17):

$$ \begin{gathered} \left( {l + 2} \right)\left( {1 + \frac{1}{\beta }} \right)\left( {l + 1} \right)\left( {l + 3} \right)F\left( {l + 3} \right) - 2\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)\left( {l - q + 1} \right)F\left( {l - q + 1} \right)} F\left( {q + 1} \right) + \hfill \\ \sum\limits_{q = 0}^{l} {\left( {l + 1} \right)\left( {l + 2} \right)} F\left( {q + 2} \right)F(l - q) - \frac{2\,Ha}{{(m^{2} + 1)}}\left( {\left( {l + 1} \right)F\left( {l + 1} \right) + mG(l)} \right) + 2\lambda \left( {T\left( l \right) + {\rm N}P\left( l \right)} \right) \hfill \\ + 2M\left( {\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)\left( {l - q + 1} \right)H\left( {l - q + 1} \right)} H\left( {q + 1} \right) - \frac{1}{2}\sum\limits_{q = 0}^{l} {\left( {l + 1} \right)} H\left( {q + 1} \right)H(l - q)} \right) = 0, \hfill \\ \end{gathered} $$

(19)

$$ \begin{gathered} \left( {l + 2} \right)\left( {1 + \frac{1}{\beta }} \right)\left( {l + 1} \right)G\left( {l + 2} \right) - 2\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)G\left( {l - q} \right)} F\left( {q + 1} \right) + \hfill \\ \sum\limits_{q = 0}^{l} {\left( {l + 1} \right)} G\left( {q + 1} \right)F(l - q) + \frac{2\,Ha}{{(m^{2} + 1)}}\left( {m\left( {l + 1} \right)F\left( {l + 1} \right) - G(l)} \right) + \hfill \\ + 2M\left( {\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)\left( {l - q + 1} \right)H\left( {l - q + 1} \right)} H\left( {q + 1} \right) - \frac{1}{2}\sum\limits_{q = 0}^{l} {\left( {l + 1} \right)} H\left( {q + 1} \right)H(l - q)} \right) = 0, \hfill \\ \end{gathered} $$

(20)

$$ \left( {l + 1} \right)\left( {l + 2} \right)T\left( {l + 2} \right) + \Pr \left\{ \begin{gathered} \sum\limits_{q = 0}^{l} {\left( {q + 1} \right)T\left( {q + 1} \right)} F\left( {l - q} \right) - 4\sum\limits_{q = 0}^{e} {\left( {q + 1} \right)F\left( {q + 1} \right)} T\left( {l - q} \right) + \hfill \\ Nb\,\,\sum\limits_{q = 0}^{e} {\left( {q + 1} \right)} \left( {l - q + 1} \right)P\left( {q + 1} \right)T\left( {l - q + 1} \right) + \hfill \\ Nt\,\,\sum\limits_{q = 0}^{e} {\left( {q + 1} \right)} \left( {l - q + 1} \right)T\left( {q + 1} \right)T\left( {l - q + 1} \right) \hfill \\ \end{gathered} \right\} = 0, $$

(21)

$$ \left( {l + 1} \right)\left( {l + 2} \right)P\left( {l + 2} \right) + Sc\left\{ \begin{gathered} \sum\limits_{q = 0}^{l} {\left( {q + 1} \right)P\left( {q + 1} \right)} F\left( {l - q} \right) - 2\chi P\left( l \right) - \hfill \\ 4\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)F\left( {q + 1} \right)} P\left( {l - q} \right) \hfill \\ \end{gathered} \right\} + \frac{Nt}{{Nb}}\left( {l + 1} \right)\left( {l + 2} \right)T\left( {l + 2} \right) = 0, $$

(22)

$$ \begin{gathered} \gamma \left( {l + 2} \right)\left( {l + 1} \right)\left( {l + 3} \right)H\left( {l + 3} \right) - \sum\limits_{q = 0}^{l} {\left( {q + 1} \right)\left( {q + 2} \right)H\left( {l - q} \right)} F\left( {q + 2} \right) + \hfill \\ \sum\limits_{q = 0}^{l} {\left( {l + 1} \right)\left( {l + 2} \right)} H\left( {q + 2} \right)F(l - q) - \sum\limits_{q = 0}^{l} {\left( {q + 1} \right)H\left( {l - q} \right)} G\left( {q + 1} \right) + 2\left( {\sum\limits_{q = 0}^{l} {\left( {q + 1} \right)G\left( {l - q} \right)} H\left( {q + 1} \right)} \right) = 0. \hfill \\ \end{gathered} $$

(23)

The transformation of boundary conditions are:

$$ \left. \begin{gathered} F\left( 0 \right) = 0,\,\,F\left( 1 \right) = 1 + \alpha Sin\left( {n\xi } \right),\,\,F\left( 2 \right) = \frac{a}{2},\,\,G\left( 0 \right) = 0,\,\,G\left( 1 \right) = b, \hfill \\ H\left( 0 \right) = 0,\,\,H\left( 1 \right) = 0,\,\,H\left( 2 \right) = \frac{c}{2},P\left( 0 \right) = 1,\,\,P\left( 1 \right) = d,\,T\left( 0 \right) = 1,\,\,T\left( 1 \right) = e. \hfill \\ \end{gathered} \right\}\,\, $$

(24)

Differential transform of $f\left( \eta \right),$$g\left( \eta \right),$$\theta \left( \xi \right),$$\phi \left( \eta \right)$ and $h\left( \eta \right)$ are $F(l),$$G(l),$$T\left( l \right),$$P\left( l \right)$ and $H\left( l \right),$ also with the help of (17), we can find constants $a,$ $b,$ $c$ and $e.$ By utilizing (24) and Eqs. (19)–(23), we get the closed form of solution.

4 Result and discussion

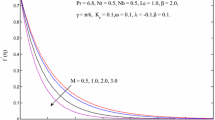
The findings are detailed in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 and displayed to show the features of the problem. The impact of the induced magnetic parameter $M$ on the velocities, temperature, concentration, and induced magnetic profiles is shown in Figs. 2a, 3b, 4a, 5a, and 6a, respectively. As the values of $M$ increases the axial velocity ($f{\prime} \left( \eta \right)$) profile in Fig. 2a increases, but it resists the transverse velocity ($g\left( \eta \right)$) in Fig. 3b. Physically, the induced magnetic field under the influence of the external magnetic field increases the body force and acts as a drag force, accelerating the velocity along the $x$-axis. The applied magnetic field also generates a resistive force known as the Lorentz force, which prohibits the $g\left( \eta \right)$.In general, a greater estimate of the $M,$ Lorentz force results in a decrease in temperature and concentration. The thickness of the thermal and concentration boundary layer decreases as a result. Hence, temperature and concentration profiles reduce as $M$ rises in Figs. 4a and 5a. When the values of $M$ grow, the thickness of the induced magnetic field boundary layer increases in Fig. 6a. This occurs as a result of the applied magnetic field and induced magnetic field being in the same direction. The influence of the Hartman number $Ha$ on velocities, temperature, and concentration profiles is depicted in Figs. 2b, 3c, 4b and 5b, respectively. According to Fig. 2b, $f{\prime} \left( \eta \right)$ is decreasing as the value $Ha$ of rises. By applying a uniform magnetic field that is perpendicular to the flow direction, the Lorentz force is generated. The fluid will often move more slowly as a result of this force. Consequently, as $Ha$ is increased, $f{\prime} \left( \eta \right)$ reduces. As the values of $Ha$ rises, $g\left( \eta \right)$ rises in Fig. 3c. The $g\left( \eta \right)$ values significantly rise as a result of the Lorentz force, which exerts its influence in the direction of increase in $Ha$ values and tends to speed up fluid flow in that direction. The thermal and concentration boundary layer thickens rises as $Ha$ values rise, as shown in Figs. 4b and 5b. By slowing down the fluid's velocity and thickening the thermal and concentration boundary layer, the magnetic field's application produces a resistive-type force that raises the fluid’s temperature and concentration. The impact of Hall parameter $m$ on the velocities, temperature, and concentration profiles is shown in Figs. 2c, 3a, 4d, and 5c, respectively. Figure 2c shows that as the values of $m$ enhances,$f{^\prime} \left( \eta \right)$ enhances. Higher values of $m$ decrease the effective conductivity $\frac{\sigma }{{1 + m^{2} }}$ which, reduces the magnetic damping force on $f{\prime} \left( \eta \right)$ and this reduction results in an assisting effect on $f{\prime} \left( \eta \right)$. In Fig. 3a, as the values of $m$ enhances the transverse flow first enhances gradually with $m$, reaches a greatest profile and then diminishes. This is due to the fact that for larger values of $m$, the term $\frac{1}{{1 + m^{2} }}$ becomes very small and hence resistive effect of the magnetic field is diminished. It is seen from Figs. 4d and 5c that both temperature and nanoparticle volume fraction profiles decrease with increasing $m$. This is due to the fact that an increase in $m$ decreases the effective conductivity $\frac{\sigma }{{1 + m^{2} }}$ and hence the magnetic damping decreases which in turn decreases $\theta \left( \eta \right),$ and $\phi \left( \eta \right)$.The effect of Casson fluid parameter $\beta$ on the axil velocity, temperature, and concentration profiles is shown in Figs. 2e, 4c, and 5e, respectively. In Fig. 2e, it can be seen that by increasing $\beta$, axil velocity has decreased. Physically, increase in $\beta$ causes increase in fluid viscosity, so it is obvious that the higher viscosity results in lower velocity. Also, in Figs. 4c and 5e, it is also observed that the same increase in viscosity has led to an increase in nanofluid temperature and concentrations profiles, respectively. Figure 2d analyses the impact of the mixed convection parameter $\lambda$ on $f{\prime} \left( \eta \right)$. It is evident that the dominance of buoyant forces over viscous forces is causing the momentum boundary layer thickness and $f{\prime} \left( \eta \right)$ to rise. Fig. 5d shows that as the values of chemical reaction parameter $\chi$ rises,$\phi \left( \eta \right)$ diminishes. It is true because the higher values of chemical reaction make fall in the chemical molecular diffusivity. Fig. 6b shows that as magnetic Prandtl number $\gamma$ rises, induced magnetic profile ($h{\prime} \left( \eta \right)$) rises. As $\gamma$ grows, the magnetic diffusivity declines, which causes the resistive forces to decrease. As a result, the $h{\prime} \left( \eta \right)$ increases with higher $\gamma$.

Fig. 2

a–e Variation of $f{\prime} \left( \eta \right)$. a $M$ when $\lambda = 0.1,N = 0.1,m = 0.1,\beta = 0.1,Ha = 0.1,Nb = 0.1,\Pr = 2,Sc = 0.5,$$Nt = 0.1,\alpha = 0.5,n = 50,\upxi = 0.5,\gamma = 0.1,\chi = 0.55.$ b $Ha$ when $\lambda = 0.1,N = 0.1,\beta = 0.1,m = 0.1,M = 0.55,Nb = 0.1,\gamma = 0.1,$$\alpha = 0.5,n = 50,\upxi = 0.5,\chi = 0.55.$ c $m$ when $\lambda = 0.1,N = 0.1,\beta = 0.1,Ha = 0.1,M = 0.55,Nb = 0.1,\Pr = 2,Sc = 0.5,Nt = 0.1,$$\alpha = 0.5,\xi = 0.5,\gamma = 0.1,\chi = 0.55,n = 50.$(d $\lambda$ when $m = 0.1,N = 0.1,\beta = 0.1,Ha = 0.1,M = 0.55,Nb = 0.1,\Pr = 2,Nt = 0.1,$ $\alpha = 0.5,\xi = 0.5,n = 50,\gamma = 0.1,\chi = 0.55,Sc = 0.5.$ e$\beta$ when $\lambda = 0.1,N = 0.1,m = 0.1,Ha = 0.1,Nb = 0.1,\Pr = 2,Sc = 0.5,$$\alpha = 0.5,n = 50,\upxi = 0.5,M = 0.55,\gamma = 0.1,Sc = 0.5,Nt = 0.1$

Fig. 3

a–c Variation of $g\left( \eta \right)$ on a $m$ when $\alpha = 0.5,n = 50,\upxi = 0.5,N = 1,\gamma = 0.1,\chi = 0.5,Nt = 0.1,M = 0.5,$$\lambda = 0.1,\beta = 1,Ha = 1,Nb = 0.1,\Pr = 2,Sc = 10.$ b $M$ when $Nt = 0.1,\lambda = 0.1,\beta = 1,Ha = 1,Nb = 0.1,\Pr = 2,Sc = 10,\gamma = 0.1,$$\alpha = 0.5,n = 50,\upxi = 0.5,\gamma = 0.1,\chi = 0.5.$ c $Ha$ when $\lambda = 0.1,N = 1,M = 0.5,m = 1,\beta = 1,Nb = 0.1,\Pr = 2,Sc = 10,\chi = 0.5,$$Sc = 10,\alpha = 0.5,n = 50,\upxi = 0.5,\gamma = 0.1$

Fig. 4

a–d Variation of $\theta \left( \eta \right)$ on a $M$ when $\lambda = 0.1,N = 1,m = 1,Ha = 1,Nb = 0.1,\Pr = 2,\gamma = 0.1,\beta = 1,Nt = 0.1,$$Sc = 10,\chi = 0.55.$ b $Ha$ when $Nt = 0.1,$$\beta = 1,$$\lambda = 0.1,N = 1,m = 1,M = 0.55, Nb = 0.1,\Pr = 2, Sc = 10,\gamma = 0.1,\chi = 0.55.$ c $\beta$ when $\lambda = 0.1,\,N = 1,\,m = 1,\,M = 0.55,\,\,Nb = 0.1,\,\,\Pr = 2,\,\,Sc = 10,\gamma = 0.1,Ha = 1,\chi = 0.55,Nt = 0.1.$ d $m$ when $\lambda = 0.1,N = 1,\chi = 0.55,M = 0.55,Nb = 0.1,\Pr = 2,Sc = 10,\gamma = 0.1,Ha = 1,Nt = 0.1,\beta = 1$

Fig. 5

a–e Variation of $\phi \left( \eta \right)$ on a $M$ when $Ha = 1.$ b $Ha$ when $\lambda = 0.1,N = 1,\chi = 0.3,Nb = 0.1,\Pr = 2,M = 0.3,Sc = 10,\gamma = 0.1,\beta = 1,Nt = 0.1$ c $\beta$ when $\lambda = 0.1,$$Nb = 0.1,\Pr = 2,Sc = 10,Nt = 0.1,M = 0.3,Nb = 0.1,\Pr = 2,Sc = 10,Nt = 0.1,Ha = 1,N = 1,\chi = 0.3,\gamma = 0.1.$ d$\chi$ when $Ha = 1,$$\lambda = 0.1,N = 1,Nb = 0.1,\Pr = 2,Sc = 10,\gamma = 0.1,M = 0.3,\beta = 1,Nt = 0.1.$ e$\beta$ when $Ha = 1,Nt = 0.1,N = 1,\chi = 0.3,Nb = 0.1,$$\lambda = 0.1,M = 0.3,\Pr = 2,Sc = 10,\gamma = 0.1$

Fig. 6

a, b Variation of $h{\prime} \left( \eta \right)$ on a $M$ when $Nt = 0.1,m = 1.5,\beta = 1,N = 1,\gamma = 0.1,\lambda = 0.1,Ha = 1,Nb = 0.1,$$\Pr = 2,\chi = 0.5,Sc = 10,n = 50,\alpha = 0.5,\upxi = 0.5.$ b $\gamma$ when $Nt = 0.1,m = 1.5,\beta = 1,N = 1,M = 0.5,\lambda = 0.1,Ha = 0.1,$$\Pr = 2,\chi = 0.5,Sc = 10,\,Nb = 0.1,n = 50,\alpha = 0.5,\upxi = 0.5,Ha = 0.1$

Fig. 7

a–c Effect of $\alpha$ and $n$ on ${\text{Re}}^{\frac{1}{2}} C_{f}$ for $Nt = 0.0,m = 0.1,\beta = 0.1,\lambda = 10,Ha = 0.1,Nb = 0.0,\,Sc = 0.0,\,$$M = 0.1$

Fig. 8

a–c Effect of $\alpha$ and $n$ on ${\text{Re}}^{\frac{1}{2}} C_{f}$ for $Nt = 0.1,m = 0.1,\lambda = 10,\beta = 0.1,Ha = 0.1,Nb = 0.1,\,Sc = 10,\,M = 0.1,$$\chi = 0.1,\Pr = 6,\,N = 0.1$

Fig. 9

a–g Effect of $\alpha$ and $n$ on ${\text{Re}}^{{ - \frac{1}{2}}} Nu$ for $Nt = 0.0,\beta = 0.1,Ha = 0.1,Nb = 0.0,\,Sc = 0.0,\,\Pr = 6,\,N = 0.0$

Fig. 10

a–f Effect of $\alpha$ and $n$ on ${\text{Re}}^{{ - \frac{1}{2}}} Nu$ for $Nt = 0.1,\chi = 0.1,m = 0.1,\beta = 0.1,Ha = 0.1,Nb = 0.1,\,\,\Pr = 6,\,\,$$Sc = 10,\,\,{\text{and}}\,\,N = 0.1$

Fig. 11

a–h Effect of $\alpha$ and $n$ on ${\text{Re}}^{{ - \frac{1}{2}}} NSh$ for $Nt = 0.1,\chi = 0.1,\,\,\,Nb = 0.1,\,\,\Pr = 6,\,\,Sc = 10,\,\,{\text{and}}\,\,N = 0.1$

The variations of the skin-friction coefficient ${\text{Re}}^{\frac{1}{2}} C_{f}$ along $\upxi$ are shown in Figs. 7a–c and 8a–c for various values of small parameter $\alpha$ ($\alpha$ = 0, 0.03, 0.05, and 0.1) and frequency parameter $n$ ($n$ = 10, 15, and 20) respectively, for the non-existence and existence of nanoparticles. In particular, the enhancement in $\alpha$ and $n$ considerably enhances the resistance between the wall and fluid particles in Fig. 7a–c, in the absence of nanoparticles. The stretching wall has a greater number of cavities that may be seen in greater depth due to rising of $\alpha$ and $n$ values. Hence, skin-friction coefficient enhances with values of $\alpha$ and $n$.The same influences of $\alpha$ and $n$ on ${\text{Re}}^{\frac{1}{2}} C_{f}$ can be seen in the Fig. 8a–c, when nanoparticles are present. The effects of $n$ ($n$ = 50, 75, 100) and $\alpha$ ($\alpha$ = 0, 0.01, 0.1, 0.2, 0.3, 0.4, 0.5) on the wall heat transfer rate (${\text{Re}}^{{ - \frac{1}{2}}} Nu$) along $\upxi$ are shown in Figs. 9a–g and 10a–f, respectively, for the non-existence and existence of nanoparticles. In particular, in Fig. 9a–g, the heat transfer rate shows the sinusoidal changes in the occurrence of surface roughness, which increase with the rise in the values of $\alpha$ and $n$. Heat is transferred from the heated area to the cold one more easily in cavities with more depth. Figure 10a–f show that the presence of nanoparticles causes the heat transfer rate to rise in the direction of the origin, achieve a maximum value, then drop in the opposite direction for larger values of $\alpha$ and $n$.When nanoparticles are introduced to a fluid, they first collect on a stretched wall, speeding up the rate of heat transfer. Once they have enough energy, they move away from the heated wall after a particular period of time. The heat transfer rate decreases considerably as a result of this. Further, the surface roughness effects are more prominent for $\alpha \ge 0.5$, which can be seen in the Figs. 9a–g and 10a–f. The effects of $n$ ($n$ = 50, 75, 100) and $\alpha$ ($\alpha$ = 0, 0.01, 0.1, 0.2, 0.3, 0.4, 0.5) on the nanoparticle mass transfer rate (${\text{Re}}^{{ - \frac{1}{2}}} NSh$) along $\upxi$ are shown in Fig. 11a–h. As values of $\alpha$ and $n$ rise, the magnitude and number of sinusoidal changes in ${\text{Re}}^{{ - \frac{1}{2}}} NSh$ rise, respectively. The wall with a larger surface area and those changes in the mass transfer rate are shown by the greater values of $\alpha$ and $n$.

5 Conclusions

The current work examines the mixed convective Casson nanofluid flow along an exponential sheet in presence of induced magnetic field, surface roughness, hall current and chemical reaction. The key observations are provided below.

• As values of $M$ enhances, same behavior can be seen in both velocities and induced magnetic profiles but reverse trend can be observed in temperature, volume fraction profiles.

• As values of $Ha$ enhances, same behavior can be seen in the $g(\eta )$, $\theta (\eta )$, and $\phi (\eta )$ profiles, but reverse nature can be seen in $f{\prime} (\eta )$ profile.

• As values $m$ enhances, both velocity profiles enhances, but reverse nature can be observed in temperature profile.

• The ambient base fluid’s nanoparticles increase friction close to the wall and slow the rate at which heat is transferred from the warm wall to the cool ambient fluid.

• When nanoparticles are introduced to the base fluid, ${\text{Re}}^{{ - \frac{1}{2}}} Nu$ is reduced by around 88% in both smooth ($\alpha = 0$) and rough ($\alpha = 0.5$) surface situations at ${\upxi = 1}$.