1 Introduction

With the rapid development of modern industry, CNC processing is focusing on high even ultra high precision. As a kind of primary precision processing tools, CNCs directly affect development of the entire manufacturing industry [1,2,3]. Geometric and thermal errors dominate CNCs [4, 5]. The former dominates the overall error of a tool. Study of modeling and compensation of spatial geometric errors has a history of ages. Especially, modeling and compensation of spatial geometric errors of multi-axis CNCs are becoming more popular and challenging recently [6,7,8,9]. The tool error modeling theory is also based on spatial errors. The more representative modeling methods are based on the rigid body dynamics [10, 11] and homogeneous coordinate transformation method [12, 13]. Ferreira et al. applied the rigid body kinematics in 1986 to establish the parameterized relationship between the working point error vector and coordinates in the working space of a 3-axis CNC. Their work laid the foundation for study of space errors [14]. Okafor also applied the rigid body kinematics in 2000 to model a homogeneous transformation matrix of uniaxial geometric errors and derived a homogeneous transformation matrix of spatial errors between the tool and the workpiece under the assumption of small angular errors. The space error vector of the tool was calculated out finally by means of the inverse kinematics solution [15]. Jung et al. identified the elements in the error model based on measurement of the diagonal positioning errors and then established a mathematical model of spatial errors with 21 error elements by means of a homogeneous transformation matrix to verify its validity by machining hemispherical workpieces [16]. Yang Jianguo et al. derived geometric and thermal error models of a turning machining center based on a homogeneous coordinate transformation matrix and achieved real-time compensation [17]. Zhang Hu et al. deduced the error model of a CNC based on the rigid kinematics and homogeneous coordinate transformation and proposed a compensation method by modifying G codes. They experimentally achieved a good error compensation on a 3-axis CNC [18]. Xia Xiaojun applied the theory of multiple rigid body kinematics, the homogeneous transformation matrix and its differentiation to study the comprehensive arbitrary structure of a machine geometric error transformation matrix, and established a high-grade CNC of arbitrary structure by means of integration of the multi rigid-body kinematic model of geometric errors. He proposed error separation (identification) method for the original error terms [19]. Zhang Yueming established the error-free motion equations between adjacent bodies by means of the multi-body theory. The adjacent body kinematics theory was applied to establish a topological structure relationship of each moving part and the low-order body array, and model errors of a tool grinding system to predict the machining accuracy [20]. Zhao et al. established an error compensation model based on application of the single-axis error data and the combined interpolation algorithm of the motion shape function. With reference to the position and posture of the driving motor, its prediction errors were compensated based on correction of the motion command to achieve high-precision machining error compensation [21]. Xia et al. established a spatial error model of the grinder based on the homogeneous transformation matrix, the kinematic chain and measurements of the single-axis motion errors. Moreover, they put forward an actual compensation method based on IKM to compensate the position-related geometric errors of the worktable [22]. Huang analyzed the homogeneous transformation matrix method by means of modeling tool spatial errors and found that the measured point error data are not directly related to the tool point errors in terms of the generalized homogeneous transformation theory. The famous Abbe principle and the Bryan principle were applied based on the above analysis to derive the error terms in the parallel and perpendicular directions of motion, respectively. On this basis, a high-precision error model was established [23].

Study of error detection, modeling and compensation of 3-axis CNCs [24,25,26] is relatively comprehensive while some problems remain challenging so far. As those error modeling methods were based on the multi-body theory and homogeneous coordinate transformation, the measurement points were constrained but the positional relationship between the measurement and compensation points and effects of angular errors on the spatial errors were not taken into account in actual measurement. The homogeneous coordinate transformation requires establishment of multiple local coordinate systems, which is a tedious process. Most of compensation methods adopt the modification of G-codes [27], or external mounted compensators [28]. The compensation process is tedious or poor in real time but also the accuracy is not good at the same time. Based on the screw theory, the single-axis motion errors of a laser interferometer measurement point are expressed as a motion screw matrix. Also, the topology of the 3-axis CNC is coupled to analyze the kinematic chain. Finally, the tool containing the measurement point position and angular and spatial errors of the tool tip point in the working space is modeled. A comprehensive compensation module for spatial errors is developed based on the open CNC system (HNC818) and the compensation effect is evaluated in view of spatial error simulation and spatial diagonal error measurement.

The purpose of the study reported here is twofold: (1) To compensate for the machine tool error, a new modeling method for the machine tool spatial error is established based on the screw theory for improving the accuracy of the machine tool. (2) A method combining quantitative evaluation of the machine tool diagonal and the spatial error simulation is proposed, which is more accurate and intuitive compared with the traditional accuracy evaluation method of the whole machine tool. In Sect. 2, the method of model establishing is described. Section 3 discusses the compensation effect of the model based on the examples. Finally, conclusions are given in Sect. 4.

2 Modeling approach

Accurate measurement of motion errors of the bed axes of a 3-axis CNC machine is the prerequisite for error modeling and compensation. The error measurement of the laser interferometer on the tool is the motion error of the laser head on the working platform, instead of that of the tool point. Due to the inevitable occurrence of angular errors, there is a certain difference between measurements and tool point errors. Thus, it is more reasonable to set up the spatial error model of tools in accordance with the rigid body and screw theory.

2.1 Modeling of uniaxial motion errors

As shown in Fig. 1, the tool point shall be ideally positioned at \({\mathbf{p}}_{{\mathbf{d}}}\) in Reference Coordinate System XYZ while it is actually positioned at p. The ideal angular velocity is \({{\varvec{\upomega}}}_{{\mathbf{d}}}\), and the actual angular velocity is \({\uptheta }_{{\text{e}}}\) at a certain angle from \({{\varvec{\upomega}}}_{{\mathbf{d}}}\). Its ideal and actual screws of motion can be expressed as:

$$\xi_{d} = \left[ {{\varvec{q}}_{{\varvec{d}}} \times {\varvec{\omega}}_{{\varvec{d}}} \;{\varvec{\omega}}_{{\varvec{d}}} } \right]^{T} ,\;\xi = \left[ {{\varvec{q}} \times {\varvec{\omega}}\; {\varvec{\omega}}} \right]^{T}$$
Fig. 1
figure 1

Error screw

Full size image

There are position and angular errors (d and \({\uptheta }_{{\text{e}}}\)) between the ideal and actual positions. Thus, errors can be regarded as results of the screw motion with a moving screw of \({\upxi }_{{\text{e}}}\). The which is expressed as:

$$\left\{ {\begin{array}{*{20}c} {{{\varvec{\upomega}}}_{{\mathbf{e}}} = \frac{{{{\varvec{\upomega}}}_{{\mathbf{d}}} \times {{\varvec{\upomega}}}}}{{\sin {\uptheta }_{{\text{e}}} }},{\text{h}}_{{\text{e}}} = \frac{{\text{d}}}{{{\uptheta }_{{\text{e}}} }} = \frac{{{\mathbf{q}} - {\mathbf{q}}_{{\mathbf{d}}} }}{{{\uptheta }_{{\text{e}}} }}} \\ {{\mathbf{v}}_{{\mathbf{e}}} = \frac{{{\mathbf{q}} \times \left( {{{\varvec{\upomega}}}_{{\mathbf{d}}} \times {{\varvec{\upomega}}}} \right)}}{{\sin {\uptheta }_{{\text{e}}} }} + {\text{h}}_{{\text{e}}} \frac{{{{\varvec{\upomega}}}_{{\mathbf{d}}} \times {{\varvec{\upomega}}}}}{{\sin {\uptheta }_{{\text{e}}} }} = \frac{{{\mathbf{q}}_{{\mathbf{d}}} \times {\mathbf{q}}}}{{\text{d}}} + \frac{{{\mathbf{q}} - {\mathbf{q}}_{{\mathbf{d}}} }}{{{\uptheta }_{{\text{e}}} }}} \\ \end{array} } \right.$$
(1)

In Eq. (1): "d" represents the position error between the ideal and the actual position of the tool tip; "ve" represents the instantaneous motion velocity of the tool tip; and "he" represents the screw distance of the tool tip.

2.1.1 Modeling of position errors

It can be shown in Fig. 2, as the research object the measuring point of a laser interferometer is focused in Global Reference Coordinate System \({\text{O}}_{1} {\text{X}}_{1} {\text{Y}}_{1} {\text{Z}}_{1}\) where after the operation of the workbench its ideal coordinate vector becomes \({\mathbf{q}}_{{\mathbf{d}}} = \left[ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{O}}1}} } & {{\text{Y}}_{{{\text{O}}1}} } & {{\text{Z}}_{{{\text{O}}1}} } \\ \end{array} } \right]^{{\mathbf{T}}}\) Actually, its coordinate vector is \({\mathbf{q}} = \left[ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{O}}2}} } & {{\text{Y}}_{{{\text{O}}2}} } & {{\text{Z}}_{{{\text{O}}2}} } \\ \end{array} } \right]^{{\mathbf{T}}}\) due to the positioning error of \({\updelta }_{{\text{x}}} \left( {\text{x}} \right)\). At this point, the error screw can be expressed as:

$${\upxi }_{{\text{e}}} = \left[ {\begin{array}{*{20}c} {\frac{{{\mathbf{q}} - {\mathbf{q}}_{{\mathbf{d}}} }}{{\text{d}}}} \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\left[ {\begin{array}{*{20}c} {X_{O2} - X_{O1} } \\ {Y_{O2} - Y_{O1} } \\ {Z_{O2} - Z_{O1} } \\ \end{array} } \right]}}{d}} \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(2)
Fig. 2
figure 2

The positional motion error screw of the measurement point

Full size image

The corresponding rigid body transformation matrix due to the positioning error is calculated out as follows:

$${\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{x}}} \left( {\text{x}} \right)}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {{\updelta }_{{\text{x}}} \left( {\text{x}} \right)} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(3)

where \({\updelta }_{{\text{x}}} \left( {\text{x}} \right)\) indicates the positioning error of the measuring point, which is our research object.

Similarly, when linearity errors in Directions Y and Z only exist during the movement of the table along Axis X, the error screw can be expressed as \(\left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\) and \(\left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ \end{array} } \right]^{{\text{T}}}\), respectively. The rigid body transformation matrix can be calculated as follows:

$${\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{y}}} \left( {\text{x}} \right)}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & {{\updelta }_{{\text{y}}} \left( {\text{x}} \right)} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]{\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{z}}} \left( {\text{x}} \right)}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & {{\updelta }_{{\text{z}}} \left( {\text{x}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(4)

where \(\updelta _{{\text{y}}} {\text{(x)}}\;{\text{and}}\;\updelta _{{\text{z}}} {\text{(x)}}\) represent the errors of Y and Z straightnesses of the measuring point.

2.1.2 Modeling of angular errors

In the light of the above equations, when an angular error only exists, the error screw can be expressed as:

$${\upxi }_{{\text{e}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{{\mathbf{e}}} } \\ {{{\varvec{\upomega}}}_{{\mathbf{e}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{{\mathbf{q}} \times \left( {{{\varvec{\upomega}}}_{{\mathbf{d}}} \times {{\varvec{\upomega}}}} \right)}}{{\sin {\uptheta }_{{\text{e}}} }}} \\ {\frac{{{{\varvec{\upomega}}}_{{\mathbf{d}}} \times {{\varvec{\upomega}}}}}{{\sin {\uptheta }_{{\text{e}}} }}} \\ \end{array} } \right]$$
(5)

where \({{\varvec{\upomega}}}_{{\mathbf{e}}}\) indicates the direction of error rotation, which is used to describe the angular error in the motion error of the bed axis of a CNC and often refers to the direction of the motion axis.

As shown in Fig. 3, the measurement point of a laser interferometer is taken as our research object in \({\text{O}}_{1} {\text{X}}_{1} {\text{Y}}_{1} {\text{Z}}_{1}\). While the workbench moves a certain distance in Direction x and g only has angular error around Axis Y, \({\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)\) can be written as:

$$\left\{ {\begin{array}{*{20}c} {{{\varvec{\upomega}}}_{{\mathbf{e}}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ \end{array} } \right]^{{\text{T}}} } \\ {{\mathbf{v}}_{{\mathbf{e}}} = q \times {{\varvec{\upomega}}}_{{\text{e}}} = \left[ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{O}}_{2} }} } \\ {{\text{Y}}_{{{\text{O}}_{2} }} } \\ {{\text{Z}}_{{{\text{O}}_{2} }} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right]} \\ \end{array} } \right.$$
(6)

On this basis, when the table moves along Axis X, the rigid body transformation matrix is expressed as:

$${\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)}} = \left[ {\begin{array}{*{20}c} 1 & 0 & {{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} & { - {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} \\ 0 & 1 & 0 & 0 \\ { - {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} & 0 & 1 & {{\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(7)

where \({\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)\) represents the pitch angular error measured by the laser interferometer at Command Position x.

Fig. 3
figure 3

The angular motion error screw of the measurement point

Full size image

Similarly, if there is an angular error around Axis X orZ while the table moves along Axis X-axis, the error screws can be expressed as:

$$\begin{aligned} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)}} = & \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & { - {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} & {{\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} \\ 0 & {{\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} & 1 & { - {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)}} = & \left[ {\begin{array}{*{20}c} 1 & { - {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} & 0 & {{\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} \\ {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} & {1{ }} & 0 & { - {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(8)

where \(\upvarepsilon _{{\text{x}}} {\text{(x)}}\;{\text{and}}\;\upvarepsilon _{{\text{z}}} {\text{(x)}}\) represent the measured roll angle and yaw angular errors at Commanded Position X of the measuring point; \({\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)}}\) represents the attitude change of the workbench in case that there is an angular error around Axis Y, which indicates the change of position error due to the angular error in the fourth column vectors (\(- {\text{Z}}_{{{\text{O}}_{2} }}\upvarepsilon _{{\text{y}}} ({\text{x}})\) and \({\text{X}}_{{{\text{O}}_{2} }}\upvarepsilon _{{\text{y}}} ({\text{x}})\))\(.\)

2.1.3 Comprehensive modeling of single-axis motion errors

While a machine tool uniaxially moving, the existed 6-motion errors can be regarded as 6 differential rotating motions around Axes X, Y and Z. Thus, such 6 motion errors can be multiplied in turn to represent the screw transformation matrix of the uniaxial motion errors; namely, the rigid body transformation matrix is as follows (Fig. 4):

$$\begin{aligned} {\text{e}}^{{\widehat{{{\xi }}}{\text{X}}_{{\text{e}}} }} = & {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{x}}} \left( {\text{x}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{y}}} \left( {\text{x}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{z}}} \left( {\text{x}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)}} \\ = & \left[ {\begin{array}{*{20}c} 1 & { - {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} & {{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} & {{\updelta }_{{\text{x}}} \left( {\text{x}} \right) + {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right) - {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} \\ {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} & 1 & { - {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} & {{\updelta }_{{\text{y}}} \left( {\text{x}} \right) + {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right) - {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right)} \\ { - {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right)} & {{\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} & 1 & {{\updelta }_{{\text{z}}} \left( {\text{x}} \right) + {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right) - {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{x}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(9)
$$\begin{aligned} {\text{e}}^{{\widehat{{{\xi }}}{\text{Y}}_{{\text{e}}} }} = & {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{x}}} \left( {\text{y}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{y}}} \left( {\text{y}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{z}}} \left( {\text{y}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{x}}} \left( {\text{y}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)}} \\ = & \left[ {\begin{array}{*{20}c} 1 & { - {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} & {{\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)} & {{\updelta }_{{\text{x}}} \left( {\text{y}} \right) + {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right) - {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)} \\ {{\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} & 1 & { - {\upvarepsilon }_{{\text{x}}} \left( {\text{y}} \right)} & {{\updelta }_{{\text{y}}} \left( {\text{y}} \right) + {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{y}} \right) - {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} \\ { - {\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)} & {{\upvarepsilon }_{{\text{x}}} \left( {\text{y}} \right)} & 1 & {{\updelta }_{{\text{z}}} \left( {\text{y}} \right) + {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right) - {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{y}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(10)
$$\begin{aligned} {\text{e}}^{{\widehat{{{\xi }}}{\text{Z}}_{{\text{e}}} }} = & {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{x}}} \left( {\text{z}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{y}}} \left( {\text{z}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\updelta }_{{\text{z}}} \left( {\text{z}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{x}}} \left( {\text{z}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)}} {\text{e}}^{{\widehat{{{\xi }}}{\upvarepsilon }_{{\text{z}}} \left( {\text{z}} \right)}} \\ = & \left[ {\begin{array}{*{20}c} 1 & { - {\upvarepsilon }_{{\text{z}}} \left( {\text{z}} \right)} & {{\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)} & {{\updelta }_{{\text{x}}} \left( {\text{z}} \right) + {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{z}} \right) - {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)} \\ {{\upvarepsilon }_{{\text{z}}} \left( {\text{z}} \right)} & 1 & { - {\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)} & {{\updelta }_{{\text{y}}} \left( {\text{z}} \right) + {\text{Z}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{z}} \right) - {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{z}}} \left( {\text{z}} \right)} \\ { - {\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)} & {{\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right)} & 1 & {{\updelta }_{{\text{z}}} \left( {\text{z}} \right) + {\text{X}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{y}}} \left( {\text{z}} \right) - {\text{Y}}_{{{\text{O}}_{2} }} {\upvarepsilon }_{{\text{x}}} \left( {\text{z}} \right)} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$
(11)
Fig. 4
figure 4

The uniaxial motion error screw of the measurement point

Full size image

2.2 Spatial error modeling based on the error screw matrix

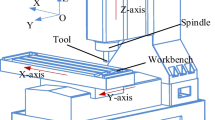
As per requirements of ISO 10791-6, the kinematic chain of Tool XYTZ can describe the composition of the tool and workpiece kinematic chains. Its kinematic chain is analyzed here (Fig. 5). Its tool kinematic chain is made up of z-axis, spindle tool and connecting parts while its workpiece kinematic chain contains Axes X and Y, worktable, workpiece and connecting parts. Their coordinated movement achieves the movement of the tool in the workspace relative to the worktable.

Fig. 5
figure 5

Analysis of kinematic chains of Tool XYTZ

Full size image

2.2.1 Modeling of workpiece movement chains

The kinematic chain of the workpiece includes Axes X and Y. As per the theory of screw, its transformation matrix of the kinematic chain in relation to Reference Coordinate System is ideally expressed as:

$${\text{g}}_{{{\text{bw}}}}^{{\text{i}}} ({\text{x}},{\text{y}}) = {\text{e}}^{{{\hat{\xi }}_{{\text{Y}}} \cdot {\text{y}}}} \cdot {\text{e}}^{{{\hat{\xi }}_{{\text{X}}} \cdot {\text{x}}}} \cdot {\text{g}}_{{{\text{bw}}}}^{{\text{i}}} (0)$$
(12)

where \({\hat{\xi }}_{{\text{Y}}} \cdot {\text{y}}\) and \({\hat{\xi }}_{{\text{X}}} \cdot {\text{x}}\) are ideal motion screws along Motion Axes x and y; and \({\text{g}}_{{{\text{bw}}}}^{{\text{a}}} \left( 0 \right)\) is the initial position and attitude matrix of the measurement point; namely, the installation position of a laser interferometer relative to Reference Coordinate System is expressed as:

$${\text{g}}_{{{\text{bw}}}}^{{\text{i}}} \left( 0 \right) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {{\text{X}}_{{{\text{O}}1}} } \\ 0 & 1 & 0 & {{\text{Y}}_{{{\text{O}}1}} } \\ 0 & 0 & 1 & {{\text{Z}}_{{{\text{O}}1}} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$
(13)

Because there are 6 motion errors in the straight spool of a 3-axis tool, the error motion screw is now added to the motion transformation matrix. The actual transformation matrix of the tool point position relative to Reference Coordinate System on the workbench can be expressed as:

$${\text{g}}_{{{\text{bw}}}}^{{\text{a}}} ({\text{x}},{\text{y}}) = {\text{e}}^{{{\hat{\xi }}_{{{\text{Ya}}}} \cdot {\text{ya}}}} \cdot {\text{g}}_{{{\text{bwY}}}}^{{\text{a}}} (0) \cdot {\text{e}}^{{{\hat{\xi }}_{{{\text{Xa}}}} \cdot {\text{xa}}}} \cdot {\text{g}}_{{{\text{bwX}}}}^{{\text{a}}} (0) = {\text{e}}^{{{\hat{\xi }}_{{\text{Y}}} \cdot {\text{y}}}} \cdot {\text{e}}^{{\widehat{{{\xi }}}{\text{Y}}_{{\text{e}}} }} \cdot {\text{e}}^{{{\hat{\xi }}_{{\text{X}}} \cdot {\text{x}}}} \cdot {\text{e}}^{{\widehat{{{\xi }}}{\text{X}}_{{\text{e}}} }} \cdot {\text{g}}_{{{\text{bw}}}}^{{\text{a}}} (0)$$
(14)

where \({\hat{\xi }}_{{{\text{Ya}}}}\) and \({\hat{\xi }}_{{{\text{Xa}}}}\) are the actual screw of motion; \({\text{ya and xa}}\) are the directions of the actual axis of motion; \({\text{e}}^{{\widehat{{{\xi }}}{\text{Y}}_{{\text{e}}} }}\) and \({\text{e}}^{{\widehat{{{\xi }}}{\text{X}}_{{\text{e}}} }}\) are the Y- and X-axis error screw transformation matrices, respectively; and \({\text{g}}_{{{\text{bw}}}}^{{\text{a}}} \left( 0 \right) = {\text{g}}_{{{\text{bw}}}}^{{\text{i}}} \left( 0 \right)\) is the rigid body transformation matrix of the actual measurement point relative to Reference Coordinate System.

For a linear axis, its motion screw and screw motion can be deduced from Eq. (14), which are expressed as:

$${\hat{\xi }}_{{\text{i}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{{\mathbf{i}}} } \\ 0 \\ \end{array} } \right]{\text{e}}^{{{\hat{\xi }}_{{\text{i}}} \cdot {\uptheta }_{{\text{i}}} }} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{3 \times 3} } & {{\mathbf{v}}_{{\mathbf{i}}} {\uptheta }_{{\text{i}}} } \\ {0_{1 \times 3} } & 1 \\ \end{array} } \right]$$
(15)

where \({\mathbf{v}}_{\mathbf{i}}\) represents the unit vector in the direction of the moving axis; for example, \({\mathbf{v}}_{\mathbf{x}}=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\),\({\mathrm{and \theta }}_{\mathrm{i}}=\mathrm{x}\) exist for Axis X.

In this respect, the position and angular errors of the workpiece movement chain can be expressed as the difference between the actual and ideal positions and attitudes of the tool point:

$$\left[ {\begin{array}{*{20}c} {\Delta {\mathbf{P}}_{{{\mathbf{bw}}}} } \\ 0 \\ \end{array} } \right] = \left( {{\text{g}}_{{{\text{bw}}}}^{{\text{a}}} - {\text{g}}_{{{\text{bw}}}}^{{\text{i}}} } \right)\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{{\mathbf{w}}} } \\ 0 \\ \end{array} } \right]$$
(16)

where \(\Delta {\mathbf{P}}_{{{\mathbf{bw}}}}\) represents the error of the tool point in Reference Coordinate System, and \({\mathbf{p}}_{{\mathbf{w}}} = \left[ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{tw}}}} } & {{\text{Y}}_{{{\text{tw}}}} } & {{\text{Z}}_{{{\text{tw}}}} } \\ \end{array} } \right]\) represents the coordinates of the tool point in Local Coordinate System where the measuring point is taken as the origin.

Integration of Eqs. (12), (14) and (16) can result in the following equations:

$$\left\{ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{P}}_{{{\text{bw}}}} }} = {\updelta }_{{\text{x}}} \left( {\text{x}} \right) + {\updelta }_{{\text{x}}} \left( {\text{y}} \right) - {\text{Y}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} \right) + {\text{Z}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)} \right)} \\ {{\text{Y}}_{{{\text{P}}_{{{\text{bw}}}} }} = {\updelta }_{{\text{y}}} \left( {\text{x}} \right) + {\updelta }_{{\text{y}}} \left( {\text{y}} \right) + {\text{X}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} \right) - {\text{Z}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} \right)} \\ {{\text{Z}}_{{{\text{P}}_{{{\text{bw}}}} }} = {\updelta }_{{\text{z}}} \left( {\text{x}} \right) + {\updelta }_{{\text{z}}} \left( {\text{y}} \right) - {\text{X}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{y}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{y}}} \left( {\text{y}} \right)} \right) + {\text{Y}}_{{{\text{tw}}}} \left( {{\upvarepsilon }_{{\text{z}}} \left( {\text{x}} \right) + {\upvarepsilon }_{{\text{z}}} \left( {\text{y}} \right)} \right)} \\ \end{array} } \right.$$
(17)

2.2.2 Kinematic error modeling of a tool kinematic chain

A tool chain is composed of z-axis and the tool. Ideally, its pose transformation matrix relative to Reference Coordinate System is expressed as:

$${\text{g}}_{{{\text{bw}}}}^{{\text{i}}} ({\text{z}}) = {\text{e}}^{{{\hat{\xi }}_{{\text{Z}}} \cdot {\text{z}}}} \cdot {\text{g}}_{{{\text{bw}}}}^{{\text{i}}} (0)$$
(18)

Similarly, the error motion screw is introduced due to the existence of motion errors of the straight spool. The actual transformation matrix of the tool point position on the workbench relative to Reference Coordinate System can be expressed as:

$${\text{g}}_{{{\text{bw}}}}^{{\text{a}}} ({\text{x}},{\text{y}}) = {\text{e}}^{{{\hat{\xi }}_{{{\text{Za}}}} \cdot {\text{za}}}} \cdot {\text{g}}_{{{\text{bw}}}}^{{\text{a}}} (0) = {\text{e}}^{{{\hat{\xi }}_{{\text{Z}}} \cdot {\text{z}}}} \cdot {\text{e}}^{{\widehat{{{\xi }}}{\text{Z}}_{{\text{e}}} }} {\text{g}}_{{{\text{bw}}}}^{{\text{a}}} (0)$$
(19)

where \({\hat{\xi }}_{{{\text{Za}}}}\) is the actual screw of motion; \({\text{za}}\) is the direction of the actual axis of motion; \({\text{e}}^{{\widehat{{{\xi }}}{\text{Z}}_{{\text{e}}} }}\) is the z-axis error screw transformation matrix; and \({\text{g}}_{{{\text{bw}}}}^{{\text{a}}} \left( 0 \right)\) is the actual rigid body transformation matrix relative to Reference Coordinate System.

Given all this, the position and angular error of the workpiece kinematic chain can be expressed as the difference between the actual and ideal positions and postures of the tool point:

$$\left[ {\begin{array}{*{20}c} {\Delta {\mathbf{P}}_{{{\mathbf{bt}}}} } \\ 0 \\ \end{array} } \right] = \left( {{\text{g}}_{{{\text{bw}}}}^{{\text{a}}} - {\text{g}}_{{{\text{bw}}}}^{{\text{i}}} } \right)\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{{{\mathbf{tt}}}} } \\ 0 \\ \end{array} } \right]$$
(20)

where \(\Delta {\mathbf{P}}_{{{\mathbf{bt}}}}\) represents the error of the tool point in the workpiece coordinate system; and \({\mathbf{p}}_{{{\mathbf{tt}}}} = \left[ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{tt}}}} } & {{\text{Y}}_{{{\text{tt}}}} } & {{\text{Z}}_{{{\text{tt}}}} } \\ \end{array} } \right]\) represents the coordinates of the tool point in the coordinate system where the measuring point is taken as the origin.

Equations (9), (10) and (11) are solved simultaneously, and the error of the tool movement chain relative to Reference Coordinate System is written as:

$$\left\{ {\begin{array}{*{20}c} {{\text{X}}_{{{\text{P}}_{{{\text{bt}}}} }} = \delta_{{\text{x}}} ({\text{z}}) - {\text{Y}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{z}}} ({\text{z}}) + {\text{Z}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{y}}} ({\text{z}})} \\ {{\text{Y}}_{{{\text{P}}_{{{\text{bt}}}} }} = \delta_{{\text{y}}} ({\text{z}}) + {\text{X}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{z}}} ({\text{z}}) - {\text{Z}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{x}}} ({\text{z}})} \\ {{\text{Z}}_{{{\text{P}}_{{{\text{bt}}}} }} = \delta_{{\text{z}}} ({\text{z}}) - {\text{X}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{y}}} ({\text{z}}) + {\text{Y}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{x}}} ({\text{z}})} \\ \end{array} } \right.$$
(21)

2.3 Modeling of spatial errors

As per analysis of the motion error of the tool and workpiece kinematic chains of the CNC, the motion errors of the entire kinematic chain relative to the fixed coordinate system are obtained. The error function of position in directions x, y and z of the uniaxial direction can be obtained by analyzing the uniaxial motion. The spatial error of the tool point is based on interaction effects of both tool chains. Thus, the spatial error model of the CNC is expressed as:

$$\begin{aligned} & \left\{ {\begin{array}{*{20}c} {{\text{E}}_{{\text{x}}} = {\text{X}}_{{\Delta {\text{P}}_{{{\text{bt}}}} }} - {\text{X}}_{{\Delta {\text{P}}_{{{\text{bw}}}} }} } \\ {{\text{E}}_{{\text{y}}} = {\text{Y}}_{{\Delta {\text{P}}_{{{\text{bt}}}} }} - {\text{Y}}_{{\Delta {\text{P}}_{{{\text{bw}}}} }} } \\ {{\text{E}}_{{\text{z}}} = {\text{Z}}_{{\Delta {\text{P}}_{{{\text{bt}}}} }} - {\text{Z}}_{{\Delta {\text{P}}_{{{\text{bw}}}} }} } \\ \end{array} \Rightarrow } \right. \\ & \left\{ {\begin{array}{*{20}l} {{\text{E}}_{{\text{x}}} = \delta_{{\text{x}}} ({\text{z}}) - \delta_{{\text{x}}} ({\text{x}}) - \delta_{{\text{x}}} ({\text{y}}) - {\text{Y}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{z}}} ({\text{z}}) + {\text{Z}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{y}}} ({\text{z}}) + {\text{Y}}_{{{\text{tw}}}} (\varepsilon_{{\text{z}}} ({\text{x}}) + \varepsilon_{{\text{z}}} ({\text{y}})) - {\text{Z}}_{{{\text{tw}}}} (\varepsilon_{{\text{y}}} ({\text{x}}) + \varepsilon_{{\text{y}}} ({\text{y}}))} \hfill \\ {{\text{E}}_{{\text{y}}} = \delta_{{\text{y}}} ({\text{z}}) - \delta_{{\text{y}}} ({\text{x}}) - \delta_{{\text{y}}} ({\text{y}}) + {\text{X}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{z}}} ({\text{z}}) - {\text{Z}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{x}}} ({\text{z}}) - {\text{X}}_{{{\text{tw}}}} (\varepsilon_{{\text{z}}} ({\text{x}}) + \varepsilon_{{\text{z}}} ({\text{y}})) + {\text{Z}}_{{{\text{tw}}}} (\varepsilon_{{\text{x}}} ({\text{x}}) + \varepsilon_{{\text{x}}} ({\text{y}}))} \hfill \\ {{\text{E}}_{{\text{z}}} = \delta_{{\text{z}}} ({\text{z}}) - \delta_{{\text{z}}} ({\text{x}}) - \delta_{{\text{z}}} ({\text{y}}) - {\text{X}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{y}}} ({\text{z}}) + {\text{Y}}_{{{\text{tt}}}} \cdot \varepsilon_{{\text{x}}} ({\text{z}}) + {\text{X}}_{{{\text{tw}}}} (\varepsilon_{{\text{y}}} ({\text{x}}) + \varepsilon_{{\text{y}}} ({\text{y}})) - {\text{Y}}_{{{\text{tw}}}} (\varepsilon_{{\text{x}}} ({\text{x}}) + \varepsilon_{{\text{x}}} ({\text{y}}))} \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(22)

3 Application verification

A 3-axis vertical machining center (Model: XHK715; manufacturer: Hubei Jiangshan Huake Digital Equipment Technology Co., Ltd.) is focused here, whose overall structure characteristic dimensions are as follows:

Travels: 1400 mm (Axis X); 800 mm (Axis Y); and 800 mm (Axis Z).

Overall dimensions of its table (width × length): 500 mm × 1050 mm.

Positioning accuracy: ± 5 μm; and Positioning repeatability: ± 2 μm (Fig. 6).

Fig. 6.
figure 6

3-axis vertical machining center

Full size image

A laser interferometer (Renishaw XM-60) is used in our example verification, of which linear error resolution is 1 nm, and the angular error resolution is 0.03 microradians. A laser head is equipped at the workbench. A 6-D sensor is equipped at the tool spindle. As per the principle of dimming, the laser head and the 6-D sensor are aligned to establish their communication. The measurement starting point, spacing, interval time and other parameters are set in the measurement software and the tool table moves in parallel to measure the tool geometric errors in Axes X, Y and Z (Fig. 7).

Fig. 7
figure 7

Laser measurement

Full size image

3.1 Machine error data acquisition

In case of non-collision and considering the rationality of the experiment, the travels of Axes X, Y and Z are selected as follows: 0–1300 mm, − 650 to 0 mm, and − 650 to 0 mm. In case of meeting the national relevant measurement requirements, the measurement spacing is taken as 100 mm, 50 mm and 50 mm. Axes X, Y and Z are divided into 13 segments, respectively. Six geometric errors of Axes X, Y and Z are measured with the laser interferometer successively. The measurements are shown in Figs. 8, 9 and 10.

Fig. 8.
figure 8

6 errors of Axis X

Full size image
Fig. 9.
figure 9

6 errors of Axis Y

Full size image
Fig. 10.
figure 10

6 errors of Axis Z

Full size image

Figure 8 indicates that the measured travel of Axis X and distance are [0, 1300] mm and 100 mm, respectively. The positioning, straightness and angular errors are among 15.1 to − 19.4 μm, 6.1 to − 10.3 μm and 6.2 μm to − 40.9 μm, respectively.

Figure 9 shows that the measured travel of Axis Y and interval are [− 650, 0] mm and 50 mm, respectively. The positioning, straightness and angular errors are among − 7.5 to − 18.2 μm, 6.5 to − 5.9 μm and 27.8 to − 75.5 μm, respectively.

Also, Fig. 10 shows that the measured travel of Axis Z is [− 650, 0] mm, and its interval is 50 mm. The positioning, straightness and angular errors are among − 6.6 to − 27.5 μm, 4.9 to − 3.8 μm and 38.5 to − 26.1 μm, respectively.

3.2 Evaluation of the tooling accuracy

3.2.1 Simulation evaluation

The MATLAB simulation method is applied here. The measurements and the error model and the single-axis error measurement file are imported into the spatial error measurement software for calculation. The spatial errors (εx, εy and εz) of feature points in the spatial error field are obtained. The color separation diagram of the error field is obtained by means of the Matlab simulation tool (Fig. 11). This method can be applied to qualitatively evaluate the overall spatial accuracy of the tool.

Fig. 11
figure 11figure 11

Simulation of Axis-X, Y and Z spatial error fields before performance of compensation. Columns (a), (b) and (c) represent the simulation of the error fields in Axes X, Y and Z, respectively

Full size image

Figure 11a presents εx of the tool in the whole space. The space errors of X (0–1300) mm, Y (− 650 to 0) mm and Z (− 650 to − 300) mm are within 20–40 μm. Some spatial errors are among 0–20 μm. The space errors of X (400–1300) mm, Y (− 550 to 0) mm and Z (− 650 to 450) mm are up to 60 μm.

Figure 11b shows εy in the entire space. The space errors of X (500–1200) mm, Y (− 650 to 0) mm and Z (− 650 to 0) mm is below 20 μm. A certain spatial errors falls in 20–40 μm. The space errors of X (0–200) mm, Y (− 650 to 0) mm and Z (− 250 to 0) mm exceeds 40 μm.

Figure 11c presents εz in the entire space. The space errors of X (0–1300) mm, Y (− 650 to 600) mm and Z (− 650 to 450) mm is within 20 μm. The space errors of X (400–1300) mm, Y (− 400 to 0) mm, Z (− 650 to 0) mm are above 60 μm.

3.2.2 Evaluation of the body diagonal accuracy

Evaluation of the spatial accuracy of a tool is usually based on the diagonal precision index so far. In a 3-axis CNC space, there are 4 body diagonals which can reflect the overall spatial accuracy of the tool. The 4 body diagonal lines of the machine tool are indicated by PPP, NPP, NPN and PPN, respectively. In general, its accuracy can only be shown while the diagonal accuracy indexes of its 4 bodies are simultaneously high. There is no international standard for the body diagonal accuracy as of now. Our study shows that the accuracy indexes of 4 body diagonal accuracy of a CNC can be controlled within 20 μm at the same time but also the accuracy of the tool is very high. For evaluating the spatial accuracy of a tool, a laser doppler instrument and a step-step diagonal measuring mirror group are utilized to measure its whole travel space (Fig. 12).

Fig. 12
figure 12

Body diagonal error measurement

Full size image

Sizes of the working space of our tool for measuring the diagonal of the laser step-step body are 1300 × 650 × 650 mm, and the total length of the diagonal of each body is 1592.16 mm which are divided into 13 grids. X, Y and Z are measured step by step in each lattice. The corresponding moving vectors of each step are (100, 0, 0), (0, 50, 0) and (0, 0, 50). The measurements of the diagonal errors of the positive and negative bodies are shown in Fig. 13.

Fig. 13
figure 13

Body diagonal errors before performance of compensation

Full size image

Figure 13 shows the positioning error curves of Diagonals PPP, NPP, PNP and NNP of the spatial body of 3-axis CNC (Fig. 10). The maximum positioning errors of Diagonals PPP, PNP and NNP are − 58.2 μm, − 51.5 μm, 57.5 μm and − 7.3 μm, respectively.

3.3 Error compensation

3.3.1 Development of our compensation software

After obtaining the compensation data of the tool execution end, an error compensation module was developed on the Huazhong 8-CNC system platform based on the tool space error model. This error module contains functions such as basic measurement interval, grid spacing, grid point setting and compensation file reading. The interface of our compensation module is shown in Fig. 14.

Fig. 14
figure 14

Compensation module interface

Full size image

3.3.2 Precision evaluation after performance of compensation

Firstly, the machine tool spatial error compensation model established is input into the system compensation software (Sect. 3.3.1), which can calculates out the trip point error compensation value \((E_{x} ,\;E_{y} \;{\text{and}}\;E_{z} )\) according to the travel position point coordinates (x,y,z) of the machine tool. Then, the machine tool control system stores the error compensation value into the compensation list within the system. Lastly, when the machine tool runs to a specific travel position, the system obtains the corresponding error compensation value in the compensation list to implement the real-time error compensation of the machine tool. Then the tool spatial errors are compensated by means of our system compensation software. The tool space error field is simulated. The tool spatial error field is shown in the Fig. 15.

Fig. 15
figure 15figure 15

Simulation of XYZ 3-D spatial field error after performance of compensation. Columns (a), (b) and (c) represent simulations of X, Y and Z-direction error fields, respectively

Full size image

Figure 15a presents εx of the tool in the whole space after compensation of the system. The space errors of X (0–1300) mm, Y (− 150 to 0) mm and Z (− 550 to 0) mm are within 5 μm. The errors of X (0–1300) mm, Y (− 650 to 150) mm and Z (− 650 to 50) mm space are among 5–10 μm. They are rarely above 10 μm.

Figure 15b shows εy in the entire space after compensation of the system. The space errors of X (500–1200) mm, Y (− 650 to 0) mm and Z (− 200 to 0) mm are below 5 μm. The space errors of X (400–1100) mm, Y (− 650 to 0) mm and Z (− 650 to 450) mm are among 10–20 μm. Only a few errors fall in 5–10 μm.

Figure 15c shows εz in the entire space after compensation of the system. The space errors of X (0–1200) mm, Y (− 650 to 0) mm and Z (− 400 to 0) mm are among 10–20 μm. The space errors of X (600–1200) mm, Y (− 650 to − 200) mm and Z (− 650 to 0) mm are above 25 μm. Few space errors are less than 10 μm.

After the tool errors are compensated by means of our compensation software, the tool diagonal errors are measured. The measurements are shown in Fig. 16.

Fig. 16
figure 16

Diagonal body error after performance of compensation

Full size image

Figure 16 shows that the maximum positioning errors of PPP, NPP, PNP and NNP are − 11.9 μm, − 11.4 μm, 11.8 μm and 1.5 μm, respectively. Their diagonal accuracies in the tool space meet the requirements of high precision and our compensation effects are remarkable.

Based on comparison of our space simulation and spatial diagonal quantitative evaluation before and after performance of compensation, the specific compensation effects are shown in Table 1.

Table 1 Compensation data comparison
Full size table

In terms of the qualitative evaluation of simulated tool spatial errors, Axis-X, Y and Z errors without compensation are among 0 to − 60 μm, 40 to − 55 μm and 0 to − 100 μm, respectively. In contrast, Axis-X, Y and Z errors are among 1 to − 13 μm, 20 to − 23 μm and − 2 to − 29 μm after performance of compensation. Comparison of simulated tool space errors indicates that the overall tool space errors fall greatly.

In terms of quantitative evaluation of the body diagonal errors, the compensated maximum errors of NPP, PNP, NPP and PPP are up to 58.2 μm, 51.5 μm, 57.5 μm and 7.3 μm, respectively. Their errors peak up to 11.9 μm, 11.4 μm, 11.8 μm and 1.5 μm, respectively. Comparison of the diagonal error data indicates that their diagonal accuracies can meet the high-precision requirements after performance of compensation. Thus, our compensation effects are significant.

3.3.3 Discussion

In our previous published article [29], a comprehensive error model of the machine tool based on the spatial feature point is proposed, but it does not take into account for the distance of the motion direction between the compensation point (tool point) and the measurement point, so that the compensation effect is not ideal. Therefore, our author considers the machine tool error change as the motion screw of the machine arm from the perspective of robotics to establish a machine tool spatial error model based on the screw theory which effectively circumvents the deficiencies in previous studies. Comparison with the comprehensive error model of the machine tool proposed in the previous paper, the proposed method greatly improves the compensation effect, which provides new ideas for the spatial error modeling of machine tool.

4 Conclusions

The errors of the measuring points are utilized to perform tool error compensation currently. Because of effects of the angular errors and measuring positions, the measured point errors cannot represent the position errors of the actual compensation points (tool points) so that the compensation system may be mostly unable to achieve real-time comprehensive compensation. For overcoming the above shortcomings, the spatial error fields are modeled based on the travel theory to simulate the workpiece and tool motion chains. In accordance with our model, a quantitative precision evaluation method is put forward here for the tool diagonals. The precision of a body diagonal represents the partial precision of the spatial area of a tool due to the multi-axis coupling effects. Thus, the error status of all spatial positions of a tool cannot be fully reflected. In this regard, a simulation method of the whole spatial error field of a tool is presented here by means of the Matlab analysis method, which can be utilized to qualitatively evaluate the spatial accuracy of the whole tools. In addition, a spatial error compensation system where there are functions of original error analysis, high-precision modeling, diagonal error calculation and error field simulation is specially developed here to verify the compensation effects. An empirical analysis is introduced to verify the effectiveness of our error compensation model and accuracy evaluation method. For a 3-axis tool, its 3-axis positional accuracies are compensated to 19.4 μm, 18.2 μm and − 27.6 μm, respectively; and their four-bar diagonal errors are 58.2 μm, 51.5 μm, 57.5 μm and 7.3 μm, respectively. After performance of our compensation, its 3-axis positional accuracies fall to 3.9 μm, 3.1 μm and − 5.8 μm, respectively; and its four-bar diagonal errors are 11.9 μm, 11.4 μm, 11.8 μm and 1.5 μm, respectively. Our compensation effects are comparatively clear. Such achievements show that our high precision compensation method is feasible and effective. To improve the tool’s accuracy, ensuring the quality of parts and reducing wasteful spending, the current method may be further researched. In fact, the real-time compensation techniques of tooling spatial errors will be more complicated and difficult. How to interpolate real-time error data into a CNC system to achieve real-time dynamic compensation will be much more difficult and challenging. This will be our next focus of the study.