1 Introduction

CNC machine is one of the most important components in modern manufacturing area. The vigorous development of science and technology and electronic information technology requires it to have higher performance[1, 2]. During the long-term use of CNC machine tool, geometric errors are caused by wear, deformation and other reasons, so that its machining accuracy is degraded. Therefore, it is extremely necessary to improve its machining accuracy [3]. Error compensation [4,5,6,7] is an effective technique to achieve high accuracy with low cost, and the geometric error is systematic and measurable [8,9,10].

Many researchers have developed lots of methods on the geometric error compensation of CNC machine tools in the past decades, aiming to improve the machining accuracy of the machine tools. As the foundation of error compensation, it is a key issue to establish the correct compensation model. A number of methods or techniques on error modeling are designed in past years, such as HTM, multi-body system (MBS) theory [11, 12], rigid body kinematics [13], screw theory [14,15,16], sequential decoupling compensation method [17], etc. HTM is a popular modeling method, and plenty of papers presented the HTM techniques for CNC machines compensation with HTM. Wang et al. [18] established spatial coordinate models on the upper and lower platforms and branches of the Stewart platform with six degrees of freedom by using Denavit-Hartenberg (D-H) method based on HTM, which improved the accuracy of the model and reduced the error. Chen et al. [19] established a 3d micro-milling surface model considering the influence of machining nonlinear dynamics by using HTM, and accurately predicted the surface topography generation and roughness under different processing conditions of CNC machine tools. Liang et al. [20] deduced the error model between the geometrical error parameters of the rotating axis and the change of the length of the ball rod on the CFXYZA five-axis CNC machine tools through the HTM, and determined the parameters accordingly to deduce the displacement deviation caused by the linkage motion of the straight axis and the rotating axis. Wu et al. [21] established a comprehensive error model of CATT gear milling machine by using D-H homogeneous transformation matrix and lower position matrix method. This model provides theoretical basis for error analysis, precision design and geometric error compensation of CATT gear milling machine. In addition to the above literature, many scholars at home and abroad have used this method to model the spatial geometric errors of machine tools [22,23,24,25]. In the above literatures, these models derived by them have obtained good compensation effect, which greatly improves the machining accuracy of the machine tools. Unfortunately, the additional angle errors generated by the influence on lower guide rail to the upper guide rail of the machine table are not considered, which can further improve its machining accuracy. Therefore, according to the different composition structures of machine tools, it is of great significance to further carry out the research on the spatial geometric error model of machine tools considering the two-dimensional angle errors.

Considering the additional impact of two-dimensional angle error to further improve the machining accuracy of CNC machine tools, this paper takes a CNC machine tool with three axes of X, Y and Z in series as the object of research to do the following work: In Sect. 2, the principle of two-dimensional angle error is analyzed. In Sect. 3, an optimized spatial geometric error compensation model of CNC machine tool based on two-dimensional angle error is established. Section 4 verifies the validity of the optimized compensation model according to the experiment, and the conclusions are given in Sect. 5.

2 Theoretical analysis of two-dimensional angle error

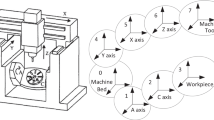
The CNC machine tool studied in this paper adopts the structure of X, Y and Z coordinate axes in series, with Z-direction guide rail installed on Y-direction guide rail, which installed on X-direction guide rail at the same time, as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of CNC machine workbench structure

Full size image

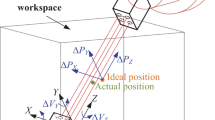
When the table rail system is moving, the angle errors of the X-direction guide system will be transmitted to the Y-direction guide system installed on it by the slide structure, which make additional angle errors, and it is showed in Fig. 2. The influence of the angle errors of the X-direction guide system is two-dimensional, and there is correlation and compensation between it and the Y-direction motion error of the table. Therefore, it is more reasonable to take the additional angle errors generated by the X-direction guide in the Y-direction guide into account when modeling the spatial error of the CNC machine tools. Similarly, the additional angle errors of the Y-axis guide system in the Z-axis should also be counted in error compensation model for CNC machine tool. Without considering the influence of temperature on the angle errors of the guide system, the comprehensive yaw angle, pitch angle and roll angle of the Y-direction guide system can be formulated as follows:

$$\left\{\begin{array}{c}{\epsilon }_{z(x,y)}={\epsilon }_{zy}+{{\upepsilon }}_{\text{z}\text{x}}\\ {\epsilon }_{x(x,y)}={\epsilon }_{xy}+{{\upepsilon }}_{\text{x}\text{x}}\\ {\epsilon }_{y(x,y)}={\epsilon }_{yy}+{{\upepsilon }}_{\text{y}\text{x}}\end{array}\right.$$
(1)

where: \({\epsilon }_{z(x,y)},{\epsilon }_{y(x,y)},{\epsilon }_{x(x,y)}\) are the comprehensive yaw angle, comprehensive pitch angle and comprehensive roll angle of the Y-direction guide system, respectively. In the X-direction, \({\epsilon }_{zx},{\epsilon }_{yx}\) and \({\epsilon }_{xx}\) are yaw angle, pitch angle and roll angle of guide system, respectively. In the Y-direction, \({{\upepsilon }}_{\text{z}\text{y}},{{\upepsilon }}_{\text{x}\text{y}}\) and \({{\upepsilon }}_{\text{y}\text{y}}\) are yaw angle, pitch angle and roll angle of guide system, respectively.

Fig. 2
figure 2

Additional angle errors generated by lower guide rail to upper guide rail

Full size image

The comprehensive yaw angle, pitch angle and roll angle of the Z-direction guide system can be written as follows:

$$\left\{\begin{array}{c}{\epsilon }_{x(x,y,z)}={{{\upepsilon }}_{\text{x}\text{z}}+\epsilon }_{x(x,y)}\\ {\epsilon }_{y(x,y,z)}={{\upepsilon }}_{\text{y}\text{z}}+{\epsilon }_{y(x,y)}\\ {\epsilon }_{z(x,y,z)}={{\upepsilon }}_{\text{z}\text{z}}+{\epsilon }_{z(x,y)}\end{array}\right.$$
(2)

where: \({\epsilon }_{x(x,y,z)},{\epsilon }_{y(x,y,z)},{\epsilon }_{z(x,y,z)}\) are the comprehensive yaw angle, comprehensive pitch angle and comprehensive roll angle of the Z-direction guide system, respectively. In the Z-direction, \({\epsilon }_{yz},{\epsilon }_{xz}\) and \({\epsilon }_{zz}\) are yaw angle, pitch angle and roll angle of guide system, respectively.

We will give a geometric error compensation model in next section.

3 Modeling method

We need to derive a sequence of formulation according to a structure of CNC machine for geometric error compensation modeling with HTM. As mentioned above, Fig. 1 shows the structure of CNC machine, and Fig. 3 gives a coordinate system that related to the structure of CNC machine. The origin of the absolute coordinate system (denoted by Oo) is fixed on a out corner of the workbench. The origin of the first relative coordinate system (denoted by Ox) locates on outside the center of the saddle, and it is X-axis displacement relative to the absolute coordinate system. The origin of the second relative coordinate system (denoted by Oy) is set in the outside the center point above the machine column, and it is Y axial displacement relative to the first relative coordinate system. The origin of the third relative coordinate system (denoted by Oz) is lied at the outside the center of the spindle head, and it is Z axis displacement relative to the second coordinate system. Combined with the composition of the machine structure, according to the modeling method of the reference [26, 27], the modeling process is as follows.

Fig. 3
figure 3

The establishment of reference coordinate systems

Full size image

3.1 Uniaxial motion error modeling

When the workbench is located at x on the x axis in the absolute coordinate system, a ideal position matrix of Ox depended on the origin denoted by Oo is given by:

$${}_{}{}^{o}{T}_{x}=\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& x\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]$$
(3)

The six-term geometric errors coordinate matrix of X mobile platform is:

$${E}_{x}=\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zx}\\ {\epsilon }_{zx}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yx}& {\delta }_{xx}\\ -{\epsilon }_{xx}& {\delta }_{yx}\end{array}\\ \begin{array}{cc}{-\epsilon }_{yx}& {\epsilon }_{xx}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]$$
(4)

Therefore, the actual position matrix of relative coordinate system Ox can be transformed absolute coordinate system Oo. That:

$${}_{}{}^{o}{T}_{x}{\text{E}}_{\text{x}}=\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& x\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zx}\\ {\epsilon }_{zx}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yx}& {\delta }_{xx}\\ -{\epsilon }_{xx}& {\delta }_{yx}\end{array}\\ \begin{array}{cc}{-\epsilon }_{yx}& {\epsilon }_{xx}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zx}\\ {\epsilon }_{zx}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yx}& {\delta }_{xx}+x\\ -{\epsilon }_{xx}& {\delta }_{yx}\end{array}\\ \begin{array}{cc}{-\epsilon }_{yx}& {\epsilon }_{xx}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]$$
(5)

3.2 Traditional machine tools’ spatial geometric error modeling

The actual position offset of the machining point and the origin of the absolute coordinate system, that is, the spatial geometric error formula of the machine tools is the product of the transformation matrix of the homogeneous coordinate of the geometric error between the corresponding coordinate systems. The traditional spatial geometric error model of machine tool is:

$$\begin{aligned}\left[{}^{ref}{T}_{tool}\right]&=\left[{}_{}{}^{ref}{T}_{saddle}{\text{E}}_{\text{s}\text{a}\text{d}\text{d}\text{l}\text{e}}\right]\left[{}^{saddle}{T}_{column}{\text{E}}_{\text{c}\text{o}\text{l}\text{u}\text{m}\text{n}}\right]\times\left[{}^{column}{T}_{head}{\text{E}}_{\text{h}\text{e}\text{a}\text{d}}\right]\\&=\left[{}_{}{}^{o}{T}_{x}{\text{E}}_{\text{x}}\right]\left[{}^{x}{T}_{y}{\text{E}}_{\text{y}}\right]\left[{}_{}{}^{y}{T}_{z}{\text{E}}_{\text{z}}\right]\\&=\left[\begin{array}{cc}\begin{array}{cc}{\varDelta }_{11}+{\epsilon }_{zz}{\varDelta }_{12}-{\epsilon }_{yz}{\varDelta }_{13}& -{\epsilon }_{zz}{\varDelta }_{11}+{\varDelta }_{12}+{\epsilon }_{xz}{\varDelta }_{13}\\ {\varDelta }_{21}+{\epsilon }_{zz}{\varDelta }_{22}-{\epsilon }_{yz}{\varDelta }_{23}& -{\epsilon }_{zz}{\varDelta }_{21}+{\varDelta }_{22}+{\epsilon }_{xz}{\varDelta }_{23}\end{array}& \begin{array}{cc}{\epsilon }_{yz}{\varDelta }_{11}-{\epsilon }_{xz}{\varDelta }_{12}+{\varDelta }_{13}& {\delta }_{xz}{\varDelta }_{11}+{\delta }_{yz}{\varDelta }_{12}+({\delta }_{zz}+z){\varDelta }_{13}+{\varDelta }_{14}\\ {\epsilon }_{yz}{\varDelta }_{21}-{\epsilon }_{xz}{\varDelta }_{22}+{\varDelta }_{23}& {\delta }_{xz}{\varDelta }_{21}+{\delta }_{yz}{\varDelta }_{22}+({\delta }_{zz}+z){\varDelta }_{23}+{\varDelta }_{24}\end{array}\\ \begin{array}{cc}{\varDelta }_{31}+{\epsilon }_{zz}{\varDelta }_{32}-{\epsilon }_{yz}{\varDelta }_{33}&-{\epsilon }_{zz}{\varDelta }_{31}+{\varDelta }_{32}+{\epsilon }_{xz}{\varDelta }_{33}\\ 0& 0\end{array}& \begin{array}{cc}{\epsilon }_{yz}{\varDelta }_{31}-{\epsilon }_{xz}{\varDelta }_{32}+{\varDelta }_{33}& {\delta }_{xz}{\varDelta }_{31}+{\delta }_{yz}{\varDelta }_{32}+({\delta }_{zz}+z){\varDelta }_{33}+{\varDelta }_{34}\\ 0& 1\end{array}\end{array}\right]\end{aligned}$$
(6)

where: for the convenience of writing, let \(\varDelta =\left[{}_{}{}^{o}{T}_{x}{\text{E}}_{\text{x}}\right]\left[{}_{}{}^{x}{T}_{y}{\text{E}}_{\text{y}}\right]\), then we have:

$$\begin{aligned}\varDelta &=\left[{}_{}{}^{o}{T}_{x}{\text{E}}_{\text{x}}\right]\left[{}_{}{}^{x}{T}_{y}{\text{E}}_{\text{y}}\right]=\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zx}\\ {\epsilon }_{zx}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yx}& {\delta }_{xx}+x\\ -{\epsilon }_{xx}& {\delta }_{yx}\end{array}\\ \begin{array}{cc}{-\epsilon }_{yx}& {\epsilon }_{xx}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& -{\epsilon }_{zy}\\ {\epsilon }_{zy}& 1\end{array}& \begin{array}{cc}{\epsilon }_{yy}& {\delta }_{xy}-{\alpha }_{xy}y\\ -{\epsilon }_{xy}& {\delta }_{yy}+y\end{array}\\ \begin{array}{cc}{-\epsilon }_{yy}& {\epsilon }_{xy}\\ 0& 0\end{array}& \begin{array}{cc}1& {\delta }_{zy}\\ 0& 1\end{array}\end{array}\right]\\&=\left[\begin{array}{cc}\begin{array}{cc}1-{\epsilon }_{zx}{\epsilon }_{zy}-{\epsilon }_{yx}{\epsilon }_{yy}& -{\epsilon }_{zy}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{xy}\\ {\epsilon }_{zx}+{\epsilon }_{zy}+{\epsilon }_{xx}{\epsilon }_{yy}& -{\epsilon }_{zx}{\epsilon }_{zy}+1-{\epsilon }_{xx}{\epsilon }_{xy}\end{array}& \begin{array}{cc}{\epsilon }_{yy}+{\epsilon }_{zx}{\epsilon }_{xy}+{\epsilon }_{yx}& {\delta }_{xy}-{\epsilon }_{zx}({\delta }_{yy}+y)+{\epsilon }_{yx} {\delta }_{zy}+({\delta }_{xx}+x)\\ {\epsilon }_{zx}{\epsilon }_{yy}-{\epsilon }_{xy}-{\epsilon }_{xx}& {\epsilon }_{zx}{\delta }_{xy}+({\delta }_{yy}+y)-{\epsilon }_{xx}{\delta }_{zy}+{\delta }_{yx}\end{array}\\ \begin{array}{cc}-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{zy}-{\epsilon }_{yy}& {\epsilon }_{yx}{\epsilon }_{zy}+{\epsilon }_{xx}+{\epsilon }_{xy}\\ 0& 0\end{array}& \begin{array}{cc}-{\epsilon }_{yx}{\epsilon }_{yy}-{\epsilon }_{xx}{\epsilon }_{xy}+1& {-\epsilon }_{yx}{\delta }_{xy}+{\epsilon }_{xx}({\delta }_{yy}+y)+{\delta }_{zy}+ {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]\end{aligned}$$
(7)

The traditional spatial geometric error model of machine tool on the direction X,Y and Z can be described \({E}_{x},{E}_{y}\) and \({E}_{z}\), respectively:

$$\left\{\begin{array}{c}{E}_{x}=(-{\epsilon }_{zx}{\epsilon }_{zy}-{\epsilon }_{yx}{\epsilon }_{yy})x+{\epsilon }_{zz}(-{\epsilon }_{zy}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{xy})x-{\epsilon }_{yz}({\epsilon }_{yy}+{\epsilon }_{zx}{\epsilon }_{xy}+{\epsilon }_{yx})x-{\epsilon }_{zz}(1-{\epsilon }_{zx}{\epsilon }_{zy}-{\epsilon }_{yx}{\epsilon }_{yy})y+(-{\epsilon }_{zy}-{\epsilon }_{zx}\\ +{\epsilon }_{yx}{\epsilon }_{xy})y+{\epsilon }_{xz}({\epsilon }_{yy}+{\epsilon }_{zx}{\epsilon }_{xy}+{\epsilon }_{yx})y+{\epsilon }_{yz}(1-{\epsilon }_{zx}{\epsilon }_{zy}-{\epsilon }_{yx}{\epsilon }_{yy})z-{\epsilon }_{xz}(-{\epsilon }_{zy}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{xy})z+({\epsilon }_{yy}+{\epsilon }_{zx}{\epsilon }_{xy}+{\epsilon }_{yx})z+\\ {\delta }_{xz}(1-{\epsilon }_{zx}{\epsilon }_{zy}-{\epsilon }_{yx}{\epsilon }_{yy})+{\delta }_{yz}(-{\epsilon }_{zy}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{xy})+({\delta }_{zz}+z)({\epsilon }_{yy}+{\epsilon }_{zx}{\epsilon }_{xy}+{\epsilon }_{yx})+{\delta }_{xy}-{\epsilon }_{zx}({\delta }_{yy}+y)+{\epsilon }_{yx} {\delta }_{zy}+{\delta }_{xx}\\ {E}_{y}=({\epsilon }_{zx}+{\epsilon }_{zy}+{\epsilon }_{xx}{\epsilon }_{yy})x+{\epsilon }_{zz}(-{\epsilon }_{zx}{\epsilon }_{zy}+1-{\epsilon }_{xx}{\epsilon }_{xy})x-{\epsilon }_{yz}({\epsilon }_{zx}{\epsilon }_{yy}-{\epsilon }_{xy}-{\epsilon }_{xx})x-{\epsilon }_{zz}({\epsilon }_{zx}+{\epsilon }_{zy}+{\epsilon }_{xx}{\epsilon }_{yy})y+(-{\epsilon }_{zx}{\epsilon }_{zy}-\\ {\epsilon }_{xx}{\epsilon }_{xy})y+{\epsilon }_{xz}({\epsilon }_{zx}{\epsilon }_{yy}-{\epsilon }_{xy}-{\epsilon }_{xx})y+{\epsilon }_{yz}({\epsilon }_{zx}+{\epsilon }_{zy}+{\epsilon }_{xx}{\epsilon }_{yy})z-{\epsilon }_{xz}(-{\epsilon }_{zx}{\epsilon }_{zy}+1-{\epsilon }_{xx}{\epsilon }_{xy})z+({\epsilon }_{zx}{\epsilon }_{yy}-{\epsilon }_{xy}-{\epsilon }_{xx})z+\\ {\delta }_{xz}({\epsilon }_{zx}+{\epsilon }_{zy}+{\epsilon }_{xx}{\epsilon }_{yy})+{\delta }_{yz}(-{\epsilon }_{zx}{\epsilon }_{zy}+1-{\epsilon }_{xx}{\epsilon }_{xy})+({\delta }_{zz}+z)({\epsilon }_{zx}{\epsilon }_{yy}-{\epsilon }_{xy}-{\epsilon }_{xx})+{\epsilon }_{zx}{\delta }_{xy}+{\delta }_{yy}-{\epsilon }_{xx}{\delta }_{zy}+{\delta }_{yx}\\ {E}_{z}=(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{zy}-{\epsilon }_{yy})x+{\epsilon }_{zz}({\epsilon }_{yx}{\epsilon }_{zy}+{\epsilon }_{xx}+{\epsilon }_{xy})x-{\epsilon }_{yz}(-{\epsilon }_{yx}{\epsilon }_{yy}-{\epsilon }_{xx}{\epsilon }_{xy}+1)x-{\epsilon }_{zz}(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{zy}-{\epsilon }_{yy})y+({\epsilon }_{yx}{\epsilon }_{zy}+\\ {\epsilon }_{xx}+{\epsilon }_{xy})y+{\epsilon }_{xz}(-{\epsilon }_{yx}{\epsilon }_{yy}-{\epsilon }_{xx}{\epsilon }_{xy}+1)y+{\epsilon }_{yz}(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{zy}-{\epsilon }_{yy})z-{\epsilon }_{xz}({\epsilon }_{yx}{\epsilon }_{zy}+{\epsilon }_{xx}+{\epsilon }_{xy})z+(-{\epsilon }_{yx}{\epsilon }_{yy}-{\epsilon }_{xx}{\epsilon }_{xy})z+\\ {\delta }_{xz}(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{zy}-{\epsilon }_{yy})+{\delta }_{yz}({\epsilon }_{yx}{\epsilon }_{zy}+{\epsilon }_{xx}+{\epsilon }_{xy})+({\delta }_{zz}+z)(-{\epsilon }_{yx}{\epsilon }_{yy}-{\epsilon }_{xx}{\epsilon }_{xy}){-\epsilon }_{yx}{\delta }_{xy}+{\epsilon }_{xx}({\delta }_{yy}+y)+{\delta }_{zy}+{\delta }_{zx}\end{array}\right.$$
(8)

3.3 Optimized spatial geometric error modeling of CNC machine tool based on two-dimensional angle error

In order to reduce the error and improve the compensation accuracy, the influence of two-dimensional angle error should be taken into account when modeling the spatial geometric error of CNC machine tools. In Sect. 2, the principle of two-dimensional angle error has been explained, and obtained the corresponding calculation Eqs. (1) and (2). Therefore, By substituting Eqs. (1) and (2) into the above traditional machine tool spatial geometric error model, the machine tool spatial geometric error model considering two-dimensional angle error can be obtained.

$$\left[{}_{}{}^{ref}{T}_{tool}\right]^{\prime}=\left[\begin{array}{cc}\begin{array}{cc}{\varDelta ^{\prime }}_{11}+{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{12}-{\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{13}& -{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{11}+{\varDelta ^{\prime }}_{12}+{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{13}\\ {\varDelta ^{\prime }}_{21}+{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{22}-{\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{23}& -{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{21}+{\varDelta ^{\prime }}_{22}+{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{23}\end{array}& \begin{array}{cc}{\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{11}-{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{12}+{\varDelta ^{\prime }}_{13}& {\delta }_{xz}{\varDelta ^{\prime }}_{11}+{\delta }_{yz}{\varDelta ^{\prime }}_{12}+({\delta }_{zz}+z){\varDelta ^{\prime }}_{13}+{\varDelta ^{\prime }}_{14}\\ {\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{21}-{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{22}+{\varDelta ^{\prime }}_{23}& {\delta }_{xz}{\varDelta ^{\prime }}_{21}+{\delta }_{yz}{\varDelta ^{\prime }}_{22}+({\delta }_{zz}+z){\varDelta ^{\prime }}_{23}+{\varDelta ^{\prime }}_{24}\end{array}\\ \begin{array}{cc}{\varDelta ^{\prime }}_{31}+{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{32}-{\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{33}& -{\epsilon }_{z(x,y,z)}{\varDelta ^{\prime }}_{31}+{\varDelta ^{\prime }}_{32}+{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{33}\\ 0& 0\end{array}& \begin{array}{cc}{\epsilon }_{y(x,y,z)}{\varDelta ^{\prime }}_{31}-{\epsilon }_{x(x,y,z)}{\varDelta ^{\prime }}_{32}+{\varDelta ^{\prime }}_{33}& {\delta }_{xz}{\varDelta ^{\prime }}_{31}+{\delta }_{yz}{\varDelta ^{\prime }}_{32}+({\delta }_{zz}+z){\varDelta ^{\prime }}_{33}+{\varDelta ^{\prime }}_{34}\\ 0& 1\end{array}\end{array}\right]$$
(9)

where:

$$\varDelta ^{\prime }=\left[\begin{array}{cc}\begin{array}{cc}1-{\epsilon }_{zx}{\epsilon }_{z(x,y)}-{\epsilon }_{yx}{\epsilon }_{y(x,y)}& -{\epsilon }_{z(x,y)}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{x(x,y)}\\ {\epsilon }_{zx}+{\epsilon }_{z(x,y)}+{\epsilon }_{xx}{\epsilon }_{y(x,y)}& -{\epsilon }_{zx}{\epsilon }_{z(x,y)}+1-{\epsilon }_{xx}{\epsilon }_{x(x,y)}\end{array}& \begin{array}{cc}{\epsilon }_{y(x,y)}+{\epsilon }_{zx}{\epsilon }_{x(x,y)}+{\epsilon }_{yx}& {\delta }_{xy}-{\epsilon }_{zx}({\delta }_{yy}+y)+{\epsilon }_{yx} {\delta }_{zy}+({\delta }_{xx}+x)\\ {\epsilon }_{zx}{\epsilon }_{y(x,y)}-{\epsilon }_{x(x,y)}-{\epsilon }_{xx}& {\epsilon }_{zx}{\delta }_{xy}+({\delta }_{yy}+y)-{\epsilon }_{xx}{\delta }_{zy}+{\delta }_{yx}\end{array}\\ \begin{array}{cc}-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{z(x,y)}-{\epsilon }_{y(x,y)}& {\epsilon }_{yx}{\epsilon }_{z(x,y)}+{\epsilon }_{xx}+{\epsilon }_{x(x,y)}\\ 0& 0\end{array}& \begin{array}{cc}-{\epsilon }_{yx}{\epsilon }_{y(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)}+1& {-\epsilon }_{yx}{\delta }_{xy}+{\epsilon }_{xx}({\delta }_{yy}+y)+{\delta }_{zy}+ {\delta }_{zx}\\ 0& 1\end{array}\end{array}\right]$$
(10)

When we take into the two-dimensional angle error, the optimized spatial geometric error model of the machine tool can be derived as follows:

$$\left\{\begin{array}{c}{E}_{x}=(-{\epsilon }_{zx}{\epsilon }_{z(x,y)}-{\epsilon }_{yx}x+{\epsilon }_{z(x,y,z)}(-{\epsilon }_{z(x,y)}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{x(x,y)})x-{\epsilon }_{y(x,y,z)}({\epsilon }_{y(x,y)}+{\epsilon }_{zx}{\epsilon }_{x(x,y)}+{\epsilon }_{yx})x-{\epsilon }_{z(x,y,z)}(1-{\epsilon }_{zx}{\epsilon }_{z(x,y)}\\ -{\epsilon }_{yx}{\epsilon }_{y(x,y)})y+(-{\epsilon }_{z(x,y)}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{x(x,y)})y+{\epsilon }_{x(x,y,z)}({\epsilon }_{y(x,y)}+{\epsilon }_{zx}{\epsilon }_{x(x,y)}+{\epsilon }_{yx})y+{\epsilon }_{y(x,y,z)}(1-{\epsilon }_{zx}{\epsilon }_{z(x,y)}\\ -{\epsilon }_{yx}{\epsilon }_{y(x,y)})z-{\epsilon }_{x(x,y,z)}(-{\epsilon }_{z(x,y)}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{x(x,y)})z+({\epsilon }_{y(x,y)}+{\epsilon }_{zx}{\epsilon }_{x(x,y)}+{\epsilon }_{yx})z+{\delta }_{xz}(1-{\epsilon }_{zx}{\epsilon }_{z(x,y)}-{\epsilon }_{yx}{\epsilon }_{y(x,y)})\\ +{\delta }_{yz}(-{\epsilon }_{z(x,y)}-{\epsilon }_{zx}+{\epsilon }_{yx}{\epsilon }_{x(x,y)})+({\delta }_{zz}+z)({\epsilon }_{y(x,y)}+{\epsilon }_{zx}{\epsilon }_{x(x,y)}+{\epsilon }_{yx})+{\delta }_{xy}-{\epsilon }_{zx}({\delta }_{yy}+y)+{\epsilon }_{yx} {\delta }_{zy}+{\delta }_{xx}\\ {E}_{y}=({\epsilon }_{zx}+{\epsilon }_{z(x,y)}+{\epsilon }_{xx}{\epsilon }_{y(x,y)})x+{\epsilon }_{z(x,y,z)}(-{\epsilon }_{zx}{\epsilon }_{z(x,y)}+1-{\epsilon }_{xx}{\epsilon }_{x(x,y)})x-{\epsilon }_{y(x,y,z)}({\epsilon }_{zx}{\epsilon }_{y(x,y)}-{\epsilon }_{x(x,y)}-{\epsilon }_{xx})x-{\epsilon }_{z(x,y,z)}({\epsilon }_{zx}+\\ {\epsilon }_{z(x,y)}+{\epsilon }_{xx}{\epsilon }_{y(x,y)})y+(-{\epsilon }_{zx}{\epsilon }_{z(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)})y+{\epsilon }_{x(x,y,z)}({\epsilon }_{zx}{\epsilon }_{y(x,y)}-{\epsilon }_{x(x,y)}-{\epsilon }_{xx})y+{\epsilon }_{y(x,y,z)}({\epsilon }_{zx}+{\epsilon }_{z(x,y)}+\\ {\epsilon }_{xx}{\epsilon }_{y(x,y)})z-{\epsilon }_{x(x,y,z)}(-{\epsilon }_{zx}{\epsilon }_{z(x,y)}+1-{\epsilon }_{xx}{\epsilon }_{x(x,y)})z+({\epsilon }_{zx}{\epsilon }_{y(x,y)}-{\epsilon }_{x(x,y)}-{\epsilon }_{xx})z+{\delta }_{xz}({\epsilon }_{zx}+{\epsilon }_{z(x,y)}+{\epsilon }_{xx}{\epsilon }_{y(x,y)})\\ +{\delta }_{yz}(-{\epsilon }_{zx}{\epsilon }_{z(x,y)}+1-{\epsilon }_{xx}{\epsilon }_{x(x,y)})+({\delta }_{zz}+z)({\epsilon }_{zx}{\epsilon }_{y(x,y)}-{\epsilon }_{x(x,y)}-{\epsilon }_{xx})+{\epsilon }_{zx}{\delta }_{xy}+{\delta }_{yy}-{\epsilon }_{xx}{\delta }_{zy}+{\delta }_{yx}\\ {E}_{z}=(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{z(x,y)}-{\epsilon }_{y(x,y)})x+{\epsilon }_{z(x,y,z)}({\epsilon }_{yx}{\epsilon }_{z(x,y)}+{\epsilon }_{xx}+{\epsilon }_{x(x,y)})x-{\epsilon }_{y(x,y,z)}(-{\epsilon }_{yx}{\epsilon }_{y(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)}+1)x-{\epsilon }_{z(x,y,z)}(-\\ {\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{z(x,y)}-{\epsilon }_{y(x,y)})y+({\epsilon }_{yx}{\epsilon }_{z(x,y)}+{\epsilon }_{xx}+{\epsilon }_{x(x,y)})y+{\epsilon }_{x(x,y,z)}(-{\epsilon }_{yx}{\epsilon }_{y(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)}+1)y+{\epsilon }_{y(x,y,z)}(-{\epsilon }_{yx}+\\ {\epsilon }_{xx}{\epsilon }_{z(x,y)}-{\epsilon }_{y(x,y)})y-{\epsilon }_{x(x,y,z)}({\epsilon }_{yx}{\epsilon }_{z(x,y)}+{\epsilon }_{xx}+{\epsilon }_{x(x,y)})z+(-{\epsilon }_{yx}{\epsilon }_{y(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)})z+{\delta }_{xz}(-{\epsilon }_{yx}+{\epsilon }_{xx}{\epsilon }_{z(x,y)}-\\ {\epsilon }_{y(x,y)})+{\delta }_{yz}({\epsilon }_{yx}{\epsilon }_{z(x,y)}+{\epsilon }_{xx}+{\epsilon }_{x(x,y)})+({\delta }_{zz}+z\left)\right(-{\epsilon }_{yx}{\epsilon }_{y(x,y)}-{\epsilon }_{xx}{\epsilon }_{x(x,y)}){-\epsilon }_{yx}{\delta }_{xy}+{\epsilon }_{xx}({\delta }_{yy}+y)+{\delta }_{zy}+{\delta }_{zx}\end{array}\right.$$
(11)

4 Experimental validation

In order to validate the error model developed in this paper, we have done a sequence of experiment on a three-axis vertical machine center produced by Baoji Machine Tool Factory in China. The working stroke of the machine tool are 1800 mm, 1500 mm in and 1200 mm in the direction of X-axis, Y-axis and Z-axis, respectively.

4.1 Machine tool geometric error data collection

In the case of no collision, considering the rationality of the experiment, the travel of X, Y and Z axes is selected as follows: X axis is − 800 to 0 mm; Y-axis is − 500 to 0 mm; Z-axis is − 500 to 0 mm. In the case of meeting the relevant national measurement requirements, the measurement spacing is 50 mm on each coordinate axis. Both Y axis and Z axis are divided into 11 segments, and X axis is divided into 17 segments. Six geometric errors of each coordinate axis can be measured with laser interferometer. The measurement site and measurement results are shown in Figs. 4 and 5, respectively.

Fig. 4
figure 4

Measurement site

Full size image
Fig. 5
figure 5

Measurement results

Full size image

Figure 5 shows the value of positioning error, angle error and straightness error for each coordinate axis. The detail for each error mentioned above is given in Table 1.

Table 1 Range of positioning error, angle error and straightness error on each coordinate axis
Full size table

The accuracy of the spatial body diagonal [28,29,30], as an important index, is usually applied to evaluate the accuracy of machine tools. According to the ISO 230-6 [31], in a 3-axis CNC space, there are 4 body diagonals which can reflect the overall spatial accuracy of the tool. The 4 body diagonal lines of the machine tool are indicated by PPP, NPP, NPN and PPN, respectively. Figure 6 gives a measurement stroke of the bodies diagonal in our study.

Fig. 6
figure 6

Body diagonal measurement

Full size image

The measuring space of the machine tool is 800 mm × 500 mm × 500 mm, and the measuring spacing (interval) is selected as 80 mm, 50 mm, and 50 mm for X axis, Y axis and Z axis, respectively. Each body diagonals is divided into 10 sections. Figure 7 shows the measurement results measured by laser interferometer for four body diagonals.

Fig. 7
figure 7

Body diagonal measurement results

Full size image

Where: NPP, NPN, PPN and PPP represent the four body diagonals of the machine tool space, and their positioning errors are − 0.6 to −  70.68 μm, 6.01 to −  52.55 μm, −  0.09 ~ 57.56 μm, and − 0.93 to −  58.23 μm, respectively.

4.2 Angle error analysis considering two-dimensional angle error

According to Eqs. (1) and (2), the angle errors after considering two-dimensional angle error are shown in Fig. 8.

Fig. 8
figure 8

The angle errors after two dimensional angle error optimization

Full size image

The angle errors of axes X, Y and Z are improved when is two-dimensional angle error is applied in our model, and the improved angle errors are − 31.05 ~ 37.51 μm, -34.02 ~ 50.5 μm and − 34.72 ~ 66.42 μm for X,Y and Z axis ,respectively.

4.3 Error compensation

With the spatial geometric error compensation module of the machine tool developed on the Huazhong8-CNC system platform, the geometric error is compensated, and the compensation interface is shown in Fig. 9. In the process of error compensation in CNC system, first of all, according to the real-time position of machine tool, on the one hand, the interpolation works out the amount of feeding (x, y, z) in the next interpolation period according to the G code instructions. On the other hand, error compensation module calls compensation algorithm to calculate the compensation amount (Ex, Ey, Ez) according to the next instruction coordinates. Then, they are added together into the driver to control the motor position and realize error compensation.

Fig. 9
figure 9

Compensation interface

Full size image

4.3.1 Quantitative evaluation of body diagonal of machine tool

When compensation are applied, according to the traditional machine tools’ spatial geometric error compensation model, the diagonal errors of the four bodies are measured, and results are shown in Fig. 10.

Fig. 10
figure 10

Measurement results of body diagonals compensated by traditional model

Full size image

When the two-dimensional angle error is not applied in compensation model, the positioning errors of NPP, NPN, PPN and PPP of the four bodies diagonals are 0.65 to − 19.19 μm, 0.94 to − 18.19 μm, 0.97–18.82 μm and − 0.26 to − 19.06 μm, respectively.

According to the improved spatial geometric error compensation model of the machine tool, errors of the diagonal errors for the four bodies are shown in Fig. 11.

Fig. 11
figure 11

Measurement results of body diagonals compensated by optimized model

Full size image

Clearly, when the two-dimensional angle error is applied into our error compensation model, the positioning errors of the diagonal NPP, NPN, PPN and PPP of the four bodies are: 0.17 ~ 8.67 μm, 0.63 ~ 3.55 μm, 0.43 ~ 5.68 μm, 0.74 ~ 5.57 μm.

4.3.2 Comparison of body diagonal precision of machine tool

The bodies diagonal errors of improved model are given in Table 2 compared with the traditional model.

Table 2 Comparison of error data
Full size table

In Table 2: the maximum diagonal error of the machine tool is − 70.68 μm without compensation; the maximum error is − 19.19 μm after compensating with the traditional machine tools’ spatial geometric error compensation model; the maximum error is only − 8.67 μm after the compensation model based on two-dimensional angle error. Clearly, the body-diagonal accuracy after compensation based on the optimized model is 87.73% higher than that before compensation, and 54.82% higher than that of the traditional model after compensation.

5 Conclusion

Traditional machine tools’ spatial geometric error compensation model does not take into account the additional angle errors generated by a transmission from the angle error of lower guide rail to the upper guide rail. This paper presents a machine tools’ spatial geometric error compensation model including the additional angle errors to further improve compensation accuracy, and the compensation ability of improved compensation model is verified by measuring the accuracy of bodies diagonal with a sequence of experiment.

In this study the elastic deformation of machine structural components and the magnitude of these effects on part accuracy is not considered, and we plan to conduct into them in future. Furthermore, it is fundamental to study on proper interfaces for metrology equipment and the documentation of the respective compensation data.