Convection in a horizontal layer of water with three diffusing components

Abstract

Triple diffusive convection in water is modelled with properties like density, specific heat, thermal conductivity, thermal diffusivity and thermal expansion, modified in the presence of salts. The Ginzburg–Landau equation is derived to study heat and mass transports of different combinations of salts in water. A table is prepared documenting the actual values of thermophysical properties of water with different salts and the critical Rayleigh number is calculated. This information is used in the estimation of Nusselt and Sherwood numbers and their relative magnitudes are commented upon. A detailed study on different single, double and triple diffusive systems is done and comparison is made of the results. The local nonlinear stability analysis made via a Ginzburg–Landau model mimics many properties of the original governing equations, namely, Hamiltonian character and a bounded solution.

1 Introduction

Double diffusive convection is a well-studied topic when compared to systems with more than two components. Turner [1] was the first person to consider the two-component convection problem by considering heat and solute as two components having their influence on density and which lead to the instability of the system. Huppert and Turner [2] studied experimentally the influence of heat and salinity in Lake Vanda and concluded that the obtained experimental results are applicable to large scale motions. Double diffusive convection and its applications are well documented in the book by Turner [3]. Rudraiah and Siddheshwar [4] and Mokhtar and Khalidah [5] investigated the effects of cross-diffusion coefficients in a double diffusive system and they concluded that diffusive and finger instabilities are possible by choosing suitable sign and magnitude of cross-diffusion coefficients. Motivated by the above works, Malashetty and Kollur [6], Malashetty et al. [7] and Narayana et al. [8] studied the effect of external constraints like magnetic field and rotation on the stability of a double diffusive system and concluded that these external constraints stabilize the system and reduce the heat and mass transports. The competing influences of various diffusing components on the onset of convection in a three-component system make it a very interesting problem. Griffiths [9] pioneered the study of the linear stability of a triple diffusive system in a horizontal fluid layer of infinite horizontal extent. Griffiths [10] and Griffiths [11] reported an experimental investigation of a three-component system and measured simultaneous fluxes of many dissolved solutes through the diffusive interface of thermohaline convection. A good account of practical situations in which triple diffusive system arises is documented by Corriel et al. [12], Noulty and Leaist [13] and Terrones and Pearlstein [14]. One of the most comprehensive studies on triple diffusive convection is the work of Pearlstein et al. [15]. He showed that instabilities arise in an otherwise stable double diffusive system due to the presence of a third diffusing component. Moroz [16] studied two-dimensional convection problem in a three diffusive system proposed by Griffiths [9]. Lopez et al. [17] was the first to investigate the influence of a rigid boundary on the onset of a triple diffusive system. It was Terrones [18] who considered the effect of coupled molecular diffusion (cross diffusion) on the convective instability in a triple diffusive system. Straughan and Walker [19] examined various aspects of penetrative convection in three-component systems. Straughan and Tracey [20] considered the influence of internal heating (or cooling) on multi-component convection. Rionero [21] obtained conditions in closed-form that are sufficient for inhibiting the onset of convection and that which guarantee the global nonlinear stability of the thermal conduction solution. Gentile and Straughan [22] studied tridispersive thermal convection in a porous medium of which one of the diffusive components is temperature. Raghunath et al. [23] investigated the problem of triple diffusive convection in an Oldroyd-B fluid with cross-diffusion. They found that viscoelastic parameters influence the stability of the stationary bifurcation.

Most of the reported works on single, double and triple diffusive systems that have been investigated are in very general contexts and do not pay attention to the thermophysical properties of the base liquid (mainly water) and the aqueous solutions that are added to them. Bringing into focus this unconsidered aspect of single, double and triple diffusive systems is the main objective of the paper. The analysis of the paper also differs from those of earlier investigations in the sense that the Ginzburg–Landau equation with cubic non-linearity is chosen to make a non-linear stability analysis. In this paper the obtained Ginzburg–Landau equation is tractable and hence an analytical solution is found. Alternately, one can use the HOBW method/Haar wavelet method used by Ali et al. [24,25,26,27,28,29].

2 Mathematical formulation

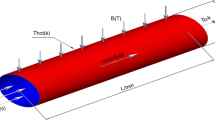
Consider a layer of Newtonian liquid confined between two infinite horizontal surfaces separated by a distance d apart. The z-axis is directed vertically upwards with the lower boundary in the xy−plane. A Cartesian coordinate system is taken with origin in the lower boundary and z-axis vertically upwards (see Fig. 1). Let $\varDelta T, \varDelta S_1$ and $\varDelta S_2$ be the differences in temperature and solute concentrations of the lower and the upper boundaries.

Fig. 1

Physical configuration of the triple diffusive convective system

The governing equations of the two-dimensional triple diffusive thermoconvective problem in terms of stream function, $\psi$ , are:

Conservation of linear momentum

$$\begin{aligned} \rho _0 \frac{\partial }{\partial t}\bigg ( \frac{\partial \psi }{\partial z}\bigg )= & {} -\frac{\partial p}{\partial x} +\mu \nabla ^2\bigg (\frac{\partial \psi }{\partial z}\bigg ), \end{aligned}$$

(1)

$$\begin{aligned} \rho _0 \frac{\partial }{\partial t}\bigg ( \frac{\partial \psi }{\partial x}\bigg )= & {} -\frac{\partial p}{\partial z} -\mu \nabla ^2 \bigg (\frac{\partial \psi }{\partial x}\bigg )-\rho _0 [1-\alpha _{t}(T-T_{0})\nonumber \\&+ \alpha _{S_{1}}(S_{1}-S_{10})+\alpha _{S_{2}}(S_{2}-S_{20})], \end{aligned}$$

(2)

Conservation of Energy

$$\begin{aligned} \frac{\partial T}{\partial t}= \chi \nabla ^2 T + \frac{\partial (\psi ,T)}{\partial (x,z)}, \end{aligned}$$

(3)

Conservation of concentration of solute 1

$$\begin{aligned} \frac{\partial S_{1}}{\partial t}= \chi _{S_{1}} \nabla ^2 S_{1}+ \frac{\partial (\psi ,S_{1})}{\partial (x,z)}, \end{aligned}$$

(4)

Conservation of concentration of solute 2

$$\begin{aligned} \frac{\partial S_{2}}{\partial t}= \chi _{S_{2}} \nabla ^2 S_{2}+ \frac{\partial (\psi ,S_{2})}{\partial (x,z)}, \end{aligned}$$

(5)

where $\rho _{0}$ is the density of the fluid, $\psi$ is the stream function, t is the dimensional time, p is the dimensional dynamic pressure, $\mu$ is the dynamic coefficient of viscosity, $\alpha _{t}$ is the coefficient of thermal expansion, T is the dimensional temperature, $S_{1}$ is the concentration of solute 1, $\alpha _{S_{1}}$ is the coefficient of thermal expansion of the solute 1, $S_{2}$ is the concentration of solute 2, $\alpha _{S_{2}}$ is the solutal analog of the coefficient of thermal expansion of the solute 2, g is acceleration due to gravity, $\chi _{S_{1}}$ is the thermal diffusivity of solute 1, $\chi _{S_{2}}$ is the thermal diffusivity of solute 2, d is the dimensional liquid layer depth, x is the dimensional horizontal coordinate and z is the dimensional vertical coordinate.

The boundary conditions for momentum, heat and mass transport are given by:

$$\begin{aligned} \left. \begin{aligned} \frac{\partial \psi }{\partial x}=0,\,\,\frac{\partial \psi }{\partial z}=0, T=T_{0}+\varDelta T\,\\ S_{1}=S_{10}+\varDelta S_{1}, S_{2}=S_{20}+\varDelta S_{2}, \end{aligned} \right\} z=0 \left. \begin{aligned} \frac{\partial \psi }{\partial x}=0,\frac{\partial \psi }{\partial z}=0; T=T_{0}\\ S_{1}=S_{10},S_{2}=S_{20}\,\,\,\, \end{aligned} \right\} z=d \end{aligned}$$

(6)

These are the boundary conditions on the initial static state of the problem.

3 Stability analysis

The stability of the basic state is analyzed by introducing the following decomposition of the quantities as the sum of the basic state and the perturbed state values:

$$\begin{aligned} \left. \begin{array}{c} \psi =\psi ^{\prime },\\ \rho = \rho _{0}g\left[ 1-\{\alpha _{S_{1}}\varDelta S_{1}-\alpha _{S_{2}}\varDelta S_{2}\}(1-\frac{z}{d})\right] dz +p^{\prime }+C, \\ T=T_{0}+\varDelta T (1- \frac{z}{d})+T^{\prime },\\ S_{1}=S_{10}+\varDelta S^{\prime }_{1}\bigg (1-\frac{z}{d}\bigg )+S_{1}^{\prime },\\ S_{2}=S_{20}+\varDelta S^{\prime }_{2}\bigg (1-\frac{z}{d}\bigg )+S_{2}^{\prime }, \end{array}\right\} \end{aligned}$$

(7)

where the primes indicate that the quantities are perturbed.

Substituting Eq. (7) into the basic governing Eqs. (1)–(5), eliminating the pressure, making the resulting equations dimensionless using the following definitions:

$$\begin{aligned} \left. \begin{array}{c} (x^*,y^*,z^*)=\big (\frac{x}{d},\,\frac{y}{d},\,\frac{z}{d}\big ),\,t^{*}=\frac{t^{\prime }}{\frac{d^2}{\chi }},\,\,\,\,\, \psi ^{*}=\frac{\psi ^{\prime }}{\chi },\,\,\,\,\,\,\,\\ \theta ^{*}=\frac{T^{\prime }}{\varDelta T},\,\,\,\, \phi ^* S_{1}=\frac{S^{\prime }_{1}}{\varDelta S_{1}},\,\,\,\, \phi ^{*}S_{2}=\frac{S^{\prime }_{2}}{\varDelta S_{2}}, \end{array}\right\} \end{aligned}$$

(8)

we obtain the following dimensionless equations (after dropping the asterisk) :

$$\begin{aligned}&\left[ {\begin{array}{cccc} -\nabla ^4 &{} \quad R_{T}\frac{\partial }{\partial x} &{} \quad -R_{S_{1}}\frac{\partial }{\partial x} &{} \quad -R_{S_{2}}\frac{\partial }{\partial x} \\ \frac{\partial }{\partial x} &{} \quad -\nabla ^2 &{} \quad 0 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad -\tau _{1}\nabla ^2 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad 0 &{} \quad -\tau _{2}\nabla ^2 \\ \end{array} } \right] \left[ {\begin{array}{c} \psi \\ \theta \\ \phi _{S_{1}}\\ \phi _{S_{2}} \\ \end{array} } \right] \nonumber \\&\quad = \, \left[ {\begin{array}{c} -\frac{1}{Pr}\frac{\partial }{\partial t}(\nabla ^2 \psi )+\frac{1}{Pr}\frac{\partial (\psi , \nabla ^2 \psi )}{\partial (x,z)} \\ -\frac{\partial \theta }{\partial t}+\frac{\partial (\psi , \theta )}{\partial (x,z)}\\ -\frac{\partial \phi _{S_{1}}}{\partial t}+\frac{\partial (\psi , \phi _{S_{1}})}{\partial (x,z)}\\ -\frac{\partial \phi _{S_{2}}}{\partial t}+\frac{\partial (\psi , \phi _{S_{2}})}{\partial (x,z)}\\ \end{array} } \right] \end{aligned}$$

(9)

where $R_{T}$ is the Rayleigh number, $R_{S_{1}}$ is the Rayleigh number of solute 1, $R_{S_{2}}$ is the Rayleigh number of solute 2, Pr is the Prandtl number, $\psi$ is the dimensionless stream function, $\theta$ is the dimensionless temperature, $\phi _{S_{1}}$ is the dimensionless concentration of solute 1 , $\phi _{S_{2}}$ is the dimensionless concentration of solute 2, $\tau _{1}$ is the ratio of diffusivity of solute1 and the heat diffusivity and $\tau _{2}$ is the ratio of the diffusivity of solute 2 and the heat diffusivity.

4 Weakly nonlinear analysis

In this section, a local non-linear stability analysis of triple diffusive convection is performed using the Ginzburg–Landau model. To make this study, we take Jacobians in the system (9) to be non-zero. We now introduce the following perturbation expansion:

$$\begin{aligned} \left. \begin{array}{l} R_{T}= R_{0}+\delta ^2 R_{2}+\delta ^4 R_{4}+...,\\ \psi = \delta \psi _{1}+\delta ^2 \psi _{2}+\delta ^3 \psi _{3}+...,\\ \theta = \delta \theta _{1}+\delta ^2 \theta _{2}+\delta ^3 \theta _{3}+...,\\ \phi _{S_{1}} = \delta \phi _{S_{11}}+\delta ^2 \phi _{S_{12}}+\delta ^3\phi _{S_{13}} +...,\,\,\,\,\\ \phi _{S_{2}} = \delta \phi _{S_{21}}+\delta ^2 \phi _{S_{22}}+\delta ^3\phi _{S_{23}} +...,\,\,\,\,\\ \end{array}\right\} \end{aligned}$$

(10)

where $R_0$ is the Rayleigh number at the onset of steady and triple−diffusive convection, $R_2$ is the second−order correction to $R_0$ , $R_4$ is the fourth-order correction to $R_0$ , $\psi _{i}, \theta _{i}, \phi _{S_{1i}}, \phi _{S_{2i}} (i=1,2,3)$ are the first, second and third order solutions to $\psi , \theta , \phi _{S_{1}}, \phi _{S_{2}}$ and $\delta$ is the perturbation parameter.

Substituting Eq. (10) in Eq. (9) and introducing a small time scale $\tau ^{*}=\delta ^{2}t_{1}$ and comparing the coefficients of like powers of $\delta$ on either side of the resulting equations, we get the systems of linear inhomogeneous equations of different orders.

The first-order system is given by

$$\begin{aligned} \left[ {\begin{array}{cccc} -\nabla ^4 &{} \quad R_{0}\frac{\partial }{\partial x} &{} \quad -R_{S_{1}}\frac{\partial }{\partial x} &{} \quad -R_{S_{2}}\frac{\partial }{\partial x} \\ \frac{\partial }{\partial x} &{} \quad -\nabla ^2 &{} \quad 0 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad -\tau _{1}\nabla ^2 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad 0 &{} \quad -\tau _{2}\nabla ^2 \\ \end{array} } \right] \left[ {\begin{array}{c} \psi _{1} \\ \theta _{1}\\ \phi _{S_{11}}\\ \phi _{S_{21}} \\ \end{array} } \right] \,\, = \,\, \left[ {\begin{array}{c} 0 \\ 0\\ 0\\ 0\\ \end{array} } \right] . \end{aligned}$$

(11)

The boundary conditions to solve this first-order system are given by

$\frac{\partial \psi _{1}}{\partial x}=\frac{\partial \psi _{1}}{\partial z}=\theta _{1}=\phi _{S_{11}}=\phi _{S_{21}}=0; \,at\, z=0,1.$

The solution of the first-order system subject to the above conditions

$$\begin{aligned} \left. \begin{array}{l} \psi _{1}= A(\tau ^*) sin(\alpha x) sin(\pi z)\\ \theta _{1} = -\frac{\alpha }{k^2}A(\tau ^*) cos( \alpha x) sin(\pi z),\\ \phi _{S_{11}} =-\frac{\alpha }{k^2\tau _{1}}A(\tau ^*) cos( \alpha x) sin(\pi z),\\ \phi _{S_{21}} =-\frac{\alpha }{k^2\tau _{2}}A(\tau ^*) cos( \alpha x) sin(\pi z),\\ \end{array}\right\} \end{aligned}$$

(12)

where $k^{2}= \pi ^{2}+\alpha ^{2}$ is the wave number, $A(\tau ^*)$ is the amplitude and $R_0$ is the eigen value of the system which is given by

$$\begin{aligned} R^{st}_{0}=\frac{R_{S_{1}}}{\tau _{1}}+\frac{R_{S_{2}}}{\tau _{2}}+\frac{k^6}{\pi ^{2}\alpha ^{2}}. \end{aligned}$$

(13)

At the second-order, we have

$$\begin{aligned} \left[ {\begin{array}{cccc} -\nabla ^4 &{} \quad R_{0}\frac{\partial }{\partial x} &{} \quad -R_{S_{1}}\frac{\partial }{\partial x} &{} \quad -R_{S_{2}}\frac{\partial }{\partial x} \\ \frac{\partial }{\partial x} &{} \quad -\nabla ^2 &{} \quad 0 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad -\tau _{1}\nabla ^2 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad 0 &{} \quad -\tau _{2}\nabla ^2 \\ \end{array} } \right] \left[ {\begin{array}{c} \psi _{2} \\ \theta _{2}\\ \phi _{S_{12}}\\ \phi _{S_{22}} \\ \end{array} } \right] \,\, = \,\, \left[ {\begin{array}{c} R_{21} \\ R_{22}\\ R_{23}\\ R_{24}\\ \end{array} } \right] , \end{aligned}$$

(14)

where

$$\begin{aligned} \left. \begin{array}{l} R_{21}= 0,\\ R_{22} = \frac{\partial (\psi _{1}, \theta _{1})}{\partial (x,z)}=-\frac{\alpha ^2 \pi }{2 k^2} A^2(\tau ^*) sin(2\pi z),\\ R_{23} = \frac{\partial (\psi _{1}, \phi _{S_{11}})}{\partial (x,z)}=-\frac{\alpha ^2 \pi }{2 k^2 \tau ^{2}_{1}} A^2(\tau ^*) sin(2\pi z),\\ R_{24} = \frac{\partial (\psi _{1}, \phi _{S_{21}})}{\partial (x,z)}=-\frac{\alpha ^2 \pi }{2 k^2 \tau ^{2}_{2}} A^2(\tau ^*) sin(2\pi z).\\ \end{array}\right\} . \end{aligned}$$

(15)

The boundary conditions to solve this second order system are given by

$$\begin{aligned} \frac{\partial \psi _{2}}{\partial x}=\frac{\partial \psi _{2}}{\partial z}=\theta _{2}=\phi _{S_{12}}=\phi _{S_{22}}=0; at\,\, z=0,1 \end{aligned}$$

The second order system (14) has solutions as follows:

$$\begin{aligned} \left. \begin{array}{l} \psi _{2} = 0, \\ \theta _{2} =-\frac{\alpha ^2 }{8 \pi k^2} A^2(\tau ^*) sin(2\pi z), \\ \phi _{S_{12}} = -\frac{\alpha ^2 \pi }{8 \pi k^2 \tau ^{2}_{1}} A^2(\tau ^*) sin(2\pi z), \\ \phi _{S_{22}} = -\frac{\alpha ^2 \pi }{8 \pi k^2 \tau ^{2}_{2}} A^2(\tau ^*) sin(2\pi z). \\ \end{array}\right\} \end{aligned}$$

(16)

In this section, we focus attention primarily on the Nusselt number and the Sherwood numbers. The horizontally averaged Nusselt number, Nu, and the Sherwood number corresponding to solute 1, $Sh_1$ , and the Sherwood number corresponding to solute 2, $Sh_2$, are given by

$$\begin{aligned} Nu(\tau ^*)= & {} 1+\frac{\left[ \dfrac{\alpha }{2 \pi } \int _{0} ^ {\frac{2 \pi }{\alpha }} \frac{d}{dz}(1-z+\theta _{2})dx \right] _{z=0}}{\left[ \frac{\alpha }{2 \pi } \int _{0}^ {\frac{2 \pi }{\alpha }} \frac{d}{dz} (1-z)dx \right] _{z=0}}, \end{aligned}$$

(17)

$$\begin{aligned} Sh_{1}(\tau ^*)= & {} 1+\frac{\left[ \dfrac{\alpha }{2 \pi } \int _{0} ^ {\frac{2 \pi }{\alpha }} \frac{d}{dz}(1-z+\phi _{S_{12}})dx \right] _{z=0}}{\left[ \frac{\alpha }{2 \pi } \int _{0}^ {\frac{2 \pi }{\alpha }} \frac{d}{dz} (1-z)dx \right] _{z=0}}, \end{aligned}$$

(18)

$$\begin{aligned} Sh_{2}(\tau ^*)= & {} 1+\frac{\left[ \dfrac{\alpha }{2 \pi } \int _{0} ^ {\frac{2 \pi }{\alpha }} \frac{d}{dz}(1-z+\phi _{S_{22}})dx \right] _{z=0}}{\left[ \frac{\alpha }{2 \pi } \int _{0}^ {\frac{2 \pi }{\alpha }} \frac{d}{dz} (1-z)dx \right] _{z=0}}. \end{aligned}$$

(19)

Substituting $\theta _{2}$, $\phi _{S_{12}}$ and $\phi _{S_{22}}$ from Eq. (16) into the Eqs. (17) to (19) and simplifying, we obtain:

$$\begin{aligned} Nu(\tau ^*)= & {} 1+\frac{\alpha ^2 }{4 k^2} A^2(\tau ^*), \end{aligned}$$

(20)

$$\begin{aligned} Sh_{1}(\tau ^*)= & {} 1+\frac{\alpha ^2 }{4 k^2 \tau ^{2}_{1}} A^2(\tau ^*), \end{aligned}$$

(21)

$$\begin{aligned} Sh_{2}(\tau ^*)= & {} 1+\frac{\alpha ^2 }{4 k^2 \tau ^{2}_{2}} A^2(\tau ^*). \end{aligned}$$

(22)

At the third order, we have

$$\begin{aligned} \left[ {\begin{array}{cccc} -\nabla ^4 &{} \quad R_{0}\frac{\partial }{\partial x} &{} \quad -R_{S_{1}}\frac{\partial }{\partial x} &{} \quad -R_{S_{2}}\frac{\partial }{\partial x} \\ \frac{\partial }{\partial x} &{} \quad -\nabla ^2 &{} \quad 0 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad -\tau _{1}\nabla ^2 &{} \quad 0 \\ \frac{\partial }{\partial x} &{} \quad 0 &{} \quad 0 &{} \quad -\tau _{2}\nabla ^2 \\ \end{array} } \right] \left[ {\begin{array}{c} \psi _{3} \\ \theta _{3}\\ \phi _{S_{13}}\\ \phi _{S_{23}} \\ \end{array} } \right] \,\, = \,\, \left[ {\begin{array}{c} R_{31} \\ R_{32}\\ R_{33}\\ R_{34}\\ \end{array} } \right] , \end{aligned}$$

(23)

where

$$\begin{aligned} \left. \begin{array}{l} R_{31}= -\frac{1}{Pr}\frac{\partial }{\partial \tau ^*}\{\nabla ^2 \psi _{1}\}-Ra \frac{\partial }{\partial x}\{\theta _{1}\}, \\ R_{32} = - \frac{\partial }{\partial \tau ^*}\{\theta _{1}\}+\frac{\partial (\psi _{1}, \theta _{2})}{\partial (x,z)}, \\ R_{33} =- \frac{\partial }{\partial \tau ^*}\{\psi _{S_{11}}\}+\frac{\partial (\psi _{1}, \phi _{S_{12}}}{\partial (x,z)}, \\ R_{34} = - \frac{\partial }{\partial \tau ^*}\{\psi _{S_{21}}\}+\frac{\partial (\psi _{1}, \phi _{S_{22}}}{\partial (x,z)}. \\ \end{array}\right\} \end{aligned}$$

(24)

The boundary conditions to solve this second-order system are given by $\frac{\partial \psi _{3}}{\partial x}=\frac{\partial \psi _{3}}{\partial z}=\theta _{3}=\phi _{S_{13}}=\phi _{S_{23}}=0; \,\,at\,\, z=0,1$.

Table 1 Thermophysical properties of aqueous solutions at 300K

Table 2 Ratio of diffusivity, solutal Rayleigh number and Prandtl number of different aqueous solutions

For the existence of the solution of the third-order system (23), the Fredholm solvability condition needs to apply which is given by:

$$\begin{aligned} \int _{z=0}^{1} \int _{x=0}^{\frac{2 \pi }{\alpha }} [ \hat{\psi _{1}} R_{31}+\hat{\theta _{1}} R_{32}+\hat{\phi _{S_{11}}} R_{33}+\hat{\phi _{S_{22}}} R_{34} ]dxdz=0. \end{aligned}$$

(25)

where $[ \hat{\psi _{1}}, \hat{\theta _{1}}, \hat{\phi _{S_{11}}}, \hat{\phi _{S_{22}}} ]^{T}$ is the solution of the adjoint of the first-order system, viz.,

$$\begin{aligned} \left[ {\begin{array}{cccc} -\nabla ^4 &{} -\frac{\partial }{\partial x} &{} -\frac{\partial }{\partial x} &{} -\frac{\partial }{\partial x} \\ -R_{0}\frac{\partial }{\partial x} &{} -\nabla ^2 &{} 0 &{} 0 \\ -R_{s_{1}}\frac{\partial }{\partial x} &{} 0 &{} -\tau _{1}\nabla ^2 &{} 0 \\ -R_{s_{2}} \frac{\partial }{\partial x} &{} 0 &{} 0 &{} -\tau _{2}\nabla ^2 \\ \end{array} } \right] \left[ {\begin{array}{c} \hat{\psi _{1}} \\ \hat{\theta _{1}}\\ \hat{\phi _{S_{11}}}\\ \hat{\phi _{S_{22}}}\\ \end{array} }\right] \,\, = \,\, \left[ {\begin{array}{c} 0 \\ 0\\ 0\\ 0\\ \end{array} } \right] . \end{aligned}$$

(26)

The solution of the system (26) is given by

$$\begin{aligned} \left. \begin{array}{l} \hat{\psi _{1}}= A(\tau ^*) sin(\alpha x) sin(\pi z), \\ \hat{\theta _{1}} = \frac{\alpha R_{0}}{k^2}A(\tau ^*) cos( \alpha x) sin(\pi z), \\ \hat{\phi _{S_{11}}} = -\frac{\alpha R_{s_{1}}}{k^2}A(\tau ^*) cos( \alpha x) sin(\pi z), \\ \hat{\phi _{S_{22}}} =-\frac{\alpha R_{s_{2}}}{k^2}A(\tau ^*) cos( \alpha x) sin(\pi z). \\ \end{array}\right\} \end{aligned}$$

(27)

Substituting Eqs. (24) and (27) into Eq. (25), we arrive at the autonomous Ginzburg–Landau equation in the form:

$$\begin{aligned} A_{1}\frac{d}{ d \tau ^*}[A(\tau ^*)]=A_{2}A(\tau ^*)-A_{3}A^{3}(\tau ^*), \end{aligned}$$

(28)

where

$$\begin{aligned} \left. \begin{array}{c} A_{1}=\frac{k^2}{Pr}-\frac{\alpha ^2}{k^4}\bigg [R_0-\frac{R_{s_{1}}}{\tau ^{2}_{1}}-\frac{R_{s_{2}}}{\tau ^{2}_{2}}\bigg ];\,\,A_{2} = \frac{Ra_{2}\alpha ^2}{k^2}; A_{3}=\bigg (R_0-\frac{R_{s_{1}}}{\tau ^{3}_{1}}-\frac{R_{s_{2}}}{\tau ^{3}_{2}}\bigg )\frac{\alpha ^4}{8 k^4}\\ \end{array}\right\} . \end{aligned}$$

(29)

The analytical solution of the Ginzburg–Landau equation (28), subject to the initial condition $A(0)= 1$ , is given by

$$\begin{aligned} A(\tau ^*) = \frac{Exp\bigg [\frac{A_{2}}{A_{1}} \tau ^* \bigg ]}{\sqrt{1+ \frac{A_{3}}{A_{2}}\left\{ Exp\bigg [\frac{2A_{2}}{A_{1}}\tau ^*\bigg ]-1\right\} }}. \end{aligned}$$

(30)

5 Results and discussion

Triple diffusive convection in water is studied in the paper with heat as one diffusing component and two aqueous solutions as the other two components. Aqueous solutions of KCl, NaCl, $CaCl_2$, $BaCl_2$ are considered in the paper and the thermophysical properties of water and the aqueous solutions are used in making definite predictions about thermal convection in water, four different double diffusive systems and six triple diffusive systems. The thermophysical properties of water and the four aqueous solutions are shown in Tables 1 and 2. The tables provide a clear picture on the typical values of thermophysical quantities, and the predictions on onset and heat and mass transports are quite accurate.

Table 3 Critical Rayleigh number and wave number of different aqueous solutions in double diffusive convection

Table 4 Critical Rayleigh number and wave number of different aqueous solutions in triple diffusive convection

A linear stability analysis of the thermal system, four double-diffusive systems and six triple diffusive systems gives identical results in terms of the critical wave number. The cell size at onset is same for all the eleven systems and these have the wave length to be 8.88576. This result is documented in Tables 3 and 4 which further reveals that

$$\begin{aligned}&R^{BaCl_{2}}_{c}> R^{NaCl}_{c}> R_{c}^{KCl}>R_{c}^{CaCl_{2}},\\&\quad R^{NaCl+BaCl_{2}}_{c}>R^{KCl+BaCl_{2}}_{c}>R^{BaCl_{2}+CaCl_{2}}_{c}> R^{KCl+NaCl}_{c}>R^{NaCl+CaCl_{2}}_{c}\\&\quad >R_{c}^{KCl+CaCl_{2}}. \end{aligned}$$

If one were to analyse this result then it is pretty obvious that the thermal conductivity of the aqueous solutions predominantly dictate such results. In respect of thermal conductivity, we have the result $k_{c}^{BaCl_{2}}< k_{c}^{NaCl}< k_{c}^{KCl}< k_{c}^{CaCl_{2}}$.

Though the other thermophysical properties of the other aqueous solutions do not have an ordering like that of the thermal conductivity, it is apparent that the thermal conductivity is the deciding factor. From Table 4, it becomes clear that the addition of one more diffusing component to the double diffusive systems does not alter the cell size. These, however, contribute to the critical Rayleigh number. Table 5 and Figs. 2 and 3 present the following results in the case of the Nusselt and the Sherwood numbers:

$$\begin{aligned}&Nu^{BaCl_{2}}<Nu^{NaCl}<Nu^{KCl}<Nu^{CaCl_{2}}\\&Sh_{1}^{KCl}>Sh_{1}^{NaCl}<Sh_{1}^{CaCl_{2}}>Sh_{1}^{BaCl_{2}}. \end{aligned}$$

Table 5 Comment on Nusselt and Sherwood numbers of different aqueous solutions in double diffusive convection

From this finding, we may conclude that heat transport is the highest in that double diffusive system in which the onset is earlier. We also find that the Nusselt number of aqueous solution of $CaCl_2$ and $BaCl_2$ is greater than the Sherwood number whereas it is opposite in the case of KCl and NaCl. The value of the diffusivity ratio of such solutions decides this result.

Fig. 2

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for double diffusive convection

Fig. 3

Plot of Sherwood number, $Sh_1$, versus time, t, for different aqueous solutions for double diffusive convection

Table 6 and Figs. 4, 5 and 6 present several important results on triple diffusive systems. The results tabulated in Table 6 essentially decide the nature of results on heat transfer in triple diffusive systems. There is a discernible pattern pertaining to Sherwood and Nusselt numbers in the case of triple diffusive systems. This can be seen in Table 5 and Figs. 4, 5 and 6. The values of the diffusivity ratios $\tau _{1}$ and $\tau _{2}$ being less than unity or greater than unity will decide on whether heat transport is more or mass transport is more in the system. Further which of the diffusing components facilitates higher heat transfer and in combination with which other components can be seen in Table 5 and Figs. 4, 5 and 6.

Table 6 Comment on Nusselt and Sherwood numbers of different aqueous solutions in triple diffusive convection

The results on this observation are mentioned below:

$$\begin{aligned}&Nu^{KCl+CaCl_{2}}< Nu^{NaCl+CaCl_{2}}< Nu^{KCl+NaCl}< Nu^{CaCl_{2}+BaCl_{2}}<\\&Nu^{KCl+BaCL_{2}}<Nu^{NaCl+BaCl_{2}},\\&Sh_{1}^{BaCl_{2}+CaCl_{2}}< Sh_{1}^{NaCl+CaCl_{2}}< Sh_{1}^{KCl+CaCl_{2}}< Sh_{1}^{KCl+NaCl}<\\&Sh_{1}^{NaCl+BaCl_{2}}< Sh_{1}^{KCl+BaCL_{2}},\\&Sh_{2}^{KCl+CaCl_{2}}< Sh_{2}^{NaCl+CaCl_{2}}< Sh_{2}^{BaCl_{2}+CaCl_{2}}< Sh_{2}^{KCl+BaCL_{2}}<\\&Sh_{2}^{NaCl+KCl } < Sh_{2}^{NaCl+BaCL_{2}}. \end{aligned}$$

In order to compare the quantum of heat and mass transport, we consider Eqs. (20)–(22) to obtain the following results (Table 6):

$$\begin{aligned}&\frac{Sh_{1}(\tau ^*)-1}{Nu(\tau ^*)-1}=\frac{1}{\tau _{1}^{2}};\,\,\,\,\,\,\, \frac{Sh_{2}(\tau ^*)-1}{Nu(\tau ^*)-1}=\frac{1}{\tau _{2}^{2}};\\&\quad \frac{Sh_{1}(\tau ^*)-1}{Sh_{2}(\tau ^*)-1}=\frac{\tau _{2}^{2}}{\tau _{1}^{2}} \end{aligned}$$

Fig. 4

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for triple diffusive convection

Fig. 5

Plot of Sherwood number, $Sh_1$, versus time, t, for different aqueous solutions for triple diffusive convection

Fig. 6

Plot of Sherwood number, $Sh_2$, versus time, t, for different aqueous solutions for triple diffusive convection

Table 7 presents qualitative results on the quantum of heat and mass transports. The value of the diffusivity ratio, being less than or greater than unity decides whether heat transport dominates or the mass transport.

Table 7 Comparison of Nusselt and Sherwood numbers in double diffusive convection

Table 8 Comparison of Nusselt and Sherwood numbers in triple diffusive convection

Table 8 carries a summary of the results of table 5.

Figures 7, 8, 9 and 10, consider four different possibilities with $Rs_1$ and $Rs_2$, namely,

• 1. $Rs_1> 0\,\, and\,\, Rs_2 > 0,$

• 2. $Rs_1< 0\,\, and\,\, Rs_2 < 0,$

• 3. $Rs_1 > 0\,\, and\,\, Rs_2 < 0,$

• 4. $Rs_1 < 0\,\, and\,\, Rs_2 > 0.$

The general results obtained in the case 1 above is qualitatively different from other three cases. Figures 7, 8, 9 and 10 clearly indicate such a result.

Fig. 7

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for both $Rs_1$ and $Rs_2$ positive

Fig. 8

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for both $Rs_1$ and $Rs_2$ negative

Fig. 9

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for $Rs_1$ positive and $Rs_2$ negative

Representative single, double and triple diffusive systems are considered and conclusions of a general nature are made. In these representative aqueous solutions, we obtained the following results from Figs. 11 and 12:

$$\begin{aligned}&Nu^{Water + KCl + NaCl}> Nu ^{Water+ KCl}> Nu^{Water},\\&Sh_{1}^{Water + KCl + NaCl} > Sh_{1}^{Water+ KCl}. \end{aligned}$$

We have refrained from making a plot of $Sh_2$ versus $\tau ^{*}$ for $water + KCl + NaCl$, as this variation is similar to the corresponding variation of $Sh_1$ in Fig. 12.

Fig. 10

Plot of Nusselt number, Nu, versus time, t, for different aqueous solutions for $Rs_1$ negative and $Rs_2$ positive

Fig. 11

Plot of Nusselt number, Nu, versus time, t, for single, double and triple diffusive convections, where $Rs_1 > 0$ and $Rs_2 > 0$

Fig. 12

Plot of Sherwood number, $Sh_1$, versus time, t, for double and triple diffusive convections, $Rs_1 > 0$ and $Rs_2 > 0$

6 Conclusion

The following are the conclusions drawn from the study:

• 1. The critical values of the Rayleigh, Nusselt and Sherwood numbers obtained in the study are based on best estimated values of the thermophysical properties of the aqueous solutions.

• 2. The values of diffusivity ratios in triple diffusive convection decide whether the heat transport is more or mass transport is more, but in the case of double diffusive convection heat transport is more always.

• 3. Water as a heat transport medium may be inadequate in some situations and hence there is a need for using aqueous solutions in it.

• 4. Use of $CaCl_{2}$ and $BaCl_{2}$ with other salts enhances the heat transport which seems a very attractive proposition for cooling, whereas use of KCl and NaCl increases the mass transport and seems a good proposition for thermal storage.