A novel approach for the edge rolling force and dog-bone shape by combination of slip-line and exponent velocity field

Abstract

This study presents a new mathematical model for edge rolling force and dog-bone shape using the combination of slip-line and exponent velocity field. The slip-line field of the dog-bone area is drawn out based on the deformation characteristics of edge rolling and the maximal depth of dog-bone zone is determined. Then a new exponent velocity field and corresponding strain rate field which satisfy kinematically admissible condition are proposed to analyze the edge rolling force based on upper bound approach. The upper bound solutions of dog-bone shape and rolling force are obtained by minimizing the total power which contains the internal plastic power, frictional and shear powers. The effects of reduction rate, initial thickness and roll radius on dog-bone shape size and edge rolling force are discussed. The results obtained by the combined solution in this paper are compared with measured data in strip hot rolling field and finite element method (FEM) simulation results, and a good agreement is found.

1 Introduction

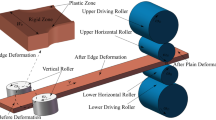
The width accuracy of hot rolled strip steel products is a very important technical indicator in the hot rolling process. In order to obtain desired size of slabs, the edge rolling process plays an important role in regulating and controlling slab width in actual production, as shown in Fig. 1. In edge rolling progress, owing to the high ratio of width to thickness, the plastic deformation of slab is mainly restricted in a small area on the edge. As a result, significant double drum shape appears on the slab cross-section, as illustrated in Fig. 2, which is called dog-bone shape [1]. Due to the complex environment of hot rolling production field, a mechanical model is usually established to predict the edge rolling force, and the dog-bone shape is predicted based on the relationship between the rolling force and the shape. Therefore, improve the prediction accuracy of edge rolling force and dog-bone shape is conducive to high precision width control to enhance the quality of hot rolling products.

Fig. 1

Edge-horizontal rolling process in roughing mill

Fig. 2

Dog-bone profile after edge rolling

About edge rolling force and dog bone shape, a lot of experimental investigations and FEM simulations have been done by many scholars. Okado et al. [2] used pure lead to simulate vertical rolling on a laboratory mill, four parameters including peak height of dog-bone area, thickness of contact between slab and vertical roll, location of dog-bone peak and deformation area’s width were firstly proposed to represent the cross section characteristics of dog-bone shape after edge rolling, then an empirical formula which considered above four parameters, the effects of slab thickness and reduction was given. Toaze [3] added roll radius and slab width in these equations on the basis of experimental data obtained by Shibahara et al. [4], and concluded that the width of dog-bone area and the position of dog-bone peak were proportional to the unilateral reduction. Ginzburg [5] modified these formulas later, the results obtained are consistent with those obtained by Huismann [6]. However these formulas are empirical and partial due to limitations of experimental conditions, the results may be unstable under different rolling conditions.

The finite element method (FEM) is one of the most suitable ways to investigate edge rolling which provides complex calculations under actual process constraints and various deformation conditions. Huisman and Huetink [7] investigated the effect of different vertical roll radius on the dog-bone shape after edge rolling, and verified the FEM results by using plasticine as experimental material, the velocity field of particle flow was used to explain the formation process of dog bone, and the stress–strain distribution during vertical rolling was obtained. The simulated peak height of dog-bone was in good agreement with the experimental value, and it is considered that the width reduction efficiency of large roll diameter is significantly higher than that of small roll diameter. David et al. [8] studied the influence of friction coefficient on the dog-bone formation process in edge rolling by using the penalty function calculation method of visco-plastic FEM, and the calculated value of dog-bone shape parameters was consistent with the measured data, but the result of rolling force was greatly deviated. Xiong et al. [9] proposed a 3-dimensional model to discuss the utilization of the slightly compressible FEM to analyze edge rolling force and dog-bone shape, and obtained the relationships among section profile after edge rolling, rolling parameters and other influence factors. Unfortunately, although the results obtained by the FEM are accurate, it is not applicable for on-line automatic control in practical production due to the large amount of computation time.

The analytical solution based on energy approach is another method to study edge rolling process by establishing kinematically admissible velocity field and then calculate the deformation power and force. Lundberg et al. [10] hypothesized that the edge rolling process was plane deformation, respectively established the triangular velocity field in the deformation zone with and without friction, and obtained the hodograph of metal flow during vertical rolling, thus the rolling torque was calculated. However, the specific steps to calculate the dog-bone shape are not given in this paper and it is considered that friction has little influence on the calculation of vertical rolling torque. Yun et al. [11] proposed an abstract dog-bone shape model composed of exponential function and quaternary function, and the kinematically admissible velocity field was established based on stream function and constant volume principle. The parameters of dog-bone shape and edge rolling force were obtained by fitting FEM simulation data. Finally, the predicted value of dog-bone shape was compared with the results obtained by Okado’s model and Shibahara’s physical simulation and the errors were within 5%. However, the analytical solution of dog-bone shape and edge rolling force are not obtained. Liu et al. [12] established the sine function dog-bone shape model and corresponding velocity and strain rate fields on the basis of the incompressibility condition and stream function. The solutions of edge rolling force and dog-bone shape were presented based on upper bound method, then these results are compared with previous models and FEM simulation and the errors were within 6.7%. But the maximum depth of the dog-bone region was obtained indirectly by incompressibility condition and the total power functional minimization.

The slip-line method is a classical algorithm for solving plane deformation problems which was firstly proposed by Hencky in 1923, and improved by Pandtl, Geiringer and Hill et al. [13]. In 1953, Alexander [14] applied the slip-line method to analyze the hot rolling process, and obtained the slip-line solution of the rolling force. During the study of vertical rolling process, it is found that the vertical rolling deformation after entering the stable rolling stage satisfies the plane deformation characteristics and is suitable to be solved by slip-line method. Since the plasticity condition used in the slip-line method is accurate, the slip-line method can accurately predict the size of plastic zone. Thus the maximum depth of dog-bone area can be determined according to the geometric characteristics of the slip- line field of slab plastic deformation zone during edge rolling.

Therefore, in case of the shortage of analytical solution model in edge rolling process, the maximum depth of dog-bone area is obtained directly by slip-line method in this paper, then a new exponent velocity and corresponding strain rate field are established. And an analytical solution of edge rolling force and the shape parameters of dog-bone are obtained based on the upper bound theory. The calculated edge rolling force and dog-bone shape parameters are compared with other models and on-line measured data.

2 Exponent velocity field

2.1 Determination of deformation zone

As shown in Fig. 3, slip-line field and hodograph for edge rolling per unit length under the full adhesion condition are drawn out according to Cauchy problem [15]. Due to the complete adhesion between the vertical roll and the slab, according to Prandtl problem [16], $\vartriangle ABC$ is a uniform linear field with contact surface of 45° and $BC$ is $\beta$ line. It is noticed that $BD$ is a free surface, based on first boundary condition in the slip-line theory, $\vartriangle BCD$ is also a uniform linear field and $CD$ is $\alpha$ line with free surface of 45°. Therefore, on the basis of the geometric characteristics of edge rolling slip-line, the relation shape between initial thickness $2h_{0}$ and the deformation area’s maximum width $b$ is determined as follows [17]:

$$ b = B^{\prime } D^{\prime } = BD = AB = 2h_{0} $$

(1)

Fig. 3

Slip-line field and hodograph for edge rolling

2.2 Velocity field

As shown in Figs. 2 and 4, while the slab is rolled by a pair of edge rolls of radius $R$, the width of slab is reduced from $2W_{0}$ to $2W_{E}$ (unilateral reduction ∆W = W₀ − W_E). A rectangular coordinate system is set up in the center of the entrance cross section and the axes $x$,$y$ and $z$ represent rolling, width and thickness directions of the slab. The projected length of the contact arc is given by $l$, $l = \sqrt {2R\Delta W}$, peripheral velocity is given by $v_{R}$ and entrance velocity $v_{0} = v_{R} \cos \varphi$. The bite angle is $\theta$ and the contact angle is $\varphi$. Due to the symmetry of deformation area, only a quarter is considered and divided the deformation zone into rigid zoneIand plastic zoneIIand III. Essentially the vertical rolling process can be thought of as the joint extrusion of the vertical roll and rigid zone [18], which causes the metal in the plastic area to flow along z-direction. Therefore, plastic zone II and III can be considered symmetric about $y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}$, and $v_{{y{\text{II}}}} = - v_{{y{\text{III}}}}$.

Fig. 4

Definition sketch of the bite zone in edge rolling

From the geometry, the contact equation (half-width) and parameter equation are expressed as follows:

$$ W_{x} = W_{E} + R - \sqrt {R^{2} - \left( {l - x} \right)^{2} } $$

(2)

W_x is the half of the width in the bite zone in Eq. (2).

$$ \left\{ {\begin{array}{*{20}l} {W_{x} = W_{\varphi } = W_{0} - R\left( {\cos \varphi - \cos \theta } \right)} \hfill \\ {b_{\varphi } = R - R\cos \varphi + 2h_{0} - \Delta W} \hfill \\ {\theta = \sin^{ - 1} \left( {l/R} \right)} \hfill \\ \end{array} } \right. $$

(3)

where $b_{\varphi }$ is the deformation area’s width during vertical rolling.

From Eq. (3) the pressing velocity $v_{y}$ is:

$$ v_{y} = v_{{y{\text{III}}}} - v_{{y{\text{II}}}} = \frac{{d\left( {W_{0} - W_{\varphi } } \right)}}{dt} = R\sin \varphi \frac{d\varphi }{dt} = \omega R\sin \varphi = v_{R} \sin \varphi $$

(4)

ω in Eq. (4) is angular velocity.

To facilitate the calculation, the authors pan the ordinate origin $o$ along $y$-axis to $o^{{\prime }}$ where $y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}$ and suppose the dog-bone extending velocity $v_{z}$ along $y$-axis by exponential function [19] as follows:

$$ \left\{ {\begin{array}{*{20}l} {v_{{z{\text{II}}}} = Av_{R} \sin \varphi \frac{2z}{{b_{\varphi } }}e^{{{{2cy} \mathord{\left/ {\vphantom {{2cy} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} ,} \hfill & { - {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2} \le y \le 0} \hfill \\ {v_{{z{\text{III}}}} = Av_{R} \sin \varphi \frac{2z}{{b_{\varphi } }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} ,} \hfill & {0 \le y \le {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}} \hfill \\ \end{array} } \right. $$

(5)

A and $c$ are undetermined parameters in Eq. (5). Because of the symmetry, only zone III is analyzed below.

According to the incompressibility condition and plane deformation assumption [20] $\left( {\dot{\varepsilon }_{x} = 0} \right)$:

$$ \dot{\varepsilon }_{{z{\text{III}}}} = \frac{{\partial v_{{z{\text{III}}}} }}{\partial z} = \frac{{2Av_{R} \sin \varphi }}{{b_{\varphi } }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} {b\varphi }}} \right. \kern-0pt} {b\varphi }}}} = - \dot{\varepsilon }_{{y{\text{III}}}} = - \frac{{\partial v_{{y{\text{III}}}} }}{\partial y} $$

(6)

Based on the geometric equation [21] of the relationship between strain rate and displacement velocity, $v_{{y{\text{III}}}}$ is obtained as follows:

$$ v_{{y{\text{III}}}} = \int {\dot{\varepsilon }_{{y{\text{III}}}} } \text{dy} = - \frac{{2Av_{R} \sin \varphi }}{{b_{\varphi } }}\int {e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} } \text{d} y = \frac{{Av_{R} \sin \varphi }}{c}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} + {\text{f}}\left( z \right) $$

(7)

while $y = 0,\;v_{y} = 0$, substituting this boundary condition to Eq. (7), $\text{f} \left( z \right)$ is obtained:

$$ {\text{f}}\left( z \right) = - \frac{{Av_{R} \sin \varphi }}{c} $$

(8)

Then the following expression is the velocity field in plastic zone III:

$$ \left\{ {\begin{array}{*{20}l} {v_{{x{\text{III}}}} = v_{R} } \hfill \\ {v_{{y{\text{III}}}} = \frac{{Av_{R} \sin \varphi }}{c}\left( {e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} - 1} \right)} \hfill \\ {v_{{z{\text{III}}}} = Av_{R} \sin \varphi \frac{2z}{{b_{\varphi } }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} } \hfill \\ \end{array} } \right. $$

(9)

while $y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2},\;v_{{y{\text{III}}}} = - \frac{{v_{R} \sin \varphi }}{2},$ substituting this boundary condition to Eq. (9)

$$ v_{y} |_{{y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}}} = \frac{{Av_{R} \sin \varphi }}{c}\left( {e^{{{ - }c}} - 1} \right) = - \frac{{v_{R} \sin \varphi }}{2} $$

(10)

Thus, $\frac{A}{c} = \frac{1}{{2\left( {1 - e^{{{ - }c}} } \right)}}$ is calculated by Eq. (10), then substituting it to Eq. (9) yields velocity field as follows:

$$ \left\{ {\begin{array}{*{20}l} {v_{{x{\text{III}}}} = v_{R} } \hfill \\ {v_{{y{\text{III}}}} = \frac{{v_{R} \sin \varphi }}{{2\left( {1 - e^{{{ - }c}} } \right)}}\left( {e^{{{{ - 2c{\text{y}}} \mathord{\left/ {\vphantom {{ - 2c{\text{y}}} b}} \right. \kern-0pt} b}_{\varphi } }} - 1} \right)} \hfill \\ {v_{{z{\text{III}}}} = \frac{{cv_{R} \sin \varphi }}{{1 - e^{{{ - }c}} }}\frac{z}{{b_{\varphi } }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} } \hfill \\ \end{array} } \right. $$

(11)

That leaves only one undetermined parameter c in Eq. (11) which is called bulge parameter [22]. According to Cauchy equation [23], the strain rate field is determined as follows:

$$ \left\{ {\begin{array}{*{20}l} {\dot{\varepsilon }_{{y{\text{III}}}} = \frac{{\partial v_{{y{\text{III}}}} }}{\partial y} = - \dot{\varepsilon }_{{z{\text{III}}}} = \frac{{cv_{R} \sin \varphi }}{{b_{\varphi } \left( {e^{ - c} - 1} \right)}}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} } \hfill \\ {\dot{\varepsilon }_{{yz{\text{III}}}} = \frac{1}{2}\left( {\frac{{\partial v_{{y{\text{III}}}} }}{\partial z} + \frac{{\partial v_{{z{\text{III}}}} }}{\partial y}} \right) = \frac{1}{2}\frac{{\partial v_{{z{\text{III}}}} }}{\partial y} = \frac{{c^{2} v_{R} \sin \varphi }}{{\left( {e^{{{ - }c}} - 1} \right)}}\frac{z}{{b_{\varphi }^{2} }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} } \hfill \\ {\dot{\varepsilon }_{zx} = \dot{\varepsilon }_{yx} = \dot{\varepsilon }_{x} = 0} \hfill \\ \end{array} } \right. $$

(12)

In Eqs. (11)–(12), $\dot{\varepsilon }_{x} + \dot{\varepsilon }_{y} + \dot{\varepsilon }_{z} = 0$; $v_{{y{\text{III}}}} |_{{y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2},\varphi = \theta }} = - \frac{{v_{R} \sin \theta }}{2}$; $v_{{y{\text{III}}}} |_{{y = {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2},\varphi = 0}} = 0$;$v_{{y{\text{III}}}} |_{y = 0,\varphi = \theta } = 0$; $v_{{y{\text{III}}}} |_{y = 0,\varphi = 0} = 0$. So, they are kinematically admissible velocity and strain rate field.

3 Total power functional

According to the first variation principle of rigid-plastic material [24], the total power functional is:

$$ J^{ * } = \dot{W}_{i} + \dot{W}_{s} + \dot{W}_{f} $$

(13)

where $\dot{W}_{i}$ is the internal deformation power; $\dot{W}_{s}$ is the shear power and $\dot{W}_{f}$ is the friction power.

3.1 Inter-deformation power

The inter-deformation power per unit length can be calculated as follows:

$$ \begin{aligned} \dot{W}_{i} = & 2\left( {\dot{W}_{{i{\text{II}}}} + \dot{W}_{{i{\text{III}}}} } \right) = 4\int_{\text{V} } {\sigma_{{e{\text{III}}}} \dot{\varepsilon }_{{e{\text{III}}}} } \text{dV} = 4\sqrt {\frac{2}{3}} \sigma_{s} \int_{\text{V} } {\sqrt {\dot{\varepsilon }_{ij} \dot{\varepsilon }_{ij} } } \text{dV} \\ = & 4\sqrt {\frac{2}{3}} \sigma_{s} \int_{0}^{{h_{0} }} {\int_{0}^{{\frac{{b_{\varphi } }}{2}}} {\sqrt {\dot{\varepsilon }_{{y{\text{III}}}}^{2} + \dot{\varepsilon }_{{z{\text{III}}}}^{2} + 2\dot{\varepsilon }_{{yz{\text{III}}}}^{2} } \text{dydz} } } \\ = & \frac{{2\sigma_{s} v_{R} \sin \varphi }}{\sqrt 3 }\left[ {h_{0} \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } + \frac{{b_{\varphi } }}{c}\ln \left( {\frac{{ch_{0} }}{{b_{\varphi } }} + \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } } \right)} \right] \\ \end{aligned} $$

(14)

3.2 Shear power and friction power

From Eq. (11), the tangential discontinuity exists at the interface between roll and slab, and the tangential velocity discontinuity is:

$$ \Delta v_{f} = v_{z} = \frac{{cv_{R} \sin \varphi }}{{1 - e^{{{ - }c}} }}\frac{z}{{b_{\varphi } }}e^{ - c} $$

(15)

Considering symmetry, the shear power is:

$$ \begin{aligned} \dot{W}_{s} = \dot{W}_{f} = & \int_{{F_{f} }} {\tau_{f} \left| {\Delta v_{f} } \right|\text{dF} } \\ = & 4mk\int_{0}^{{h_{0} }} {\frac{{cv_{R} \sin \varphi }}{{1 - e^{ - c} }}\frac{z}{{b_{\varphi } }}e^{ - c} \text{dz} } \\ = & \frac{{2mkcv_{R} \sin \varphi h_{0}^{2} }}{{\left( {e^{c} - 1} \right)b_{\varphi } }} \\ \end{aligned} $$

(16)

3.3 Total power and its minimization

Summarizing Eqs. (14) and (16), the total power per unit length $\dot{W}$ can be obtained as follows:

$$ \begin{aligned} \dot{W} = & \dot{W}_{i} + \dot{W}_{s} + \dot{W}_{f} \\ = & \frac{{2\sigma_{s} v_{R} \sin \varphi }}{\sqrt 3 }\left[ {h_{0} \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } + \frac{{b_{\varphi } }}{c}\ln \left( {\frac{{ch_{0} }}{{b_{\varphi } }} + \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } } \right)} \right] + \frac{{4mkcv_{R} \sin \varphi h_{0}^{2} }}{{\left( {e^{c} - 1} \right)b_{\varphi } }} \\ \end{aligned} $$

(17)

Then integrating $\dot{W}$ over the whole contact arc and the analytical solution of total power $J^{*}$ is:

$$ \begin{aligned} J^{*} = \int_{0}^{\theta } {\dot{W}} R\text{d} \varphi = & \frac{{2\sigma_{s} v_{R} R}}{\sqrt 3 }\int_{0}^{\theta } {\left\{ {\left[ {h_{0} \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } + \frac{{b_{\varphi } }}{c}\ln \left( {\frac{{ch_{0} }}{{b_{\varphi } }} + \sqrt {1 + \left( {\frac{{ch_{0} }}{{b_{\varphi } }}} \right)^{2} } } \right)} \right] + \frac{{2mch_{0}^{2} }}{{\left( {e^{c} - 1} \right)b_{\varphi } }}} \right\}} \sin \varphi \text{d} \varphi \\ = & \frac{{2\sigma_{s} v_{R} h_{0}^{2} c}}{\sqrt 3 }\left\{ {\ln \left[ {\frac{{\frac{{ch_{0} }}{{2h_{0} - \Delta W}} + \sqrt {1 + \left( {\frac{{ch_{0} }}{{2h_{0} - \Delta W}}} \right)^{2} } }}{{\frac{c}{2} + \sqrt {1 + \frac{{c^{2} }}{4}} }}} \right] - \sqrt {1 + \left( {\frac{{2h_{0} - \Delta W}}{{ch_{0} }}} \right)^{2} } + \sqrt {\frac{4}{{c^{2} }} + 1} } \right\} \\ & \quad + \frac{{2\sigma_{s} v_{R} h_{0}^{2} c}}{\sqrt 3 }\int_{{\frac{c}{2}}}^{{\frac{{ch_{0} }}{{2h_{0} - \Delta W}}}} {\frac{{\ln \left( {t + \sqrt {1 + t^{2} } } \right)}}{{t^{3} }}} dt + \frac{{4m\sigma_{s} v_{R} h_{0}^{2} c}}{{\sqrt 3 \left( {e^{c} - 1} \right)}}\ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}} \\ \end{aligned} $$

(18)

According to the mean value theorem of integrals, the total power $J^{*}$ is:

$$ \begin{aligned} J^{*} { = } & \frac{{2\sigma_{s} v_{R} h_{0}^{2} c}}{\sqrt 3 }\left\{ {\ln \left[ {\frac{{\frac{{ch_{0} }}{{2h_{0} - \Delta W}} + \sqrt {1 + \left( {\frac{{ch_{0} }}{{2h_{0} - \Delta W}}} \right)^{2} } }}{{\frac{c}{2} + \sqrt {1 + \frac{{c^{2} }}{4}} }}} \right] - \sqrt {1 + \left( {\frac{{2h_{0} - \Delta W}}{{ch_{0} }}} \right)^{2} } + \sqrt {\frac{4}{{c^{2} }} + 1} } \right\} \\ & \quad + \frac{{\sigma_{s} v_{R} h_{0}^{2} c}}{\sqrt 3 }\ln \left[ {\varepsilon + \sqrt {1{ + }\varepsilon^{2} } } \right]\left[ {\frac{4}{{c^{2} }}{ - }\left( {\frac{{2h_{0} - \Delta W}}{{ch_{0} }}} \right)^{2} } \right] + \frac{{4m\sigma_{s} v_{R} h_{0}^{2} c}}{{\sqrt 3 \left( {e^{c} - 1} \right)}}\ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}} \\ \end{aligned} $$

(19)

In Eq. (19), due to the mean value $\varepsilon \in \left[ {\frac{c}{2},\frac{{ch_{0} }}{{2h_{0} - \Delta W}}} \right]$ and this interval is very small, $\varepsilon { = }\frac{c}{2}$ is selected in this paper to facilitate the calculation.

$J^{*}$ is only relevant to bulge parameter c when the deformation resistance $\sigma_{s}$, the peripheral velocities $v_{R}$, initial thickness of slabs $2h_{0}$ and friction factor of edge roll-slab arc $m$ are given. The optimal value of $c = 1.617$ is obtained by MATLAB searching algorithm when $J^{*}$ attains the minimum value $J^{*}_{\hbox{min} }$ as shown in Fig. 5, and the search results are shown in Fig. 6. Then the minimum of total power functional $J^{*}_{\hbox{min} }$ is obtained by substituting the optimal value of c into Eq. (19).

Fig. 5

Flow chart of calculation

Fig. 6

Results of the research for the minimum value of the ${{J^{*} } \mathord{\left/ {\vphantom {{J^{*} } {\sigma_{s} }}} \right. \kern-0pt} {\sigma_{s} }}$

According to the relationship between rolling power $J^{*}_{\hbox{min} }$ and rolling force $\bar{P}$:

$$ J^{*}_{\hbox{min} } = M\omega = 4\bar{b}_{\varphi } h_{0} \bar{P}\chi R\Delta W\omega $$

(20)

where $M$ is rolling torque, $M{ = }P \cdot a$; $P$ is the total edge rolling force, $P{ = }\bar{P} \cdot F$, $\bar{P}$ is rolling force per unit slab thickness and width, $F$ is the projection of the contact area between the slab and edge roll in the width direction, $F{ = }l \cdot \bar{b}_{\varphi }$, $l$ is the projected length of contact arc, $l{ = }\sqrt {2R\Delta W}$, $\bar{b}_{\varphi }$ is the average width of plastic zone and $\bar{b}_{\varphi } = 2h_{0} - \frac{\Delta W}{2}$, $a$ is the arm of force and $a{ = }\chi \cdot l = \chi \sqrt {2R\Delta W}$;$\omega$ is roll angular velocity. The arm factor $\chi = 0.3\sim0.6$ was researched in hot rolling process by Lundberg [25]. And $\chi { = }0.5$ is selected in this paper under equipment and process parameters.

4 Exponent function dog-bone shape model

Exponent function dog-bone shape model is proposed based on plastic flow rules and the deformation characteristics in vertical rolling, as shown in Fig. 7, $h_{e}$ is the height of the dog-bone area.

Fig. 7

Sketch of exponent function dog-bone profile

According to the velocity field Eq. (11), the distribution of the metal flow along z-direction in the deformation zone IIand III is:

$$ \left\{ {\begin{array}{*{20}l} {v_{{z{\text{II}}}} = \frac{{cv_{R} \sin \varphi }}{{1 - e^{{{ - }c}} }}\frac{z}{{b_{\varphi } }}e^{{{{2cy} \mathord{\left/ {\vphantom {{2cy} b}} \right. \kern-0pt} b}_{\varphi } }} ,} \hfill & { - {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2} \le y \le 0} \hfill \\ {v_{{z{\text{III}}}} = \frac{{cv_{R} \sin \varphi }}{{1 - e^{{{ - }c}} }}\frac{z}{{b_{\varphi } }}e^{{{{ - 2cy} \mathord{\left/ {\vphantom {{ - 2cy} b}} \right. \kern-0pt} b}_{\varphi } }} ,} \hfill & {0 \le y \le {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}} \hfill \\ \end{array} } \right. $$

(21)

Then substituting the optimal value $c = 1.617$ obtained above into Eq. (21), the extended velocity of dog-bone area is:

$$ \left\{ {\begin{array}{*{20}l} {v_{{z{\text{II}}}} = \frac{{1.617v_{R} \sin \varphi }}{{1 - e^{{{ - 1} . 6 1 7}} }}\frac{z}{{b_{\varphi } }}e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} b}} \right. \kern-0pt} b}_{\varphi } }} ,} \hfill & { - {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2} \le y \le 0} \hfill \\ {v_{{z{\text{III}}}} = \frac{{1.617v_{R} \sin \varphi }}{{1 - e^{{{ - 1} . 6 1 7}} }}\frac{z}{{b_{\varphi } }}e^{{{{ - 3.234y} \mathord{\left/ {\vphantom {{ - 3.234y} b}} \right. \kern-0pt} b}_{\varphi } }} ,} \hfill & {0 \le y \le {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}} \hfill \\ \end{array} } \right. $$

(22)

Consequently, the average velocity of particles in the plastic deformation region II is derived as follows:

$$ \begin{aligned} \bar{v}_{{z{\text{II}}}} = & \frac{{\int_{0}^{\theta } {v_{{z{\text{II}}}} R{\text{d}}\varphi } }}{l} = \int_{0}^{\theta } {\frac{{1.617v_{R} \sin \varphi R}}{{l\left( {1 - e^{{{ - 1} . 6 1 7}} } \right)}}\frac{z}{{b_{\varphi } }} \cdot e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} } {\text{d}}\varphi \\ = & \int_{{2h_{0} - \Delta W}}^{{2h_{0} }} {\frac{{1.617v_{R} }}{{l\left( {1 - e^{ - 1.617} } \right)}}\frac{z}{{b_{\varphi } }} \cdot e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} } {\text{d}}b\varphi \\ = & \frac{{1.617zv_{R} }}{{l\left( {1 - e^{ - 1.617} } \right)}}\int_{{2h_{0} - \Delta W}}^{{2h_{0} }} {\frac{{e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} }}{{b_{\varphi } }}d} b\varphi \\ \end{aligned} $$

(23)

Similarly, in region III:

$$ \bar{v}_{{z{\text{III}}}} = \frac{{1.617zv_{R} }}{{l\left( {1 - e^{ - 1.617} } \right)}}\int_{{2h_{0} - \Delta W}}^{{2h_{0} }} {\frac{{e^{{{{ - 3.234y} \mathord{\left/ {\vphantom {{ - 3.234y} {b_{\varphi } }}} \right. \kern-0pt} {b_{\varphi } }}}} }}{{b_{\varphi } }}db\varphi } $$

(24)

Thus, on the basis of integral mean value theorem, the result of Eqs. (23)–(24) can be expressed as follows:

$$ \bar{v}_{{z{\text{II}}}} { = }\frac{{1.617zv_{R} }}{{l\left( {1 - e^{ - 1.167} } \right)}} \cdot e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} \xi }} \right. \kern-0pt} \xi }}} \cdot \ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}} $$

(25)

$$ \bar{v}_{{z{\text{III}}}} { = }\frac{{1.617zv_{R} }}{{l\left( {1 - e^{ - 1.167} } \right)}} \cdot e^{{{{ - 3.234y} \mathord{\left/ {\vphantom {{ - 3.234y} \xi }} \right. \kern-0pt} \xi }}} \cdot \ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}} $$

(26)

In Eqs. (25)–(26), the mean value $\xi { = }2h_{0} - \frac{\Delta W}{2}$ is chosen in present paper.

Based on the Euler method [26] of studying the movement of continuum:

$$ {{{\text{d}}\left( {h_{e} - h_{0} } \right)} \mathord{\left/ {\vphantom {{{\text{d}}\left( {h_{e} - h_{0} } \right)} {dt}}} \right. \kern-0pt} {dt}} = \bar{v}_{z} $$

(27)

In addition, it is noticed that the time for the roll to rotate from inlet to outlet of the slab is:

$$ t = l/v_{R} $$

(28)

Summarizing Eqs. (25)–(28), the function of the dog-bone area height’s distribution along the y-direction at outlet of slab can be obtained as follows:

$$ h_{e} = \left\{ {\begin{array}{*{20}l} {h_{0} + \frac{{1.617h_{0} }}{{\left( {1 - e^{ - 1.617} } \right)}} \cdot e^{{{{3.234y} \mathord{\left/ {\vphantom {{3.234y} \xi }} \right. \kern-0pt} \xi }}} \cdot \ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}},} \hfill & {{{ - b_{\varphi } } \mathord{\left/ {\vphantom {{ - b_{\varphi } } {2 \le y \le 0}}} \right. \kern-0pt} {2 \le y \le 0}}} \hfill \\ {h_{0} + \frac{{1.617h_{0} }}{{\left( {1 - e^{ - 1.617} } \right)}} \cdot e^{{{{ - 3.234y} \mathord{\left/ {\vphantom {{ - 3.234y} \xi }} \right. \kern-0pt} \xi }}} \cdot \ln \frac{{2h_{0} }}{{2h_{0} - \Delta W}},} \hfill & {0 \le y \le {{b_{\varphi } } \mathord{\left/ {\vphantom {{b_{\varphi } } 2}} \right. \kern-0pt} 2}} \hfill \\ \end{array} } \right. $$

(29)

Equation (29) shows that $h_{e}$ is a function of the slabs’ initial half thickness $h_{0}$, the width coordinate y, edge roll radius $R$ and the unilateral reduction $\Delta W$.

5 Results

5.1 Edge rolling force

For the purpose of verifying the validity of the analytical solution model proposed in this paper, the results obtained from Eq. (20) are compared with the measured data of vertical rolling force in a hot strip mill. The slabs’ width were reduced from 1.518 m-1.524 m to 1.48 m-1.51 m, initial thickness 2 h₀ = 0.18–0.23 m, R = 0.6 m and $\omega { = }3.09\;{\text{rad/s}}$. More than 1500 records of rolling force $\bar{P}$ were collected while changing the vertical roll radius $R$, the engineering strain ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ and initial half thickness $h_{0}$, and the comparison between the analytical model and measured ones was shown in Fig. 8. The error of the vertical rolling force calculated by analytical model is within 10% compared with the practical data. Results indicate that the proposed exponent velocity field can be successfully applied to analyze the edge rolling process. Furthermore, the results show that the proportion (predicted results greater than the actual measured ones) is about 70%, that because the method used to calculate the vertical rolling force in this paper is based on the upper bound analysis.

Fig. 8

Comparison rolling force predicted by proposed model with on-line measured data

5.2 Dog-bone shape

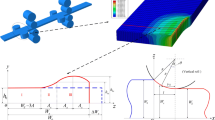
The slab’s shape at exit is another key parameter to measure the quality of hot rolled products. The following sections will discuss the relationship between height of the dog-bone area $h_{e}$ and associated parameters (initial half thickness $h_{0}$ and engineering strain ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$). Figure 9 shows the comparisons between exponent function dog-bone shape model in this paper and Yun’s model [11], FEM simulation’s results and Liu’s sine function model [12]. It can be seen that the exponent function’s error is less than 1.24% compared with Liu’s model and within 1.53% compared with FEM simulation. The maximum error with Yun’s model is slightly higher and it can reach 8.19%. This is because Yun assumed that the entire deformation can be extended across the width direction, then the final dog-bone shape was obtained by FEM fitting. This led the length of plastic deformation zone was larger and the peak height of dog-bone was lower than other models. But considering the deformation characteristics of large width-thickness ratio in vertical rolling, it is more reasonable to assume the middle position of slab as rigid zone in exponent function model. This feature is also proved by FEM simulation, as shown in Fig. 10.

Fig. 9

Comparison of exponent function, Liu’s, FEM and Yun’s models

Fig. 10

Slab cross section shape in FEM model

6 Discussion

6.1 Edge rolling force

Then, we analyzed how ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$, $R$ and $h_{0}$ affect the stress state coefficient $n_{\sigma }$, where $n_{\sigma } = {{\bar{P}} \mathord{\left/ {\vphantom {{\bar{P}} {\sigma_{s} }}} \right. \kern-0pt} {\sigma_{s} }}$. Figure 11 shows the variation of $n_{\sigma }$ caused by ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ and $R$ when $h_{0}$ is constant, and it is evident from Fig. 11 that the rolling force increases with the increasing of ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ and $R$. This is due to the increase of ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ making the deformed area closer to the center of the slab, and the total volume of plastic deformed metal increases, which makes the vertical rolling force increase. And when the edge roll radius increases, the arc length of the contact area and contacting area increase, which lead the increasing of deformed metal volume and vertical rolling force. In addition, the effect of ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ on $n_{\sigma }$ is more direct than that of $R$. The reason is that the volume of compressed metal increase caused by the increasing of $\Delta W$ is larger than that caused by the increase of edge roll radius $R$. Figure 12 gives the effects of initial half thickness $h_{0}$ and the engineering strain ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$ on $n_{\sigma }$ when $R$ is constant. It can be seen that $n_{\sigma }$ decreases as $h_{0}$ increases, this is because the plastic deformation of edge rolling is mainly concentrated on the edge of slabs, as the initial thickness $h_{0}$ increases, the volume of the rigid region also increases, although the increase of thickness can make the total rolling force larger, the rolling force that acts on each metal particle will be smaller. Figure 13 illustrates that the influence of initial half thickness $h_{0}$ on the stress state coefficient $n_{\sigma }$ is stronger than roll radius $R$.

Fig. 11

Effect of $\Delta W/W_{0}$ and $R/W_{0}$ on stress state coefficient $n_{\sigma }$ while ${{h_{0} } \mathord{\left/ {\vphantom {{h_{0} } {W_{0} = 0.143}}} \right. \kern-0pt} {W_{0} = 0.143}}\left( {W_{0} { = 0} . 7\;{\text{m}}} \right)$

Fig. 12

Effect of $h_{0} /W_{0}$ and $\Delta W/W_{0}$ on stress state coefficient $n_{\sigma }$ while $R/W_{0} = 0.857\left( {W_{0} { = 0} . 7\;{\text{m}}} \right)$

Fig. 13

Effect of $h_{0} /W_{0}$ and $R/W_{0}$ on stress state coefficient $n_{\sigma }$ while $\Delta W/W_{0} = 0.0571\left( {W_{0} { = 0} . 7\;{\text{m}}} \right)$

6.2 Dog-bone shape

The variations of the value of $h_{e} /W_{0}$ are obtained under different initial half thickness $h_{0}$ and engineering strain ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$. The comparative results between exponent function model with Liu’s model and FEM simulation’s results are given in Figs. 14 and 15. The error of exponent function model is below 6.27% compared with FEM simulation’s results and less than 8.88% with Liu’s model.

Fig. 14

Effect of $\Delta W$ on $h_{e} /W_{0}$ while $h_{0} /W_{0} = 0.143$

Fig. 15

Effect of $h_{0}$ on $h_{e} /W_{0}$ while $\Delta W/W_{0} = 0.0286$

In Fig. 14, it is evident that the value of $h_{e}$ increases linearly with the increasing of engineering strain ${{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_{0} }}} \right. \kern-0pt} {W_{0} }}$. This is due to the increasing of the volume of metal in deformation zone resulting in the height of dog-bone area increasing. In addition, due to the edge rolling as a plane deformation process in the calculation of the exponential function of the dog bone model, that is, the metal under pressure in the width direction is all transformed into the metal bulging in the thickness direction, while Liu’s model takes into account the slab deformation in the rolling direction, resulting in the reduction of the metal volume transformed into the dog-bone shape. Figure 15 illustrates that the value of $h_{e}$ increases with the increasing of $h_{0}$. This is because when the slab thickness increases only, the contact arc length between the slab and the vertical roll remains unchanged, but the contact area and the volume of the deformed metal increase, so the deformation gradually penetrates into the center of the slab, which lead the increasing of the value of $h_{e} /W_{0}$.

Through the above verification of the edge rolling force model and dog-bone shape model in present paper, the accuracy is very close to the numerical solution, which can play a guiding role in the actual production.

Moreover, compared with Liu’s model, because the exponent function model combines the maximum depth of the dog-bone region derived from the theory of slip-line, it has more theoretical significance. And in the case of similar accuracy, the exponent function model is simpler and more efficient in predicting the shape of dog-bone under different rolling conditions.

7 Conclusions

• 1. The combination of slip-line and exponent velocity field is firstly applied to determine the maximum depth of the dog-bone zone and establish the kinematically admissible velocity field and corresponding strain rate field in edge rolling process.

• 2. Using the above velocity field and according to the first variation principle of rigid-plastic material, the analytical solutions of total power, rolling torque, rolling force and dog-bone shape model are derived by minimizing the total power functional.

• 3. The predicted rolling force and final dog-bone shape dimensions of edge rolled slab show a good agreement with those of experimental data in reference and FEM simulation.

• 4. The stress state coefficient $n_{\sigma }$ increases with the increasing of engineering strain and edge roll radius, but decreases while initial thickness increases. The altitude of the dog-bone shape increases while engineering strain or initial thickness increases.