1 Introduction

Over the past several years, certain perovskite (simple or complex) materials of a general chemical formula ABO3 (A = mono-divalent, B = tri to hexavalent ions) having giant dielectric permittivity (\(\in\)r\(\approx\)105) have been found useful in the field of microelectronics for the fabrication of devices including spintronics and energy storage devices [21]. Subramanian et al. first reported a giant dielectric constant (~ 104) in CaCu3Ti4O12 (CCTO) over a wide temperature and frequency range [24]. Since then, extensive studies have been performed to tailor the dielectric properties (i.e., enhancement of dielectric constant and decrease the tangent loss factor) of CCTO by suitable substitution at its different atomic sites and/or fabrication of solid solution/composites with other perovskites. In this process, modification of CCTO with a Ca-site of a general chemical composition ACu3Ti4O12 (A = Na½Y1/2, Y2/3, Bi2/3) and other related materials exhibits enormously high dielectric permittivity (\(\in\)r) with weak frequency and temperature dependence over a wide range [5]. In order to understand the origin of the giant dielectric constant and low loss factor of CCTO, several models or mechanisms have been proposed, including local dipole moments associated with off-center displacement of Ti ions [20], multi-layer capacitance (MLC) [14], nano-barrier layer capacitor (NBLC) [35], nanoscale disorder (NSD), surface barrier layer capacitor (SBLC), and internal domain [8, 19] models. Amongst all the models, the internal barrier layer capacitor (IBLC) model has been found to be the most acceptable mechanism and/or explanation for the high dielectric constant of CCTO. According to the IBLC model, CCTO behaves as an electrically heterogeneous ceramic containing insulating grain boundaries (GBs) and semiconducting grains (Gs), as reported by Adams et al. [1] and Zhang et al. [36]. Hence, if we can alter the electrical properties of GBs and Gs, we can induce good dielectric properties (\(\in\)r and tan\(\delta\)) in the material.

Generally, dielectric properties are strongly dependent on various factors, which include the concentration of doped ions into the parent compound, sintering conditions and microstructure. Recent works have reported on doping the suitable ions at the Ca, Cu and/or Ti sites of CCTO to enhance the dielectric properties [2, 30]. The Ca and Cu disorder in CCTO (at nanometer scale) was analyzed using superior quantitative electron diffraction (QED) and extended X-ray absorption fine structure (EXAFS) analysis. The increased permittivity was proposed to be a result of the modified electronic structure of the defect Cu cation on the A site [29]. The relaxation and conduction mechanism using dielectric and modulus spectroscopy of 15 wt% of Sr in CCTO was not extensively reported as discerned from the vast literature. Similar composition was reported by Vangchangyia et al. [31], showing a dielectric constant of 11432 and loss tangent of 0.025 at 20 °C and 1 kHz. Among the Sr-CCTO specimens reported by Xue et al. [33], Sr-CCTO-2, with Sr doping concentration of 10%, exhibited the highest permittivity and the lowest nonlinear coefficient. In a study by Li et al. [15] the dielectric properties demonstrated that, with dopant weight %  ≤ 0.15, Sr doping in CCTO not only increased dielectric permittivity but also reduced dielectric loss; however, it also reduced the dependence on frequency at low frequencies. In addition, we have taken different particle size of starting ingredients for the preparation of CSCTO-15.

In the present communication, we primarily report the basic crystal data, morphology, and dielectric and impedance characteristics of strontium-modified CaCu3Ti4O12, (i.e., Ca0.85Sr0.15Cu3Ti4O12), fabricated with nano-sized powders of CuO (< 50 nm, particle size) and TiO2 (21 nm, particle size) and micro-sized powders of CaCO3 and SrCO3, which is the main motivation behind this attempt.

2 Experimental details

High-purity (> 99.99%) starting materials of different particle sizes, including SrCO3 (M/s Sigma Aldrich), CaCO3, (M/s Sigma Aldrich), CuO (< 50 nm) and TiO2 (21 nm) (M/S Sigma Aldrich), in required stoichiometric amounts, were used for the fabrication of polycrystalline samples of CSCTO-15. Fine powders of the materials were mixed in dry and wet medium for 2 h with the help of a pestle and an agate mortar. The mixed powder was set aside in a high-purity alumina crucible and heated in a muffle furnace at 600 °C for 4 h. Preferably, the kinetics of the quick conventional solid-state reaction at a microscopic level at high temperature is promoted with the use of TiO2 and CuO2 nano-sized powders at the start of sample preparation with micron-sized CaCO3 and SrCO3 powders. The room-temperature X-ray powder diffraction (XRD) data were obtained using a high-resolution Bruker D8 diffractometer for structural characterization of CSCTO-15. Cylindrical pellets of 12 mm in diameter and 1.8 mm thick were then prepared from the calcined powder at a pressure of 4 × 107 N/m2 with the help a uniaxial hydraulic press. After making a pellet, it was sintered at 1200 °C for 12 h (total programming time) and furnace-cooled to room temperature. The presence of a minor peak of TiO2 in a pure CCTO sample with sintering at 1200 °C for 8 h was also reported by Hu et al. [10]; thus this sintering temperature was preferred. However, thermogravimetric and dilatometry testing could provide more relevant information about the calcination and sintering temperature, but this was not possible due to limitation of instruments. Scanning electron microscopy (Zeiss EVO-18) was utilized to explore the microstructure of the CSCTO-15 pellet and pure CCTO. Then, both surfaces of the disc-shaped pellet were made even as well as parallel. The (sintered) pellet was coated with a thin layer of silver paste to create an electrode, followed by heat treatment at 250 °C for about 1 h in order to make it moisture free and further characterize its impedance and dielectric properties. The electrical parameters (dielectric constant, dissipation factors, impedance data, etc.) were recorded using a computer-controlled LCR meter (M/S PSM 1735, N4L) over a broad frequency range (1 kHz to 2 MHz) at different temperatures (25–315 °C).

3 Results and discussion

3.1 Structural and microstructural analysis

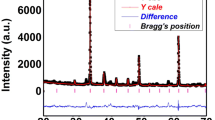
The room-temperature XRD pattern of CCTO and the sintered specimen (CSCTO-15) showed highly crystalline behavior (Fig. 1a, b). Rietveld structural analysis of the sample was carried out for the refinement of crystal data using the XRD pattern. The phase of the parent compound (CCTO) has been identified with some major peaks including (220), (400) and (422) peaks, which obey the extinction rule of the reported space group (i.e., for h k l reflection h + k + l = 2n, for h h l: reflection l = 2n, for h 0 0 reflections h = 2n, for 0 k l reflections k + l = 2n” [25]. A few small-intensity impurity peaks are also observed. The sharp peaks confirm that the synthesized compound (CSCTO-15) is highly crystalline in nature. The reliability and correctness of the structural refinement were demonstrated using index parameters including weighted residual error (Rw), Bragg factor (Rb), expected factor (Rexp), and goodness of fit expressed by the Rw/Rexp ratio. The software used for Rietveld refinement is POWD MULT. The JCPDS card number 75-2188 is used to refine the structure. Table 1 shows the reliability parameters of pure CCTO and 15 wt% Sr-doped CCTO. This suggests the best-quality fitting of the experimental data with the theoretical data. The little high R-factors may originate by a little high of noise at the background of the XRD spectra, as described by Jansen et al. [12].

Fig. 1
figure 1

Structural refinement of sintered a CCTO and b CSCTO-15 samples

Full size image
Table 1 Refinement coefficient (Rwp, Rexp, Rp, GoF and R-Bragg) of pure CCTO and Sr-doped CCTO
Full size table

The grains and grain boundaries of pure CCTO were observed from micrographs to have high densification [25]. Figure 2a, b shows the SEM micrographs of the CCTO and CSCTO-15 sintered pellet. The figure clearly shows the distinct grains of almost equal dimensions. Interlinking between grains (boundary) is also clearly visible. The size of some grains for CSCTO-15 was calculated using ImageJ image analysis software. Due to the influence of chemical homogenization, the microstructure of the product and very clear grain boundaries are depicted. The grain morphology indicates that said compound is fully dense. During the sintering stage, these are intimately connected with the presence of the liquid phase of (CuO) and oxygen vacancy at grains and grain boundaries (GBs), respectively [34]. The stoichiometric/elemental composition of CSCTO-15 was analyzed by EDX from the same SEM micrograph. Figure 2b shows the peaks of Ca, Sr, Cu, Ti and O and their respective band energies, suggesting it is consistent with the base composition, with no impurities. The wt% and at.% are summarized in Fig. 2c (inset).

Fig. 2
figure 2

Surface micrographs of a CCTO and b CSCTO-15, and c EDX inset showing the at.% and wt% of CSCTO-15

Full size image
Table 2 Values of Rg (Ω), Cg, Rgb (Ω), Cgb, Re and Ce of CSCTO-15
Full size table

3.2 Dielectric behavior

The temperature dependence of the relative dielectric constant and loss factor for CSCTO-15 at various frequencies is shown in Fig. 3. Here it is observed that both remain temperature-independent in the low-temperature region and then rapidly increase with increasing temperature (Table 2). Such a low value of dielectric constant in the low-temperature region indicates the absence of any significant dipolar interaction under the action of the applied electric field [22]. The rate of increase is greater at lower frequencies than at higher frequencies. Together, these observations indicate that the Maxwell–Wagner mechanism controls the polarization mechanism. However, the dielectric constant increases sharply in the high-temperature region. Furthermore, the trend in the increase of the dielectric constant in the high-temperature region decreases with the increase in applied frequency. A conducting grain with an insulating grain boundary produces an SBLC and IBLC, and also explains the high dielectric permittivity of the prepared sample. Similarly, a sharp increase in the dielectric loss in the high-temperature region may be attributed to the increased mobility of charge carriers due to defects or vacancies in the sample [23]. Also, the increased conductivity at elevated temperatures, thermally assisted electric charge carriers and relaxation process may cause the sharp increase in the tangent loss factor [16, 32]. Therefore, it is believed that said sample with high dielectric constant and low dissipation factor at higher temperatures is best suited for high-temperature applications, and also in devices such as transistors and microelectronic devices. [6, 37]. Both dielectric constant and tangent loss are also high at lower frequency, but fall with rising frequency, as shown in Fig. 3. For CSCTO-15, the dielectric permittivity of 30,000 and loss factor of 2.4 is observed for 1 kHz at 300 °C. It indicates the presence of dipolar relaxation phenomena in our composition. Xue et al. reported a dielectric constant of 4 × 104 and loss of 0.5 for 10 wt% Sr-doped CCTO at 10 kHz and 120 °C.

Fig. 3
figure 3

Variation in a permittivity and b loss factor with temperature of CSCTO-15 at different frequencies

Full size image

A comprehensive effort has been made to understand the conduction mechanism in CSCTO-15 using different characterization techniques. One strategy for understanding the electrode performance is to understand the charge transport mechanism with respect to the temperature and frequency. The study of the frequency and temperature dependence of the dielectric constant may provide an opportunity to gain a better understanding of the details of electronic/ionic migration mechanisms [17].

3.3 Electrical conductivity studies

The conductance remains constant in the region of low frequency and rises on increasing the field for pure CCTO, as observed from frequency-dependent ac electrical conductivity [25]. Figure 4a illustrates the variation in ac electrical conductivity (σac) of CSCTO-15 relative to the frequency of the supplied electric field at different temperatures. The ac electrical conductivity has been analyzed using the equation σac= 2πtanδ εr εo. In this equation, dielectric data (i.e. εr, εo), f = linear frequency of the ac field, and tan δ = tangent loss are used. From Fig. 4a, it is concluded that at all temperatures, conductivity strongly depends on the frequency. In the low-frequency domain, a plateau region is viewed in the compound. It indicates the existence of dc conductivity at low frequency.

Fig. 4
figure 4

a, b Variation in ac conductivity (σac) of CSCTO-15 at different temperatures and frequencies

Full size image

These observations show the behavior of conductivity as a function of temperature and frequency. The Arrhenius plot for electrical conductivity of CSCTO-15 at different frequencies is merely shown in Fig. 4b. For the conduction process, the activation energy (EA) can be considered from the slope of the line according to Arrhenius equation [26]:

$$\sigma = B\exp ( -\, E_{\text{A}} /k_{\text{B}} T)$$

where EA is the activation energy, kBis the Boltzmann constant, B is the pre-exponential factor, and T is the absolute temperature. Using this expression, the calculated activation energy is found to be 0.7, 0.64, 0.6 and 0.31 eV at 10, 100, 500 kHz and 1 MHz frequency, respectively. In general, at high temperatures, the anion vacancies (holes) are more activated [18], since more activation energy is required for them than electrons. Hence, the value of conductivity is increased with a rise in temperature. Conduction in the high-temperature region is due to holes as well as electrons, whereas in the low-temperature region it is mainly due to electrons [18]. However, at low temperatures, the smaller activation energy may be attributed to the hopping process of electrons between ions of different valences [9]. Low electrical conductivity in the sample may be due to high grain boundary density [7]. The ferroelectric behavior of the prepared materials is linked to the conduction mechanisms. For the perovskite ferroelectrics, oxygen vacancies are one of the mobile charge carriers. In these systems, the Kröger–Vink notation is used to represent ionized oxygen vacancies that can be formed when the oxygen releases electrons [28]

$${\text{O}}_{0} = \frac{1}{2}{\text{O}}_{2} + V_{o}^{\prime } + e^{ - }$$
(1)
$${\text{O}}_{0} = \frac{1}{2}{\text{O}}_{2} + V_{0}^{{\prime \prime }} + 2e^{ - }$$
(2)

During this process, Ti4+ ions may capture these liberated electrons to form Ti3+ ions, and the electron hopping from Ti4+ to Ti3+ causes the overall electronic conductivity, which is both frequency- and temperature-dependent [13].

3.4 Impedance spectrum analysis

Impedance spectrum analysis is used to interpret the real (resistive) and imaginary (reactive) components of the complex impedance (Z*) of the materials. In order to explain the electrical response of grains and GBs of sintered CSCTO-15 ceramic, a non-destructive technique such as impedance spectroscopy is used.

Generally, using the two quantities, (a) complex capacitive and (b) impedance, quantities of dielectric properties of materials can be described as a function of frequency.

$${\text{Complex}}\;{\text{dielectric}}\;{\text{constant}}\;(\varepsilon^{*} ),\quad \varepsilon^{*} = \varepsilon^{{\prime }} - j\varepsilon^{{\prime \prime }}$$
(3)
$${\text{Complex}}\;{\text{impedance}}\;\left( {Z^{*} } \right),\quad Z^{*} = Z' - jZ'' = R_{s} - \frac{j}{{\omega c_{s} }}$$
(4)
$${\text{Dielectric}}\;{\text{modulus}}\,\left( {M^{*} } \right),\quad M^{*} = M^{\prime } + jM^{\prime \prime } = j\omega {\text{Co}}Z*\omega$$
(5)
$${\text{Dielectric}}\;{\text{loss}}\,\left( {\tan \delta } \right)\tan \delta = \frac{{\varepsilon^{{\prime \prime }} }}{{\varepsilon^{{\prime }} }} = \frac{{ - Z^{{\prime }} }}{{Z^{{\prime \prime }} }} = \frac{{M^{{\prime \prime }} }}{{M^{{\prime }} }}$$
(6)

The parameters ω, Rs and Cs are known as angular frequency, resistance and capacitance, respectively, in the above equations. Using Eqs. (1)–(4), there is a wide scope for graphical representation to estimate the contributions of the above parameters of the electrode/ceramic/electrode system. Figure 5a, b shows the variation in Z´ (resistivity component) and Z″ (reactive component) as a function of frequency. Resistivity and reactive components are expressed as below.

$$Z^{{\prime }} = \frac{R}{{1 + (\omega \tau )^{2} }}$$
(7)
$$Z^{{\prime \prime }} = \frac{{\omega R\tau }}{{1 + (\omega \tau )^{2} }}$$
(8)

To a great extent, in the lower-frequency range, there is a reduction in the value of \(Z'\) with an increase in temperature, demonstrating NTCR (semiconducting) behavior. The Negative temperature cofficient resistance (NTCR) property is altered considerably in the high-frequency region, presenting complete fusion of \(Z'\) curves over a definite frequency. At higher frequencies, the magnitude of Z’ for every temperature converges, indicating the possible release of space charge [11].

Fig. 5
figure 5

Frequency dependence of a Z′ and b Z″ of CSCTO-15 at selected temperatures

Full size image

Figure 5b reveals that as the temperature increases, the loss peaks shift towards the higher-frequency region, and all Z″ curves converge at high frequencies (for all temperatures). This is a sign of the nature of bulk resistance, possible release of space charge at the grain boundaries and the presence of the dielectric relaxation process in the compound is expected [3]. The relaxation process may occur as a result of the existence of immobile/electron species at lower temperatures and defects/vacancies at high temperatures [27]. Also, the value of Z˝ decreases steadily with a shift in the characteristic frequency towards the high-frequency side, and hence they ultimately converge in the higher-frequency side; due to the accumulation of space charge [11]. Further, a large broadening of the peaks relative to temperature again indicates the occurrence of the temperature-dependent relaxation process in the material. The widths of the peaks suggest a spread of relaxation times.

3.5 Nyquist plot

The Nyquist plot of the pure CCTO showed the contribution of grain, grain boundary and electrode effects, and a non-Debye relaxation process was reported [25]. The Nyquist diagram (Fig. 6a, b) illustrates the relationship between the real and imaginary parts of the impedance at different temperatures and frequencies. It helps to identify the role of the electrode interface, grain boundary and grain effects associated with the polarization mechanism. It is observed that successive semicircle arcs are formed in the diagram which describe these three effects. Extension of the intercept of semicircles on the x-axis (real axis) and its number in the spectrum provide information regarding electrical processes occurring within the sample. The connection between these arcs and microstructure of the compound is recognized by sketching an equivalent electrical circuit. In polycrystalline specimens, grains are semiconducting, whereas the grain boundaries are insulating. The semiconducting nature of the grains in ceramic samples is believed to be owing to the loss of oxygen during the high-temperature sintering route.

Fig. 6
figure 6

a, b Nyquist plot of CSCTO-15 at different temperatures with c, d equivalent circuit diagrams

Full size image

We can model an equivalent circuit (Fig. 6d, f) to describe a physical mechanism occurring in the sample with the help of impedance spectra. A computer-controlled software package (ZSimpWin version 2.0) is used to fit the theoretically calculated data with experimental data to determine the type of the relaxation mechanism (Debye or non-Debye). The simulated circuit consists of a parallel arrangement of bulk capacitance (Cg) and resistance (Rb), with grain boundary capacitance (Cgb), which corresponds to the constant phase element (CPE = Q) coefficient and grain boundary resistance (Rgb) connected in a series arrangement. The nature of the material (experimental and theoretical fit plot) was analyzed using software and is summarized in Table 1. Due to inhomogeneous distribution of grains, depressed semicircles or arcs will be observed in impedance spectroscopy plots; to fit the ideal capacitor to the data is not possible. The ideal capacitor is used only when exact semicircles are formed, in the case of homogeneous distribution of grains and when grain growth takes place; however, in practice, it is not possible to obtain exact semicircles. Thus, by using the CPE, it is possible to extract C values. The phase angle of the CPE impedance has a value of −(90*n)°. For n = 1, it behaves like a capacitor. For n = 0, it behaves like a resistor, and for n = −1, like an inductor. The Kröger–Vink notation was used by Cortes et al. to understand the dielectric and non-ohmic properties of low-Sn4+-substituted samples (x = 0.1 and x = 0.2) into a CCTO/CTO composite [4].

4 Conclusion

In summary, the hopping type of conduction and dielectric phenomena have been systematically investigated for CSCTO-15 sample. The prepared sample crystallizes in a cubic crystal system, which was confirmed from the structural refinement of X-ray diffraction data. The surface morphology shows grain (various sizes) and clear grain boundaries suggesting a highly densified ceramic sample. The Maxwell–Wagner model and interfacial polarization explains the higher dielectric constant of the material at higher temperatures. As the tangent loss was low and the Q factor (quality factor) of the compound very high, the material can be used for various applications, including microwave laminates and appliances. The conductivity vs. temperature graph, confirms that in the low-temperature region, the conductivity of CSCTO-15 is relatively low. This may be due to high grain boundary density, which results in increased grain boundary resistance. The graphs of complex impedance show that the sample reveals semiconducting behavior and the relaxation phenomenon.