P-wave Interaction by an Asymmetric Crack in an Orthotropic Strip

Abstract

Diffraction of p-wave by a Griffith crack at an asymmetric position in an infinite orthotropic strip is analyzed. Fourier and Abel transforms are used to reduce the problem to a system of dual integral equation. The system of dual integral equation is further reduced to a Fredholm integral equation of second kind and finally the integral equation is solved numerically. The Stress Intensity Factor has been calculated and illustrated graphically to show the effect of asymmetry of the position of the crack and material orthotropy.

Introduction

Cracks and inclusions are common in almost all fabricated materials. The study of diffraction of waves due to crack is interesting and active research area in solid mechanics. There are a number of researchers Chen [1], Cinar and Erdogan [2], Dhaliwal [5], Gard [7], Kassir and Tse [9] who studied diffraction of waves in orthotropic medium. Das, Patra and Debnath [4] solved the problem of determining the stress intensity factor for an interfacial crack between two orthotropic half planes bonded to a dissimilar orthotropic layer with a punch. They reduced the problem to a system of simultaneous integral equations which are solved by Chebyshev polynomials. The problem of two perfectly bonded dissimilar orthotropic strip with an interfacial crack is studied by Li [10]. He derived the analytical expression for the stress intensity factor. Sarkar, Mandal and Ghosh [15] solved the problem of diffraction of elastic waves by three coplanar Griffith cracks in an orthotropic medium. Diffraction of p-waves by edge crack in an infinitely long elastic strip is studied by Munshi and Mandal [14]. Elastostatic problem of an infinite row of parallel cracks in an orthotropic medium is analyzed by Sinharoy [16]. Monfared and Ayatollahi [12] investigated the problem of determining the dynamic stress intensity factors of multiple cracks in an orthotropic strip with functionally graded materials coating. They solved the problem by reducing it to a singular integral equation of Cauchy type. The problem of Interaction of three interfacial Griffith cracks between bonded dissimilar orthotropic half planes has been studied by Mukherjee and Das [13]. Das, Chakraborty, Srikanth and Gupta [3] solved the problem of determining the stress intensity factors due to symmetric edge cracks in an orthotropic strip under normal loading. They derived an analytical expression for the stress intensity factor at the crack tip. The problem of finding The Stress Intensity Factors for two parallel interface cracks between a nonhomogeneous bonding layer and two dissimilar orthotropic half-planes under tension has been studied by Itou [8].

In our paper, diffraction of p-wave by a Griffith crack at an asymmetric position in an infinite orthotropic strip is analyzed. The mixed boundary value problem is reduced to a system of dual integral equation by using Fourier transform and Abel transform technique. The system of dual integral equation is again reduced to a Fredholm integral equation of second kind and finally the Fredholm integral equation is solved numerically by Fox and Goodwin [6] method. The stress intensity factor is calculated numerically and plotted graphically against the dimensionless frequency to show the effect of the position of the crack and material orthotropy.

Formulation of the Problem

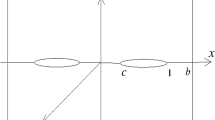
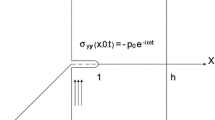
Let us consider the problem of diffraction of p-wave by a Griffith crack in an infinite orthotropic strip given by $-b_{1}\le x_{1} \le c_{1}$. The crack is located in the region $-a\le x_{1} \le a,\,\, -\infty <z_{1}<\infty ,\,\,y_{1}=0$. Normalizing all the lengths with respect to ‘$a$’ and putting $\frac{x_{1}}{a}=x, \frac{y_{1}}{a}=y,\,\frac{z_{1}}{a}=z,\,\frac{b_{1}}{a}=b,\,\frac{c_{1}}{a}=c,$ it is found that the location of the crack is $-1\le x \le 1,\,\, -\infty <z<\infty ,\,\,y=0$ (Fig. 1) referred to Cartesian co-ordinate system $(x,y,z)$. Let us consider a normally incident time harmonic wave travels in the direction of the positive $y$-axis. The oscillatory term $e^{-i\omega t}$, which is common to all field variables, is omitted in the formulation.

Fig. 1

Geometry of the problem

Displacement components are also made dimensionless with respect to ‘$a$’. The dimensionless displacement components in $x,$ $y$ directions are assumed to be $u,\,v$ respectively, where

$$\begin{aligned} u=u(x,y,t) \hbox { and } v=v(x,y,t) \end{aligned}$$

(1)

The nonzero stress components $\tau _{xx},\,\tau _{yy},\, \tau _{xy}$ are given by

$$\begin{aligned}&\tau _{xx}\big /\mu _{12}=C_{11}\frac{\partial u}{\partial {x}}+C_{12}\frac{\partial v}{\partial {y}}\end{aligned}$$

(2)

$$\begin{aligned}&\tau _{yy}\big /\mu _{12}=C_{12}\frac{\partial u}{\partial {x}}+C_{22}\frac{\partial v}{\partial {y}}\end{aligned}$$

(3)

$$\begin{aligned}&\tau _{xy}\big /\mu _{12}=\frac{\partial u}{\partial {y}}+\frac{\partial v}{\partial {x}} \end{aligned}$$

(4)

where $C_{11},C_{12}$ and $C_{22}$ are non-dimensional parameters related to the elastic constants by the relations

$$\begin{aligned}&C_{11}=E_{1}\big /\mu _{12}(1-\nu _{12}^{2}E_{2}\big /E_{1})\end{aligned}$$

(5)

$$\begin{aligned}&C_{22}=E_{2}\big /\mu _{12}(1-\nu _{12}^{2}E_{2}\big /E_{1})=C_{11}E_{2}\big /E_{1}\end{aligned}$$

(6)

$$\begin{aligned}&C_{12}=\nu _{12}E_{2}\big /\mu _{12}(1-\nu _{12}^{2}E_{2}\big /E_{1})=\nu _{12}C_{22}=\nu _{21}C_{11} \end{aligned}$$

(7)

The constants $E_{i}$ and $\nu _{ij}$ satisfy Maxwell’s relation:

$$\begin{aligned} \nu _{ij}\big /E_{i}=\nu _{ji}\big /E_{j} \end{aligned}$$

(8)

The displacement equations of motion for orthotropic material are

$$\begin{aligned}&C_{11}\frac{\partial ^{2}u}{\partial {x^{2}}}+\frac{\partial ^{2}u}{\partial {y^{2}}}+(1+C_{12})\frac{\partial ^{2}v}{{\partial {x}}{\partial {y}}} =\frac{a^{2}}{c_{s}^{2}}\frac{\partial ^{2}u}{\partial {t^{2}}}\end{aligned}$$

(9)

$$\begin{aligned}&\frac{\partial ^{2}v}{\partial {x^{2}}}+C_{22}\frac{\partial ^{2}v}{\partial {y^{2}}}+(1+C_{12})\frac{\partial ^{2}u}{{\partial {x}}{\partial {y}}} =\frac{a^{2}}{c_{s}^{2}}\frac{\partial ^{2}v}{\partial {t^{2}}} \end{aligned}$$

(10)

where $c_{s}$ is the wave velocity.

Let us substitute $u(x,y,t)=u(x,y)e^{-i\omega t}$ and $v(x,y,t)=v(x,y)e^{-i\omega t}$ in Eqs.(9) and (10) to obtain

$$\begin{aligned}&C_{11}\frac{\partial ^{2}u}{\partial {x^{2}}}+\frac{\partial ^{2}u}{\partial {y^{2}}}+(1+C_{12})\frac{\partial ^{2}v}{{\partial {x}}{\partial {y}}} +k_{s}^{2}u=0\end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial ^{2}v}{\partial {x^{2}}}+C_{22}\frac{\partial ^{2}v}{\partial {y^{2}}}+(1+C_{12})\frac{\partial ^{2}u}{{\partial {x}}{\partial {y}}} +k_{s}^{2}v=0 \end{aligned}$$

(12)

with $k_{s}^{2}=a^{2}\omega ^{2}\big /c_{s}^{2}$, . The boundary conditions are given by

$$\begin{aligned}&\tau _{yy}(x,0 +)=\tau _{yy}(x,0 -)=-\tau _{0}\quad -1<x<1 \end{aligned}$$

(13)

$$\begin{aligned}&v(x,0)=0,\quad -b<x<-1,~~1<x<c \end{aligned}$$

(14)

$$\begin{aligned}&\tau _{xy}(-b,y)=0\quad -\infty <y<\infty \end{aligned}$$

(15)

$$\begin{aligned}&\tau _{xy}(c,y)=0\quad -\infty <y<\infty \end{aligned}$$

(16)

$$\begin{aligned}&\tau _{xx}(-b,y)=0\quad -\infty <y<\infty \end{aligned}$$

(17)

$$\begin{aligned}&\tau _{xx}(c,y)=0\quad -\infty <y<\infty \end{aligned}$$

(18)

$$\begin{aligned}&\tau _{xy}(x,0)=0\quad -b\le x\le c \end{aligned}$$

(19)

where $\tau _{0}$ is a constant.

The solutions of Eqs. (11) and (12) with the help of the boundary condition (19) are

$$\begin{aligned} u(x,y)&= \int _{-\infty }^{\infty }[ e^{-\upgamma _{1}y}-\beta e^{-\upgamma _{2}y}]A_{1}(\xi ) e^{i \xi x} d \xi \nonumber \\&\quad +\int _{0}^{\infty }[A_{3}(\zeta )e^{\upgamma _{3} x}+A_{4}(\zeta )e^{-\upgamma _{3}x}+A_{5}(\zeta )e^{\upgamma _{4}x}+A_{6}(\zeta )e^{-\upgamma _{4}x}]\cos (\zeta y)d\zeta \nonumber \\ \end{aligned}$$

(20)

and

$$\begin{aligned} v(x,y)&= \int _{-\infty }^{\infty }\left[ \frac{\alpha _{1}}{\xi } e^{-\upgamma _{1}y}-\beta \frac{\alpha _{2}}{\xi }e^{-\upgamma _{2}y}\right] A_{1}(\xi )i e^{i \xi x} d \xi \nonumber \\&\quad +\int _{0}^{\infty }\left[ \frac{\alpha _{3}}{\zeta }A_{3}(\zeta )e^{\upgamma _{3} x}-\frac{\alpha _{3}}{\zeta }A_{4}(\zeta )e^{-\upgamma _{3}x}\right. \nonumber \\&\quad \left. +\frac{\alpha _{4}}{\zeta }A_{5}(\zeta )e^{\upgamma _{4}x}-\frac{\alpha _{4}}{\zeta }A_{6}(\zeta )e^{-\upgamma _{4}x}\right] \sin (\zeta y)d\zeta \end{aligned}$$

(21)

and the non vanishing stress components are given by

$$\begin{aligned} \tau _{xx}\big /\mu _{12}&= \int _{-\infty }^{\infty }\left[ (C_{11}\xi -\frac{C_{12}\alpha _{1}\upgamma _{1}}{\xi })e^{-\upgamma _{1}y}-\beta (C_{11}\xi -\frac{C_{12}\alpha _{2}\upgamma _{2}}{\xi })e^{-\upgamma _{2}y}\right] A_{1}(\xi )i e^{i\xi x}d\xi \nonumber \\&\quad +{\int _{0}^{\infty }}\Big [(C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})A_{3}(\zeta )e^{{\upgamma }_{3}x}-(C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})A_{4}(\zeta )e^{-\upgamma _{3}x}\nonumber \\&\quad +\,(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})A_{5}(\zeta )e^{\upgamma _{4}x}-(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})A_{6}(\zeta )e^{-\upgamma _{4}x}\Big ] \cos (\zeta y)d\zeta \end{aligned}$$

(22)

$$\begin{aligned} \tau _{yy}\big /\mu _{12}&= \int _{-\infty }^{\infty }[(C_{12}\xi -\frac{C_{22}\alpha _{1}\upgamma _{1}}{\xi })e^{-\upgamma _{1}y}-\beta (C_{12}\xi -\frac{C_{22}\alpha _{2}\upgamma _{2}}{\xi })e^{-\upgamma _{2}y} ]A_{1}(\xi )i e^{i\xi x}d\xi \nonumber \\&\quad +\int _{0}^{\infty }[(C_{12}{\upgamma }_{3}+C_{22}\alpha _{3})A_{3}(\zeta )e^{\upgamma _{3}x}-(C_{12}{\upgamma }_{3}+C_{22}\alpha _{3})A_{4}(\zeta )e^{-\upgamma _{3}x}\nonumber \\&\quad +\,(C_{12}{\upgamma }_{4}+C_{22}\alpha _{4})A_{5}(\zeta )e^{\upgamma _{4}x}-(C_{12}{\upgamma }_{4}+C_{22}\alpha _{4})A_{6}(\zeta )e^{-\upgamma _{4}x}] \cos (\zeta y)d\zeta \end{aligned}$$

(23)

$$\begin{aligned} \tau _{xy}\big /\mu _{12}&= -\int _{-\infty }^{\infty }[({\upgamma }_{1}+\alpha _{1})(e^{-\upgamma _{1}y}-e^{-\upgamma _{2}y})A_{1}(\xi ) e^{i\xi x}d\xi \nonumber \\&\quad -\int _{0}^{\infty }[(\zeta -\frac{\alpha _{3}\upgamma _{3}}{\zeta })A_{3}(\zeta )e^{\upgamma _{3}x}+(\zeta -\frac{\alpha _{3}\upgamma _{3}}{\zeta })A_{4}(\zeta )e^{-\upgamma _{3}x}\nonumber \\&\quad +\,(\zeta -\frac{\alpha _{4}\upgamma _{4}}{\zeta })A_{5}(\zeta )e^{\upgamma _{4}x}+(\zeta -\frac{\alpha _{4}\upgamma _{4}}{\zeta })A_{6}(\zeta )e^{-\upgamma _{4}x}]sin(\zeta y)d\zeta \end{aligned}$$

(24)

where

$$\begin{aligned} \alpha _{i}&= \frac{C_{11}\xi ^{2}-k_{s}^{2}-\upgamma _{i}^{2}}{(1+C_{12})\upgamma _{i}}\qquad (i=1,2)\\ \alpha _{j}&= \frac{\zeta ^{2}-k_{s}^{2}-C_{11}\upgamma _{j}^{2}}{(1+C_{12})\upgamma _{j}}\qquad (j=3,4)\\ \beta&= \frac{\upgamma _{1}+\alpha _{1}}{\upgamma _{2}+\alpha _{2}} \end{aligned}$$

where $\upgamma _{1}^{2}$ and $\upgamma _{2}^{2}$ are the roots of the equation

$$\begin{aligned} C_{22}{\upgamma }^{4}+\left\{ (C_{12}^{2}+2 C_{12}-C_{11}C_{22})\xi ^{2}+(1+C_{22})k_{s}^{2}\right\} {\upgamma }^{2}+(\xi ^{2}-k_{s}^{2})(C_{11}\xi ^{2}-k_{s}^{2})=0 \end{aligned}$$

and, $\upgamma _{3}^{2}$ and $\upgamma _{4}^{2}$ are the roots of the equation

$$\begin{aligned} C_{11}{\upgamma }^{4}+\left\{ (C_{12}^{2}+2 C_{12}-C_{11}C_{22})\zeta ^{2}+(1+C_{11})k_{s}^{2}\right\} {\upgamma }^{2}+(\zeta ^{2}-k_{s}^{2})(C_{22}\zeta ^{2}-k_{s}^{2})=0 \end{aligned}$$

Formulation of the Dual Integral Equations

Using the boundary condition (13) and (14), the problem is reduced to the following system of dual integral equations for determining the unknown function $A(\xi )$

$$\begin{aligned}&\int _{-\infty }^{\infty }A(\xi )e^{i\xi x} d\xi =0 \quad -b\le x \le -1,\quad 1\le x\le c\end{aligned}$$

(25)

$$\begin{aligned}&\int _{-\infty }^{\infty }\xi [1+H(\xi )]A(\xi )e^{i\xi x} d\xi = -\frac{p_{0}(x)}{ i \theta } \quad -1\le x\le 1 \end{aligned}$$

(26)

where,

$$\begin{aligned} A(\xi )=\frac{\alpha _{1}-\beta \alpha _{2}}{\xi }A_{1}(\xi ) \end{aligned}$$

(27)

also

$$\begin{aligned} H(\xi )&= \frac{(C_{12}\xi ^{2}-C_{22}\alpha _{1}\upgamma _{1})-\beta (C_{12}\xi ^{2}-C_{22}\alpha _{2}\upgamma _{2})}{(\alpha _{1}-\beta \alpha _{2})\xi \theta }-1 \quad \rightarrow 0 \quad as \quad \xi \rightarrow \infty \end{aligned}$$

(28)

$$\begin{aligned} \theta&= \frac{(C_{12}^{2}\!+\!C_{12}\!-\!C_{11}C_{22})(C_{12}N_{1}N_{2}\!-\!C_{11})\!-\!C_{22}\left\{ C_{12}N_{1}^{2}N_{2}^{2}\!+\!C_{11}(N_{1}^{2}\!+\!N_{1}N_{2}\!+\!N_{2}^{2})\right\} }{C_{11}(1\!+\!C_{12})(N_{1}\!+\!N_{2})}\quad \end{aligned}$$

(29)

$$\begin{aligned} N_{1}^{2}&= \frac{-(C_{12}^{2}+2 C_{12}-C_{11}C_{22})+\sqrt{(C_{12}^{2}+2 C_{12}-C_{11}C_{22})^{2}-4 C_{11}C_{22}}}{2 C_{22}}\end{aligned}$$

(30)

$$\begin{aligned} N_{2}^{2}&= \frac{-(C_{12}^{2}+2 C_{12}-C_{11}C_{22})-\sqrt{(C_{12}^{2}+2 C_{12}-C_{11}C_{22})^{2}-4 C_{11}C_{22}}}{2 C_{22}} \end{aligned}$$

(31)

and

$$\begin{aligned} p_{0}(x)&= \frac{\tau _{0}}{\mu _{12}}+\int _{0}^{\infty }\left[ \left( C_{12} {{\upgamma }_{3}}+C_{22}\alpha _{3}\right) \left( A_{3}(\zeta )e^{\upgamma _{3}x}-A_{4}(\zeta )e^{-\upgamma _{3}x}\right) \right. \nonumber \\&\quad \left. +\left( C_{12}{{\upgamma }_{4}}+C_{22}\alpha _{4})(A_{5}(\zeta )e^{\upgamma _{4}x}-A_{6}(\zeta )e^{-\upgamma _{4}x}\right) \right] d\zeta \end{aligned}$$

(32)

Again using the boundary conditions (15),(16),(17) and (18)and applying Fourier inverse transform technique, the unknown functions $A_{3}(\zeta ),A_{4}(\zeta ),A_{5}(\zeta )$ and $A_{6}(\zeta )$ are obtained from the following linear equations

$$\begin{aligned}&\left( \frac{\alpha _{3}\upgamma _{3}}{\zeta }-\zeta \right) \left( A_{3}(\zeta ) e^{-b\upgamma _{3}}+A_{4}(\zeta )e^{b\upgamma _{3}}\right) +\left( \frac{\alpha _{4} \upgamma _{4}}{\zeta }-\zeta \right) \left( A_{5}(\zeta )e^{-b\upgamma _{4}}+A_{6}(\zeta ) e^{b\upgamma _{4}}\right) \nonumber \\&\qquad =\frac{2}{\pi (\upgamma _{3}^{2}-\upgamma _{4}^{2})}\int _ {-\infty }^{\infty }\left( \frac{q_{1}\upgamma _{3}^{2}-q_{2}}{\xi ^{2}+\upgamma _{3}^{2}} -\frac{q_{1}\upgamma _{4}^{2}-q_{2}}{\xi ^{2}+\upgamma _{4}^{2}}\right) \xi \zeta A(\xi )e^{-i b\xi }d\xi \end{aligned}$$

(33)

$$\begin{aligned}&\left( \frac{\alpha _{3}\upgamma _{3}}{\zeta }-\zeta \right) \left( A_{3}(\zeta ) e^{c\upgamma _{3}}+A_{4}(\zeta )e^{-c\upgamma _{3}}\right) +\left( \frac{\alpha _{4}\upgamma _{4}}{\zeta }-\zeta \right) \left( A_{5}(\zeta )e^{c\upgamma _{4}}+A_{6}(\zeta ) e^{-c\upgamma _{4}}\right) \nonumber \\&\qquad =\frac{2}{\pi (\upgamma _{3}^{2}-\upgamma _{4}^{2})}\int _ {-\infty }^{\infty }\left( \frac{q_{1}\upgamma _{3}^{2}-q_{2}}{\xi ^{2}+\upgamma _{3}^{2}} -\frac{q_{1}\upgamma _{4}^{2}-q_{2}}{\xi ^{2}+\upgamma _{4}^{2}}\right) \xi \zeta A(\xi )e^{i c\xi }d\xi \end{aligned}$$

(34)

$$\begin{aligned}&\left( C_{11}{{\upgamma }_{3}}+C_{12}\alpha _{3}\right) \left( A_{3}(\zeta )e^{-b\upgamma _{3}}-A_{4} (\zeta )e^{b\upgamma _{3}}\right) +\left( C_{11}{{\upgamma }_{4}}+C_{12}\alpha _{4})(A_{5} (\zeta )e^{-b\upgamma _{4}}-A_{6}(\zeta )e^{b\upgamma _{4}}\right) \nonumber \\&\qquad =-\frac{2}{\pi (\upgamma _{3}^{2}-\upgamma _{4}^{2})}\int _{-\infty }^{\infty } \left( \frac{q_{3}\upgamma _{3}^{2}-q_{4}}{\xi ^{2}+\upgamma _{3}^{2}}-\frac{q_{3} \upgamma _{4}^{2}-q_{4}}{\xi ^{2}+\upgamma _{4}^{2}}\right) A(\xi )i e^{-i b\xi }d\xi \end{aligned}$$

(35)

and

$$\begin{aligned}&(C_{11}{{\upgamma }_{3}}\!+\!C_{12}\alpha _{3})(A_{3}(\zeta )e^{c\upgamma _{3}}-A_{4} (\zeta )e^{-c\upgamma _{3}})\!+\!(C_{11}{{\upgamma }_{4}}+C_{12}\alpha _{4})(A_{5} (\zeta )e^{c\upgamma _{4}}\!-\!A_{6}(\zeta )e^{-c\upgamma _{4}})\nonumber \\&\qquad =-\frac{2}{\pi (\upgamma _{3}^{2}-\upgamma _{4}^{2})}\int _{-\infty }^{\infty } \left( \frac{q_{3}\upgamma _{3}^{2}-q_{4}}{\xi ^{2}+\upgamma _{3}^{2}}-\frac{q_{3} \upgamma _{4}^{2}-q_{4}}{\xi ^{2}+\upgamma _{4}^{2}}\right) A(\xi )i e^{i c\xi }d\xi \end{aligned}$$

(36)

where

$$\begin{aligned} q_{1}&= \frac{C_{11}C_{22}-C_{12}^{2}}{C_{11}}\\ q_{2}&= -\frac{(C_{12}+C_{22})k_{s}^{2}}{C_{11}}\\ q_{3}&= \frac{C_{12}^{2}\zeta ^{2}-C_{11}C_{22}\zeta ^{2}+C_{12}k_{s}^{2}}{C_{11}}\\ q_{4}&= \frac{C_{12}k_{s}^{2}(\zeta ^{2}-k_{s}^{2})}{C_{11}} \end{aligned}$$

Method of Solution

To solve the dual integral equations given by (25) and (26), we consider

$$\begin{aligned} A(\xi )=-\frac{\tau _{0}}{2 i \mu _{12}\theta }\int _{0}^{1}t g(t) J_{0}(\xi t)dt \end{aligned}$$

(37)

so that, the integral Eq. (25) is automatically satisfied. The Eq. (26),with the help of Abel’s transform technique, is reduced to a Fredholm integral equation of second kind given by

$$\begin{aligned} g(u)+\int _{0}^{1}t g(t) L(u,t) dt=1 \end{aligned}$$

(38)

where the kernel $L(u,t)$ is the sum of two functions

$$\begin{aligned} L(u,t)=L_{1}(u,t)+L_{2}(u,t) \end{aligned}$$

(39)

given by

$$\begin{aligned} L_{1}(u,t)=\int _{0}^{\infty }\xi H(\xi )J_{0}(\xi t) J_{0}(\xi u) d\xi \end{aligned}$$

(40)

and

$$\begin{aligned} L_{2}(u,t)=-\sum \limits _{i=3}^{4}\sum \limits _{j=3}^{4}\int _{0}^{\infty }\left[ g_{ij} (\zeta )I_{0}({\upgamma }_{i}t)I_{0}({\upgamma }_{j}u)+{h}_{ij}(\zeta )I_{0} ({\upgamma }_{i}t)L_{0}({\upgamma }_{j}u)\right] d\zeta \end{aligned}$$

(41)

where

$$\begin{aligned} g_{33}(\zeta )&= \frac{C_{12}\upgamma _{3}+C_{22}\alpha _{3}}{\theta \Delta } (q_{33}-q_{43}),\quad h_{33}(\zeta )=\frac{C_{12}\upgamma _{3}+C_{22} \alpha _{3}}{\theta \Delta }(q_{33}+q_{43})\nonumber \\ g_{43}(\zeta )&= \frac{C_{12}\upgamma _{3}+C_{22}\alpha _{3}}{\theta \Delta } (q_{34}-q_{44}),\quad h_{43}(\zeta )=\frac{C_{12}\upgamma _{3}+C_{22} \alpha _{3}}{\theta \Delta }(q_{34}+q_{44})\nonumber \\ g_{34}(\zeta )&= \frac{C_{12}\upgamma _{4}+C_{22}\alpha _{4}}{\theta \Delta } (q_{53}-q_{63}),\quad h_{34}(\zeta )=\frac{C_{12}\upgamma _{4}+C_{22} \alpha _{4}}{\theta \Delta }(q_{53}+q_{63})\\ g_{44}(\zeta )&= \frac{C_{12}\upgamma _{4}+C_{22}\alpha _{4}}{\theta \Delta } (q_{54}-q_{64}),\quad h_{44}(\zeta )=\frac{C_{12}\upgamma _{4}+C_{22} \alpha _{4}}{\theta \Delta }(q_{54}+q_{64})\nonumber \end{aligned}$$

(42)

The function $\Delta$ is given by

$$\begin{aligned} \Delta&= 8\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3} +C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times [\cosh (b+c){\upgamma }_{3}\cosh (b+c){\upgamma }_{4}-1]-4 \left[ \left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) ^{2} \left( C_{11}{\upgamma }_{4}+C_{12}\alpha _{4}\right) ^{2}\right. \nonumber \\&\quad \left. +\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) ^{2} (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})^{2}\right] \sinh (b+c){\upgamma }_{3}\sinh (b+c){\upgamma }_{4} \end{aligned}$$

(43)

Also

$$\begin{aligned} q_{33}&= 4h_{1}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})^{2}e^{-c{\upgamma }_{3}}\cosh b{\upgamma }_{3}\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad -\,4h_{1}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})e^{-c{\upgamma }_{3}}\nonumber \\&\quad \times [\sinh b{\upgamma }_{3}\cosh (b+c){\upgamma }_{4}+\sinh c{\upgamma }_{3}]\nonumber \\&\quad -\,4h_{3}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})e^{-c{\upgamma }_{3}}\sinh b{\upgamma }_{3}\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad +\,4h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})e^{-c{\upgamma }_{3}}\nonumber \\&\quad \times [\cosh b{\upgamma }_{3}\cosh (b+c){\upgamma }_{4}-\cosh c{\upgamma }_{3}]\end{aligned}$$

(44)

$$\begin{aligned} q_{43}&= -4h_{1}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})^{2}e^{-b{\upgamma }_{3}}\cosh c{\upgamma }_{3} \sinh (b+c){\upgamma }_{4}\nonumber \\&\quad +\,4h_{1}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12} \alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})e^{-b{\upgamma }_{3}}\nonumber \\&\quad \times [\sinh c{\upgamma }_{3}\cosh (b+c){\upgamma }_{4}+\sinh b{\upgamma }_{3}]\nonumber \\&\quad +\,4h_{3}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{3} +C_{12}\alpha _{3})e^{-b{\upgamma }_{3}}\sinh c{\upgamma }_{3}\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad -\,4h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})e^{-b{\upgamma }_{3}}\nonumber \\&\quad \times [\cosh c{\upgamma }_{3}\cosh (b+c){\upgamma }_{4}-\cosh b{\upgamma }_{3}]\end{aligned}$$

(45)

$$\begin{aligned} q_{34}&= -2h_{2}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})^{2} (e^{b{\upgamma }_{3}-c{\upgamma }_{4}}+e^{-c{\upgamma }_{3}-b{\upgamma }_{4}})\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad +\,2h_{2}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{b{\upgamma }_{3}-c{\upgamma }_{4}}-e^{-c{\upgamma }_{3}-b{\upgamma }_{4}}) \cosh (b+c){\upgamma }_{4}+(e^{b{\upgamma }_{3}-b{\upgamma }_{4}}-e^{-c{\upgamma }_{3}-c{\upgamma }_{4}})\right\} \nonumber \\&\quad +\,2h_{4}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(e^{b{\upgamma }_{3}-c{\upgamma }_{4}}-e^{-c{\upgamma }_{3}-b{\upgamma }_{4}})\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad -\,2h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{b{\upgamma }_{3}-c{\upgamma }_{4}}+e^{-c{\upgamma }_{3}-b{\upgamma }_{4}})\cosh (b+c){\upgamma }_{4}-(e^{b{\upgamma }_{3}-b{\upgamma }_{4}}+e^{-c{\upgamma }_{3}-c{\upgamma }_{4}})\right\} \end{aligned}$$

(46)

$$\begin{aligned} q_{44}&= 2h_{2}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})^{2}(e^{c{\upgamma }_{3}-b{\upgamma }_{4}}+e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad -\,2h_{2}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{c{\upgamma }_{3}-b{\upgamma }_{4}}-e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\cosh (b+c){\upgamma }_{4}+(e^{c{\upgamma }_{3}-c{\upgamma }_{4}}-e^{-b{\upgamma }_{3}-b{\upgamma }_{4}})\right\} \nonumber \\&\quad -\,2h_{4}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(e^{c{\upgamma }_{3}-b{\upgamma }_{4}}-e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\sinh (b+c){\upgamma }_{4}\nonumber \\&\quad +\,2h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{c{\upgamma }_{3}-b{\upgamma }_{4}}+e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\cosh (b+c){\upgamma }_{4}-(e^{c{\upgamma }_{3}-c{\upgamma }_{4}}+e^{-b{\upgamma }_{3}-b{\upgamma }_{4}})\right\} \end{aligned}$$

(47)

$$\begin{aligned} q_{53}&= 2h_{1}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})^{2}(e^{b{\upgamma }_{4}-c{\upgamma }_{3}}+e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad -\,2h_{1}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{b{\upgamma }_{4}-c{\upgamma }_{3}}-e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\cosh (b+c){\upgamma }_{3}+(e^{-b{\upgamma }_{3}+b{\upgamma }_{4}}-e^{-c{\upgamma }_{3}-c{\upgamma }_{4}})\right\} \nonumber \\&\quad -\,2h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})(e^{b{\upgamma }_{4}-c{\upgamma }_{3}}-e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad +\,2h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})\nonumber \\&\quad \times \left\{ (e^{b{\upgamma }_{4}-c{\upgamma }_{3}}+e^{-b{\upgamma }_{3}-c{\upgamma }_{4}})\cosh (b+c){\upgamma }_{3}-(e^{-b{\upgamma }_{3}+b{\upgamma }_{4}}+e^{-c{\upgamma }_{3}-c{\upgamma }_{4}})\right\} \end{aligned}$$

(48)

$$\begin{aligned} q_{63}&= -2h_{1}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})^{2}(e^{c{\upgamma }_{4}-b{\upgamma }_{3}}+e^{-b{\upgamma }_{4}-c{\upgamma }_{3}})\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad +\,2h_{1}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})\nonumber \\&\quad \times \left\{ (e^{c{\upgamma }_{4}-b{\upgamma }_{3}}-e^{-b{\upgamma }_{4}-c{\upgamma }_{3}})\cosh (b+c){\upgamma }_{3}-(e^{-b{\upgamma }_{3}-b{\upgamma }_{4}}-e^{-c{\upgamma }_{3}+c{\upgamma }_{4}})\right\} \nonumber \\&\quad +\,2h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})(e^{c{\upgamma }_{4}-b{\upgamma }_{3}}-e^{-b{\upgamma }_{4}-c{\upgamma }_{3}})\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad -\,2h_{3}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})\nonumber \\&\quad \times \left\{ (e^{c{\upgamma }_{4}-b{\upgamma }_{3}}+e^{-b{\upgamma }_{4}-c{\upgamma }_{3}})\cosh (b+c){\upgamma }_{3}-(e^{-b{\upgamma }_{3}-b{\upgamma }_{4}}+e^{-c{\upgamma }_{3}+c{\upgamma }_{4}})\right\} \end{aligned}$$

(49)

$$\begin{aligned} q_{54}&= -4h_{2}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})^{2}e^{-c{\upgamma }_{4}}\cosh b{\upgamma }_{4}\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad +\,4h_{2}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4}) e^{-c{\upgamma }_{4}}\nonumber \\&\quad \times [\sinh b{\upgamma }_{4}\cosh (b+c){\upgamma }_{3}+\sinh c{\upgamma }_{4}]\nonumber \\&\quad +\,4h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) ^{2}(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4})e^{-c {\upgamma }_{4}}\sinh b{\upgamma }_{4} \sinh (b+c){\upgamma }_{3}\nonumber \\&\quad -\,4h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3}) e^{-c{\upgamma }_{4}}\nonumber \\&\quad \times [\cosh b{\upgamma }_{4} \cosh (b+c){\upgamma }_{3}-\cosh c{\upgamma }_{4}] \end{aligned}$$

(50)

$$\begin{aligned} q_{64}&= 4h_{2}\left( \frac{\alpha _{4}{\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})^{2}e^{-b{\upgamma }_{4}}\cosh c{\upgamma }_{4}\sinh (b+c){\upgamma }_{3}\nonumber \\&\quad -\,4h_{2}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3})(C_{11}{\upgamma }_{4}+C_{12}\alpha _{4}) e^{-b{\upgamma }_{4}}\nonumber \\&\quad \times [\sinh c{\upgamma }_{4}\cosh (b+c){\upgamma }_{3}+\sinh b{\upgamma }_{4}]\nonumber \\&\quad -\,4h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) ^{2}(C_{11} {\upgamma }_{4}+C_{12}\alpha _{4})e^{-b{\upgamma }_{4}}\sinh c{\upgamma }_{4} \sinh (b+c) {\upgamma }_{3}\nonumber \\&\quad +\,4h_{4}\left( \frac{\alpha _{3}{\upgamma }_{3}}{\zeta }-\zeta \right) \left( \frac{\alpha _{4} {\upgamma }_{4}}{\zeta }-\zeta \right) (C_{11}{\upgamma }_{3}+C_{12}\alpha _{3}) e^{-b{\upgamma }_{4}}\nonumber \\&\quad \times [\cosh c{\upgamma }_{4} \cosh (b+c){\upgamma }_{3}-\cosh b{\upgamma }_{4}] \end{aligned}$$

(51)

$$\begin{aligned} h_{1}&= \frac{(q_{1}{\upgamma }_{3}^{2}-q_{2})\zeta }{{\upgamma }_{3}^{2} -{\upgamma }_{4}^{2}},\quad h_{2}=\frac{(q_{1}{\upgamma }_{4}^{2}-q_{2})\zeta }{{\upgamma }_{3}^{2}-{\upgamma }_{4}^{2}}\nonumber \\ h_{3}&= \frac{q_{3}{\upgamma }_{3}^{2}-q_{4}}{({\upgamma }_{3}^{2} -{\upgamma }_{4}^{2}){\upgamma }_{3}},\quad h_{4}=\frac{q_{3} {\upgamma }_{4}^{2}-q_{4}}{({\upgamma }_{3}^{2}-{\upgamma }_{4}^{2}){\upgamma }_{4}} \end{aligned}$$

(52)

Using the contour integration technique, discussed by Mandal and Ghosh [11] the kernel $L_{1}(u,t)$ can be transformed to integrals with finite limits given by

$$\begin{aligned} L_{1}(u,t)&= -i\left[ \int _{0}^{\frac{k_{s}}{\sqrt{C_{11}}}}(\overline{X}_{1}\overline{\upgamma }_{1}-\overline{X}_{2}\overline{\upgamma }_{2})J_{0}(\xi t)H_{0}^{(1)}(\xi u)d\xi \right. \nonumber \\&\quad \left. +\int _{\frac{k_{s}}{\sqrt{C_{11}}}}^{ks}X_{2}^{'}{\upgamma }_{2}^{'}J_{0}(\xi t)H_{0}^{(1)}(\xi u)d\xi \right] \quad \qquad u>t \end{aligned}$$

(53)

where

$$\begin{aligned} \overline{X}_{1}&= \frac{[C_{12}(1+C_{12})\xi ^{2}-C_{22}(C_{11}\xi ^{2}-k_{s}^{2}+\overline{\upgamma }_{1}^{2})](C_{11}\xi ^{2}-k_{s}^{2}-C_{12}\overline{\upgamma }_{2}^{2})}{(1+C_{12})(C_{11}\xi ^{2}-k_{s}^{2})(\overline{\upgamma }_{1}^{2}-\overline{\upgamma }_{2}^{2})\theta }\\ \overline{X}_{2}&= \frac{[C_{12}(1+C_{12})\xi ^{2}-C_{22}(C_{11}\xi ^{2}-k_{s}^{2}+\overline{\upgamma }_{2}^{2})](C_{11}\xi ^{2}-k_{s}^{2}-C_{12}\overline{\upgamma }_{1}^{2})}{(1+C_{12})(C_{11}\xi ^{2}-k_{s}^{2})(\overline{\upgamma }_{1}^{2}-\overline{\upgamma }_{2}^{2})\theta }\\ X_{2}^{'}&= \frac{[C_{12}(1+C_{12})\xi ^{2}-C_{22}(C_{11}\xi ^{2}-k_{s}^{2}+{{\upgamma }_{2}^{'}}^{2})](C_{11}\xi ^{2}-k_{s}^{2}+C_{12}{{\upgamma }_{1}^{'}}^{2})}{(1+C_{12})(C_{11}\xi ^{2}-k_{s}^{2})({{\upgamma }_{1}^{'}}^{2}+{{\upgamma }_{2}^{'}}^{2})\theta }\\ \overline{\upgamma }_{1}&= \left[ \frac{1}{2}(B_{1}-(B_{1}^{2}-4\overline{B}_{2})^{\frac{1}{2}})\right] ^{\frac{1}{2}}\\ \overline{\upgamma }_{2}&= \left[ \frac{1}{2}(B_{1}+(B_{1}^{2}-4\overline{B}_{2})^{\frac{1}{2}})\right] ^{\frac{1}{2}}\\ {\upgamma }_{1}^{'}&= \left[ \frac{1}{2}(-B_{1}+(B_{1}^{2}+4B_{2}^{'})^{\frac{1}{2}})\right] ^{\frac{1}{2}}\\ {\upgamma }_{2}^{'}&= \left[ \frac{1}{2}(B_{1}+(B_{1}^{2}+4B_{2}^{'})^{\frac{1}{2}})\right] ^{\frac{1}{2}}\\ B_{1}&= \frac{(C_{12}^{2}+2C_{12}-C_{11}C_{22})\xi ^{2}+(1+C_{22})k_{s}^{2}}{C_{22}}\\ \overline{B}_{2}&= \frac{(\xi ^{2}-k_{s}^{2})(C_{11}\xi ^{2}-k_{s}^{2})}{C_{22}}\\ B_{2}^{'}&= \frac{(k_{s}^{2}-\xi ^{2})(C_{11}\xi ^{2}-k_{s}^{2})}{C_{22}} \end{aligned}$$

For the case $u<t$ the expression for the kernel $L_{1}(u,t)$ can be obtained by interchanging $u$ and $t$ in (53).

Quantities of Physical Interest: the Stress Intensity Factor (SIF)

It has been found that the normal stress component $\tau _{yy}$ outside the crack has a square root singularity at $x=1$. This leads to the concept of Stress Intensity Factor(SIF). The SIF(K) is defined by

$$\begin{aligned} K=Lt_{x\rightarrow 1^{+}} \Big \vert \frac{\tau _{yy}(x,0)(x-1)^{\frac{1}{2}}}{\tau _{0}} \Big \vert \end{aligned}$$

(54)

The SIF determines the state of stress at the crack tip. After some manipulation it can be shown that

$$\begin{aligned} K=\,\Big \vert \frac{g(1)}{\sqrt{2}} \Big \vert \end{aligned}$$

(55)

Numerical Results and Discussions

The Fredholm integral Eq. (38) is solved numerically by Fox and Goodwin method. In this method the integral in the Eq. (38) is represented by a quadrature formula involving the values of the desired function $g(t)$ at the pivot points inside the range of integration. Then the Eq. (38) is converted to a system of linear equations with the pivot points of $g(t)$ as unknown variables. The solution of which gives the first approximation of the required pivot values of $g(t)$ which can be improved by using the difference correction technique. Once the value of $g(1)$ is calculated, the SIF is calculated and plotted graphically against the dimensionless frequency for two different orthotropic materials whose elastic constants are given by the following table (Table 1).

Table 1 Engineering elastic constants

The SIF(K) is plotted graphically against the dimensionless frequency($k_{s}$) for different strip length, position of the crack for two orthotropic materials. Figs. 2, 3, and 4 show the variation of SIF against the dimensionless frequency for different values of the strip length for type I material. Figs. 5, 6, and 7 display the same for type II material.

Fig. 2

SIF versus the dimensionless frequency for type I material and $b=1.5$

Fig. 3

SIF versus the dimensionless frequency for type I material and $b=2.0$

Fig. 4

SIF versus the dimensionless frequency for type I material and $b=2.5$

Fig. 5

SIF versus the dimensionless frequency for type II material and $b=1.5$

Fig. 6

SIF versus the dimensionless frequency for type II material and $b=2.0$

Fig. 7

SIF versus the dimensionless frequency for type II material and $b=2.5$

From Figs. 2, 3 and 4 it is clear that the SIF for type I material increases initially with the increasing value of the dimensionless frequency and after reaching a maximum value it decreases and shows wave like nature. Moreover the maximum height of the SIF becomes slightly lower with the increment of $b$.

From Figs. 5, 6 and 7 it can be stated that SIF for the type II material increases initially with the increasing value of the frequency and after reaching a highest value it decreases rapidly and then shows wave like nature. Moreover it is noted that the maximum value of the SIF for the type II material is little higher than that for the type I material.

Conclusions

From all the graphs of SIF, it can be concluded that though the SIF increases initially with the increment of the frequency($k_{s}$), after reaching a maximum value it decreases and tends to zero for large frequency. Therefore the value of SIF can be arrested within a certain range.