P-wave Diffraction by a Crack Under Impact Load

Abstract

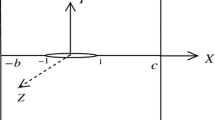
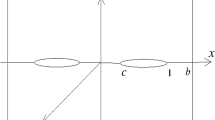
The focus of this paper is centered on diffraction of P-wave by a Griffith crack in an infinite isotropic elastic medium on which impact load is applied. Suddenly applied equal but opposite normal stresses on crack faces causes the separation of the crack faces. Laplace and Fourier transforms have been employed to convert the problem to a Fredholm integral equation of second kind in the Laplace transform plane which has been solved by perturbation method. Stress intensity factor has been computed numerically by Laplace inversion using Zakian’s algorithm and plotted graphically against time for different isotropic materials.

Appendix

In this algorithm f(t) is computed as a sum of weighted evaluations of F(p).

$$\begin{aligned} \displaystyle f(t)=\sum _{i=1}^NK_iF(p_i), \end{aligned}$$

where the values of $K_i, p_i$ and N are dictated by a particular method. The development of Zakian’s algorithm is given in Rice et al. [25]. The time function can be related to a finite series of exponential functions

$$\begin{aligned} \displaystyle \sum _{i=1}^N K_ie^{\alpha _it} \end{aligned}$$

Table 1 Complex constants

The significance of this specification is that Zakian’s algorithm is very accurate for over-damped and slightly under-damped systems. But it is not accurate for systems with prolonged oscillations.

Given F(p) and a value of time t, the following equations implements Zakian’s algorithm and allows us to calculate the numerical value of f(t).

$$\begin{aligned} \displaystyle f(t)=\frac{2}{t}\sum _{i=1}^{5}{\textit{REAL}}\left( K_iF \left( \frac{\alpha _i}{t}\right) \right) \end{aligned}$$

Table 1 gives the set of five complex constants for $\alpha _i$ and $K_i$.

Zakian’s algorithm is simple to implement and computes quickly. But note that the initial value of f(t) at $t=0$, cannot be computed. Also, when there are oscillatory systems, f(t) becomes inaccurate after approximately the second cycle.