Introduction

Infectious diseases have been part of humanity history since ancient times, and historically, one can remember the great plague, also known as Black Death, which in the 14th century killed millions in Europe (Benedictow 2005; Prentice and Rahalison 2007). Six centuries has passed until the Great influenza pandemic, or the Spanish Flu emerged. Several influenza epidemic waves between 1918 and 1920 left behind millions of fatal victims which precise number is not known (Nickol and Kindrachuk 2019)

Mycobacterium tuberculosis is the infectious agent of Tuberculosis (TB). It is a highly infectious disease of global public health concern, being among the top ten leading causes of death from a single disease according to the World Health Organization, (WHO 2001). However, of all people infected with TB, approximately only \(10\%\) will progress to the disease active state. Out of these \(10\%\), only \(5\%\) will be sick in a period of two years, what is called fast progression. The remaining individuals, for some reason, will have the pathogens activated at some point of their lives, i.e., slow progression (CDC 2000; Blower et al. 1995). Then, though the number of TB human hosts is large, most of them will remain latent for all their lifetime.

Severe acute respiratory syndrome that first emerged in December 2019 in Wuhan, China, became the newest pandemic. Its causative agent is the coronavirus SARS-CoV-2 (Zu et al. 2020; Andersen et al. 2020; Wu et al. 2020). From this date on, SARS-CoV-2 viruses have spread in more than 190 countries, and approximately 230 million cases have been recorded as reported by WHO (COVID-19 2021). Prior to the availability of pharmaceutical measures (treatment and vaccination), for some time, the world has relied on non therapeutic interventions such as quarantine, face masks wearing, self isolation, social/physical distancing, and lock down. Since the end of 2020, several vaccines have been approved to start a worldwide immunization campaign, and countries with increasing immunization rates already have the number of SARS-CoV-2 deaths drastically reduced (Swan et al. 2021), despite the multiple strains that have emerged so far.

Infectious diseases threats are constantly evolving with continuous changes in disease landscape (Crisan-Dabija et al. 2020; Ewald 2004; Schrag and Wiener 1995). The emergence of SARS-CoV-2 pandemic and its geographical overlap with TB, a long-standing diseases is of great public health concerns (Crisan-Dabija et al. 2020). On the other hand, SARS-CoV-2 displays clinical and radiological similarities with pulmonary tuberculosis (Vanzetti et al. 2020). Both diseases can have a deadly outcome if not diagnosed and treated timely (Tadolini et al. 2020). SARS-CoV-2 has been the main concern at the heart of ravaging pandemic, and overlapping respiratory diseases also termed the great imitators such as tuberculosis within differential diagnoses should not be forgotten Petrone et al. (2021). While tuberculosis is a potential risk factor for SARS-CoV-2 patients through severity, morbidity and mortality (Tamuzi et al. 2020), it could also impact the ability to mount a strong response in co-infected subjects due to their symptoms similarities (Petrone et al. 2021). Thus, due their similar clinical manifestations, TB testing should be performed for SARS-CoV-2 patients especially in TB-burden countries such as Indonesia (Tolossa et al. 2021). In fact, the it has been noted that SARS-CoV-2 and TB are a cursed duo that needs immediate attention (TB/COVID-19 Global Group 2022).

The first study describing the co-infection of tuberculosis and SARS-CoV-2 was published by Khurana and Aggarwal (2020). This co-infection has also been reported in Motta et al. (2020), Stochino et al. (2020), Martinez Orozco et al. (2020), Yao et al. (2020) and Mishra et al. (2021). Co-existence of TB and SARS-CoV-2 is almost evident due to the their worldwide geographic overlap (Khurana and Aggarwal 2020). This co-infection poses a great challenge due to their differential diagnosis (Tadolini et al. 2020). Also, active TB patients are quite vulnerable to potential infection with SARS-CoV-2 due to the chronic nature of TB, and their synergistic impact on socio-economic life worldwide (Khurana and Aggarwal 2020), with health systems in poor and overcrowded areas most vulnerable (Wingfield et al. 2018). In fact, mortality due to both diseases is about 12.3% in patients with dual infections, which is higher than isolated SARS-CoV-2 deaths (Guan et al. 2020). Morbidity and mortality are a concern in patients with other co-morbidities such as HIV, dengue, diabetes, etc., among others (Wingfield et al. 2018; Sarinoglu et al. 2020; Tamuzi et al. 2020). Thus, lethal synergism of SARS-CoV-2 and TB could contribute to severe cases (Crisan-Dabija et al. 2020; Visca et al. 2021).

TB high burden countries worldwide (including Indonesia) account for about 80% of the world’s tuberculosis infections (WHO 2021). Indonesia has been hit with more than 4 million reported SARS-CoV-2 infections and 144 thousand deaths (WHO 2021). Consequently, due to the large geographic overlap of the two diseases (TB and SARS-CoV-2), synergistic epidemics (or syndemics) cannot be ruled out. For this reason, we selected Indonesia as our case study country.

Theoretical studies on SARS-CoV-2 dynamics abound in the literature (Bandekar and Ghosh 2021; Asamoah et al. 2020; Nkwayep et al. 2020; Wang et al. 2020; Asamoah et al. 2022; Kucharski et al. 2020; Ferguson et al. 2020; Maier and Brockmann 2020). However, we are interested in its co-dynamics with tuberculosis which is also a disease of global public health concern. Recently, some co-infection models for SARS-CoV-2 and TB have been studied (Goudiaby et al. 2022; Mekonen et al. 2022; Bandekar and Ghosh 2022). For instance, Goudiaby et al. (2022) investigated in general settings the impact of implementing optimal control measures in a co-infection of SARS-CoV-2 and tuberculosis model. They considered 5 controls which do not include vaccination, but instead they included control against co-infection with a second disease. On the other hand, Bandekar and Ghosh (2021) dwelled more into the sensitivity analyses of a tuberculosis and SARS-CoV-2 co-infection model, but they only considered two control measures, early SARS-CoV-2 detection and TB treatment. There are key distinct features of our proposed model with that in Goudiaby et al. (2022). For example, their model has ten compartment depending on individual’s disease status compared to the nine classes in ours. However, our proposed model is seemingly the first theoretical modeling work to investigate the co-dynamics of tuberculosis and SARS-CoV-2 with key control strategies to mitigate the rapid spread of these two diseases in a specific country, using real data. Also, our model is more complex as we considered most of the possible transmission routes and recovery from one or both of the diseases. It complements previous tuberculosis and SARS-CoV-2 co-infection models with a validation performed through a model fit to the reported Indonesia SARS-CoV-2 cases using the fmincon function in the MATLAB Optimization Toolbox. Finally, we also investigated the impact of various control strategies on the co-interaction of both diseases.

The following outlines how the rest of this paper is organized. Details on the formulation of the proposed co-dynamics model of SARS-CoV-2 and TB is given in Sect. 2. The invariant region where the model is biological relevant is presented in Sect. 2.1. Theoretical results such as stability and bifurcation analysis of the sub-models (TB and SARS-CoV-2) equilibrium points are presented in Sect. 3. To mitigate the spread of these two diseases, time variant controls are incorporated into the full model. The optimal control problem is then analyzed using the well-known Pontragyn’s Maximum Principle in Sect. 4. Numerical simulations to support the analytical results are provided in Sect. 5, while Sect. 6 concludes the paper.

Model formulation

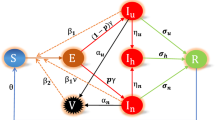
Consider a homogeneously mixing population, that is, individuals have equal probability of contact with one another. Both diseases transmission dynamics are described via a deterministic compartmental model. Based on individuals’ disease status, at any time t, the total population N(t) is subdivided into nine compartments: unvaccinated susceptibles \({\mathcal {S}}(t)\), vaccinated susceptibles, \(({\mathcal {V}}(t))\), SARS-CoV-2 infected individuals \({\mathcal {I}}(t)\), recovered from SARS-CoV-2 \({\mathcal {R}}(t)\), TB infected (in latent stage) \({\mathcal {E}}(t)\), TB infected (in active stage) \({\mathcal {A}}(t)\), TB treatment class \({\mathcal {T}}(t)\), individuals infected with latent TB and SARS-CoV-2 \({\mathcal {I}}_{\textsc {e}}(t)\), and individuals infected with both active TB and SARS-CoV-2 \({\mathcal {I}}_{\textsc {a}}(t)\).

The parameter \(\Psi _{\textsc {h}}\) represents the inflow (or recruitment) into the susceptible class \({\mathcal {S}}\). Individuals in this group are reduced at the rate, \(\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\) when infected with SARS-CoV-2, and are also reduced at the rate \(\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\) when infected with TB. The parameter \(\eta ~(\eta \ge 1)\) denotes the potential high infectivity due to co-infection with TB. All persons in each epidemiological states suffer natural death at the rate \(\omega _{\textsc {h}}\). Individuals infected with SARS-CoV-2 can get infected with TB at the rate \(\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\). Those already infected with TB can get additional infection with SARS-CoV-2 at the rate \(\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\). Infected individuals can suffer SARS-CoV-2-induced death at the rate \(\delta _1\) or TB induced death at the rate \(\delta _2\). Individuals co-infected with both diseases can also suffer disease-induced death, either due to SARS-CoV-2 or TB. Co-infected individuals can equally recover either from SARS-CoV-2 or TB. Upon recovery from SARS-CoV-2, an individual gains immunity against re-infection. However, there is possibility of infection with TB at the rate \(\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\). Upon recovery from TB, an individual can either get re-infected with TB at the rate \(\varpi \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\) (where \(\varpi\) is the TB re-infection rate) or get infected with SARS-CoV-2 at the rate \(\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\). All other transitions in the model are described in Eq. (1), with the model flow diagram shown in Fig. 1. The description of the model parameters, their values and the source are provided in Table 1.

From the aforementioned, we derive the following non-linear system of ordinary differential equations

Fig. 1
figure 1

SARS-CoV-2 and tuberculosis model flow diagram

Full size image
$$\begin{aligned} \begin{aligned} \frac{{\text {d}} {\mathcal {S}}}{{\text {d}}t}&= \Psi _{\textsc {h}} - \left( \frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}+ \omega _{\textsc {h}} + \lambda + \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {S}},\\ \frac{{\text {d}} {\mathcal {V}}}{{\text {d}}t}&= \lambda {\mathcal {S}} - \left( (1-\chi )\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}+ \omega _{\textsc {h}} + \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {V}},\\ \frac{{\text {d}} {\mathcal {I}}}{{\text {d}}t}&= \frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}[{\mathcal {S}} + (1-\chi ){\mathcal {V}} + {\mathcal {T}}] + \Lambda _{\textsc {2}}{\mathcal {I}}_{\textsc {a}} \\&\quad - \left( \phi _{\textsc {1}} + \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} + \omega _{\textsc {h}} + \delta _{\textsc {1}} \right) {\mathcal {I}},\\ \frac{{\text {d}} {\mathcal {R}}}{{\text {d}}t}&= \phi _{\textsc {1}}{\mathcal {I}} - \left( \omega _{\textsc {h}} + \kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} \right) {\mathcal {R}},\\ \frac{{\text {d}} {\mathcal {E}}}{{\text {d}}t}&= (1 - \vartheta _{\textsc {1}})\kappa _{\textsc {2}}\frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) + \xi _1 {\mathcal {I}}_{\textsc {e}}\\&\quad - \left( \psi _{1}\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} + \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) {\mathcal {E}},\\ \frac{{\text {d}} {\mathcal {A}}}{{\text {d}}t}&= \vartheta _{\textsc {1}}\kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} + {\mathcal {V}}+ {\mathcal {R}} + \varpi {\mathcal {T}}) + \gamma _{\textsc {1}}{\mathcal {E}} + \xi _2 {\mathcal {I}}_{\textsc {a}} \\&\quad - \left( \Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} + \psi _{2}\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\right) {\mathcal {A}},\\ \frac{{\text {d}} {\mathcal {T}}}{{\text {d}}t}&= \Lambda _{\textsc {1}}{\mathcal {A}} \\&\quad - \left( \frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} + \varpi \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} + \omega _{\textsc {h}}\right) {\mathcal {T}},\\ \frac{{\text {d}} {\mathcal {I}}_{\textsc {e}}}{{\text {d}}t}&= (1-\vartheta _{\textsc {2}})\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} + \psi _{1}\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {E}} \\&\quad - (\gamma _{\textsc {2}} + \omega _{\textsc {h}} + \xi _1 + \delta _{\textsc {1}} ){\mathcal {I}}_{\textsc {e}},\\ \frac{{\text {d}} {\mathcal {I}}_{\textsc {a}}}{{\text {d}}t}&= \vartheta _{\textsc {2}}\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} \\&\quad + \gamma _{\textsc {2}}{\mathcal {I}}_{\textsc {e}} + \psi _{2}\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {A}} - (\Lambda _{\textsc {2}} + \omega _{\textsc {h}} + \xi _2 + \delta _{\textsc {3}}){\mathcal {I}}_{\textsc {a}},\\ \end{aligned} \end{aligned}$$
(1)

with the initial conditions

$$\begin{aligned} \begin{array}{ll} {\mathcal {S}}(0) \ge 0,\;{\mathcal {V}}(0) \ge 0,\;{\mathcal {I}}(0) \ge 0,\;{\mathcal {R}}(0) \ge 0,\;{\mathcal {E}}(0) \ge 0,\;{\mathcal {A}}(0) \ge 0,\;{\mathcal {T}}(0) \ge 0,\; {\mathcal {I}}_{\textsc {e}}(0) \ge 0,\; {\mathcal {I}}_{\textsc {a}}(0) \ge 0. \end{array} \end{aligned}$$
(2)

Invariant region

The model system (1) is biological relevant, that is epidemiologically and mathematically well-posed, when all model parameters and state variables are non-negative for all time \(t\ge 0\). The SARS-CoV-2 and Tuberculosis transmission dynamic model (1) will therefore be analyzed in a suitable feasible region, obtained as follows.

Lemma 2.1

The region \(\Omega = \left\{ ( {\mathcal {S}},{\mathcal {V}},{\mathcal {I}},{\mathcal {R}},{\mathcal {E}},{\mathcal {A}},{\mathcal {T}}, {\mathcal {I}}_{\textsc {e}}, {\mathcal {I}}_{\textsc {a}} ) \in {\mathbb {R}}_+^9 : N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}} \right\}\) is positively-invariant for the model system (1) with non-negative initial conditions in \({\mathbb {R}}_+^9\).

Proof

Let, \(( {\mathcal {S}},{\mathcal {V}},{\mathcal {I}},{\mathcal {R}},{\mathcal {E}},{\mathcal {A}},{\mathcal {T}}, {\mathcal {I}}_{\textsc {e}}, {\mathcal {I}}_{\textsc {a}} ) \in {\mathbb {R}}_+^9\) be any solution of the model system (1). Then, adding all the differential equations of the model system (1), we have

$$\begin{aligned} \frac{{\text {d}}N}{{\text {d}}t} = \Psi _{\textsc {h}}-\omega _{\textsc {h}}N-[({\mathcal {I}} +{\mathcal {I}}_{\textsc {e}})\delta _{\textsc {1}}+ \delta _{\textsc {2}}{\mathcal {A}}+\delta _{\textsc {3}}{\mathcal {I}}_{\textsc {a}}]\le \Psi _{\textsc {h}}-\omega _{\textsc {h}}N. \end{aligned}$$

Owing to the conditions (2) that guarantee \(N(0)\ge 0\), and since the region \(\Omega\) is positively-invariant and attracting, \(N(t)\ge 0\) is bounded \(\forall t > 0\). By applying Birkhoff and Rota’s comparison Theorem of differential inequality (Birkhoff and Rota 1989), we can show using the theory of integration that

$$\begin{aligned} N(t) \leqslant N(0)e^{-\omega _{\textsc {h}}t}+\dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}(1-e^{-\omega _{\textsc {h}}t}). \end{aligned}$$

In particular, \(N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\) if \(N(0) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\). Thus, the conclusion follows from Hethcote (2000) that the region \(\Omega\) is positively invariant. It is then sufficient to consider the dynamics of the flow generated by the model system (1) in \(\Omega\). In this region, solutions of the model system (1) with initial conditions in \(\Omega\) will remain in \(\Omega\) for all time \(t>0\). \(\square\)

Table 1 Description of the model parameters
Full size table

Model analysis

For mathematical tractability and convenience and the fact that the full model dynamics is driven by that of its sub-models, we investigate the dynamics of the two sub-models.

SARS-CoV-2 sub-model

Set \({\mathcal {E}}={\mathcal {A}}={\mathcal {T}}= {\mathcal {I}}_{\textsc {e}}= {\mathcal {I}}_{\textsc {a}} =0\) in (1), we obtain the following SARS-CoV-2 only sub-model.

$$\begin{aligned} \begin{aligned} \frac{{\text {d}} {\mathcal {S}}}{{\text {d}}t}&= \Psi _{\textsc {h}} - \left( \frac{\kappa _{\textsc {1}}{\mathcal {I}}}{N}+ \omega _{\textsc {h}} + \lambda \right) {\mathcal {S}},\\ \frac{{\text {d}} {\mathcal {V}}}{{\text {d}}t}&= \lambda {\mathcal {S}} - \left( (1-\chi )\frac{\kappa _{\textsc {1}}{\mathcal {I}}}{N}+ \omega _{\textsc {h}} \right) {\mathcal {V}},\\ \frac{{\text {d}} {\mathcal {I}}}{{\text {d}}t}&= \frac{\kappa _{\textsc {1}}{\mathcal {I}}}{N}[{\mathcal {S}} + (1-\chi ){\mathcal {V}}] - \left( \phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}} \right) {\mathcal {I}},\\ \frac{{\text {d}} {\mathcal {R}}}{{\text {d}}t}&= \phi _{\textsc {1}}{\mathcal {I}} - \omega _{\textsc {h}} {\mathcal {R}}, \end{aligned} \end{aligned}$$
(3)

with \(N(t)={\mathcal {S}}(t) +{\mathcal {V}}(t) +{\mathcal {I}}(t) + {\mathcal {R}}(t).\)

The sub-model CovidModel feasible region is given by \(\Omega _{\textsc {c}} = \lbrace ( {\mathcal {S}},{\mathcal {V}},{\mathcal {I}},{\mathcal {R}}) \in {\mathbb {R}}_+^4: N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\rbrace .\)

Positivity and boundedness of solutions

Positivity Recall that the model variables represent human population, and it can be shown as in the case of the full model system (1) above that the solution of the sub-model system (3) with the given positive initial conditions will remain non-negative for all time \(t>0\).

Lemma 3.1

If \({\mathcal {S}}(0) \ge 0,\;{\mathcal {V}}(0) \ge 0,\;{\mathcal {I}}(0) \ge 0\) and \({\mathcal {R}}(0) \ge 0\), then the solutions of the model system (3) remain non-negative for all time \(t > 0\).

Proof

From the first two equation of (3), we have

$$\begin{aligned} \begin{aligned} \frac{{\text {d}} {\mathcal {S}}}{{\text {d}}t} |_{{\mathcal {S}} = 0,{\mathcal {V}}\ge 0,{\mathcal {I}}\ge 0,{\mathcal {R}}\ge 0,{\mathcal {E}}\ge 0,{\mathcal {A}}\ge 0,{\mathcal {T}}\ge 0,{\mathcal {I}}_{\textsc {e}}\ge 0,{\mathcal {I}}_{\textsc {a}}\ge 0} = \Psi _{\textsc {h}} > 0,\\ \frac{{\text {d}} {\mathcal {V}}}{{\text {d}}t} |_{{\mathcal {S}}\ge 0,{\mathcal {V}} = 0,{\mathcal {I}}\ge 0,{\mathcal {R}}\ge 0,{\mathcal {E}}\ge 0,{\mathcal {A}}\ge 0,{\mathcal {T}}\ge 0,{\mathcal {I}}_{\textsc {e}}\ge 0,{\mathcal {I}}_{\textsc {a}}\ge 0} = \lambda {\mathcal {S}} \ge 0. \end{aligned} \end{aligned}$$
(4)

All the remaining seven equations can be written similar to the second equation above, and since the transfer rates are non-negative at the boundary of the positive cone \({\mathbb {R}}_+^9\), the direction of the vector field will point inward Guo and Li (2021). That is, the trajectory of all solutions remains in the positively invariant region when starting from a non-negative point. Hence, the proof. \(\square\)

Boundedness

Lemma 3.2

All solutions of the SARS-CoV-2 only model (3) with non-negative initial conditions are bounded, with \(N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\) for all time \(t > 0\).

Proof

Adding all the equations in (3), we obtain

$$\begin{aligned} \frac{{\text {d}} N}{{\text {d}}t} = \Psi _{\textsc {h}} -\omega _{\textsc {h}}N - \delta _{\textsc {1}}{\mathcal {I}}\;\Rightarrow \;\frac{{\text {d}}N}{{\text {d}}t} \le \Psi _{\textsc {h}} -\omega _{\textsc {h}}N. \end{aligned}$$

Lemma (3.1) ensures that \(N(t)\ge 0\) for all time \(t > 0\).

Clearly, \(\displaystyle \lim _{t\rightarrow \infty } \mathrm{sup}\; N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\). Hence, \(0\leqslant N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}}\) for all time \(t > 0\). This implies that \({\mathcal {S}}(t),\; {\mathcal {V}}(t),\; {\mathcal {I}}(t),\) and \({\mathcal {R}}(t)\) are all bounded above by the lim sup and below by 0. \(\square\)

Computation of the Reproduction Numbers \({\mathcal {R}}_{\textsc {0c}}\) and \({\mathcal {R}}_{\textsc {vc}}\)

The threshold parameter \({\mathcal {R}}_{\textsc {0c}}\) denotes the basic reproduction number of system (3) when no vaccination program is implemented, while \({\mathcal {R}}_{\textsc {vc}}\) is the vaccination-induced reproduction number representing infections newly generated by an infected in a community in which a vaccination program is being implemented. The DFE of the SARS-CoV-2 only sub-model (3) is given by

$$\begin{aligned} E_{\textsc {c}}^0=({\mathcal {S}}^0,\;{\mathcal {V}}^0,\;{\mathcal {I}}^0,\;{\mathcal {R}}^0)=\left( \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}+\lambda },\dfrac{\Psi _{\textsc {h}}\lambda }{\omega _{\textsc {h}}(\omega _{\textsc {h}}+\lambda )}, 0,0 \right) . \end{aligned}$$

The threshold quantity, \({\mathcal {R}}_{\textsc {vc}}\) derived using the next generation matrix operator (van den Driessche and Watmough 2002), is the spectral radius of the matrix \(FV^{-1}\) at the DFE \((E_{\textsc {c}}^0)\), with F and V respectively given by

$$\begin{aligned} F= \left[ {\begin{array}{cc} \frac{\kappa _{\textsc {1}}[{\mathcal {S}}^0 + (1-\chi ){\mathcal {V}}^0]}{N} &{} 0 \\ 0 &{} 0 \\ \end{array}}\right] = \left[ {\begin{array}{cc} \frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda } &{} 0 \\ 0 &{} 0 \\ \end{array}}\right] , \end{aligned}$$

and

$$\begin{aligned} V= \left[ {\begin{array}{cc} \phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}} &{} 0 \\ -\phi _{\textsc {1}} &{} \omega _{\textsc {h}} \\ \end{array}}\right] . \end{aligned}$$

The vaccination-induced reproduction number of the SARS-CoV-2 only sub-model (3) is given by

$$\begin{aligned} {\mathcal {R}}_{\textsc {vc}}=\rho (FV^{-1})=\frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{(\omega _{\textsc {h}} + \lambda )(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})}. \end{aligned}$$
(5)

The basic reproduction number when there is no vaccination (\(\lambda =0\)) is given by

$$\begin{aligned} {\mathcal {R}}_{\textsc {0c}}=\frac{\kappa _{\textsc {1}}}{\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}}}. \end{aligned}$$
(6)

Note that

$$\begin{aligned} {\mathcal {R}}_{\textsc {vc}}=\frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{(\omega _{\textsc {h}} + \lambda )(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})}={\mathcal {R}}_{\textsc {0c}}\frac{[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda }={\mathcal {R}}_{\textsc {0c}}\zeta , \end{aligned}$$

where \(\zeta =\frac{[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda }.\) Since \(\zeta <1,\) as expected \({\mathcal {R}}_{\textsc {vc}}<{\mathcal {R}}_{\textsc {0c}}\). The higher the vaccine efficacy (large value of \(\chi \in (0, 1]\)), the smaller is the value of \(\zeta\). The parameter \(\zeta\) which depends on the rate of vaccination and vaccine efficacy represents the effect of SARS-CoV-2 vaccine implementation in reducing the vaccine-induced reproduction number.

Local stability of the SARS-CoV-2 only DFE

The local stability of the disease-free equilibrium (DFE) of the SARS-CoV-2 only sub-model (3) is determined by its vaccination-induced reproduction number \(({\mathcal {R}}_{\textsc {vc}})\). The Jacobian matrix of the SARS-CoV-2 only model (3) at the DFE is given by

$$\begin{aligned} J(E_{\textsc {c}}^0)= \left[ {\begin{array}{cccc} -(\omega _{\textsc {h}} +\lambda ) &{} 0 &{} -\frac{\kappa _{\textsc {1}}\omega _{\textsc {h}}}{\omega _{\textsc {h}} + \lambda } &{} 0 \\ \lambda &{} -\omega _{\textsc {h}}&{}-\frac{\kappa _{\textsc {1}} (1-\chi )\lambda }{\omega _{\textsc {h}} + \lambda }&{}0 \\ 0&{}0&{}\frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda }-(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})&{}0\\ 0&{}0&{} \phi _{\textsc {1}} &{} -\omega _{\textsc {h}} \\ \end{array}}\right] , \end{aligned}$$

and the corresponding eigenvalues are \(\lambda _{\textsc {1}}=-(\omega _{\textsc {h}} +\lambda ),\; \lambda _{\textsc {2}}=-\omega _{\textsc {h}},\; \lambda _{\textsc {3}}=\frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda }-(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})\) and \(\lambda _{\textsc {4}}= -\omega _{\textsc {h}}.\) The DFE is locally asymptotically stable if all eigenvalues of the Jacobian matrix have negative real parts. The following eigenvalues \(\lambda _{\textsc {1}},\; \lambda _{\textsc {2}}\) and \(\lambda _{\textsc {4}}\) are negative. Thus, the local stability of the DFE \((E_{\textsc {c}}^0)\) depends on the sign of \(\lambda _{\textsc {3}}.\) That is,

$$\begin{aligned} \lambda _{\textsc {3}}=\frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{\omega _{\textsc {h}} + \lambda }-(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}}) =(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})\left[ \frac{\kappa _{\textsc {1}}[\omega _{\textsc {h}} + (1-\chi )\lambda ]}{(\omega _{\textsc {h}} + \lambda )(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})}-1\right] =(\phi _{\textsc {1}} + \omega _{\textsc {h}} + \delta _{\textsc {1}})\left[ {\mathcal {R}}_{\textsc {vc}}-1\right] \end{aligned}$$

Thus, the following result have been established.

Lemma 3.3

The DFE of the SARS-CoV-2 only sub-model (3) is locally asymptotically stable if \({\mathcal {R}}_{\textsc {vc}}<1\), and unstable otherwise.

Proof

Since all the eigenvalues of \(J(E_{\textsc {c}}^0)\) are negative except \(\lambda _{\textsc {3}},\) it follows that the DFE is locally asymptotically stable whenever \(\lambda _{\textsc {3}}<0\), and unstable if \(\lambda _{\textsc {3}}>0.\) Because \(\lambda _{\textsc {3}}<0\) if and only if \({\mathcal {R}}_{\textsc {vc}}<1\), the result follows. \(\square\)

TB only sub-model

By setting \({\mathcal {V}}={\mathcal {I}}={\mathcal {R}}= {\mathcal {I}}_{\textsc {e}}= {\mathcal {I}}_{\textsc {a}} =0\) in (1), the following TB only sub-model is obtained.

$$\begin{aligned} \begin{aligned} \frac{{\text {d}} {\mathcal {S}}}{{\text {d}}t}&= \Psi _{\textsc {h}} - \left( \frac{\kappa _{\textsc {2}}{\mathcal {A}} }{N}+\omega _{\textsc {h}}\right) {\mathcal {S}},\\ \frac{{\text {d}} {\mathcal {E}}}{{\text {d}}t}&= (1 - \vartheta _{\textsc {1}})\frac{\kappa _{\textsc {2}}{\mathcal {A}} }{N}({\mathcal {S}} + \varpi {\mathcal {T}}) - \left( \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) {\mathcal {E}},\\ \frac{{\text {d}} {\mathcal {A}}}{{\text {d}}t}&= \vartheta _{\textsc {1}} \frac{\kappa _{\textsc {2}}{\mathcal {A}}}{N}({\mathcal {S}} + \varpi {\mathcal {T}}) + \gamma _{\textsc {1}}{\mathcal {E}} - \left( \Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} \right) {\mathcal {A}},\\ \frac{{\text {d}} {\mathcal {T}}}{{\text {d}}t}&= \Lambda _{\textsc {1}}{\mathcal {A}} - \left( \varpi \frac{\kappa _{\textsc {2}}{\mathcal {A}}}{N} + \omega _{\textsc {h}}\right) {\mathcal {T}}, \end{aligned} \end{aligned}$$
(7)

with \(N(t)={\mathcal {S}}(t) +{\mathcal {E}}(t) +{\mathcal {A}}(t) +{\mathcal {T}}(t).\) Analogously to Lemma 2.1, it can be shown that the region

$$\begin{aligned} \Omega _{\textsc {t}} = \lbrace ( {\mathcal {S}},{\mathcal {E}},{\mathcal {A}},{\mathcal {T}} ) \in {\mathbb {R}}_+^4 : N(t) \leqslant \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}} \rbrace . \end{aligned}$$

is positively invariant. Thus, we consider the dynamics of the TB only sub-model (7) in \(\Omega _{\textsc {t}}\).

Local stability of the DFE of TB only sub-model

The DFE of the TB only sub-model (7) is given by

$$\begin{aligned} E_{\textsc {t}}^0=({\mathcal {S}}^0,\;{\mathcal {E}}^0,\;{\mathcal {A}}^0,\;{\mathcal {T}}^0)=\left( \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}},0, 0,0 \right) , \end{aligned}$$

and the associated matrices F and V are respectively given by

$$\begin{aligned} F= \left[ {\begin{array}{cc} 0 &{}(1 - \vartheta _{\textsc {1}})\frac{\kappa _{\textsc {2}} }{N^0}({\mathcal {S}}^0 + \varpi {\mathcal {T}}^0) \\ 0 &{} \vartheta _{\textsc {1}}\frac{\kappa _{\textsc {2}} }{N^0}({\mathcal {S}}^0 + \varpi {\mathcal {T}}^0) \\ \end{array}}\right] = \left[ {\begin{array}{cc} 0 &{} (1 - \vartheta _{\textsc {1}})\kappa _{\textsc {2}} \\ 0 &{} \vartheta _{\textsc {1}}\kappa _{\textsc {2}} \\ \end{array}}\right] , \end{aligned}$$

and

$$\begin{aligned} V= \left[ {\begin{array}{cc} \gamma _{\textsc {1}} + \omega _{\textsc {h}} &{} 0 \\ -\gamma _{\textsc {1}} &{} \Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} \\ \end{array}}\right] . \end{aligned}$$

From van den Driessche and Watmough (2002), the basic reproduction number of the TB only sub-model (7) is given by

$$\begin{aligned} {\mathcal {R}}_{\textsc {0t}}=\frac{\kappa _{\textsc {2}}\left( \gamma _{\textsc {1}}+ \vartheta _{\textsc {1}} \omega _{\textsc {h}} \right) }{(\gamma _{\textsc {1}} + \omega _{\textsc {h}} )(\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}})}, \end{aligned}$$
(8)

and from Theorem 2 in van den Driessche and Watmough (2002), the following result holds.

Lemma 3.4

The DFE of the TB only sub-model (7) is locally asymptotically stable if \({\mathcal {R}}_{\textsc {0t}}<1\), and unstable if \({\mathcal {R}}_{\textsc {0t}}>1\).

From Lemma 3.4, TB could be eliminated when \({\mathcal {R}}_{\textsc {0t}}<1\) (if the initial size of the sub-populations of the model are in the basin of attraction of \(E_{\textsc {t}}^0\)). Since at \({\mathcal {R}}_{\textsc {0t}}=1\), the DFE \(E_{\textsc {t}}^0\) of the TB only sub-model (7) may undergo backward bifurcation (Wangari and Stone 2018; Sulayman et al. 2021), we wish to investigate (1) whether the sub-model (7) could also exhibit that phenomenon (2) the forward/transcritical or backward/subcritical direction of the bifurcation.

Bifurcation analysis

Using the Centre manifold theory (Castillo-Chavez and Song 2004), let \(x = (x_{1}, x_{2}, x_{3}, x_{4})^{T} = ({\mathcal {S}}, {\mathcal {E}}, {\mathcal {A}}, {\mathcal {T}})^{T}.\) Next, rewrite the TB-only sub-model (7) as \(\dfrac{{\text {d}}x}{{\text {d}}t} = f(x)\), with \(f(x)=(f_{1}(x), f_{2}(x),f_{3}(x), f_{4}(x))\). Thus,

$$\begin{aligned} \begin{aligned} \dfrac{{\text {d}}x_{1}}{{\text {d}}t}= f_{1}(x)&= \Psi _{\textsc {h}} - \left( \frac{\kappa _{\textsc {2}}x_{3} }{x_{1}+x_{2}+x_{3}+x_{4}}+\omega _{\textsc {h}}\right) x_{1},\\ \frac{{\text {d}} x_{2}}{{\text {d}}t}=f_{2}(x)&= (1 - \vartheta _{\textsc {1}})\frac{\kappa _{\textsc {2}}x_{3} }{x_{1}+x_{2}+x_{3}+x_{4}}(x_{1} + \varpi x_{4}) - \left( \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) x_{2},\\ \frac{{\text {d}} x_{3}}{{\text {d}}t}=f_{3}(x)&= \vartheta _{\textsc {1}} \frac{\kappa _{\textsc {2}}x_{3}}{x_{1}+x_{2}+x_{3}+x_{4}}(x_{1} + \varpi x_{4}) + \gamma _{\textsc {1}}x_{2} - \left( \Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} \right) x_{3},\\ \frac{{\text {d}} x_{4}}{{\text {d}}t} =f_{4}(x)&= \Lambda _{\textsc {1}}x_{3} - \left( \varpi \frac{\kappa _{\textsc {2}}x_{3}}{x_{1}+x_{2}+x_{3}+x_{4}} + \omega _{\textsc {h}}\right) x_{4}. \end{aligned} \end{aligned}$$
(9)

The Jacobian of system (9) at the DFE \(E_{\textsc {t}}^0 = \left( \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}},0, 0,0 \right)\) is given by

$$\begin{aligned} J(E_{\textsc {t}}^0 )=\left( \begin{array}{cccccccc} -\omega _{\textsc {h}} &{} 0 &{} -\kappa _{\textsc {2}} &{} 0\\ \\ 0 &{} - \left( \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) &{} (1 - \vartheta _{\textsc {1}})\kappa _{\textsc {2}}&{}0\\ \\ 0&{} \gamma _{\textsc {1}} &{} \vartheta _{\textsc {1}}\kappa _{\textsc {2}}- \left( \Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} \right) &{}0\\ \\ 0&{}0&{}\Lambda _{\textsc {1}}&{}- \omega _{\textsc {h}} \end{array} \right) . \end{aligned}$$

Choosing the bifurcation parameter as \(\kappa _{\textsc {2}}\), and setting \({\mathcal {R}}_{\textsc {0t}}=1\), we obtain

$$\begin{aligned} \kappa _{\textsc {2}}= \kappa _{\textsc {2}}^{*} = \dfrac{(\gamma _{\textsc {1}} + \omega _{\textsc {h}} )(\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}})}{(1 - \vartheta _{\textsc {1}})\gamma _{\textsc {1}}+ \vartheta _{\textsc {1}}(\gamma _{\textsc {1}} + \omega _{\textsc {h}}) } = \dfrac{(\gamma _{\textsc {1}} + \omega _{\textsc {h}} )(\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}})}{\gamma _{\textsc {1}}+ \vartheta _{\textsc {1}} \omega _{\textsc {h}} }. \end{aligned}$$
(10)

By applying Theorem 4.1 in Castillo-Chavez and Song (2004), we can show that system (9) may undergo forward or a backward bifurcation when \({\mathcal {R}}_{\textsc {0t}}=1\). We consider the DFE \(E_{\textsc {t}}^0 = \left( \dfrac{\Psi _{\textsc {h}}}{\omega _{\textsc {h}}},0, 0,0 \right)\) and \(\kappa _{\textsc {2}}= \kappa _{\textsc {2}}^{*} = \dfrac{(\gamma _{\textsc {1}} + \omega _{\textsc {h}} )(\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}})}{\gamma _{\textsc {1}}+ \vartheta _{\textsc {1}} \omega _{\textsc {h}} }=\dfrac{\alpha _{0}\alpha _{1}}{\alpha _{2}}\) at \({\mathcal {R}}_{\textsc {0t}}=1\), where \(\alpha _{0}=\gamma _{\textsc {1}} + \omega _{\textsc {h}},\; \alpha _{1}=\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}}\) and \(\alpha _{2}=\gamma _{\textsc {1}}+ \vartheta _{\textsc {1}} \omega _{\textsc {h}}\). By adopting the notation in Castillo-Chavez and Song (2004), the right eigenvector \(w= (w_{1}, w_{2}, w_{3}, w_{4})^{T}\) is defined such that \(J(E_{\textsc {t}}^0).w = 0\) at \(\kappa _{\textsc {2}} = \kappa _{\textsc {2}}^{*}\). Similarly, the left-eigenvector \(v= (v_{1}, v_{2}, v_{3}, v_{4})\) is such that \(v. J(E_{\textsc {t}}^0) = 0\). These eigenvectors w and v a respectively given by

$$\begin{aligned} w_{1} = -\dfrac{\alpha _{0}\alpha _{1}}{\omega _{\textsc {h}}\alpha _{2}} w_{3}, \; w_{2} = \dfrac{(1 -\vartheta _{\textsc {1}}) \alpha _{1}}{\alpha _{2}} w_{3},\; w_{3}=w_{3},\; w_{4}=\dfrac{\Lambda _{\textsc {1}}}{\omega _{\textsc {h}}}w_{3}, \end{aligned}$$

where

$$\begin{aligned} w_{3}>0. \end{aligned}$$

and

$$\begin{aligned} v_{1} = 0, \; v_{2} = \dfrac{\gamma _{\textsc {1}}}{\alpha _{0}} v_{3},\; v_{3}=v_{3}, v_{4}=0, \end{aligned}$$

where \(v_{3} > 0.\)

The condition \(v .w = 1.\) must be satisfied. That is,

$$\begin{aligned}&(w_{1}, w_{2}, w_{3}, w_{4})^{T} (v_{1}, v_{2}, v_{3}, v_{4}) = \dfrac{(1 -\vartheta _{\textsc {1}}) \alpha _{1}}{\alpha _{2}} \dfrac{\gamma _{\textsc {1}}}{\alpha _{0}} w_{3} v_{3} + w_{3} v_{3} \\&\quad = w_{3} v_{3} \left( 1 +\dfrac{(1 -\vartheta _{\textsc {1}}) \alpha _{1}\gamma _{\textsc {1}} }{\alpha _{0}\alpha _{2}}\right) =1. \end{aligned}$$

To determine the direction of the bifurcation, we compute and determine the sign of the bifurcation parameters a and b defined as

$$\begin{aligned} \begin{array}{lllll} a &{}= &{} \displaystyle \sum _{k,i,j=1}^{4}v_{k}w_{i}w_{j}\dfrac{\partial ^{2} f_{k}}{\partial x_{i} \partial x_{j}}(E_{\textsc {t}}^0,\kappa _{\textsc {2}}^{*}), \\ \end{array} \end{aligned}$$
(11)

and

$$\begin{aligned} \begin{array}{llllll} b &{}= &{} \displaystyle \sum _{k,j=1}^{4}v_{k}w_{j}\dfrac{\partial ^{2} f_{k}}{\partial x_{j} \partial \kappa _{\textsc {2}} }(E_{\textsc {t}}^0,\kappa _{\textsc {2}}^{*}). \\ \end{array} \end{aligned}$$
(12)

From the model system (9), we have

$$\begin{aligned}&\dfrac{\partial ^{2} f_{2}}{\partial x_{2} \partial x_{3} }=\dfrac{-(1 -\vartheta _{\textsc {1}})\kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\; \dfrac{\partial ^{2} f_{2}}{\partial x_{3} \partial x_{3} }=\dfrac{-2(1 -\vartheta _{\textsc {1}})\kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\\&\dfrac{\partial ^{2} f_{2}}{\partial x_{3} \partial x_{4} }=(1 -\vartheta _{\textsc {1}}) \dfrac{(\varpi -1)\kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\\&\dfrac{\partial ^{2} f_{3}}{\partial x_{2} \partial x_{3} }=\dfrac{-\vartheta _{\textsc {1}}\kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\\&\dfrac{\partial ^{2} f_{3}}{\partial x_{3} \partial x_{3} }=\dfrac{-2\vartheta _{\textsc {1}}\kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\; \dfrac{\partial ^{2} f_{4}}{\partial x_{3} \partial x_{4} }=\dfrac{-\varpi \kappa _{\textsc {2}}^{*}}{x_{1}^{*}},\\&\dfrac{\partial ^{2} f_{1}}{\partial x_{3} \partial \kappa _{\textsc {2}}}=-1,\; \dfrac{\partial ^{2} f_{2}}{\partial x_{3} \partial \kappa _{\textsc {2}}}=1 -\vartheta _{\textsc {1}},\; \dfrac{\partial ^{2} f_{3}}{\partial x_{3} \partial \kappa _{\textsc {2}}}=\dfrac{\vartheta _{\textsc {1}}}{x_{1}^{*}}. \end{aligned}$$

The other second partial derivatives in equations (11) and (12) are zero. Hence, since \(\vartheta _{\textsc {1}} \le 1\) and \(\varpi \le 1)\), after some algebraic manipulations and rearrangements,

$$\begin{aligned} \begin{array}{llllll} a &{}= &{} \displaystyle \sum _{k,i,j=1}^{4}v_{k}w_{i}w_{j}\dfrac{\partial ^{2} f_{k}}{\partial x_{i} \partial x_{j}}(E_{\textsc {t}}^0,\kappa _{\textsc {2}}^{*}),\\ \\ &{}= &{}-2\dfrac{\kappa _{\textsc {2}}^{*}}{x_{1}^{*}}v_{3}w_{3}w_{3}\left[ \left( \dfrac{(1 -\vartheta _{\textsc {1}}) \alpha _{1}+\alpha _{2}}{\alpha _{0}}\right) -\dfrac{\Lambda _{\textsc {1}}\gamma _{\textsc {1}}(1-\vartheta _{\textsc {1}})(\varpi -1)}{\alpha _{0}\omega _{\textsc {h}}}\right] ,\\ \\ &{}= &{}-2\dfrac{\alpha _{1}}{\alpha _{2}\Psi _{\textsc {h}}}v_{3}w_{3}^{2}\left[ ((1 -\vartheta _{\textsc {1}}) \alpha _{1}+\alpha _{2} )\omega _{\textsc {h}}+\Lambda _{\textsc {1}}\gamma _{\textsc {1}}(1-\vartheta _{\textsc {1}})(1-\varpi ) \right] ,\\ \\ &{}= &{}-2\dfrac{\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}}}{(\gamma _{\textsc {1}}+ \vartheta _{\textsc {1}} \omega _{\textsc {h}})\Psi _{\textsc {h}}}v_{3}w_{3}^{2}{\mathcal {Q}} <0,\\ \\ \end{array} \end{aligned}$$

where \({\mathcal {Q}}= [\alpha _{1}(1 -\vartheta _{\textsc {1}}) +\alpha _{2}]\omega _{\textsc {h}}+\Lambda _{\textsc {1}}\gamma _{\textsc {1}}(1-\vartheta _{\textsc {1}})(1-\varpi ) >0\), and

$$\begin{aligned} \begin{array}{lllllll} b &{}= &{} \displaystyle \sum _{k,j=1}^{4}v_{k}w_{j}\dfrac{\partial ^{2} f_{k}}{\partial x_{j} \partial \kappa _{\textsc {2}} }(E_{\textsc {t}}^0,\kappa _{\textsc {2}}^{*}) =(1 -\vartheta _{\textsc {1}})v_{2}w_{3} +\dfrac{\vartheta _{\textsc {1}}}{x_{1}^{*}}v_{3}w_{3}>0.\\ \\ \end{array} \end{aligned}$$

The above results is summarized as follows.

Theorem 3.1

Since the parameters \(a<0\) and \(b>0\), the direction of the bifurcation of the model system (7) at \({\mathcal {R}}_{\textsc {0t}}=1\) is forward.

Because the model system (7) undergoes a forward/transcritical bifurcation at \({\mathcal {R}}_{\textsc {0t}}=1\), this precludes the co-existence of a dual equilibria (that is when a stable DFE co-exists with a stable endemic equilibrium when \({\mathcal {R}}_{\textsc {0t}}<1\)). Consequently, the DFE equilibrium of model (7) is globally asymptotically stable. For this reason, we will forgo the routine theoretical proof of the global stability of the endemic equilibrium of the Tb only sub-model, see Silva and Torres (2013) for a detail proof. While most TB models exhibit subcritical/backward bifurcation, it has been shown that this phenomenon arises due to imperfect vaccine and exogenous re-infection Gumel (2012). These processes are neither incorporated into the TB-only sub-model nor in our complex SARS-CoV-2 and TB co-dynamic model.

As mentioned above, the dynamics of the full model is driven by that of its sub-models, therefore, since both sub-models exhibit a forward bifurcation, the disease-free and endemic equilibria of the full model system (1) cannot co-exist when the reproduction number \({\mathcal {R}}_{\textsc {0t}} = \max ({\mathcal {R}}_{\textsc {vc}},{\mathcal {R}}_{\textsc {0t}}) < 1\). Consequently, the DFE and endemic equilibrium of (1) will exist, be unique, locally and globally asymptotically stable. For these reasons, we will forgo the detailed theoretical analysis here and instead focus on formulating and analyzing the optimal control problem.

The optimal control problem

In order to investigate the potential impact of implementing intervention measures to mitigate the spread of both diseases, we incorporate five time varying controls \(u_1(t)\), \(u_2(t)\), \(u_3(t)\), \(u_4(t)\), and \(u_5(t)\) into (1). These five controls are defined as follows

  1. (i)

    \(u_1\): Face mask usage,

  2. (ii)

    \(u_2\): time-dependent SARS-CoV-2 vaccination rate,

  3. (iii)

    \(u_3\): TB prevention,

  4. (iv)

    \(u_4\): SARS-CoV-2 treatment (palliative),

  5. (v)

    \(u_5\): TB treatment

Tuberculosis treatment is assumed to be based on the isoniazid INH in combination with three other drugs rifampin, pyrazinamide and ethambutol regimen. We note that although usage of mask could be an important prevention measure for TB, herein, for the sake of simplicity and mathematical tractability, we consider the effect of the use of face mask via the control \(u_1\) mainly as a prevention of SARS-CoV-2. Based on how this control is accounted for in the model, we recognize that this drawback (limitation) will imply that the control \(u_1\) has no or little effect in reducing the TB transmission rate from a TB infected person.

The controls \(u_1\), \(u_2\) and \(u_3\) satisfy \(0 \le u_1, u_2, u_3 < 0.90\) while, SARS-CoV-2 and TB treatment controls \(u_4\) and \(u_5\) are bounded as follows: \(0 < u_4,u_5 \le 0.80\). Treatment is assumed to be at most 80% effective. The model system with the control measures is given by

$$\begin{aligned} \begin{aligned} \frac{{\text {d}} {\mathcal {S}}}{{\text {d}}t}&= \Psi _{\textsc {h}} - \left( (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}+ \omega _{\textsc {h}} \right. \\&\quad \left. + u_2 + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {S}},\\ \frac{{\text {d}} {\mathcal {V}}}{{\text {d}}t}&= u_2 {\mathcal {S}} - \left( (1-\chi )(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\right. \\&\quad \left. + \omega _{\textsc {h}} + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {V}},\\ \frac{{\text {d}} {\mathcal {I}}}{{\text {d}}t}&= (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}[{\mathcal {S}} \\&\quad + (1-\chi ){\mathcal {V}} + {\mathcal {T}}] + (1+u_5)\Lambda _{\textsc {2}}{\mathcal {I}}_{\textsc {a}} \\&\quad - \left( (1+u_4)\phi _{\textsc {1}} + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} + \omega _{\textsc {h}} + \delta _{\textsc {1}} \right) {\mathcal {I}},\\ \frac{{\text {d}} {\mathcal {R}}}{{\text {d}}t}&= (1+u_4)\phi _{\textsc {1}}{\mathcal {I}} - \left( \omega _{\textsc {h}} + (1-u_3)\kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} \right) {\mathcal {R}},\\ \frac{{\text {d}} {\mathcal {E}}}{{\text {d}}t}&= (1 - \vartheta _{\textsc {1}})(1-u_3)\kappa _{\textsc {2}}\frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} \\&\quad + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) + (1+u_4)\xi _1 {\mathcal {I}}_{\textsc {e}}\\&\quad - \left( \psi _{1}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} + \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) {\mathcal {E}},\\ \frac{{\text {d}} {\mathcal {A}}}{{\text {d}}t}&= (1-u_3)\vartheta _{\textsc {1}}\kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} \\&\quad + {\mathcal {V}}+ {\mathcal {R}} + \varpi {\mathcal {T}}) + \gamma _{\textsc {1}}{\mathcal {E}} + (1+u_4)\xi _2 {\mathcal {I}}_{\textsc {a}} \\&\quad - \left( (1+u_5)\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} + \psi _{2}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\right) {\mathcal {A}},\\ \frac{{\text {d}} {\mathcal {T}}}{{\text {d}}t}&= (1+u_5)\Lambda _{\textsc {1}}{\mathcal {A}} - \left( (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} \right. \\&\quad \left. + \varpi (1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} + \omega _{\textsc {h}}\right) {\mathcal {T}},\\ \frac{{\text {d}} {\mathcal {I}}_{\textsc {e}}}{{\text {d}}t}&= (1-\vartheta _{\textsc {2}})(1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} \\&\quad + \psi _{1}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {E}} \\&\quad - (\gamma _{\textsc {2}} + \omega _{\textsc {h}} + (1+u_4)\xi _1 + \delta _{\textsc {1}} ){\mathcal {I}}_{\textsc {e}},\\ \frac{{\text {d}} {\mathcal {I}}_{\textsc {a}}}{{\text {d}}t}&= \vartheta _{\textsc {2}}(1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} \\&\quad + \gamma _{\textsc {2}}{\mathcal {I}}_{\textsc {e}} + \psi _{2}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {A}} \\&\quad - ((1+u_5)\Lambda _{\textsc {2}} + \omega _{\textsc {h}} + (1+u_4)\xi _2 + \delta _{\textsc {3}}){\mathcal {I}}_{\textsc {a}}. \end{aligned} \end{aligned}$$
(13)

The problem is to minimize the following cost functional defined as

$$\begin{aligned} J\big [u_{\textsc {1}}, u_{\textsc {2}}, u_{\textsc {3}}, u_{\textsc {4}}, u_{\textsc {5}} \big ] = \int _{0}^{T} \big [ {\mathcal {I}}(t) + {\mathcal {E}}(t) + {\mathcal {A}}(t) + {\mathcal {I}}_{\textsc {e}}(t) + {\mathcal {I}}_{\textsc {a}}(t) + \frac{\theta _1}{2}u_{\textsc {1}}^2 + \frac{\theta _2}{2}u_{\textsc {2}}^2+ \frac{\theta _3}{2}u_{\textsc {3}}^2 + \frac{\theta _4}{2}u_{\textsc {4}}^2 + + \frac{\theta _5}{2}u_{\textsc {5}}^2\big ]dt, \end{aligned}$$
(14)

where T is the final time. Because the total cost includes the cost of TB and SARS-CoV-2 prevention and treatment, we use a quadratic cost functional. Thus, we need to find \(u_{\textsc {1}}^*, u_{\textsc {2}}^*, u_{\textsc {3}}^*, u_{\textsc {4}}^*, u_{\textsc {5}}^*\), such that

$$\begin{aligned}&J(u_{\textsc {1}}^*, u_{\textsc {2}}^*, u_{\textsc {3}}^*, u_{\textsc {4}}^*, u_{\textsc {5}}^*)=\min \{J(u_{\textsc {1}}^*, u_{\textsc {2}}^*, u_{\textsc {3}}^*, u_{\textsc {4}}^*,\nonumber \\&\quad u_{\textsc {5}}^*)|u_{\textsc {1}}, u_{\textsc {2}}, u_{\textsc {3}}, u_{\textsc {4}}, u_{\textsc {5}}\in U\}, \end{aligned}$$
(15)

where \(U= \{(u_{\textsc {1}}^*, u_{\textsc {2}}^*, u_{\textsc {3}}^*, u_{\textsc {4}}^*)\in L^2[0,T]\}\) is the control set, such that \(u_{\textsc {1}}^*, u_{\textsc {2}}^*, u_{\textsc {3}}^*\) are measurable with \(0\le u_{\textsc {1}}^* \le 0.9, 0\le u_{\textsc {2}}^* \le 0.9, 0\le u_{\textsc {3}}^* \le 0.9\), \(0\le u_{\textsc {4}}^* \le 1\), \(0\le u_{\textsc {5}}^* \le 1\) for \(t\in [0,T]\).

To derive the optimality conditions, the Hamiltonian is formulated from the cost functional (14), and is given by

$$\begin{aligned} \begin{aligned} {\mathcal {M}}&= {\mathcal {I}} (t) + {\mathcal {E}}(t) + {\mathcal {A}}(t) + {\mathcal {I}}_{\textsc {e}}(t) + {\mathcal {I}}_{\textsc {a}}(t) \\&\quad + \frac{\theta _1}{2}u_{\textsc {1}}^2+ \frac{\theta _2}{2}u_{\textsc {2}}^2+ \frac{\theta _3}{2}u_{\textsc {3}}^2 + \frac{\theta _4}{2}u_{\textsc {4}}^2 + \frac{\theta _5}{2}u_{\textsc {5}}^2\\&\quad + \lambda _1 \left( \Psi _{\textsc {h}} - \left( (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}+ \omega _{\textsc {h}} + u_2 \right. \right. \\&\quad \left. \left. + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {S}} \right) \\&\quad + \lambda _2 \left( u_2 {\mathcal {S}} - \left( (1-\chi )(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\right. \right. \\&\quad \left. \left. + \omega _{\textsc {h}} + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}\right) {\mathcal {V}} \right) \\&\quad +\lambda _3 \left( (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}[{\mathcal {S}} + (1-\chi ){\mathcal {V}} + {\mathcal {T}}] \right. \\&\quad + (1+u_5)\Lambda _{\textsc {2}}{\mathcal {I}}_{\textsc {a}} - \left( (1+u_4)\phi _{\textsc {1}} + (1-u_3) \frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} \right. \\&\quad \left. \left. + \omega _{\textsc {h}} + \delta _{\textsc {1}} \right) {\mathcal {I}} \right) \\&\quad +\lambda _4 \left( (1+u_4)\phi _{\textsc {1}}{\mathcal {I}} - \left( \omega _{\textsc {h}} + (1-u_3)\kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} \right) {\mathcal {R}}\right) \\&\quad + \lambda _5 \left( (1 - \vartheta _{\textsc {1}})(1-u_3)\kappa _{\textsc {2}}\frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} \right. \\&\quad + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) + (1+u_4)\xi _1 {\mathcal {I}}_{\textsc {e}}\\&\quad \left. - \left( \psi _{1}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} + \gamma _{\textsc {1}} + \omega _{\textsc {h}}\right) {\mathcal {E}} \right) \\&\quad + \lambda _6 \bigg ( (1-u_3)\vartheta _{\textsc {1}}\kappa _{\textsc {2}} \frac{({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}({\mathcal {S}} \\&\quad + {\mathcal {V}}+ {\mathcal {R}} + \varpi {\mathcal {T}}) + \gamma _{\textsc {1}}{\mathcal {E}} + (1+u_4)\xi _2 {\mathcal {I}}_{\textsc {a}} \\&\quad - \left( (1+u_5)\Lambda _{\textsc {1}} + \omega _{\textsc {h}} +\delta _{\textsc {2}} \right. \\&\quad \left. + \psi _{2}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}\right) {\mathcal {A}} \bigg )\\&\quad + \lambda _7 \left( (1+u_5)\Lambda _{\textsc {1}}{\mathcal {A}} - \left( (1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N} \right. \right. \\&\quad \left. \left. + \varpi (1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N} + \omega _{\textsc {h}}\right) {\mathcal {T}} \right) \\&\quad + \lambda _8 \left( (1-\vartheta _{\textsc {2}})(1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} \right. \\&\quad + \psi _{1}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {E}} \\&\quad \left. - (\gamma _{\textsc {2}} + \omega _{\textsc {h}} + (1+u_4)\xi _1 + \delta _{\textsc {1}} ){\mathcal {I}}_{\textsc {e}}\right) ,\\&\quad + \lambda _9 \left( \vartheta _{\textsc {2}}(1-u_3)\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})}{N}{\mathcal {I}} \right. \\&\quad + \gamma _{\textsc {2}}{\mathcal {I}}_{\textsc {e}} + \psi _{2}(1-u_1)\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})]}{N}{\mathcal {A}} \\&\quad \left. - ((1+u_5)\Lambda _{\textsc {2}} + \omega _{\textsc {h}} + (1+u_4)\xi _2 + \delta _{\textsc {3}}){\mathcal {I}}_{\textsc {a}} \right) \end{aligned} \end{aligned}$$
(16)

Theorem 4.1

Suppose the cost functional J is minimized by the set \(\{u_1 , u_2 , u_3, u_4, u_5\}\). Then, the adjoint variables \(\lambda _1 , \lambda _2,\ldots , \lambda _{8}\) (the expressions of \(\frac{{\text {d}} \lambda _i}{{\text {d}}t}\) are provided in the Appendix) satisfy the following adjoint equations

$$\begin{aligned} -\frac{\partial \lambda _i}{\partial t} = \frac{\partial {\mathcal {M}}}{\partial i}, \end{aligned}$$

with

$$\begin{aligned} \lambda _i(t_f) = 0, \quad \quad \text {where}, \quad i= {\mathcal {S}}, {\mathcal {V}}, {\mathcal {I}}, {\mathcal {R}}, {\mathcal {E}}, {\mathcal {A}}, {\mathcal {T}}, {\mathcal {I}}_{\textsc {e}}, {\mathcal {I}}_{\textsc {a}}. \end{aligned}$$
(17)

Furthermore,

$$\begin{aligned} \begin{aligned} u_1^*&=\min \left\{ 1,\max \left( 0,\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})][{\mathcal {S}}(\lambda _3 - \lambda _1) + (1-\chi ){\mathcal {V}}(\lambda _3 - \lambda _2) + {\mathcal {T}}(\lambda _3 - \lambda _7) + \psi _1 {\mathcal {E}}(\lambda _5 - \lambda _5) + \psi _2 {\mathcal {A}}(\lambda _9 - \lambda _6)]}{\theta _1N_{\textsc {h}}}\right) \right\} ,\\ u_2^*&=\min \left\{ 1,\max \left( 0,\frac{{\mathcal {S}}(\lambda _1 - \lambda _2)}{\theta _2}\right) \right\} ,\\ u_3^*&=\min \left\{ 1,\max \left( 0,\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})[({\mathcal {S}} + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) \left\{ (1-\vartheta _1)\lambda _5 + \vartheta _1\lambda _6 \right\} - \lambda _1 {\mathcal {S}} - \lambda _2 {\mathcal {V}} - \lambda _4 {\mathcal {R}} - \lambda _7 \varpi {\mathcal {T}} + {\mathcal {I}}\left\{ (1-\vartheta _2)\lambda _8 + \vartheta _2\lambda _9 - \lambda _3 \right\} ]}{\theta _3 N_{\textsc {h}}}\right) \right\} ,\\ u_4^*&=\min \left\{ 1,\max \left( 0,\frac{[\phi _1 {\mathcal {I}}(\lambda _3 -\lambda _4) + \xi _2 {\mathcal {I}}_{\textsc {e}}(\lambda _8 -\lambda _5) + \xi _3 {\mathcal {I}}_{\textsc {a}}(\lambda _9 -\lambda _6)]}{\theta _4}\right) \right\} ,\\ u_5^*&=\min \left\{ 1,\max \left( 0,\frac{{\mathcal {A}}\Lambda _{\textsc {1}}(\lambda _6-\lambda _1) + {\mathcal {I}}_{\textsc {a}}\Lambda _{\textsc {2}}(\lambda _9-\lambda _3)}{\theta _5}\right) \right\} ,\\ \end{aligned} \end{aligned}$$
(18)

Proof of Theorem 4.1

Consider the associated solutions \(U^*=(u_1^*,u_2^*, u_3^*, u_4^*, u_5^*)\) and \({\mathcal {S}}^*, {\mathcal {V}}^*, {\mathcal {I}}^*, {\mathcal {R}}^*, {\mathcal {E}}^*, {\mathcal {A}}^*, {\mathcal {T}}^*, {\mathcal {I}}_{\textsc {e}}^*, {\mathcal {I}}_{\textsc {a}}^*\). Appying Pontryagin’s Maximum Principle, there exist adjoint variables satisfying

$$\begin{aligned} \begin{aligned} - \frac{{\text {d}}\lambda _1}{{\text {d}}t}&=\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {S}}}, \quad \lambda _1(t_f)=0, \quad - \frac{{\text {d}}\lambda _2}{{\text {d}}t}=\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {V}}}, \quad \lambda _2(t_f)=0, \quad - \frac{{\text {d}}\lambda _3}{{\text {d}}t} =\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {I}}}, \quad \lambda _3(t_f)=0,\\ - \frac{{\text {d}}\lambda _4}{{\text {d}}t}&=\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {R}}}, \quad \lambda _4(t_f)=0, - \frac{{\text {d}}\lambda _5}{{\text {d}}t}=\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {E}}}, \quad \lambda _5(t_f)=0, \quad - \frac{{\text {d}}\lambda _6}{{\text {d}}t} =\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {A}}}, \quad \lambda _6(t_f)=0, \\ - \frac{{\text {d}}\lambda _7}{{\text {d}}t}&=\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {T}}}, \quad \lambda _7(t_f)=0, \quad - \frac{{\text {d}}\lambda _8}{{\text {d}}t} =\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {I}}_{\textsc {e}}}, \quad \lambda _8(t_f)=0, \quad - \frac{{\text {d}}\lambda _9}{{\text {d}}t} =\frac{ \partial {\mathcal {M}}}{\partial {\mathcal {I}}_{\textsc {a}}}, \quad \lambda _9(t_f)=0,\\ \end{aligned} \end{aligned}$$
(19)

with \(\lambda _1(t_f)=\lambda _2(t_f)=\lambda _3(t_f)=\lambda _4(t_f)=\lambda _5(t_f)=\lambda _6(t_f)=\lambda _7(t_f)=\lambda _8(t_f)=0\).

On the interior of the control set U where \(0<u_j<1\) for all (\(j=1,2,3,4,5\)), we have

$$\begin{aligned} \begin{aligned} 0&=\frac{\partial {\mathcal {M}}}{\partial u_1}=\theta _1N_{\textsc {h}}u_1^*-\kappa _{\textsc {1}}[{\mathcal {I}}\\&\quad + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})][{\mathcal {S}}(\lambda _3 - \lambda _1) + (1-\chi ){\mathcal {V}}(\lambda _3 - \lambda _2) + {\mathcal {T}}(\lambda _3 - \lambda _7) + \psi _1 {\mathcal {E}}(\lambda _5 - \lambda _5) + \psi _2 {\mathcal {A}}(\lambda _9 - \lambda _6)], \\ 0&=\frac{\partial {\mathcal {M}}}{\partial u_2}=\theta _2N_{\textsc {h}}u_2^*- {\mathcal {S}}(\lambda _1 - \lambda _2),\\ 0&=\frac{\partial {\mathcal {M}}}{\partial u_3}=\theta _3N_{\textsc {h}}u_3^* - \kappa _{\textsc {2}}({\mathcal {A}} \\&\quad + {\mathcal {I}}_{\textsc {a}})[({\mathcal {S}} + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) \left\{ (1-\vartheta _1)\lambda _5 + \vartheta _1\lambda _6 \right\} - \lambda _1 {\mathcal {S}} \\&\quad - \lambda _2 {\mathcal {V}} - \lambda _4 {\mathcal {R}} - \lambda _7 \varpi {\mathcal {T}} + {\mathcal {I}}\left\{ (1-\vartheta _2)\lambda _8 + \vartheta _2\lambda _9 - \lambda _3 \right\} ],\\ 0&=\frac{\partial {\mathcal {M}}}{\partial u_3}=\theta _4u_4^* - [\phi _1 {\mathcal {I}}(\lambda _3 -\lambda _4) \\&\quad + \xi _2 {\mathcal {I}}_{\textsc {e}}(\lambda _8 -\lambda _5) + \xi _3 {\mathcal {I}}_{\textsc {a}}(\lambda _9 -\lambda _6) ],\\ 0&=\frac{\partial {\mathcal {M}}}{\partial u_3}=\theta _5u_5^* - [{\mathcal {A}}\Lambda _{\textsc {1}}(\lambda _6-\lambda _1) \\&\quad + {\mathcal {I}}_{\textsc {a}}\Lambda _{\textsc {2}}(\lambda _9-\lambda _3)].\\ \end{aligned} \end{aligned}$$
(20)

\(\square\)

Therefore,

$$\begin{aligned} \begin{aligned} u_1^*&=\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})][{\mathcal {S}}(\lambda _3 - \lambda _1) + (1-\chi ){\mathcal {V}}(\lambda _3 - \lambda _2) + {\mathcal {T}}(\lambda _3 - \lambda _7) + \psi _1 {\mathcal {E}}(\lambda _5 - \lambda _5) + \psi _2 {\mathcal {A}}(\lambda _9 - \lambda _6)]}{\theta _1N_{\textsc {h}}},\\ u_2^*&=\frac{{\mathcal {S}}(\lambda _1 - \lambda _2)}{\theta _2},\\ u_3^*&=\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})[({\mathcal {S}} + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) \left\{ (1-\vartheta _1)\lambda _5 + \vartheta _1\lambda _6 \right\} - \lambda _1 {\mathcal {S}} - \lambda _2 {\mathcal {V}} - \lambda _4 {\mathcal {R}} - \lambda _7 \varpi {\mathcal {T}} + {\mathcal {I}}\left\{ (1-\vartheta _2)\lambda _8 + \vartheta _2\lambda _9 - \lambda _3 \right\} ]}{\theta _3 N_{\textsc {h}}},\\ u_4^*&=\frac{[\phi _1 {\mathcal {I}}(\lambda _3 -\lambda _4) + \xi _2 {\mathcal {I}}_{\textsc {e}}(\lambda _8 -\lambda _5) + \xi _3 {\mathcal {I}}_{\textsc {a}}(\lambda _9 -\lambda _6)]}{\theta _4},\\ u_5^*&=\frac{{\mathcal {A}}\Lambda _{\textsc {1}}(\lambda _6-\lambda _1) + {\mathcal {I}}_{\textsc {a}}\Lambda _{\textsc {2}}(\lambda _9-\lambda _3)}{\theta _5}.\\ \end{aligned} \end{aligned}$$
(21)
$$\begin{aligned} \begin{aligned} u_1^*&=\min \left\{ 1,\max \left( 0,\frac{\kappa _{\textsc {1}}[{\mathcal {I}} + \eta ({\mathcal {I}}_{\textsc {a}} + {\mathcal {I}}_{\textsc {e}})][{\mathcal {S}}(\lambda _3 - \lambda _1) + (1-\chi ){\mathcal {V}}(\lambda _3 - \lambda _2) + {\mathcal {T}}(\lambda _3 - \lambda _7) + \psi _1 {\mathcal {E}}(\lambda _5 - \lambda _5) + \psi _2 {\mathcal {A}}(\lambda _9 - \lambda _6)]}{\theta _1N_{\textsc {h}}}\right) \right\} ,\\ u_2^*&=\min \left\{ 1,\max \left( 0,\frac{{\mathcal {S}}(\lambda _1 - \lambda _2)}{\theta _2}\right) \right\} ,\\ u_3^*&=\min \left\{ 1,\max \left( 0,\frac{\kappa _{\textsc {2}}({\mathcal {A}} + {\mathcal {I}}_{\textsc {a}})[({\mathcal {S}} + {\mathcal {V}} + {\mathcal {R}} + \varpi {\mathcal {T}}) \left\{ (1-\vartheta _1)\lambda _5 + \vartheta _1\lambda _6 \right\} - \lambda _1 {\mathcal {S}} - \lambda _2 {\mathcal {V}} - \lambda _4 {\mathcal {R}} - \lambda _7 \varpi {\mathcal {T}} + {\mathcal {I}}\left\{ (1-\vartheta _2)\lambda _8 + \vartheta _2\lambda _9 - \lambda _3 \right\} ]}{\theta _4}\right) \right\} ,\\ u_5^*&=\min \left\{ 1,\max \left( 0,\frac{{\mathcal {A}}\Lambda _{\textsc {1}}(\lambda _6-\lambda _1) + {\mathcal {I}}_{\textsc {a}}\Lambda _{\textsc {2}}(\lambda _9-\lambda _3)}{\theta _5}\right) \right\} ,\\ \end{aligned} \end{aligned}$$
(22)

Optimal control model simulations

The numerical simulations carried out on the control system (13), adjoint equations (19) and characterizations of the control (22) are run in MATLAB using the Runge-Kutta forward backward sweep method. To compute the total cost for each strategy implemented over time, we use the quadratic cost functions \(\frac{1}{2}\theta _1u_{\textsc {1}}^2, \frac{1}{2}\theta _2u_{\textsc {2}}^2, \frac{1}{2}\theta _3u_{\textsc {3}}^2\), \(\frac{1}{2}\theta _4u_{\textsc {4}}^2\) and \(\frac{1}{2}\theta _5u_{\textsc {5}}^2\) are. The following weight constants are assumed in order to investigate the cost of each implemented strategy: \(\theta _1=900, \theta _2=1500, \theta _3=2000, \theta _4=1000\) and \(\theta _5=1200\). Also, the implementation cost to preventing SARS-CoV-2 infections (face-mask usage and vaccination) is assumed to be less than the cost of implementing the TB prevention control. Similarly, TB treatment cost is assumed to be higher than the cost of SARS-CoV-2 treatment.

Initial conditions and model fitting

The population of Indonesia is estimated to be 273,523,621 (Indonesia 2021). Thus, let \({\mathcal {S}}(0) = 270,000,000\). By February 11, 2021, the total number fully vaccinated individuals against SARS-CoV-2 in Indonesia was 345,605 (Indonesia 2021), hence \({\mathcal {V}}(0) = 345,605\). The total number of recovered individuals was 627,044, Indonesia (2021), that is \({\mathcal {R}}(0)=627,044\). Total confirmed SARS-CoV-2 infections was 1, 191, 990, and active cases 166, 492, thus, we set \({\mathcal {I}}(0)=166,492\). The remaining initial conditions are: \({\mathcal {E}}(0) = 450,000\), \({\mathcal {A}}(0) = 12000\), \({\mathcal {T}}(0)=0\), \({\mathcal {I}}_{\textsc {e}}(0) = 50000\), \({\mathcal {I}}_{\textsc {a}}(0) = 5000\) as reported in TB cases (2021).

For the model fitting, we used the approach in McCall (2005), which is based on the fmincon optimization toolbox in MATLAB. The fmincon’s optimization routine syntax: \(x = fmincon(\textit{@modelfun},x0,A,b,Aeq,beq,lb,ub,nonlcon,options),\) starts at x0 (the initial guesses) and finds an optimum x to the function described in \(\textit{@modelfun}\) that fits the model to a given data set, subject to the nonlinear inequalities c(x) or equalities ceq(x) defined in nonlcon, and also subject to the linear inequalities \(A.x \le b\) and linear equalities \(Aeq.x = beq\), defined in A, b, Aeq, beq, respectively. x0 can be a scalar, vector, or matrix. lb and ub are the bounds on the parameters to be estimated. The optimization parameters and error tolerance are specified in options.

From the Indonesia daily cumulative number SARS-CoV-2 infections (Indonesia 2021), we estimated some of the model parameters. The model system (1) fitted to the cumulative confirmed daily SARS-CoV-2 cases for Indonesia from February 11, 2021 to August 26, 2021 is shown in Fig. 2. It is evident from Fig. 2 that our proposed model fits the Indonesia’s data pretty well.

Fig. 2
figure 2

Model fitting to the cumulative daily Indonesia SARS-CoV-2 infections

Full size image

Discussion

In this section, we shall investigate the impact of the implementation of various possible control strategies on the co-interaction of the two diseases in Indonesia.

Strategy A: Face-mask usage and SARS-CoV-2 vaccination (\(u_1 \ne 0, u_2 \ne 0\))

The simulations of the optimal control system (13) when the strategy that combines public use of face-mask usage and SARS-CoV-2 vaccination (\(u_1 \ne 0, u_2 \ne 0\)) is implemented, are respectively depicted in Figs. 3, 4, 5, 6 and 7. With the implementation of this intervention strategy, for \(\kappa _{\textsc {1}} =1.3337, \kappa _{\textsc {2}} = 7\) and \(\varpi = 0.6\), so that the reproduction number, \(\displaystyle {\mathcal {R}}_{\textsc {0ct}} =\max \left\{ {\mathcal {R}}_{\textsc {vc}}, {\mathcal {R}}_{\textsc {0t}} \right\} = 5.8314>1\), as expected, there is a significant reduction in the number of persons infected with SARS-CoV-2 as shown in Fig. 3. Note that despite the introduction of face mask and vaccination, there are still SARS-CoV-2 cases at the onset of their implementation, and this is not surprising because vaccination takes some time to provide protection, while those already infected who have not yet been detected or showing symptoms are being identified through testing as both intervention measures are being rolled out. This is also an indication that it is a daunting task to have any intervention measures attain their maximum early on when these are being put in place. Amazingly, this strategy against SARS-CoV-2 also avert about 27,878,840 new TB cases (as depicted in Figs. 4 and 5, respectively). Besides, this strategy has a positive population level impact on co-infected individuals. From Figs. 6 and 7, 38,539,095 new dual infections could potentially be averted). The control profile for the combined effect of the face-mask usage and SARS-CoV-2 vaccination control strategy are depicted in Fig. 8. When face-mask wearing and SARS-CoV-2 vaccination are the selected strategy, one notes that wearing face mask (control \(u_1\)) should be implemented optimally throughout the intervention period, while SARS-CoV-2 vaccination \(u_2\) uptake will start decreasing after about 4 months. Several reasons could explain such a decreasing number of reported daily infections and deaths. While this Strategy A is too optimistic because it means that during 140 days, the health system should vaccinate about 90% of the (remaining) susceptible population each day, which is likely not feasible realistically or cannot be supported from a quantitative point of view in any country’s health system.

Fig. 3
figure 3

Time series of SARS-CoV-2 infections with implementation of strategy A

Full size image
Fig. 4
figure 4

Dynamics of infected with latent TB when strategy A is implemented

Full size image
Fig. 5
figure 5

Dynamics of infected with active TB when strategy A is implemented

Full size image
Fig. 6
figure 6

Dynamics of SARS-CoV-2 and latent TB dual infection with implementation of strategy A

Full size image
Fig. 7
figure 7

Time series of SARS-CoV-2 and active TB co-infection with implementation of strategy A

Full size image
Fig. 8
figure 8

Control profile for the combined effect of controls \(u_1\) and \(u_2\)

Full size image

Strategy B: SARS-CoV-2 vaccination and treatment (\(u_2 \ne 0, u_4 \ne 0\))

The simulations of the optimal control system (13) when the strategy that combines SARS-CoV-2 vaccination and treatment (\(u_2 \ne 0, u_4 \ne 0\)) is implemented, are presented in Figs. 9, 10, 11, 12 and 13. With the implementation of this intervention strategy, for \(\kappa _{\textsc {1}} =1.3337, \kappa _{\textsc {2}} = 7\) and \(\varpi = 0.6\), so that the reproduction number, \(\displaystyle {\mathcal {R}}_{\textsc {0ct}} =\max \left\{ {\mathcal {R}}_{\textsc {vc}}, {\mathcal {R}}_{\textsc {0t}} \right\} = 5.8314>1\), as expected, the number of SARS-CoV-2 infections is reduced, see Fig. 3. Interestingly, this SARS-CoV-2 only control strategy also averts over 25 million new TB cases (Figs. 10 and 11). This strategy B tends to overestimate the number of latent and active TB cases in Indonesia, and this may not be surprising because we do not consider any TB preventive or therapeutic (treatment and vaccination) intervention measures in this strategy. However, despite this limitation, this strategy has positive population level impact on the number of co-infected individuals with SARS-CoV-2 and TB (as shown in Figs. 12 and 13, where more than 30 million new co-infections with both diseases were averted). The control profile for the combined effect of the face-mask usage and SARS-CoV-2 vaccination control strategy is presented in Fig. 14. When SARS-CoV-2 vaccination and treatment are implemented, Fig. 14 can be interpreted as follows: as expected, treatment of SARS-CoV-2 \(u_4\) started prior to vaccination and increased gradually as detected cases grew, but to mitigate the rapid spread of the pandemic, vaccination should be optimally applied at the onset of the vaccination campaign.

Fig. 9
figure 9

Dynamics of infected with SARS-CoV-2 when strategy B is implemented

Full size image
Fig. 10
figure 10

Dynamics of infected with latent TB when strategy B is implemented

Full size image
Fig. 11
figure 11

Dynamics of infected with active TB when strategy B is implemented

Full size image
Fig. 12
figure 12

Time series of SARS-CoV-2 and latent TB co-infections with implementation of strategy B

Full size image
Fig. 13
figure 13

Dynamics of co-infected with SARS-CoV-2 and active TB when strategy B is implemented

Full size image
Fig. 14
figure 14

Control profile for the combined effect of controls \(u_2\) and \(u_4\)

Full size image

Strategy C: TB prevention and treatment (\(u_3 \ne 0, u_5 \ne 0\))

Numerical simulations of the optimal control system (13) when the strategy that combines TB prevention and treatment (\(u_3 \ne 0, u_5 \ne 0\)) is implemented, are presented in Figs. 15, 16, 17, 18 and 19. When this TB only intervention strategy is implemented, for \(\kappa _{\textsc {1}} =1.3337, \kappa _{\textsc {2}} = 7\) and \(\varpi = 0.6\), the reproduction number \(\displaystyle {\mathcal {R}}_{\textsc {0ct}} =\max \left\{ {\mathcal {R}}_{\textsc {vc}}, {\mathcal {R}}_{\textsc {0t}} \right\} = 5.8314>1\). From Fig. 15, the number of SARS-CoV-2 infections is reduced, with 5,397,795 new infections averted. In fact, as expected applying this strategy will avert more than 20 million new TB cases. This is depicted by Figs. 16 and 17). Besides, this strategy also has a positive population level impact on the number of individuals co-infected with SARS-CoV-2 and TB (Figs. 18 and 19, where more than 35 million new co-infection cases were averted). The control profile for the combined effect of TB prevention and treatment controls is presented in Fig. 20. When only TB prevention and treatment are implemented, as expected, the TB prevention control \(u_3\) should be optimally implemented throughout, while the TB treatment control \(u_5\) is optimally implemented at the onset of the epidemic, but drastically decreases and only picks up again from day 120. This may be due to the fact that SARS-CoV-2 displays clinical and radiological similarities with pulmonary tuberculosis, and SARS-CoV-2 emerged with high mortality, focus may have been on saving SARS-CoV-2 patients at the detriments of TB patients.

Fig. 15
figure 15

Time series of SARS-CoV-2 infections with implementation of strategy C

Full size image
Fig. 16
figure 16

Dynamics of infected with latent TB when strategy C is implemented

Full size image
Fig. 17
figure 17

Dynamics of infected with active TB when strategy C is implemented

Full size image
Fig. 18
figure 18

Dynamics of SARS-CoV-2 and latent TB co-infections with implementation of strategy C

Full size image
Fig. 19
figure 19

Time series of SARS-CoV-2 and active TB co-infections with implementation of strategy C

Full size image
Fig. 20
figure 20

Control profile for the combined effect of controls \(u_3\) and \(u_5\)

Full size image

Conclusion

We formulated a mathematical model of the co-dynamics of COVID-19 and TB and investigated the impact of implementing various control measures to mitigate the spread of both diseases. Basic properties of the sub-models, namely TB only and SARS-CoV-2 only such as the invariant region, positivity and boundedness of solutions are provided. Their equilibria are locally asymptotically stable when the associated reproduction number is less than unity. The phenomenon of backward bifurcation where both a stable DFE co-exists with a stable endemic equilibrium when the basic reproduction number is less than unity is investigated for the TB sub-model, and results show that the direction of the bifurcation is forward. This precludes the co-existence of dual equilibria. Because the dynamics of the full model is driven by that of its sub-models, we did not carry out detailed analysis of the full model system 1, based on the transcritical/forward bifurcation of both sub-models, the full model equilibria is locally and globally asymptotically stable. Finally, using the Pontryagin’s maximum Principle, conditions for the existence of optimal control of the co-infection model are established.

Indonesia is a country where both TB and SARS-CoV-2 are endemic. Real SARS-CoV-2 daily cumulative infections are used to fit the model system 1 from February 11, 2021 to August 26, 2021, and estimated some of the model parameter values. Although model fitting to cumulative cases and then used to estimate several of the model parameter values could lead to an over fitting problem, it is not the case herein. However, if such a problem is identified (occur), one could use the corrective approach proposed in King et al. (2015).

Five control measures are incorporated into  the model 1, namely; SARS-CoV-2 vaccination, TB and SARS-CoV-2 prevention controls as well as treatment for both diseases. The highlights of the model simulations are as follows

  1. (i)

    TB prevention could avert up to 870,000 new SARS-CoV-2 infections (Fig. 15);

  2. (ii)

    Implementation of control strategy for either of the diseases could greatly reduce co-infections (see Figs. 6, 7 and 18, 19);

  3. (iii)

    The highest number of co-infections averted is observed when TB prevention and treatment controls are implemented. From Figs. 18 and 19, about 39,021,510 dual infections would have been averted.

There are definitely some limitations to our model. Face mask is also protective against TB, but because this has been widely used for protection by medical personnel only (Zhou et al. 2020; Gammaitoni and Nucci 1997), we do not apply the control \(u_1\) to TB. Due to the complexity of our proposed model, vaccination against TB and exogenous re-infection were not included. Future studies could investigate network models such as agent-based, and the cost-effectiveness of the various and potential strategies that could be implemented to mitigate the spread of these diseases. Since by construction, mechanistic models inherit the loss of information, exploring time varying or time-invariant sensitivity analysis is viable. Finally, to address possible random fluctuations, the model could be reformulated as a stochastic compartmental model that includes white noise.