Periodic transmission and vaccination effects in epidemic dynamics: a study using the SIVIS model

Abstract

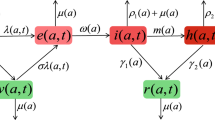
This work explores the dynamics of an epidemic considering an SIVIS (susceptible-infected-vaccinated-infected-susceptible) epidemiological model, accounting for heterogeneous susceptibility, governmental interventions, social behavioral dynamics and public reactions in both of autonomous and nonautonomous aspects. The study frames the system as an optimal control problem, considering time-dependent control strategies for strength of social behavior of public and pharmaceutical treatments. The emergence of a coexistence steady state is analyzed based on the basic reproduction number. The impact of model parameters on disease propagation is assessed through sensitivity analysis. Transcritical bifurcation-induced stability alteration is explored, and numerical simulations illustrate theoretical findings. The proposed system investigates the dynamical behavior in case of periodic transmission rate. It vividly highlights the profound impact of factors such as vaccination rates, frequency and amplitude of transmission on the enduring and evolving dynamic patterns exhibited by the disease.

Appendices

Appendix A

1.1 A.1 Reproduction number

Suppose that, $x\equiv (I,V)$. Then we have:

$$\begin{aligned}{} & {} \frac{dx}{dt}={\mathfrak {F}}(x)-\nu (x),\ \text {where}\\{} & {} {\mathfrak {F}}(x)=\begin{pmatrix} (1-\alpha )(1-D)^{k}(\theta _{1}S_{1}(t)+\theta _{2}S_{2}(t))I(t) \\ 0 \end{pmatrix}\\{} & {} \quad \text {and}\ \nu (x)=\begin{pmatrix} \left( \mu +m+\gamma \right) I-\varepsilon I V \\ -(v _1S_1+v _2S_2)-(1-\beta _1-\beta _2)\gamma I+\varepsilon IV+\mu V \end{pmatrix}. \end{aligned}$$

Here, ${\mathfrak {F}}(x)$ consists of the compartment in which infection is introduced first and $\nu (x)$ contains rest of the terms. Then, at $\displaystyle E_{0}(S_{10},S_{20},0,V_0)$, we have

$$\begin{aligned}{} & {} \displaystyle F=\left( D{\mathfrak {F}}(x)\right) _{E_{0}} \\{} & {} \quad =\begin{pmatrix} (1-\alpha )(1-D)^{k}(\theta _{1}S_{10}(t)+\theta _{2}S_{20}(t)) &{} 0 \\ 0 &{} 0 \end{pmatrix} \\{} & {} \quad \text {and}\quad \displaystyle V=\left( D\nu (x)\right) _{E_{0}}=\begin{pmatrix} \left( \mu +m+\gamma \right) -\varepsilon V_0 &{} 0\\ (1-\beta _1-\beta _2)\gamma +\varepsilon V_0 &{} \mu \end{pmatrix}. \end{aligned}$$

Reproduction number is the spectral radius of next-generation matrix. Now, $FV^{-1}$ is the next-generation matrix whose spectral radius is denoted as:

$$\begin{aligned} R_{0}=\frac{(1-\alpha )(1-D)^{k}(\theta _{1}S_{10}+\theta _{2}S_{20})}{(\mu +m+\gamma -\varepsilon V_0)}. \end{aligned}$$

Appendix B

1.1 B.1 Existence of optimal control functions

Here, we describe the existence of optimal control measures with a minimized cost function in a finite time interval.

Proof of Theorem 8.1

Model (8.2) assumes $N=S_1+S_2+I+V$ be the total population. So,

$$\begin{aligned} \frac{dN}{dt}&=\Pi -\mu S_{1}-\mu S_{2}-(\mu +m)I-\mu V \\&\le \Pi -\mu N\Rightarrow 0<N(t)\\&\le \frac{\Pi }{\mu }+\left( N(0)-\frac{\Pi }{\mu }\right) e^{-\mu t} \end{aligned}$$

where N(0) represents the overall population at initial state. As $\displaystyle t\rightarrow \infty ,\ 0<N(t)\le \frac{\Pi }{\mu }+\epsilon , ~ \mathrm{for ~ any ~} \epsilon > 0.$

Thus, when control factors are present, the solution of model (8.2) remains bounded, and the functions on the right side of system (8.2) are Lipschitz continuous within $\Xi$. Thus, according to the Picard–Lindelöf theorem, optimal control model system (8.2) exhibits nontrivial solutions within $\Xi$ [50]. Moreover, the control elements are confined within a closed and convex set $\Xi$. Each equation system (8.2) can be expressed linearly using D and $\gamma$, with coefficients dependent on time and state variables. Moreover, the control variables are of second order, leading to the integrand $L(S_1,S_2,I,V,D,\gamma )$ being a convex function on the solution set $\Xi$.

$$\begin{aligned}{} & {} \text {Again,}\ L_1(S_1,S_2,I,V,D,\gamma )= g_{1}I(t)+g_{2}D^{k}(t)\\{} & {} \quad +g_{3}\gamma ^{2}(t) \ge g_{2}D^{k}+g_{3}\gamma ^{2}. \end{aligned}$$

Let us take, ${\overline{g}} = \min (g_{2},g_{3})>0$ and $h(D,\gamma )={\overline{g}}(D^{k}+\gamma ^{2})$. Hence, $h(D,\gamma )$ is a continuous function, and $L(S_1,S_2,I,V,D,\gamma )\ge h(D,\gamma )$. Furthermore, $||(D,\gamma )||^{-1}h(D,\gamma )\rightarrow \infty$ for $||(D,\gamma )||\rightarrow \infty .$ Therefore, using the outcomes of [47, 51], it can be stated that optimal control interventions $D^{*}$ and $\gamma ^{*}$ exist such that $Z(D^{*},\gamma ^{*})=\min [Z(D,\gamma )]$. $\square$

1.2 B.2 Characterization of control interventions

The optimal control strategies are derived through the utilization of Pontryagin’s principle [51, 52]. Now, the Hamiltonian function is given by:

$$\begin{aligned}&H\left( S_1,S_2,I,V,D,\gamma ,l\right) =L_1(S_1,S_2,I,V,D,\gamma )\nonumber \\&\quad +l_{1} \frac{dS_1}{dt}+l_{2}\frac{dS_2}{dt}+l_{3}\frac{dI}{dt}+l_{4}\frac{dV}{dt}.\nonumber \\&H = g_{1}I(t)+g_{2}D^{k}(t)+g_{3}\gamma ^{2}(t) \nonumber \\&\qquad \quad + l_1\left[ q\Pi -(1-\alpha )(1-D(t))^{k}\theta _{1}S_{1}I\right. \nonumber \\&\qquad \quad \left. -v _1S_1+\beta _1\gamma I-\mu S_{1} \right] \nonumber \\&\qquad \quad + l_2 \left[ (1-q)\Pi -(1-\alpha )(1-D(t))^{k}\theta _{2}S_{2}I\right. \nonumber \\&\qquad \quad \left. -v _2S_2+\beta _2\gamma I-\mu S_{2} \right] \nonumber \\&\qquad \quad + l_3\Big [(1-\alpha )(1-D(t))^{k}(\theta _{1}S_{1}+\theta _{2}S_{2})I\nonumber \\&\qquad \quad - (\mu +m)I-\gamma I+\varepsilon IV \Big ] + l_4 \nonumber \\&\quad \Big [(v _1S_1+v _2S_2)+(1-\beta _1-\beta _2)\gamma I-\varepsilon IV-\mu V \Big ] \end{aligned}$$

(B.1)

Here $l=\left( l_{1},l_{2},l_{3},l_4\right)$ indicates adjoint variables. Our primary concern is to minimize Hamiltonian H by utilizing Pontryagin’s principle so that a minimal cost function is obtained.

Proof of Theorem 8.2

Consider $D^{*}$ and $\gamma ^{*}$ be the applied optimal control along with the corresponding optimal state variables are $S_1^{*}, S_2^*, I^{*}$ and $V^{*}$ of (8.2) which minimize the cost functional Z defined in (8.1). Therefore, we have adjoint variables $l_{i}$ for $i=1,2,3,4$, satisfying the canonical equations:

$$\begin{aligned}{} & {} \frac{dl_{1}}{dt}=-\frac{\partial H}{\partial S_1}, \qquad \frac{dl_{2}}{dt}=-\frac{\partial H}{\partial S_2}, \\{} & {} \frac{dl_{3}}{dt}=-\frac{\partial H}{\partial I}, \qquad \frac{dl_{4}}{dt}=-\frac{\partial H}{\partial V}. \end{aligned}$$

So, we have

$$\begin{aligned}&\frac{dl_1}{dt}= l_1\left[ (1-\alpha )(1-D)^{k}\theta _{1}I +v_1+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{1}I \right] - l_4\Big [v_1 \Big ]\nonumber \\&\frac{dl_2}{dt}= l_2\left[ (1-\alpha )(1-D)^{k}\theta _{2}I +v_2+\mu \right] \nonumber \\&\qquad \quad - l_3\left[ (1-\alpha )(1-D)^{k}\theta _{2}I \right] - l_4\Big [v_2 \Big ]\nonumber \\&\frac{dl_3}{dt}= -g_1 + l_1 \left[ (1-\alpha )(1-D)^{k}\theta _{1}S_1 - \beta _1 \gamma \right] \nonumber \\&\qquad \quad + l_2 \left[ (1-\alpha )(1-D)^{k}\theta _{2}S_2 - \beta _2 \gamma \right] \nonumber \\&\qquad \quad - l_3 \left[ (1-\alpha )(1-D)^{k} (\theta _{1}S_1+\theta _{2}S_2) \right. \nonumber \\&\qquad \quad \left. - (\mu +m+\gamma ) +\varepsilon V \right] \nonumber \\&\qquad \quad - l_4\Big [ (1-\beta _1 - \beta _2) \gamma - \varepsilon V \Big ]\nonumber \\&\frac{dl_4}{dt}= -l_3\Big [\varepsilon I \Big ] - l_4\Big [-\varepsilon I -\mu \Big ] \end{aligned}$$

with the transversality conditions $l_{i}(T_{f})=0$, for $i=1,2,3,4$.

$$\begin{aligned}{} & {} \text {From optimality conditions}: ~~~ \frac{\partial H}{\partial D}\bigg |_{D=D^{*}}=0, \\ {}{} & {} \text {and} \ \frac{\partial H}{\partial \gamma }\bigg |_{\gamma =\gamma ^{*}}=0. \end{aligned}$$

So, $\displaystyle D^{*}{=} \frac{\left[ \frac{(1{-}\alpha )I^*}{g_{2}}\left\{ (l_{3}{-}l_{1})\theta _1 S_1^* {+} (l_{3}{-}l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1{+}\left[ \frac{(1{-}\alpha )I^*}{g_{2}}\left\{ (l_{3}{-}l_{1})\theta _1 S_1^* {+} (l_{3}{-}l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}$

and $\displaystyle \gamma ^{*}{=}\frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\}$.

In $\Xi ,$ we have

$$\begin{aligned}{} & {} \begin{aligned} D^{*}&= {\left\{ \begin{array}{ll} 0, &{} \text {if}\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}< 0 \\ \\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}, &{} \text {if}\ 0\le \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}\le 1 \\ \\ 1, &{} \text {if}\ \frac{\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}{1+\left[ \frac{(1-\alpha )I^*}{g_{2}}\left\{ (l_{3}-l_{1})\theta _1 S_1^* + (l_{3}-l_{2})\theta _2 S_2^* \right\} \right] ^{\frac{1}{k-1}}}> 1 \end{array}\right. } \end{aligned} \\{} & {} \begin{aligned} \gamma ^{*}&= {\left\{ \begin{array}{ll} 0, &{} \text {if}\quad \frac{ I^{*}}{2g_{3}}\{(l_{4}-l_{1})\beta _1+(l_{4}-l_{2})\beta _2 -(l_{4}-l_{3})\}<0 \\ \frac{I^{*}}{2g_{3}}\{(l_{4}-l_{1})\beta _1&{}\\ +(l_{4}-l_{2})\beta _2 -(l_{4}-l_{3})\}, &{} \text {if}\quad 0\le \frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\} \le 1 \\ 1, &{} \text {if}\quad \frac{ I^{*}}{2g_{3}}\left\{ \left( l_{4}-l_{1}\right) \beta _1+\left( l_{4}-l_{2}\right) \beta _2 -\left( l_{4}-l_{3}\right) \right\} > 1 \end{array}\right. } \end{aligned} \end{aligned}$$

which is equivalent as (8.4). $\square$

1.3 B.3 Optimal system

The optimal system which includes the optimal control measures $D^{*}$ and $\gamma ^{*}$ and minimizing the Hamiltonian $H^{*}$ at $(S_1^{*},S_2^{*}, I^{*}, V^{*}, l_{1}, l_{2}, l_{3},l_4)$ is

$$\begin{aligned} \frac{dS_{1}^*}{dt}&=q\Pi -(1-\alpha )(1-D^*)^{k}\theta _{1}S_{1}^*I^*\nonumber \\&\quad -v _1S_1^*+\beta _1\gamma ^* I^*-\mu S_{1}^* \nonumber \\ \frac{dS_{2}^*}{dt}&=(1-q)\Pi -(1-\alpha )(1-D^*)^{k}\theta _{2}S_{2}^*I^*\nonumber \\&\quad -v _2S_2^*+\beta _2\gamma ^* I^*-\mu S_{2}^*\nonumber \\ \frac{dI^*}{dt}&=(1-\alpha )(1-D^*)^{k}(\theta _{1}S_{1}^*\nonumber \\&\quad +\theta _{2}S_{2}^*)I^*-\gamma ^* I^*+\varepsilon I^*V^*- (\mu +m)I^*\nonumber \\ \frac{dV^*}{dt}&=(v _1S_1^*+v _2S_2^*)\nonumber \\&\quad +(1-\beta _1-\beta _2)\gamma ^* I^*-\varepsilon I^*V^*-\mu V^*\ge 0. \end{aligned}$$

(B.2)

with non-negative initial conditions $S_1^{*}(0)>0,\ S_2^{*}(0)>0, \ I^{*}(0)\ge 0,\ V^{*}(0) \ge 0$, and the corresponding adjoint system is:

$$\begin{aligned} \frac{dl_1}{dt}&= l_1\left[ (1-\alpha )(1-D^*)^{k}\theta _{1}I^* +v_1+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D^*)^{k}\theta _{1}I^* \right] - l_4\Big [v_1 \Big ]\nonumber \\ \frac{dl_2}{dt}&= l_2\left[ (1-\alpha )(1-D^*)^{k}\theta _{2}I^* +v_2+\mu \right] \nonumber \\&\quad - l_3\left[ (1-\alpha )(1-D^*)^{k}\theta _{2}I^* \right] - l_4\Big [v_2 \Big ]\nonumber \\ \frac{dl_3}{dt}&= -g_1 + l_1 \left[ (1-\alpha )(1-D^*)^{k}\theta _{1}S_1^* - \beta _1 \gamma ^* \right] \nonumber \\&\quad + l_2 \left[ (1-\alpha )(1-D^*)^{k}\theta _{2}S_2^* - \beta _2 \gamma ^* \right] \nonumber \\&\quad - l_3 \left[ (1-\alpha )(1-D^*)^{k} (\theta _{1}S_1^*+\theta _{2}S_2^*) \right. \nonumber \\&\quad \left. - (\mu +m+\gamma ^*) +\varepsilon V^* \right] \nonumber \\&\quad - l_4\Big [ (1-\beta _1 - \beta _2) \gamma ^* - \varepsilon V^* \Big ]\nonumber \\ \frac{dl_4}{dt}&= -l_3\Big [\varepsilon I^* \Big ] - l_4\Big [-\varepsilon I^* -\mu \Big ] \end{aligned}$$

(B.3)

with transversality conditions $l_{i}(T_{f})=0$, for $i=1,2,3,4$ and the control interventions $D^{*},\ \gamma ^{*}$ are the same as in (8.4).