Dynamics of a prey-generalized predator system with disease in prey and gestation delay for predator

Abstract

In the present study, a prey-generalized predator model is proposed with disease in the prey and gestation delay for predator. The asymptotic behavior of the model is studied for all the feasible equilibrium states. The criterion for local stability of the system are established around steady states and thresholds for Hopf bifurcation are determined at the endemic as well as disease-free state. The respective sensitive indices of the variables are identified at the endemic state by performing the sensitivity analysis. Further numerical simulations have been carried out to justify our analytic findings.

Introduction

The interactions between prey and predator living in the same environment is a fascinating field in the bio-mathematical literature starting with the pioneer work of Lotka (1925) and Volterra (1926). Many mathematicians and ecologists studied the dynamical behavior of the prey-predator system in ecology and contributed to the growth of the population models (Dhar and Jatav 2013; Dubey 2007; Freedman 1980; Jeschke et al. 2002; Kooij and Zegeling 1996; Ma and Takeuchi 1998; Singh et al. 2015; Dhar et al. 2015; Sen et al. 2012; Murray 2002; Robinson 1998; Tripathi et al. 2015). Further, the correlation between the disease and the prey-predator system is a topic of significant interest, and the fusion of ecology and epidemiology is a comparatively new branch of study, known as eco-epidemiology. It is a well known fact that the predator is more vulnerable to the infected prey because the infected prey may become weaker and less active so that they may be easily caught by the predator, and the same concept was modeled by various researchers (Moore et al. 2002; Hethcote et al. 2004; Liu and Wang 2010; Hadeler and Freedman 1989). But, there is also a possibility that, the predator gets infected due to consumption of the infected prey and dies out more rapidly. In this latter case the growth of the predator will depend on the healthy prey. Further, there will be the lack of the healthy prey due to disease in the prey population and therefore, the predator depends on the alternative food for their survival. Also, in population dynamics, growth is not instantaneous, it will take some time to perform, for example, the predator populations take some time to born a new offspring after mating is known as gestation delay. The simplest prey-predator models cannot capture the rich variety of dynamics and the inclusion of the gestation delay in these models makes them more realistic (Driver 1977; Beretta et al. 1995; Brauer 1990; Jin and Ma 2006).

In this paper, we have analyzed a prey-predator model with gestation delay for predator growth. We have considered that prey population is suffered from a communicable disease and the predator depends on alternative resources for their survival. This paper is organized as follows: in Sect. 2, formulation of the mathematical model is presented. In Sect. 3, positivity and boundedness of the system has been obtained. In Sect. 4, the stability criterion of the system is discussed at all the feasible equilibrium states and obtained the conditions for the existence of Hopf bifurcation at the disease-free and endemic equilibrium states. In Sect. 5, the sensitive parameters of the state variables are identified and in Sect. 6, we presented numerical simulations in support of our analytical findings. Finally, the results has been concluded in the last section.

Formulation of mathematical model

The assumptions of the proposed model are:

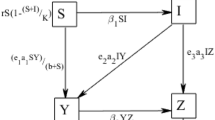
• (i) In a particular habitat, there are two populations; prey and predator. The prey population is suffered from a communicable disease, and it is divided into two mutually exclusive classes, susceptible S and infective I at any time t. The density of predator population at any time t is P.

• (ii) We suppose that due to the disease in the prey population, the infected individuals are unable to produce offsprings.

• (iii) The predator might get infected due to consumption of infected prey and dies out with a fixed rate h.

• (iv) $\tau$ is a gestation delay in predator growth.

• (v) The predator depends on healthy prey for their growth and due to lack of healthy prey, the predator also depends on alternative resources.

The proposed system is of the form:

$$\begin{aligned} \frac{dS}{dt} = aS\left( 1-\frac{S+I}{k}\right) -\frac{b SP}{S+l}-\beta S I, \end{aligned}$$

(1)

$$\begin{aligned} \frac{dI}{dt} = \beta S I-b_0IP-d_0I,\end{aligned}$$

(2)

$$\begin{aligned} \frac{dP}{dt} = cP-hIP+\frac{mbS(t-\tau )P(t-\tau )}{S(t-\tau )+l}-dP^2, \end{aligned}$$

(3)

with initial conditions:

$$\begin{aligned}& {S}(\alpha )=\psi _1(\alpha ),\ {I}(\alpha )=\psi _2(\alpha ),\ {P}(\alpha )=\psi _3(\alpha ), \hfill \\ & \quad \psi _1(0)>0,\ \psi _2(0)>0,\ \psi _3(0)>0, \end{aligned}$$

where $\alpha \in [-\tau ,0]$ and $\psi _1(\alpha )$, $\psi _2(\alpha )$, $\psi _3(\alpha ) \in \mathcal {C}([-\tau ,0], R_+^3)$, the Banach space of continuous functions mapping the interval $[-\tau ,0]$ into $R_+^3$, where $R_+^3=\{(x_1, x_2, x_3): x_i\ge 0, i=1,2,3\}$. The detail description of the parameters is stated in Table 1.

Table 1 Description of parameters for the system (1–3)

Positivity and boundedness of the system

We state and prove the following lemmas for the positivity and boundedness of the solution of the system (1–3):

Lemma 1

The solution of the Eqs. (1–3) with initial conditions are positive, for all $t\ge 0$.

Proof

For $t\in [0,\tau ]$, the Eq. (1) can be rewritten as

$$\begin{aligned} \frac{dS}{dt}\ge -aS\left( \frac{S+I}{k}\right) -\frac{b SP}{S+l}-\beta S I, \end{aligned}$$

and it follows that

$$\begin{aligned} S(t)\ge \frac{\exp \left\{ -\int _0^t\left( \frac{aI}{k}+\frac{b PS}{S(S+l)}+\beta I\right) du\right\} }{S(0)+\int _0^t a \exp \left\{ -\int _0^t\left( \frac{aI}{k}+\frac{b PS}{S(S+l)}+\beta I\right) du\right\} dv}>0. \end{aligned}$$

For $t\in [0,\tau ]$, the Eq. (2) can be rewritten as

$$\begin{aligned} \frac{dI}{dt}\ge -b_0IP-d_0I, \end{aligned}$$

which evidences that

$$\begin{aligned} I(t)\ge I(0)\exp \left\{ -\int _0^t(d_0+b_0P)du\right\} >0. \end{aligned}$$

The Eq. (3) for $t\in [0,\tau ]$ can be rewritten as

$$\begin{aligned} \frac{dP}{dt}\ge -hIP-dP^2, \end{aligned}$$

which implies that

$$\begin{aligned} P(t)\ge \frac{\exp \{ -\int _0^t hIdu\}}{P(0)+\int _0^td \exp \{ -\int _0^t hIdu\}}>0. \end{aligned}$$

Similarly, for the intervals $[\tau ,2\tau ],....,[n\tau ,(n+1)\tau ], n\in N$, it can be proved that S(t), I(t) and P(t) are positive. Thus by induction, S(t), I(t) and P(t) are positive for all $t\ge 0$. $\square$

Lemma 2

The solution of the Eqs. (1–3) with initial conditions is uniformly bounded in $\Omega$, where

$$\begin{aligned} \Omega = \left\{(S,I,P):0 \le S(t)+I(t)+P(t) \le \frac{k_2}{k_1}\right\}, \end{aligned}$$

$k_1=min\{d_1,d_2,d_3\}$ and $k_2=ak+\frac{c^2}{d}$.

Proof

Let $V(t)=S(t)+I(t)+P(t)$. Taking the derivative of V(t) with respect to t, we have

$$\begin{aligned} \begin{array}{ll} \frac{dV(t)}{dt} &= aS\left( 1-\frac{S+I}{k}\right) -\frac{b SP}{S+l}-b_0IP-d_0I+cP-hIP \\ & \quad +\frac{mb S(t-\tau )P(t-\tau )}{S(t-\tau )+l}-dP^2.\\ \end{array} \end{aligned}$$

Now $m<1$, therefore we have

$$\begin{aligned} \frac{dV(t)}{dt} \le aS\left( 1-\frac{S+I}{k}\right) -b_0IP-d_0I+cP-hIP-dP^2. \end{aligned}$$

Taking $k_1=min\{a,d_0,c\}$, we get

$$\begin{aligned} \frac{dV(t)}{dt}+k_1V\le & {} 2aS-aS\left( \frac{S+I}{k}\right) -b_0IP+2cP-hIP-dP^2.\\\le & {} 2aS-\frac{aS^2}{k}+2cP-dP^2. \end{aligned}$$

Further, we obtain

$$\begin{aligned} \frac{dV(t)}{dt}+k_1V\le k_2, \end{aligned}$$

where $k_2=ak+\frac{c^2}{d}$ is a positive constant.

On simplifying, it is obtained that

$$\begin{aligned} 0<V(t)\le V(0)e^{-k_1t}+\frac{k_2}{k_1}. \end{aligned}$$

As $t\rightarrow \infty$, we have

$$\begin{aligned} 0\le V(t)\le \frac{k_2}{k_1}. \end{aligned}$$

Therefore, V(t) is bounded. So, the solution of the system of Eqs. (1–3) with initial conditions is uniformly bounded in $\Omega$. $\square$

Dynamical behavior of the system

The system of equations (1–3) have the below mentioned equilibriums:

• (i) The equilibrium $E_0(0,0,0)$ always exists.

• (ii) The equilibrium $E_1(k,0,0)$ exists.

• (iii) The prey-free equilibrium $E_2(0,0,\frac{c}{d})$ exists.

• (iv) The predator-free equilibrium $E_3(S_3,I_3,0)$ exists, if ($\mathbf {H_1}$) holds, where

  $$\begin{aligned} S_3=\frac{d_0}{\beta },\ \ I_3=\frac{a(\beta k-d_0)}{\beta (\beta k+a)} \end{aligned}$$

  and

  $$\begin{aligned} (\mathbf {H_1}): \beta k-d_0>0. \end{aligned}$$

• (v) The disease-free equilibrium (DFE) $E_4(S_4,0,P_4)$ exists, where $S_4,$ $P_4$ is given by

  $$\begin{aligned} \left\{ \begin{array}{c} a\left( 1-\frac{S}{k}\right) -\frac{b P}{S+l}=0, \\ c+\frac{m b S}{S+l}-dP=0. \end{array} \right. \end{aligned}$$

  (4)

• (vi) The endemic equilibrium $E^*(S^*,I^*,P^*)$ exists, where $S^*,$ $I^*$, $P^*$ is given by

  $$\begin{aligned} \left\{ \begin{array}{c} a\left( 1-\frac{S+I}{k}\right) -\frac{b P}{S+l}-\beta I=0, \\ \beta S-b_0P-d_0=0,\\ c-hI+\frac{m b S}{S+l}-dP=0. \end{array} \right. \end{aligned}$$

  (5)

Now, we will discuss the local behavior of non-negative equilibria of the system (1–3).

Theorem 1

The local behavior of different equilibria of the system (1–3) is as follows;

• (i) $E_0(0,0,0)$ is unstable.

• (ii) $E_1(k,0,0)$ is unstable.

• (iii) $E_2(0,0,\frac{c}{d})$ is locally asymptotically stable for all $\tau ,$ if $(H_2)$ holds, otherwise it is unstable.

Proof

• (i) The characteristic equation for $E_0(0,0,0)$ is

  $$\begin{aligned} (\lambda -a)(\lambda +d_0)(\lambda -c)=0. \end{aligned}$$

  (6)

  The eigenvalues are $\lambda =a,$ $\lambda =-d_0,$ $\lambda =c$. The equilibrium $E_0(0,0,0)$ is unstable, because two of the eigenvalues of (6) are positive.

• (ii) The characteristic equation for $E_1(k,0,0)$ is

  $$\begin{aligned} (\lambda +a)(\lambda +d_0-\beta k)\left( \lambda -c-\frac{mb k}{k+l}e^{-\lambda \tau }\right) =0. \end{aligned}$$

  (7)

  The eigenvalues are $\lambda =-a,$ $\lambda =-(d_0-\beta k),$ $\lambda =c+\frac{m b k}{k+l}e^{-\lambda \tau }$. The equilibrium $E_1(k,0,0)$ is unstable because one eigenvalue of (7) is positive.

• (iii) The characteristic equation for $E_2(0,0,\frac{c}{d})$ is

  $$\begin{aligned} \left( \lambda -a+\frac{b c}{dl}\right) \left( \lambda +d_0+\frac{b_0c}{d}\right) (\lambda +c)=0. \end{aligned}$$

  (8)

  The eigenvalues are $\lambda =a-\frac{b c}{d l},$ $\lambda =-(d_0+\frac{b_0c}{d}),$ $\lambda =-c$. The equilibrium $E_2(0,0,\frac{c}{d})$ is locally asymptotically stable if $(\mathbf {H_2}): adl\le b c$ holds and it is unstable otherwise.

$\square$

Now similar to Ruan (2001), we will discuss the transcendental polynomial equation of the first degree

$$\begin{aligned} \lambda +r +qe^{-\lambda \tau }=0 \end{aligned}$$

(9)

for the following cases:

• $(A_1)$ $q+r>0$;

• $(A_2)$ $r^2-q^2>0$;

• $(A_3)$ $r^2-q^2<0$.

Lemma 3

For Eq. (9);

• (i) If $(A_1)-(A_2)$ holds, then for all $\tau \ge 0$, the roots of (9) are with negative real parts.

• (ii) If $(A_1)$ and $(A_3)$ hold and $\tau =\tau ^+_j$, then roots of equation (9) are purely imaginary $\pm iw_+.$ When $\tau =\tau _j^+$ then all roots of (9) except $\pm iw_+$ have negative real parts.

Proof

If $\tau =0$, then (9) can be written as

$$\begin{aligned} \lambda +r+q=0. \end{aligned}$$

(10)

Now the root of (10) is negative if and only if $(\mathbf {A_1})$: $q+r>0$ holds. If $\lambda =iw$, then from (9), we get

$$\begin{aligned} iw+r+qe^{-iw\tau }=0. \end{aligned}$$

(11)

Equating real and imaginary parts from (11), we get

$$\begin{aligned} q cosw\tau= -r, \end{aligned}$$

(12)

$$\begin{aligned} qsinw\tau= w. \end{aligned}$$

(13)

Solving (12, 13), we get

$$\begin{aligned} w^2+(r^2-q^2)=0. \end{aligned}$$

(14)

If $(\mathbf {A_2})$: $r^2-q^2>0$ holds, then (14) do not have positive roots and hence roots of (9) are not purely imaginary. If ($A_1$) holds, then the root of (10) is negative and hence by Rouche’s theorem, Eq. (9) roots with negative real parts. Therefore, if ($A_1$) and ($A_2$) holds, then the roots of (9) have negative real parts for all $\tau \ge 0.$

If $(\mathbf {A_3})$: $r^2-q^2<0$, then the Eq. (14) has a positive root and (9) has purely imaginary roots for certain values of $\tau$. The critical value of $\tau$ is given by

$$\begin{aligned} \tau _{k}^+=\frac{1}{w_0}\left[ \cos ^{-1}\left( -\frac{r}{q}\right) + 2k\pi \right] , \end{aligned}$$

where $k=0,1,2,....$

Therefore, if ($A_1$) and ($A_3$) holds and $\tau =\tau ^+_k$, then the roots of (9) have a pair of purely imaginary roots. $\square$

Theorem 2

If $(H_1)$, $(H_3$–$H_5)$ holds, then predator-free equilibrium $E_3(S_3, I_3, 0)$ is locally asymptotically stable for all $\tau$, otherwise it is unstable.

Proof

The characteristic equation at $E_3(S_3,I_3,0)$ may be written as:

$$\begin{aligned} F(\lambda )\left[ \lambda ^2-(a_1+b_2)\lambda +(a_1b_2-a_2b_1)\right] =0, \end{aligned}$$

(15)

where

$$\begin{aligned} F(\lambda )=\lambda -(d_3+c_3e^{-\lambda \tau }), \end{aligned}$$

and

$$\begin{aligned} a_1= a-\frac{2aS_3}{k}-\frac{aI_3}{k}-\beta I_3, \\ b_1= -\frac{aS_3}{k}-\beta S_3, \\ a_2= \beta I_3,\\ b_2= \beta S_3-d_0,\\ c_3= \frac{mb S_3}{S_3+l},\\ d_3= c-hI_3. \end{aligned}$$

When

$$\begin{aligned} \lambda ^2-(a_1+b_2)\lambda +(a_1b_2-a_2b_1)=0, \end{aligned}$$

(16)

then by Routh-Hurwitz criteria, the eigen values of (16) have negative real parts if $(\mathbf {H_3})$: $(a_1+b_2)<0$ and $(\mathbf {H_4})$: $(a_1b_2-a_2b_1)>0$ holds.

If $F(\lambda )=0$, then

$$\begin{aligned} \lambda -(d_3+c_3e^{-\lambda \tau })=0. \end{aligned}$$

(17)

Now (17) can be expressed as

$$\begin{aligned} \lambda +r+qe^{-\lambda \tau }=0, \end{aligned}$$

(18)

where $r=-d_3$, $q=-c_3$. Here q is always negative because $c_3$ is positive.

Using Lemma (3), $F(\lambda )=0$ have roots with negative real parts if $q+r>0$, that is, if $(\mathbf {H_5}): c_3+d_3<0$ holds. Thus the equilibrium $E_3(S_3, I_3,0)$ is locally asymptotically stable if ($H_1$), ($H_3$–$H_5$) holds.

Now, $F(\lambda )=0$ have a pair of purely imaginary roots by Lemma (3), if $-q<r<q$, which is impossible because q is negative. Therefore, Hopf bifurcation does not exists for the predator-free equilibrium $E_3(S_3, I_3,0)$. $\square$

Now, the following the second degree equation

$$\begin{aligned} \lambda ^2+p\lambda +r +(s\lambda +q)e^{-\lambda \tau }=0 \end{aligned}$$

(19)

has been studied by Ruan (2001) and discussed the following results:

• $(H_7)$ $p+s>0$;

• $(H_8)$ $q+r>0$;

• $(H_9)$ either $s^2-p^2+2r<0$ and $r^2-q^2>0$ or $(s^2-p^2+2r)^2<4(r^2-q^2)$;

• $(H_{10})$ either $r^2-q^2<0$ or $s^2-p^2+2r>0$ and $(s^2-p^2+2r)^2=4(r^2-q^2)$;

• $(H_{11})$ either $r^2-q^2>0, s^2-p^2+2r>0$ and $(s^2-p^2+2r)^2>4(r^2-q^2)$.

Lemma 4

see Ruan (2001) For Eq. (19);

• (i) If $(H_7$–$H_9)$ holds, then (19) have roots with negative real parts for all $\tau \ge 0$.

• (ii) If $(H_7)$, $(H_8)$ and $(H_{10})$ hold and $\tau =\tau ^+_j$, then (19) has a pair of purely imaginary roots $\pm iw_+.$ When $\tau =\tau _j^+$ then all roots of (19) except $\pm iw_+$ have negative real parts.

• (iii) If $(H_7)$, $(H_8)$ and $(H_{11})$ hold and $\tau =\tau ^+_j$($\tau =\tau ^-_j$ respectively) then (19) has a pair of purely imaginary roots $\pm iw_+$ ($\pm iw_-,$ respectively). Furthermore $\tau =\tau _j^+$ ($\tau _j^-,$ respectively),then all roots of (19) except $\pm iw_+$ ($\pm iw_-$, respectively) have negative real parts.

Theorem 3

Let $(H_6)$ holds. For the system (1–3), we have;

• (i) If $(H_7)$, $(H_8)$ and $(H_9)$ holds, then the disease-free equilibrium $E_4(S_4,0,P_4)$ is locally asymptotically stable for all $\tau .$

• (ii) If $(H_7)$, $(H_8)$ and $(H_{10})$ holds, then the equilibrium $E_4(S_4,0,P_4)$ is locally asymptotically stable for all $\tau \in [0,\tau _{0}^+),$ and unstable when $\tau \ge \tau _{0}^+.$

Proof

The characteristic equation of the jacobian matrix at $E_4(S_4,0,P_4)$ can be written as:

$$\begin{aligned} (\lambda -b_2)F(\lambda )=0, \end{aligned}$$

(20)

where

$$\begin{aligned} F(\lambda )=\lambda ^2-(a_1+d_3)\lambda +a_1d_3+(a_1c_3-a_3c_1-c_3\lambda )e^{-\lambda \tau }, \end{aligned}$$

and

$$\begin{aligned} a_1&= a-\frac{2aS_4}{k}-\frac{b P_4}{S_4+l}+\frac{b S_4 P_4}{(S_4+l)^2}, \\ c_1&= -\frac{b S_4}{S_4+l},\\ b_2&= \beta S_4-b_0 P_4-d_0,\\ a_3&= \frac{m b P_4}{S_4+l}- \frac{m b S_4P_4}{(S_4+l)^2},\\ c_3&= \frac{m b S_4}{S_4+l},\\ d_3&= c-2dP_4. \end{aligned}$$

Assume $(\mathbf {H_6})$: $b_2<0$ holds.

If $F(\lambda )=0$, then we have

$$\begin{aligned} \lambda ^2-(a_1+d_3)\lambda +a_1d_3+(a_1c_3-a_3c_1-c_3\lambda )e^{-\lambda \tau }=0. \end{aligned}$$

(21)

Equation (21) can be written as

$$\begin{aligned} {\lambda }^2+p\lambda +r+(s\lambda +q)e^{-\lambda \tau }=0, \end{aligned}$$

(22)

where

$$\begin{aligned} p&=-(a_1+d_3),\\ r&=a_1d_3,\\ s&=-c_3,\\ q&=a_1c_3-a_3c_1.\end{aligned}$$

Case I: In the absence of delay $\tau _2=0$, we get

$$\begin{aligned} \lambda ^2+(p+s)\lambda +(q+r)=0. \end{aligned}$$

(23)

If $({H_7})$ and $({H_8})$ holds, then all the roots of (21) have negative real parts. Hence the equilibrium $E_4(S_4, 0, P_4)$ is locally asymptotically stable.

Case II: If $\tau >0$, then we get

$$\begin{aligned} {\lambda }^2+p\lambda +r+(s\lambda +q)e^{-\lambda \tau }=0. \end{aligned}$$

(24)

Using Lemma 4, if $(H_7)$, $(H_8)$ and $(H_9)$ holds, then the system (1–3) has roots with negative real parts and hence the system is locally asymptotically stable.

Further, using Lemma 4, if $(H_7)$, $(H_8)$ and $(H_{10})$ holds, then the system (1–3) has a pair of purely imaginary roots.

Put $\lambda =iw$ in (24), we get

$$\begin{aligned} {(iw) }^2+p(iw)+r+(iws +q)e^{-iw \tau }=0. \end{aligned}$$

(25)

Equating real and imaginary parts from (25), we get

$$\begin{aligned} -w^2+r+sw\sin {w\tau }+q\cos w\tau =0,\end{aligned}$$

(26)

$$\begin{aligned} pw+sw\cos w\tau -q\sin w\tau =0. \end{aligned}$$

(27)

Solving (26) and (27), we get

$$\begin{aligned} \sin w\tau= & {} \frac{sw^3+(pq-rs)w}{s^2w^2+q^2},\end{aligned}$$

(28)

$$\begin{aligned} \cos w\tau= & {} \frac{(q-ps)w^2-qr}{s^2w^2+q^2}, \end{aligned}$$

(29)

and

$$\begin{aligned} w^4+(p^2-2r-s^2)w^2+(r^2-q^2)=0. \end{aligned}$$

(30)

We define

$$\begin{aligned} F(w)=w^4+(p^2-2r-s^2)w^2+(r^2-q^2)=0. \end{aligned}$$

By Descart’s rule of sign, there is at least one positive root of $F(w)=0$. Let $w_0$ is the positive root of $F(w)=0.$ From (29), we get

$$\begin{aligned} \tau _{k}^+=\frac{1}{w_0}\left[ \cos ^{-1}\left( \frac{(q-ps){w_0}^2-qr}{s^2{w_0}^2+q^2}\right) + 2k\pi \right] , \end{aligned}$$

where $k=0,1,2,....$

Differentiating (24) with respect to $\tau$, we get

$$\begin{aligned} \frac{d\lambda }{d\tau }=\frac{\lambda (s\lambda +q)e^{-\lambda \tau }}{2\lambda +p+se^{-\lambda \tau }-(s\lambda +q)\tau e^{-\lambda \tau }}. \end{aligned}$$

At $\lambda =iw_0$ and $\tau =\tau _{0}^+$, we have

$$\begin{aligned} Re\left( \frac{d\lambda }{d\tau }\right) ^{-1}=\frac{qG-sw_0H}{w_0(q^2+s^2w_0^2)}, \end{aligned}$$

(31)

where $G=p sin w_0 \tau _0+2w_0 cosw_0 \tau _0$ and $H=s+pcosw_0\tau _0-2w_0sinw_0\tau _0$.

Simplifying (31), we have

$Re\left[ \left( \frac{d\lambda }{d\tau }\right) ^{-1}\right] _{\tau =\tau _{0}^+}\ne 0,$ if $qG\ne sw_0H$. $\square$

Now, we state a lemma as similar as given in Song et al. (2005).

Lemma 5

For the polynomial equation $z^3+pz^2+qz+r=0$,

• (i) If $r<0$, then the equation has at least one positive root;

• (ii) If $r\ge 0$ and $\triangle ={p}^2-3q\le 0,$ the equation has no positive root;

• (iii) If $r\ge 0$ and $\triangle ={p}^2-3q>0,$ the equation has positive roots iff $z_1^*=\frac{-p+\sqrt{\triangle }}{3}$ and $h(z_1^*)\le 0,$ where $h(z)=z^3+pz^2+qz+r$.

Theorem 4

Let $(H_{12})$ holds. For the system (1–3),

• (i) The endemic equilibrium $E^*(S^*,I^*,P^*)$ is locally asymptotically stable for all $\tau \in [0,\tau _{0}^+)$.

• (ii) If $\tau \ge \tau _{0}^+$, then the endemic equilibrium $E^*(S^*,I^*,P^*)$ is unstable and undergoes Hopf bifurcation.

Proof

The characteristic equation of the jacobian matrix at $E^{*}(S^{*},I^{*},P^{*})$ can be written as:

$$\begin{aligned} {\lambda }^3+A \lambda ^2+ B \lambda + C +( F \lambda ^2 + E \lambda + D)e^{-\lambda \tau }=0, \end{aligned}$$

(32)

where

$$\begin{aligned} A &= -(a_1+b_2 + d_3),\\ B &= b_2 d_3 - b_3 c_2 - a_2 b_1+a_1d_3 +a_1 b_2,\\ C &= a_2b_1d_3+a_1b_3c_2-a_1b_2 d_3 -a_2 b_3 c_1,\\ D &= a_2 b_1 c_3 - a_1 b_2 c_3 -a_3 b_1 c_2+ a_3 b_2 c_1,\\ E& = b_2c_3+a_1c_3-a_3c_1,\\ F &= -c_3, \end{aligned}$$

and

$$\begin{aligned} a_1 & = a-\frac{2aS^*}{k}-\frac{aI^*}{k}-\frac{b P^*}{S^*+l}+\frac{b S^* P^*}{(S^*+l)^2}-\beta I^*, \\ b_1 & = -\frac{aS^*}{k}-\beta S^*, \\ c_1 &= -\frac{b S^*}{S^*+l},\\ a_2 &= \beta I^*,\\ b_2 &= \beta S^*-b_0 P^*-d_0,\\ c_2 &= -b_0I^*,\\ a_3 &= \frac{mb P^*}{S^*+l}- \frac{mb S^*P^*}{(S^*+l)^2},\\ b_3 &= -h P^*,\\ c_3 &= \frac{m b S^*}{S^*+l},\\ d_3 &= c-hI^*-2dP^*. \end{aligned}$$

In the absence of delay ($\tau =0$), the transcendental equation (32) reduces to

$$\begin{aligned} {\lambda }^3+(A+F) \lambda ^2+ (B+E) \lambda + (C+D)=0, \end{aligned}$$

(33)

where

$$\begin{aligned} \begin{array}{ll} A+F& = -(a_1+b_2 + c_3 + d_3),\\ B+E& = b_2 d_3 - b_3 c_2 - a_2 b_1+a_1d_3 +a_1 b_2+b_2c_3+a_1c_3-a_3c_1,\\ C+D&= a_2b_1d_3+a_1b_3c_2-a_1b_2 d_3 -a_2 b_3 c_1+a_2 b_1 c_3 - a_1 b_2 c_3 -a_3 b_1 c_2+ a_3 b_2 c_1. \end{array} \end{aligned}$$

By Routh-Hurwitz criterion, all the roots of Eq. (33) have negative real parts and the equilibrium $E^*$ is locally asymptotically stable if $(\mathbf {H_{12}}):$ $A+F,$ $B+E,$ $C+D>0$ and $(A+F)(B+E)-(C+D)>0$ holds.

Assume that $\lambda =iw$ is root of (32), therefore we have

$$\begin{aligned} &{(iw) }^3+A(iw)^2+B(iw)+C \hfill \\ & \quad +(F(iw)^2+E(iw) +D)e^{-iw \tau }=0. \end{aligned}$$

(34)

Equating real and imaginary parts from (34), it can be obtained

$$\begin{aligned} Ew\sin {w\tau }+(D-Fw^2)\cos w\tau =Aw^2-C,\end{aligned}$$

(35)

$$\begin{aligned} Ew\cos w\tau -(D-Fw^2)\sin w\tau =w^3-Bw. \end{aligned}$$

(36)

Solving (35) and (36), we get

$$\begin{aligned} w^6+pw^4+qw^2+r=0, \end{aligned}$$

(37)

where

$$\begin{aligned} p&=A^2-2B-F^2,\\ q&=B^2-2AC+2DF-E^2,\\ r&=C^2-D^2. \end{aligned}$$

By substituting $w^2=z$ in equation (37), we define

$$\begin{aligned} F(z)=z^3+pz^2+qz+r. \end{aligned}$$

By Lemma 5, there exists at least one positive root $w=w_0$ of equation (37) satisfying (35) and (36), which implies that (32) has a pair of purely imaginary roots $\pm iw_0$. Solving (35) and (36) for $\tau$ and substituting the value of $w=w_0$, the corresponding $\tau _k>0$ is given by

$$\begin{aligned} \tau _k^+=\frac{1}{w_0}\left[ \cos ^{-1}\left( \frac{(E-AF)w_0^4+(AD+CF-BE)w_0^2-CD}{E^2w_0^2+(D-Fw_0^2)^2}\right) + 2k\pi \right] , \end{aligned}$$

where $k=0,1,2,....$

Differentiating equation (32) with respect to $\tau$, we get

$$\begin{aligned} \left( \frac{d\lambda }{d\tau }\right) ^{-1}=\frac{(3\lambda ^2+2A\lambda +B)e^{\lambda \tau }+(2F\lambda +E)}{\lambda (F\lambda ^2+E\lambda +D)}-\frac{\tau }{\lambda }. \end{aligned}$$

At $\lambda =iw$ and $\tau =\tau _0^+$, we have

$$\begin{aligned} Re \left[ \left( \frac{d\lambda }{d\tau }\right) ^{-1}\right] =\frac{MQ-NR}{w_0(L^2+M^2)}, \end{aligned}$$

where $K=-3w_0^2+B,$ $L=2Aw_0,$ $M=D-Fw_0^2,$ $N=Ew_0,$ $Q=K$sin$w_0 \tau _0+L$cos$w_0 \tau _0+2 Fw_0$ and $R=K$cos$w_0 \tau _0-L$sin$w_0 \tau _0+E.$

Now, we have $Re\left[ \left( \frac{d\lambda }{d\tau }\right) ^{-1}\right] _{\tau =\tau _0^+}\ne 0,$ if $MQ\ne NR.$ $\square$

Sensitivity analysis

Table 2 The sensitivity indices $\gamma _{y_j}^{x_i}=\frac{\partial x_i}{\partial y_j}\times \frac{y_j}{x_i}$ of the state variables of the system (1–3) to the parameters $y_j$ for the parameter values $a = 0.5$; $k = 5$; $b = 0.4$; $l = 2$; $\beta = 0.8$; $b_0 = 0.1$; $d_0 = 0.5$; $c = 0.9$; $h = 0.04$; $m = 0.6$; $d = 0.5$

Fig. 1

The prey-free equilibrium $E_2(0,0,1.09)$ is stable for parameteric values $a = 0.8$; $k = 3$; $b = 1.6$; $l = 2$; $\beta = 0.2$; $b_0 = 0.1$; $d_0 = 0.5$; $c = 0.6$; $h = 0.04$; $m = 0.9$; $d = 0.55$

Fig. 2

The predator-free equilibrium $E_3(1,1.33,0)$ is stable for parameteric values $a = 0.5$; $k = 5$; $b = 0.25$; $l = 1.25$; $\beta = 0.2$; $b_0 = 0.01$; $d_0 = 0.2$; $c = 0.01$; $h = 0.1$; $m = 0.8$; $d = 0.1$

Fig. 3

The DFE equilibrium point $E_4(0.66,0,0.99)$ is stable for parameteric values $a = 0.8$; $k = 10$; $b= 2$; $l = 2$; $\beta = 0.2$; $b_0 = 0.1$; $d_0 = 0.2$; $c = 0.1$; $h = 0.1$; $m = 0.8$; $d = 0.5$; $\tau =1.44<\tau _0^+=1.5$

Fig. 4

The DFE equilibrium point $E_4(0.66,0,0.99)$ is unstable and Hopf bifurcation appears for the parameteric values $a = 0.8$; $k = 10$; $b = 2$; $l= 2$; $\beta = 0.2$; $b_0 = 0.1$; $d_0 = 0.2$; $c = 0.1$; $h = 0.1$; $m = 0.8$; $d = 0.5$; $\tau =1.52>\tau _0^+=1.5$

Fig. 5

The endemic equilibrium point $E^{*}$ is stable for parameteric values $a=0.5;$ $k=5;$ $b =0.4;$ $l = 2;$ $\beta = 0.8;$ $b_0 = 0.1;$ $d_0= 0.5;$ $c = 0.9;$ $h = 0.04;$ $m=0.6;$ $d=0.5;$ $\tau =6.6<\tau _0^+=6.7$

Fig. 6

The endemic equilibrium point $E^{*}$ is unstable and Hopf bifurcation appears for the parameteric values $a=0.5;$ $k=5;$ $b=0.4;$ $l=2;$ $\beta = 0.8;$ $b_0 = 0.1;$ $d_0= 0.5;$ $c = 0.9;$ $h = 0.04;$ $m=0.6;$ $d=0.5;$ $\tau =6.8>\tau _0^+=6.7$

In this section, we perform the sensitivity analysis of state variables of the system (1–3) with respect to the model parameters at the endemic equilibrium state. The respective sensitive parameters of the state variables at the endemic equilibrium are shown in the Table 2 using parameter values $a = 0.5$; $k = 5$; $b = 0.4$; $l = 2$; $\beta = 0.8$; $b_0 = 0.1$; $d_0 = 0.5$; $c = 0.9$; $h = 0.04$; $m = 0.6$; $d = 0.5$. We observe that b, $b_0$, $d_0$, c, m have a positive impact on the $S^*$ and the rest of the parameters have a negative impact. Moreover $\beta$ is the most sensitive parameter to $S^*$. Again a, b, l, $\beta$, c and d are more sensitive parameter to $I^*$ than other parameters. Further c and d are the most sensitive parameter to $P^*$ and all the other parameters are less sensitive to $P^*$.

Numerical simulations

We perform the numerical simulations of the model (1–3) to justify the analytic findings. We use initial population sizes as $S_0=2,\ I_0=0.1,\ P_0=2$. From Fig. 1, we observe that the prey-free equilibrium $E_2 (0,0,1.09)$ is stable for parameter values $a = 0.8$; $k = 3$; $b = 1.6$; $l = 2$; $\beta = 0.2$; $b_0 = 0.1$; $d_0 = 0.5$; $c = 0.6$; $h = 0.04$; $m = 0.9$; $d = 0.55$, which establish the Theorem 1.

It is observed from Fig. 2 that the predator-free equilibrium $E_3 (1,1.33,0)$ is stable for parameter values $a = 0.5$; $k = 5$; $b = 0.25$; $l = 1.25$; $\beta = 0.2$; $b_0 = 0.01$; $d_0 = 0.2$; $c = 0.01$; $h = 0.1$; $m = 0.8$; $d = 0.1$, which results that the Theorem 2 holds good.

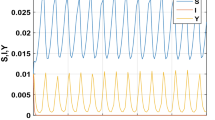
The DFE equilibrium point $E_4 (0.66,0,0.99)$ is stable for parameter values $a = 0.8$; $k = 10$; $b=2$; $l=2$; $\beta = 0.2$; $b_0 = 0.1$; $d_0 = 0.2$; $c = 0.1$; $h = 0.1$; $m = 0.8$; $d = 0.5$; $\tau =1.44<\tau _0^+=1.5$ (see Fig. 3) and Hopf bifurcation exists for $\tau =1.52>\tau _0^+=1.5$ (see Fig. 4), which shows that the Theorem 3 is true.

The endemic equilibrium point $E^ {*}$ is stable for parameter values $a=0. 5$; $k=5$; $b=0.4$; $l=2$; $\beta = 0.8$; $b_0 = 0.1$; $d_0= 0.5$; $c = 0.9$; $h = 0.04$; $m=0. 6$; $d=0. 5$; $\tau =6.6<\tau _0^+=6.7$ (see Fig. 5) and the equilibrium is unstable and Hopf bifurcation appears for $\tau =6.8>\tau _0^+=6.7$ (see Fig. 6), which is in accordance with the results stated in the Theorem 4.

Conclusions

In this paper, we proposed a prey-predator system with predator depends on alternative resources, disease in the prey and maturation delay for predator. We investigated the asymptotic stability of the model for all the feasible equilibrium states. The existence of Hopf bifurcation in the disease-free and endemic equilibrium states is explored. It is established that the disease-free equilibrium $E_4(S_4, 0, P_4)$ as well as endemic equilibrium $E^*(S^*,I^*,P^*)$, both exhibit Hopf bifurcation, when the gestation delay for predator ($\tau$) is greater than or equal to their corresponding critical value ($\tau _{0}^+$) under certain respective conditions. Finally, the normalized forward sensitivity indices are calculated for the state variables at the endemic equilibrium state with respect to the various parameters. Numerical simulations of the system are performed with a particular set of parameters to justify our analytic findings.