Impact of physical and behavioral prey refuge on the stability and bifurcation of Gause type Filippov prey-predator system

Abstract

After the pioneering theoretical studies of Lotka and Volterra, Gause and his co-workers replace the previously used linear functional response by using a saturating functional response with a discontinuity at a threshold prey density. Here we assume that prey density at below this threshold value is effectively and successfully in a refuge patch. In this situation there is no food option for predator and go to extinction. But above this threshold value surplus density of prey is available to predator for its diet. But the system does not show any future activities when prey density is in the vicinity of the threshold density, system is ill posed because the trajectories are not well defined here. In the present study, we redefine and analyze the model by using Filippov regularization method. By this continuation method, the system becomes well posed and gives more results as predicted by Gause. Also predator fully depends upon alternative diet to survive from extinction risk when prey is in refuge patch and system largely varies with the availability of alternative diet resource but in the later case predator again switches to its primary (essential) food. When prey density is in the vicinity of the threshold density, then predator may choose its deit preferentially from essential or alternative resources according to its profit. Numerical examples support these hypothesis and analytical results.

Introduction

Theoretical ecology is the scientific study and esthetic analysis of interactions among organisms and their environment. Ecosystem is composed of dynamically interacting parts including organisms, the communities they make up and the non-living components of their environment. The dynamic relationship between predator and its prey has long been and will continue to be one of the dominant themes in both ecology and mathematical ecology due to its universal existence and importance (Berryman 1992). After the pioneering theoretical studies of Lotka (1925) and Volterra (1931), their predictions are experimentally tested by Gause (1934) and his co-workers (Gause et al. 1936). Gause focuses on three experiments consisting of prey (Aleuroglyphus agilis) and predatory (Cheyletus eruditus) mites, prey (Paramecium caudatum) and predator (Didinium nasatum) protists and yeast (Saccharomyces exiguus) and protists (Paramecium bursaria). The results of these experiments are not consistent with the Lotka–Volterra neutrally stable limit cycles, such as a prolong coexistence of prey and predator are obtained by regularly adding protists and mites where as, in a completely homogeneous environment Didinium destructs all prey and it collapses subsequently.

When the environment is not homogeneous and there is a structural diversity of habitat, then the propagation of life of both prey and predator and also their interrelationship (Alstad 2001; Anderson 1984) largely depends and varies upon the structure of habitat and more prominently their habitat selection (Anderson 2001; Johnson 2006). Refuge means a place or state of safety, provides in the literature is rather elastic. An implicit definition of “refuge” is often tied into the concept of barrier for population dispersal. Meta-population, population makes up of sub populations of weak dispersal moving through weakly connected (due to, for example, the presence of population barriers) networks of patches, face limited intraspecific competition and as a consequence tend to be stable. Predator’s functional response, defines as the amount of prey catch per predator per unit of time, is affected by the structure of prey habitat and predator’s hunting ability (Alstad 2001; Anderson 1984). The use of spatial refuge by prey is one of the more relevant behavioral traits that decreases predation rate, e.g., spatial or temporal refuge, behavioral or physical refuge, prey aggregation or reducing search activity by prey. The smell, color, injection of some poisonous agent, size, skin, body cover etc may be used as different form of refuges, which can be used to save the prey species from its predator. Environmental heterogeneity enhances spatial refuges of prey which provides less accessible sites for predator to capture prey. By using refuge, some numbers of the prey population are protected against predator. The work assumes physical (non-adaptive) refuge used by prey - either a constant number or proportion of prey stays in the refuge patch (Gonzalez-Olivares and Ramos-Jiliberto 2003; Kar 2005; Chen et al. 2010; Jana 2013, 2014). However, due to the decreasing resource, prey fitness (food intake or mating opportunity) gradually decreases. In the refuge patch there is no predation risk for the prey population and if their resources are not limiting the survival rate is increased. So, it has been documented that due to increasing foraging efficiency in an open patch, prey can reduce their activities and change their suitable habitat adaptively (Sih 1980, 1986, 1987; Ives and Dobson 1987; Lima and Dill 1990; Ruxton 1995; Křivan 1997, 1998, 2011, 2013; Peacor and Werner 2001; Brown and Kotler 2004). There has been a great deal of research on the effect of prey refuge (physical/ non-adaptive and behavioral/ adaptive) on the population dynamics (Kar 2005; Křivan 1997, 1998, 2011, 2013; Jana 2013, 2014).

Extinction is part of natural world. If we are to understand the causes of extinction, we shall have to comprehend many aspects of ecology and evolution. Population viability analysis (PVA) is a process of determining whether a particular recovery or restoration strategy will lead to success. PVA involves the consideration of information from all aspects of life history of the population (Ricklefs and Miller 2000). So, to rescue the population at any tropic level from extinction risk, for example, due to the lack of essential food in a diverse habitat, is a very important PVA. Alternative food source is a very important and prominent strategy when any population is suffering from lack of essential food. When a population moves through a habitat in search of food, it sequentially encounters potential or more available food with each encounter, the population is confronted with the choice of pursuing and eating the profitable food (Ricklefs and Miller 2000). Prey switching is a frequency-dependent predation, where the predator preferentially consumes the most common type of prey. The phenomenon has also been described as apostatic selection. The term ‘switching’ is first coined by the ecologist Murdoch (1969) to describe the situation where a predator eats disproportionately more of the most common type of prey. Clarke (1962) describes a similar phenomenon. The diet choice models (Charnov 1976; Stephens and Krebs 1986) assume that predator feeds potential prey type on the basis of their profitability and also predict that at low preferred prey density, the interaction possibility between prey and predator sharply decreases due to their switching tendency to alternative food temporarily or permanently. Since then the term prey switching has mainly been used by ecologists. Different aspects of frequency dependent selection is also very important for prey population. Such a situation is more complex as prey fitness not only depends on predator abundance but also their own abundance. This phenomena makes the frequency dependent prey fitness (Colombo and Křivan 1993; Cressman and Křivan 2006, 2013; Křivan 1997, 1998, 2011, 2013) and finally the predator’s optimal foraging strategy can create a behavioral prey refuge (Oaten and Murdoch 1975; Charnov 1976; Holt 1983; Fryxell and Lundberg 1994, 1997; Abrams and Matsuda 1996; Křivan 1997, 2011, 2013; Abrams 1999; Křivan and Eisner 2003; Ma et al. 2003).

Ray and Straškraba (2001) notice that the prey species, i.e., detritivorous fish and their predator species, carnivorous fish coexist in Sundarban Mangrove ecosystem. In the pristine part of the ecosystem where forest is dense, the production of detritus is high and the detritivorous fish can easily take refuge in the densely inundated bushy part of the forest to avoid predation by carnivorous fish. In this part the production and densities of both prey and predator fish are high and coexist with each other. But in the reclaimed part of the forest where there is huge anthropogenic stress, production of detritus is less and due to lack of bushy part of the forest the area for refuge of prey species is minimum. In this reclaimed area prey density (detritivorous fish) is reduced at an alarming level but predator fish population is also slightly reduced because this fish population has switched its food habit to other fish and animals (Roy et al. 2008). In a completely homogeneous environment Didinium nasatum destructs all prey and it collapses subsequently. When the environment is not homogeneous and there is a refuge of total prey population, the population survives in the refuge but the predator population collapses. The situation is different when protists fed on the yeast, here a fraction of yeast population undergoes refuse. This strong experimental evidence suggests that in this type of situation population dynamics of both prey and predator tend to a limit cycle. The above observations lead Gause et al. (1936) to search for discrepancies in assumptions of the Lotka–Volterra prey-predator model. First, they observe that protists are not able to feed on yeast at low densities because at low yeast densities the population hide into the sediment at the bottom which is not accessible to predator inhabiting the water column. Thus, prey is effectively and successfully in a refuge when at low concentrations (Kar 2005; Křivan 1997, 1998, 2011, 2013; Jana 2013, 2014; Jana et al. 2015). When prey reaches above the critical density, it reappears in the water column and becomes accessible to predator (Kar 2005; Křivan 1997, 1998, 2011, 2013; Jana 2013, 2014; Jana et al. 2015). So, when prey density is below its critical density, then there is a possibility of predator’s collapse. In that condition predator can switch their diet resources to another prey in the context of behavioral prey refuge (Oaten and Murdoch 1975; Charnov 1976; Holt 1983; Fryxell and Lundberg 1994, 1997; Abrams and Matsuda 1996; Křivan 1997, 2011, 2013; Abrams 1999; Křivan and Eisner 2003; Ma et al. 2003). This phenomena can avoid predator extinction possibility. But when prey density reaches above its critical density, predator switches to its essential (primary) food. At the vicinity of critical prey density predator starts switching from primary to alternative food sources or vice versa.

In the next section, we construct the model on the basis of Gause’s observation where the prey population is protected by a refuge of constant strength, when prey density below this threshold strength they are effectively and successfully in the refuge, above which only the surplus density is available for predation. In the vicinity of the critical value of prey density predator switches its primary to alternative food and vice versa. Mathematically till now the system is not defined in this vicinity because the trajectories are not well studied. In “Filippov regularization”, we analyze the system at this vicinity by applying Filippov regularization method for better understanding. Numerical examples support all the assumptions and their corresponding results throughout the study.

Model and analysis

Gause et al. (1936) consider the following form of Lotka–Volterra prey-predator system as

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=xf(x)-yg(x), \\ \frac{dy}{dt}=(eg(x)-m)y. \end{array} \end{aligned}$$

(1)

Here, x and y are the densities of logistically growing prey [with intrinsic growth rate r and carrying capacity k in the form $f=r(1-\frac{x}{k})$] and its predator population (with food conversion efficiency e and mortality rate m) respectively. Predator’s functional response is defined as the rate of prey captured by a predator per unit of time and here g is the Gause functional response which is specified bellow.

A constant number of the prey population is always protected from the hunting ability of predator, this is the refuge area and this sub-habitat conceives mostly a low density of prey (say, $x_c$) (Gause et al. 1936; Maynard Smith 1974). These models assume that prey prefer to be in the refuge and only when the refuge is fully occupied, the surplus of prey moves outside. So, there are three prominent distinct dynamical features of the predation process.

• 1. Up to the critical prey population threshold ($x<x_c$), prey is not consumed by predator. This situation corresponds to the refuge of prey in a constant size $x_c$.

• 2. When the prey density is above its critical value ($x>x_c$), then surplus of the prey population ($x-x_c$) is accessible for predation.

• 3. Consumption saturates with increasing prey density (Gause et al. 1936).

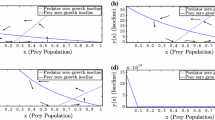
The jump at the critical prey density is motivated by their observation (Gause et al. 1936). This suggests that the functional response in the vicinity of $x=x_c$ is quite steep and can be approximated by a functional response with a jump discontinuity at $x=x_c$. Such a functional response is given by (see Fig. 1a)

Fig. 1

a Gause functional response (2). b Filipov regularization (6) of Gause functional response. Parameters: $\alpha =0.45, h=0.0437$

$$\begin{aligned} g(x)=\left\{ \begin{array}{ll} 0 \quad & x<x_c \\ \frac{\alpha (x-x_c)}{1+\alpha h (x-x_c)} \quad & x>x_c \end{array}\right. \end{aligned}$$

(2)

here $\alpha$ and h describe the attack rate and the handling time that a predator needs to process one unit of prey. $x_c$ is the intensity of prey refuge, i.e., a critical prey density below which prey are not accessible to predator. Thus, for above the critical prey density, g is the Holling type II functional response (Holling 1959). For prey population density below the threshold ($x<x_c$), prey is not being eaten by predator, grows logistically while predator dies exponentially, i.e., model (1) becomes

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=rx(1-\frac{x}{k}), \\ \frac{dy}{dt}=-my. \end{array} \end{aligned}$$

(3)

The nullclines define domains in the phase plane (xy-plane) in which the population rate of change does not change sign. The nullclines provide some insights regarding existence of equilibrium points and their stability behaviors. The equilibrium point, formed by the intersection of the prey and predator nullclines, is stable if $\frac{dy}{dx}<0$, unstable if $\frac{dy}{dx}>0$ and Hopf bifurcation occurs at local maxia and minima (Robert 1976; Rosenzweig 1969; Rosenzweig and MacArthur 1963). For small prey density which satisfying $x<x_c$ (grey regions in the xy-plane of Fig. 2a–c), there is only trivial prey nullcline, $x=0$ and trivial predator nullcline, $y=0$ and their intersection defines the trivial equilibrium point of the system ($E_0(0,0)$) and dynamically it is unstable node (UN). Thus, at each point of the prey-predator density phase plane to the left of the critical prey density $x=x_c$, trajectories move in the south-east direction (grey regions in the xy-plane of Fig. 3i–iv).

Fig. 2

Nullclines of system (4). Parameters: $r=3.3, k=900, \alpha =0.45, e=0.215, m=1.06$

For prey population density above the threshold ($x>x_c$), population dynamics (1) is given by the Lotka–Volterra model with the Holling type-II functional response [functional response (2)]

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=rx\left(1-\frac{x}{k}\right)-\frac{\alpha (x-x_c)y}{1+\alpha h (x-x_c)}, \\ \frac{dy}{dt}=\left(\frac{e\alpha (x-x_c)}{1+\alpha h (x-x_c)}-m\right)y. \end{array} \end{aligned}$$

(4)

There is only one non trivial prey nullcline $y=\frac{rx(k-x)\{1+\alpha h (x-x_c)\}}{\alpha k (x-x_c)}$, this is a sigmoid curve with vertex at $x=\underline{x}$ which is the positive root/roots of

$$\begin{aligned} (x-x_c)[r(k-2x)\{1+\alpha h(x-x_c)\}+r\alpha hx(k-x)]-rx(k-x)\{1+\alpha h(x-x_c)\}=0, \end{aligned}$$

and intersects positive x-axis at $x=k$. The predator nullclines, where $\frac{dy}{dt}=0$, are $y=0$ and the vertical line $x = \frac{m}{\alpha (e-mh)}+x_c$. If we vary intensity of prey refuge parameter $x_c$ with $h=0.17$ (other parameters are as in Fig. 1), we observe that when $x_c<184.27$, then $\frac{dy}{dx}>0$ and $E^{*}$ is unstable; $184.27<x_c<k$, then $\frac{dy}{dx}<0$ and $E^{*}$ is stable and $x_c=184.27$ there is a Hopf-bifurcation at $E^{*}$ (Fig. 2a). Similarly if we vary h with $x_c=200$ (other parameters are as in Fig. 1), then system is stable in $(0,h_1)\bigcup (h_2,h_3)$, unstable in $(h_1,h_2)$, Hopf-bifurcation occurs at $h_1$ and $h_2$ and transcritical bifurcation occurs between $E^{*}$ and $E_k$ at $h_3$, where $h_1=0.1708$ (Fig. 2b), $h_2=0.15$ (Fig. 2c), $h_3=0.199$ . Thus, the dynamical features of the model system (4) are given by Table 1.

Table 1 Equilibrium points of the model system (4), their feasibility and stability conditions

Fig. 3

a Stability region of system (4) in $x_c h$-plane where $R_i$ ($i=1,2,3,4$) are different stability sub-regions. $E^{*}$: stable node, stable focus, unstable focus and infeasible in the region $R_1, R_2, R_3$ and $R_4$ respectively. $E_k$: feasible in whole plane, unstable node and stable node in $\bigcup _{i=1}^{3}R_i$ and $R_4$. A Hopf bifurcation occurs on $H_b$ points (red line) and a transcritical bifurcation between $E^{*}$ and $E_k$ occurs on $t_b$ points (green line). Panel i are phase plane diagrams of the system (3) (grey block) and (4) (white block) corresponding to region $R_i$ where unstable and stable $E^{*}$ are indicated by red (iii) and green bullet (i, ii), stable limit cycle is shown by green closed loop (iii) and stable $E_k$ is shown by blue bullet (iv). Parameters: $r=3.3, k=900, x_c=100, \alpha =0.45, e=0.215, m=1.06$

Existence of limit cycle and its uniqueness

It is known for prey-predator system that the existence and stability of a limit cycle is related to the existence and stability of the interior equilibrium. If the interior equilibrium point $E^{*}$ exists and any limit cycle does not exist, then the equilibrium point $E^{*}$ is globally asymptotically stable. On the other hand, if an interior point exists and is unstable, there must occur at least one limit cycle. Using the Theorem 4.3 of Kuang and Freedman (1988), one can see that the system (4) has exactly one limit cycle which is globally asymptotically stable (green closed loop in Fig. 3iii, all trajectories with different initial condition (x(0), y(0)) converges to the stable limit cycle) with respect to the set $\{(x, y)/ x >0, y>0\} {\setminus } {E^{*}}$ if $0< x_c < \bar{x}_c$ (region $R_3$ in Fig. 3a), where $\bar{x}_c$ is the positive root (minimum root, if both roots are positive) of $x_c^2+px_c+q=0$ $\left[p=\frac{2m}{\alpha (e-mh)}-k-\frac{2e m}{(e-mh)^2}, q=\frac{e m k}{(e-mh)^2}-\frac{2e m^2}{\alpha (e-mh)^3}-\frac{m}{\alpha (e-mh)}(k-\frac{m}{\alpha (e-mh)})\right]$. It is interesting to observe whether prey refuge intensity is capable of preventing the cyclic behavior of system population. Suppose the system parameters are such that the system (4) admits a limit cycle. This limit cycle can be prevented if all solutions of the system approach an equilibrium point instead of a limit cycle. Let $\hat{x}_c$ be the value of $x_c$ for which the system (4) admits a limit cycle. Then definitely $\hat{x}_c\in (0, \bar{x}_c)$. Now, let $(\bar{x}, \bar{y})$ be the required limiting value for the solutions of the system. Let $\hat{x}_c$ be such that $(x^{*}(\hat{x}_c), y^{*}(\hat{x}_c))= (\bar{x}, \bar{y})$. Clearly, $(\bar{x}, \bar{y })$ will be asymptotically stable if we select $\hat{x}_c$ in such a way that $\bar{x}_c<\hat{x}_c<k-\frac{m}{\alpha (e-mh)}$ along with $h<\frac{e}{m}-\frac{1}{\alpha k}, e\alpha k>m$ (region $\bigcup _{i=1}^2R_i$ in Fig. 3a and corresponding phase plane diagrams are in Fig. 3i, ii, here all trajectories with different initial condition (x(0), y(0)) with $x(0)>x_c$ converge to the coexistence equilibrium point $E^{*}$). Therefore, it is possible to prevent oscillation of a prey-predator system to a stable state varying the intensity of prey refuge. This shows that intensity of prey refuge may increase stability of a prey-predator interaction.

Bifurcation analysis

To obtain a complete classification of the qualitative behavior of model (4), we analyze the bifurcation pattern (Jana 2013; Jana and Bairagi 2014; Jana et al. 2015; Solisa and Ku-Carrillo 2014) and illustrate the results with two parameters, say intensity of prey refuge-$x_c$ and handling time-h. The classification requires up to two codimension-one bifurcations: Hopf bifurcation points in which coexistence equilibrium point $E^{*}$ exchanges stability, limit points of cycles in which a stable and an unstable cycles collide and bifurcation points tracking a transcritical bifurcation between coexistence equilibrium point $E^{*}$ and prey only equilibrium $E_k$, where these two equilibria coincide and exchange their stability to each other.

Hopf bifurcation

One-dimensional bifurcation analysis reveals the behavior of the system when a particular system parameter is varied for a long range. Here we observe the behavior of the system when $x_c$, the prey refuge intensity is varied. It can be observed from the Eq. (4) that the characteristic roots become purely imaginary when $x_c=\bar{x}_c$. In this case, Re$(\lambda )|_{x_c=\bar{x}_c}=0$, Im$(\lambda )|_{x_c=\bar{x}_c}\ne 0$ and $\frac{d}{dc}$Re$(\lambda )|_{x_c=\bar{x}_c}<0$ (we use standard package of Mathematica to get these results) and hence the transversality condition for a Hopf-bifurcation is satisfied (Perko 2001). Therefore, there exists a Hopf-bifurcation at $x_c=\bar{x}_c$. The negative sign of $\frac{d}{dc}$Re$(\lambda )|_{x_c=\bar{x}_c}<0$ implies that the oscillations in the population densities dampen as $x_c$ passes from lower value to higher value through $\bar{x}_c$ (Fig. 4).

Fig. 4

Bifurcation diagram of system (4) with $x_c$ as the bifurcation parameter. Solid and dash lines are respectively for coexistence equilibrium $E^{*}$ and prey only equilibrium $E_k$. Grey colour represents infeasibility of $E^{*}$. Red and green for unstable and stable status of each equilibrium points. A Hopf bifurcation of $E^{*}$ occurs at $x_c=212$, $E^{*}$ is unstable focus on $100<x_c<212$ and asymptotically stable on $212<x_c<810$. A transcritical bifurcation occurs as the degree of prey refuge $x_c$ crosses the higher threshold value $x_c = 810$. Blue and black solid curves are the stable limit cycles for prey and predator around $x^{*}$ and $y^{*}$ [(the coordinates of unstable coexistence equilibrium $E^{*}$ (red solid line)]. Parameters: $r=3.3, k=900, \alpha =0.45, e=0.215, m=1.06, h=0.18$

Similarly, if we analyze Hopf bifurcation with respect to h, we see that Hopf-bifurcation occurs at $h=h_1$ and $h=h_2$ and the transversality conditions for a Hopf-bifurcation are $\frac{d}{dh}$Re$(\lambda )|_{h=h_1}>0$ and $\frac{d}{dh}$Re$(\lambda )|_{h=h_2}<0$ (Fig. 5). Also, the red line in Fig. 3a indicates the Hopf-bifurcation points in the $x_ch$-plane.

Fig. 5

Bifurcation diagram of system (4) with h as the bifurcation parameter. Solid and dash lines are respectively for coexistence equilibrium $E^{*}$ and prey only equilibrium $E_k$. Grey colour represents infeasibility of $E^{*}$. Red and green for unstable and stable status of each equilibrium points. A Hopf bifurcation of $E^{*}$ occurs at $h=h_1=0.1708$ and $h_2=0.195$, $E^{*}$ is unstable focus on $h_100<h<h_2$ and asymptotically stable on $0<h<h_1$ and $h_2<h<h_3$. A transcritical bifurcation occurs as h crosses the higher threshold value $h_3 = 0.199$. Blue and black solid curves are the stable limit cycles for prey and predator around $x^{*}$ and $y^{*}$ [the coordinates of unstable coexistence equilibrium $E^{*}$ (red solid line)]. Parameters: $r=3.3, k=900, \alpha =0.45, e=0.215, m=1.06, x_c=200$

Transcritical bifurcation

The system (4) undergoes a transcritical bifurcation involving the two equilibria $E_k$ and $E^{*}$. It has been shown that when $(0,h_1)\bigcup (h_2,h_3)$ (stability subregion $\bigcup _{i=1}^{3}R_i$ in Fig. 3a), the coexistence equilibrium $E^{*}$ is stable but the prey only equilibrium $E_k$ is unstable node. The two equilibria coincide at $h=h_3=\frac{e}{m}-\frac{1}{\alpha (k-x_c)}$ (green line in Fig. 3a) and exchange their stability. Once $h>h_3$, $E^{*}$ becomes unstable node (in this case this equilibrium point is biologically infeasible) and $E_k$ becomes stable node (stability subregion $R_4$ in Fig. 3a). Here, we will prove that the system undergoes a transcritical bifurcation at $h=h_3=\frac{e}{m}-\frac{1}{\alpha (k-x_c)}$ using $Sotomayer's$ theorem (Perko 2001). For $h=h_3=\frac{e}{m}-\frac{1}{\alpha (k-x_c)}$, there is only one prey only equilibrium point $E_k$ of the system. The Jacobian matrix evaluated at $E_k$ is

$$\begin{aligned} \begin{array}{l} J=Df(x_1,y_1;h_3)=\left( \begin{array}{cc} -r &{} -\frac{m}{e} \\ 0 &{} 0 \\ \end{array} \right) .\\ \end{array} \end{aligned}$$

J has an eigenvalue $\xi =0$. Let V and W be the eigenvectors corresponding to the eigenvalue $\xi =0$ for J and $J^T$, respectively. Then one can calculate,

$$\begin{aligned} \begin{array}{l} V=\left( \begin{array}{c} -\frac{m}{re} \\ 1 \\ \end{array} \right) ~\text{ and }~W=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right) . \end{array} \end{aligned}$$

Using the expressions for V and W, we get

• $W^Tf_h(x_1,y_1;h_3)=0,$

• $W^T[Df_h(x_1,y_1;h_3)V]=-\frac{m^2 k}{\alpha e(k-x_c)^2}<0$ and

• $W^T[D^2f(x_1,y_1;c_1)(V,V)]=-\frac{2m^2}{rke}<0$.

Thus, by Sotomayor’s theorem, we conclude that the model system undergoes a transcritical bifurcation as the parameter h passes through the critical value $h_3$. We draw a bifurcation diagram with respect to $x_c$ when h is fixed (Fig. 4) to demonstrate the system behavior more succinctly. We take initial condition as $x(0)>x_c,~y(0)>0$ always, because system (4) is not define for $x<x_c$. Observe that population oscillate (blue for prey and black for predator) around the unstable coexistence equilibrium point ($E^{*}$) (red solid lines for both $x^{*}$ and $y^{*}$) at the lower range of degree of prey refuge ($x_c$), at lower threshold value of $x_c$ (here $x_c=212$) system experiences Hopf-bifurcation and becomes stable up to the upper threshold value (here $x_c=810$) (green solid line for $x^{*}$ and blue solid line for $y^{*}$) and till now the prey only equilibrium point $E_k$ remains unstable (red dash lines). At upper threshold value of $x_c$ two equilibrium points $E^{*}$ and $E_k$ coincide and become $E_k$ and transcritical bifurcation occurs. If further we increase the value of $x_c$, $E^{*}$ becomes unstable node (here it is biologically infeasible and indicated by grey solid line) and system converges to prey only equilibrium point $E_k$ (green dash lines). It is very interesting to observe that prey density (x) never comes less the threshold density ($x=x_c$, here the black dot line represents $x=x_c$). Similarly we draw bifurcation diagram with respect to h with fixed $x_c=200$ in the similar fashion (Fig. 5).

Filippov regularization

The most interesting phenomena of Gause model is the fact when a trajectory falls on the vertical part of the prey nullcline, then it cannot be continued any further. Indeed, as the “trajectory” cannot leave the line $x=x_c$ and it follows that $\frac{dx}{dt}=0$. In other words, the Gause model is not well posed because trajectories are not defined when they fall on the vertical part of the prey nullcline. This is a consequence of the fact that the Gause functional response has a “jump” at the critical prey density, because such models may not have solutions. After Gause et al. (1936), (Filippov 1960, 1988) introduces a new solution concept for such models. The crucial step is provided through suitable definition of the vector field at the critical prey density, which we briefly describe now. The Filippov solution concept (Filippov 1960, 1988; Colombo and Křivan 1993; Utkin et al. 2009; Yang et al. 2013) applied to the Gause model defines a new vector field at the critical prey density $x_c$ as the line segment with end points given by the two adjacent vector fields $F^1$ and $F^2$. Here $F^1=(rx_c(1-\frac{x_c}{k}),-my)$ stands for the vector field is defined by the right-hand side of model (3) and $F^2=(rx_c(1-\frac{x_c}{k})-\frac{\alpha (x-x_c) y}{1+\alpha h (x-x_c)},\frac{e\alpha (x-x_c) y}{1+\alpha h (x-x_c)}-my)$ for the vector field is defined by the right-hand side of model (4). This new (multi valued) vector field is given by

$$\begin{aligned} F=\beta F^1+(1-\beta )F^2 \end{aligned}$$

(5)

where $0\le \beta \le 1$. In other words, this vector field associates to every point along the vertical part of prey nullcline, a whole set of possible directions is given by F. The definition of the Filippov field redefines the functional response (2) at the critical prey density to

$$\begin{aligned} g(x)=\left\{ \begin{array}{ll} 0 &{} x<x_c \\ \bigg [0,\frac{\alpha x_c}{1+\alpha h x_c}\bigg ] &{} x=x_c\\ \frac{\alpha (x-x_c)}{1+\alpha h (x-x_c)} &{} x> x_c \end{array}\right. \end{aligned}$$

(6)

It follows that under this new definition $g(x_c)$ is the line segment $\bigg [0,\frac{\alpha x_c}{1+\alpha h x_c}\bigg ]$ that fills the gap in Gause functional response (Fig. 1b). This definition is very natural as it reflects the fact that at the critical prey density the functional response does not specify exactly the prey consumption by predators.

Existence and uniqueness of trajectories of the Gause model

Let $n(n_x, n_y)=(1,0)$ be the vector perpendicular to the line $x=x_c$ in the prey-predator density phase plane. Projection of the two vector fields are given by the right hand sides of (3) (denoted as $F^1$) and (4) (denoted as $F^2$) are $\langle n,F^1\rangle =rx_c(1-\frac{x_c}{k})$ and $\langle n,F^2\rangle =rx_c(1-\frac{x_c}{k})-\frac{\alpha (x-x_c)}{1+\alpha h (x-x_c)}$. The existence of trajectories for the Gause model follows from general existence theorem that can be found in Filippov (1988) (Colombo and Křivan 1993). Uniqueness of trajectories for the Gause model follows from the fact that $\langle n,F^1\rangle =\langle n,F^2\rangle +\frac{\alpha (x-x_c)}{1+\alpha h (x-x_c)}$.

$$\begin{aligned} S_1=\{x: x<x_c\}, \ S_2=\{x: x>x_c\} \end{aligned}$$

and the manifold

$$\begin{aligned} \sum =\{x: x=x_c\}. \end{aligned}$$

In order to investigate the global dynamics of Filippov system [system (1) with functional response (6)], the qualitative behaviors of the subsystems which are determined by vector field $F^1$ or $F^2$ and the dynamics which is defined on the discontinuity manifold $\sum$ are crucial. The dynamics for vector fields $F^1$ and $F^2$ can be analyzed by using classical qualitative techniques of differential dynamic systems previously. However, the dynamics on the switching manifold $\sum$ can be complex and can be studied by using the well-known Filippov’s convex method (Filippov 1988) or Utkin’s equivalent control method (Utkin et al. 2009).

Let $\sigma =\langle n,F^1\rangle \langle n,F^2\rangle$, then $\sum _s=\{x\in \sum : \sigma <0\}$. The sliding mode domain $\sum _s$ can be distinguished by the following regions (Kuznetsov et al. 2003; Buzzi et al. 2006, 2010):

• 1. Escaping region: if $\langle n,F^1\rangle <0$ and $\langle n,F^2\rangle >0$ which would imply non-uniqueness of trajectories (Filippov 1988; Colombo and Křivan 1993).

• 2. Sliding region: if $\langle n,F^1\rangle >0$ and $\langle n,F^1\rangle >0$, trajectories are pushed from both below and above to the line $x=x_c$.

Thus, the state space is ($S_1\bigcup S_2\bigcup \sum$) and the model equations are

$$\begin{aligned} \frac{dn}{dt}=F^i(n,x_c)\ \text{ where }\ n\in S_i,\ i=1,2 \end{aligned}$$

(7)

where, $F^i$ are described previously. Sliding occurs on the segment $\sum$ which is delimited by two intersections $S_1$ and $S_2$ of $\sum$ with two nullclines $\frac{dy}{dt}=0$. As first pointed out by Filippov, these points which are called the tangent points (Kuznetsov et al. 2003) at which $F^2$ is tangent to $\sum$ is very important for bifurcation analysis. Sliding motion on $\sum$ obeys the smooth scalar differential equation

$$\begin{aligned} \frac{dx}{dt}=F \end{aligned}$$

(8)

where F is the unique convex combination of $F^1$ and $F^2$, which is given by (5) and $\beta =1-\frac{r(k-x_c)\{1+\alpha h x_c\}}{k\alpha y}$. Now the system is well posed and all the trajectories are defined throughout the range of x. This phenomena [system (1) with functional response (6)] is shown by Fig. 6 (each figures corresponds to the same in Fig. 3).

Fig. 6

Panel i are phase plane diagrams of the filippov system with functional response (6) corresponding to region $R_i$ of Fig. 3, where unstable and stable $E^{*}$ are indicated by red (iii) and green bullet (i, ii), stable limit cycle is shown by green closed loop (iii) and stable $E_k$ is shown by blue bullet (iv). Parameters: $r=3.3, k=900, x_c=100, \alpha =0.45, e=0.215, m=1.06$

Fig. 7

Bifurcation diagram of system (10) with increasing the proportions of prey out of the refuge $u_1$ (decreasing the proportions of prey in the refuge $u_2$) as the bifurcation parameter. Parameters: $r_1=3.3, r_2=2.5, k=900, \alpha =0.45, e=0.215, m=1.06, h=0.18, x_c=200$

Fig. 8

Phase plane diagrams of the system which shows the adaptive alternative food selection by predator. Parameters: $r=3.3, k=900, x_a=100~(i), x_a=110~(ii) \alpha =0.45, \alpha _a=0.42, e=0.215, e_a=0.25, h=0.17, h_a=0.15, m=1.06$

To analyze the Gause model (Gause 1934), it is very important to know the dynamics of the system along the vertical part of prey nullcline where the trajectories of system (1) falls on the vertical part of the prey nullcline and the predator density satisfies $y>\frac{r(k-x_c)\{1+\alpha hx_c\}}{\alpha k}=y_c$, the trajectories cannot leave the nullcline and moves vertically, i.e., $\frac{dx}{dt}=0$, i.e., along $\beta =1-\frac{r(k-x_c)\{1+\alpha h x_c\}}{k\alpha y}$. This trajectory corresponds to the vector $f^{F}=(0,erx_c(1-\frac{x_c}{k})-my)\in F$ and the population dynamics is:

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=0, \\ \frac{dy}{dt}= erx_c(1-\frac{x_c}{k})-my. \end{array} \end{aligned}$$

(9)

This equation depicts the dynamics of the system (1) along the line $x=x_c$ as long as $y>y_c$, then trajectories are forced to leave the line $x=x_c$ and enter the region $x>x_c$. This also follows from the considerations of the existence and uniqueness of trajectories of the Gause model.

Adaptive refuge use by the prey

The adaptation of an organism cannot easily be separated from the environment in which it lives. Insect larvae from stagnant aquatic environments in ditches and sloughs can survive longer without oxygen than can related species from well-aerated streams and rivers; species of marine snails that occurs high in the intertidal zone, where they are frequently exposed to air, tolerate desiccation better than do species from lower levels. These are examples of specializations that suit organisms to particular, restricted ranges of environmental conditions (Ricklefs and Miller 2000). It is very convenient that when predators are present in the system, naturally prey decreases its activities or changes suitable habitat to avoid predation risk (Werner and Gilliam 1984; Holbrook and Schmitt 1988; Brown and Alkon 1990; Brown 1998; Lima 1998a, b; Sih 1998; Peacor and Werner 2001; Preisser et al. 2005). Reduction in prey activities is a prominent example of a behavioral refuge whether prey reduces their activities or moves to a physical refuge leads to a trade-off due to live in the refuge (behavioral or physical) which increases the survival rate and decreases the predation rate and other components of prey fitness. The model of this trade-off is:

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=r_1 u_1 x \left(1-\frac{u_1 x}{(k-x_c)}\right)-\frac{\alpha u_1 xy}{1+\alpha hu_1 x}+r_2 u_2 x\left(1-\frac{u_2 x}{x_c}\right), \\ \frac{dy}{dt}= \left(\frac{e\alpha u_1 x}{1+\alpha hu_1 x}-m\right)y. \end{array} \end{aligned}$$

(10)

Here, $u_1$ is the proportions of prey out of the refuge and $u_2$ is so for refuge and $u_1+u_2=1$. Maximum refuge size is $x_c$, so in the reserve area prey grows logistically up to the size $x_c$ and naturally in the unreserve area prey grows logistically up to $(k-x_c)$, because k is the maximum strength of prey in the total habitat in absence of predation. $r_1$ and $r_2$ are the intrinsic growth rates of prey out and inside the refuge. Figure 7 depicts the behavior of the system with increasing the proportion of prey out of the refuge $u_1$ (decreasing the proportion of prey in the refuge $u_2$) as the bifurcation parameter. When $u_1<u_2$, i.e., maximum population can avoid the foraging efficiency of predator, then predator either goes to extinction or survive with very low density and at the intermediate range of $u_1,~ u_2$ and $u_1>u_2$, then both population can survive at their commensurate equilibrium density or at fluctuating mode, this adaptive nature is validated by Fig. 7. Now the question: What is the optimal prey strategy $(u_1,u_2)$?

If proportion $u_1$ of prey is out of the refuge, so their payoff is $V_1=r_1(1-\frac{u_1 x}{(k-x_c)})-\frac{\alpha y}{1+\alpha hu_1 x}$. As the proportion of prey out side the refuge $(u_1)$ increases, payoff will increase, because the chance that a single prey will be captured by a predator decreases due to the risk dilution effect (Foster and Treherne 1981). As we assume that prey in the refuge is completely protected from predation, the payoff in the refuge is $V_2=r_2(1-\frac{u_2 x}{x_c})$. Thus, fitness of a mutant prey (with strategy $\tilde{u}=(\tilde{u}_1,\tilde{u}_2)$) in a monomorphic resident population (with distribution $u=(u_1,u_2)$) is given by the mean payoff

$$\begin{aligned} W(\tilde{u},u)=\tilde{u}_1 V_1+\tilde{u}_2 V_2 =r_1 \tilde{u}_1\left(1-\frac{u_1 x}{(k-x_c)}\right)-\frac{\alpha \tilde{u}_1y}{1+\alpha hu_1 x}+r_2 \tilde{u}_2\left(1-\frac{u_2 x}{x_c}\right). \end{aligned}$$

(11)

Mutant fitness is not only density dependent but also frequency dependent, because it depends on the resident strategy.

Adaptive alternative food selection by predator

Optimization of diet choice by predator has been explored theoretically by number of authors (Schoner 1969, 1971; Rapport 1971; Cody 1974; Orians and Pearson 1979; Townsend and Hughes 1981; Charnov and Stephens 1988; Krebs and Kacelnik 1991). These treatments agree with MacArthur and Pianka’s prediction (MacArthur and Pianka 1966). Mathematically, the problem of optimal diet choice has been characterized by the switching phenomena of “classic” model of diet choice (Ricklefs and Miller 2000). Prey switching is frequency-dependent predation, where the predator preferentially consumes the most common type of prey. The reason a predator may switch from eating one prey to another, is because it may increase an individual’s foraging efficiency and therefore its inclusive fitness (Hughes and Croy 1993; Cornell 1976). It has been argued that frequency-dependent predation is predicted from optimal foraging theory (Hubbard et al. 1982). Predator’s preference for prey might stabilize prey-predator dynamics (Oaten and Murdoch 1975). Oaten and Murdoch (1975) assume that the proportion of prey in the predator’s diet choice increases with increasing prey proportion in the environment faster than linearly what they call switching. So, the Holling type II functional response for the primary resource is (Holt 1983; Abrams 1999)

$$\begin{aligned} g(x)=\frac{u\alpha (x-x_c)}{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a}, \end{aligned}$$

(12)

where $u~(u_a=1-u)$ is the predator’s preference for the primary (alternative) prey $x~(x_a)$. At the extreme case where predators attack on the more abundant species and the functional response is piece-wise continuous (Fig. 1b)

$$\begin{aligned} g(x)=\left\{ \begin{array}{ll} 0 &{} x<x_a \\ \frac{\alpha (x-x_c)}{1+\alpha h (x-x_c)} &{} x> x_a \end{array}\right. \end{aligned}$$

(13)

and corresponding numerical response is

$$\begin{aligned} G(x)=\left\{ \begin{array}{ll} \frac{e_a \alpha _a x_a}{1+\alpha _a h_a x_a} &{} x<x_a \\ \frac{e\alpha (x-x_c)}{1+\alpha h (x-x_c)} &{} x> x_a \end{array}\right. \end{aligned}$$

(14)

where $x_a$ is the alternative prey abundance and $\alpha _a,~h_a,~e_a$ are the attack rate, handling time and food conversion efficiency of predator for their alternative prey. So, our model system (1) becomes when $x<x_a$

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=rx\left(1-\frac{x}{k}\right), \\ \frac{dy}{dt}=\frac{e_a \alpha _a x_a y}{1+\alpha _a h_a x_a}-my, \end{array} \end{aligned}$$

(15)

at each point to the left of $x=x_c$ in the prey-predator phase space, prey population grows logistically and predator increases (decreases) if $x_a>\frac{m}{\alpha _a(e_a-h_a m)}$ $(x_a<\frac{m}{\alpha _a(e_a-h_a m)})$. When prey population density above the critical prey density ($x>x_c$), then system (1) becomes

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=rx\left(1-\frac{x}{k}\right)-\frac{\alpha (x-x_c)y}{1+\alpha h (x-x_c)}, \\ \frac{dy}{dt}=\frac{e\alpha (x-x_c)y}{1+\alpha h (x-x_c)}-my. \end{array} \end{aligned}$$

(16)

The prey population decreases if predator population is very large ($y>y^c=\frac{rx(k-x)\{1+\alpha h(x-x_c)\}}{\alpha (x-x_c)}$) in the vicinity and to the right of $x=x_c$. For $x=x_c$ population dynamics is

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=rx\left(1-\frac{x}{k}\right)-\frac{u\alpha (x-x_c)y}{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a}, \\ \frac{dy}{dt}=\bigg (\frac{eu\alpha (x-x_c)+e_au_a\alpha _ax_a}{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a}-m\bigg )y. \end{array} \end{aligned}$$

(17)

Here the trajectories can not leave the switching line $x=x_c$ when predator density is higher than $y^c$, then corresponding preference is

$$\begin{aligned} u=\frac{rx(k-x)(1+\alpha _ah_ax_a)}{k\alpha (x-x_c)y+rx(k-x)\{\alpha _ah_ax_a-\alpha h(x-x_c)\}}. \end{aligned}$$

Then Eq. (17) becomes

$$\begin{aligned} \begin{array}{l} \frac{dx}{dt}=0, \\ \frac{dy}{dt}=\bigg (\frac{erx(k-x)}{k}+\frac{e_a\alpha _au_ax_ay}{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a}\bigg )-my. \end{array} \end{aligned}$$

(18)

This system has the equilibrium as

$$\begin{aligned} E_a^{*}=(x_a^{*},y_a^{*})=\bigg (x_a,\frac{erx(k-x)\{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a\}}{k\{m+(mh_a-e_a)\alpha _au_ax_a+m\alpha hu(x-x_c)\}}\bigg ). \end{aligned}$$

There are three distinguish features depending upon the abundance of alternative food source ($x_a$).

• When alternative resource is very small, i.e., $x_a<x^{*}$ [$x^{*}$ is the equilibrium density of prey of model system (4)], i.e., when predator feeds on primary prey only, then both population coexist in limit cycle (Fig. 8i).

• When alternative food size is intermediate, i.e., $x^{*}<x_a<X_a=x_c+\frac{m}{\alpha _a (e_a-mh_a)}$, then there exists a stable coexistence equilibrium point $E_a^{*}(x_a^{*},y_a^{*})$ where $x_a^{*}=x_a$ and $y_a^{*}=\frac{erx(k-x)\{1+\alpha h u (x-x_c)+\alpha _a h_a u_a x_a\}}{k\{m+(mh_a-e_a)\alpha _au_ax_a+m\alpha hu(x-x_c)\}}$ (Fig. 8ii).

• If alternative food resource approaches to $X_a$, then predator equilibrium is tending to infinity and when $x_a>X_a$, then there coexistence is not possible because it is very unrealistic to assume that alternative resource can reach such a high density and not be influenced by predation or competition with essential resource directly or apparently.

Discussion

In the present study, we have analyzed a prey-predator system which is introduced by Gause (1934) and his co-workers (Gause et al. 1936) to examine some cycles of prey-predator interaction in some experiments. They replace the linear functional response of Lotka and Volterra by some saturating functional response which is zero below a critical prey density and is saturating above which with respect to prey density. At the critical prey density there is discontinuity as well as a “jump” of the functional response of predator. So, trajectories are not well defined throughout the range of prey density and also not well posed. So, at the vicinity of the critical prey density there is some confusion. But in nature any population may increase or decrease their density over time. So, naturally it is very convenient that prey density must cross this critical density at any time, so analysis at that critical prey density is very essential not only the purpose of ecological clarification but also for mathematical interest. Natural habitat, mostly, is patchy. Different patches or sites characterize differently. Some sites are suitable for prey or some are for predator. So patch selection by both population is a very essential and important ecological phenomena. In this present study, we consider that there is two patches, one is reserve for prey and other is non reserve. In the reserve patch prey population can successfully refuse the foraging efficiency of predator. Here we consider the critical prey density, the size of refuse limit of Gause model. After successful refusing, the remaining prey population is not able to take shelter in the reserve patch and then they come into the interaction with predator. Here at this critical prey density the system is not well defined. Below this critical density predator is forced to go extinction due to lack of food and prey population grows logistically without any predation risk. But when prey density is above this critical density, then surplus of prey and predator populations can survive in the fashion of classical prey-predator relation and can coexist in either limit cycle mode or at equilibrium. Where as Gause et al. (1936) show that a prey refuge can lead to prey-predator coexistence as the same model without refuge. Also, here the cyclic behavior of both population coincides with coexistence equilibrium or vice versa through Hopf-bifurcation due to the size of refuse patch or food handling ability of predator and also the decreasing availability of food can able to make predator extinction from the coexistence of population through transcritical bifurcation. For searching the answer of discontinuity of Gause model in this article, an approach is developed by Filippov (1960) is used, we show how the trajectories in the Gause model can be defined at the vicinity of prey density. This technique can explain mathematically and ecologically the movement of trajectories in the vicinity of prey density.

Generally, predator depends on more than a single prey population. Predator population’s growth under a given set of conditions behaves uniquely to the level of each of its prey resources (Ricklefs and Miller 2000; Murdoch 1969; Clarke 1962; Charnov 1976; Stephens and Krebs 1986). According to Liebig’s law of minimum (Liebig 1840) whichever the resources is reduced to the value of critical density, first it limits the growth of predator population. Here, in this model the primary prey is referred ecologically as essential resources, an interaction of the predator and the prey resources is considered when one of the prey resource is essential and other is not. If essential prey resource density drops at the critical level, the predator population for their survival switches to non essential resources (Ricklefs and Miller 2000; Murdoch 1969; Clarke 1962; Charnov 1976; Stephens and Krebs 1986). Our model depicts that the survivability and stability of predator depend on switching behavior from essential to non essential prey resources. Ecologically it is established that if essential resource is decreased to the critical level and if predator switch to the non essential one, then more non essential resources will be consumed because non essential resource will provide less nutrient than that of essential resource. So, the condition i.e., the dependency of predator on alternative prey (non essential resource) does not persist for the long time. But during this time essential prey density will again be increased due to the absence of predation pressure on them and exceeds the critical density and predator’s dependency on alternative prey is again switched back to primary prey population.