Applications of graph’s complete degree with bipolar fuzzy information

Abstract

Due to the presence of two opposite directional thinking in relationships between countries and communication systems, the systems may not always be balanced. Therefore, the perfectness between countries relations are highly important. It comes from how much they were connected to each other for communication. In this study, first perfectly regular bipolar fuzzy graph is introduced and examined the regularity of nodes. Then, the relationship between the adjacent nodes and their regularity are visualized as a perfectly edge-regular bipolar fuzzy graphs. The totally accurate communication between all connected nodes is explained by introducing completely open neighborhood degree and completely closed neighborhood degree of nodes and edges in a bipolar fuzzy graph. Some algorithms and flowcharts of the proposed methods are given. Finally, two applications of these cogitation are exhibited in two bipolar fuzzy fields. The first one is in international relationships between some countries during cold-war era and the second one is in decision-making between teachers–students communication system for the improvement of teaching.

Introduction

Research background

In daily life of humanity, decision structure is build upon the human thinking potency. Graph theory plays an essential part to maintain the relationship and communication in various types of connected fields including computer network, artificial intelligence, decision-making, engineering science, signal processing, pattern recognition, image segmentation, and medical science. If the nodes as well as edges in a graph become uncertain [33], then fuzzy graph theory [26] gives us more accuracy for decision-making in some real problems. Therefore, at present, fuzzy graph theory is one of the important research areas. But once in while human decision generated two antithetical sides [35, 37] which can come positive and negative sides, increasing and decreasing side, good and bad relation, profit and loss, effect, and side effect.

Due to the existence of bipolar judgemental thinking, the bipolar fuzzy sets and relations play a major role in extensive number of real-life bipolar fuzzy fields including qualitative model, cognitive mapping, cooperation, clustering, analysis of multi-agent data mining, strategic decision in international relationship, neurological modeling, analysis of diagnose of major depressive, granular computing, etc. When the effects of the nodes are positive and negative in the graphs, then the notion of bipolar fuzzy graphs gives us more accurate result for decision-making. During the recent time, the Wi-Fi network system has been placed in many places of a big town including office, court, educational field, town, bus stand, railway station, etc. The speed of Wi-Fi network becomes slow due to certain reasons like for excessive users, mechanical disturbances, and natural disaster. Therefore, the speed of Wi-Fi is uncertain. For natural disturbance and excessive user, the Internet speed is not fixed. Then, there exists a bipolarity in the Wi-Fi machines as well as between every pair of Wi-Fi machines. To handle these types of graphical systems, bipolar fuzzy graph plays an essential role. To control the total power of the Wi-Fi machine and the Internet speed between two Wi-Fi machines, open and closed neighborhood degrees of nodes and edges are introduced.

In fuzzy graphs [26], there is only one character of nodes and edges whose membership values lie in [0, 1]. However, if there is another opposite character for the nodes and edges whose membership values lie in $[-1,0]$, then these types situations cannot be handled by means of fuzzy graphs. Bipolar fuzzy graphs (BFGs) [5, 31] gives the two opposite side information about the nodes and edges. However, it cannot give any information whether the system is perfectly regular or not. The degree of nodes in BFGs gives the total information and contribution of the positive and negative characters separately. Therefore, we do not have any idea about the highest and lowest connected nodes and edges. Therefore, we cannot order the nodes and edges in this case.

Motivation

Many events related to our real life can be modeled using BFG. For instance, some people are connected by a group in social media. Their relationships and communications to each other are uncertain. Often, it may happen that between any two friends, one may agree with an incident and disagree with another incident. Therefore, there exists bipolarity between each pair of friends. To handle these type of situations, BFGs always conduct an essential part. It happens many times that some friends send ‘Good Morning’ or ‘Good Night’ message in the group and personally to others. However, others may not reply to these type of messages. All of these types of communication explain how much a man perfectly related and communicated to the others in that group and personally. This type of social network group is called a perfectly regular group if all people in this group are perfect and is called a perfectly irregular group if all people in this group are imperfect. This motivates us to introduce perfectly regular and edge-regular BFG. However, a man can agree or disagree about an information with his friends personally and also in locally. This can be explained by open and closed neighborhood degree of nodes and edges. Consequently, it motivates us to define completely open neighborhood degree and completely closed neighborhood degree.

Framework of this study

This manuscript is organized as follows: The next section contains literature of review and some basic definitions related to this manuscript. Perfectly regular and perfectly edge-regular bipolar fuzzy graph with their properties are initiated in “Perfectly regular and perfectly edge-regular BFG”. The terms completely open neighborhood degree and completely closed neighborhood degree are initiated with their properties in “Completely open neighborhood degree (COND) and completely closed neighborhood degree (CCND) in a BFG”. Algorithms and flowcharts for calculating various types of degrees are described in “Algorithm and flowchart for calculating COND and CCND in BFG”. Applications of these substantive thoughts are conferred to maintain international relationship and decision-making in such real-life communication systems in “Applications of BFG using COND and CCND”. Finally, a conclusion of all these works is given in “Conclusion and future works”.

Literature review and preliminaries

Due to the presence of fuzziness or uncertainty in human thinking, Zadeh [33] originated the concept of fuzzy sets. Liao et al. [18] discussed about several types of fuzzy sets with operations and applications in various multi-attribute decision-making. Hesitancy degree-based correlation measures for hesitant fuzzy sets are described in [17]. Citil [8] investigated many fuzzy problems based on Laplace transform. Yuan et. al. [32] explained application of graph kernel which is based on link prediction for signed in social networks. Gao et al. [12, 13], respectively, introduced different algorithms for partial multi-dividing ontology and Wiener number in bicyclic molecular structures. Nguyen et al. [21] established a notable techniques to handle knowledge graph fusion in smart systems. Imran et al. [16] introduced different types of network based on graph. Currently, fuzzy graph theory [26] is extensively used in numerous fields. Mordeson and Nair [19, 20] created disjoint arcs and cycles in fuzzy graphs. Strength of arcs in fuzzy graphs is explained in [7]. Gross et al. [15] gives an approach of fuzzy graph matching in intelligent analysis to maintain continuous situational awareness. Different types of picture fuzzy graph and their application are described in [9, 29]. Fan et al. [11] explained the intuition about bipartite fuzzy graph with its real-life approach. Based on bipolarity of fuzzy sets, Zhang [35] presented the conceptual idea of bipolar fuzzy sets. Different types of operations and properties of bipolar fuzzy sets and bipolar fuzzy relations with their applications in various real fields are briefly discussed in [30, 37]. Akram [1, 2] first introduced the concept of BFG, isomorphism on BFGs, complement, and its application. After that, Yang et. al. [31] gave the generalized concept of BFGs. Then, Akram et al. [3,4,5] defined trees, cycles, paths, metric, forest, and cut node in BFG. Different types of applications of BFGs founded in [6]. The concept of fuzzy soft and bipolar fuzzy soft graphs and their application in wireless Internet founded in [27, 28]. Poulik and Ghorai [23] initiated geodesic distance and different types of nodes in BFGs with their applications. Different types of indices and degrees in bipolar fuzzy graphs with applications are explained in [22, 25]. Poulik et al. [24] described different operations and applications of interval-valued fuzzy graph. Ghorai [14] characterized regular bipolar fuzzy graphs using fundamental sequences.

Now, we represent some elementary definitions in the next sections.

Definition 1

[35] Let X be a non-empty set.

• The set $A=\{(x,\nu ^p_A (x),\nu ^n_A (x)):x\in X\}$ is said to be a bipolar fuzzy set in X, where $\nu ^p_A:X\rightarrow [0,1]$ and $\nu ^n_A:X\rightarrow [-1,0]$ are mappings.

• A mapping $A=(\nu ^p_A,\nu ^n_A):X\times X \rightarrow [0,1]\times [-1,0]$ is said to be a bipolar fuzzy relation on X, where $\nu ^p_A (x,y)\in [0,1]$ and $\nu ^n_A (x,y)\in [-1,0]$.

The positive membership value $\nu ^p_A (x), x\in V$ is the positive satisfaction degree of x corresponding to bipolar fuzzy set A and the negative membership value $\nu ^n_A (x), x\in V$ is the negative satisfaction degree of x.

Definition 2

[35] Let X be a non-empty set. Then, $B=(\nu ^p_B, \nu ^n_B) : X\times X\rightarrow [0, 1]\times [-1, 0]$ is called a bipolar fuzzy relation on X, such that $\nu ^p_B(a,b)\in [0,1]$ and $\nu ^n_B(a,b)\in [-1,0]$.

Let $A=(\nu ^p_A, \nu ^n_A)$ be a bipolar fuzzy set on a set X. If $B=(\nu ^p_B, \nu ^n_B)$ is a bipolar fuzzy relation on a set X, then $B=(\nu ^p_B, \nu ^n_B)$ is a bipolar fuzzy relation on $A=(\nu ^p_A, \nu ^n_A)$ if $\nu ^p_B(a,b)\le \min \{\nu ^p_A(a),\nu ^p_A(b)\}$ and $\nu ^n_B(a,b)\ge \max \{\nu ^n_A(a),\nu ^n_A(b)\}$ for all $a,b\in X$.

In 2011, Akram [5] first defined BFG as follows.

Definition 3

[5] A BFG G on a non-empty set X is a pair $G=(A, B)$, where $A : X \rightarrow [0, 1] \times [-1, 0]$ is a bipolar fuzzy set on X and $B : X\times X \rightarrow [0, 1] \times [-1, 0]$ is a bipolar fuzzy relation in X, such that $\nu ^p_B(ab)\le \min \{\nu ^p_A(a),\nu ^p_A(b)\}$ and $\nu ^n_B(ab)\le \min \{\nu ^n_A(a),\nu ^n_A(b)\}$, for all $a, b\in X$.

For a given set V, an equivalence relation $\sim$ on $V \times V - \{(x,x) |x\in V\}$ is defined as $(x_1,y_1)\sim (x_2,y_2)$ $\Leftrightarrow$ either $(x_1,y_1) = (x_2,y_2)$ or $x_1 = y_2, x_2 = y_1$. The quotient set obtained in this way is denoted by $\widetilde{V^2}$ , and the equivalent class which contains the element (x,y) is denoted by xy or yx. Yang et al. [31] defined the BFG in 2013.

Definition 4

[31] A BFG G is a triplet (V, A, B) of the crisp graph $G^*=(V, E)$, where $A=(\nu ^p_A, \nu ^n_A)$ and $B=(\nu ^p_B, \nu ^n_B)$ are the bipolar fuzzy sets in V and $\widetilde{V^2}$, respectively, for which

$$\begin{aligned} \nu ^p_B(ab) \le \min \{\nu ^p_A(a), \nu ^p_A(b)\} \end{aligned}$$

and

$$\begin{aligned} \nu ^n_B(ab) \ge \max \{\nu ^n_A(a), \nu ^n_A(b)\} \end{aligned}$$

for all $ab\in \widetilde{V^2}$ with $\nu ^p_B(ab)=\nu ^n_B(ab)=0$ for all $ab\in (\widetilde{V^2}-E)$.

Fig. 1

Example of a BFG G

Example 1

In Fig. 1, we consider a graph $G^*=(V, E)$, where $V=\{ a_1, a_2, a_3, a_4, a_5, a_6 \}$ and $E=\{ a_1a_2, a_1a_4, a_1a_6, a_2a_3, a_2a_5, a_3a_6, a_4a_5, a_5a_6 \}$. Every node and edge has two components, positive and negative. All the positive and negative components of all the nodes and edges lie in [0, 1] and $[-1, 0]$, respectively. This means that $\nu ^p_A(a_i), \nu ^p_B(a_ja_j)\in [0, 1]$ and $\nu ^n_A(a_i), \nu ^n_B(a_ja_j)\in [-1, 0]$, $\forall a_i\in V, \forall a_ia_j\in \widetilde{V^2}$. Here $(\nu ^p_A(a_1), \nu ^n_A(a_1))=(0.7, -0.8), (\nu ^p_A(a_2), \nu ^n_A(a_2))=(0.6, -0.4)$. $(\nu ^p_A(a_1a_2), \nu ^n_A(a_1a_2))=(0.2, -0.1)$. Therefore, $\nu ^p_B(a_1a_2)<\min \{ \nu ^p_A(a_1), \nu ^p_A(a_2) \}$ and $\nu ^n_B(a_1a_2)>\max \{ \nu ^n_A(a_1), \nu ^n_A(a_2) \}$. Similarly, all the other edges and vertices satisfy the condition $\nu ^p_B(a_ia_j)\le \min \{ \nu ^p_A(a_i), \nu ^p_A(a_j) \}$ and $\nu ^n_B(a_ia_j)\ge \max \{ \nu ^n_A(a_i), \nu ^n_A(a_j) \}, 1\le i\ne j\le 6$. Therefore, G is a BFG.

The open neighborhood degree (OND) of a node $a\in V$ in a BFG G is denoted by $deg(a)=(deg^p(a), deg^n(a))$ and is defined as $deg^p(a)=\sum _{\begin{array}{c} a\ne b \\ ab\in \widetilde{V^2} \end{array}} \nu ^p_B(ab)$ and $deg^n(a)=\sum _{\begin{array}{c} a\ne b \\ ab\in \widetilde{V^2} \end{array}} \nu ^n_B(ab)$. If $deg(a)=(d_1, d_2)$, $\forall a\in V$, G is called $(d_1, d_2)$-regular.

For example, the BFG G of Fig. 1, we have $deg(a_i)=(0.8,-0.4)\forall a_i$. Therefore, G is a $(0.8,-0.4)$-regular BFG.

The order of a BFG G is denoted by $O(G)=(O^p(G), O^n(G))$ and is defined as $O^p(G)=\sum _{a\in V}\nu ^p(a)$ and $O^n(G)=\sum _{a\in V}\nu ^n(a)$. Also, $S(G)=(S^p(G),S^n(G))$ is the size of G , where $S^p(G)=\sum _{ab\in \widetilde{V^2}}\nu ^p_B(ab)$ and $S^n(G)=\sum _{ab\in \widetilde{V^2}}\nu ^n_B(ab)$.

From the BFG G of Fig. 1, we see that $O(G)=(4.3,-4.0)$ and $S(G)=(2.4,-1.2)$.

The closed neighborhood degree (CND) of a node $a\in V$ in a BFG G is denoted by $deg[a]=(deg^p[a], deg^n[a])$ and is defined as $deg^p[a]= deg^p(a) + \nu ^p_A(a)$ and $deg^n[a]= deg^n(a) + \nu ^n_A(a)$. If $deg[a]=(f_1, f_2)$ $\forall a\in V$, then G is called $(f_1, f_2)$-totally regular.

For the BFG G of Fig. 1, $deg[a_2]=(1.4,-0.8)\ne (1.8,-1.4)=deg[a_5]$. Therefore, G is not totally regular.

The degree of an edge $ab\in E$ in a BFG G is denoted by $deg(ab)=(deg^p(ab), deg^n(ab))$ and is defined as $deg^p(ab)=\sum _{\begin{array}{c} a\ne c \\ ac\in \widetilde{V^2} \end{array}}\nu ^p_B(ac) + \sum _{\begin{array}{c} b\ne c \\ bc\in \widetilde{V^2} \end{array}}\nu ^p_B(bc) = \sum _{ac\in \widetilde{V^2}} \nu ^p_B(ac) + \sum _{bc\in \widetilde{V^2}} \nu ^p_B(bc) - 2\nu ^p_B(ab)$ and $deg^n(ab)=\sum _{\begin{array}{c} a\ne c \\ ac\in \widetilde{V^2} \end{array}}\nu ^n_B(ac) + \sum _{\begin{array}{c} b\ne c \\ bc\in \widetilde{V^2} \end{array}}\nu ^n_B(bc) = \sum _{ac\in \widetilde{V^2}} \nu ^n_B(ac) + \sum _{bc\in \widetilde{V^2}} \nu ^n_B(bc) - 2\nu ^n_B(ab)$.

If $deg(ab)=(k_1, k_2)$, $\forall ab\in \widetilde{V^2}$, then G is called $(k_1, k_2)$-edge regular.

For the BFG G of Fig. 1, $deg(a_1a_2)=(1.2,-0.6)\ne (0.8,-0.4)=deg(a_4a_5)$. Therefore, G is not edge regular.

The total degree of an edge ab in a BFG G is denoted by

$deg[ab]=(deg^p[ab], deg^n[ab])$ and is defined as $deg^p[ab]=deg^p(ab) + \nu ^p_B(ab)$ and $deg^p[ab]=deg^p(ab) + \nu ^p_B(ab)$. If $deg[ab]=(t_1, t_2)$, $\forall ab\in \widetilde{V^2}$, G is called $(t_1, t_2)$-totally edge-regular.

For the BFG G of Fig. 1, $deg[a_1a_2]=(1.4, -0.7)\ne (1.2,-0.6)=deg(a_4a_5)$. Therefore, G is not totally edge-regular.

Definition 5

[22] The connectivity index of a BFG $G = (V,A,B)$ denoted by $CI_{BF}(G)$ is defined as

$$\begin{aligned} CI_{BF}(G)&= \left( CI^p_{BF}(G), CI^n_{BF}(G)\right) \\&=\left( \sum \limits _{a_i, a_j\in V} \nu ^p_A(a_i) \nu ^p_A(a_j) CONN^p_G(a_i,a_j), \right. \\&\quad \left. \quad \sum \limits _{a_i, a_j\in V} \nu ^n_A(a_i) \nu ^n_A(a_j) CONN^n_G(a_i,a_j)\right) , \end{aligned}$$

where $CI^p_{BF}(G)$ and $CI^n_{BF}(G)$, respectively, denote the positive connectivity index and negative connectivity index of G and $CONN^p_G(a_i,a_j)= (\nu ^p_B((a_i,a_j))^\infty )$ and $CONN^n_G(a_i,a_j) = (\nu ^n_B((a_i,a_j))^\infty )$, respectively, denote the positive strength of connectedness and negative strength of connectedness between every pair of vertices $(a_i,a_j)$ in G.

Also, the average connectivity index of G denoted by $ACI_{BF}(G)$ is defined as

$$\begin{aligned} ACI_{BF}(G)&= (ACI^p_{BF}(G), (ACI^n_{BF}(G))\\&= \frac{1}{{^{m}}{C_{2}}} \left[ \sum \limits _{a_i, a_j\in V} \nu ^p_A(a_i) \nu ^p_A(a_j) CONN^p_G(a_i,a_j), \right. \\&\left. \quad \sum \limits _{a_i, a_j\in V} \nu ^n_A(a_i) \nu ^n_A(a_j) CONN^n_G(a_i,a_j)\right] , \end{aligned}$$

where $|V| = m$.

Definition 6

[25] The Wiener index of a BFG $G=(V, A, B)$ is defined as

$$\begin{aligned} WI_{BF}(G)&= \left( WI^p_{BF}(G), WI^n_{BF}(G)\right) \\&=\left( \sum _{a_i,a_j\in V}\nu ^p_A(a_i) \nu ^p_A(a_j) d^p_{g(G)}(a_i,a_j), \right. \\&\left. \quad \sum _{a_i,a_j\in V}\nu ^n_A(a_i)\nu ^n_A(a_j) d^n_{g(G)}(a_i,a_j)\right) , \end{aligned}$$

where $WI^p_{BF}(G)$ and $WI^n_{BF}(G)$ represent the positive and negative Wiener index of G, respectively. $d^p_{g(G)}(a_i,a_j)$ and $d^n_{g(G)}(a_i,a_j)$ are, respectively, the minimum and maximum values of the sums of all positive and negative membership values of all the edges on the geodesics from $a_i$ to $a_j$.

Perfectly regular and perfectly edge-regular BFG

In a BFG, we cannot justify a node, with a single node according to the exceptional and unexceptional contributions. It would be better, if the justification can be made with all the nodes at the same time. In this matter, the OND and CND of the nodes and their regularity in a BFG play an important factor. Therefore, the equal contribution of all the nodes and all the edges in a BFG system are extremely helpful to maintain the equivalency of the system. In this section, perfectly regular BFG is defined and some theorems connected to these are discussed with examples. Perfectly edge regular BFG is defined with its boundedness. Some properties related to this are also established with examples.

Definition 7

A BFG is said to be a perfectly regular if it is both regular BFG and totally regular BFG.

We consider a perfectly regular BFG $G=(V,A,B)$. Therefore, G must be regular BFG and totally regular BFG. Then, the OND and CND of all the nodes of G are equal. Hence, the positive and negative membership values of all the nodes of G must be equal. Thus, we have the following proposition.

Proposition 1

For a perfectly regular BFG $G=(V, A, B)$, $A=(\nu ^p_A, \nu ^n_A)$ is a constant function.

Proof

Let G is perfectly regular BFG. Therefore, G is both $(d_1, d_2)$-regular and $(f_1, f_2)$-totally regular. Therefore, $deg^p[a]=deg^p(a)+\nu ^p_A(a)=deg^p(b)+\nu ^p_A(b)=deg^p[b]$ and $deg^n[a]=deg^n(a)+\nu ^n_A(a)=deg^n(b)+\nu ^n_A(b)=deg^n[b]$, $\forall a, b\in V$.

However, $deg^p(a)=d_1=deg^p(b)$, $deg^n(a)=d_2=deg^n(b)$ and $deg^p[a]=f_1=deg^p[b]$, $deg^n[a]=f_2=deg^n[b]$, $\forall a, b\in V$. $\Rightarrow \nu ^p_A(a)=\nu ^p_A(b)=f_1-d_1=constant$ and $\nu ^n_A(a)=\nu ^n_A(b)=f_2-d_2=constant$, $\forall a, b\in V$.

Hence, $A=(\nu ^p_A, \nu ^n_A)$ is a constant function. $\square$

Fig. 2

A BFG G with membership values of all nodes as $(0.7, -0.8)$

Example 2

From the BFG G of Fig. 2, we see that $A=(\nu ^p_A, \nu ^n_A)$ is constant. However, $deg(a_1)\ne deg(a_3)$. Hence, G is not perfectly regular. Therefore, the converse of the Proposition  1 is not true for all BFG.

Remark 1

The truthfulness of the converse of the Proposition 1 needs not be essential.

The measure of the total contribution between every pair of nodes in a BFG actually depend upon the size of a BFG. Therefore, when we want to determine the size of a perfectly regular BFG, every edge comes two times in total. This is explained in the next Theorem.

Theorem 1

Let $G=(V, A, B)$ be a perfectly regular BFG of the graph $G^*=(V, E)$. Then, size of G is $S(G)=\frac{|V|}{2}(d_1,d_2)$, where $(d_1, d_2)$ is the OND of a node in G.

Proof

Since G is a perfectly regular BFG and $(d_1, d_2)$ is the OND of a node of G. Then, $deg(a)=(d_1,d_2)\forall a\in V$.

Now, $\sum _{a\in V}deg(a)=|V|(d_1,d_2)\Rightarrow \big (\sum _{a\in V}\sum _{a\ne b}\nu ^p_B(ab), \sum _{a\in V}\sum _{a\ne b}\nu ^n_B(ab)\big )=|V|(d_1,d_2)$

$\Rightarrow \big (2\sum _{ab\in \widetilde{V^2}}\nu ^p_B(ab), 2\sum _{ab\in \widetilde{V^2}}\nu ^n_B(ab)\big )=|V|(d_1,d_2)\Rightarrow S(G)=\frac{|V|}{2}(d_1,d_2)$. $\square$

Fig. 3

A $(0.6,-0.8)$-regular BFG G

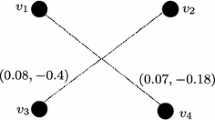
Example 3

Consider the BFG G of Fig. 3. Here, $S(G)=\frac{|V|}{2}(d_1,d_2)=(1.5, -2.0)$. However, $deg[a_1]\ne deg[a_2]$. Therefore, G is not perfectly regular. Hence, the converse of the Proposition 1 is not true in this BFG and the general case is stated in Remark 2.

Remark 2

The converse of the Theorem 3 does not hold in general.

An edge in a BFG maintains the relationship between the two corresponding nodes. Therefore, the total contribution of every edge of the BFG has an important sustainability. The intuition about perfect regularity of a BFG in the sense of edges is definitely important. Thus, we have introduced the concept of perfectly edge-regular BFG in the next definition.

Definition 8

A BFG is said to be a perfectly edge-regular BFG if it is both edge-regular and totally edge-regular.

We consider now a perfectly edge-regular BFG $G=(V,A,B)$. Then, the degree and total degree of all the edges of G are equal. Therefore, the positive and negative membership values of all the edges of G remain same. Thus, we have the proposition.

Proposition 2

For a perfectly edge-regular BFG $G=(V, A, B)$ of the graph $G^*=(V, E)$, $B=(\nu ^p_B, \nu ^n_B)$ is a constant function.

Fig. 4

A BFG G with membership values of all edges as $(0.4, -0.5)$

Example 4

Consider the BFG G of Fig. 4. Here, $B=(\nu ^p_B, \nu ^n_B)$ is constant. However, $deg(a_1a_3)\ne deg(a_1a_2)$ and this implies that G is not perfectly regular. Thus, the converse of Proposition 2 does not hold in general.

The maximum and minimum values of the total positive and negative communication powers of all the nodes in a BFG G are important factor to control a bipolar fuzzy connected field. This means that the total of the positive membership values and the total of the negative membership values of all the nodes in a BFG G represent the order of the BFG G, i.e., $O(G)=(\sum \nolimits _{a\in V}\nu ^p(a), \sum \nolimits _{a\in V}\nu ^n(a))$. This implies that the lower and upper boundary of the order of a BFG is very important, which is stated in the next Theorem.

Theorem 2

(Boundedness property for the order of a perfectly edge-regular BFG) Let G be a perfectly edge-regular BFG and $|V|=k$. Then,

$\sum \nolimits _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j) | i\ne j\}\le O^p(G)\le k$ and

$-k\le O^n(G)\le \sum \nolimits _{a_i\in V}\{\min \ \nu ^n_B(a_ia_j) | i\ne j\}$,

$1\le i,j\le k$.

Proof

Since $|V|=k$, let $V=\{a_1, a_2, \ldots , a_k\}$. $\nu ^p_A(a_i)\le 1$ and $-1\le \nu ^n_A(a_i)$, $1\le i\le k$.

Therefore, $\sum _{a_i\in V}\nu ^p_A(a_i)\le k$ and $-k\le \sum _{a_i\in V}\nu ^n_A(a_i)$.

This implies $O^p(G)\le k$ and $-k\le O^n(G)$. $\ldots$(i)

Now, $\nu ^p_B(a_ia_j)\le \min \{\nu ^p_A(a_i), \nu ^p_A(a_j)\}$ and $\nu ^n_B(a_ia_j)\ge \max \{\nu ^n_A(a_i), \nu ^n_A(a_j)\}$,

$1\le i,j\le k, i\ne j$

$\Rightarrow \max \ \nu ^p_B(a_ia_j)\le \{ \nu ^p_A(a_i), \nu ^p_A(a_j)\}$ and $\min \nu ^n_B(a_ia_j)\ge \{ \nu ^n_A(a_i), \nu ^n_A(a_j)\}$, $1\le i,j\le k, i\ne j$

$\Rightarrow \sum _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j)|i\ne j\} \le \sum _{a_i\in V} \nu ^p_A(a_i)$ and $\sum _{a_i\in V}\{\min \ \nu ^n_B(a_ia_j)|i\ne j\} \ge \sum _{a_i\in V} \nu ^n_A(a_i)$, $1\le i,j\!\le \! k, i\!\ne j$

$\Rightarrow \sum _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j)|i\ne j\}\le O^p(G)$ and $\sum _{a_i\in V}\{\min \nu ^n_B(a_ia_j)|i\ne j\} \ge O^n(G)$. $\ldots$ (ii)

Combining (i) and (ii), we have

$\sum _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j) | i\ne j\}\le O^p(G)\le k$ and

$-k\le O^n(G)\le \sum _{a_i\in V}\{\min \ \nu ^n_B(a_ia_j) | i\ne j\}$, $1\le i,j\le k$. $\square$

Fig. 5

Example of a BFG G which satisfies Theorem  2

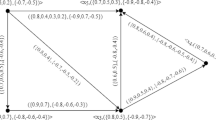
Example 5

From the BFG of Fig. 5, it is clearly seen that

$|V|=4$, $(O^p(G), O^n(G))=(2.4, -2.5)$, $\sum _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j)|i\ne j\} = 0.5+0.5+0.5+0.5= 2.0$, $\sum _{a_i\in V}\{\min \ \nu ^n_B(a_ia_j)|i\ne j\} = -0.5-0.5-0.5-0.5=-2.0$.

Now, $2.0\le 2.4\le 4$ and $-4\le -2.5\le -2.0$

$\Rightarrow \sum _{a_i\in V}\{\max \ \nu ^p_B(a_ia_j) | i\ne j\}\le O^p(G)\le 4$ and

$-4\le O^n(G)\le \sum _{a_i\in V}\{\min \ \nu ^n_B(a_ia_j) | i\ne j\}$, $1\le i,j\le 4$. Thus, G satisfies Theorem 2.

In chemical graph theory, different types of indices are initiated likes connectivity index, Wiener index, Randic index, Zagreb index, etc. The concept of connectivity index and Wiener index of BFGs and real applications are presented in [22, 25]. However, if BFGs are perfectly regular and perfectly edge regular, then the connectivity index and Wiener index can be found easily, which are explained in the following theorems.

Theorem 3

Let $G=(V,A,B)$ be a perfectly regular BFG, such that $|V|=m$ and $(\nu ^p_B(a_ia_j), \nu ^p_B(a_ia_j))=(e_1,e_2), \forall a_i,a_i\in V$. Then $CI^p_{BF}(G)=\frac{m(m-1)}{2}v^2_1e_1$ and $CI^n_{BF}(G)=\frac{m(m-1)}{2}v^2_2e_2$, where $(v_1, v_2)=(\nu ^p_A(a_i), \nu ^n_A(a_i))$.

Proof

Since G is a perfectly regular BFG, so by Proposition 1, we have $A=(\nu ^p_a, \nu ^n_a)$ must be constant. Since $(v_1, v_2)=(\nu ^p_A(a_i), \nu ^n_A(a_i)), \forall a_i\in V$.

Again, since $(\nu ^p_B(a_ia_j), \nu ^p_B(a_ia_j))=(e_1,e_2), \forall a_i,a_i\in V$, then there exists an edge between every pair of nodes in G and the membership values of all the nodes are same i.e, $(e_1,e_2)$. Therefore, the total number of edges in G is ${{^{m}}{C_{2}}=\frac{m(m-1)}{2}}$.

Again, the strength of connectedness between two vertices lies on an edge and is equal to the membership value of that edge. So, $CONN^p_G(a_i,a_j)=e_1$ and $CONN^n_G(a_i,a_j)=e_2, \forall a_i, a_j\in V$.

Now, ${CI^p_{BF}(G)=\sum \nolimits _{a_i,a_j\in V}\nu ^p_A(a_i) \nu ^p_A(a_j)CONN^p_G(a_i,a_j)}{ =\sum \nolimits _{a_i,a_j\in V}v_1.v_1.CONN^p_G(a_i,a_j) =v^2_1 {^{m}}{C_{2}} e_1=\frac{m(m-1)}{2}v^2_1e_1}$

and

${CI^n_{BF}(G)=\sum \nolimits _{a_i,a_j\in V}\nu ^n_A(a_i) \nu ^n_A(a_j)CONN^n_G(a_i,a_j)}{ =\sum \nolimits _{a_i,a_j\in V}v_2.v_2.CONN^n_G(a_i,a_j) =v^2_2 {^{m}}{C_{2}} e_2=\frac{m(m-1)}{2}v^2_2e_2}$. $\square$

Note 1

If the perfectly regular BFG G of the Theorem 3 is complete, then $e_1=\nu ^p_B(a_ia_j)=\min \{ \nu ^p_A(a_i), \nu ^p_A(a_j) \}=v_1$ and $e_2=\nu ^n_B(a_ia_j)=\max \{ \nu ^n_A(a_i), \nu ^n_A(a_j) \}=v_2$. Then, $CI^p_{BF}(G)=\frac{m(m-1)}{2}v^3_1$ and $CI^n_{BF}(G)=\frac{m(m-1)}{2}v^3_2$.

Corollary 1

For the BFG G of Note 1, $ACI_{BF}(G)=(v^3_1, v^3_2)$.

Proof

Since the G satisfies all the conditions of Note 1, so we have

$e_1=v_1$ , $e_2=v_2$, $CONN^p_G(a_i,a_j)=e_1=v_1$ and $CONN^n_G(a_i,a_j)=e_2=v_2, \forall a_i, a_j\in V$. Since G is complete and $|V|=m$, so there is an edge between every pair of vertices and the total number of edges in G is ${{^{m}}{C_{2}}}$.

Now, from the Definition 5, we have

$$\begin{aligned} ACI^p_{BF}(G)&=\frac{1}{{^{m}}{C_{2}}} \sum \limits _{a_i, a_j\in V} \nu ^p_A(a_i) \nu ^p_A(a_j) CONN^p_G(a_i,a_j)\\&=\frac{{^{m}}{C_{2}}}{{^{m}}{C_{2}}}v_1.v_1.e_1=v^3_1 and\\ ACI^n_{BF}(G)&=\frac{1}{{^{m}}{C_{2}}} \sum \limits _{a_i, a_j\in V} \nu ^n_A(a_i) \nu ^n_A(a_j) CONN^n_G(a_i,a_j)\\&=\frac{{^{m}}{C_{2}}}{{^{m}}{C_{2}}}v_2.v_2.e_2=v^3_2. \end{aligned}$$

$\therefore ACI_{BF}(G)=(ACI^p_{BF}(G), ACI^n_{BF}(G))=(v^3_1, v^3_2)$. $\square$

Theorem 4

Let $G=(V,A,B)$ be perfectly regular complete BFG, such that $|V|=m$ and $(\nu ^p_A(a_i), \nu ^n_A(a_i))=(v_1,v_2)$. Then, $WI^p_{BF}(G)=\frac{m(m-1)}{2}v^3_1$ and $WI^n_{BF}(G)=\frac{m(m-1)}{2}v^3_2$.

Proof

Since G is perfectly regular complete BFG and $|V|=m$, so from the Note 1, we have

$\nu ^p_B(a_ia_j)=\min \{ \nu ^p_A(a_i), \nu ^p_A(a_j) \}=v_1$ and $\nu ^n_B(a_ia_j)=\max \{ \nu ^n_A(a_i), \nu ^n_A(a_j) \}=v_2$.

Now, $d^p_{g(G)}(a,b)=$ minimum value of the sums of all positive membership values of all the edges on the geodesics from a to b is equal to $v_1$ and $d^n_{g(G)}(a,b)=$ maximum value of the sums of all negative membership values of all the edges on the geodesics from a to b is equal to $v_2$.

Therefore, ${WI^p_{BF}(G)=\sum _{a_i,a_j\in V}\nu ^p_A(a_i) \nu ^p_A(a_j) d^p_{g(G)}(a_i,a_j)}{={^{m}}{C_{2}}v_1.v_1.v_1=\frac{m(m-1)}{2}v^3_1}$ and

${WI^n_{BF}(G)=\sum _{a_i,a_j\in V}\nu ^n_A(a_i) \nu ^n_A(a_j) d^n_{g(G)}(a_i,a_j)}{={^{m}}{C_{2}}v_2.v_2.v_2=\frac{m(m-1)}{2}v^3_2}$. $\square$

Completely open neighborhood degree (COND) and completely closed neighborhood degree (CCND) in a BFG

We can measure the importance of a nodes not only by its positive and negative characters but also by the sum of their positive and negative characters. The positive neighborhood degree of a node in a BFG equals or not-equals to the negative neighborhood degree of that node. Therefore, the complete neighborhood degrees, i.e., COND and CCND, of nodes are very essential. In this section, COND and CCND of nodes in a BFG are defined with their properties and examples.

Definition 9

The COND of a node $a_1$ in a BFG G is denoted by COND$(a_1)$ and is defined as COND$(a_1)=deg^p(a_1) + deg^n(a_1)$.

The CCND of a node $a_1$ in a BFG G is denoted by CCND$[a_1]$ and is defined as CCND$[a_1]=deg^p[a_1] + deg^n[a_1]$.

If all the nodes in a BFG G have equal contribution for communication means, then G is perfectly regular BFG. Then, using the Proposition 1, we can say that the positive and negative membership values of every node of G are equal. Now, using the Definition 9, we can effortlessly determine the COND and CCND of a perfectly regular BFG, which is stated in Proposition 3.

Proposition 3

For a perfectly regular BFG

• (i) the CONDs of all the nodes are same and

• (ii) the CCNDs of all the nodes are same.

Fig. 6

A connected BFG G

Example 6

For the BFG G of Fig. 6, we have $COND(a_i)=0.8$ and $CCND(a_i)=0.7, i=1,2,3,4,5$. Thus, the CONDs and CCNDs of all the nodes of G are same. However, the membership values of some nodes are different. Therefore, by Proposition 1, we have G which is not perfectly regular BFG. Therefore, the converse part of the Proposition 3 is not true in this case.

We can also measure the edges not only their positive and negative communications but also their total communications. Therefore, the concepts of completely degrees of nodes in a BFG, i.e., COND and CCND, are very essential.

Definition 10

The COND of an edge ab in a BFG G is denoted by COND(ab) and is defined as COND$(ab)=deg^p(ab) + deg^n(ab)$. The CCND of a edge ab in a BFG G is denoted by CCND[ab] and is defined as CCND$[ab]=deg^p[ab] + deg^n[ab]$ for all $ab\in \widetilde{V^2}$.

If the communication between every pair of nodes in a BFG G is same, i.e., if the BFG G is perfectly edge-regular BFG, then by Proposition 2 we have, the positive and negative membership values of every edge in G are same. Then, using the Definition 10, we can effortlessly determine the COND and CCND of all the edges which is stated in Proposition 4.

Proposition 4

For a perfectly edge-regular BFG

• (i) the CONDs of all the edges are same and

• (ii) the CCNDs of all the edges are same.

Example 7

For the BFG G of Fig. 6, we have $COND(a_ia_j)=1.2, CCND(a_ia_j)=1.4$, for all edges $a_ia_j$ in G. However, the membership values of some edges of G are different. Therefore, by Proposition 2, we have G which is not perfectly edge-regular BFG. Therefore, the converse part of the Proposition 4 is not true in this case.

Theorem 5

(Relation between COND and CCND in a BFG) Let $G=(V,A,B)$ be a BFG. Then

• (i) $COND(a_i)\ge CCND(a_i)\Leftrightarrow \nu ^p_A(a_i)\le |\nu ^n_A(a_i)|$,

  $COND(a_i)\le CCND(a_i)\Leftrightarrow \nu ^p_A(a_i) \ge |\nu ^n_A(a_i)|$, $\forall a_i\in V$,

  and

• (ii) $COND(a_ia_j)\ge CCND(a_ia_j)\Leftrightarrow \nu ^p_B(a_ia_j)\le |\nu ^n_B(a_ia_j)|$,

  $COND(a_ia_j)\le CCND(a_ia_j)\Leftrightarrow \nu ^p_B(a_ia_j) \ge |\nu ^n_B(a_ia_j)|$, $\forall a_ia_j\in \widetilde{V^2}$.

Proof

Let $G=(V,A,B)$ be a BFG.

• (i) Let $a_i\in V$. Therefore, from the definition of COND and CCND of a node, we have $COND(a_i)-CCND(a_j)=-(\nu ^p_A(a_i)+\nu ^n_A(a_i))\ge (\le ) 0 \Leftrightarrow \nu ^p_A(a_i)\le (or \ge )|\nu ^n_A(a_i)|$.

  Since $a_i$ is a arbitrary node in G, therefore $COND(a_i)\ge CCND(a_i)\Leftrightarrow \nu ^p_A(a_i)\le |\nu ^n_A(a_i)|$, $\forall a_i\in V$.

  Similarly, $COND(a_i)\le CCND(a_i)\Leftrightarrow \nu ^p_A(a_i) \ge |\nu ^n_A(a_i)|$, $\forall a_i\in V$

• (ii) Let $a_ia_j\in E$. Then, from the definition of COND and CCND of an edge, we have

  $COND(a_ia_j)-CCND(a_ia_j)=-(\nu ^p_B(a_ia_j)+\nu ^n_B (a_ia_j))\ge (\le ) 0 \Leftrightarrow \nu ^p_B(a_ia_j)\le (or \ge )|\nu ^n_B(a_ia_j)|$. Since $a_ia_j$ is an arbitrary edge in G, therefore

  $COND(a_ia_j)\ge CCND(a_ia_j)\Leftrightarrow \nu ^p_B(a_ia_j)\le |\nu ^n_B(a_ia_j)|$, $\forall a_ia_j\in \widetilde{V^2}$.

  Similarly, $COND(a_ia_j)\le CCND(a_ia_j)\Leftrightarrow \nu ^p_B(a_ia_j) \ge |\nu ^n_B(a_ia_j)|$, $\forall a_ia_j\in \widetilde{V^2}$.

$\square$

Algorithm and flowchart for calculating COND and CCND in BFG

In this section, the algorithms to determine the CONDs and CCNDs of all the nodes and edges are proposed. Then, the flowcharts of the proposed algorithms are presented.

Algorithm and flowchart to determine most communicable nodes in a BFG using COND and CCND

Fig. 7

Flowchart to determine most communicable nodes in BFG

Using the Dijkstra’s algorithm [10] first draws a crisp graph $G^*=(V, E)$, where V and E are, respectively, denote the set of all nodes and edges with $|V|=n$ and $|E|=m$.

Step 1. Put the membership values $\nu _A(a_i)=(\nu ^p_A(a_i), \nu ^n_A(a_i))$ of the nodes $a_i$’s, $i=1, 2, \ldots , n$, $\nu ^p_A(a_i)\in [0, 1]$, $\nu ^n_A(a_i)\in [-1, 0]$.

Step 2. Write the membership values $\nu _B(a_ia_j)=(\nu ^p_B(a_ia_j), \nu ^n_B(a_ia_j))$ of the edges $a_ia_j\in E$, such that $\nu ^p_B(a_ia_j)\le \min \{ \nu ^p_A(a_i), \nu ^p_A(a_j) \}$, $\nu ^n_B(a_ia_j)\ge \max \{ \nu ^n_A(a_i), \nu ^n_A(a_j) \}$, $\nu ^p_B(a_ia_j)\in [0, 1], \nu ^n_B(a_ia_j)\in [-1, 0]$.

Step 3. Calculate ONDs of the nodes $a_i, i=1,2,\ldots , n$, $deg(a_i)=(deg^p(a_i), deg^n(a_i))$, where $deg^p(a_i)=\sum \limits _{\begin{array}{c} i\ne j \\ a_ia_j\in \widetilde{V^2} \end{array}}\nu ^p_B(a_ia_j)$, $deg^n(a_i)=\sum \limits _{\begin{array}{c} i\ne j \\ a_ia_j\in \widetilde{V^2} \end{array}}\nu ^n_B(a_ia_j)$.

Step 4. Calculate CNDs of the nodes $a_i, i=1,2,\ldots , n$, $deg[a_i]=(deg^p[a_i], deg^n[a_i])$, where $deg^p[a_i]=deg^p(a_i)+\nu ^p_A(a_i)$ and $deg^n[a_i]=deg^n(a_i)+\nu ^n_A(a_i)$.

Step 5. Calculate $COND(a_i)=deg^p(a_i)+deg^n(a_i)$ and $CCND(a_i)=deg^p[a_i]+deg^n[a_i]$, $i=1, 2, \ldots , n$.

Step 6. Select $maximum \{ COND(a_i) \}$ and $maximum \{ CCND(a_i) \}$ , $i=1, 2, \ldots , n$.

Step 7. Most communicable nodes.

Algorithm and flowchart to determine most communicable edges in a BFG using COND and CCND

Fig. 8

Flowchart to determine most communicable edges in BFG

Using the Dijkstra’s algorithm [10] first draws a crisp graph $G^*=(V, E)$, where V and E are, respectively, denote the set of all nodes and edges with $|V|=n$ and $|E|=m$.

Step 1. Put the membership values $\nu _A(a_i)=(\nu ^p_A(a_i), \nu ^n_A(a_i))$ of the nodes $a_i$’s, $i=1, 2, \ldots , n$, $\nu ^p_A(a_i)\in [0, 1]$, $\nu ^n_A(a_i)\in [-1, 0]$.

Step 2. Write the membership values $\nu _B(a_ia_j)\!=\!(\nu ^p_B(a_ia_j), \nu ^n_B(a_ia_j))$ of the edges $a_ia_j\in \widetilde{V^2}$, such that $\nu ^p_B(a_ia_j)\le \min \{ \nu ^p_A(a_i), \nu ^p_A(a_j) \}$, $\nu ^n_B(a_ia_j)\ge \max \{ \nu ^n_A(a_i), \nu ^n_A(a_j) \}$, $\nu ^p_B(a_ia_j)\in [0, 1], \nu ^n_B(a_ia_j)\in [-1, 0]$.

Step 3. Calculate ONDs of the edges $a_ia_j\in \widetilde{V^2}$, $deg(a_ia_j)=(deg^p(a_ia_j), deg^n(a_ia_j))$, where $deg^p(a_ia_j)=\sum _{\begin{array}{c} i\ne k \\ a_ia_k\in \widetilde{V^2} \end{array}}\nu ^p_B(a_ia_k)+\sum _{\begin{array}{c} j\ne k \\ a_ja_k\in \widetilde{V^2} \end{array}}\nu ^p_B(a_ja_k)$, $deg^n(a_ia_j)=\sum _{\begin{array}{c} i\ne k \\ a_ia_k\in \widetilde{V^2} \end{array}}\nu ^n_B(a_ia_k)+\sum _{\begin{array}{c} j\ne k \\ a_ja_k\in \widetilde{V^2} \end{array}}\nu ^n_B(a_ja_k)$.

Step 4. Calculate CNDs of the edges $a_ia_j\in E$, $deg[a_ia_j]=(deg^p[a_ia_j], deg^n[a_ia_j])$, where $deg^p[a_ia_j]=deg^p(a_ia_j)+\nu ^p_B(a_ia_j)$ and $deg^n[a_ia_j]=deg^n(a_ia_j)+\nu ^n_B(a_ia_j)$.

Step 5. Calculate $COND(a_ia_j)=deg^p(a_ia_j)+deg^n(a_ia_j)$ and $CCND(a_ia_j)=deg^p[a_ia_j]+deg^n[a_ia_j]$, for all $a_ia_j\in \widetilde{V^2}$.

Step 6. Select $maximum \{ COND(a_ia_j) \}$ and $maximum \{ CCND(a_ia_j) \}$ , for all $a_ia_j\in \widetilde{V^2}$.

Step 7. Most communicable edges.

Applications of BFG using COND and CCND

In this section, we have constructed two real-life bipolar fuzzy models. First, one is international relationship between east and west countries during the cold-war era and second one is communication between teachers and students. Using the COND and CCND, the selection of the highest communicated countries and best pair of countries according to internal communication is determined for the first one and the best communicated teachers for the second one are shown.

International relationship between countries during the cold-war era

The original work is to find the most communicated countries in bipolar fuzzy decision-making problems. In a BFG $G=(V,A,B)$ with n nodes and m edges, $COND(a_i)=deg^p(a_i)+deg^n(a_i)$ and $CCND(a_i)=deg^p[a_i]+deg^n[a_i]$. Now, using $\max \{ COND(a_i) \}$ and $\max \{ CCND(a_i) \}$ for all i, we have to find the top most communicated nodes for which COND and CCND are maximum. Similarly, we have to find the edges between two corresponding nodes for which $COND(a_ia_j)$ and $CCND(a_ia_j)$, $i\ne j$ are maximum are the top most connected nodes according to communications.

At the time of cold war in 1950s, the race of confrontation and all armament between the east and west countries accrued a huge amount of energy. The energy could have been a major possible cause of the Third World War. This dangerous energetic relation and its computation have been discussed as a bipolar crisp relational graph in [36], before the enemies between USSR and China. The main interesting fact is that the releasing of this accrued energy was disequilibrium. The China card performed a main role at the end of cold war. However, China and USSR reduced their own enemies in the late 1960s. Since China and the U.S. were facing the same enemy with USSR, so this was a common enemy between China and the U.S. At that time, the president of U.S. understood that the Taiwan problem is a major interruption between China and the U.S. He made a plan to open the door to China, and he fetched the relationship between China and the U.S. that is a normalization course, which was followed by western allies and Japan. After that, the USSR collapse into some parts. However, there arises a question that is “why the other countries agreed with this normalization course between China and the U.S. ?”

Representation of membership values

The reason depended upon the relationship and communication in the sense of power, facility, security, import–export, etc., and all these things depend upon a bipolar fuzzy relation that has been discussed in [34]. Here, we represent all the good and bad relationships between every pair of countries as a BFG, which is shown in Fig. 9, that has been taken from [34]. In Fig. 9, the nodes represent the countries Japan, Vietnam, Cuba, Nato, U.S., Russia, E. European countries, S. Korea, Taiwan, China, and N. Korea, and they are denoted by J, V, C, N, US, R, ER, SK, T, CH, and NK, respectively.

Fig. 9

Modeling of countries during the post-world war era as a BFG with membership degree of the nodes as $(1,-1)$

Table 1 Nodes and their corresponding COND, CCND of the BFG G of Fig. 9

Table 2 Edges and their corresponding CCND of the BFG G of Fig.  9

Decision-making

From Table 1, we see that the COND and CCND between the nodes CH and the US are more than the other nodes. This means that the total connection (direct and indirect) of China and the U.S. with other countries was better than the other countries. From Table 2, we have the CCND of the edge between the nodes CH and US is more than the other edges. Therefore, the total relationship and communication (direct and indirect) between China and the U.S. was at the top level from the other countries.

Why the other countries agreed with the normal relationship between China and the U.S.? The answer of the question is “the total aggregate relation and communication of China and the U.S. was at the highest level from the other countries. Also the total internal relationship (for showing normalized to the other countries) between China and the U.S. was maximum than the other pair of countries.”

Therefore, China and the U.S was the most communicated countries and the total internal communication between China and the U.S was at the highest level.

Modeling of a communication system for improvement of students

Here, first, we will model the communications between teachers and students as a BFG. Then, using the COND and CCND of the nodes, we have to select that nodes for which the COND and CCND both are maximum. Then, we can find that the most communicated teachers for the corresponding nodes have the maximum COND and maximum CCND.

Model construction

During recent time, the improvement of student is very indispensable in educational field. Now, most of the improvement of a student depends upon (i) students’ skill, (ii) communication with each other, (iii) good results in various examinations, (iv) taking part in various competitive examinations, (v) study plan, etc. All these matters mainly depend upon the communication between the students with each other and the communication between the students and teachers. Therefore, communications are very needed in the present time. Now, we presume that, in an Institution, there are five teachers in Mathematics Department. Here, we demonstrate this communication system in this Institution as a BFG (Fig. 10) between teachers and students.

Fig. 10

Modeling of a communication system as a BFG G

Description of membership values

Here, each node performs as a teacher. The positive membership value of each node represents the communication power of a teacher with students. The communication varies teacher to teacher due to lack of time, pressure of official works, etc. Therefore, this is uncertain. Its value is 0 if the communication is $\le 10 \%$, and its value is 1 if the communication is $\ge 90\%$. Therefore, this lies between 0 and 1. Also the negative membership value of each node represents the incapability of teachers to maintain this communication (because of lacks of time, pressure of official works, etc). Therefore, this is uncertain. Its value is − 1 if the incapability is $\ge 85 \%$ and it’s value is 0 if the incapability is $\le 10\%$. Therefore, this lies between − 1 and 0.

The positive membership value of each edge represents that the communication between two teachers for students and its varies also due to lack of time, pressure of official works, etc. Therefore, this is again uncertain. Its value is 0 if the communication is $\le 15\%$, and its value is 1, if the communication is $\ge 80\%$. Therefore, this lies between 0 and 1. The negative membership value of each edge represents the incapability of teachers to maintain this communication. Therefore, this is uncertain. Its value is - 1 if the incapability is $\ge 85 \%$ and its value is 0 if the incapability is $\le 10\%$. Therefore, this lies between - 1 and 0.

Table 3 Nodes and their corresponding COND, CCND of the BFG G of Fig. 10

Decision-making

From Table 3, we have $COND(t_1)<COND(t_3)<COND(t_4)<COND(t_2)=COND(t_5)$ and $CCND(t_1)<CCND(t_3)<CCND(t_4)<CCND(t_2)<CCND(t_5)$.

$\max \{ COND(t_i) \} =1.20=COND(t_2)=COND(t_5)$ and $\max \{ CCND[t_i] \}=1.55= CCND[t_5]$, for all $i =1, 2, 3, 4, 5$. Thus, for the node $t_5$, both the value $COND(t_5)$ and $CCND[t_5]$ are maximum. $\min \{ COND(t_i) \} =0.98=COND(t_3)$ and $\min \{ CCND[t_i] \}=1.27= CCND[t_3]$, for all $i =1, 2, 3, 4, 5$. Thus, for the node $t_3$, both the value $COND(t_3)$ and $CCND[t_3]$ are minimum.

Since the COND and CCND of the node $t_5$ both are highest, therefore the totally accurate communication of the node $t_5$ is maximum. Hence, the teacher $t_5$ is the most communicable teacher for development of future of students.

Therefore, using the help of maximum value of COND and maximum value of CCND of the nodes, the selection of the $t_5$ teacher as a best communicate teacher is depicted.

Comperative analysis

In a fuzzy graphical model, there exists only one side membership value of each node and edge. Akram et al. [5, 6] and Poulik and Ghorai [25] have described different types of applications of BFGs in wireless network, determination of journey’s order using path, connectivities, and indices. However, in this work, different types of degrees of nodes have been used. In our first model, there exists some good and bad relations between countries which are of opposite to each other and uncertain. Therefore, in this type of situations, bipolar fuzzy graph can be used to get better explanation. Also, the degree of vertices in a fuzzy graph gives the total contribution of the nodes in the system only. However, the degree of nodes in a bipolar fuzzy graph gives the total information and contribution of the positive and negative characters separately. Many decision-making problems on bipolar fuzzy graphs had been done previously. However, in our proposed methods, there are positive as well as negative relations. Here, the COND and CCND give the total combined (both positive and negative side) contribution of the countries in the system. Based on COND and CCND, the highest communicated countries in international communication systems and the most communicated teacher in teacher–students communication system are determined.

Advantages and limitations

The main advantages of the proposed method are as follows:

• The relation of communication between some countries have been analyzed here

• The most communicated countries are shown using COND and CCND in a BFG.

• This method can be applied to explain teacher–student communication in education system for the improvement of study under bipolar fuzzy information.

Some of the limitations of this work are as follows:

• This work mainly focused on BFG and its related network systems.

• This method is applicable only when two opposite-sided directional thinking exist in a connected bipolar fuzzy graphical system.

• If the membership values of the characters are given in different environment, then the concept of BFG cannot be applicable.

• Collection of real data may not be possible always.

Conclusion and future works

The degree of nodes and edges in a BFG have been applied to analyze the international relationship between some countries and teacher students’ communication in education field. The regularity of nodes and edges in a BFG plays an important factor in many decision-making problem with bipolar fuzzy environment for instances, shortest path, boundary and interior stations in a wireless network, water and electric connection, etc. First, it contains perfectly regular BFG, which is an interpretation of the degrees of nodes with their characteristic. Second, regular interconnections between nodes are visualized as a perfectly edge-irregular BFG with their properties. Third, the total complete communication of nodes in a bipolar fuzzy environment has been described in terms of COND and CCND with some theorems. Some algorithms with corresponding flowcharts are exhibited to calculate the most communicable nodes and edges in a BFG. Two applications of our research work have been discussed using COND and CCND of BFGs. First one is to select the most communicated countries between countries at the time of cold-war era. The second one is in decision-making to select the best communicated teacher in a teacher–student communication system. At last, a comparative analysis and some advantages and limitations of this work have been described.

Based on the multiple characteristics of the nodes and edges in graphs, there are a lot of future research scope, such as: (i) complete degree in intuitionistic fuzzy graphs, (ii) complete degree in pythagorean fuzzy graphs, (iii) complete degree in m-polar fuzzy graphs, etc.