Explicitly represented polygon wall boundary model for the explicit MPS method

Abstract

This study presents an accurate and robust boundary model, the explicitly represented polygon (ERP) wall boundary model, to treat arbitrarily shaped wall boundaries in the explicit moving particle simulation (E-MPS) method, which is a mesh-free particle method for strong form partial differential equations. The ERP model expresses wall boundaries as polygons, which are explicitly represented without using the distance function. These are derived so that for viscous fluids, and with less computational cost, they satisfy the Neumann boundary condition for the pressure and the slip/no-slip condition on the wall surface. The proposed model is verified and validated by comparing computed results with the theoretical solution, results obtained by other models, and experimental results. Two simulations with complex boundary movements are conducted to demonstrate the applicability of the E-MPS method to the ERP model.

1 Introduction

The smoothed particle hydrodynamics (SPH) method [11, 25] and the moving particle semi-implicit/simulation (MPS) [23] method have been widely used for the analysis of free-surface flows.

One of the characteristics of these methods is that they discretize strong form partial differential equations in the Lagrangian description, without node connectivity information. This characteristic allows them to deal with turbulent-free surfaces and moving boundaries without the difficulties faced by mesh-based methods, such as the finite element method (FEM). In those situations, it is often necessary for mesh-based methods to remesh or renode, which reduces both the accuracy and the parallel efficiency. They also require special treatment for free surfaces and moving boundaries; these treatments include the volume of fluid (VOF) method [13] and the level set method [9, 38].

Another important characteristic is that mass conservation is automatically satisfied, assuming each node (particle) has its own mass. In addition to this assumption, Koshizuka and Oka [23] applied a density validation term to the right-hand side of the pressure Poisson equation in the derivation of the MPS algorithm, instead of the velocity divergence term generally used in the finite difference method (FDM) with the projection method [4]. Since this term has the effect of recovering the fluid volume and contributes robustness to the computations, it has been widely employed with both MPS and SPH computations [16, 20, 22] as a stabilization term. Therefore, mesh-free particle methods have the significant advantages of convenience and robustness in long-term analyses of free-surface flows with moving boundaries.

However, they have problems with accuracy. Because particles are moving in a Lagrangian fashion, it is difficult to let the spatial resolution vary with position, such as by using smaller particles near wall boundaries in order to treat boundary layer flows. In addition, since a nonhomogeneous distribution of particles harms the accuracy of the computation, stabilization techniques, such as artificial viscosities [26, 30, 33] or collision forces, are often required.

Examples of simulations that can take advantage of mesh-free particle methods include disasters involving water, such as tsunamis [6, 35] and sloshing problems [7]. These kinds of problems generally have large analytical areas, so fully explicit algorithms, such as the Weakly compressible SPH (WCSPH) method [31, 42] and the explicit MPS (E-MPS) method [37, 43, 47] have often been adopted. Since the explicit methods have high scalability for parallel computing, distributed-memory parallel algorithms have been investigated and developed [10, 21].

Research has made great progress with the SPH methods for treating wall boundaries. The repulsive-force model [29, 31, 32] was developed in order to prevent fluid particles from penetrating wall boundaries. Although this model is relatively easy to implement, the fluid particles near wall boundaries are unstable because the boundary conditions are not satisfied. On the other hand, the mirror (ghost) particle approach [34] is widely used to satisfy the boundary conditions on walls. In this approach, a virtual particle is generated across the wall at the location of the mirror image of each fluid particle. These mirror particles are given pressure and velocity values such that the pressure Neumann boundary condition and slip/no-slip condition are satisfied. However, this approach has several problems, including a high computational cost caused by the need to generate the virtual particles, and the leakage of particles at the angled edges of surfaces; thus, some improvements have been presented [49]. A method similar to the mirror particle approach is taken by the virtual marker (fixed ghost particle) approach [3, 26]. In this approach, wall particles are fixed and given the value of their mirror point; this is accomplished by using moving least squares instead of by generating mirror particles. This approach is widely used, but it requires a special technique to determine the position of the virtual markers near the curved and complex-shaped surfaces.

Recently, the research community using the MPS method developed the polygon wall boundary model, which treats wall boundaries as a set of arbitrary planes. Compared to conventional models that represent wall boundaries as particles, with the polygon wall boundary model, it is easier to prepare the initial configuration data during the design process, since polygon or surface patch data generated by computer-aided design (CAD) software or a commercial finite element method solver can be used for the wall boundaries. The polygon model can also reduce memory usage in the case of large-scale and flat geometry, such as tsunami simulations, which require many particles for the wall boundaries. Harada et al. [12] used the impulse–momentum relationship at the wall to derive the force exerted on a fluid particle by a wall. This can be classified as a repulsive-force model, and thus Harada’s model will have the same problems of instability and strangely behaving fluid particles near the wall. Yamada et al. [47] focused on the E-MPS method, and they proposed another formulation for the polygon model. Although it is an expansion of the differential operator models, it results in excessive pressure oscillations.

In this study, we developed a new polygon wall boundary model for fully explicit algorithms, called the explicitly represented polygon (ERP) wall boundary model. It is based on the mirror particle approach and can satisfy the boundary conditions on walls, and it is versatile enough to treat arbitrarily shaped boundaries and arbitrary movements. The ERP model has the following characteristics.

• Wall boundaries are represented explicitly.

• Generation of virtual particles and the need to make special adaptations for angled edges are not required.

• The pressure Neumann boundary condition and the slip/no-slip condition on the walls are satisfied.

Although in this study we apply the ERP model to the E-MPS method, the ERP model could also be applied to the WCSPH method, because there are differential operator approximations in the WCSPH methods that can be formulated in the same way by the ERP model.

2 Explicit MPS method

2.1 Governing equations

The Navier–Stokes equations and the continuity equation for a quasi-incompressible Newtonian fluid in a Lagrangian reference frame are given as follows:

$$\begin{aligned}&\frac{D \varvec{v}}{Dt} = -\frac{1}{\rho } \nabla p + \nu \nabla ^2 \varvec{v} + \varvec{g}, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{1}{\rho } \frac{D \rho }{D t} + \nabla \cdot \varvec{v} = 0, \end{aligned}$$

(2)

where $\rho$ is the density of the fluid, $\varvec{v}$ is the velocity vector, $p$ is the pressure, $\nu$ is the kinetic viscosity, and $\varvec{g}$ is the gravitational acceleration vector.

2.2 MPS discretization of differential operators

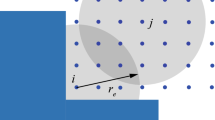
In the MPS discretization, the differential operators acting on a particle $i$ are evaluated using the neighboring particles $j$ located within an effective radius $r_e$. Let $\mathbb {P}_i$ be the set of particles that neighbor particle $i$, as follows:

$$\begin{aligned} \mathbb {P}_i \equiv \big \{j \mid r_e > |\varvec{x}_{ij}| \wedge j \ne i \big \} . \end{aligned}$$

(3)

In this study, $\phi _{ij}$ denotes the difference between particles $i$ and $j, \phi _j - \phi _i$, where $\phi$ represents a property of the particle.

The neighboring particles are weighted using a function of their separation from particle $i, r = |\varvec{x}_{ij}|$. In the original MPS, the weight function is given as

$$\begin{aligned} w(r) = {\left\{ \begin{array}{ll} \frac{r_e}{r} - 1 &{}\quad (0 \le r < r_e) \\ 0 &{}\quad (r_e \le r) . \end{array}\right. } \end{aligned}$$

(4)

A normalization factor, the particle number density, is defined as

$$\begin{aligned} n_i \equiv \sum _{j \in \mathbb {P}_i} w\big (|\varvec{x}_{ij}|\big ). \end{aligned}$$

(5)

This represents the density of the fluid.

The E-MPS method models the differential operators in the governing equations as follows:

$$\begin{aligned}&\langle \nabla p \rangle _i = \frac{d}{n^0} \sum _{j \in \mathbb {P}_i} \left[ \frac{p_j + p_i}{| \varvec{x}_{ij}|} \frac{ \varvec{x}_{ij}}{| \varvec{x}_{ij}|} w\big (| \varvec{x}_{ij}|\big ) \right] , \end{aligned}$$

(6)

$$\begin{aligned}&\langle \nabla ^2 \varvec{v} \rangle _i = \frac{2d}{{\uplambda }^0 n^0} \sum _{j \in \mathbb {P}_i} \left[ \varvec{v}_{ij} w\big (|\varvec{x}_{ij}|\big ) \right] . \end{aligned}$$

(7)

Here $d$ is the number of dimensions, $n^0$ is the initial value of the particle number density given by Eq. (5) and calculated for the initial particle geometry, and the angle brackets $\langle \rangle$ indicate discretization by the MPS differential model. ${\uplambda }^0$ is a correction parameter that ensures that the increase in the variance is equal to that of the analytical solution, and like $n^0$, it is calculated for the initial geometry:

$$\begin{aligned} {\uplambda }_i \equiv \frac{ \sum _{j \in \mathbb {P}_i} |\varvec{x}_{ij}|^2 w\big (|\varvec{x}_{ij}|\big )}{ \sum _{j \in \mathbb {P}_i} w\big (|\varvec{x}_{ij}|\big )} . \end{aligned}$$

(8)

2.3 Algorithm

In the E-MPS method, the fractional step algorithm is applied for time discretization, hence each time step is divided into prediction and correction steps. In this study, in order to reduce the computational cost of calculating the distance between particles and polygons, the Navier–Stokes equations are partitioned as follows:

(1) Prediction step

$$\begin{aligned} \frac{\varvec{v}^* - \varvec{v}^n}{{\varDelta }t} = \varvec{g}, \end{aligned}$$

(9)

(2) Correction step

$$\begin{aligned} \frac{\varvec{v}^{n+1} - \varvec{v}^{*}}{{\varDelta }t} = \nu \big \langle \nabla ^2 \varvec{v} \big \rangle ^n - \frac{1}{\rho ^0} \big \langle \nabla p \big \rangle ^{n+1}, \end{aligned}$$

(10)

where $\varvec{v}^*$ is the intermediate velocity, and $\rho ^0$ is the constant density of the fluid.

To calculate the correction step, Eq. (10), the pressure values in the next time step $p^{n+1}$ are required. In the E-MPS method, which assumes that fluids are weakly compressible, the pressure values required in the correction step, Eq. (10), are calculated as

$$\begin{aligned} p_i^{n+1} = c^2 \rho ^0 \left( \frac{n^*_i}{n^0} -1 \right) , \end{aligned}$$

(11)

where $c$ is a parameter that is set such that the conditions of numerical stability are satisfied.

2.4 Free-surface criterion

The condition for free-surface particle recognition is given as follows:

$$\begin{aligned} n^*_i < \beta n_0 . \end{aligned}$$

(12)

Here $\beta$ is a threshold coefficient, and in the E-MPS model, we set $\beta = 1.0$ to prevent instability caused by negative pressure. For particles on a free surface, we apply the Dirichlet condition for the pressure, $p = 0$.

3 Existing polygon wall boundary model

3.1 Wall weight function

There are two existing studies [12, 47] on the polygon wall boundary model for the MPS methods. In these studies, polygon walls are implicitly represented using the distance function: the nearest distance between particle $i$ and all polygons, $d^{wall}_{i}$, and the outward unit normal vector, $\varvec{n}^{wall}_i$, are given by the distance function and its gradient, using background grids.

To implement a polygon wall without using wall particles, it is necessary to interpolate between the contributing parts of the walls that are used in the particle number density computation. The wall weight function is defined as the sum of the weights of the virtual wall particles that are created inside the wall. Using the distance between particle $i$ and the nearest wall, $d^{wall}_i$, the wall weight function, $z(|d^{wall}_i|)$, is defined as

$$\begin{aligned} z\big (d^{wall}_{i}\big ) \equiv \sum _{j \in wall} w(|\varvec{x}_{ij}|) . \end{aligned}$$

(13)

Within the neighboring particles $j \in \mathbb {P}_i$ of particle $i$, we define the fluid particles as $j \in particle$ and the virtual wall particles as $j\in wall$. The particle number density Eq. (5) can be partitioned into the contribution of the fluid particles and that of the wall weight function, as follows:

$$\begin{aligned} n_i= & {} \sum _{j \in particle} w\big (|\varvec{x}_{ij}|\big ) + \sum _{j \in wall} w\big (|\varvec{x}_{ij}|\big ) \nonumber \\= & {} \sum _{j \in particle} w\big (|\varvec{x}_{ij}|\big ) + z\big (d^{wall}_{i}\big ) . \end{aligned}$$

(14)

In the actual computation, the wall weight function is determined by a linear interpolation of the values at a given discrete distance; these are calculated prior to this computation.

3.2 Viscosity term

The viscosity term discretized by the Laplacian model (7) is partitioned into the contributions from the fluid particles and those from the polygon walls:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i = \big \langle \nabla ^2 \varvec{v} \big \rangle _i^{particle} + \big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall} . \end{aligned}$$

(15)

Assuming that the velocity of the wall is a constant value $\varvec{v}^{wall}$ within the effective radius of the particle $i$, the contributing region of the polygon wall can be rewritten as follows:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall}&= \frac{2d}{{\uplambda }^0 n^0} \big ( \varvec{v}^{wall} - \varvec{v}_{i}\big ) \sum _{j \in wall} w\big (|\varvec{x}_{ij}|\big ) \end{aligned}$$

(16)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \big ( \varvec{v}^{wall} - \varvec{v}_{i} \big ) \ z\big (|\varvec{x}_{ib}|\big ) . \end{aligned}$$

(17)

3.3 Pressure gradient term

As is the case with the viscosity term, the pressure gradient term is partitioned into the contributions from the fluid particles and those from the polygon walls, as follows:

$$\begin{aligned} \big \langle \nabla p \big \rangle _i = \big \langle \nabla p \big \rangle _i^{particle} + \big \langle \nabla p \big \rangle _i^{wall} . \end{aligned}$$

(18)

3.3.1 Harada’s model

Harada et al. [12] derived the contribution from the wall $\langle \nabla p \rangle ^{wall}_i$ from the impulse–momentum change equation

$$\begin{aligned} \frac{D \varvec{x}}{D t} = -\frac{1}{\rho ^0} \int ^{t + {\varDelta }t}_t \nabla p dt \end{aligned}$$

(19)

as the force exerted on the particles in contact with the polygons

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i =- \frac{\rho ^0}{{\varDelta }t^2} \left( l^0 - d^{wall}_{i}\right) \varvec{n}^{wall}_{i}. \end{aligned}$$

(20)

Since this force is repulsive on the walls, this model can be classified as a repulsive-force model [31, 32].

Harada et al. claimed that, in the semi-implicit MPS (SI-MPS) [23] computation, the pressure Poisson equation can be computed using only the degrees of freedom of the fluid particles. However, the derivation of Eq. (20) implies that $p^{n+1} \simeq p^n$, hence the pressures near the wall are confined to explicit accuracy, although these pressures are obtained implicitly by solving systems of linear equations. In the E-MPS computation, Harada’s model causes strange behavior in the particles that are in contact with polygons. The result of a dam-break problem computed by the E-MPS method with Harada’s pressure gradient model is shown in Fig. 1. As can be seen in the figure, particles near the wall boundaries stick to the wall and have unnatural pressure values.

Fig. 1

Problem solved using Harada’s pressure gradient model

3.3.2 Yamada’s model

Yamada et al. [47] derived the wall part of the pressure gradient term based on the E-MPS gradient model given by Eq. (6). Assuming that the pressures of the neighboring particles $j$ that are within the walls are equal to the pressure of particle $i$, that is, $p_j = p_i$, the wall part can be rewritten as follows:

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i&= \frac{d}{n^0} \sum _{j \in wall} \left[ \frac{\varvec{x}_{ij}}{| \varvec{x}_{ij}|} \, \frac{ p_j + p_i }{|\varvec{x}_{ij}|} w\big (| \varvec{x}_{ij}|\big ) \right] \end{aligned}$$

(21)

$$\begin{aligned}&= \frac{d}{n^0} (2 p_i) \sum _{j \in wall} \left[ \frac{\varvec{x}_{ij} \cdot \varvec{n}^{wall}_{i}}{| \varvec{x}_{ij}|^2} w\big (| \varvec{x}_{ij}|\big ) \right] \varvec{n}^{wall}_{i}. \end{aligned}$$

(22)

Using the wall weight function for the gradient model,

$$\begin{aligned} z^{grad}(d^{wall}_{i}) \equiv \sum _{j \in wall} \left[ \frac{\varvec{x}_{ij} \cdot \varvec{n}^{wall}_{i}}{| \varvec{x}_{ij}|^2} w\big (| \varvec{x}_{ij}|\big ) \right] , \end{aligned}$$

(23)

Eq. (22) can be rewritten as

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i = \frac{d}{n^0} \left\{ 2 p_i \, z^{grad}\big (d^{wall}_{i}\big ) \right\} \varvec{n}^{wall}_{i}. \end{aligned}$$

(24)

Yamada’s model is a polygon wall boundary model for the E-MPS computations, and it is naturally derived from the MPS gradient model. This model, however, has a problem in that at the wall, there are non-physical oscillations in the vertical direction as shown in Fig. 2; these disturb the pressure field and decrease the accuracy. This problem is seen in the calculations for verifying the hydrostatic pressure, in Sect. 5.1; it is attributed to the assumption that $p_j = p_i$.

Fig. 2

Problem in Yamada’s pressure gradient model

4 Explicitly represented polygon wall boundary model

4.1 Explicit polygon representation

In the ERP model, the polygon walls are represented explicitly, without constructing the distance function. Let us denote the nearest point on the polygon $k$ from the particle $i$ as $\varvec{x}^{near}_{i,k}$. As illustrated in Fig. 3, the ERP model assumes that the force exerted on the wall by the particle $i$ acts on only the nearest point, $\varvec{x}^{wall}_i$, for all the points $\varvec{x}^{near}_{i,k}$, and that it can be written as

$$\begin{aligned} \varvec{x}^{wall}_i \equiv {\mathop {\hbox {argmin}}\limits _{\varvec{x}^{near}_{i,k}}} \big |\varvec{x}_i - \varvec{x}^{near}_{i, k}\big | \quad (k = 1, 2, \ldots , n_{pol}). \end{aligned}$$

(25)

In this study, $\varvec{x}^{wall}_i$ is called the force-acting point of particle $i$. In this operation, calculation of the distance between the particle and wall is conducted by using a fast algorithm ([8], pp 136–142) to compute in which of the triangle polygon’s Voronoi feature regions the particle lies.

Fig. 3

Point of application of force from particle $i$, and its unit normal vector

The outward unit normal vector of the force acting on the point $\varvec{x}^{wall}_i$ is defined as follows:

$$\begin{aligned} \varvec{n}^{wall}_i \equiv \frac{\varvec{x}_i - \varvec{x}^{wall}_i}{\big |\varvec{x}_i - \varvec{x}^{wall}_i\big |}. \end{aligned}$$

(26)

4.2 Mirror particle

In SPH computations, the mirror particle (ghost particle) method [34] is widely used to satisfy the homogeneous pressure Neumann boundary condition

$$\begin{aligned} \nabla p \cdot \varvec{n} = 0. \end{aligned}$$

(27)

For particles close to the wall, mirror particles are placed on the other side of the wall, as shown in Fig. 4. These methods, however, have high computational costs, because the mirror particles are regenerated at each time step, and the fluid particles leak out at angled edges. Instead of generating mirror particles, fixed wall particles can be given the value of their mirrored point (virtual marker) [3, 26], but special techniques are required to deal with curved surfaces.

Fig. 4

Mirror particles

The mirror particle corresponding to particle $i$ is denoted by $i'$. The position of particle $i', \varvec{x}_{i'}$, is

$$\begin{aligned} \varvec{x}_{i'} = \varvec{x}_i + 2 \big (\varvec{x}^{wall}_i - \varvec{x}_i\big ). \end{aligned}$$

(28)

The transformation matrix for reflection across the plane whose unit normal vector is $\varvec{n}, \varvec{R}^{ref} (\varvec{n})$, and the inverse transformation matrix, $\varvec{R}^{inv}$, are defined as:

$$\begin{aligned} \varvec{R}^{ref}(\varvec{n})&\equiv \varvec{I} - 2\varvec{n} \otimes \varvec{n} \end{aligned}$$

(29)

$$\begin{aligned} \varvec{R}^{inv}&\equiv - \varvec{I}. \end{aligned}$$

(30)

The reflection transformation matrix for the particle $i$ and the unit normal vector $\varvec{n}^{wall}_i, \varvec{R}^{ref}(\varvec{n}^{wall}_i)$, will be abbreviated below as $\varvec{R}^{ref}_i$.

4.3 Pressure boundary condition

The set of mirror particles corresponding to the particles neighboring particle $i$ is expressed as $j' \in virtual$. To satisfy the pressure Neumann boundary condition, the wall part of the pressure gradient is

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i = \frac{d}{n^0} \sum _{j' \in virtual} \left[ \frac{\varvec{x}_{ij'}}{|\varvec{x}_{ij'}|}\frac{p_{i} + p_{j'}}{|\varvec{x}_{ij'}|} w\big (|\varvec{x}_{ij'}|\big ) \right] . \end{aligned}$$

(31)

In terms of the two particles $i$ and $j$ and their mirror particles $i'$ and $j'$, which are reflected across the same plane, we have the following relations:

$$\begin{aligned} \varvec{x}_{ij'}&= \varvec{R}^{ref}_i \varvec{x}_{i'j}, \end{aligned}$$

(32)

$$\begin{aligned} |\varvec{x}_{ij'}|&= |\varvec{x}_{i'j}|. \end{aligned}$$

(33)

The isotropic weight functions used in the general MPS computations, including Eq. (4), satisfy the equation:

$$\begin{aligned} w\big (|\varvec{x}_{ij'}|\big ) = w\big (|\varvec{x}_{i'j}|\big ). \end{aligned}$$

(34)

If we set the pressure exerted by the mirror particle $j'$ to be the same as that of the particle $j$, that is, $p_{j'} = p_j$, and use Eqs. (32)–(34), Eq. (31) can be rewritten as follows:

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i&= \frac{d}{n^0} \sum _{j \in \mathbb {P}_{i'}} \left[ \frac{\varvec{R}^{ref}_i\varvec{x}_{i'j}}{|\varvec{x}_{i'j}|}\frac{p_{i} + p_{j}}{|\varvec{x}_{i'j}|} w\big (|\varvec{x}_{i'j}|\big ) \right] \end{aligned}$$

(35)

$$\begin{aligned}&= \frac{d}{n^0} \varvec{R}^{ref}_i \sum _{j \in \mathbb {P}_{i'}} \left[ \frac{\varvec{x}_{i'j}}{|\varvec{x}_{i'j}|}\frac{p_{i} + p_{j}}{|\varvec{x}_{i'j}|} w\big (|\varvec{x}_{i'j}|\big ) \right] \end{aligned}$$

(36)

$$\begin{aligned}&= \varvec{R}^{ref}_i \big \langle \nabla p \big \rangle ^{particle}_{i'} \end{aligned}$$

(37)

The wall part of the pressure gradient, $\langle \nabla p \rangle ^{wall}_i$, is equal to the reflection transformed pressure gradient from the position of the mirror particle $i'$, as implied by Eq. (37) and illustrated in Fig. 5.

Fig. 5

ERP model calculations without using virtual particles

It is worth noting that when there are no particles above the wall, the particles neighboring the mirror particle $i'$ contain the original particle and its neighbors

$$\begin{aligned} \mathbb {P}_{i'} \subset \mathbb {P}_{i} + \{ i \}. \end{aligned}$$

(38)

Because of this, it is not necessary to search for the particles neighboring the mirror particle $i'$, and this greatly reduces the computational cost.

Since the ERP model is based on the mirror particle method, there is the same problem of particle leakage at the angled edges of the polygons. To deal with this problem, a repulsive force is added to the particles for which the distance to the nearest polygon is less than $\frac{1}{2}l^0$:

$$\begin{aligned} \varvec{f}^{rep}_i = {\left\{ \begin{array}{ll} - \alpha ^{rep} \left( \dfrac{\frac{1}{2} l^0}{r} - 1 \right) \varvec{n}_i^{wall} &{}\quad \left( 0 < r < \frac{1}{2}l^0\right) \\ 0 &{}\quad \left( \frac{1}{2}l^0 \le r\right) \end{array}\right. }. \end{aligned}$$

(39)

where $\alpha ^{rep}$ is a repulsive coefficient added to ensure the computation is stable. It is clear, however, that this approach cannot satisfy the boundary conditions near angled edges, but it is quite reasonable in terms of having versatile and robust computations when the boundaries undergo arbitrary motions. The pressure gradient in the ERP model, when including the pressure Neumann boundary condition, is

$$\begin{aligned}&\big \langle \nabla p \big \rangle _i = \big \langle \nabla p \big \rangle ^{particle}_{i} + \varvec{R}^{ref}_i \langle \nabla p \rangle ^{particle}_{i'} + \varvec{f}^{rep}_i \end{aligned}$$

(40)

$$\begin{aligned}&= \frac{d}{n^0} \sum _{j \in \mathbb {P}_i} \left[ \frac{\varvec{x}_{ij}}{|\varvec{x}_{ij}|}\frac{p_i + p_j}{|\varvec{x}_{ij}|} w\big (|\varvec{x}_{ij}|\big ) \right] \nonumber \\&\quad +\, \frac{d}{n^0} \varvec{R}^{ref}_i \sum _{j \in \mathbb {P}_{i'}} \left[ \frac{\varvec{x}_{i'j}}{|\varvec{x}_{i'j}|}\frac{p_{i} \!+\! p_j}{|\varvec{x}_{i'j}|} w\big (|\varvec{x}_{i'j}|\big ) \right] \!+\! \varvec{f}^{rep}_i \end{aligned}$$

(41)

$$\begin{aligned} \big \langle \nabla p \big \rangle ^{wall}_i= & {} \varvec{R}^{ref}_i \big \langle \nabla p \big \rangle ^{particle}_{i'} + \varvec{f}^{rep}_i. \end{aligned}$$

(42)

4.4 Velocity boundary condition

The slip and no-slip boundary conditions result in different velocities being given to the mirror particles. Similar to what we did for the pressure gradient, we will derive the Laplacian for the velocity model that satisfies the slip/no-slip boundary condition, using only fluid particles.

4.4.1 Slip boundary condition

To impose the slip boundary condition, the velocity of the mirror particle $j'$ is given to the reflection transformed velocity of the original particle $j$ as

$$\begin{aligned} \varvec{v}_{j'} = \varvec{R}^{ref}_j \varvec{v}_j. \end{aligned}$$

(43)

In this case, the wall part of the Laplacian of the velocity in the viscosity term is

$$\begin{aligned}&\big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall} = \frac{2d}{{\uplambda }^0 n^0} \sum _{j' \in virtual} \left[ \big (\varvec{v}_{j'} - \varvec{v}_{i}\big ) w\big (|\varvec{x}_{ij'}|\big )\right] \end{aligned}$$

(44)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \sum _{j' \in virtual} \left[ \big (\varvec{R}^{ref}_j \varvec{v}_{j} - \varvec{v}_{i}\big ) w\big (|\varvec{x}_{ij'}|\big )\right] . \end{aligned}$$

(45)

Assuming that the nearest polygon wall of the particle $i$ and its neighboring particle $j$ have the same unit normal vector,

$$\begin{aligned} \varvec{n}^{wall}_j \simeq \varvec{n}^{wall}_i, \qquad \varvec{R}^{ref}_j \simeq \varvec{R}^{ref}_i, \end{aligned}$$

(46)

Equation (45) can be rewritten as follows:

$$\begin{aligned}&\big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall}\nonumber \\&= \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{ref}_i \cdot \varvec{R}^{ref}_i\nonumber \\&\qquad \sum _{j' \in virtual} \left[ \big (\varvec{R}^{ref}_i \varvec{v}_{j} - \varvec{v}_{i}\big ) w\big (|\varvec{x}_{ij'}|\big )\right] \end{aligned}$$

(47)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{ref}_i \sum _{j' \in virtual} \left[ \big (\varvec{v}_{j} - \varvec{R}^{ref}_i \varvec{v}_{i}\big ) w\big (|\varvec{x}_{ij'}|\big )\right] \end{aligned}$$

(48)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{ref}_i \sum _{j \in \mathbb {P}_{i'}} \left[ \big (\varvec{v}_{j} - \varvec{v}_{i'}\big ) w\big (|\varvec{x}_{i'j}|\big )\right] \end{aligned}$$

(49)

$$\begin{aligned}&= \varvec{R}^{ref}_i \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_{i'}. \end{aligned}$$

(50)

Note that the reflection transformation matrix has the property

$$\begin{aligned} \varvec{R}_{i}^{ref} \cdot \varvec{R}_{i}^{ref} = \varvec{I}. \end{aligned}$$

(51)

Finally, the Laplacian of the velocity when the slip boundary condition is imposed can be written as follows:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i&= \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_i + \varvec{R}^{ref}_i \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_{i'} \end{aligned}$$

(52)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \sum _{j \in \mathbb {P}_i} \left[ \varvec{v}_{ij} w\big (|\varvec{x}_{ij}|\big )\right] \nonumber \\&\quad + \frac{2d}{{\uplambda }^0 n^0} \varvec{R}_{i}^{ref} \sum _{j \in \mathbb {P}_{i'}} \left[ \varvec{v}_{i'j} w\big (|\varvec{x}_{i'j}|\big )\right] \end{aligned}$$

(53)

$$\begin{aligned} \varvec{v}_{i'}&= \varvec{R}^{ref}_i \varvec{v}_{i}. \end{aligned}$$

(54)

4.4.2 No-slip boundary condition

When the no-slip boundary condition is imposed on a wall whose velocity is $\varvec{v}^{wall}$ and whose unit normal vector is $\varvec{n}$, we have

$$\begin{aligned} (\varvec{v}-\varvec{v}^{wall}) - \varvec{n}\cdot (\varvec{v}-\varvec{v}^{wall})\varvec{n} = 0, \end{aligned}$$

(55)

and the velocity of the mirror particle $j'$ is given as

$$\begin{aligned} \varvec{v}_{j'}= & {} \varvec{R}^{inv} \varvec{v}_j + 2 \tilde{\varvec{v}}^{wall}_j , \end{aligned}$$

(56)

$$\begin{aligned} \tilde{\varvec{v}}^{wall}_j= & {} \varvec{v}^{wall}_j - \big (\varvec{n}^{wall}_j \cdot \varvec{v}^{wall}_j \big ) \varvec{n}^{wall}_j , \end{aligned}$$

(57)

where $\varvec{v}^{wall}_j$ is the velocity of the wall at the point at which it is acted on by the force of particle $j, \varvec{x}^{wall}_j$.

Using the definition of the inverse transformation matrix,

$$\begin{aligned} \varvec{R}^{inv} \cdot \varvec{R}^{inv} = \varvec{I}, \end{aligned}$$

(58)

the wall part of the Laplacian of the velocity can be rewritten as follows:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall}&= \frac{2d}{{\uplambda }^0 n^0} \sum _{j' \in virtual} \left[ \big (\varvec{v}_{j'} - \varvec{v}_{i}\big ) w\big (|\varvec{x}_{ij'}|\big )\right] \end{aligned}$$

(59)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \sum _{j' \in virtual} \left[ \left\{ \big (\varvec{R}^{inv} \varvec{v}_{j} + 2\tilde{\varvec{v}}^{wall}_j\big )\right. \right. \nonumber \\&\qquad \left. \left. - \varvec{v}_{i}\right\} w\big (|\varvec{x}_{ij'}|\big )\right] \end{aligned}$$

(60)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{inv}\sum _{j' \in virtual} \left[ \left\{ \varvec{v}_{j} - \varvec{R}^{inv}\right. \right. \nonumber \\&\qquad \left. \left. \big (\varvec{v}_{i} - 2 \tilde{\varvec{v}}^{wall}_j\big ) \right\} w\big (|\varvec{x}_{ij'}|\big ) \right] . \end{aligned}$$

(61)

In addition to the assumption of Eq. (46), assuming that the velocity on $\varvec{x}^{wall}_j$ is equal to the one on $\varvec{x}^{wall}_i$,

$$\begin{aligned} \varvec{v}^{wall}_j \simeq \varvec{v}^{wall}_i, \end{aligned}$$

(62)

Equation (61) can be rewritten as follows:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i^{wall}&= \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{inv} \sum _{j \in \mathbb {P}_{i'}} \left[ \big ( \varvec{v}_{j} - \varvec{v}_{i'} \big ) w\big (|\varvec{x}_{i'j}|\big )\right] \end{aligned}$$

(63)

$$\begin{aligned}&= \varvec{R}^{inv} \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_{i'}. \end{aligned}$$

(64)

Finally, the Laplacian of the velocity when the no-slip boundary condition is imposed can be written as follows:

$$\begin{aligned} \big \langle \nabla ^2 \varvec{v} \big \rangle _i&= \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_{i} + \varvec{R}^{inv} \big \langle \nabla ^2 \varvec{v} \big \rangle ^{particle}_{i'} \end{aligned}$$

(65)

$$\begin{aligned}&= \frac{2d}{{\uplambda }^0 n^0} \sum _{j \in \mathbb {P}_i} \left[ \varvec{v}_{ij} w\big (|\varvec{x}_{ij}|\big )\right] \nonumber \\&\quad + \frac{2d}{{\uplambda }^0 n^0} \varvec{R}^{inv} \sum _{j \in \mathbb {P}_i{'}} \left[ \varvec{v}_{i'j} w\big (|\varvec{x}_{i'j}|\big )\right] \end{aligned}$$

(66)

$$\begin{aligned} \varvec{v}_{i'}&= \varvec{R}^{inv} \left[ \varvec{v}_{i} - 2 \left\{ \varvec{v}^{wall}_i - \big (\varvec{n}^{wall}_i \cdot \varvec{v}^{wall}_i\big ) \varvec{n}^{wall}_i \right\} \right] . \end{aligned}$$

(67)

4.5 Force exerted on the polygon wall

The force on the polygon wall exerted by particle $i, \varvec{f}^{particle}_i$, is determined by the reaction to the wall parts of the pressure gradient and viscosity terms:

$$\begin{aligned} \varvec{f}^{particle}_i = -m_i \left( -\frac{1}{\rho ^0} \big \langle \nabla p \big \rangle ^{wall}_i + \nu \big \langle \nabla ^2 \varvec{v} \big \rangle ^{wall}_i \right) , \end{aligned}$$

(68)

where $m_i$ is the mass of particle $i$, defined as $m_i = \rho ^0 (l^0)^d$ in the MPS method, and the force is regarded as the point load at the acting point, $\varvec{x}^{wall}_i$, in the ERP model. In this study, the load distributions on the polygons were calculated by applying the shape functions used in the FEM.

In conventional MPS computations using wall particles, the surface forces calculated by the pressures of the wall particles are not consistent with the forces exerted on the fluid particles by the walls. Although the imbalance between these forces on the boundaries is not exposed during flow analysis, in the case of fluid–rigid or fluid–structure interaction analyses, Mitsume et al. [27] pointed out that the force imbalance causes instability near the interfaces in their study on the development of a coupling method using the E-MPS method and FEM applied a conventional polygon wall boundary model. In addition, because the wall particles are set in uniform grids to ensure correct calculations, the surfaces represented by the wall particles are not consistent with the real surfaces. Therefore, it is difficult to determine the surface area of each wall particle. In contrast with the wall particle approach, the ERP model does not encounter such problems.

4.6 Algorithm of the E-MPS method with the ERP model

The procedure of the E-MPS method with the ERP model at the $n$th step is summarized below.

• 1. Intermediate velocities $\varvec{v}^*$ are determined by the prediction calculation given by Eq. (9).

• 2. Using only fluid particles, the fluid part of the particle number density, the pressure gradient $\langle \nabla p \rangle _i^{particle}$, and the velocity Laplacian $\langle \nabla ^2 \varvec{v} \rangle _i^{particle}$ of each particle $i$ are calculated.

• 3. The acting points of each particle $i, \varvec{x}^{wall}_i$, are calculated.

• 4. Intermediate particle number densities $n^*$ are determined using the wall weight function $z$ given by Eq. (13).

• 5. Pressures $p^{n+1}$ are determined by Eq. (11).

• 6. Free-surface particles are determined by Eq. (12).

• 7. Viscosity forces are determined by the ERP calculation of the wall part of the velocity Laplacian, $\langle \nabla ^2 \varvec{v} \rangle _i^{wall}$, given by Eqs. (52) or (66).

• 8. Pressure gradient forces are determined by the ERP calculation of the wall part of the pressure gradient, $\langle \nabla p \rangle _i^{wall}$, given by Eq. (41).

• 9. Forces on polygon walls are calculated by summing Eq. (68) over $i$.

• 10. The updated velocities $\varvec{v}^{n+1}$ and particle positions $\varvec{x}^{n+1}$ are determined by the collection step calculation given by Eq. (10).

5 Verification and validation

For verification and validation of the ERP model, we conducted two-dimensional computations of a hydrostatic pressure problem, a Couette flow, Poiseuille flow, and a dam break problem.

5.1 Hydrostatic pressure

In order to verify quantitatively the accuracy of using the pressure gradient model in the ERP model, as given by Eq. (41), and applied to the E-MPS method, we analyzed a hydrostatic pressure problem in a rectangular vessel. The numerical results were compared with the theoretical solution

$$\begin{aligned} p = \rho ^0 |\varvec{g}| h, \end{aligned}$$

(69)

where $h$ is the depth of the static water surface.

The initial configuration of the hydrostatic pressure problem, in which the depth of the rectangular vessel is $0.1(\mathrm{m})$ and the width is $0.04(\mathrm{m})$, is shown in Fig. 6. In the E-MPS computation, weak compressibility causes vertical vibrations of the fluid surface. To reach the static state as quickly as possible, we chose a relatively high value for the kinematic viscosity (but not so high that it would destabilize the computations). The conditions used in the analysis are listed in Table 1.

Table 1 Hydrostatic pressure: analysis conditions

Fig. 6

Hydrostatic pressure: initial configuration

The pressures of fluid particles computed by the ERP model, the ERP model using only the repulsive force in Eq. (41), Harada’s model, Yamada’s model, and the conventional wall particle model are shown in Figs. 8, 9, 10, 11 and 12, respectively. These are the results at the $200{\!,}000$th step, at which the pressure field can be regarded to be in a steady state. In Fig. 7, snapshots obtained by each models at the $200{\!,}000$th step are shown; the pressure on the fluid particles is indicated by color [(unit $(\mathrm{N/m^2})$, min: $0$, max: $1000$].

Fig. 7

Hydrostatic pressure: visualization of results

Fig. 8

Pressure on particles (ERP model)

Fig. 9

Pressure on particles (repulsive model)

Fig. 10

Pressure on particles (Harada’s model)

Fig. 11

Pressure on particles (Yamada’s model)

Fig. 12

Pressure on particles (wall particle model)

As indicated in Figs. 9 and 10, the results from using only the repulsive force show the same tendency as those from Harada’s pressure gradient model, which is one of the repulsive force models that we mentioned in Sect. 3.3.1. Both of the results exhibit two strange lines that indicate pressures that are higher than the theoretical values. These results indicate that the pressures on the particles in contact with polygons have not been evaluated correctly, as shown in Fig. 7. Therefore, the model using only the repulsive force encounters the same problems as are found with Harada’s model, as shown in Fig. 1. On the other hand, Fig. 11 shows that Yamada’s pressure gradient model results in a disturbed pressure field that has a wide dispersion compared to that found with the other methods, as mentioned in Sect. 3.3.2.

Unlike the existing polygon wall boundary models, the ERP model doesn’t have the problems that occur with Harada’s and Yamada’s models, and it obtains a better pressure distribution that is in agreement with the theoretical solution. The results of the ERP model are also in better agreement with the theoretical solution than are the results obtained by the wall particle model, shown in Fig. 12. This is because the pressure gradient in the ERP model satisfies the pressure Neumann boundary condition, whereas the pressure gradient obtained using the wall particles in the original E-MPS method do not satisfy it rigorously.

The results of the polygon wall boundary model involving the ERP model, however, have highly dispersed pressures near the bottom of the vessel, because the accuracy deteriorates at the angled edges of polygons. Although this may be avoided by applying a procedure similar to that of the virtual marker method [3, 26], the ERP model does not adopt such a procedure because the versatility and robustness are given priority over accuracy at angled edges. The influence of the edges can be reduced by enhancing the spatial resolution by using smaller particles.

Next, we verify the pressures on the polygon wall that are calculated by the ERP model. We begin by defining for the polygons the first-order shape functions of the one-dimensional natural coordinate $\xi$:

$$\begin{aligned} N_1(\xi )= & {} 1 - \xi , \nonumber \\ N_2(\xi )= & {} \xi . \end{aligned}$$

(70)

Using these shape functions, the point loads given by Eq. (68), $\varvec{f}^{particle}_i$, are distributed on the nodes of a polygon as follows:

$$\begin{aligned} \varvec{f}^{node}_1&= \sum _i N_1\big (\xi _i\big ) \varvec{f}^{particle}_i ,\nonumber \\ \varvec{f}^{node}_2&= \sum _i N_2\big (\xi _i\big ) \varvec{f}^{particle}_i , \end{aligned}$$

(71)

where $\xi _i$ is the point in the one-dimensional natural coordinate, $\xi$, corresponding to the force acting on point $\varvec{x}^{wall}_i$. In what follows, the pressures on a polygon $k, p^{wall}_k$, are evaluated at the center of the polygon, as follows:

$$\begin{aligned} p^{wall}_k&= \int ^1_0 \varvec{f}^{node} \cdot (-\varvec{n}) d\xi \end{aligned}$$

(72)

$$\begin{aligned}&= \int ^1_0 \left\{ N_1(\xi ) \varvec{f}^{node}_1 + N_2(\xi ) \varvec{f}^{node}_2 \right\} \cdot (-\varvec{n}) d\xi . \end{aligned}$$

(73)

As illustrated in Fig. 6, we performed computations with the left-hand wall divided into various numbers of polygons.

The average and standard variation of the pressures from the $200{\!,}001$th to the $201{\!,}000$th step, with the left-hand wall comprising $30, 50$, and $100$ polygons, are shown in Figs. 13, 14 and 15, respectively. In these results, the average pressures are in good agreement with the theoretical values, and no serious pressure oscillations are observed except for at several polygons near the bottom. A large pressure oscillation is also seen at the angled edges. Within the effective radius, $r_e$, from the edge nodes, the pressure Neumann boundary condition is not satisfied, and the fluid particles are dominated by the repulsive force. Also, because the ERP model assumes that each particle receives a force from only a single polygon, since the nearest polygon changes at the edges, the direction of the force changes momentarily. This problem can be reduced by using more particles and smaller polygons.

Fig. 13

Pressure on the left wall (30 polygons)

Fig. 14

Pressure on the left wall (50 polygons)

Fig. 15

Pressure on the left wall (100 polygons)

5.2 Couette flow and Poiseuille flow

In order to verify the no-slip formulation of the ERP model given by Eq. (66), we analyzed the Couette and Poiseuille flows. In both situations, two parallel plates are separated by a distance $L = 1.0\, (\mathrm{m})$, under the no-slip condition and the other conditions shown in Table 2. Twenty fluid particles were placed vertically between two plates.

Table 2 Couette flow and Poiseuille flow: analysis conditions

In the Couette flow analysis, the upper plate moved in the $x$-direction at a velocity $v_0 = 1.0\,(\mathrm{m/s})$. The numerical results were compared with the theoretical solution of the Couette flow, which is

$$\begin{aligned} v_x(y, t)= & {} \frac{y}{L} v^0 - \sum ^{\infty }_{n=1} \frac{2 v^0}{n \pi } (-1)^{n+1} \nonumber \\&\mathrm {exp}\left\{ -(n \pi )^2 \frac{\nu t}{L^2} \right\} \sin \left( n \pi \frac{y}{L} \right) . \end{aligned}$$

(74)

In the Poiseuille flow analysis, fluid particles were given the pressure gradient force, $F = 0.08 \,(\mathrm{N})$, and the results were compared with the theoretical solution of the Poiseuille flow:

$$\begin{aligned} u_x (y, t )= & {} \frac{F}{2\nu } y (L-y) - \sum ^{\infty }_{n=0} \frac{4FL^2}{\nu (2n+1)^3 \pi ^3 } \nonumber \\&\mathrm {exp} \left\{ -(2n+1)^2 \pi ^2 \frac{\nu t}{L^2} \right\} \sin \left\{ \frac{(2n+1)\pi }{L} y \right\} \end{aligned}$$

(75)

$$\begin{aligned}&F = -\frac{1}{\rho ^0}\frac{\partial p}{\partial x} . \end{aligned}$$

(76)

In Figs. 16 and 17, the results of the Couette flow and the Poiseuille flow, respectively, are compared with the theoretical solution at times $t=0.5, 3.0, 10.0$, and $50.0 \,(\mathrm{s})$ . The theoretical values were obtained by truncating the infinite series in Eqs. (74) and (75) at $n=1{\!,}000{\!,}000$. Both the results are in quite good agreement with the theoretical values, including the velocities in the transient states. Therefore, the no-slip formulation in the ERP model is adequately accurate.

Fig. 16

Couette flow: velocity in $x$-direction in transient state

Fig. 17

Poiseuille flow: velocity in $x$-direction in transient state

5.3 Pressure in comparison with experiment of dam break

For validation of the E-MPS computation with the ERP model, we analyzed a dam break problem, and the numerical results were compared with the experimental results obtained by Hu and Kashiwagi [14]. The initial configuration is illustrated in Fig. 18. In the experiment, a pressure sensor was installed on the right-hand vertical wall at point $A$, as shown in Fig. 18. The experiment was repeated eight times, and the mean value was calculated for comparison with the numerical results. The conditions used in the E-MPS computation are reported in Table 3, and the pressures were calculated at the point $A$ by using Eq. (73).

Fig. 18

Dam break: initial configuration

Table 3 Dam break: analysis conditions

The computed pressures at each time step were computed using $5440\times 980=5{,}331{,}200$ fluid particles with the no-slip condition on the walls; the results are shown in Fig. 19. The average and standard variation of the pressure at each $2{\!,}000$th step are shown in Fig. 20. Although pressure oscillations, such as occur with mesh-free particle methods in general, were observed, overall, the results were in good agreement with those measured in the experiment. These pressure oscillations, which are a common problem in mesh-free particle methods, can be reduced by using smoothing schemes [5, 40] or other approaches [26], but we did not do this because it could mask issues caused by the ERP model.

Fig. 19

Dam break: pressure time history

Fig. 20

Dam break: pressure time history averaged over 2000 steps

Hu and Kashiwagi [14] analyzed the dam break problem using the constrained interpolation profile (CIP) method [45, 46], and they argued that the no-slip condition is crucial for obtaining agreement with the experimental results. They showed that under the no-slip condition, a vortex near the lower-right corner reduces the pressure at point $A$ after the pressure peaks, but this is not seen under the slip condition. The results obtained by using the slip and no-slip conditions are compared with the results obtained by using the CIP method in Fig. 21. By $0.7\,(\mathrm{s})$, both the slip and no-slip conditions give results that are in good agreement with the CIP results. This indicates that the ERP model can simulate fluid flow behavior in the boundary layer when the particles being used are small enough. The results from using various particle sizes under the no-slip condition are shown in Fig. 22, and we can see that, after the pressure peaks, the pressures obtained using a larger particle size are closer to the results obtained using the slip condition. This means that the velocity field near the walls better simulated when using a higher spatial resolution.

Fig. 21

Dam break: results with slip and no-slip conditions compared with results computed by the CIP method

Fig. 22

Dam break: results with slip and no-slip conditions obtained using different particle sizes

6 Application

6.1 Rotating gear

To demonstrate the applicability of the ERP model, we simulated the situation of water inflow with a rotating gear. The gear had $12$ teeth and rotates in a vessel in a counterclockwise direction with an angular velocity $8.0\pi \,(\mathrm{rad/s})$, as illustrated in Fig. 23. In this simulation, the number of fluid particles was $120{\!,}000$ placed in the rectangular space, and the time step width was $2.0\times 10^{-6} \,(\mathrm{s})$. The water was assumed to be at 25 $^\circ$C, and the slip boundary condition was used.

Fig. 23

Rotating gear: initial configuration

Snapshots at several time steps are shown in Fig. 24; the fluid particles are colored according to the magnitude of their velocity [unit $(\mathrm{m/s})$]. Fluids are pushed out by rotation of the gear, and this creates a very complex free surface. The results indicate that the E-MPS method applied to the ERP model can, in a relatively simple way, simulate such a complex phenomenon involving free surfaces and moving boundaries.

Fig. 24

Rotating gear: visualization of results

6.2 Water vessel with a moving bottom surface

In the rotating gear problem introduced in the previous section, the wall boundaries are rigidly moved, hence, an implicit surface representation utilizing the distance function can be effective. Here, we consider a situation in which there is arbitrary movement of the boundaries; this requires a recalculation of the distance function. We conducted this simulation in order to demonstrate the versatility and robustness of the proposed model. As illustrated in Fig. 25, we consider a fluid-filled vessel in which the bottom surface moves with the following harmonic oscillation:

$$\begin{aligned} y = \frac{1}{3} \sin (2 \pi x) \sin (\pi t). \end{aligned}$$

(77)

In this simulation, the number of fluid particles is $250{,}000$, and the time step width is $2.0\times 10^{-5} [\mathrm{s}]$. The temperature of the water was assumed to be 25 $^\circ$C, and the no-slip boundary condition was used. The bottom surface was divided into $100$ polygons. Because of the no-slip condition on the moving walls, the velocity of wall at the acting point of particle $i, \varvec{v}^{wall}_i$, is determined from the velocities on the polygon nodes, $\varvec{v}^{node}_1$ and $\varvec{v}^{node}_2$, and the shape functions given by Eq.(71):

$$\begin{aligned} \varvec{v}^{wall}_i = N_1\big (\xi _i\big ) \varvec{v}^{node}_1 + N_2\big (\xi _i\big ) \varvec{v}^{node}_2. \end{aligned}$$

(78)

Snapshots at several time steps are shown in Fig. 26; the fluid particles are colored according to the magnitude of their respective velocities [unit $(\mathrm{m/s})$]. The results indicate that the ERP model is able to conduct stable simulations and to impose the boundary conditions dynamically even if the movement of the boundaries is arbitrary. The simulation was conducted by $1{\!,}000{\!,}000$ steps in $10$ oscillation cycles, and the volume of the fluid was conserved and no instability was observed in the behavior of the particles. We also note that since the grid size for the distance function should be smaller than the particle spacing in order to accurately evaluate the distance in the implicit surface representation, the explicit polygon representation can be potentially more efficient and effective when solving problems that require recalculation of the distance function (e.g., fluid–structure interaction analyses).

Fig. 25

Water vessel with moving bottom surface: initial configuration

Fig. 26

Water vessel with a moving bottom surface: visualization of results

7 Conclusions

In this study, we developed and verified the explicitly represented polygon (ERP) wall boundary model for the E-MPS method. It can deal with arbitrarily shaped boundaries and movements, and it can accurately impose boundary conditions for free-surface flow analysis.

The ERP model is formulated such that it satisfies the pressure Neumann boundary condition and the slip/no-slip boundary condition, without requiring the generation of virtual particles or treating angled edges as exceptional cases. Moreover, the ERP model eliminates the problem of force imbalance on the boundaries, which occurs in conventional models. Because of this, the E-MPS method applied to the ERP model can conduct stable and accurate computations, especially in coupled analyses with rigid or elastic bodies.

For verification and validation of the proposed model, we performed simulations for a hydrostatic pressure problem, a Couette flow, a Poiseuille flow, and a dam break problem. The results were compared with the theoretical values, the results obtained by other models and methods, and experimental results. We confirmed that the boundary conditions of the ERP model were appropriately modeled, and the E-MPS method with the ERP model can achieve adequate accuracy.

Finally, we demonstrated the applicability and versatility when the method was applied to the proposed model by conducting simulations involving boundaries that had moving and complex shapes.

In the ERP model, each particle receives a force from only a single polygon, and this results in robustness and eliminates the need to handle angled edges as exceptions. However, if the force is appropriately distributed to multiple polygons without loss of robustness, accuracy at angled edges could be improved. This is a challenge for future work.

As briefly stated in Sect. 4.5, the ERP model can achieve a consistent force on the wall boundaries. This characteristic is beneficial, especially when the ERP model applies to a coupled problem, such as fluid–rigid body or fluid–structure interactions with free surfaces, for which hybrid coupling approaches that use mesh-free particle methods for free-surface flows and the FEM for structures have been developed [15, 24, 27, 28, 48]. Much work has been done for this kind of coupled problem, such as by using the FEM with the arbitrary Lagrangian–Eulerian method [1] or an interface tracking method, such as the level set method [44], the mesh-free particle methods [2, 17, 39], or the Particle-FEM [18, 19, 36, 41]. As an area of future work, we plan to apply the ERP model to a hybrid coupling approach and investigate its stability, accuracy, and applicability. This approach could inherit the FEM’s advantages of high reliability and accuracy for structural analysis, and the robustness and flexibility of mesh-free particle methods in free-surface flow analysis.