1 Introduction

In high-speed rail vehicle systems, the main problem is related to the interaction between the train pantograph and the catenary. Indeed, when the train runs, the pantograph deforms the catenary and oscillatory motions are induced. Moreover, when the train speed increases, these oscillations may become larger and the loss of contact between the pantograph head and the collector wire could occur. Thus, when the pantograph moves along the catenary, it is fluctuated due to propagation and reflection of the wave on the catenary, which leads to a modification in its dynamics depending on the position [1].

Actually, both the pantograph and the catenary could be damaged if the contact force is too large as this could cause a contact wire breaking and stop the current collection. On the other hand, the pantograph and the catenary could lose their contact if the contact force is too small, which could cause an electric arc and accelerate the degradation of the contact wire. Therefore, considering at least these effects, many researchers have tried to design active controllers in order to ensure that the contact force remains as constant as possible [2]. Thus, to deal with this problem, the catenary device was first modeled with a constant stiffness. Then, optimal control strategies have been proposed [3]. This solution was sufficiently effective to reject external disturbances, but finding the optimal control gains while satisfying simultaneous objectives and hard constraints was beyond the adopted strategy. Thereafter, in order to improve the active control system performances, approximate models of the pantograph–catenary (PAC) system were considered [4, 5]. Accordingly, many researchers assumed that the complex dynamics of the catenary might be well approximated by a linear mechanical system with space-varying lumped parameters. In this sense, the catenary parameters could be considered time-varying with a rate determined by the train speed [6]. Then, as uncertainties are present in almost all designed models, use of robust control techniques was proposed [7], while sometimes the problem was solved by tuning standard PID controllers [6]. More recently, a second-order sliding mode-based control scheme [8, 9] that estimates the contact force using the measured displacements of the upper and lower pantograph frames was formally presented using the algebraic observability theory [10]. Nonetheless, this approach turns out to require more knowledge, as it requires the value of the control force applied to the upper frame, the velocity and the acceleration of the upper and lower frames, which could render the control system complex and expensive. Alternately, in other works, to perform output feedback, the contact force is evaluated by means of load cells whose measurements are compensated by accelerometers [11], which could also be very expensive mainly for their quick deterioration during the runs of the train.

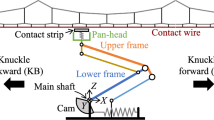
In this work, our aim is to attenuate the time-varying stiffness fluctuation between the pantograph head and the contact wire. To this aim, the pantograph frames are modelled in terms of lumped masses, springs and dampers [4]. Without loss of generality, the mechanical parameters of the pantograph mechanism model (Fig. 1) are usually supposed to be constant and known. Then, to tackle this design task, we begin by constructing an adaptive observer that allows estimating both the system state and the unknown catenary equivalent stiffness. Thereafter, taking benefit of the asymptotic behavior of an adaptive observer, we synthesize a backstepping controller to ensure the output tracking of a nominal reference trajectory. In this sense, the proposed control strategy is peculiar as it joins control action with parameter estimation. Finally, analyzing the control system, we show that the proposed solution is appropriate to deal with the considered problem. Indeed, first rudiments of this work have been presented in [12] with a simplifying hypothesis that the catenary stiffness is known, which not the case is the present work.

Fig. 1
figure 1

Schema of 2-DOF pantograph

Full size image

The organization of the paper is as follows: Sect. 2 presents the PAC system modelling and the problem statement. Section 3 describes the adaptive observer. Then, Sect. 4 presents the controller synthesis, Sect. 5 gives the main results of the paper, and Sect. 6 presents a numerical example. Finally, Sect. 7 outlines some concluding remarks. To lighten the paper reading, all proofs are appended.

2 PAC system model and problem statement

2.1 PAC model

The pantograph and the catenary form a dynamically coupled vibrating system interacting through the contact force. Roughly, when the pantograph runs along the catenary, the variation of the catenary stiffness produces a periodic excitation that causes the pantograph vibration and leads to contact force fluctuation. As a result, the contact force is composed of a lift force that is static, and a dynamic force that depends on the vibration of the pantograph–catenary system and the vehicle speed.

Historically, a variety of catenary models are proposed in the literature from simpler models that consider only static variation of stiffness along a span to a complete finite element model (FEM) which describes the nonlinear dynamic interaction between the pantograph and the catenary system [13]. Especially, high accuracy models are required in the high-speed range, as the wave reflection becomes a major cause of contact loss [14]. Moreover, sometimes, the effect of other elements such as brackets, registration arms, and droppers is also taken into consideration. Nonetheless, without loss of generality, the simplified models with lumped and possibly time-varying parameters have been shown to be sufficiently accurate for control analysis and design purposes [6]. Thus, it turns out that a time-varying linear system can approximate the PAC dynamics with sufficient accuracy around a working configuration profile [4, 7]. For this reason, to present the main idea of this paper, we consider a 2-DOF representation of the PAC system where, on one hand, the pantograph is modelled in terms of lumped masses, springs and dampers and, on the other hand, the catenary is modeled by a time-varying equivalent stiffness \(k (t )\) [15]. Indeed, a simplified railway overhead contact line model, which neglects the wave propagation effects, may consider only the stiffness variation along a span. In this sense, if \(k_{ \hbox{max} }\) and \(k_{ \hbox{min} }\) are respectively the largest and smallest stiffness values in a span, the catenary average stiffness \(k_{ 0}\) and the stiffness variation coefficient \(\alpha\) may be approximated by

$$k_{ 0} = {{ (k_{ \hbox{max} } + k_{ \hbox{min} } )} \mathord{\left/ {\vphantom {{ (k_{ \hbox{max} } + k_{ \hbox{min} } )} { 2\,\,\,\,\,{\text{and}}\,\,\,\alpha = {{ (k_{ \hbox{max} } - k_{ \hbox{min} } )} \mathord{\left/ {\vphantom {{ (k_{ \hbox{max} } - k_{ \hbox{min} } )} { (k_{ \hbox{max} } + k_{ \hbox{min} } )}}} \right. \kern-0pt} { (k_{ \hbox{max} } + k_{ \hbox{min} } )}}}}} \right. \kern-0pt} { 2\,\,\,\,\,{\text{and}}\,\,\,\alpha = {{ (k_{ \hbox{max} } - k_{ \hbox{min} } )} \mathord{\left/ {\vphantom {{ (k_{ \hbox{max} } - k_{ \hbox{min} } )} { (k_{ \hbox{max} } + k_{ \hbox{min} } )}}} \right. \kern-0pt} { (k_{ \hbox{max} } + k_{ \hbox{min} } )}}}}.$$
(1)

Then, if we omit the stiffness variation between the vertical droppers, it is commonly assumed that the catenary equivalent stiffness can be written as

$$k(t) = k_{ 0} \left( {1 + \alpha \cos \left( {wt - \beta } \right)} \right)\, \quad {\text{and}}\quad w = 2\pi \lambda /L,$$
(2)

where \(k_{ 0}\) is the average stiffness, \(\alpha\) is the stiffness variation coefficient in a span, \(\lambda\) is the vehicle speed, and L is the span length. In addition, in this paper, we denote by \(\beta\) a possible phase shift at time t = 0, in the time-varying expression of the stiffness \(k(t)\).

On the other hand, although the pantographs present several differences between each other, the two degrees of freedom (2-DOF) lumped-parameters (Figs. 1 and 2) may be considered as a reference model.

Fig. 2
figure 2

PAC system 2-DOF lumped-parameters model

Full size image

Roughly speaking, when the railway vehicle is running, this vibration system is in contact and its dynamics could be described by the following mathematical equations:

$$\left\{ \begin{aligned} & m_{ 2} {\ddot{z}}_{2} + b_{ 2} \dot{z}_{2} + b_{ 1} \text{(}\dot{z}_{2} - \dot{z}_{1} )+ k_{ 1} (z_{2} - z_{1} )= u\,, \\ & m_{ 1} {\ddot{z}}_{1} + b_{ 1} (\dot{z}_{1} - \dot{z}_{2} )+ k_{ 1} (z_{1} - z_{2} )= - F, \\ & kz_{1} = F, \\ \end{aligned} \right.$$
(3)

where the subscript i = 1, 2 stand for the upper and the lower frame respectively, \(z_{i}\) is the vertical coordinate of the pantograph frames, \(\dot{z}_{i}\) and \({\ddot{z}}_{i}\) denote the first and the second derivative of displacement \(z_{i}\), \({{m}}_{i}\) is the mass, \(k_{i}\) is the frame stiffness, \(b_{i}\) is the damping coefficient, k is the time-varying catenary stiffness, F is the contact force applied by the pan-head on the catenary lower wire, and u is the external actuator control action applied on the PAC system.

Now, considering the displacements (\(z_{1},\,z_{2}\)) and their respective derivatives (\(\dot{z}_{1},\,\dot{z}_{2}\)) as the state system, it follows that:

$$\varvec{z} = \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & {\dot{z}_{1} } & {\dot{z}_{2} } \\ \end{array} } \right]^{{\,\text{T}}} \, = \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & {z_{3} } & {z_{4} } \\ \end{array} } \right]^{{\,{\text{T}}}} .$$
(4)

Using this choice, it follows that the pantograph–catenary system could be described by the following linear time-varying representation [1]:

$$\left\{ \begin{array}{l} \dot{z}_{1} = z_{3} \,, \hfill \\ \dot{z}_{2} = z_{4} \,\,,\, \hfill \\ \dot{z}_{3} = \, - {{ [(k_{ 1} + k )} \mathord{\left/ {\vphantom {{ [k_{ 1} + k )} {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }}]z_{1} + {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }})z_{2} - {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )z_{3\,} + {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )z_{4} \,, \hfill \\ \dot{z}_{4} = {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }} )z_{1} - {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }} )z_{2} + {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }} )z_{3} - {{ [ (b_{ 1} + b_{ 2} )} \mathord{\left/ {\vphantom {{ [ (b_{ 1} + b_{ 2} )} {{\text{m}}_{ 2} }}} \right. \kern-0pt} {{\text{m}}_{ 2} }}]z_{4} + {u \mathord{\left/ {\vphantom {u {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }}\,, \hfill \\ \end{array} \right.$$
(5)
$$F = kz_{1} ,$$
(6)

where the time-variable t is here omitted in order to alleviate the text. Then, k has the approximated form mentioned in Eq. (2) and recalled here for clarity:

$$k = k_{0} [1 + \alpha \cos \left( {wt - \beta } \right)],$$
(7)

with \(w = 2\pi \lambda /L.\)

Now, using Eq. (7), the (unknown) parameters of the stiffness k can be extracted by writing it as follows:

$$k: = \varvec{v}^{\text{T}}\varvec{\theta},$$
(8)

where

$$\left\{ \begin{array}{l} \varvec{v}^{\text{T}} : = \left[ {\begin{array}{*{20}l} 1 & {{\text{cos(}}wt )} & {{\text{sin(}}wt )} \\ \end{array} } \right]\,, \hfill \\\varvec{\theta} : = \left[ {\begin{array}{*{20}l} {k_{0} } & {k_{0} \alpha \cos (\beta )} & {k_{0} \alpha {\text{sin(}}\beta )} \\ \end{array} } \right]^{\text{T}} \,: = \,\,\left[ {\begin{array}{*{20}l} {\theta_{1} } & {\theta_{2} } & {\theta_{3} } \\ \end{array} } \right]^{\text{T}} . \hfill \\ \end{array} \right.$$
(9)

2.2 Problem statement

In this paper, our main objective is to regulate the output contact force F around its nominal reference F r despite the time-varying catenary parameters. Then, as the catenary stiffness k, the output contact force F, and the state z are assumed to be unknown, our strategy is based on an output feedback control. Thus, assuming that only the frame positions (namely, \(z_{1}\) and \(z_{2}\)) are measurable, it becomes necessary to recover all the unavailable variables and parameters using an adaptive observer. Thus, in the next Section, the aim is to compute an estimate of the state \(\varvec{z}\), the catenary equivalent stiffness k, and the actual contact force F.

3 Observer synthesis

In this section, we propose to design an observer that estimates both the system state z and the stiffness k. First, let us define the measured output vector:

$$\varvec{y}: = \left[ {\begin{array}{*{20}c} {z_{ 1} } & {z_{ 2} } \\ \end{array} } \right]^{{\,{\text{T}}}} .$$
(10)

Now, using Eqs. (5) and (9), one can easily verify that the considered PAC system can be described by the following state-affine representation:

$$\left\{ \begin{array}{l} \dot{\varvec{z}} = \varvec{Az} + \varvec{\varphi } (u )+\varvec{\psi}(\varvec{y} )\varvec{\theta}, \hfill \\ \varvec{y}\, = \varvec{Cz}, \hfill \\ \end{array} \right.\,$$
(11)

where A is a constant matrix; the components of the vector \(\varvec{\varphi }\left( u \right)\) and the matrix \(\varvec{\psi}\left( \varvec{y} \right)\) are known, uniformly bounded, continuous functions that depend on the input u (that is here assumed to be bounded) and the measured output y; z denotes the unknown system state vector and \(\varvec{\theta}\) is the unknown catenary parameters vector.

Comparing Eq. (5) with Eq. (12), it follows that:

$$\varvec{A} = \left[ {\begin{array}{*{20}c} 0& 0& 1& 0\\ 0& 0& 0& 1\\ { - k_{ 1} /m_{ 1} } & {k_{ 1} /m_{ 1} } & { - b_{ 1} /m_{ 1} } & {b_{ 1} /m_{ 1} } \\ {k_{ 1} /m_{ 2} } & { - k_{ 1} /m_{ 2} } & {b_{ 1} /m_{ 2} } & { - (b_{ 1} + b_{ 2} ) /m_{ 2} } \\ \end{array} } \right]\,,$$
(12)
$$\varvec{C} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ \end{array} } \\ \end{array} } \right] = \,\left[ {\begin{array}{*{20}c} {\varvec{I}_{2} } & {\mathbf{0}_{2} } \\ \end{array} } \right]\,,$$
(13)
$$\varvec{\varphi } (u )^{{^{\text{T}} }} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {{u \mathord{\left/ {\vphantom {u {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }}} \\ \end{array} } \right]\,,$$
(14)
$$\varvec{\psi}(\varvec{y} )= \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ { - \frac{{z_{1} }}{{m_{1} }}} & { - \frac{{z_{1} }}{{m_{1} }}\cos (wt)} & { - \frac{{z_{1} }}{{m_{1} }}{ \sin }(wt)} \\ 0 & 0 & 0 \\ \end{array} } \right],$$
(15)

where \(\varvec{I}_{n}\) and \(\mathbf{0}_{n}\) are respectively the \((n , { }n )\) identity and null matrices.

As mentioned above, the representation Eq. (11) shows that we are considering a state affine system, where the state z and the parameters vector θ are both involved in affine relationships. Moreover, let us notice that the matrix \(\varvec{\psi}\left( \varvec{y} \right)\) and the vector \(\varvec{\varphi }\left( u \right)\) depend on measured signals \(\left( {u,\varvec{y}} \right)\).

Remark 1

Actually, it can easily be checked that the pair (A, C) is observable. Then, there exists a bounded K such that A−KC is Hurwitz, which means that any system \(\left\{ {\dot{\varvec{x}} (t )= (\varvec{A} - \varvec{KC} )\varvec{x} (t )} \right\}\) is exponentially stable. Consequently, in order to estimate both z and θ, we propose to use an adaptive observer whose estimation state error does vanish asymptotically.

Assumption 1

The solution \(\varvec{\varLambda}(t )\) of \(\left\{ {\dot{\varvec{\varLambda }} (t )= \left[ {\varvec{A} - \varvec{KC}} \right]\varvec{\varLambda}(t )+\varvec{\psi}(t )} \right\}\) is persistently exciting in the sense that, for some \(t \ge t_{0}\) and some bounded positive definite matrix \(\varvec{\varSigma}\), there exist α 1, β 1 and T1 such that:

$$\alpha_{1} \varvec{I}\,\le \int\limits_{t}^{{t + {\text{T}}_{1} }} {\varvec{\varLambda}(\tau )^{\text{T}} \varvec{C}^{\text{T}} \varvec{\varSigma} (\tau )\varvec{C}(\tau )\varvec{\varLambda}(\tau ){\text {d}}} \tau\; \le\; \beta_{1} \varvec{I},\quad \forall t \;\ge\; t_{0}.$$
(16)

Then, as candidate observer for system Eq. (11), we propose to use the following one [16]:

$$\left\{ \begin{array}{l} {\dot{\hat{\varvec{z}}}} = \varvec{A}{\hat{\varvec{z}}} + {\varvec{\varphi }}(u)+\varvec{\psi}(\varvec{y} )\hat{\varvec{\theta }} + \left\{ {\varvec{\varLambda S}_{{\theta}}^{ - 1}\varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} + \varvec{S}_{z}^{ - 1} \varvec{C}^{\text{T}} } \right\}\varvec{\varSigma} (\varvec{y} - \varvec{C}{\hat{\varvec{z}}} ) ,\hfill \\ {\dot{\hat{\varvec{\theta}}}} = \varvec{S}_{{\theta}}^{ - 1} \varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} \varvec{\varSigma }(\varvec{y} - \varvec{C}{\hat{\varvec{{z}}}}), \hfill \\ \dot{\varvec{\varLambda }} = \left\{ {\varvec{A} - \varvec{S}_{z}^{ - 1} \varvec{C}^{\text{T}} \varvec{\varSigma C}} \right\}\,\varvec{\varLambda}+\varvec{\psi}({\varvec{y}}), \hfill \\ \dot{\varvec{S}}_{z} = - \rho_{z} \varvec{S}_{z} - \varvec{A}^{\text{T}} \varvec{S}_{z} - \varvec{S}_{z} \varvec{A} + \varvec{C}^{\text{T}} \varvec{\varSigma}\varvec{C}, \hfill \\ \dot{\varvec{S}}_{\theta } = - \rho_{{\theta}} \varvec{S}_{{\theta}}+\varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} \varvec{\varSigma C\varLambda },\quad \varvec{S}_{z} (0)> 0,\,\quad \varvec{S}_{{\theta}} (0)> 0, \hfill \\ \end{array} \right.$$
(17)

where \(\rho_{z}\) and \(\rho_{\theta }\) are sufficiently large positive constants, and \(\varvec{\varSigma}\) is a bounded positive definite matrix,

$$\hat{\varvec{z}} = \left[ {\begin{array}{*{20}c} {\hat{z}_{1} } & {\hat{z}_{2} } & {\hat{z}_{3} } & {\hat{z}_{4} } \\ \end{array} } \right]^{\text{T}} \; \in \,\;{\mathbf{R}}^{4} ,$$
(18)

where R is the vector of real numbers.

Now, let us consider the state and the parameters estimation errors, which are defined by

$$\left\{ \begin{array} {l} \varvec{e}_{z} : = \varvec{z} - \hat{\varvec{z}} ,\hfill \\ \varvec{e}_{\theta } : =\varvec{\theta}- \,\hat{\varvec{\theta }} .\hfill \\ \end{array} \right.$$
(19)

Then, if Assumption 1 holds, the above system Eq. (17) is an asymptotic observer for system Eq. (11), in the sense that for any set of initial conditions z(0) and \(\varvec{\theta}( 0 )\), both e z and \(\varvec{e}_{\theta }\) do exponentially decay to zero. Specifically, the analysis of this observer dynamics, described by Eq. (17), states the following lemma [16].

Lemma 1

Consider the system described by Eq. (11), where the parameters \(\varvec{\theta}\) and the state z are both estimated using the observer dynamics Eq. (17). Then, \(\exists \,\rho > 0,\,\) \(\forall \hat{\varvec{z}} ( 0 )\; \in \,\;{\mathbf{R}}^{4}, \,\forall \hat{\varvec{\theta }} ( 0 )\; \in {\mathbf{R}}^{3}\), the state estimation error \(\varvec{e}_{z}\) and the parameters vector estimation error \(\varvec{e}_{\theta }\) , exponentially go to zero with a rate driven by \(\rho = { \hbox{min} }(\rho_{z} ,\rho_{\theta } )\), where the estimation errors \(\varvec{e}_{z}\) and \(\varvec{e}_{\theta }\) , defined in Eq. (19), involve any trajectory \(\hat{\varvec{z}}\) and any parameters vector \(\hat{\varvec{\theta }}\) associated to the input u and the measured output vector \({\varvec{y}}\) □

For sake of clarity, the proof of Lemma 1 is placed in Appendix 1.

Remark 2

  1. (i)

    The above global convergence result is obtained thanks to the fact that \(\varvec{\psi}(\varvec{y} )\) is globally Lipchitz in \({\varvec{y}}\), and \(\varvec{\varphi }\left( u \right)\) is locally Lipchitz in u. This property is a direct consequence of the fact that \(\varvec{\varphi }\left( u \right)\) is linear in z and the signal k is bounded.

  2. (ii)

    Using Eqs. (11), (17) and (19), we can easily verify that:

    $$\begin{aligned} \left\{ {\varvec{\varLambda S}_{\theta }^{ - 1}\varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} + \varvec{S}_{x}^{ - 1} \varvec{C}^{\text{T}} } \right\}{\varvec{\varSigma}} (\varvec{y} - \varvec{C}{\hat{\mathbf{z}}} )= \left\{ {\varvec{\varLambda S}_{\theta }^{ - 1}\varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} {\varvec{\varSigma}} + \varvec{S}_{x}^{ - 1} \varvec{C}^{\text{T}} \varvec{\varSigma}} \right\}\,\varvec{Ce}_{z} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,: = \left[ {\begin{array}{*{20}c} {g_{11} } & {g_{12} } \\ {g_{21} } & {g_{22} } \\ {g_{31} } & {g_{32} } \\ {g_{41} } & {g_{42} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\tilde{z}_{1} } \\ {\tilde{z}_{2} } \\ \end{array} } \right]\,. \hfill \\ \end{aligned}$$
    (20)

In this sense, bearing in mind Eq. (20), the observer dynamics Eq. (17) can be rewritten as follows:

$$\left\{ {\begin{array}{l} {\dot{\hat{z}}_{1} = \hat{z}_{3} + g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2}}, \\ {\dot{\hat{z}}_{2} = \hat{z}_{4} + g_{21} \tilde{z}_{1} + g_{22} \tilde{z}_{2} ,} \\ {\dot{\hat{z}}_{3} = f_{1} (\hat{z}_{1} ,\hat{z}_{2} ,\hat{z}_{3} )+ {\text{b}}_{ 1} \hat{z}_{4} /m_{ 1} - (z_{ 1} /m_{ 1} )\varvec{v}^{\text{T}} \hat{\varvec{\theta }} + g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2},} \\ {\dot{\hat{z}}_{4} = f_{2} (\hat{\varvec{z}} )+ ( 1 /m_{ 2} )\,u\, + g_{41} \tilde{z}_{1} + g_{42} \tilde{z}_{2},} \\ \end{array} } \right.$$
(21)

where

$$\left\{ {\begin{array}{*{20}l} {f_{1} (\hat{z}_{1} ,\,\hat{z}_{2} ,\hat{z}_{3} ) \;=\; - {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )\hat{z}_{1} + {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 1} )}}} \right. \kern-0pt} {m_{ 1} )}}\hat{z}_{2} - {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )\hat{z}_{3} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {f_{2} (\hat{\varvec{z}} )= ({{k_{ 1} } \mathord{\left/ {\vphantom {{k_{ 1} } {m_{ 2} )}}} \right. \kern-0pt} {m_{ 2} )}}\hat{z}_{1} - {{ (k_{ 1} } \mathord{\left/ {\vphantom {{ (k_{ 1} } {m_{ 2} }}} \right. \kern-0pt} {m_{ 2} }} )\hat{z}_{2} + ({{b_{ 1} } \mathord{\left/ {\vphantom {{b_{ 1} } {m_{ 2} )}}} \right. \kern-0pt} {m_{ 2} )}}\hat{z}_{3} - {{ [ (b_{ 1} + b_{ 2} )} \mathord{\left/ {\vphantom {{ [ (b_{ 1} + b_{ 2} )} {m_{ 2} ]}}} \right. \kern-0pt} {m_{ 2} ]}}\hat{z}_{4} \,.} \\ \end{array} } \right.$$
(22)

4 Controller synthesis

Recall that our aim is to ensure the output regulation of the PAC system. Namely, we wish to ensure that the contact force \(F(t)\) remains constant, despite the fluctuation of the catenary equivalent stiffness \(k(t)\). Thereafter, as we are dealing with a linear time-varying system, we use backstepping techniques [17] since this control tool could ensure a robust regulation.

Hence, as \(F(t) = k(t)z_{1} (t)\) (where \(k(t) > 0\)), aiming to force the contact force \(F(t)\) to track constant reference \(F_{\text{r}} (t)\) turns out to make \(z_{1} (t)\) track the following reference signal:

$$z_{{1{\text{r}}}} (t): = - F_{\text{r}} (t )/k (t )\, .$$
(23)

Now, getting benefit of the fact that the state estimation error \(\tilde{\varvec{z}} (t )\) vanishes exponentially, the proposed regulator may be performed based on Eq. (21). To this end, let us assume that the output reference \(F_{\text{r}} (t )\) and the catenary equivalent stiffness \(k(t)\) are differentiable as many times as necessary. Roughly, this is possible as \(F_{\text{r}} (t )\) could be made continuous using an appropriate low-pass filter. In addition, the stiffness \(k(t)\) is continuous as it is a physical signal.

Then, using the backstepping approach, it follows from the representation Eq. (17) that the control design will include three steps.

  • Step 1 Introducing the output tracking error:

    $$e_{1} = \hat{z}_{1} - z_{{ 1 {\text{r}}}} .$$
    (24)

Using (21), it follows that

$$\dot{e}_{1} = \hat{z}_{3} + g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2} - \dot{z}_{{ 1 {\text{r}}}} \,,$$
(25)

where \(\hat{z}_{3}\) stands for a virtual control. Let the corresponding stabilizing function be denoted by \(\alpha_{1}\). Then, to stabilize Eq. (25) around \(e_{1} = 0\), let us consider the Lyapunov function:

$$V_{1} = {{e_{1}^{2} } \mathord{\left/ {\vphantom {{e_{1}^{2} } 2}} \right. \kern-0pt} 2}\,.$$
(26)

Then, using Eq. (25), deriving \(V_{1}\) with respect to time yields

$$\dot{V}_{1} = e_{1} \dot{e}_{1} = e_{1} \left(\hat{z}_{3} + g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2} - \dot{z}_{{ 1 {\text{r}}}}\right)\,.$$
(27)

This suggests that the virtual control \(\hat{z}_{3}\) is chosen equal to \(\alpha_{1}\), with

$$\alpha_{1} = \dot{z}_{{1{\text{r}}}} - c_{1} e_{1} \,,$$
(28)

where \(c_{1}\) is positive real.

As \(\hat{z}_{3}\) is not the actual control action, it cannot be forced to \(\hat{z}_{3} = \alpha_{1}\). Then, let us retain the expression of \(\alpha_{1}\) and introduce the following error:

$$e_{2} = \hat{z}_{3} - \alpha_{1} \,.$$
(29)

Now, from Eqs. (25), (27) and (29), \(\dot{e}_{1}\) and \(\dot{V}_{1}\) can be rewritten as follows:

$$\dot{e}_{1} = e_{2} - c_{1} e_{1} + g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{21} \,,$$
(30)
$$\dot{V}_{1} = e_{1} e_{2} - c_{1} e_{1}^{2} + e_{1} \left(g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2}\right)\, .$$
(31)

  • Step 2 Let us notice that, as \(\alpha_{1}\) depends on measurable signals, it follows that \(\dot{\alpha }_{1}\) does exist. Then, using Eqs. (21) and (29), \(\dot{e}_{2}\) can be computed as

    $$\dot{e}_{2} = f_{1} \left(\hat{z}_{1} ,\hat{z}_{2} ,\hat{z}_{3}\right)+ \frac{{b_{ 1} }}{{m_{ 1} }}\hat{z}_{4} - \frac{{z_{ 1} }}{{m_{ 1} }}\varvec{v}^{\text{T}} \hat{\varvec{\theta }}\, + g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2} - \dot{\alpha }_{1} \,,$$
    (32)

    where \(\hat{z}_{4}\) stands for a virtual control. Let the corresponding stabilizing function be denoted by \(\alpha_{ 2}\). To stabilize Eq. (32) around \(e_{2} = 0\), let us consider the Lyapunov function:

    $$V_{2} = V_{1} + {{e_{2}^{2} } \mathord{\left/ {\vphantom {{e_{2}^{2} } 2}} \right. \kern-0pt} 2}\,.$$
    (33)

Now, using Eqs. (31) and (32), deriving \(V_{2}\) with respect to time yields

$$\begin{aligned} \dot{V}_{2} & = e_{1} e_{2} - c_{1} e_{1}^{2} + e_{1} (g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2} )\, \hfill \\ &\, + \,e_{2} \left({f_{1} \left(\hat{z}_{1} ,\hat{z}_{2} ,\hat{z}_{3}\right)+ \left(b_{ 1} /m_{ 1})\hat{z}_{4} - (z_{ 1} /m_{ 1}\right)\varvec{v}^{\text{T}} \hat{\varvec{\theta }} +\,g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2} \, - \dot{\alpha }_{1} } \right)\,. \hfill \\ \end{aligned}$$
(34)

Equation (34) suggests that \(\hat{z}_{4}\) should be chosen equal to \(\alpha_{2}\) with

$$\alpha_{2} = (m_{ 1} /b_{ 1} )\left( { - c_{2} e_{2} - e_{1} - f_{1} \left(\hat{z}_{1} ,\hat{z}_{2} ,\hat{z}_{3} )+ (z_{ 1} /m_{ 1}\right)\varvec{v}^{\text{T}} \hat{\varvec{\theta }} + \dot{\alpha }_{1} } \right),$$
(35)

where \(c_{2}\) is positive real constant number. However, as \(\hat{z}_{4}\) is not the actual control action, it cannot be forced to \(\hat{z}_{4} = \alpha_{2}\). Then, let us retain the expression of \(\alpha_{2}\) and introduce the following error

$$e_{3} = \hat{z}_{4} - \alpha_{2} \,.$$
(36)

Afterwards, from Eqs. (32), (34) and (36), \(\dot{e}_{2}\) and \(\dot{V}_{2}\) can be rewritten in terms of \(e_{1}\),\(e_{2}\) and \(e_{3}\) as follows:

$$\dot{e}_{2} = - e_{1} - c_{2} e_{2} + {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )e_{3} + g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2} \,,$$
(37)
$$\dot{V}_{2} = - c_{1} e_{1}^{2} - c_{2} e_{2}^{2} + {{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )e_{2} e_{3} \, + e_{1} \left(g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2}\right)\, + e_{2} \left(g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2}\right)\,.$$
(38)

  • Step 3 From Eqs. (21) and (36), the computation of \(\dot{e}_{3}\) yields

    $$\dot{e}_{3} = f_{2} (\hat{z}) + (1/m_{2} )u\, + g_{41} \tilde{z}_{1} + g_{42} \tilde{z}_{2} - \dot{\alpha }_{2} .$$
    (39)

To stabilize Eq. (39) around \(e_{3} = 0\), let us consider the Lyapunov function:

$$V_{c} = V_{2} + {{e_{3}^{2} } \mathord{\left/ {\vphantom {{e_{3}^{2} } 2}} \right. \kern-0pt} 2}\,.$$
(40)

Using Eqs. (38) and (39), we can derive \(V_{c}\) with respect to time as:

$$\begin{aligned} \dot{V}_{c} =& - c_{1} e_{1}^{2} - c_{2} e_{2}^{2} + e_{3} \,\left[ {{{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )e_{2} \, + f_{2} (\hat{\varvec{z}} )+ ( 1 /m_{ 2} )\,u\, - \dot{\alpha }_{2} } \right] \hfill \\ & + e_{1} (g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2} )+ e_{2} (g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2} )+ e_{3} (g_{41} \tilde{z}_{1} + g_{42} \tilde{z}_{2} )\, .\hfill \\ \end{aligned}$$
(41)

Then, letting

$${{ (b_{ 1} } \mathord{\left/ {\vphantom {{ (b_{ 1} } {m_{ 1} }}} \right. \kern-0pt} {m_{ 1} }} )e_{2} + f_{2} (\hat{\varvec{z}} )+ ( 1 /m_{ 2} )u - \dot{\alpha }_{2} = - c_{3} e_{3} \,,$$
(42)

with \(c_{3} > 0\), it follows that:

$$u = {{m}}_{ 2} (- c_{3} e_{3} + \dot{\alpha }_{2} - f_{2} (\hat{\varvec{z}} )-{{ ( {{b}}_{ 1} } \mathord{\left/ {\vphantom {{ ( {\text{b}}_{ 1} }{{\text{m}}_{ 1} }}} \right. \kern-0pt} {{{m}}_{ 1} }} )e_{2} )\, .$$
(43)

Now, from Eqs. (39), (41), and (43), \(\dot{V}_{c}\) and \(\dot{e}_{3}\) can be rewritten as follows:

$$\dot{V}_{c} = - c_{1} e_{1}^{2} - c_{2} e_{2}^{2} - c_{3} e_{3}^{2} + \left[e_{1} \left(g_{11} \tilde{z}_{1} + g_{12} \tilde{z}_{2} \right)+ e_{2} \left(g_{31} \tilde{z}_{1} + g_{32} \tilde{z}_{2}\right)+ e_{3} \left(g_{41} \tilde{z}_{1} + g_{42} \tilde{z}_{2}\right)\right]\, ,$$
(44)
$$\dot{e}_{3} = - c_{3} e_{3} - {{(b_{1} } \mathord{\left/ {\vphantom {{(b_{1} } {m_{1} )}}} \right. \kern-0pt} {m_{1} )}}e_{2} + k_{41} \tilde{z}_{1} + k_{42} \tilde{z}_{2} \,.$$
(45)

The output feedback controller established consists of the observer dynamics Eq. (17) and the control law Eq. (43). Then, for sake of clarity, before analyzing the closed loop control system, let us define the following error vector:

$$\varvec{e}_{c} = \left[ {\begin{array}{*{20}c} {e_{1} } & {e_{2} } & e \\ \end{array}_{3} } \right]^{\text{T}} \; \in \;{\mathbf{R}}^{3} .$$
(46)

From Eqs. (30), (37) and (45), one gets

$$\varvec{e}_{c} = \varvec{H}_{c} \varvec{e}_{c} \,\, + \varvec{G}_{y} \tilde{\varvec{y}},$$
(47)

where

$$\varvec{H}_{c} : = \left[ {\begin{array}{*{20}c} { - c_{1} } & 1 & 0 \\ { - 1} & { - c_{2} } & {b_{ 1} /m_{ 1} } \\ 0 & { - b_{ 1} /m_{ 1} } & { - c_{3} } \\ \end{array} } \right],$$
(48)
$$\varvec{G}_{y} : = \left[ {\begin{array}{*{20}c} {g_{11} } & {g_{12} } \\ {g_{31} } & {g_{32} } \\ {g_{41} } & {g_{42} } \\ \end{array} } \right]\,,$$
(49)
$$\tilde{\varvec{y}}: = \varvec{Ce}_{z} = \,\left[ {\begin{array}{*{20}c} {\tilde{z}_{1} } & {\tilde{z}_{2} } \\ \end{array} } \right]^{\text{T}} .$$
(50)

5 Control system analysis

Based on Eqs. (17) and (43), the performance of the output feedback controller will now be formally analyzed. First, let us use the following transformation [18]:

$$\varvec{\varepsilon}_{z} : = \,\varvec{e}_{z} - \varvec{\varLambda e}_{\theta } .$$
(51)

Afterwards, the closed loop control system could be described by the following error vector:

$$\varvec{e} = \left[ {\begin{array}{*{20}c} {\varvec{e}_{c}^{\text{T}} } & {\varvec{\varepsilon}_{z}^{\text{T}} } & {\varvec{e}_{\theta }^{\text{T}} } \\ \end{array} } \right]\; \in \;{\mathbf{R}}^{10} .$$
(52)

Now, the main result is summarized in the following theorem:

Theorem 1

Consider the control system consisting of the PAC system described by Eq. (11) and the output feedback controller consisting of the state observer dynamics Eq. (17) with the control law Eq. (43). Then,

  1. (1)

    The closed-loop control system is described by the following representation:

    $$\left\{ \begin{array}{l} \dot{\varvec{e}}_{c} = \,\varvec{H}_{c} \varvec{e}_{c} \, + \varvec{G}_{y} \varvec{C}\, (\varvec{\varepsilon}_{z} + \varvec{\varLambda e}_{\theta } ) ,\hfill \\ \dot{\varvec{\varepsilon }}_{z} = \left\{ {\varvec{A} - \varvec{S}_{z}^{ - 1} \varvec{C}^{\text{T}} \varvec{\varSigma C}} \right\}\,\varvec{\varepsilon}_{z} , \hfill \\ \dot{\varvec{e}}_{\theta } = - \varvec{S}_{\theta }^{ - 1}\varvec{\varLambda}^{\text{T}} \varvec{C}^{\text{T}} \varvec{\varSigma C} (\varvec{\varepsilon}_{z} + \varvec{\varLambda e}_{\theta } )\, .\hfill \\ \end{array} \right.$$
    (53)
  2. (2)

    The error vector \(\varvec{e} = \left[ {\begin{array}{*{20}c} {\varvec{e}_{c}^{\text{T}} } & {\varvec{e}_{z}^{\text{T}} } & \varvec{e} \\ \end{array}_{\theta }^{\text{T}} } \right]^{\text{T}}\) defined by Eqs. (19), (46) and (51) is globally asymptotically stable around the origin; i.e. whatever \(\varvec{e}_{c} ( 0 )\), \(\varvec{\varepsilon}_{z} ( 0 )\) and \(\varvec{e}_{\theta } ( 0 )\) are, one has \(\varvec{e}_{c}^{\text{T}} (t )\), \(\varvec{\varepsilon}_{z}^{\text{T}} (t )\) and \(\varvec{\varepsilon}_{\theta }^{\text{T}} (t )\mathop{\longrightarrow}\limits_{t \to \infty }{}{\mathbf{0}}.\) □

For sake of clarity, the proof of the Theorem 1 is placed in Appendix 2.

6 Numerical example

In order to show the effectiveness of the proposed control scheme and the derived results, the control system including the PAC system, the adaptive observer and the backstepping regulator, have been simulated considering mechanical parameters with common values (Table 1). Of course, these parameters are only used in the implementation of the PAC system model. For controller synthesis, all the catenary parameters (\(k_{0}\),\(\alpha\), \(\beta\)) are obviously assumed to be unknown.

Table 1 Typical mechanical parameters of a 2-DOF PAC system [15]
Full size table

The (continuous) contact force reference \(F_{\text{r}} (t )\) is obtained by filtering a square sequence \(F_{\text{c}} (t )\) switching between 0 and \(F_{\text{N}} = 100\,\,{\text{N}}\) (that is a common nominal value in real context). Afterwards, using a constant low acceleration, the vehicle velocity is assumed to have reached its high speed nominal value \(\lambda = 360\,\,\text{km/h}\,\), which means that the control system operates in steady state. Then, using a simulation tool, it turns out that good behaviour of the closed loop system can be ensured with the following controller and observer parameters:

$$c_{1} = 400,\;c_{2} = 400,\;c_{3} = 50,\;\rho_{z} = 40 ,\;\rho_{\theta } = 20,\;\varvec{\varSigma} = 100\varvec{I}_{ ( 4 ,\, 4 )},\;\varvec{S}_{z} ( 0 )= \varvec{I}_{ ( 4 ,\, 4 )}, \quad {\rm and} \quad \varvec{S}_{\theta } ( 0 )= \varvec{I}_{ ( 3 ,\, 3 )}.$$

The simulation results are illustrated in Figs. 3, 4 and 5. First, in Fig. 3, we can see that the contact force \(F(t)\) is almost confounded with the filtered reference \(F_{\text{r}} (t )\). The corresponding closed-loop control action \(u ( {\text{t)}}\) is given in Fig. 4 and the approximated catenary equivalent stiffness is shown in Fig. 5. Therefore, as the contact force \(F(t)\) is almost constant (negligible fluctuation), it turns out that the proposed control strategy could provide almost good robustness despite the stiffness variation and good tracking performances even in high speed context.

Fig. 3
figure 3

Contact force \(F(t)\) (dashed) versus the filtered reference \(F_{\text{r}} (t )\) (solid)

Full size image
Fig. 4
figure 4

Closed-loop control action \(u(t)\)

Full size image
Fig. 5
figure 5

Catenary equivalent stiffness estimate \(\hat{k}(t)\) (dashed) versus its actual value k(t)

Full size image

7 Conclusion

In this paper, we deal with the problem of contact force regulation and tracking control design with respect to the time-varying catenary parameters in active train pantographs. The proposed control strategy is based on the backstepping approach and the adaptive observer. The main result of this work ensures that the contact force applied on the catenary could be maintained almost constant despite the time-varying catenary parameters. Interestingly, a Kalman-like adaptive observer provides the estimation of the catenary parameters, which means that the use of a contact force sensor is here avoided. A numerical example and a formal detailed analysis of the closed-loop control system show that both output regulation and tracking objectives of step-like contact force references can be asymptotically guaranteed. Additional perspectives of this study include the extension to the case of parameter uncertainties and the consideration of a more complex model of the PAC system.