Mechanism and suppression of friction-induced vibration in catenary-pantograph system

Abstract

An unexplained instability phenomenon in railways is known to be caused by sliding friction in a catenary-pantograph system at low speeds. This is an important engineering problem because this instability phenomenon contributes to increased wear of contact wires and requires a train driver to confirm safety, which leads to train delays. Tribological analyses have found an increase in the friction coefficient at low speeds. Pantograph models based on the finite element method, multibody dynamics, and pin-disk model have been proposed for kinematic analyses. However, the mechanism is still uncertain, and no experimental investigations have been conducted. In this study, experimental and numerical investigations are conducted on the instability phenomenon caused by sliding friction. A method for estimating the friction coefficient for an actual pantograph is proposed and applied to experimentally investigate the instability phenomenon. A dynamic model is constructed based on various experiments. The frequency and the stable-unstable boundary of the instability phenomenon obtained in the simulations agree with those obtained in the experiment. From the dynamic model, it is found that the instability is a flutter-type instability caused by the asymmetry of the stiffness matrix due to Coulomb friction. Countermeasures for preventing the instability phenomenon based on the determined mechanism are proposed, and their effectiveness is verified by simulations and experiments. The results could contribute to the design of new pantographs to improve stability and the development of countermeasures for existing pantographs that experience instability.

1 Introduction

Instability phenomena in railways include the hunting motion of rolling stock [1,2,3], negative stiffness in maglev systems [4, 5], wire galloping [6,7,8,9], and parametric excitation in vehicle-bridge systems, wheel-rail systems, and catenary-pantograph systems [10,11,12,13,14,15,16,17,18]. As these phenomena cause various problems, it is important to understand their mechanisms and develop preventive measures.

An unexplained instability phenomenon in railways is known to be caused by sliding friction in a catenary-pantograph system at low speeds (hereafter referred to simply as the instability phenomenon) [19, 20]. In this instability phenomenon, the upper part of the pantograph is elastically deformed by the frictional force and vibrates in the direction of travel at low speeds immediately after the train starts [20]. It has also been reported that this instability phenomenon causes undulating wear on the contact wires with wavelengths ranging from 20 to 50 cm and that it disappears when the train speed increases [20]. In addition, this instability phenomenon contributes to the increased wear of contact wires on Shinkansen trains [21,22,23] and requires a train driver to confirm safety, which leads to train delays. Therefore, this is an important engineering problem.

Tribological analyses found that the friction coefficient between the contact wires and contact strips (see Fig. 1) used in the Shinkansen increases at low speeds [23, 24]. The Shinkansen uses iron-based sintered alloys as the contact strip materials [25]. This speed dependence of the friction coefficient has not been reported for carbon-based contact strips [26]. However, carbon-based contact strips generally have lower fracture toughness than that of iron-based contact strips [27]. High fracture toughness is required for the contact strips of high-speed trains, and thus measures that do not require changing the contact strip material (e.g., those based on kinematic data) are required.

Fig. 1

Conceptual diagram of single-arm pantograph. The pantograph uses a linkage mechanism consisting of elements such as an upper frame and a lower frame. A contact strip is attached to the upper surface of the panhead and in contact with a contact wire. A cam is attached to a shaft at the lower end of the lower frame, called the main shaft. The pantograph runs in two directions such as knuckle forward (KF) and knuckle backward (KB)

In a previous study on the dynamics of a pantograph-catenary system, a pantograph model based on the finite element method (FEM) was constructed [28]. However, the system was unstable even when the friction coefficient was very low (e.g., 0.1) and neither the mechanism of the instability phenomenon nor the effect of the running direction on stability was investigated. In addition, the study did not experimentally verify the instability phenomenon or the dynamical characteristics of the pantograph model. The present authors previously proposed a two-degree-of-freedom pantograph model based on multibody dynamics [29] in Ref. [30]. In Ref. [30], the results of excitation tests on an actual pantograph were used to validate the dynamical characteristics of the pantograph model at frequencies below 30 Hz. The model was found to be consistent with the experimental result that knuckle backward (KB) runs are more prone to destabilization, which is discussed later in this paper. However, the friction coefficient at which the model becomes unstable is much higher than that reported in Ref. [24] and thus the model does not quantitatively match observations. Furthermore, the mechanism of the instability phenomenon was not considered in Ref. [30]. The discrepancies regarding the friction coefficient suggest that the elastic deformation of the articulated frame should be considered in the model. The present authors also proposed another pantograph model based on the pin-disk model [31] in Ref. [32]. In Ref. [32], the contact strips and their supports were modelled as a two-degree-of-freedom system, and an analytical study was carried out. This model predicts that a flutter-type instability occurs when the friction coefficient is comparable to the values reported in Ref. [24]. However, this model was unstable irrespective of the running direction, and the frequency at which it became unstable was extremely high. Thus, the model does not qualitatively match observations. This finding suggests that the articulated frame of the pantograph should be considered in the model.

As mentioned above, previous studies have not conducted experiments on the instability phenomenon or investigated the mechanism based on experiments and simulations. Therefore, the present study conducts experimental and numerical investigations of the instability phenomenon caused by sliding friction. In the experimental investigation, the instability phenomenon observed in the field [20] is reproduced in the laboratory and its frequencies and mode shapes are measured. In addition, a method for estimating the friction coefficient for an actual pantograph is proposed and used to investigate the effects of the friction coefficient and running direction on stability. In the numerical investigation, the pantograph is modelled based on flexible multibody dynamics (FMBD) [33], and the contact between a contact wire and a pantograph is modelled based on the penalty method [34]. Each model is experimentally verified. Complex eigenvalue analysis is applied to the models under the assumption of Coulomb friction to examine the destabilization mechanism. Based on the determined mechanism, countermeasures for preventing the instability phenomenon are developed. The effectiveness of these countermeasures is verified through simulations and experiments.

2 Experimental investigation

To reproduce a high friction coefficient, it is necessary to create a sliding history at a running speed of 300 km/h for a few minutes [24]. It is difficult to do this using an actual overhead contact line (OCL). In addition, the use of an actual OCL is not suitable for the examination of the instability mechanism because it is difficult to control various parameters, including the state of the sliding surfaces, for an actual OCL.

Therefore, the high-speed test facility for pantograph/OCL systems (HiPaC) [35], shown in Fig. 2, is used here to reproduce the instability phenomenon. HiPaC is a device that reproduces the sliding motion between a pantograph and a contact wire by rotating a rigid disk to which the contact wire is attached at high speed. Although HiPaC cannot perfectly reproduce the dynamics of an OCL, it can stably reproduce high friction coefficients and is thus suitable for the assessment of the stability of actual pantographs.

Fig. 2

Schematic diagram of HiPaC. The rigid disk is rotated to simulate sliding and shaken in the horizontal direction to reproduce a stagger of an OCL

Friction-induced vibration has been reported in many studies [36], especially those on railway and automobile noise [37, 38]. Studies on automotive disc brake squeal have reported that the friction coefficient and contact area affect stability [39, 40]. Therefore, this section presents tests that reproduce the instability phenomenon and parametric studies of the key parameters.

To reproduce conditions with a high friction coefficient, the friction history was created according to the operation pattern of HiPaC, which is shown in Fig. 3. Note that some conditions were changed for various practical reasons (e.g., to accommodate the placement of sensors). The OCL has a horizontal stagger to avoid the local wear of the contact strips. A horizontal displacement (triangular wave with an amplitude of 200 mm and a frequency of 0.5 Hz) of the rigid disk was applied to reproduce this stagger.

Fig. 3

Operation pattern of HiPaC. The horizontal displacement (triangular wave with an amplitude of 200 mm and a frequency of 0.5 Hz) of the rigid disk is applied

2.1 Reproduction of friction-induced vibration

This section describes a test conducted to reproduce the instability phenomenon using HiPaC. With the application of a DC voltage, HiPaC can detect the contact loss between a contact wire and a pantograph. An electrical circuit was configured in which the potential difference between the contact strip and the rigid disk was 0 V when the contact wire and the pantograph were in contact and 8 V when they were not in contact. The contact loss criterion was set to 4 V. Copper-based contact wires and iron-based sintered alloy contact strips were used in this test. Accelerometers were placed on the top and sides of the contact strip during the test. Figure 4 shows the locations of the accelerometers.

Fig. 4

Locations of accelerometers. Accelerometers are placed on the top and sides of the contact strip

After the sliding history was created according to the operation pattern shown in Fig. 3, low-speed running at 5 km/h was performed. The time history of the contact loss at 5 km/h is shown in Fig. 5. The lower and upper parts of Fig. 5 show the results for knuckle forward (KF) and knuckle backward (KB) running, respectively. The origin of the time is the time when the running speed reached 5 km/h. The lower part of Fig. 5 shows that the pantograph is stable with almost no contact loss when running in KF. In all tests conducted for KF running, the pantograph remained stable. In contrast, the upper part of Fig. 5 shows that the pantograph was unstable in KB running, that the instability phenomenon of an actual pantograph was reproduced, and that the pantograph exhibited stable 7 Hz collisional vibration. Note that although the parametric excitation represented by Mathieu’s differential equation [41] is known to cause instability phenomena in catenary-pantograph systems, the phenomenon investigated here is not considered to be caused by parametric excitation because it was reproduced using HiPaC and has been reported to occur at low speeds [19, 20].

Fig. 5

Comparison of contact loss between KF and KB running. HiPaC can detect contact loss with the application of a DC voltage. The range above 4 V is the contact loss. The range enclosed yellow line is the FFT application area, the results of which are shown in Fig. 6 (FFT: fast Fourier transform)

Fig. 6

Power spectral density (PSD) of acceleration in ranges shown in Fig. 5

Figure 6 shows the results of applying the fast Fourier transform (number of sampling points: 512, window function: Hanning window) to the time history of acceleration in the range enclosed by the yellow line in the upper part of Fig. 5. The lower and upper parts of Fig. 6 show the results for Accelerometers 1 and 5, respectively. The results for these two accelerometers are generally similar. The results for the other accelerometers are also similar (data not shown). The results in Fig. 6 are generally consistent with the results of the pantograph excitation test (Fig. 16), which are described later. This is because the excitation due to the unevenness of the contact wire sliding surface does not have a dominant frequency component in the range below about 100 Hz and the excitation input is close to pseudo-random waves (see Appendix 1 for details). Compared to the results of the excitation test shown in Fig. 16, the response at 9.77 Hz, indicated by the solid red line in Fig. 6, is very large and therefore may be involved in the instability phenomenon. The eigenmode corresponding to this frequency is the mode of the elastic deformation of the entire frame section, mainly in the direction of travel (see Sect. 3.2).

Since the amplitude of the collision vibration was large, the shape of the vibration was recorded on video. Figure 7 shows a stroboscopic view of the collision vibration created from the video. As shown, the entire frame section vibrates vertically and horizontally, suggesting a relationship with the 9.77 Hz eigenmode mentioned above.

Fig. 7

Strobe diagram of 7 Hz collisional vibration (time increments: 1/14 s)

Since the instability phenomenon occurred even though the surface of the contact wire was milled to make the sliding surface flat, it is unlikely that the instability phenomenon is forced vibration due to the unevenness of the sliding surface or chatter vibration, which is frequently observed in machine tools [42].

It is known that the amount of wear of contact wires is proportional to the contact force between an OCL and a pantograph [43]. The contact force fluctuations corresponding to the instability phenomenon are predicted to cause undulating wear on the contact wires. When an instability phenomenon (about 7 Hz) occurs at 5–10 km/h, the wavelength of the undulating wear is 20–40 cm, which roughly corresponds to the 20–50 cm wavelength reported in Ref. [20]. It is thus considered that HiPaC can approximately reproduce the instability phenomenon reported in Ref. [20], although the pantograph and OCL types are different.

2.2 Method for estimating friction coefficient

Numerous studies have been conducted on the estimation of contact forces between an OCL and a pantograph, especially in Germany, Italy, and Japan [44,45,46,47,48]. These studies inserted load cells (or attached strain gauges) and accelerometers into the pantograph and estimated the contact force based on the equilibrium equation of force. The contact force can also be estimated by placing a sensor on the OCL [49] or using images of the pantograph or OCL [50, 51]. In addition to the contact force, frictional forces need to be estimated to examine the mechanism of the instability phenomenon. Therefore, the present study proposes a method for estimating the friction coefficient that involves inserting multi-component force transducers between the pan-head section and the frame section shown in Fig. 8. In the figure, the pantograph is divided into two sections for simplicity.

Fig. 8

Division of pantograph into two sections for simplicity

Fig. 9

Time history of estimated friction coefficient in KF (LPF: low-pass filter)

Figure 10 shows a schematic diagram and photograph of a device for estimating friction coefficient. In the device, two-component force transducers are inserted into an actual pantograph. The vertical and horizontal internal forces f_z and f_x, respectively, between the pan-head section and the frame section were measured from the combined forces of the two transducers inserted on either side. The friction coefficient μ was calculated from the ratio of these two values:

$$ \mu = f_{{\text{x}}} /f_{{\text{z}}} . $$

(1)

Fig. 10

Schematic diagram and photograph of the device for estimating friction coefficient. Two-component force transducers are inserted into an actual pantograph

Here, the value of the friction coefficient includes the effect of the inertia force of the pan-head section. The time variation of the friction coefficient is generally large. It is thus necessary to determine representative values.

Here, a low-pass filter that passes frequencies below 5 Hz was applied to the value of the friction coefficient calculated using Eq. (1) to eliminate the influence of the dynamics. Figure 9 shows an example of the time history of the estimated friction coefficient when a high friction coefficient is reproduced in KF running. The solid black and red lines in Fig. 9 represent the waveforms of the friction coefficient before and after the application of the low-pass filter, respectively. As shown, the friction coefficient increases to about 1.0 for an actual pantograph. The friction coefficient decreases with time. In this test run, even though the friction coefficient exceeded 1.0, the behaviour of the system was stable.

Figure 11 shows the time history of the contact loss, friction coefficient, and strain of the upper frame (see Fig. 1) in KB running. The strain was measured by gauges glued at the locations shown in Fig. 12 to measure the bending deformation of the upper frame. The blue dashed line in Fig. 11 and the clinometer in Fig. 12 are discussed in the next section. From Fig. 11, it can be seen that the system exhibits periodic collisional vibration when the friction coefficient is around 0.8 and that the strain in the upper frame increases before the start of contact loss, with a vibration frequency of 8 Hz. This increase in the strain in the upper frame corresponds to the articulated frame vibration described in the previous section (see Figs. 5 and 7).

Fig. 11

Time history of contact loss, estimated friction coefficient, and strain of upper frame in KB. The strain of the upper frame increases before the start of contact loss, with a vibration frequency of 8 Hz. The evaluation interval indicated by the blue dashed lines is used when explaining the statistical processing method for the friction coefficient

Fig. 12

Locations of gauges and measurement of attack angle. The attack angle is measured with a digital clinometer on the upper surface of the contact strip

2.3 Parametric study of friction coefficient and attack angle

In this section, the effects of the friction coefficient and the attack angle of the pan-head section on stability are examined. The attack angle was changed by fine-tuning the lengths of the elements that comprised the linkage mechanism and measured with a digital clinometer on the upper surface of the contact strip, as shown in Fig. 12. In the figure, the positive and negative directions of the attack angle are shown in orange.

The relationship between the attack angle and the contact area is first described. This relationship was examined using pressure-sensitive paper under static conditions. Figure 13 shows the transition of the contour map of the contact pressure with respect to the attack angle. As shown, there is a bias in the contact pressure (called one-sided contact), the contact pressure distribution changes significantly with a change in the attack angle of ± 0.2°, and the contact area correlates with the change in the attack angle. Preliminary tests on the contact range under dynamic conditions, which involve frictional sliding between the contact strip and the rigid disk, were also conducted. The tests, which were carried out on painted contact strips, confirmed that the dynamic contact range correlates with the static contact range under the conditions shown in Fig. 13.

Fig. 13

Relationship between attack angle and contact pressure. The grey dashed line indicates the range for full contact

Next, the statistical processing method for the friction coefficient is described. As shown by the fluctuating waveform of the friction coefficient after the application of the low-pass filter in Fig. 9, the trend of the friction coefficient changes over a period of about 2–4 s. For example, the average of μ is around 1.0 for the range of 3–5 s in Fig. 9, whereas it is around 0.8 for the range of 8–12 s. The average value is often used as the representative value of the friction coefficient. However, averaging over multiple trends is undesirable for understanding the trend of the instability phenomenon. Therefore, the representative value of the friction coefficient was determined by averaging the values of the friction coefficient for each trend. For the transition to collisional vibration, averaging was performed for the section up to the point before the transition to collisional vibration, as shown by the dashed blue line in Fig. 11.

Finally, Fig. 14 shows the transition of stability obtained using the method described above for various combinations of the friction coefficient and attack angle. In the figure, the stability of the system is indicated by red and blue markers. In this paper, instability is defined as a state in which the periodic collisional vibration described in Sect. 2.1 stably forms. The difference in the direction of travel is expressed by the positive and negative values of μ. In this paper, μ is defined as positive in KF running and negative in KB running. Figure 14 shows that the system is stable in KF running, regardless of the attack angle, even when μ is about 1.0. On the other hand, the system is unstable in KB running when μ is greater than about 0.7.

Fig. 14

Transition of stability for various combinations of friction coefficient and attack angle

3 Modelling of pantograph based on flexible multibody dynamics

Models developed for pantographs include the single-mass model [14, 52], double-mass model [14, 53], a model that adds the bending modes of the pan-head to the double-mass model [54], and models based on FEM and FMBD [28, 55, 56]. The double-mass model, which has very few degrees of freedom, can reproduce the dynamic characteristics of pantographs in the range of about 30 Hz or less. On the other hand, methods based on FEM and FMBD can reproduce the dynamic characteristics of pantographs up to a high-frequency range, but have a very large number of degrees of freedom and are easily affected by numerical errors. Here, we focus on the mechanistic characteristics of a pantograph and model a pantograph with as few degrees of freedom as possible to minimize the influence of numerical errors and clarify the essential mechanism on the instability. This section first describes the modelling of a pantograph and then describes the modelling of contact and friction.

3.1 Model overview

As mentioned in Sect. 1, Refs. [32] and [30] suggested the necessity of considering the articulated frame and its elastic deformation, respectively. In addition, the experiments carried out in this paper also supported this suggestion. Therefore, we propose an FMBD model that considers the articulated frame. Figure 15 shows a conceptual diagram of the pantograph model proposed in this paper. In this model, two in-plane motions are coupled, as shown in the figure. The X axis is in the direction of travel, the Y axis is in the longitudinal direction of the pan-head section, and the Z axis is in the vertical direction, with the lower end of the lower frame (main shaft shown in Fig. 1) as the origin. The pan-head section moves in the plane indicated by beige in Fig. 15, which coincides with the YZ plane when the system is in static equilibrium. On the other hand, the frame-section moves in the ZX plane indicated by light-blue in the figure. The motion in each section is modelled based on FMBD. For the connection between the frame section and the pan-head section, the displacements in the Z direction are coupled by degree-of-freedom coupling. Rigid motion is assumed for the translation of the pan-head section in the X direction and the rotation around the Y axis. A rotation spring is attached to the connection for the rotation of the pan-head section around the X axis. The damping is basically proportional viscous damping. In areas where the damping is considered to be high, the proportional coefficient is set to be 2 to 3 times higher than that of the other dampers. The main shaft is supported not by an ideal pin connection, but by springs with a spring constant of k_s in the vertical and horizontal directions.

Fig. 15

Conceptual diagram of FMBD pantograph model. In this model, two in-plane motions modelled based on FMBD are coupled by degree-of-freedom coupling and rotation spring. The main shaft is supported by springs with a spring constant of k_s in the vertical and horizontal directions

The equation of motion for the proposed model ignoring damping is given by

$$ \varvec{M}({\mathbf{x}}){\ddot{\varvec x}} + \varvec{K}_{{\text{L}}} \varvec{x} + \varvec{f}_{{{\text{int}}}} (\varvec{x}) = \varvec{f}_{{{\text{ext}}}} , $$

(2)

where x is the displacement vector, M is the global mass matrix, which contains the mass matrix of each element, K_L is the stiffness matrix, f_int is a vector that contains the element forces of each element, and f_ext is a vector that contains static external forces of each element. For the mass matrix of each element, a consistent mass matrix of a planar frame element [57] was used. It was transformed according to the posture of each element. The element forces for each element were calculated using the method of Simo [33]. Linearizing the above equation around the equilibrium point ${\overline{\varvec{x}}}$ yields

$$ \left. \begin{gathered} \varvec{M}(\varvec{\overline{x}})\delta {\ddot{\varvec x}} + \varvec{K}_{{\text{L}}} \delta \varvec{x} + \varvec{K}_{{{\text{NL}}}} (\varvec{\overline{x}})\delta \varvec{x} = \textbf{0} \hfill \\ \varvec{K}_{{\text{L}}} \varvec{\overline{x}} + \varvec{f}_{{{\text{int}}}} (\varvec{\overline{x}}) = \varvec{f}_{{{\text{ext}}}} \hfill \\ \varvec{K}_{{{\text{NL}}}} = \partial \varvec{f}_{{{\text{int}}}} /\partial \varvec{x},\;\;\varvec{x} = \varvec{\overline{x}} + \delta \varvec{x} \hfill \\ \end{gathered} \right\}, $$

(3)

where K_NL is the stiffness matrix that results from the elemental forces and δx is the component of variation from the equilibrium point.

3.2 Validation using frequency response function

To numerically investigate the instability phenomenon of an actual pantograph, it is necessary to verify the validity of the dynamic model proposed in the previous section. Therefore, in this section, excitation tests of an actual pantograph are conducted to validate the dynamic model.

First, an exciter was vertically applied to the pan-head and two excitation tests were conducted with the pantograph at the nominal working height. See Appendix 2 for details on the excitation tests. The accelerometer and excitation locations are shown in the lower part of Fig. 16 and a comparison of the frequency response function (FRF) obtained from the excitation tests and simulations is shown in the upper part of Fig. 16. The FRFs were calculated from the acceleration and excitation force values at the locations circled in green in the lower part of Fig. 16. For the simulation, the FRFs were calculated under the assumption of harmonic oscillations after linearization around the nominal working height. Figure 16 shows that the FRFs at the two locations are in good agreement, indicating that the modelling is highly accurate in the range below 100 Hz.

Fig. 16

Comparison of FRF between experiment and simulation. An exciter is vertically applied to the contact strip and the accelerometer sensitivity is directed vertically

Next, the mode shape of the pantograph around 10 Hz was compared. For the eigenmode around 10 Hz, the horizontal deformation was large, so the accelerometer sensitivity was directed horizontally and the pantograph was excited in the horizontal Direction. A comparison of the experimental and simulation results is shown in Fig. 17.

Fig. 17

Comparison of mode shape around 10 Hz between experiment and simulation. The solid light-blue line represents the posture in static equilibrium, the other lines represent the mode shape. See Appendix 2 for details on the excitation tests and the mode shape rendering

Figure 17a shows the experimental results and Fig. 17b shows the simulation results. In Fig. 17, the solid light-blue line represents the posture in static equilibrium, the other lines represent the mode shape, and the circles represent the response at the sensor location (see Appendix 2 for details). Figure 17 shows that the experimental and simulation results are in good agreement. The experimental and simulation results for the other modes (not shown in the figure) have the same degree of agreement. Note that experiments confirmed that the modelling is also highly accurate with respect to the rigid body motion. See Appendix 3 for details.

3.3 Modelling of contact and friction

Models of the contact between an OCL and a pantograph based on the penalty method [45, 54, 58], the method of Lagrangian multipliers [59], and the polygon contact model [60] have been proposed. Here, for simplicity, the penalty method is used for modelling. As done in Ref. [58], the penalty coefficients are set such that the collision phenomena between a contact wire and a pantograph obtained in the simulations agree with experimental results.

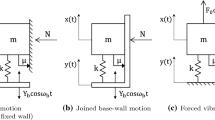
A conceptual diagram of the collision experiment is shown in Fig. 18. A load cell was attached to the contact wire of the rigid disk of HiPaC and collision experiments were conducted in which the pantograph was made to collide with the load cell from below. For the simulation, the double-mass model shown in Fig. 19a was used to simplify the calculation. f_c is the contact force between the load cell and the pantograph; it is given by

$$ \left. \begin{gathered} f_{\mathrm{c}} = \alpha y_{{\text{p}}} + \beta \dot{y}_{{\text{p}}} \hfill \\ \left. \begin{gathered} \alpha = \beta = 0\;\;(y_{{\text{p}}} < 0) \hfill \\ \beta = 0\;\;\;\;\;\;\;\;(\dot{y}_{{\text{p}}} < 0)\;\; \hfill \\ \end{gathered} \right\}\;\; \hfill \\ \end{gathered} \right\}, $$

(4)

where α is the contact stiffness, β is the contact damping. The result of the FRF verification of the double-mass model is shown in Fig. 19b. Figure 19b shows that the dynamic characteristics of the pantograph are generally well represented in the range below 50 Hz. Numerical integration was performed using the Runge–Kutta method. Since Eq. (4) requires switching the equation of motion, the switching point was precisely calculated using the bisection method to achieve high accuracy. The penalty coefficients were set such that the experimental and simulation results were consistent, resulting in α = 1.0 × 10⁷ N/m and β = 1.5 × 10³ Ns/m. A comparison of the experimental and simulated contact forces for these values is shown in Fig. 20. As shown, the order and waveform of the first and third impact forces and the period of the residual vibration obtained in the simulation agree with those obtained in the experiment, indicating that reasonable parameter identification was achieved. The collisional test was conducted several times; the experimental and simulation results had the same degree of agreement as that in Fig. 20 for all tests.

Fig. 18

Conceptual diagram of the collision experiment. A load cell is attached to the contact wire of the rigid disk of HiPaC. The pantograph was made to collide with the load cell from below

Fig. 19

Double-mass pantograph model for parameter identification of the penalty coefficients

Fig. 20

Comparison of contact force between experiment and simulation

Finally, the modelling of one-sided contact and friction is described. For the former, as shown in Fig. 21, a concentrated load was applied at a location displaced from the centre of the contact strip by a in the X direction to represent the bias of the contact pressure. Here, l is the length from the joint of the pan-head section and the frame section to the top of the contact strip. Various friction models have been proposed [61]. For simplicity, Coulomb friction is assumed here. Under the assumption that the direction in which the frictional force acts when the train runs in KF (positive X-axis direction) is positive, the positive direction of the frictional force μf_c is the direction shown in Fig. 21. If the train runs in KB (negative X-axis direction), the value of the friction coefficient μ is assumed to be negative, as in Sect. 2. The external force f exerted on the contact strips by the contact and friction model, neglecting damping, is given by

$$ \left. \begin{gathered} {\textbf{f}} = \left[ {\begin{array}{*{20}c} {f_{{\text{X}}} } \\ M \\ {f_{{\text{Z}}} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\mu f_{{\text{c}}} } \\ {(a - \mu l)f_{{\text{c}}} } \\ {f_{{\text{c}}} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} 0 & {\mu a\alpha } & {\mu \alpha } \\ 0 & {a(a - \mu l)\alpha } & {(a - \mu l)\alpha } \\ 0 & {a\alpha } & \alpha \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{{\text{j}}} } \\ {\theta_{{\text{j}}} } \\ {z_{{\text{c}}} } \\ \end{array} } \right] \hfill \\ f_{{\text{c}}} = \alpha (z_{{\text{c}}} + a\theta_{{\text{j}}} ) \hfill \\ \end{gathered} \right\}, $$

(5)

where f_x and f_z are the external forces in the X and Z directions, respectively, and M is the moment due to the external force in the ${\varTheta}$ direction (see Fig. 21) acting on the contact strips. The displacements in the X and Z directions and the angular displacements in the ${\varTheta}$ direction of the contact strips are represented by (x_c, z_c, θ_j). The displacements and angular displacement of the joints of the pan-head section and the frame section are expressed by (x_j, z_j, θ_j). Equation (5) is added to the right-hand side of Eq. (3) to obtain the final equation of motion, and the stiffness matrix becomes asymmetric. Note that Eqs. (2) and (3) are completely different from those in [32] due to the consideration of the articulated frame. In addition, Eqs. (2) and (3) are based on FMBD, whereas those in [32] are based on force equilibrium. In contrast, Eqs. (4) and (5) are similar to those in [32], because both models consider the one-sided contact and Coulomb friction. The difference between the equations in both models is due to the horizontal displacement x_j in Eq. (5).

Fig. 21

Modelling of one-sided contact and friction

4 Numerical investigation

In this section, complex eigenvalue analysis is applied to the dynamic model proposed in the previous section for stability discrimination and experimental and simulation results are compared. Based on the results of the complex eigenvalue analysis, the mechanism of the instability phenomenon is discussed.

4.1 Linear stability analysis

The model proposed in the previous section is a nonlinear model expressed in Eq. (2). When this model is linearized around the nominal working height, complex eigenvalue analysis can be applied using Eq. (3). The stability of the system can be determined by the real part of the eigenvalues λ. If even one of the eigenvalues has a positive real part, the system is dynamically unstable.

In this section, the maximum value of Re(λ), Re(λ)_max, is numerically calculated from the model proposed in the previous section. Figure 22a shows the transition of Re(λ)_max with respect to the contact location a and friction coefficient μ. In the figure, negative Re(λ)_max values (i.e., the system is stable) are shown as 0 to improve visibility. Figure 22a shows that the system is destabilised only in KB running, that it becomes unstable when μ <−­0.7, and that the transition in Re(λ)_max for a change in a is small, which is consistent with the experimental results shown in Fig. 14.

Fig. 22

Linear stability analysis results using the model proposed in the previous section. In this analysis, the model is linearized around the nominal working height

The imaginary part of the eigenvalues in Fig. 22a is shown in Fig. 22b. In the figure, the imaginary part of the eigenvalues is divided by 2π and the unit is converted to hertz. Figure 22b shows that the imaginary part of the destabilized eigenvalue is about 10 Hz throughout the entire unstable region. The frequency at which the unstable mode occurs, 10 Hz, corresponds to the frequency in the upper frame (8 Hz) shown in Fig. 11. This indicates that the dynamic model is also consistent with the experiment in terms of the frequency of the instability phenomenon. The shape of the unstable mode at μ = − 0.8 and a = 0 mm is shown in Fig. 23a. As shown, the entire articulated frame exhibits elastic deformation, and the contact strips exhibit bending deformation. For the elastic deformation of the articulated frame, the mode shape is considered to correspond to Figs. 7 and 11.

Fig. 23

Mode shapes (μ = −0.8, a = 0 mm)

The above results show that the frequencies of the instability phenomenon and the stable-unstable boundary are consistent between the experiment and simulation. The mode shapes of the instability phenomenon also show some correspondence with the experiment, as shown in Fig. 7. Therefore, it is considered that the instability phenomenon can be explained by the model. The mathematical cause of the instability of the model is the asymmetry of the stiffness matrix due to Coulomb friction. The damping matrix is also asymmetric due to the effect of Coulomb friction, but since the stability of the system did not change much from that in Fig. 22 even when β = 0, the main cause is considered to be the asymmetry of the stiffness matrix.

Note that, as shown in Appendix 4, there are also unstable modes that are sensitive to the contact location a, depending on the parameters. In these modes, the pitching motion of the pan-head section is dominant, and a has a significant effect. It is considered that these unstable modes can be explained by the pin-disk model as dealt with in Ref. [32]. On the other hand, the entire articulated frame vibrates in the unstable mode shown in Fig. 23. When the entire frame vibrates, the change in a is small relative to the scale of its motion. It is considered that this is the reason why the instability phenomenon dealt with in this study is not sensitive to a.

4.2 Examination of mechanism

In this section, we discuss the dynamical mechanism of the instability phenomenon. Since the instability modes described in the previous section were not sensitive to a, the mechanism is discussed under the assumption that a = 0. First, Fig. 24 shows the transition of eigenvalues with respect to the friction coefficient. The real and imaginary parts of the eigenvalues are respectively shown in Figs. 24a and b; the eigenvalues not involved in the instability are omitted to improve visibility. The eigenvalue whose real part is positive around μ = −0.8 (hereafter referred to as Mode 1) and the eigenvalue that changes in a coupled manner with Mode 1(hereafter referred to as Mode 2) are indicated by solid red and blue lines, respectively. Figure 24a shows that the real parts of the two eigenvalues indicated by the red and blue solid lines change in a generally line-symmetric manner with respect to Re(λ) = −4.2 and that the absolute values increase rapidly in the range of μ < −0.8. On the other hand, Fig. 24b shows that the imaginary parts of the two eigenvalues are nearly coincident in the range of μ < −0.8. Such eigenvalue transitions are derived from Hamiltonian Hopf bifurcation [62, 63] (see Appendix 5 for details). The mode shape of Mode 2 for μ = −0.8 is shown in Fig. 23b. A comparison of Figs. 23a and 23b indicates that the shapes of the two modes are very similar. The above suggests that the coupling of these two modes (hereafter referred to as mode coupling) destabilizes the system. Such instability due to mode coupling is sometimes referred to as a flutter-type instability [63]. Note that mode veering [63] occurs near μ = −0.5 and the mode involved in mode veering (hereafter Mode 3) is also shown as a solid black line; however, this mode is not involved in the instability (see Appendix 5 for details).

Fig. 24

Real parts and imaginary parts of eigenvalues as functions of friction coefficient μ for a = 0, α = 1.0 × 10⁷ N/m, β = 1.5 × 10³ Ns/m. See Appendix 5 for details on the labelling of the modes

Next, the physical causes of the mode coupling and the effect of the running direction are discussed. Figure 25 shows a conceptual diagram of the physical causes of the mode coupling. The left and right parts of the figure show the mode shapes for μ = 0 and μ = −0.8, respectively. For μ = 0, Mode 1 is the mode in which the entire articulated frame is deformed elastically and horizontally, Mode 2 is the mode of mainly vertical deformation (see Fig. 25). Mode 2 is the mode derived from a rigid body motion mode due to the linkage mechanism of the pantograph (see Appendix 6 for details). The main differences in the shapes of the two modes for μ = 0 are the displacement of the pan-head section in the X direction and the rotation around the Y axis (see Fig. 25). In KB running, when the upward displacement of the pantograph occurs, positive frictional forces and moments in the X direction and around the Y axis act on the pan-head, respectively (see Fig. 25). This effect gradually brings the mode shape of Mode 2 closer to that of Mode 1 (i.e., the eigenvalues become closer), resulting in the mode coupling. In contrast, for KF running, the frictional forces and moments act in the opposite direction. This effect diverges the eigenvalues and mode shapes of Mode 1 and Mode 2 from each other (see Fig. 24b). It is considered that this is the reason why the instability phenomenon only occurs in KB running.

Fig. 25

Conceptual diagram of the physical causes of the mode coupling. The left and right parts show the mode shapes for μ = 0 and μ = −0.8, respectively. The co-ordinate systems on the mode shapes, which are omitted to improve visibility, are the same as those in Fig. 23

Mode 1 cannot be represented by the double-mass model, as shown by the differences between the experiment and simulation near 11 Hz in Fig. 19b. This indicates that the elastic deformation of the articulated frame has to be modelled to understand the mechanism. In addition, the influence of each parameter on the modes is complex due to the linkage mechanism of the pantograph, and the quantitative evaluation of the stability requires the modelling of the linkage mechanism, as proposed in this paper.

The beam/sprag model [38, 64] is well known as one of the mechanisms of brake squeal. In this model, the stability changes depending on the sliding direction, which is similar to the instability observed in this study. In addition, as mentioned at the end of Sect. 4.1, pantographs can be unstable because of several mechanisms. An analytical model has been proposed for systems with several instability mechanisms, such as mode coupling and spragging [38] in the field of brake squeal [65]. The models proposed in Refs. [64, 65] could qualitatively explain the dependence of the instability mechanism treated in this study on the sliding direction. However, the sensitivity to the sprag angle, which is theoretically indicated by these models, was not confirmed in preliminary tests with the pantograph. This trend in the sprag angle is thought to be a unique feature of the pantograph due to the linkage mechanism, and experiments and simulations are being carried out. The results will be presented as soon as they become clear.

To verify the validity of the mechanism described based on Fig. 25, experiments were conducted using a system in which the frame section was replaced by a rigid aluminium frame. Figure 26a shows a photograph of the experiment and Fig. 26b shows the time history of the friction coefficient and the contact loss. The six-component force transducer shown in Fig. 26a was used to estimate the friction coefficient. In Fig. 26b, the potential difference in the contact state is different from that in Figs. 5 and 11 because the electrical resistance of the pan-head section and the aluminium frame is different from that of the pantograph. Figure 26b shows that contact loss does not occur and that the system is stable even when the friction coefficient exceeds 1.0. This result is consistent with the mechanism described above.

Fig. 26

Experimental investigation of dynamical mechanism of instability phenomenon

5 Construction of mechanism-based prevention measures

In this section, based on the mechanism described in the previous section, countermeasures for preventing the instability phenomenon are proposed for the frame section and the pan-head section, respectively. The effectiveness of the countermeasures is numerically and experimentally verified. The time history of the friction coefficient in the following sections shows only the results obtained after the application of the low-pass filter.

5.1 Prevention measures for frame section

As inferred from Fig. 24b and the determined mechanism, an increase in the natural frequency of Mode 1 is expected to expand the stability region. One simple way to increase the natural frequency of Mode 1 without affecting Mode 2 is to increase the support rigidity of the main shaft. In an actual pantograph, this can be done by changing the type of bearing or adjusting the clearance of the bearing of the main shaft. This method can be applied to existing pantographs. This measure does not negatively affect current collection performance in the high speed range. Therefore, this paper proposes increasing the support stiffness k_s of the main shaft as a measure for the frame section. Note that changing the support stiffness is just one example; other parameters could be changed to modify the eigenvalues of mode coupling. This issue will be addressed in a future study.

Using the model proposed in Sect. 3, we calculated the transition of the FRFs and stable-unstable boundary for various values of the support stiffness of the main shaft. The results are shown in Fig. 27. Figure 27a shows that a change in support stiffness has a limited effect on the FRFs and does not affect the dynamic characteristics at high speeds. Figure 27b shows that the stability region expands as the support stiffness increases, which numerically verifies the validity of the proposed measure. Experimental verification using an actual pantograph is a subject for future work.

Fig. 27

Transition of FRF and stable-unstable boundaries with respect to support stiffness of main shaft

5.2 Prevention measures for pan-head section

A simple preventive measure for the pan-head section is to change the flexible plate, which is a thin sheet of metal that connects several divided contact strips, as shown in Fig. 28. As shown in Fig. 23, the gain of the contact strip is large in the unstable mode, suggesting that there is sensitivity to this instability phenomenon.

Fig. 28

Schematic diagram of contact strips and surrounding structures

Therefore, this paper proposes changing the bending stiffness of the flexible plate as a measure for the pan-head section. Using the model proposed in Sect. 3, we calculated the transition of the FRFs and stable-unstable boundary for a change in the bending stiffness of the flexible plate. The results are shown in Figs. 29 and 30, where γ is the ratio of the modified bending stiffness to the original bending stiffness of the flexible plate. Figure 29 shows that a change in the bending stiffness of the flexible plate affects the FRF, mainly in the range of 20–30 Hz. However, high-speed pantographs are desirable to have a resonance point around 20 Hz, and the proposed measures meet this desire. Figure 30 shows that the stability region expands as the bending stiffness of the flexible plate decreases, thereby numerically verifying the validity of the proposed measure.

Fig. 29

Transition of FRF with respect to bending stiffness of the flexible plate

Fig. 30

Transition of stable-unstable boundaries with respect to bending stiffness

Figure 31 shows the experimental results when the bending stiffness of the flexible plate is decreased in an actual pantograph. The figure shows the results with the highest friction coefficient among the multiple tests in KB running. As shown, even when the friction coefficient exceeds 1.0, the system does not shift to collisional vibration and is stable, experimentally confirming the validity of the proposed method. Note that this measure may affect the durability of the pan-head section, and durability tests are considered necessary for practical applications. This will be an issue for future research.

Fig. 31

Time history of friction coefficient and contact loss

6 Conclusion

An unexplained instability phenomenon in railways is known to be caused by sliding friction in catenary-pantograph systems. This is an important engineering problem because this instability phenomenon contributes to increased wear of contact wires and requires a train driver to confirm safety, which leads to train delays. In this study, experimental and numerical investigations were conducted on the instability phenomenon caused by sliding friction. The instability phenomenon observed in the field was reproduced in the laboratory and its frequencies and mode shapes were experimentally investigated. A method for estimating the friction coefficient for an actual pantograph was proposed and used to experimentally investigate the effects of the friction coefficient and running direction on stability. The modelling of a pantograph and the contact between an OCL and a pantograph was carried out and the validity of the models was verified by experiments. Under the assumption of Coulomb friction, complex eigenvalue analysis was applied to the verified dynamic model. It was confirmed that the frequencies, mode shapes, and stable-unstable boundary of the instability phenomenon agreed between experiment and simulation. It was clarified that the instability phenomenon is a flutter-type instability caused by the asymmetry of the stiffness matrix due to Coulomb friction and that mode coupling can occur in KB running. The determined mechanism of the instability phenomenon was verified by an experiment using a system in which the frame section was replaced by a rigid aluminium frame. Countermeasures were developed for the frame section and the pan-head section and their effectiveness was numerically and experimentally verified. The main contributions of this study are to elucidate the mechanism of the instability phenomenon and to propose preventive measures using detailed experiments and simulations. The results could contribute to the design of new pantographs to improve stability and the development of countermeasures for existing pantographs that experience instability.

Appendices

Appendix 1: Unevenness of contact wire sliding surface

The unevenness of the contact wire sliding surface was measured with a laser displacement meter in the range of 0–355 degrees, excluding the area where the angle detection markers are located (see Fig. 32). Figure 33 shows the result of applying the fast Fourier transform (number of sampling points: 8192, window function: Hanning window) to the time history for a disk rotating at 5 km/h. As shown, the power spectral density is generally flat in the range below 50 Hz.

Fig. 32

Method for measuring unevenness of contact wire sliding surface

Fig. 33

Power spectral density (PSD) of unevenness of contact wire sliding surface at 5 km/h

Appendix 2: Details of excitation test

This appendix describes the excitation method and sensor locations for the vibration test described in Sect. 3.2 as well as the method for drawing the mode shapes. A schematic diagram of the exciter is shown in Fig. 34. As shown, the excitation test was conducted with the exciter acting vertically and horizontally on the contact strip and the pantograph at the nominal working height. The excitation force was measured by a load cell between the exciter and the pantograph. The static pressing forces for vertical and horizontal excitation were 54 N and 90 N, respectively. The excitation was applied with pseudo-random waves. The locations of the accelerometers in the test from which Fig. 17a was obtained are shown in Fig. 35.

Fig. 34

Schematic diagram of exciter

Fig. 35

Locations of accelerometers

The mode shapes were visualized by plotting the gain and phase information of the frequency response of each sensor to the excitation force at a specific frequency in three-dimensional space. In Fig. 17a, the responses of the accelerometers on the contact strips, the pan-head, and the articulated frame are represented by dark grey, light grey, and purple lines, respectively. In Fig. 17b, the mode shape of each element is represented by purple lines, and the mode shape of the pan-head section is inclined based on the angle of the connection θ_j. Each of the mode shapes in Fig. 17 was multiplied by an appropriate magnification factor to make the figure easier to see; the magnitudes of the responses are thus not comparable. Note that the experimental results in Fig. 17a do not show the shape of a single vibration mode, but rather the overlapping vibrations of neighbouring modes.

Appendix 3: Validation of modelling using pan-head trajectory

This appendix describes the validation of the dynamic model proposed in Sect. 3.1 using pan-head trajectory measurements.

The pan-head trajectory is the trajectory drawn by the pan-head in the ZX plane when the pantograph is vertically excited. The vertical and horizontal displacements of the pan-head were measured with a laser displacement meter during the vertical motion of the rigid disk of HiPaC at 5 mm/s. The same vertical motion of the pan-head was also applied to the proposed model and the results were compared. The Newmark-beta method was used for numerical integration. Figure 36 shows a stroboscopic view of the pantograph posture during numerical integration and Fig. 37 compares the experimental and simulation results. In Fig. 37, the location of the pan-head at the nominal working height is taken as the origin. The pan-head is displaced vertically within a range of approximately double the typical range of motion (± 200 mm). To confirm the reproducibility of the experimental results, two tests were conducted. Figure 37 shows that the experimental and simulation results are in good agreement.

Fig. 36

Simulation of pan-head trajectory

Fig. 37

Comparison of pan-head trajectory between experiment and simulation

Appendix 4: Unstable modes affected by contact location

This appendix describes the unstable modes affected by the contact location described in Sect. 4.1.

Figure 38a shows the transition of Re(λ)_max with respect to the contact location a and friction coefficient μ when the bending stiffness of the flexible plate and contact strips is increased by a factor of five from the original value. Figure 38a shows that there are also unstable modes that are sensitive to the contact location a, and that the system is also destabilised in KF running. The imaginary parts of the eigenvalues in Fig. 38a are shown in Fig. 38b. The figure shows that the imaginary part of the eigenvalue affected by the contact location a is about 175 Hz throughout the entire unstable region. The shape of the unstable mode at μ = −0.68 and a = −15 mm is shown in Fig. 39. In this mode, the pitching motion of the pan-head section is dominant.

The shape of the unstable region in Fig. 38 and the dominant pitching motion around the contact location are similar to those in Ref. [32] dealing with the pitching of the contact strips. It is considered that these unstable modes can be explained by the pin-disk model as dealt with in Ref. [32].

Fig. 38

Linear stability analysis results using the model proposed in Sect. 3. In this analysis, the bending stiffness of the flexible plate and contact strips was increased by a factor of five from the original value

Fig. 39

Mode shape of unstable mode (μ = −0.68, a = −15 mm)

Appendix 5: Details of mode veering and Hamiltonian Hopf bifurcation

This appendix describes the details of mode veering and Hamiltonian Hopf bifurcation described in Sect. 4.2.

First, Fig. 40 shows the transition of eigenvalues λ with respect to the friction coefficient for the damping matrix C = 0 and the contact damping β = 0 in a similar way to Fig. 24. Figure 40a shows that the real parts of Mode 1 and Mode 2 coincide for μ > −0.74 when the damping is ignored. On the other hand, Fig. 40b shows that the imaginary parts of Mode 1 and Mode 2 coincide for μ < −0.73 when the damping is ignored. Figure 40b also shows that mode veering occurs near μ = −0.5. Note that the labelling of the modes in Fig. 24 was based on Fig. 40.

Second, the root locus of the eigenvalues of Mode 1 and Mode 2 as functions of the friction coefficient μ for −25 < μ < 2.0 are shown in Fig. 41, where the damping is ignored in Fig. 41a and considered in Fig. 41b. Figure 41a shows that Hamiltonian Hopf bifurcation occurs at μ = −0.74 and that the eigenvalues of Mode1 and Mode2 become real eigenvalues at μ = −22.58. In contrast to Fig. 41a, b shows that λ is not symmetrical with respect to the vertical axis.

Fig. 40

Real parts and imaginary parts of eigenvalues λ as functions of friction coefficient μ for a = 0, α = 1.0 × 10⁷ N/m, C = 0, β = 0

Fig. 41

Root locus of the eigenvalues λ as functions of the friction coefficient μ for a = 0, α = 1.0 × 10⁷ N/m. Mode 1 and Mode 2 are represented by the red and blue lines, respectively, as done in Fig. 24. The conjugates of the eigenvalues of Mode 1 and Mode 2 are represented by yellow and green lines, respectively

Appendix 6: Eigenvalue transition for contact spring stiffness

This appendix describes the details of the transition of the eigenvalues and mode shapes with respect to the contact spring stiffness α, as described in Sect. 4.2.

For the friction coefficient μ = 0 and contact damping β = 0, the transition of the real part of the eigenvalues and mode shapes with respect to the contact spring stiffness α is shown in Fig. 42; the eigenvalues not involved in the instability are omitted to improve visibility. In the figure, Mode 1 and Mode 2 are represented by red and blue lines, respectively, as done in Fig. 24, and the eigenvalues of Mode 2 are represented by dashed blue lines when they are real eigenvalues (the eigenvalues of Mode 2 are complex eigenvalues for α > 130). Figure 42 shows that Mode 1 is the mode in which the entire articulated frame is elastically deformed for α = 0. In addition, Mode 2 is a rigid body motion mode with a zero eigenvalue for α = 0; this mode exists for all pantographs due to the linkage mechanism.

Fig. 42

Transition of eigenvalues and mode shapes with respect to α (a = 0, μ = 0, β = 0). The co-ordinate systems on the mode shapes, which are omitted to improve visibility, are the same as those in Fig. 24