1 Introduction

As we know, spectral methods have been applied for obtaining approximate solutions to various differential equations. The philosophy of spectral methods is based on expressing the approximate solution of the problem as a truncated series of polynomials, which are often orthogonal. There are three known versions of spectral methods: Galerkin, tau, and collocation. The Galerkin method, in which we choose a suitable basis satisfying the initial and boundary conditions (Youssri et al. 2022; Atta et al. 2021, 2022a, b). On the other hand, when the basis functions do not satisfy the initial and boundary conditions, the tau method is the best choice, see for example Azimi et al. (2022c), Atta et al. (2020, 2022d) and Lima et al. (2022). The collocation method is the most popular technique and can be used for all differential equations. For some articles that utilize collocation approach, see Mahdy et al. (2022), Wu and Wang (2022), Taghipour and Aminikhah (2022a) and Atta et al. (2019).

Recently, the studies of fractional calculus have attracted the attention of many mathematicians and physicists. This branch studies the possibility of taking the real number powers of the differentiation and the integration operators. Many physical systems are modeled by fractional partial differential equations, see Moghaddam and Machado (2017) and Mostaghim et al. (2018). One of the biggest problems that contain fractional derivatives is the nonlinear TFPIDE. This problem appears in the modeling heat transfer materials with memory, population dynamics (Zheng et al. 2021), and nuclear reaction theory (Sanz-Serna 1988). Moreover, it has been studied numerically in some papers. For example, the authors in Guo et al. (2020) proposed a finite difference method for solving this problem. In Taghipour and Aminikhah (2022b), the nonlinear TFPIDE is solved by using Pell collocation method.

Great attention has been paid to various versions of Chebyshev polynomials due to their importance in analysis, especially in numerical analysis. There are six classes of Chebyshev polynomials: first, second, third, fourth, fifth, and sixth kinds (Masjed-Jamei 2006). There are many old and recent studies interested in these polynomials (Abd-Elhameed et al. 2016; Türk and Codina 2019; Abd-Elhameed and Youssri 2018, 2019; Abd-Elhameed 2021; Abd-Elhameed and Alkhamisi 2021; Atta et al. 2022a). In this paper, our main focus is on the first type of Chebyshev polynomials and their shifted ones. These polynomials enjoy various interesting and useful features, in addition to the high accuracy of the approximation and the simplicity of numerical methods established based on these polynomials.

The main aims of this paper may be summarized as follows:

  • By applying the spectral collocation method, we are developing a new technique for solving the nonlinear TFPIDE via new basis functions based on the SCP1K.

  • Discussion of the error analysis of the proposed method.

  • We are presenting some examples to check the applicability and accuracy of the scheme.

The paper has the following structure: Section 2 reports a summary of the Caputo fractional derivative and some definitions and formulas linked to the SCP1K. Section 3 is devoted to presenting a numerical technique to solve the nonlinear TFPIDE using the spectral collocation method. Section 4 focuses on studying the error analysis of the proposed double expansion. Section 5 gives some numerical examples to show the theoretical results. Finally, Sect. 6 reports conclusions.

2 Preliminaries and essential relations

The main objective of this study is to give a summary of the Caputo fractional derivative. In addition, some properties and formulas related to the family of orthogonal polynomials, namely, SCP1K.

2.1 Summary on the Caputo fractional derivative

Definition 1

(Podlubny 1998) The Caputo fractional derivative of order s is defined as:

$$\begin{aligned} D_{z}^{s}h(z)=\frac{1}{\Gamma (m-s)}\displaystyle \int _{0}^{z}(z-t)^{m-s-1}h^{(m)}(t){\textrm{d}}t,\quad s>0 ,\quad z>0, \end{aligned}$$

where \(m-1\leqslant s<m,\quad m\in {\mathbb {N}}.\)

The following properties are satisfied by the operator \(D_{z}^{s}\) for \(m-1\leqslant s<m,\quad m\in {\mathbb {N}},\)

$$\begin{aligned} D_{z}^{s}b= & {} 0, \quad (b \hbox { is a constant})\\ D_{z}^{s}\,z^m= & {} {\left\{ \begin{array}{ll} 0, &{} \text{ if } m\in {{\mathbb {N}}}_0 \quad \hbox {and} \quad m<\lceil s\rceil , \\ \frac{(m)!}{(m-s)!}\,z^{m-s}, &{} \text{ if } m\in {{\mathbb {N}}}_0 \quad \hbox {and} \quad m\ge \lceil s\rceil , \end{array}\right. } \end{aligned}$$

where \({{\mathbb {N}}}=\{1,2,3,\ldots \},\) \({{\mathbb {N}}}_0=\{0\}\cup {\mathbb {N}} \) and the notation \(\lceil \alpha \rceil \) denotes the ceiling function.

2.2 Some properties and formulas of the SCP1K

The SCP1K \(T^{*}_{m}(x)\) are defined as:

$$\begin{aligned} T^{*}_{m}(x):=T_{m}\left( \frac{2\,x}{\ell }-1\right) ,\quad m\ge 0,\quad x\in [0,\ell ], \end{aligned}$$

and satisfying this orthogonality relation (Abd-Elhameed et al. 2016)

$$\begin{aligned} \int _{0}^{\ell }\frac{1}{\sqrt{x\,(\ell -x)}}\,T^{*}_{m}(x) \,T^{*}_{n}(x)\,{\textrm{d}}x=h_{\ell ,m}\,\delta _{m,n}, \end{aligned}$$

where

$$\begin{aligned} h_{\ell ,m}={\left\{ \begin{array}{ll} \pi ,&{} \text{ if } \ m=0,\\ \frac{\pi }{2},&{} \text{ if } \ m>0, \end{array}\right. } \end{aligned}$$
(1)

and

$$\begin{aligned} \delta _{m,n}={\left\{ \begin{array}{ll} \displaystyle 1,&{} \text{ if } m=n,\\ 0,&{} \text{ if } m\not =n. \end{array}\right. } \end{aligned}$$

Moreover, \(T^{*}_{m}(x)\) can be generated using the recurrence formula shown below

$$\begin{aligned} T^{*}_{m+1}(x)=2\,\left( {\frac{2\,x}{\ell }-1}\right) \,T^{*}_{m}(x)-T^{*}_{m-1}(x), \end{aligned}$$

where \(T^{*}_{0}(x)=1,\quad T^{*}_{1}(x)=\frac{2\,x}{\ell }-1.\)

One of the most important formulas of \(T^{*}_{m}(x)\) is the power form representation and its inversion formula (Abd-Elhameed and Youssri 2018)

$$\begin{aligned} T^{*}_{m}(x)= & {} m\, \sum _{k=0}^m \frac{ (-1)^{m-k}\,2^{2\,k}\,(m+k-1)!}{\ell ^{k}\,(m-k)!\,(2\,k)!}\, x^k, \quad m>0,\\ x^j= & {} 2^{1-2\, j}\, (2\, j)!\, \ell ^j \sum _{p=0}^j \frac{\epsilon _{p}}{(j-p)! (j+p)!}\ T^{*}_{p}(x),\quad j\ge 0, \end{aligned}$$

where

$$\begin{aligned} \epsilon _{m}={\left\{ \begin{array}{ll} \frac{1}{2}, &{} \text{ if } m=0, \\ 1 ,&{} \text{ if } m>0. \end{array}\right. } \end{aligned}$$

3 Collocation technique for handling the nonlinear TFPIDE

Herein, a numerical technique is presented to solve the nonlinear TFPIDE using the spectral collocation method.

Consider the following nonlinear TFPIDE:

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$
(2)

assuming that the initial and boundary conditions are as follows:

$$\begin{aligned}{} & {} \chi (x,0)=0,\quad 0< x\le \ell ,\nonumber \\{} & {} \chi (0,t)=0,\quad \chi (\ell ,t)=0, \quad 0< t\le \tau , \end{aligned}$$

where g(x, t) is the source term.

3.1 Basis functions

Suppose that

$$\begin{aligned} \phi _m(t)=&t\,T^{*}_{m}(t),\\ \psi _n(x)=&x\,(\ell -x)\,T^{*}_{n}(x). \end{aligned}$$

Then the orthogonality relations of the last basis functions are given by:

$$\begin{aligned} \int _{0}^{\tau }\frac{1}{t^{\frac{5}{2}}\,(\tau -t)^{\frac{1}{2}}}\, \phi _p(t)\,\phi _q(t)\,{\textrm{d}}t=h_{\tau ,p}\,\delta _{p,q}, \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{\ell }\frac{1}{x^{\frac{5}{2}}\,(\ell -x)^{\frac{5}{2}}} \,\psi _p(x)\,\psi _q(x)\,{\textrm{d}}x=h_{\ell ,p}\,\delta _{p,q}, \end{aligned}$$

where \(h_{\ell ,p}\) is as given in (1).

Now, define

$$\begin{aligned}{} & {} P_{N}=\mathrm{{span}}\{{\psi _{p}(x)}\,{\phi _{q}(t)}:p,q=0,1 \ldots ,N\},\\{} & {} \tilde{P_{N}}=\{y\in P_{N}:y(0,t)=y(\ell ,t)=y(x,0)=0,\, 0<x\le \ell ,\,0<t\le \tau \}, \end{aligned}$$

then, any function \(\chi _{N}(x,t)\in \tilde{P_{N}}\) can be expanded as

$$\begin{aligned} \chi _{N}(x,t)=\sum _{i=0}^{N}\sum _{j=0}^{N}\nu _{ij}\,\psi _i(x)\, \phi _{j}(t)={\varvec{\Phi }}^{\textrm{T}}(t)\, {\hat{\varvec{\nu }}}\,{\varvec{\psi }}(x), \end{aligned}$$
(3)

where

$$\begin{aligned} {\varvec{\Psi }}(x)=[\psi _{0}(x),\psi _{1}(x),\ldots ,\psi _{N}(x)]^{\textrm{T}},\\ {\varvec{\Phi }}(t)=[\phi _{0}(t),\phi _{1}(t),\ldots ,\phi _{N}(t)]^{\textrm{T}}, \end{aligned}$$

and \({\hat{\varvec{\nu }}}=(\nu _{i,j})_{0\le i,j\le N}\) is the matrix of unknowns coefficients of order \((N+1)\times (N+1).\)

3.2 Some formulas concerned with the basis functions

Lemma 1

(Abd-Elhameed et al. 2016) The first-derivative of \(\psi _{r}(x)\) is

$$\begin{aligned} \frac{{\textrm{d}}\,{\psi _{r}(x)}}{{\textrm{d}}\,x}=\frac{4}{\ell }\, \sum _{\begin{array}{c} m=0\\ (r+m)\ \textrm{odd} \end{array}}^{r-1 }\epsilon _{m}\, (3\,r-2\,m)\,\psi _{m}(x)+{\zeta }_{r}(x), \end{aligned}$$
(4)

where

$$\begin{aligned} {\zeta }_{r}(x)={\left\{ \begin{array}{ll} \ell -2\,x, &{} \text{ if } r\ \text {even}, \\ -\ell , &{} \text{ if } r\ \text {odd}. \end{array}\right. } \end{aligned}$$

Theorem 1

The second-derivative of \(\psi _{j}(x)\) is

$$\begin{aligned} \frac{{\textrm{d}}^{2}\,{\psi _{j}(x)}}{{\textrm{d}}\,x^{2}}=\frac{4}{\ell ^{2}}\, \sum _{\begin{array}{c} m=0 \\ (j+m)\ \text {even} \end{array}}^{j-2 }\epsilon _{m}\, (j-m)\,\left( 5\, j^2-3\, m\, j+4\right) \,\psi _{m}(x)+o_{j}(x), \end{aligned}$$

where

$$\begin{aligned} o_{j}(x)=-2\, \left( 2 j^2+1\right) \,{\left\{ \begin{array}{ll} 1, &{} \text{ if } j\ \text {even}, \\ \frac{2\, x}{\ell }-1, &{} \text{ if } j\ \text {odd}. \end{array}\right. } \end{aligned}$$

Proof

Differentiating Eq. (4) with respect to the variable x,  one has

$$\begin{aligned} \frac{{\textrm{d}}^{2}\,{\psi _{j}(x)}}{{\textrm{d}}\,x^{2}}= & {} \frac{4}{\ell }\, \sum _{\begin{array}{c} m=0\\ (j+m)\ \text {odd} \end{array}}^{j-1 }\epsilon _{m}\, (3\,j-2\,m)\,\frac{{\textrm{d}}\,{\psi _{m}(x)}}{{\textrm{d}}\,x}+ \frac{{\textrm{d}}\,{\zeta }_{j}(x)}{{\textrm{d}}\,x}\nonumber \\= & {} \frac{16}{\ell ^2}\, \sum _{\begin{array}{c} m=0\\ (j+m) \ \text {odd} \end{array}}^{j-1 }\sum _{\begin{array}{c} k=0\\ (m+k)\ \text {odd} \end{array}}^{m-1 }\epsilon _{m}\,\epsilon _{k}\, (3\,j-2\,m)\, (3\,m-2\,k)\,\psi _{k}(x)\nonumber \\{} & {} +\frac{4}{\ell }\, \sum _{\begin{array}{c} m=0\\ (j+m) \ \text {odd} \end{array}}^{j-1 }\epsilon _{m}\, (3\,j-2\,m)\,{\zeta }_{m}(x)+{\bar{\zeta }}_{j}, \end{aligned}$$
(5)

where

$$\begin{aligned} {\bar{\zeta }}_{m}={\left\{ \begin{array}{ll} -2 &{} \text{ if } m\ \text {even}, \\ 0, &{} \text{ if } m\ \text {odd}. \end{array}\right. } \end{aligned}$$

Expanding the right-hand side of formula (5) and rearranging the similar terms lead to the following relation

$$\begin{aligned} \frac{{\textrm{d}}^{2}\,{\psi _{j}(x)}}{{\textrm{d}}\,x^{2}}=\frac{4}{\ell ^{2}}\, \sum _{\begin{array}{c} m=0\\ (j+m)\ \text {even} \end{array}}^{j-2 }\epsilon _{m}\,Y_{m,j}\,\psi _{m}(x)+\frac{4}{\ell }\, \sum _{\begin{array}{c} m=0\\ (j+m)\ \text {odd} \end{array}}^{j-1 }\epsilon _{m}\, (3\,j-2\,m)\,{\zeta }_{m}(x)+{\bar{\zeta }}_{j}, \end{aligned}$$

where

$$\begin{aligned} Y_{m,j}={\left\{ \begin{array}{ll} \sum _{k=\left\lfloor \frac{m}{2}\right\rfloor }^{\left\lfloor \frac{j-1}{2}\right\rfloor } 4 (3\, j-4\, k-2)\, (6\, k-2\, m+3) &{} \text{ if } j\ \text {even}, \\ \sum _{k=\left\lfloor \frac{m}{2}\right\rfloor }^{\left\lfloor \frac{j-2}{2}\right\rfloor } 4\, (3 \,j-4\, k-4)\, (6\, k-2 \,m+6), &{} \text{ if } j\ \text {odd}. \end{array}\right. } \end{aligned}$$

Now, with the aid of Maple program, the following relations can be summed to give the following reduced forms

$$\begin{aligned} Y_{m,j}=(j-m)\,\left( 5\, j^2-3\, m\, j+4\right) , \end{aligned}$$

and

$$\begin{aligned} \frac{4}{\ell }\, \sum _{\begin{array}{c} m=0\\ (j+m) \ \text {odd} \end{array}}^{j-1 }\epsilon _{m}\, (3\,j-2\,m)\,{\zeta }_{m}(x)={\left\{ \begin{array}{ll} 2-2\, \left( 2 j^2+1\right) , &{} \text{ if } j\ \text {even}, \\ -2\, \left( 2 j^2+1\right) \,(\frac{2\, x}{\ell }-1), &{} \text{ if } j\ \text {odd}, \end{array}\right. } \end{aligned}$$

and therefore, the following formula can be obtained

$$\begin{aligned} \frac{{\textrm{d}}^{2}\,{\psi _{j}(x)}}{{\textrm{d}}\,x^{2}}=\frac{4}{\ell ^{2}}\, \sum _{\begin{array}{c} m=0\\ (j+m)\ \text {even} \end{array}}^{j-2 }\epsilon _{m}\, (j-m)\,\left( 5\, j^2-3\, m\, j+4\right) \,\psi _{m}(x)+o_{j}(x), \end{aligned}$$

where

$$\begin{aligned} o_{j}(x)=-2\, \left( 2 j^2+1\right) \,{\left\{ \begin{array}{ll} 1, &{} \text{ if } j\ \text {even}, \\ \frac{2\, x}{\ell }-1, &{} \text{ if } j\ \text {odd}. \end{array}\right. } \end{aligned}$$

\(\square \)

Remark 1

Lemma 1 and Theorem 1 can be written in matrix form as:

$$\begin{aligned}{} & {} \frac{{\textrm{d}}\,{\varvec{{\psi }}(x)}}{{\textrm{d}}\,x}= {\textbf{Q}}\,{\varvec{\psi }}(x)+{\varvec{\zeta }}(x),\\{} & {} \frac{{\textrm{d}}^{2}\,{\varvec{{\psi }}(x)}}{{\textrm{d}}\,x^{2}}= {\textbf{M}}\,{\varvec{{\psi }}}(x)+{\textbf{o}}(x), \end{aligned}$$

where \({\textbf{Q}}=(q_{j,m})\) and \({\textbf{M}}=(m_{j,m})\) are matrices of order \((N+1) \times (N+1).\) In addition, \({\varvec{\zeta }}(x)=[\zeta _{0}(x),\zeta _{1}(x),\ldots ,\zeta _{N}(x)]^{\textrm{T}},\) \({\textbf{o}}(x)=[o_{0}(x),o_{1}(x),\ldots ,o_{N}(x)]^{\textrm{T}},\) and

$$\begin{aligned}{} & {} q_{j,m}=\frac{4\, \epsilon _{m}\, (3\,j-2\,m)}{\ell },\quad j>m,\quad (j+m)\ \text {odd},\\{} & {} m_{j,m}=\frac{4\,\epsilon _{m}\, (j-m)\,\left( 5\, j^2-3\, m\, j+4\right) }{\ell ^{2}},\quad j>m,\quad (j+m)\ \text {even}. \end{aligned}$$

Theorem 2

For \(0<\beta <1,\) the following approximation relation holds

$$\begin{aligned} \int _{0}^{t}(t-s)^{\beta -1}\,\phi _{i}(s)\,{\textrm{d}}s\approx \sum _{r=0}^N C_{i,r}\,\phi _{r}(t), \quad i=1,\ldots ,N, \end{aligned}$$

where

$$\begin{aligned} C_{i,r}=\sum _{k=0}^i {\frac{ \left( -1 \right) ^{r}\,\sqrt{\pi }\,\tau ^{k+\beta }\,(k+1)!\,\Gamma {(\beta )}\,\lambda _{k,i}\,\Gamma \left( \beta +k+\frac{1}{2} \right) \, \Gamma \left( r-k-\beta \right) }{h_{\tau ,r}\,(k+1+\beta )!\,\Gamma \left( -k-\beta \right) \, \Gamma \left( r+ 1+k+\beta \right) }}. \end{aligned}$$

Proof

Using the power form representation of \(\phi _{i}(t),\) we obtain

$$\begin{aligned} \int _{0}^{t}(t-s)^{\beta -1}\,\phi _{i}(s)\,{\textrm{d}}s= & {} \sum _{k=0}^i \lambda _{k,i}\,\int _{0}^{t}(t-s)^{\beta -1}\,s^{k+1}\,{\textrm{d}}s\nonumber \\= & {} \sum _{k=0}^i \lambda _{k,i}\,\frac{\Gamma {(\beta )}\,\Gamma {(k+2)} }{\Gamma {(k+\beta +2)}}\,t^{k+\beta +1}, \end{aligned}$$
(6)

where

$$\begin{aligned} \lambda _{k,i}=\frac{ (-1)^{i-k}\,2^{2\,k}\,i\,(i+k-1)!}{\tau ^{k}\,(i-k)!\,(2\,k)!}, \end{aligned}$$
(7)

we can approximate \(t^{k+\beta +1}\) in the form

$$\begin{aligned} t^{k+\beta +1}\approx \sum _{r=0}^N g^{k,\beta }_{r}\,\phi _{r}(t), \end{aligned}$$
(8)

where

$$\begin{aligned} g^{k,\beta }_{r}=\frac{1}{h_{\tau ,r}}\,\int _{0}^{\tau }\, \frac{t^{k+\beta +1}}{t^{\frac{5}{2}}\,(\tau -t)^{\frac{1}{2}}}\,\phi _r(t)\,{\textrm{d}}t. \end{aligned}$$
(9)

Using the power form representation of \(\phi _{i}(t),\) and integrating the right hand side of Eq. (9), yields

$$\begin{aligned} g^{k,\beta }_{r}=\frac{\sqrt{\pi }\,\tau ^{k+\beta }\,r}{h_{\tau ,r}}\sum _{n=0}^r \frac{2^{2\, n}\, (-1)^{r-n} (n+r-1)!\, \Gamma \left( k+n+\beta +\frac{1}{2}\right) }{(2\, n)! \,(r-n)!\, (k+n+\beta )!}. \end{aligned}$$
(10)

Now, to reduce the summation in the right-hand side of Eq. (10), set

$$\begin{aligned} H^{\beta }_{r,k}=\sum _{n=0}^r \frac{2^{2\, n}\, (-1)^{r-n} (n+r-1)!\, \Gamma \left( k+n+\beta +\frac{1}{2}\right) }{(2\, n)! \,(r-n)!\, (k+n+\beta )!}, \end{aligned}$$

and using Zeilberger algorithm (Koepf 1998) to show that \(H^{\beta }_{r,k},\) satisfies the following recurrence relation

$$\begin{aligned}{} & {} -r\,(k+\beta -r)\,H^{\beta }_{r,k}+(r+1+k+\beta )\,(r+1)H^{\beta }_{r+1,k}=0,\\{} & {} \quad H^{\beta }_{1,k}={\frac{ \left( k+\beta \right) \Gamma \left( \beta +k+\frac{1}{2} \right) }{\Gamma \left( k+\beta +2 \right) }}, \end{aligned}$$

which can be exactly solved to give

$$\begin{aligned} H^{\beta }_{r,k}={\frac{ \left( -1 \right) ^{r}\,\Gamma \left( \beta +k+\frac{1}{2} \right) \, \Gamma \left( r-k-\beta \right) }{r\,\Gamma \left( -k-\beta \right) \, \Gamma \left( r+ 1+k+\beta \right) }}. \end{aligned}$$

And therefore, Eq. (10) becomes

$$\begin{aligned} g^{k,\beta }_{r}={\frac{ \left( -1 \right) ^{r}\,\sqrt{\pi }\,\tau ^{k+\beta }\,\Gamma \left( \beta +k+\frac{1}{2} \right) \, \Gamma \left( r-k-\beta \right) }{h_{\tau ,r}\,\Gamma \left( -k-\beta \right) \, \Gamma \left( r+ 1+k+\beta \right) }}. \end{aligned}$$

Now, inserting Eq. (8) into Eq. (6), the desired result of Theorem 2 may be obtained. \(\square \)

Lemma 2

For \(0<\beta <1,\) the following approximation relation holds

$$\begin{aligned} \int _{0}^{t}(t-s)^{\beta -1}\,\phi _{0}(s)\,{\textrm{d}}s\approx \sum _{r=0}^N {\bar{C}}_{0,r}\,\phi _{r}(t), \end{aligned}$$

where

$$\begin{aligned} {\bar{C}}_{0,r}={\frac{ \left( -1 \right) ^{r}\,\sqrt{\pi }\,\tau ^{\beta }\,\Gamma \left( \beta +\frac{1}{2} \right) \, \Gamma \left( r-\beta \right) }{\beta \,(\beta +1)\,h_{\tau ,r}\,\Gamma \left( -\beta \right) \, \left( r+ \beta \right) ! }}. \end{aligned}$$

Remark 2

Theorem 2 and Lemma 2 can be combined to give the following matrix form

$$\begin{aligned} \int _{0}^{t}(t-s)^{\beta -1}\,{\varvec{\phi }}({\textbf{t}}){\textrm{d}}s\approx {\textbf{C}}^{\beta }\,{\varvec{\phi }}({\textbf{t}}), \end{aligned}$$

where

$$\begin{aligned} {\textbf{C}}^{\varvec{\beta }}= \begin{bmatrix} {\bar{C}}_{0,0} &{} {\bar{C}}_{0,1} &{} \dots &{} {\bar{C}}_{0,N} \\ C_{1,0} &{} C_{1,1} &{} \dots &{} C_{1,N} \\ C_{2,0} &{} C_{2,1} &{} \dots &{} C_{2,N} \\ \vdots &{} \vdots &{} \dots &{} \vdots \\ C_{N,0} &{} C_{N,1} &{} \dots &{} C_{N,N} \end{bmatrix}_{(N+1 \times N+1)}. \end{aligned}$$

Theorem 3

For \(0<\alpha <1,\) the following approximation formula is valid

$$\begin{aligned} D_{t}^{\alpha }\phi _{i}(t)\approx \sum _{r=0}^N A_{i,r}\,\phi _{r}(t),\quad i=1,\ldots ,N, \end{aligned}$$

where

$$\begin{aligned} A_{i,r}=\sum _{k=0}^i {\frac{ \left( -1 \right) ^{r}\,\sqrt{\pi }\,\tau ^{k-\alpha }\,(k+1)!\,\lambda _{k,i}\,\Gamma \left( k-\alpha +\frac{1}{2} \right) \, \Gamma \left( r-k+\alpha \right) }{h_{\tau ,r}\,(k+1-\alpha )!\,\Gamma \left( -k+\alpha \right) \, \Gamma \left( r+ 1+k-\alpha \right) }}. \end{aligned}$$

Proof

The application of the operator \(D_{t}^{\alpha }\) on the power form representation of \(\phi _{i}(t),\) enables us to write

$$\begin{aligned} D_{t}^{\alpha }\phi _{i}(t)= \sum _{k=0}^i \lambda _{k,i}\,\frac{(k+1)! }{(k+1-\alpha )!}\,t^{k+1-\alpha }, \end{aligned}$$

where \(\lambda _{k,i}\) is defined in (7).

Now, using similar steps as in follow in Theorem 2 to approximate \(t^{k+1-\alpha },\) the results in Theorem 3 can be easily obtained. \(\square \)

Lemma 3

For \(0<\alpha <1,\) the following approximation formula is valid

$$\begin{aligned} D_{t}^{\alpha }\phi _{0}(t)\approx \sum _{r=0}^N {\bar{A}}_{0,r}\,\phi _{r}(t), \end{aligned}$$

where

$$\begin{aligned} {\bar{A}}_{0,r}= {\frac{ \left( -1 \right) ^{r}\,\sqrt{\pi }\,\tau ^{-\alpha }\,\Gamma \left( -\alpha +\frac{1}{2} \right) \, \Gamma \left( r+\alpha \right) }{h_{\tau ,r}\,\Gamma \left( \alpha \right) \,(1-\alpha )!\, \Gamma \left( r+ 1-\alpha \right) }}. \end{aligned}$$

Remark 3

Theorem 3 and Lemma 3 can be combined to give the following matrix form

$$\begin{aligned} D_{t}^{\alpha }{\varvec{\phi }}({\textbf{t}})\approx {\textbf{D}}^{\varvec{\alpha }}\,{\varvec{\phi }}({\textbf{t}}), \end{aligned}$$

where

$$\begin{aligned} {\textbf{D}}^{\varvec{\alpha }}= \begin{bmatrix} {\bar{A}}_{0,0} &{} {\bar{A}}_{0,1} &{} \dots &{} {\bar{A}}_{0,N} \\ A_{1,0} &{} A_{1,1} &{} \dots &{} A_{1,N} \\ A_{2,0} &{} A_{2,1} &{} \dots &{} A_{2,N} \\ \vdots &{} \vdots &{} \dots &{} \vdots \\ A_{N,0} &{} A_{N,1} &{} \dots &{} A_{N,N} \end{bmatrix}_{(N+1 \times N+1)}. \end{aligned}$$

3.3 Collocation solution for nonlinear TFPIDE

Now, we are in a position to deduce our collocation scheme for treating the nonlinear TFPIDE in (2).

Remarks 1,2 and 3 enable us to get the following approximations after approximating \(\chi (x,t)\) as in (3)

$$\begin{aligned}{} & {} {D_{t}^{\alpha }}\chi _{N}(x,t)\approx {\varvec{\Phi }}^{\textrm{T}}(t)\,{{\mathbf {{D}}}^{\varvec{\alpha }}}^{\textrm{T}}\, {\hat{\varvec{\nu }}}\,{\varvec{\psi }}(x),\nonumber \\{} & {} \chi _{N}(x,t)\,{\chi _{N}}_{x}(x,t)=\left[ {\varvec{\Phi }}^{\textrm{T}}(t)\, {\hat{\varvec{\nu }}}\,{\varvec{\psi }}(x)\right] \, \left[ {\varvec{\Phi }}^{\textrm{T}}(t)\, {\hat{\varvec{\nu }}}\,({\textbf{Q}}\, {\varvec{\psi }}(x)+{\varvec{\zeta }}(x))\right] ,\nonumber \\{} & {} \int _{0}^{t}(t-s)^{\beta -1}\,{\chi _{N}}_{xx}(x,s)\,{\textrm{d}}s \approx {\varvec{\Phi }}^{\textrm{T}}(t)\,{{\mathbf {{C}}}^{\varvec{\beta }}}^{\textrm{T}}\, {\hat{\varvec{\nu }}}\,({\textbf{M}}\,{\varvec{{\psi }}}(x)+{\textbf{o}}(x)). \end{aligned}$$
(11)

With the aid of the last relations (11), the residual \({\textbf{R}}(x,t)\) of Eq. (2) can be written as

$$\begin{aligned} {\textbf{R}}(x,t)= & {} {\varvec{\Phi }}^{\textrm{T}}(t)\, {{\mathbf {{D}}}^{\varvec{\alpha }}}^{\textrm{T}}\, {\hat{\varvec{\nu }}}\,{\varvec{{\psi }}}(x)+\left[ {\varvec{\Phi }}^{\textrm{T}}(t)\, {\hat{\varvec{\nu }}}\,{\varvec{{\psi }}}(x)\right] \, \left[ {\varvec{\Phi }}^{\textrm{T}}(t)\, {\hat{\varvec{\nu }}}\,({\textbf{Q}}\,{\varvec{{\psi }}}(x)+{\varvec{\zeta }}(x))\right] \nonumber \\{} & {} -{\varvec{\Phi }}^{\textrm{T}}(t)\,{{\mathbf {{C}}}^{\varvec{\beta }}}^{\textrm{T}}\, {\hat{\varvec{\nu }}}\,({\textbf{M}}\,{\varvec{{\psi }}}(x)+{\textbf{o}}(x))-g(x,t). \end{aligned}$$
(12)

Now, we enforce Eq. (12) to be satisfied exactly at the following roots

$$\begin{aligned} x_r&=\frac{1}{2} \left( 1+\cos \left( \frac{(2\,r+1)\,\pi }{2\,(N+1)} \right) \right) ,\quad r=0,1,\ldots ,N,\\ t_s&=\frac{1}{2} \left( 1+\cos \left( \frac{(2\,s+1)\,\pi }{2\,(N+1)}\right) \right) , \quad s=0,1,\ldots ,N, \end{aligned}$$

to obtain

$$\begin{aligned} {\textbf{R}}(x_{r},t_{s})\approx 0. \end{aligned}$$
(13)

Equation (13), produce a nonlinear system of algebraic equations of dimension \((N+1)\times (N+1)\) in the unknown expansion coefficients \(\nu _{ij}\), that may be solved using Newton’s iterative method.

figure a

3.4 Transformation to homogeneous conditions

assuming that the nonlinear TFPIDE

$$\begin{aligned} {D_{t}^{\alpha }}y(x,t)+y(x,t)\,y_{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,y_{xx}(x,s)\,{\textrm{d}}s+\ddot{g}(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

subject to the non-homogeneous initial and boundary conditions

$$\begin{aligned}{} & {} y(x,0)=f(x),\quad 0<x\le \ell ,\\{} & {} y(0,t)=Z_{1}(t), \quad y(\ell ,t)=Z_{2}(t), \quad 0< t\le \tau . \end{aligned}$$

Using the following transformation:

$$\begin{aligned} \chi (x,t)=y(x,t)-\left( 1-\frac{x}{\ell }\right) \, \left( Z_{1}(t)-f(0)\right) -\frac{x }{\ell }\,\left( Z_{2}(t)-Z_{2}(0)\right) -f(x), \end{aligned}$$

where \(f(0)=Z_{1}(0),\) the nonlinear TFPIDE (2), with non-homogeneous conditions will be transformed into its homogeneous ones.

4 Error analysis

This section is confined to study the error analysis of the double expansion of new basis based on SCP1K used in approximation. This study is built on the results given in Ref. Abd-Elhameed et al. (2016). The expression \(z\lessapprox {\bar{z}}\) means \(z\le n\,{\bar{z}},\) where n is a generic positive constant independent of N and of any function.

Lemma 4

(Stewart 2015) Let f(x) be continuous,  positive and decreasing function for \(x\ge n.\) If \(f(k)=a_{k}\) such that \(\sum {a_{n}}\) is convergent and \(R_{n}=\sum _{k=n+1}^{\infty }a_{k},\) then \(R_{n}\le \int _{n}^{\infty }f(x){\textrm{d}}\,x.\)

Theorem 4

Any function \(\chi (x,t)=x\,t\,(\ell -x)\,g_{1}(x)\,g_{2}(t)\in \tilde{P_{N}},\) with \(g_{1}(x)\) and \(g_{2}(t)\) have bounded second derivative can be expanded as : 

$$\begin{aligned} \chi (x,t)=\sum _{r=0}^{\infty }\sum _{s=0}^{\infty }\nu _{ij}\,\psi _i(x)\,\phi _{j}(t). \end{aligned}$$
(14)

The above series is uniformly convergent. Moreover,  the expansion coefficients in (14) satisfy : 

$$\begin{aligned} |\nu _{rs}|\lessapprox \frac{1}{r^{2}\,s^{2}}, \quad \forall \ r,s\ge 2. \end{aligned}$$

Proof

Based on the following separability \(\chi (x,t)=x\,t\,(\ell -x)\,g_{1}(x)\,g_{2}(t)\) and imitating similar steps to those given in Abd-Elhameed et al. (2016), the desired result may be obtained. \(\square \)

Theorem 5

If \(\chi (x,t)\) satisfies the hypothesis of Theorem 4, and if \(\chi _{N}(x,t)=\sum _{r=0}^{N} \sum _{s=0}^{N}\nu _{rs}\, \psi _r(x)\,\phi _{s}(t),\) then the following truncation error estimate is satisfied

$$\begin{aligned} |\chi (x,t)-\chi _{N}(x,t)|\lessapprox \frac{1}{N}. \end{aligned}$$
(15)

Proof

According to the definitions of \(\chi (x,t)\) and \(\chi _{N}(x,t),\) we have

$$\begin{aligned} |\chi (x,t)-\chi _{N}(x,t)|\le & {} \left| \sum _{r=2}^{N}\sum _{s=N+1}^{\infty }\nu _{rs}\, \psi _r(x)\,\phi _{s}(t)\right| +\left| \sum _{r=N+1}^{\infty } \sum _{s=2}^{\infty }\nu _{rs}\,\psi _r(x)\,\phi _{s}(t)\right| \\{} & {} +\left| \sum _{s=N+1}^{\infty }[\,\nu _{0s}\,\psi _{0}(x)+\nu _{1s} \,\psi _{1}(x)\,]\,\phi _{s}(t)\right| \\{} & {} +\left| \sum _{r=N+1}^{\infty } [\,\nu _{r0}\,\phi _{0}(t)+\nu _{r1}\,\phi _{1}(t)\,]\,\psi _{r}(x)\right| . \end{aligned}$$

As in Theorem 4 followed in Abd-Elhameed et al. (2016), it is easy to obtain the following inequalities

$$\begin{aligned}{} & {} |\nu _{0s}|\lessapprox \frac{1}{s^{2}}, \quad |\nu _{1s}|\lessapprox \frac{1}{s^{2}},\nonumber \\{} & {} |\nu _{r0}|\lessapprox \frac{1}{r^{2}}, \quad |\nu _{r1}|\lessapprox \frac{1}{r^{2}}. \end{aligned}$$
(16)

Now, the direct application of inequalities (16), Theorem 4 and the two identities

$$\begin{aligned}{} & {} |\psi _r(x)|\lessapprox 1,\\{} & {} |\phi _s(t)|\lessapprox 1, \end{aligned}$$

lead to

$$\begin{aligned} |\chi (x,t)-\chi _{N}(x,t)|\le&\, \sum _{r=2}^{N}\sum _{s=N+1}^{\infty }\left| \nu _{rs}\right| + \sum _{r=N+1}^{\infty }\sum _{s=2}^{\infty }\left| \nu _{rs}\right| +\sum _{s=N+1}^{\infty }[\,\left| \nu _{0s}\right| +\left| \nu _{1s} \right| \,]+\sum _{r=N+1}^{\infty }[\,\left| \nu _{r0}\right| +\left| \nu _{r1}\right| \,],\\ \lessapprox&\,\sum _{r=2}^{N}\sum _{s=N+1}^{\infty }\frac{1}{r^{2}\,s^{2}}+ \sum _{r=N+1}^{\infty }\sum _{s=2}^{\infty }\frac{1}{r^{2}\,s^{2}} +\sum _{s=N+1}^{\infty }\frac{1}{s^{2}}+\sum _{r=N+1}^{\infty }\frac{1}{r^{2}}. \end{aligned}$$

Using Lemma 4 along with the following approximation

$$\begin{aligned} \sum _{i=a+1}^{b}f(i)\le \int _{x=a}^{b}f(x)\,{\textrm{d}}x, \end{aligned}$$

where f is decreasing function, one has

$$\begin{aligned}{} & {} |\chi (x,t)-\chi _{N}(x,t)|\lessapprox \int _{1}^{N}\int _{N}^{\infty }\frac{1}{x^{2}\,y^{2}}\,{\textrm{d}}x\,{\textrm{d}}y+ \int _{N}^{\infty }\int _{1}^{\infty }\frac{1}{x^{2}\,y^{2}}\,{\textrm{d}}x\,{\textrm{d}}y \\{} & {} \quad +\int _{N}^{\infty }\frac{1}{y^{2}}\,{\textrm{d}}y+\int _{N}^{\infty }\frac{1}{x^{2}} \,{\textrm{d}}x,\lessapprox \frac{1}{N}. \end{aligned}$$

This completes the proof of Theorem 5. \(\square \)

Remark 4

As shown in Theorem 5, we find that the truncation error estimate (15) leads to an exponential rate of convergence.

5 Illustrative examples

In this section, we apply our approximate spectral scheme which is presented in Sect. 3 on four examples. All results show that our method is applicable and effective when we compare it with results in Taghipour and Aminikhah (2022b).

Example 1

(Taghipour and Aminikhah 2022b; Guo et al. 2020) Consider the following equation

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

along with the following initial and boundary conditions:

$$\begin{aligned}{} & {} \chi (x,0)=0, \quad 0<x\le 1,\\{} & {} \chi (0,t)=0,\quad \chi (1,t)=0, \quad 0< t\le 1, \end{aligned}$$

where

$$\begin{aligned} g(x,t)=\sin (\pi \, x)\, \left( \frac{6\, t^{3-\alpha }}{\Gamma (4-\alpha )}+\frac{\left( 6\, \pi ^2 \Gamma (\beta )\right) \, t^{\beta +3}}{\Gamma (\beta +4)}+\pi \, t^6 \,\cos (\pi \, x)\right) . \end{aligned}$$

The exact solution of this problem is \(\chi (x,t)=t^{3}\,\sin (\pi \,x).\)

Tables 1 and 2 show the comparison of the absolute errors between our method at \(N=12\) with the method developed in Taghipour and Aminikhah (2022b) at different values of \(\alpha \) and \(\beta .\) In addition, Fig. 1 shows the \(L_{\infty }\) error for the case corresponding to \(\alpha =0.7,\) \(\beta =0.4\) and \(\alpha =0.3,\) \(\beta =0.8\) at \(N=12.\) It can be seen that the approximate solution is quite near to the precise one.

Table 1 Comparison of absolute errors for Example 1
Full size table
Table 2 Comparison of absolute errors for Example 1
Full size table
Fig. 1
figure 1

The \(L_{\infty }\) error of Example 1

Full size image

Example 2

(Taghipour and Aminikhah 2022b) Consider the following equation with the exact solution \(\chi (x,t)=t^2 \,x \,(1-x)\)

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

along with the following initial and boundary conditions:

$$\begin{aligned}{} & {} \chi (x,0)=0, \quad 0<x\le 1,\\{} & {} \chi (0,t)=0,\quad \chi (1,t)=0, \quad 0< t\le 1, \end{aligned}$$

where

$$\begin{aligned} g(x,t)=\frac{4\, t^{\beta +2}}{\beta ^3+3\, \beta ^2+2 \,\beta }+\frac{(2\, x\, (1-x))\, t^{2-\alpha }}{\Gamma (3-\alpha )}+t^4\, x\, (1-x) \,(1-2\, x). \end{aligned}$$

Table 3 shows the absolute errors at different values of \(\alpha \) and \(\beta \) at \(N=1.\) The results in the last table show that our method is more accurate when we compare our results with those obtained in table 2 at Taghipour and Aminikhah (2022b).

Table 3 The absolute errors of Example 2
Full size table

Example 3

(Akram et al. 2021; Guo et al. 2020) Consider the following equation

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

along with the following initial and boundary conditions:

$$\begin{aligned}{} & {} \chi (x,0)=(1-x)^2 x^2, \quad 0<x\le 1,\\{} & {} \chi (0,t)=0,\quad \chi (1,t)=0, \quad 0< t\le 1, \end{aligned}$$

where

$$\begin{aligned} g(x,t)= & {} 2\, \left( t^{5/2}+1\right) ^2\, (1-x)^3\, x^3\, (1-2 x)+\frac{ \Gamma \left( \frac{7}{2}\right) }{\Gamma \left( \frac{7}{2}-\alpha \right) }\,(1-x)^2\, x^2\, t^{\frac{5}{2}-\alpha }\\{} & {} -2\, \left( 6\, x^2-6\, x+1\right) \, \left( \frac{\Gamma \left( \frac{7}{2}\right) \,\Gamma (\beta )}{\Gamma \left( \beta +\frac{7}{2}\right) }\, t^{\beta +\frac{5}{2}}+\frac{t^{\beta }}{\beta }\right) . \end{aligned}$$

The exact solution of this problem is \(u(x,t)=\left( t^{\frac{5}{2}}+1\right) \, x^2 \,(1-x)^2.\)

Table 4 show the comparison of the absolute errors between our method at \(N=12\) with the method developed in Akram et al. (2021) at \(\beta =0.15\) and different values of \(\alpha .\) Also, Fig. 2 shows the \(L_{\infty }\) error for the case corresponding to \(\alpha =0.95,\) \(\beta =0.15\) and \(N=12.\)

Table 4 Comparison of absolute errors of Example 3
Full size table
Fig. 2
figure 2

The \(L_{\infty }\) error of Example 3

Full size image

Example 4

(Taghipour and Aminikhah 2022b) Consider the following equation

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

along with the following initial and boundary conditions:

$$\begin{aligned}{} & {} \chi (x,0)=0, \quad 0<x\le 1,\\{} & {} \chi (0,t)=t^3,\quad \chi (1,t)=e \,t^3, \quad 0< t\le 1, \end{aligned}$$

where

$$\begin{aligned} g(x,t)=\frac{\left( 6\, e^x\right) \, t^{3-\alpha }}{\Gamma (4-\alpha )}-\frac{6\, e^x\, \Gamma (\beta ) t^{\beta +3}}{\Gamma (\beta +4)}+t^6\, e^{2\, x}. \end{aligned}$$

The exact solution of this problem is \(\chi (x,t)=t^3\, e^x.\)

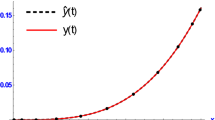
Table 5 shows the absolute errors at \(N=9,\) \(N=12\) and \(\alpha =\beta =0.5.\) Also Table 6 presents the maximum absolute errors at \(\alpha =0.9\) and \(\beta =0.3.\) The results in Tables 5 and 6 show that our method is more accurate when we compare our results with those obtained in table 4 at Taghipour and Aminikhah (2022b). Figure 3 indicates the advantage of our method for obtaining the maximum absolute errors at small values of N. This figure proves that our method is in good agreement with the analytical solution.

Table 5 The absolute errors of Example 4
Full size table
Table 6 Maximum absolute errors of Example 4
Full size table

Example 5

(Taghipour and Aminikhah 2022b) Consider the following equation

$$\begin{aligned} {D_{t}^{\alpha }}\chi (x,t)+\chi (x,t)\,\chi _{x}(x,t)= \int _{0}^{t}(t-s)^{\beta -1}\,\chi _{xx}(x,s)\,{\textrm{d}}s+g(x,t), \quad 0<\alpha ,\beta <1, \end{aligned}$$

along with the following initial and boundary conditions:

$$\begin{aligned}{} & {} \chi (x,0)=0, \quad 0<x\le 1,\\{} & {} \chi (0,t)=t^2,\quad \chi (1,t)=0, \quad 0< t\le 1, \end{aligned}$$

where

$$\begin{aligned} g(x,t)= & {} \frac{t^{2-\alpha } (2 \,(1-x)\, \cos (x))}{\Gamma (3-\alpha )}-\frac{\left( 2\, \Gamma (\beta )\, t^{\beta +2}\right) \, (2\, \sin (x)+(x-1) \,\cos (x))}{\Gamma (\beta +3)}\\{} & {} +t^4\, (1-x)\, \cos (x)\, (x \sin (x)-\sin (x)-\cos (x)). \end{aligned}$$

The exact solution of this problem is \(\chi (x,t)=t^2 \,(1-x)\, \cos (x).\)

Fig. 3
figure 3

The maximum absolute errors of Example 4

Full size image
Fig. 4
figure 4

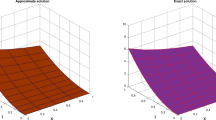
(Left) Approximate solution, (Right) \(L_{\infty }\) error for Example 5

Full size image
Table 7 The absolute errors of Example 5
Full size table
Table 8 The absolute errors of Example 5
Full size table
Table 9 The \(L_{2}\) error of Example 5
Full size table

Figure 4 shows the approximate solution and \(L_{\infty }\) error for \(\alpha =\beta =0.7,\) at \(N=10.\) In addition, Table 7 displays the absolute errors at \(\alpha =0.6,\) \(\beta =0.9\) and \(N=10.\) Moreover, Table 8 shows the absolute errors at different values of N when \(\alpha =0.3,\) \(\beta =0.8.\) Finally, Table 9 presents a comparison of \(L_{2}\) error at \(\alpha =\beta =0.5.\) It can be seen that the approximate solution is quite near to the precise one.

6 Concluding remarks

This paper presents suitable basis functions to solve the nonlinear TFPIDE subject to homogeneous initial and boundary conditions. Based on this basis, we developed new operational matrices of differentiation and integration that enable us to get the approximate spectral solution. Moreover, the error analysis of the suggested approximate double expansion was studied in depth. In the end, the proposed numerical examples illustrated the presented technique’s high accuracy, applicability, and efficiency. As an expected future work, we aim to employ the developed theoretical results in this paper along with suitable spectral methods to treat some other problems numerically. All codes were written and debugged by Mathematica 11 on HP Z420 Workstation, Processor: Intel (R) Xeon(R) CPU E5-1620—3.6 GHz, 16 GB Ram DDR3, and 512 GB storage.