1 Mean stress and residual stress in fatigue design

1.1 Residual stress in cyclically loaded components

Residual stresses are the consequence of a heterogeneous plastic deformation. In the context of fatigue of welded structures, the term of residual stress refers to macroscopic residual stresses [1, 2]. These are homogenously distributed over several grains and result from the thermally induced extension and compression of heated material volumes. This extension and compression is restrained by colder adjacent material resulting in locally differing plastic strains after cooling to ambient temperature. Furthermore, various materials, e.g., structural steels, show the phenomena of a phase transformation during heating and cooling, which goes along with a change of the packing density and thus leads to restrained expansion [3, 4]. The mechanisms behind welding residual stress generation are nowadays well understood. Details on different effects and their interaction can be found in the literature, for instance, amongst others [4,5,6,7,8,9,10,11,12,13].

Next to residual stress origins, structural engineers often distinguish the residual stress equilibrium in welded components [14]. Hereby, “short and medium range” residual stresses (equilibrium over sheet thickness respectively the weld cross section) are to expect in most small-scale laboratory specimens. “Long range” residual stress (equilibrium in the entire component) can be treated as load mean stress due to its similarity to membrane stresses [15, 16]. IIW’s mean stress correction treats such “long range” equilibriums as residual stress typically for restrained structures, for instance, resulting from repair welds or on-site assembly joints.

The general residual stress effect on fatigue strength of welded components is understood [17, 18]. Tensile residual stress decreases fatigue strength, while compressive residual stress causes an increase of fatigue life. It was observed that relaxation of residual stress under mechanical loading needs to be addressed if this effect is to be quantified specifically. Residual stress has a lower impact on fatigue strength at high stress levels than at low stress levels [19, 20]. This includes both high tensile mean stress and high stress ranges corresponding to low numbers of tolerable load cycles. The fundamental cause of these phenomena is the relaxation of residual stress [1, 21, 22]. The criterion for yielding is, next to the yield limit of the material and the load level itself, the stress concentration at the weld. Local yielding causes plastic strains resulting in changes of the residual stress field. General behavior of residual stress under mechanical loading can be classified according to [23] in either static or cyclic residual stress relaxation or various combinations of those. The principal mechanism of residual stress relaxation in welded steels under cyclic loading is the static residual stress relaxation during the first full load cycle [24, 25]. Cyclic softening may further increase the magnitude of cyclic residual stress relaxation but is usually of second order compared with initial loading effects.

1.2 Interaction of residual stress and mean stress

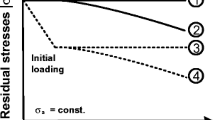
Mean stress influence on fatigue strength is commonly described by means of the sensitivity to mean stress m*. This value describes the decrease of fatigue strength from pure alternating loading (stress ratio R = σmin/σmax = − 1) to pure pulsating tension (R = 0) and it is valid between −∝ ≤ R ≤ 0 [26]. Tests using un-notched and annealed specimens proved an increase of m* with increasing ultimate strength [4], solid line in Fig. 1. According to the graph, unalloyed structural steels, widely used for welded structures and components, theoretically show 0.1 ≤ m* ≤ 0.3 (500 MPa ≤ Rm ≤ 1200 MPa, Rm ultimate strength) in an un-notched condition. Welds in structures are geometric notches at weld toe and weld root. However, the sensitivity to mean stress of different weld joint types [27,28,29,30] was determined to comparable values of 0.2 ≤ m* ≤ 0.44 [31] disregarding the residual stress condition. Similar results were obtained for welded joints made from a wide range of unalloyed structural steels with varying ultimate strengths [20]. According to these studies, the sensitivity to mean stress of welded structures appears to be independent of the steel grade. This result is contrary to the behavior of un-notched specimens and can be explained by the local microstructure in the vicinity of the fatigue critical heat-affected zone (HAZ) at the weld toe and weld root respectively. After welding, the local microstructure and mechanical properties of the HAZ in unalloyed structural steels of varying base metal strengths are comparable to each other in many cases due to similar chemical composition and the welding thermal cycle. The similarity of m* of welded joints made from varying steel grades may also be a consequence of disregarding residual stress conditions. Usually, test results are based on laboratory tests using relatively small specimens neglecting the individual residual stress conditions. This indicates either a generally low influence of residual stress on m* or, more likely, a low residual stress effect due to low residual stress magnitudes in the small-scale specimens used. The only derivation from this behavior can be observed using specimens of the longitudinal stiffener type, containing experimentally proven high tensile residual stress [32,33,34]. Longitudinal stiffeners show mean stress–dependent fatigue strength after thermal annealing but not in the as-welded condition [35].

Fig. 1
figure 1

Sensitivity to mean stress m* and sensitivity to residual stress m of steels in dependence of ultimate strength Rm, according to [4]

Full size image

Extensive literature research has led to m* values of m* = 0.33 [36] respectively m* = 0.2 [37] for fatigue design of thermally annealed weldments. The m* value of these annealed specimens depends on the R ratio applied which is also considered by design codes, for instance, the FKM guideline [38]. The magnitude of m* = 0.33 at −∝ ≤ R ≤ 0 is higher than between 0 ≤ R ≤ 0.5 (m* = 0.1). Mean stress–independent fatigue strength is generally assumed at stress ratios above R = 0.5.

The sensitivity to residual stress m also increases with increasing ultimate strength Rm, dashed line in Fig. 1. The effects of residual stress are smaller in comparison with mean stress in equivalent steels. This is explained by a possible relaxation of residual stress under fatigue loading [19]. Thus, the dependence of m on the ultimate steel strength is a result of increasing stability of residual stress in high-strength steels.

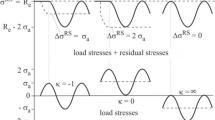
Gurney has introduced the model of constant upper load stress describing the phenomenon of mean stress–independent fatigue strength of residual stress–containing weldments [17]. Basically, the assumption is that the presence of tensile residual stress in the magnitude of the yield strength σy is a result of high shrinkage constraints in welded structures. This results in a constantly high “effective” maximum stress (sum of residual stress and load stress) in the magnitude of the yield limit due to load-induced plasticity even though residual stress may have been reduced. Accordingly, this approach does not distinguish between load mean stress and residual stress although the following significant differences exist: Mean stress can be locally increased due to notch effects and is not subject to change due to local plasticity, while residual stress may be relaxed or enhanced [4]. More specific, residual stress may be treated similar to mean stress in the case of residual stress stability under mechanical loading [20]. Based on these newer findings, residual stress may be treated as cyclically stable in constant amplitude load conditions at load numbers of N = 10,000 (and higher) where static and cyclic relaxation already has mainly occurred. By means of this assumption one can describe the decrease of the endurance limit with increasing combined effects of stabilized residual stress and mean stress (Fig. 2). Concluding, residual stress effects can only be estimated under consideration of residual stress relaxation. Further, small magnitudes (small in relation to the yield limit) of cyclically stable residual stress may have severe influence on the fatigue strength. Nowadays, residual stress fields can be determined quantitatively quite accurate by experiments or numerical simulations [39,40,41] leading to a demand for a more precise treatment of residual stress and mean stress in the nominal stress concept.

Fig. 2
figure 2

Decrease of the endurance limit of butt welds with increasing combined effects of load mean stress and residual stress, according to [20]. σv: calculated van Mises stress from transverse and longitudinal residual stress

Full size image

From the aforementioned context, it becomes obvious that m* and m interact with each other. More precise, m* can only be determined from thermally stress-relieved specimens without any residual stress influence while m can only be determined at a stress ratio of R = − 1 without interference of load mean stress. In typical welds, both residual stress and load mean stress are normally present and must therefore be considered together. As a consequence, the underlying investigation uses the approach of “effective mean stress,” where both the load mean stress and the cyclically stabilized residual stress are taken into account (see Section 1.4).

1.3 Mean stress correction in current fatigue design concepts

Fatigue design based on nominal stress is widely used in the welding industry due to its simplicity, time efficiency, reliability, and applicability to most standard design cases. Structures for which the definition of nominal stress becomes more difficult can be designed based on local concepts such as structural and notch stress approaches [36, 42]. In the nominal stress design concept, the weld detail of interest is evaluated with regard to reference S-N curves (respectively FAT classes) provided in technical design codes such as [36, 43]. These reference S-N curves are valid for a given probability of survival and a defined load stress ration (IIW: R = 0.5) taking unfavorable residual stress conditions according to Gurney’s approach [17] into account. IIW recommendations for fatigue design provide a bonus factor f(R) for the adjustment of the design FAT class with respect to the applied mean stress and the residual stress condition, as Fig. 3 depicts. This bonus factor is used to enhance the design FAT value of the specific weld detail. However, it becomes visible from this diagram that the interdependency of mean stress and residual stress is considered qualitatively. The bonus factor f(R) increases with decreasing mean stress and residual stress.

Fig. 3
figure 3

Mean stress correction factor f(R) in dependence of the stress ratio R and the residual stress condition, according to [36]

Full size image

Here, it should be noted that the application limits of this diagram are zero load mean stress (R = − 1) and “low” residual stress. Compressive mean stress or even compressive residual stress cannot be treated by current IIW recommendations for fatigue design [36]. Some approaches for the treatment of compressive mean stress are covered by other design codes, for instance, in [43], but compressive residual stress is generally neglected conservatively. Exceptions of this are novel design guidelines [44, 45] for post-weld treated weldments which allow beneficial fatigue design of compressive residual stress–containing welds. However, these guidelines treat the residual stress effect together with improvement of notch effects and strain hardening without further distinction. Bonus factors were derived empirically and depend mainly on the steel grade and the joint type but not on the magnitude of compressive residual stress induced. The importance of the residual stress field for HFMI (high-frequency mechanical impact)-treated joints was demonstrated [46] where compressive residual stress retained crack propagation of short cracks initiating from flaws in the vicinity of the peened weld toes.

IIW’s residual stress term covers welding residual stress and also additional mounting stress from assembly or other sources. The regular design case in absence of any knowledge on residual stress conditions or complex welded components is the conservative application of a mean stress correction bonus factor of f(R) = 1. In any case of better knowledge, the residual stress influence is considered by a modification of the mean stress influence. For this purpose, the residual stress condition is classified in three groups, “low,” “medium,” and “high” residual stress. All these relative terms apply to tensile residual stress and are used for all kinds of different steels and aluminum. Furthermore, the terms “low” to “high” are used in relation to the yield strength of the un-welded base material. In the further course of the current study, in particular in Section 1.5, it will be shown that the yield strength is not suitable to characterize the residual stress influence on fatigue strength. However, residual stress below 20% of the yield strength may be treated as low which means residual stress magnitudes of approximately 70 MPa in the case of regular structural steel S355 and 190 MPa in the case of high-strength quenched and tempered steel S960 respectively. In practice, this kind of treatment of residual stress is not necessarily conservative because effects of low residual stress (in relation to the yield strength) are neglected and designers may assume that low residual stress magnitudes are irrelevant to fatigue strength. In addition, the full potential for light weight design is difficult to be tapped, since the classification of residual stress conditions to one of the three groups is difficult. It would be favorable to treat specific residual stress conditions based on their magnitudes. This treatment is possible, for instance, by the effective mean stress approach described below.

1.4 Concept of local endurance limits and effective mean stress

An alternative approach for fatigue design under consideration of residual stress is the concept of local endurance limits [4]. This approach was developed for the fatigue evaluation of surface layers with locally altered material properties, for instance, by means of heat treatments (e.g., case hardening) or mechanical surface treatments like shot peening. It is based on the assumption that heterogeneous local material properties (microstructure, hardness, and residual stress) result in different local endurance limits in depth direction. Hence, an increase of hardness and compressive residual stress by local surface treatment causes an increase of the local endurance limit depending on the penetration depth of the treatment. The determination of the local endurance limit is made by means of m and m* (Fig. 1) under consideration of local hardness respectively Rm and the residual stress–free reference fatigue strength σa,R at R = − 1:

$$ {\sigma}_{\mathrm{a},\mathrm{R}}\left({\sigma}_{\mathrm{m}};{\sigma}_{RS}\right)={\sigma}_{a,R}\left({\sigma}_{\mathrm{m}}=0;{\sigma}_{\mathrm{RS}}=0\right)-\left({m}^{\ast}\cdotp {\sigma}_{\mathrm{m}}+m\cdotp {\sigma}_{\mathrm{RS}}\right)\cdotp $$
(1)

Of course, the hardness as well as the magnitude of load mean stress σm and residual stress σRS has to be determined. Residual stress relaxation is already considered in m to an unknown extend. This approach was adopted for welded joints earlier [20]. Moreover, residual stress relaxation has to be considered more detailed than by a general application of m as weldments are notched, which leads to geometry and material specific behavior.

The cyclically stabilized residual stress can be determined by either experimental or numerical methods. Another approach is the estimation of cyclically stabilized residual stress based on empirical models. For longitudinal stiffeners, such an empirical model was presented earlier [47, 48]. It estimates cyclically stabilized residual stress at N = 10,000 load cycles σRS, N = 10,000 in dependence of the material’s yield limit σy, the highest load stress σLS, and the initial residual stress at the fatigue critical location σRS,N = 0:

$$ \frac{\sigma_{\mathrm{RS},N=\mathrm{10,000}}}{\sigma_{\mathrm{y}}}=\frac{\sigma_{\mathrm{RS},N=0}}{\sigma_{\mathrm{y}}}\cdotp \left|\frac{\sigma_{\mathrm{LS}}}{\sigma_{\mathrm{y}}}\right|+\frac{\sigma_{\mathrm{RS},N=0}}{\sigma_{\mathrm{y}}}\cdotp $$
(2)

The highest load stress σLS reflects the maximum and minimum stress during fatigue loading depending on the sign of the initial residual stresses (tensile initial residual stresses: σLS = σmax; compressive initial residual stresses: σLS=σmin). The criterion of N = 10,000 load cycles was already used before [20] and it was proven to reflect both static and cyclic residual stress relaxation quite well. Of course, such a model has the downside of relative low accuracy in terms of the residual stress magnitude but on the other hand it is simple to apply. However, if more detailed information on stabilized residual stress is available, designers are encouraged to make use of it.

Cyclically stabilized residual stress (here σRS,stab = σRS, N = 10,000) is used to introduce the effective mean stress σm,eff, which is the sum of load mean stress and cyclically stabilized residual stress:

$$ {\sigma}_{\mathrm{m},\mathrm{eff}}={\sigma}_{\mathrm{m}}+{\sigma}_{\mathrm{RS},\mathrm{stab}}\cdotp $$
(3)

However, the cyclically stabilized residual stress is determined; Eq. (1) can now be simplified to:

$$ {\sigma}_{\mathrm{a},\mathrm{R}}\left({\sigma}_{\mathrm{m}};{\sigma}_{\mathrm{RS}}\right)={\sigma}_{a,R}\left({\sigma}_{\mathrm{m}}=0;{\sigma}_{\mathrm{RS}}=0\right)-{m}^{\ast}\cdotp {\sigma}_{\mathrm{m},\mathrm{eff}}\cdotp $$
(4)

This expression has the advantage of a combined treatment of residual stress and mean stress. Both stress component effects on fatigue can be evaluated by means of the more precise sensitivity to mean stress m*. Further, m* can be determined using stress-relived specimens without any uncertainties of unknown residual stress influence on m* as described above. The concept of local endurance limits uses the fatigue strength at R = − 1 of residual stress–free specimen as reference. However, for welds, it is more common to refer to the FAT values as reference when applying mean stress correction factors. Hence, this is adopted here and the reference fatigue strength is determined at stress ratios of Reff = 0.5.

1.5 Estimation of fatigue strength based on effective mean stress

The evaluation of fatigue strength of welds based on effective mean stress as described above requires the knowledge of two parameters. One is the magnitude of load mean stress and cyclically stabilized residual stress. The other is the sensitivity to mean stress m*. Both parameters can be obtained from the literature or experiments as mentioned earlier. Within own studies m* was determined experimentally using the specimen type longitudinal stiffener with different residual stress conditions [34, 47]. Here, the uniaxial residual stress component perpendicular to the crack opening is used for simplicity reasons. Figure 4 (left) shows the results of fatigue tests at different stress ratios under variation of the initial residual stress conditions. The fatigue strength at two million load cycles (probability of survival 50%) is plotted over the effective mean stress, using the nominal load mean stress and cyclically stabilized residual stress at N = 10,000 load cycles. According to this figure, m* depends on the effective stress ratio:

Fig. 4
figure 4

Left: Fatigue strength of longitudinal stiffeners (50% probability of survival at two million load cycles) as function of effective mean stress. Right: Derived bonus factor and slope exponent of the S-N curve in dependence of the effective mean stress

Full size image
$$ {R}_{\mathrm{eff}}=\frac{\sigma_{\mathrm{min}}+{\sigma}_{\mathrm{RS},\mathrm{stab}}}{\sigma_{\mathrm{max}}+{\sigma}_{\mathrm{RS},\mathrm{stab}}}\cdotp $$
(5)

The sensitivity to effective mean stress m*eff becomes 0 at high effective stress ratios Reff ≥ 0.5. At compressive effective mean stress (Reff < − 1), m* becomes approximately 0.4. In between, it equals 0.2. These values are in accordance with results of residual stress–free weldments as mentioned above. The data shown in Fig. 4 (left) contains results from fatigue tests of structural steels, in particular of regular steel (S355NL, 1.0546) and high-strength steel (S960QL, 1.8933). Both steel grades led to comparable results.

According to the graph shown, mean stress–independent fatigue strength of longitudinal stiffeners can be expected at effective mean stress of approximately σm,eff = 120 MPa and more. In relation to the yield strength of typical structural steels, this equals quite low fractions, denoted here as “critical effective mean stress in relation to the yield strength” (see Table 1). Depending on the steel grade, these values vary between 52 and 13%. IIW recommendations on fatigue design [36] consider residual stress magnitudes of 20% in simple welded components as “low” meaning mean stress correction factors f(R) (Fig. 3) may be applied. Table 1 points out that the yield limit of structural steels should not be used as criterion for the evaluation of residual stress effects as currently suggested by design codes. Especially the examples of high-strength steels prove this fact. It is rather recommended to evaluate residual stress effects based on the effective load ratio Reff under consideration of cyclically stabilized residual stress.

Table 1 Critical effective mean stress in longitudinal stiffeners leading to mean stress–independent fatigue strength. Values given in relation to different structural steels’ yield limits
Full size table

Figure 4 (right) shows a suggestion for an enhanced bonus factor f(σm,eff) which is based on the effective stress ratio Reff rather than on the nominal stress ratio R. The bonus factor can be obtained for residual stress–free and residual stress–containing weldments in dependence on the actual effective mean stress σm,eff. Thereby, σm,eff is normalized to the FAT value of the corresponding weld type for general application to different joint types. With the help of the bonus factor, the reference fatigue strength (for instance, the corresponding FAT class) can be adjusted to determine the fatigue strength at two million load cycles.

The magnitude of the enhanced bonus factor is identical to the current IIW bonus factor for thermally annealed welds and stress ratios above R ≥ − 1. For instance, it leads to the identical bonus factors of f(σm,eff) = 1 at R = 0.5 and f(σm,eff) = 1.6 at R = − 1. It expands the existing bonus factor concept to compressive effective mean stress and is thus applicable to welds containing compressive residual stress or under compressive mean stress (or a combination of both). Further, it is applicable to welded joints containing any kind of residual stress without the need of a subjective differentiation in “low, medium, or high” residual stress.

Another effect often observed in fatigue tests of residual stress–containing welds is the change of the inclination of the S-N curve. Usually, the S-N curves become shallower with increasing fatigue strength. This effect is considered here with the aid of an increase of the slope exponent k with increasing bonus factor and decreasing effective mean stress. The stepped function of k as suggested is based on the same experimental results as used in Fig. 4 (left).

2 Application of the effective mean stress approach

The approach described above is applied to longitudinal stiffeners in three different residual stress conditions in the following. The data for all three cases is available in the literature. However, the reader is encouraged to apply the model described above to own fatigue and residual stress data.

The influence of weld geometry and residual stress in the fatigue strength of longitudinal stiffeners was studied by [49] in detail. This work considers residual stress and clamping stress from welding distortion and its influence on fatigue initiation and propagation. The specimens used were tested as-welded (containing tensile residual stress at the location of crack initiation), case 1, and thermally annealed, case 2. The steel grade used was structural steel S460NL (1.8903). The applied nominal stress ratios were R = − 1 and R = 0. However, the authors determined “local” stress ratios at the fatigue critical weld toe considering distortion-induced clamping stresses for every test series.

Furthermore, longitudinal stiffeners with additionally applied LTT (low-temperature transformation) filler metal [50] are used in case 3. The LTT filler metal was applied at the fatigue critical weld notches on both sides of the stiffener. It was welded on top of a fusion weld of regular filler metal.

2.1 Case 1: Longitudinal stiffeners in as-welded condition

Longitudinal stiffeners were tested as-welded without any kind of mechanical correction of welding distortion [49]. Thus, specimens were additionally stressed due to clamping into the hydraulic test rig. The magnitude of residual stress and clamping stress was determined at increasing numbers of load cycling by the help of X-ray diffraction in the test rigs. The stabilized magnitude of residual stress and clamping stress was found to be in the range of approximately 220 to 300 MPa at 5000 load cycles. Residual stress relaxation was observed at the initial load cycle. Typical welding residual stress of this sample type ranged in unclamped condition between 50 and 200 MPa at the weld toe.

The fatigue data of both test series at R = − 1 and R = 0 is shown in Fig. 5. The data of the two different test groups was located within the same scatter band with a fatigue strength of approximately σa,R = 50 MPa at two million load cycles. The welding distortion caused a shift of the stress ratios to higher local stress rations Rlocal of − 0.4 to 0.8. However, it should be noted that this does only include additional load stress from clamping but not residual stress.

Fig. 5
figure 5

Fatigue test results of longitudinal stiffeners made from S460NL at nominal stress ratios of R = − 1 and R = 0 in as-welded condition. Effective stress ratios are given for both test series under consideration of the individual specimen distortion. Residual stress not included in Reff. Data taken from [49]

Full size image

The data shows no sensitivity to mean stress as a result of the high local stress ratios and the welding residual stress. To evaluate this data set based on the effective stress approach (Section 1.5), effective mean stress of 220 MPa shall be considered according to the diffraction experiments. Following the context of Fig. 4 and Table 1, this value is beyond the knee point in the Haigh diagram describing the mean stress influence. In other words, the effective mean stress under consideration of clamping stress and residual stress is larger than Reff > 0.5. Hence, no fatigue strength increase from R = 0 to R = −1 is to be expected, the bonus factor f(σm,eff = 220 MPa) = 1. The modified FAT(σm,eff) results to:

$$ \mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)=\mathrm{FAT}\cdotp f\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)\ \mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff}}=220\ \mathrm{MPa}\right)=63\ \mathrm{MPa}\cdotp 1.0=63\ \mathrm{MPa}\cdotp $$
(6)

Figure 4 (right) further provides the estimated expected slope exponent of the modified design S-N curve. At high effective stress ratios (Reff > 0.5), the slope exponent equals k = 3. The modified design S-N curve FAT(σm,eff) is added to Fig. 5 using the determined k and FAT values. It can be seen, the fatigue data is described conservatively by FAT 63.

2.2 Case 2: Thermally stress-relieved longitudinal stiffeners

The fatigue data of thermally annealed specimens indicates, contrary to the as-welded conditions, sensitivity to mean stress, as depicted in Fig. 6 (left). The fatigue strength at two million load cycles was determined to approximately 64 MPa (R = − 1) and 51 MPa (R = 0) based on nominal stress amplitudes. Hence, fatigue strength increases with decreasing mean stress. However, the welding distortion in these specimens also led to a shift of the local stress ratios. These ranged from Rlocal = − 0.2 to 0.8. It can be noted that these local stress ratios comply with the definition of effective stress ratios used in Section 1.5 since residual stresses are small due to the annealing heat treatment.

Fig. 6
figure 6

Left: Fatigue test results of longitudinal stiffeners made from S460NL at nominal stress ratios of R = − 1 and R = 0 in thermally annealed condition. Local stress ratios Rlocal are given for both test series under consideration of the individual specimen distortion. Right: Fatigue test data mean stress corrected to R = − 1 under consideration of individual specimen distortion–induced clamping stress, according to [49]

Full size image

The authors of [49] conducted a mean stress transformation for every test specimen to a uniform stress ratio Reff = − 1, shown in Fig. 6 (right). The result is a significant reduction of scatter and a fatigue strength of approximately 82 MPa at two million load cycles. The fatigue strength enhancement from the reference fatigue strength of 50 MPa (case 1, Section 2.1) to 82 MPa (R = − 1, free of residual stress) results in a factor of 82 MPa/50 MPa = 1.64. This factor is in good agreement with the proposed bonus factor f(σm,eff) = 1.6 at Reff = − 1. Hence, the modified design S-N curves result in:

$$ \mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)=\mathrm{FAT}\cdotp f\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)\mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff}}=0\ \mathrm{MPa}\right)=63\ \mathrm{MPa}\cdotp 1.6=100\ \mathrm{MPa}\cdotp $$
(7)

The slope exponent of the design S-N curve changes, too. According to Fig. 4 (right), a slope exponent of k = 4 would be appropriate. The determined modified design S-N curve is added in Fig. 6 (right) and describes the fatigue data well.

2.3 Case 3: Longitudinal stiffeners with LTT filler metal

The third case comprises longitudinal stiffeners with and without LTT filler metal [50]. The LTT filler metal was applied in addition to regular filler metal to reduce residual stress at the fatigue critical weld toes. All samples were made from S355NL (1.0546). Corresponding residual stress profiles are presented in Fig. 7. It can be seen that the residual stress in loading direction was significantly reduced by the application of the additional LTT filler metal. Conventionally welded samples showed residual stresses of approximately 140 MPa at the weld toe, compared with − 50 MPa for those welded with LTT filler metal. The welding distortion was corrected without affecting welding residual stress before fatigue testing. This was achieved by plastic three-point bending of the specimen ends far away from the weld, until parallel clamping areas were accomplished (more details in [34]). Hence, clamping stress can be neglected for these samples. The applied nominal stress ratio was R = 0.1 for both test series. The fatigue data is shown in Fig. 8. It can be seen from the diagram that the use of LTT filler metal led to an increase in fatigue strength at two million load cycles. The cyclically stabilized residual stress for these test series can be estimated using Eq. (2). The effective mean stress is determined to approximately 150 MPa (conventional filler metal) and − 10 MPa (LTT) by help of Eq. (3). Thus, the adjusted FAT values are:

Fig. 7
figure 7

Residual stress in longitudinal stiffeners made with conventional and LTT filler metal. Stress component in axial loading direction, determined using X-ray diffraction at the surface of the base plate. Weld toe (x = 0 mm) corresponds to the fatigue crack initiation site

Full size image
Fig. 8
figure 8

Fatigue test results of longitudinal stiffeners made from S355NL at a nominal stress ratio of R = 0.1. Specimens welded with conventional and LTT filler metal resulting in different welding residual stresses. Data taken from [50]

Full size image
$$ \mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)=\mathrm{FAT}\cdotp f\left({\sigma}_{\mathrm{m},\mathrm{eff}}\right)\mathrm{FAT}\left({\upsigma}_{\mathrm{m},\mathrm{eff},\mathrm{conv}}=150\ \mathrm{MPa}\right)=63\ \mathrm{MPa}\cdotp 1.0=63\ \mathrm{MPa}\ \mathrm{FAT}\left({\sigma}_{\mathrm{m},\mathrm{eff},\mathrm{LTT}}=-10\ \mathrm{MPa}\right)=63\ \mathrm{MPa}\cdotp 1.73=109\ \mathrm{MPa}\cdotp $$
(8)

The slope exponent of LTT-welded samples is affected by the effective mean stress. It can be determined to k = 5 (Fig. 4). The adjusted design S-N curves for both test series are given in Fig. 8. It can be noted that the fatigue data is described conservatively.

3 Summary and conclusions

The effective mean stress approach is capable to describe the change of S-N curves with a change of the effective mean stress. More detailed knowledge on actual loading conditions is required as residual stress and additional mean stress components (for instance, distortion induced) have severe influence on the fatigue strength. However, the results presented in the current study emphasize a common misunderstanding clearly: Residual stress effects in welded structures cannot be evaluated with the help of the yield strength of the base metal, as commonly performed in engineering practice and design codes. Residual stress effects can only be assessed by the magnitude of residual stress and its relation to the applied load stress level. Even relatively low residual stress, compared with the yield strength, may have a huge impact on the resulting fatigue strength, as shown in Table 1.

The data base used for the determination of the proposed enhanced bonus factor should be expanded by fatigue data of different joint types (butt welds, cruciform joints, transverse stiffeners, overlap joints, and others) and material grades. Further cyclic residual stress relaxation should be studied in more detail, especially for different joint types with varying stress concentrations. Furthermore, future studies should address residual stress from post-weld treatment methods (hammer peening including HFMI, shot peening, and others) including their specific local material behavior. Finally, these results should be tested with variable amplitude fatigue data of specimen with varying residual stress conditions.