Charged analogues of isotropic compact stars model with buchdahl metric in general relativity

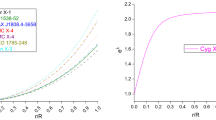
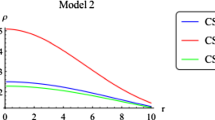
Abstract

In this work, we examine a spherically symmetric compact body with isotropic pressure profile. In this context we obtain a new class of exact solutions of Einstein-Maxwell field equation for compact stars with uniform charged distributions on the basis of Pseudo-spheroidal space-time with a particular form of electric field intensity and the metric potential $g_{11}$. Taking these two parameters into account further examination has been done to decide unknown constants and to depict several compact strange star candidates. By the isotropic Tolman-Oppenhimer-Volkoff(TOV) equation, we explore the equilibrium among hydrostatic, gravitational and electric forces. Then, we analyze the stability of the model through adiabatic index($\gamma$) and velocity of sound ($0<\frac{dp}{c^{2}d\rho }<1$). We additionally talk about other physical features of this model e.g. pressure, redshift, density, energy conditions and mass-radius ratio of the stars in detail and demonstrated that our results satisfied all the basic prerequisites of a physically legitimate stellar model, showing density, pressure, pressure-density ratio, redshift and speed of sound are monotonically decreasing. The outcomes acquired are valuable in exploring the strength of other compact objects like white dwarfs, gravastars and neutron stars. Finally, we have shown that the obtained solutions are compatible with observational data for compact objects.

Appendix

The expression for coefficients used in Eq. (17)

$$\begin{aligned} L =&(E5\times E2)\times M1\times (E1\times E2+E3\times E4) \\ &{}+M7 \bigl[(E5 \times E2) \bigl((B2+B3)\times E2+E1\times B4 \\ &{}+E3\times B6+E4\times B5 \bigr) \\ &{}-(E1\times E2+E3\times E4) (B7\times E2+B4\times E5) \bigr], \end{aligned}$$

$$\begin{aligned} M1=\frac{2\sqrt{Cx}(1-2K-x)}{K(1+x)^{2}\sqrt{(1-K)(K+x)}}, \end{aligned}$$

$$\begin{aligned} M7= \frac{2(K+x)}{K(1+x)\sqrt{(1-K)(K+x)}}, \end{aligned}$$

$$\begin{aligned} E8= \biggl[K-1+\frac{2-3Y^{2}}{4(1+Y^{2})^{2}}+ \frac{2\eta ^{2}(1+Y^{2})}{(Y^{2}\eta ^{2}+Yb)} \biggr], \end{aligned}$$

$$\begin{aligned} E10= \frac{x}{2K(1+x)^{2}}, \end{aligned}$$

$$\begin{aligned} E9 =&\frac{5(K-1)\sqrt{Cx}}{2K(1+x)^{2}}- \frac{-2\eta ^{2}}{(Y^{2}\eta ^{2}+b)}\frac{2\sqrt{Cx}}{K(1-K)} \\ &{}- \frac{(1+Y^{2})}{K} \frac{2\eta ^{2}\sqrt{Cx}(2\eta ^{2}+b/Y)}{(1-K)(Y^{2}\eta ^{2}+b)^{2}}, \end{aligned}$$

$$E7=\frac{\sqrt{Cx}(1-x)}{(1+x)^{3}}, $$

$$\begin{aligned} B2= \frac{\sqrt{Cx}}{(1-K)} \biggl[ \frac{(1+Y^{2}) (\frac{3}{2}Y\eta ^{2}+b )-\frac{3}{4}Y^{2} (Y\eta ^{2}+b )}{(1+Y^{2})^{7/4}} \biggr], \end{aligned}$$

$$B3=\frac{2\sqrt{Cx}}{(1-K)(1+Y^{2})^{3/4}} \biggl[ \biggl(\frac{1}{2}Y \eta ^{2}+b \biggr)+\bigl(1+Y^{2}\bigr)\frac{\eta ^{2}}{Y} \biggr], $$

$$E11= \frac{2\sqrt{Cx}(1-K)(5-x)}{K(1+x)^{3}}, $$

$$B4=\frac{\eta ^{3}\sqrt{Cx}}{2b^{5/2}(1-K) (b+Y\eta ^{2} )} \times E4, $$

$$B5=\frac{\eta ^{3}\sqrt{Cx}}{4b^{5/2}(1-K)} \bigl[\bigl(1+Y^{2}\bigr)^{-3/4}Y^{1/2}\!+\! \bigl(1+Y^{2}\bigr)^{1/4}Y^{3/2}\bigr], $$

$$\begin{aligned} B6 =&\frac{\eta \sqrt{Cxb}}{Y^{3/2}(1-K)(b+Y\eta ^{2})} \bigl[\cos 2 (\Phi ) \\ &{}-2\csc ^{2} (\Phi )\times \cot ^{2} (\Phi )-2\csc ^{4} (\Phi )+\csc ^{2} (\Phi ) \bigr], \end{aligned}$$

$$\begin{aligned} B7 =&\frac{\sqrt{Cx}}{2(1-K)(1+Y^{2})^{3/4}}\bigl(Y^{2}\eta ^{2}+bY\bigr) \\ &{}+ \frac{2(1+Y^{2})^{1/4}\sqrt{Cx}}{(1-K)} \biggl(\eta ^{2}+\frac{b}{Y} \biggr). \end{aligned}$$