1 Introduction

Chalcopyrite Cu(In,Ga)Se2 (CIGS) compounds have been drawing significant consideration as capable and appropriate candidates for cost-effective, efficient photovoltaic devices due to their remarkable physical and electrical properties [1,2,3]. They crystallize in a tetragonal chalcopyrite structure derived from the cubic sphalerite structure. One consequence of this structure is the possibility of varying its bandgap values (Eg). The Eg varies from pure CIS to pure CGS from approximately 1.0 to 1.7 eV, subject to gallium and indium percentages in the composition [4]. Additionally, they possess a high absorption coefficient in the range of 104 cm−1, which implies that 95% of the solar radiance with photons has energy above the Eg that can be absorbed within 1 μm of CIGS film, whereas, for example, crystalline Si might need more than 100-μm thickness to absorb that much of solar energy [5, 6]. High efficiency of 20.3% has been recorded for a laboratory-scale CIGS solar cell [7]. Other efficiencies of around 19.9% [8] and 17.4% [9] for the CIGS thin-lm sub-module have been achieved. Moreover, in the CIGS-based thin-film solar cells, molybdenum is the most commonly employed material for the back contact. For an efficient CIGS solar cell, the Mo layer shall establish a low-resistance ohmic back contact with the CIGS layer. Else, substantial resistive losses due to the Schottky barrier at the CIGS/Mo contact occur. It has been found that forming a proper intermediate layer between the CIGS absorber and Mo provides low resistance quasi-ohmic contact. For example, a skinny p-MoSe2 layer might be grown on Mo back contact within the deposition of the CIGS layers, and the contact between Mo and CIGS reveals an ohmic character [10,11,12]. It is currently believed that for many solar cell structures, the existence of such an interfacial layer can promote a quasi-ohmic electrical contact across the CIGS–Mo interface. Accordingly, a p-MoSe2 intermediate layer is added to the investigated structure in the study.

Even though the CIGS has become an excellent absorber for thin-film solar cells, optimizing the buffer layer is still a dispute for improving cell performance. The buffer layer is an n-type material used to form the p–n junction of the photovoltaic devices. So far, the most common buffer layer in the CIGS solar cells is the CdS. Introducing a suitable buffer layer was a significant step in developing higher-efficiency solar cells [13]. However, the disadvantages of CdS cannot be disregarded. Cadmium used in the buffer layer is a toxic material with restricted use in electronics. Disposition of the Ca-containing outputs evokes injurious effects on human health, and appropriate treatment of large quantities of toxic waste might be an enormous and costly duty. Apart from toxicity, the bandgap of CdS is about 2.40 to 2.50 eV, which results in significant optical absorption fall in the short wavelength range, limiting the overall performance of solar cells. Because of the disadvantages of the CdS buffer, considerable efforts have been put into finding Cd-free alternative buffer candidates, e.g., ZnS, Ins, ZnSe, Zn(O, OH), Zn(O, S, OH), and ZrO [14,15,16,17]. The potentiality of other transition metal dichalcogenide materials (TMDCs), namely the MoS2 as a buffer layer for CZTS and CIGS solar cells, has been studied [17, 18]. This paper explores the potential of a novel material as a buffer layer, namely, the zirconium sulfoselenide (ZrSxSe2−x) TMDCs. They have a bunch of remarkable characteristics as 2D materials. Additionally, one can engineer their bandgap values between ∼ 1.2 and 2.7 eV, using what has been termed chemical architecture by changing the sulfur content, i.e., the x parameter. The TMDCs exhibit a broad spectrum of electronic properties varying from metals or semimetals through semiconducting to insulating [19, 20]. Also, the materials exhibit an unusual morphology as thin, flexible, high-quality surfaces with no dangling bonds, introducing their suitability for thin-film fabrications. The general expression of the TMDC material is MX2, composed of X-M-X planes, where a layer of metal atoms lies between two chalcogens layers with a strong covalent bonding for the in-plane sheets and a weak Van der Waals coupling held the sheets [21,22,23]. Furthermore, using environmentally friendly abundant, nontoxic, and cheap materials is essential for solar cell fabrications and valid for the TMDC semiconductors. Moreover, the implementation of TMDC as a buffer layer resolves other parameters that might directly impact the cell performance, like the lattice parameter mismatch and the coefficient of the thermal expansion match between the absorber and the buffer layers. The advantage of TMDCs is that they have thermal and chemical stabilities of the n-type character associated with high carrier mobility.

In this study, our efforts have focused on a quantitative numerical study on the performance of a new proposed CIGS-based solar cell using the nontoxic n-ZrSxSe2−x as a buffer layer and a p-MoSe2 TMDC material as an interfacial layer between Mo and the absorber. The structure of the solar cell is Al/n-ZnO/i-ZnO/ZrSxSe2−x/CIGS/p-MoSe2/Mo/SLG. First, we touch upon the effect of the p-MoSe2 interfacial layer. The CIGS absorber thickness is optimized. Then, solar cell performance parameters such as open-circuit voltage Voc, short circuit current density Jsc, fill factor FF, and the conversion efficiency η are investigated as a function of the bandgap values, the thickness, and the acceptor carrier concentration (NA) of the ZrSxSe2−x buffer layer. Finally, the influence of the device operating temperature, in the range from 275 to 475 K, on the overall cell performance is investigated and discussed.

2 Device Modeling and Simulation

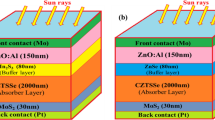
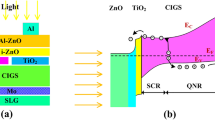
A numerical simulation is a powerful tool that leads to a comprehensive understanding of solar cells, identifying the main parameters that affect their performance and designing new experimental production structures. Many simulation programs have been used for the CIGS solar cells, such as SILVACO ATLAS [23], AMPS [24], and SCAPS [25, 26]. All simulations were obtained using the solar cell capacitance simulator (SCAPS) in this work. SCAPS is numerical simulation software that was prepared at the University of Gent [27]. It has been widely employed to simulate the electrical characteristics, performance, and spectral response of several crystallines and thin film–based photovoltaic cells, such as perovskite, CZTS, Si, CdTe, and CIGS solar cells. One of its advantages is that the SCAPS simulation results agreed well with the corresponding experimental results, such as perovskite, CZTS, Si, CdTe, and CIGS solar cells [26, 28,29,30,31]. SCAPS employs Poisson’s and continuity equations for electrons and holes to estimate the steady-state band diagram, recombination profile, and carrier transport in one dimension. Figure 1a depicts the layer structure of the proposed model CIGS device. The Mo/MoSe2/CIGS/ZrSxSe2−x/ZnO/ZnO/Al structure is a heterojunction, i.e., a junction between semiconductors of different bandgaps. On the other hand, Fig. 1b shows the corresponding energy band diagram of the proposed CIGS solar cell model using the ZrSxSe2−x buffer layer. The ZnO plays the role of the conventional window layer. The parameters used for the window layer are taken as the thickness of 150 nm, doping of 5 × 18 cm−3, and bandgap of 3.3 eV. For all simulations, this work applies the AM1.5 light spectrum illumination, and light intensity of 1000 (W/m2) at a room temperature of 300 K. The surface recombination velocities are assumed to be \({10}^{7}\) cm/s, and the coefficients of reflection of back and front surfaces are approximated to 10%. As per all simulation work, the input data for each material considered here have been collected and listed in Table 1 [32,33,34]. SCAPS simulates the energy diagrams in steady states and calculates the electron–hole recombination profile with the charge carrier transport in one dimension by solving the fundamental semiconductor equations. These equations are Poisson’s equations that connect the electrostatic potential to the charge (Eq. 1) and the continuity equations for electrons and holes (Eqs. 2 and 3):

$$\frac{\partial }{\partial x}\left({\varepsilon }_{0}{\varepsilon }_{r}\frac{\partial\Psi }{\partial x}\right)=-q(p-n+{N}_{D}^{+}-{N}_{A}^{-}+\frac{\rho }{q}$$
(1)
$$-\left(\frac{1}{q}\right)\frac{\partial {J}_{n}}{\partial x}-{U}_{n}+G=\frac{\partial n}{\partial t}$$
(2)
$$-\left(\frac{1}{q}\right)\frac{\partial {J}_{p}}{\partial x}-{U}_{p}+G=\frac{\partial p}{\partial t}$$
(3)

where \(\Psi\) is the electrostatic potential function, \(\rho\) is the charge density of defects, n and p are the free carrier concentrations whereas \({N}_{A}^{-}\) and \({N}_{D}^{-}\) are the densities of ionized acceptors and donors, \({\varepsilon }_{0}\) and \({\varepsilon }_{r}\) are the absolute and relative permittivities of the material, respectively. G is the generation rate, and \({J}_{p}\) and \({J}_{n}\) are the hole and electron current densities, respectively.

Fig. 1
figure 1

a Schematic diagram of the novel CIGS solar cell structure based on ZrSxSe2−x buffer layer and MoSe2 layer. b The energy band diagram for both valance band and conduction band the investigated CIGS solar cell structure

Full size image
Table 1 The material parameters of the proposed model incorporated into SCAPS simulations at 300 K [32,33,34]
Full size table

3 Results and Discussion

In the first stage of our study, we gain insight into the impact of the inserted p-MoSe2 as an interfacial layer between Mo back contact and the CIGS absorber. Among the prime research findings in the CIGS thin-film solar cell is the capability of CIGS to form an ohmic contact with Mo back contact [10]. Figure 2 shows the obtained results of the simulated device with and without using the interfacial p-MoSe2 layer. Figure 2a shows the current–voltage characteristics (J–V) as a log scale of the CIGS solar cell at temperature 298 K. The simulations are performed using 200 nm as the p-MoSe2 thickness with a bandgap value of 1.3 eV, and acceptor carrier concentration (NA) of about 1016 cm−3, using a CIGS absorber layer thickness of 470 nm. The result implies that the Mo/p-CIGS heterojunction without the insertion of the p-MoSe2 layer is Schottky-like contact rather than an ohmic one. From Fig. 2a, one can observe that the insertion of the p-MoSe2 layer improves the solar cell ‘s performance, and an increase in the J-V curve steepness is observed, i.e., the slope (∆I/∆V) is greater than that without using the interfacial layer. The obtained results imply that the p-MoSe2 layer at the CIGS/Mo interface beneficially on the CIGS/Mo heterojunction, mediating the ohmic-type contact from a Schottky-type contact. Additionally, developing such an ohmic contact is essential to reduce series resistance, Rs. Our observation is consistent and verified by previous numerical modeling of the effect of the MoSe2 TMDC layer of Mo back contact in Se-containing CZTSe devices [35]. It has been reported that the Cu deficiency of the CIGS films causes the formation of the ordered defect or order vacancy compounds (ODC/OVC phases) at the film surface between the absorber and buffer layers. The claimed thickness of such an ODC layer is about 15 nm, with an n-type in electrical conduction nature, which results in beneficial device performance. It causes an increase in the absorber bandgap at the buffer-absorber interface by lowering the valence band maximum (VBM) relative to the Fermi level, which reduces the rate of the interface recombinations. Due to Cu vacancies, the valence band bending near the junction interface creates a barrier for the hole transport and lowers the current recombination rate [36, 37]. The quantum efficiency (QE) versus wavelength for the solar cell without and with the interfacial layer (solid and dotted lines, respectively) is displayed in Fig. 2b. The QE is exploited to measure the spectral response of the device. The QE (λ) is defined as the ratio of the number of the collected electrons I (λ)/q to the number of incident photons φp (λ) [38], where q is the elementary charge, the I (λ) is the photogenerated current, and φp (λ) represents the photon flow. Figure 2b reveals an increase in the spectral response (QE) in the short wavelength between 300 and 400 nm for the optimized cell. The spectral response curves of both reference and optimal cells show a delightful flat one between 400 and 900 nm on a high level of approximately 93%. It discloses a decrease of QE in the long wavelength between 900 and 1100 nm. This is most feasible due to the incomplete absorption of the long-wavelength photons. The obtained results agree well with prior work by others [38].

Fig. 2
figure 2

a The current–voltage (J–V) characteristic curves of the CIGS solar cell with the interfacial layer MoSe2 layer (solid-line) and without MoSe2 layer (dashed line). b The spectral response and the external quantum efficiency (QE) of CIGS device using with the interfacial layer MoSe2 layer (solid-line) and without MoSe2 layer (dashed line)

Full size image

Regarding the impact of the thickness of the p-MoSe2 interfacial layer, a correlated study is performed, considering the absorber layer thickness. The latter is one of the critical parameters that optimize solar cell performance. It should be carefully selected to absorb the highest number of photons and not too large to control and minimize the reverse saturation current. The obtained results of the photovoltaic parameters such as open-circuit voltage Voc, short circuit current density Jsc, fill factor FF, and the conversion efficiency η are shown in Fig. 3. The thicknesses of the absorber and the interfacial layers vary from 0.2 to 1.0 μm and from 0.05 to 0.2 μm, respectively. The results show an η of 23.48%, corresponding to an absorber thickness of 0.8 μm and an interfacial layer of thickness of 0.16 μm. A constant Jsc (i.e., horizontal curve) is observed with the increase of p-MoSe2 thickness. For example, its value is 33.32 mA/cm2 at a thickness of 0.8 μm of the CIGS. This is because the Jsc parameter depends mainly on the change in the absorber thickness. On the other hand, Jsc increases from 31.69 to 38.16 mA/cm2 as the CIGS absorber thickness increases from 0.2 to 0.85 μm. The parameter Voc has increased from 0.703 to 0.743 V, increasing the p-MoSe2 thickness from 0.05 to 0.2 μm, and the efficiency improves from 22.16 to 23.48%. Figure 3d reveals an optimum value of FF of 83%, which corresponds to maximum efficiency at the possible thinnest absorber thickness. Indeed, the results indicate an enhancement of the performance by increasing the thickness of the absorber layer. We observe an increase in the device efficiency of ~ 3.5% with the increase of CIGS thickness from 0.17 to 0.9 μm. Beyond this value of CIGS thicknesses, no dramatic improvement is observed. It can be concluded that a CIGS thickness of 0.9 μm with a high doping concentration of 1 × 1018 cm−3 is enough to keep the device operating at its optimum efficiency since it is useless to consume extra materials. The above results are discussed regarding the back contact recombination and its relation to the absorber thickness. Many photogenerated carriers are likely to suffer from the recombination process at the back contact, and fewer ones can contribute to quantum efficiency. Increasing the absorber layer thickness leads to more photogenerated carriers than can be collected before the recombination process, and that is why the efficiency is enhanced. Additionally, the back contact recombination current density is reduced in a cell with a thick absorber layer since the back contact is placed farther from the depletion region. Nonetheless, we cannot increase the absorber thickness excessively, and optimization is still needed. Based on the simulation results, with a thickness of more than 0.9 μm, the efficiency only increases barely and is considered almost saturated. Indeed, with the absorber layer thickness increasing further, some incoming photons are absorbed deep into the absorber layer, away from the depletion region. The resulting carriers will not reach the space charge region during the assigned lifetime, recombining in the absorber bulk. In other words, increasing the thickness of the absorber layer raises the opportunity for bulk recombination. For the impact of the interfacial layer, a thinner p-MoS2 layer reduces the shunt resistance, and potential barriers would exist at the CZTS/p-MoS2 interface and p-MoS2/Mo interface. These barriers impede the drift of the photogenerated holes. Increasing the thickness of the MoS2 interfacial layer reveals an increase in the optical absorption, which in turn shows a higher photogenerated charge carrier. When the thickness of p-MoS2 is increased, the height of the barrier at the CIGS/p-MoS2 interface is reduced. This is because the work function and bandgap values of the p-MoS2 decrease with increasing thickness. Hence, the collection of photogenerated holes from CIGS to Mo is improved, providing better CZTS solar cell photovoltaic parameters. It is interesting to mention here that it has been noted that the MoS2 layer might form a back-surface field for the photogenerated electrons [39]. This back-surface field (BSF) causes a reduction in back-contact recombination and leads to improve cell performance, as it works as a hole transport layer (HTL) at the back contact. The relationship between the BSF and the recombination rate at the back contact has been investigated experimentally, e.g., [40].

Fig.3
figure 3

(Color online) The photovoltaic performance parameters as a function of both CIGS (x-axis) and MoSe2 (y-axis) thicknesses, the contour color-maps represent: a conversion efficiency (η), b short-circuit current density (Jsc), c fill factor (FF), d open-circuit voltage (Voc), at different CIGS absorber thicknesses ranging from 800 to 1600 nm

Full size image

Figure 4a–d depict the impact of the bandgap values of the ZrSxSe2−x buffer layer and its thickness in a contour plot in the range of 0.02 to 0.2 μm (y-axis) and from 1.3 to 1.9 eV (x-axis) on the photovoltaic performance parameters. The results show that by increasing the buffer layer thickness from 0.025 to 0.15 μm, one observes a neglected decrease in the Jsc from 37.85 to 37.80 mA/cm2. This might be because the existing hole concentrations close to the semiconductor junction could increase the possibility of facing interface recombination [41,42,43]. It is worthy to say that bandgap values above 1.5 eV cause a detrimental effect on the cell performance. In buffer layers with a larger bandgap, photons cannot gain the energy needed to absorb the photons with higher wavelengths and, accordingly, will not generate electron–hole pairs. In other words, because of the buffer layer’s parasitic absorption, the absorber/buffer interface prevents the electrons from entering the junction [43]. A more quantitative picture of the results can be discussed by referring to the absorber-buffer interface. Considering the bandgap values for the CIGS/ZrSxSe2−x system, it is well accepted that a cliff-like band alignment is assumed, where the valence band maximum (VBM) and conduction band minimum (CBM) of the ZrSxSe2−x buffer is less than that of the CIGS absorber. This develops the type-II heterojunction, a supportive structure for efficient charge separation [44]. Previous device simulations in literature have shown that the ideal conduction band offset (CBO), in a moderate cliff-like, ranges from 0 to 0.4 eV [45]. When the value of the bandgap increases, most likely because of the downward shift in the valence band Ev, this increase in valence band offset (ΔEv) value blocks the charge separation promoted to the p-type absorber. Noting that, a slight increase in ∆Ec value will not dramatically affect the electron diffusion. Similar behavior was observed in previous studies on various chalcogenides of ZTSSe and CIGS [46, 47]. The optimum values obtained suggest an optimum efficiency of about 25.08% at a low bandgap energy of 1.3 eV, corresponding to buffer layer thicknesses of 180 nm. The optimum values of the FF, Jsc, and Voc were observed of 85.17%, 37.87 mA, and 0.77 V, respectively. According to our previous investigation of the bandgap values as a function of the sulfur content (i.e., the x parameter), we conclude that the obtained optimum bandgap corresponds to ZrS0.8Se1.2 [48]. Many studies recommended an optimal thickness of the CdS buffer layer to be between 50 and 100 nm [49], and the solar cell performance decreased out of this range. However, this limitation of the ZrS0.8Se1.2 buffer layer thickness is relaxed since we introduce a nontoxic, abundant, and Cd-free alternative.

Fig. 4
figure 4

a–d (Color online) The simulated photovoltaic performance parameters versus the buffer ZrSxSe2−x layer thickness bandgap energy (1.3–1.9 eV) (y-axis). The contour color maps of the device represent: a conversion efficiency (η), b short-circuit current density (Jsc), c filling factor (FF), d open-circuit voltage (Voc) at different buffer layer thicknesses in the range from 20 to 200 nm (x-axis)

Full size image

Furthermore, the influence of buffer carrier concentration of ZrSxSe2−x on the solar cell performance parapets is studied. The doping level of the buffer is assumed to vary from 1 × 1011 to 1 × 1018 cm−3. The impact of increasing the carrier concentration on the photovoltaic parameters is demonstrated in Fig. 5. The results reveal a significant increase in the cell performance at doping levels above 1 × 1016 cm−3. The Jsc is almost constant at about 37.875 mA/cm2. Since the absorber thickness is held constant, no change in Jsc is observed. According to the literature, this parameter is most affected by the decrease in absorber thickness. The observation agrees with previous results using other TMDC buffer layers such as the MoS2 [17, 18]. The solar cell performance parameter FF increases by 11%, i.e., from 75.4 to 84.1%. At the same time, an increase in FF will collectively increase the conversion efficiency of the solar cells. The efficiency enhances from 22.88 to 25.52% with the increase of the doping level from 1012 to 1019 cm−3. It is recommended to have heavily doped with a donor concentration of 1 × 1018 cm−3 to keep the device operating at optimal efficiency of 25.52%. The results can be discussed as follows. The highly doped layer produces the suited conduction band downward bending at the interface and benefits the photoelectron collection [50]. As the carrier density of the buffer layer increases, more atoms can be ionized, and accordingly, more electrons are photogenerated. Besides, the electrostatic potential barrier in buffer/absorber ZrSxSe2−x/CIGS and window/buffer ZnO/ZrSxSe2−x heterojunctions decreases and allows an enlargement in the space charge zone, improving the collection of the photogenerated carriers, and increasing the conversion efficiency output can be achieved. The results are consistent with previously reported behavior, showing that the conversion efficiency increases with the carrier densities [18].

Fig. 5
figure 5

The photovoltaic performance parameters versus the doping concentration (log-scale) of ZrSxSe2−x buffer layer in the range of 1 × 1011 to 1 × 1018 cm.−3

Full size image

Figure 6 illustrates the obtained optical response of the ZrSxSe2−x buffer layer thickness. From Fig. 6, we can say that the transmittance of the sample appears to be nearly independent of the buffer layer thickness. However, an improvement of QE from 86.1 to 89.6% was observed at longer wavelengths ranging from 700 to 820 nm. The inset of Fig. 6 is the enlargement of the observed results in the investigated range. One acceptable explanation is that increasing the buffer layer thickness leads to the generation of more charge carriers. This wavelength matches the bandgap energy of the buffer layer. The enhancement behavior is due to the expected greater amount of atoms ionized to photogenerate more electrons.

Fig. 6
figure 6

The obtained quantum efficiency (QE) of the CIGS structure versus the incident wavelengths simulated. The inset is an enlargement of the QE between 720 and 820 nm, at different buffer layer thicknesses ranging from 10 to 160 nm

Full size image

Finally, this section focuses on the device operating temperature effect on the overall cell performance. The temperature was tuned in the range of 275 to 475 K. The simulated results are illustrated in Fig. 7. The device maintained a very high performance with device efficiency greater than 24% at operating temperatures below 340 K. A significant device performance drop in all performance parameters was observed at operating temperatures above this value. The Voc, FF, and efficiency values decrease with increasing the temperature while Jsc reduces slightly. Jsc decreases from 37.820 to 37.40 mA/cm2 as the temperature increases from 340 to 475 K. The conversion efficiency decreases from 17.55 to 12.89%, about a 9% drop. The CIGS solar cell devices obtained J–V characteristic curves at different temperatures are shown in Fig. 7b. It displays a significant increase in the current density of the operating temperature in the range of 275 to 475 K. The observed decline in the Voc is due to the increase in the reverse saturation current associated with the temperature rise. The decrease in the Voc with the increase in temperature is validated by Eq. (4), which relates the Voc and the saturation current Io [51, 52]:

Fig. 7
figure 7

a The obtained photovoltaic performance parameters as a function of the novel CIGS structure as a function with the operating temperature tuned in the range of 275 K to 475 K. b The J–V characteristic curves of the CIGS solar cell device with the operating temperature in the range of 275 K up to 475 K

Full size image
$${V}_{oc}=n{V}_{T}\mathrm{ln}\left(\frac{{i}_{p}+{I}_{o}}{{I}_{o}}\right)$$
(4)

The increase in the saturation current density is mainly due to the increase of the intrinsic carrier concentration ni and the decrease in the bandgap of the semiconductors. Additionally, the rise in temperature affects the material conductivity resulting in degradation of the solar cell performances. The material’s bandgap becomes narrower when the temperature increases, i.e., negative dEg/dT. Two significant reasons explain the temperature dependence of the energy gap in semiconductors–the explicit effect of the electron–phonon interaction and the implicit lattice dilation of the thermal expansion. As the temperature increases, the electrons in the cell gain more energy and become less stable, and they do not recombine with the holes before reaching the charging zone. As a result, the recombination rate of the internal carrier increases, resulting in decreasing Voc and efficiency [53, 54].

4 Conclusions

In this paper, we have investigated a CIGS-based solar cell using SCAPS-1D simulation. The structure involves a new ZrSxSe2−x as a nontoxic buffer layer and p-MoSe2 as an interfacial between Mo back contact and the absorber. A p-type MoSe2 layer in CIGS devices facilitates quasi-ohmic-contact development, increasing the J-V curve steepness and improving the cell performance. Additionally, the effect of thickness, band gap values, and carrier concentration of the buffer layer of the Mo/p-MoSe2/CIGS/n-ZrSxSe2−x/ZnO structure solar cell on the photovoltaic parameters was investigated. The optimal performance parameters obtained are η 25.56%, Jsc of 37.92 mA/cm2, Voc of 0.77 V, and FF of 85.28% at a buffer thickness of 180 nm and Eg of 1.3 eV. The increase in the ZrSxSe2−x bandgap above 1.3 eV results in a detrimental effect on the cell’s performance due to the possibility of electrons drifting toward the back contact and recombining. Moreover, we investigated the impact of the device operating temperature on the cell performance in the range of 275 to 475 K. The observed decline in the Voc is due to the increase in the saturation current. The study presents a promising solution for Cd-free nontoxic, and efficient CIGS solar cell devices, using the ZrSxSe2−x buffer layer for the first time in CIGS solar cells.