Introduction

Currently, the demand for energy increase year by year, which is important for technological and industrial development worldwide although limited fossil fuels1. Solar cells are considered one of the highly significant renewable energy sources since they are environmental ecofriendly technology to reduce global CO2 emissions1.

Recently, transition metal dichalcogenides (TMDCs) have received high attention to become potential candidates instead of traditional materials for various applications especially solar cells2,3 as well as batteries4, photodetector5,6, biomedical7, and catalysis8. In these materials, the d- d transition positioned at a metal site producing large band-edge excitation and therefore unique electronic properties leading for such various applications.

Zirconium disulfide (ZrS2), belongs to group IV of TMDCs, is n-type semiconductor which reveals a low mismatch lattice with other absorber materials because of Van-der-Waals force (VdW) force2,9. ZrS2 is considered as a powerful applicant to fabricate optoelectronics particularly photovoltaics since it has high absorption coefficient and bandgap energy that could be easily engineered to be in the range of 1.2–2.2 eV2,3,10. Moreover, ZrS2 has several unique electronic and optical properties owing to quasi 2D characteristic2. Based on these properties, ZrS2 could be utilized in many fields besides solar cells2,3 such as field-effect transistors (FETs)11, lithium-ion batteries12, water-splitting13, photocatalysis14, lubricant additives15, and photodetectors16.

Tunable of bandgap energy as well as electronic and optical properties for ZrS2 thin film could be achieved employing several growth techniques like chemical vapor deposition (CVD)11, chemical vapor transport (CVT)17, atomic layer deposition (ALD)13,18, sputtering19, and liquid exfoliation method9.

On the other hand, CuO is a semiconductor that has bandgap in the range of 1.2–1.5 eV, good thermal and electronic features and generally used in superconductors, supercapacitors, and solar energy purposes20. In addition, Cu2O is a non-toxic material and has a narrow direct optical band gap in the range of 1.9–2.3 eV and therefore employed on optoelectronic devices21. The combination of n-ZrS2 thin films with other p-type semiconductors with appropriate energy level alignment such as CuO and Cu2O as well as buffer layers like graphene oxide could be future key to have solar cells with higher efficiency22,23,24,25.

The predication of the optimum parameters for the materials is considered one the most promising keys to fabricate high performance solar cells. The simulation is a valuable approach to examine the influence of changes in material properties on the solar cell basic parameters and study the complex heterogeneous absorber/buffer interfaces. Therefore, many papers were published to predicate the solar cells efficiencies employing Solar Cell Capacitance Simulator Structures (SCAPS-1D) software, which is a one-dimensional (1D) windows-oriented program and has the largest number of simulation parameters26,27,28,29.

Consequently, we present here for the first-time SCAPS numerical simulation of novel inorganic ZrS2/CuO heterojunction solar cell devices. Typically, the effect of the thickness, carrier concentration, and bandgap for both the window and absorber layers on the solar cell fundamental parameters will be investigated deeply. Our simulated results will be step forwards to know the optimum parameters to experimental produce high efficiency photovoltaic devices.

Materials and methods

Inorganic solar cell structure

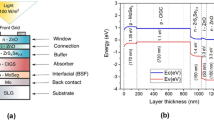
Figure 1 represents a schematic diagram of the heterojunction device structure that was employed in the simulation. Typically, n-ZrS2 thin film was used as the window layer, while p-CuO thin film was employed as the absorber layer to shape our inorganic p–n heterojunction solar cells. Transparent conductive oxide (TCO) and Gold (Au) were utilized as the front and the back metal contacts for the device.

Figure 1
figure 1

Schematic structure of inorganic ZrS2/CuO heterojunction solar cell.

Full size image

Numerical simulation and parameters of materials

In our current research, SCAPS-1D software30,31,32, as a powerful and valuable numerical simulation tool to recognize and clarify the physical phenomena arising in photovoltaic devices, was utilized to simulate and evaluate our inorganic solar cells. The light intensity of AM 1.5 light spectrum (100 mW/cm2), as standard testing conditions (STC), were employed in all SCAPS-1D simulation calculations. Here, impact of bandgap, thickness, and carrier concentration of both the absorber and window layers on the solar cell fundamental parameters were analyzed intensely where different values for input variable were used to obtain optimum values to have higher performance of solar cell devices.

The following Poisson and continuity equation for holes and electrons are used in SCAPS-1D numerical simulation calculations33,34

$$\frac{{d}^{2}}{{dx}^{2}}\Psi \left(x\right)=\frac{e}{{\varepsilon }_{0}{\varepsilon }_{r}} \left(p\left(x\right)-\mathrm{n}\left(\mathrm{x}\right)+{N}_{D}- {N}_{A}+{\rho }_{defect}(\mathrm{p}\left(\mathrm{x}\right),\mathrm{n}\left(\mathrm{x}\right)) \right)$$
(1)
$$\frac{d{J}_{n}}{dx}= \mathrm{G}-\mathrm{R \,and\, } \frac{d{J}_{p}}{dx}= \mathrm{G}-\mathrm{R}$$
(2)

where Ψ, e, ε0, εr, p, n, ND, NA, ρdefect, Jn, Jp, R, and G are electrostatic potential, charge of electron, vacuum permittivity, relative permittivity, hole density, electron density, donor impurities, acceptor impurities, distribution of defects, current densities of electron, current densities of hole, recombination rate, and generation rate, respectively. The parameters of ZrS2 and CuO thin films applied to execute our numerical simulations are scheduled in Table 1 according to Refs.2,25,35,36.

Table 1 Material parameters employed in our simulations2,25,35,36.
Full size table

Results and discussion

Impact of CuO thickness, bandgap, and carrier concentration on basic parameters of solar cells

In this section, we firstly study effect of the absorber layer thickness, band gap, and carrier concentrations on the photovoltaic fundamental parameters (open circuit voltage (Voc), short circuit current density (Jsc), fill factor (FF), and cell efficiency (η)) where the window layer thickness, band gap, and carrier concentration are fixed at 0.2 μm, 1.7 eV, 1019 cm−3, respectively.

Figure 2 demonstrates the gained contour plot of the modelled solar cell basic parameters including Voc, Jsc, FF, and η as the CuO layer thickness and the band gap vary from 1 to 6 μm (the x-axis) and from 1 to 1.5 eV (the y-axis), respectively.

Figure 2
figure 2

The simulated solar cells basic parameters including Voc (a), Jsc (b), FF (c), and η (d) as function on the absorber layer thickness (x-axis) and the band gap (y-axis) at acceptor concentration 1016 cm−3.

Full size image

It is clear from Fig. 2a that Voc increases from about 0.61 V at Eg of 1 eV to about 1 V at Eg of 1.5 eV while the variation of the Voc with CuO thickness rise from 1 to 6 µm for any Eg did not excess more than 0.1 V. The Jsc value is observed to decline from about 39.5 to 17.7 mA/cm2 with the increase of the Eg from 1 to 1.5 eV as presented in Fig. 2b. The Jsc values remain almost constant for each CuO thickness which varied from 1 to 6 µm.

Figure 2c indicates that the FF values are varying in different ways where firstly FF decreases from about 55% to about 41.7% with increasing of the Eg from 1 to 1.5 eV and this at the same time of increasing CuO thickness from about 0.1–1.5 µm (thinner CuO thin films). Secondly, FF grows from about 55% to about 65.8% with raising of the Eg from 1 to 1.5 eV and this take place with CuO thickness increasing from about 1.5–6 µm (thicker CuO thin films) with reducing on the value of FF of about 3%.

Figure 2d reveals that the η values have different zones where η of about 13.3% is detected at the Eg of about 1 eV with thickness increasing from about 0.5 to 6 µm. η with average value of about 12.5% is achieved for almost variation of the Eg from 1 to 1.5 eV expect zone located at the Eg from 1.3 to 1.45 eV and the thickness from 3 to 6 µm where higher performance of about 13.86% is obtained.

These results could be clarified as the band gap increasing, the local collection efficiency of light absorption increase inside the interface of the p-CuO thin film and n-ZrS2 thin film and enhances the carrier generation rate and therefore increasing the value of the Voc dramatically according to the following equation37:

$${V}_{oc}=\frac{{k}_{B}\mathrm{T }}{\mathrm{q}}\mathrm{ln} \left(1+\frac{{I}_{ph}}{{I}_{0}}\right)$$
(3)

Also, this explained whereas based on the ZrS2 and CuO bandgap values, band alignment of a cliff-like is supposed leading to improve the charge separation process2. When the bandgap energy raises, the valence band Ev shifts downward while the conduction band Ec shifts upper producing decreasing on the conduction band offset (ΔEc) value2. The lowered ΔEc helps the charge separation process with more approachable promotion electrons to the absorber layer and transport through the interface into the window layer and therefore enhancement of the Voc2. While band gap increasing producing high hole concentrations close to the interface junction. Therefore, increasing the probability of the recombination rate happens through surface and facing interface recombination. Consequently, this explained reducing of the Jsc with increasing band gap2,38. Moreover, the wavefunction intersecting between vibrational excited states of the lower and the higher lying electronic states produce capture centers for charge carriers38.

The behavior of the FF is always effected by many factors especially the series and shunt resistance as well as partially the Voc values as presented in the following equation39:

$$\mathrm{FF}=\frac{{{\varvec{\upupsilon}}}_{oc}-\mathrm{ln}({{\varvec{\upupsilon}}}_{oc}+0.72)}{{{\varvec{\upupsilon}}}_{oc}+1},$$
(4)

where υoc = qVoc/AkT.

The η behavior could be illustrated by the behavior and the values of the Voc, the Jsc, and the FF where the η given by the following equation40:

$$\upeta =\frac{{FF V}_{oc}{ J}_{sc}}{{ P}_{in}}.$$
(5)

From above results we concluded that to have higher efficiencies solar cells, the CuO band gap and thickness should be in the range of 1.35 eV and from 3 to 6 µm, respectively. Therefore, JV curves with basic parameters of solar cells as function of CuO thickness from 3 to 6 µm at constant band gap of 1.35 eV are simulated as described in Fig. 3. It is clear from such figure that the Voc has value from 0.88 to 0.90 V, the Jsc has constant value of 25.1 mA/cm2, the FF has value from 59.9 to 61.3% and the η has value from 13.2 to 13.86 with increasing thickness from 3 to 6 µm, respectively where the η value follows mainly the Voc, and the FF values.

Figure 3
figure 3

The simulated JV curves with basic parameters of solar cells as function on CuO thickness from 3 to 6 µm.

Full size image

Figure 4 displays the achieved contour plot of the obtained photovoltaic basic parameters consist of Voc, Jsc, FF, and η as function on the CuO thin film thickness and the acceptor concentration differ from 1 to 6 μm (the x-axis) and from 1 × 1014 to 1 × 1021 cm−3 (the y-axis), respectively.

Figure 4
figure 4

The simulated solar cells basic parameters including Voc (a), Jsc (b), FF (c), and η (d) as function on the absorber layer thickness (x-axis) and the carrier concentration (y-axis) at Eg = 1.35 eV.

Full size image

It is apparent from Fig. 4a that the Voc improves from about 0.72 V to 1 eV as acceptor concentration enhances from 1014 to 1021 cm−3 with small variation in the Voc values with rising of CuO thickness. From Fig. 4b, the value of Jsc increases from about 29.5–31.4 mA/cm2 with increasing of acceptor concentration from 1017 to 1021 cm−3 and the value stays constant at about 29.5 mA/cm2 for carrier concentration less than 1017 and this at CuO thickness above 1.5 µm. For CuO thickness less than 1.5 µm, the Jsc continues of about 28.3 mA/cm2 for carrier concentration less than 1018 cm−3, while the Jsc value change for carrier concentration above 1018 cm−3 from 24 to 29.5 mA/cm2 with CuO thickness increasing.

Figure 4c implies that the FF values remain mainly constant at value of about 56% for all carrier concentration and thickness expect for carrier concentration from 1014 to 1017 cm−3, the FF increase from about 50–55% in thickness range from 1 to 3 5 µm. The FF higher value of about 61% is obtained for carrier concentration of 1021 cm−3 and for thickness less than 1 µm.

Figure 4d shows that the η values have the same shape as the Voc where η increase from about 9.8% to about 12.5% as the carrier concentration increase from 1014 to 1017 cm−3 and this with thickness growing. The η value of about 12.5% increase to about 18.9% with rising of the carrier concentration from 1017 to 1021 cm−3.

Such results could be explained as the carrier concentration increasing, the electron diffusion increases from the p-CuO thin film to n-ZrS2 thin film and enhances the value of the device built-in voltage (Vbi) which formed mainly by the depletion width (Wd) and therefore the Voc increases dramatically37,38. Moreover, the photogenerated current (electron hole pairs) (Iph) increase and therefore the recombination rate and the reverse saturation current (Io) will be reduced and therefore enhancement of the Voc values41 as presented in Eq. (3) which clear the relation between the Voc, Iph, and Io _42:

On other hand, the Jsc values improves with increasing of carrier concentration because also enhancement of the photogenerated charge carriers and decreasing of both the leakage current and the recombination current especially for CuO thickness higher than 1.5 µm.

For the absorber thickness less than 1.5 µm and carrier concentration above 1018 cm−3, the Jsc raise with CuO thickness growing could be ascribed to the CuO charge collection length and hence the collection of electron hole pairs in the junction will be improved43. This indicates that the charge carriers will be split up and stored clearly with thickness increasing. For higher carrier concentration than 1018 cm−3 and CuO thickness higher than 1.5 µm, the charge collection length reached the maximum and the carrier collection probability increasing and the recombination rate and leakage current reducing which producing higher values for the Jsc2.

The behavior of the η could be described by the whole behavior of the Voc, the Jsc, and the FF where the η is a factor of these parameters as shown before in Eq. (5)40:

In this case, the shape of the η follows mainly the Jsc shape since the acceptor concentration influence mainly the photogenerated current. Therefore, the external quantum efficiency (EQE) as function on CuO thickness, band gap, and the carrier concentration is recorded as presented in Fig. 5. It is noticeable that EQE have the same shape with all CuO thickness with value of 40% at 200 nm and 100% at 800 nm. With increasing of the band gap from 1 to 1.5 eV, the area under curve for higher EQE part moved downward from 1200 to 800 nm. By increasing the carrier concentration from 1014 to 1021 cm−3, EQE value improve from around 40–52% for wavelength from 200 to 700 nm, while EQE value reduce from 100 to 90% for higher wavelength from 700 to 1050 nm. Moreover, there is intrinsic absorption edge in the short-wavelength region of the spectrum41,42 where it positions change with the variation of the carrier concentration as presented in Fig. 5d and this could be attributed to the reflection from the Au back contact41,42. The results indicate the photogenerated current increasing with high energy photon while decreasing for lower one and this suppose the different generation and recombination rate of charge carriers that controlled the Jsc. The results confirmed and supported that the η will affect mainly by the Jsc. We can conclude from the above simulations that the CuO band gap, thickness, and carrier concentration should be in the range of 1.35 eV, 5.5 µm, and above 1018 cm−3, respectively to achieve higher efficiencies for ZrS2/CuO heterojunction solar cell devices.

Figure 5
figure 5

The simulated external quantum efficiency as function on CuO thickness (a), band gap (b), and the carrier concentration (c,d) respectively.

Full size image

Impact of ZrS2 thickness, bandgap, and carrier concentration on basic parameters of solar cells

Secondly, the influence of the ZrS2 thin film, as window layer, thickness, band gap, and carrier concentrations on the basic parameters of photovoltaic devices will be explored deeply while the CuO layer thickness, band gap, and carrier concentrations are fixed at 5.5 μm, 1.35 eV, 1018 cm−3, respectively.

Figure 6 proves the achieved contour plot of the simulated basic parameters of solar cell as a function on the ZrS2 thin film thickness and the band gap vary from 0.1 to 1 μm (the x-axis) and from 1.3 to 1.8 eV (the y-axis), respectively.

Figure 6
figure 6

The simulated solar cells basic parameters including Voc (a), Jsc (b), FF (c), and η (d) as function on the window layer thickness (x-axis) and the band gap (y-axis) at donor concentration 1019 cm−3.

Full size image

The Voc has different values with different zones as shown in Fig. 6a. It decreases mainly from about 0.96 V to about 0.87 V with band gap increasing from 1.3 to 1.8 eV. For lower band gap from 1.3 eV to about 1.45 eV, the Voc value improving for each individual Eg value with rising ZrS2 thickness. While for intermediate ones from 1.45 eV to about 1.6 eV, the Voc values remains nearly constant with increasing ZrS2 thickness. For higher band gap than 1.6 eV, the Voc reducing with increasing ZrS2 thickness.

Figure 6b appears that the Jsc value remains constant at average of about 33.5 mA/cm2 for the Eg value below 1.55 eV even with increasing ZrS2 thickness. For the Eg from 1.55 to 1.65 eV, the Jsc value also remains nearly constant with thickness rising with rang from 18 to 25 mA/cm2 for each the Eg value. On another hand, for higher Eg values, the Jsc reduces from about 28 mA/cm2 to about 10 mA/cm2 with thickness increasing from 0.1 to 1 µm.

Figure 6c suggests that the FF has different values with the Eg values. For the Eg below 1.55 eV, FF increasing with ZrS2 thickness increasing for each individual value of the Eg. For example, at 1.4 eV, FF value increase from about 64% to about 71% with thickness increasing from 0.1 to 1 µm. For intermediate Eg from 1.55 to 1.65 eV, FF remains constant with thickness growing. For higher Eg than 1.65 eV, FF values enhance with thickness increasing but with smaller values than lower band gaps. Overall, the FF value increases mainly with ZrS2 thickness increasing.

Figure 6d recognizes that the η has different values where it decreases with thickness increasing for the Eg below 1.5 eV. For example, at 1.4 eV, the η increases from about 20% to about 23.6% with thickness growth from 0.1 to 1 µm. While for intermediate Eg values between 1.55 and 1.65 eV, the η values remains nearly constant with thickness increasing. On another hand, for higher Eg, the η reduces with thickness rising for each individual Eg value. Generally, the η has the same shape as the the Voc values.

The obtained results could be elucidated as the band gap rising, more light path through interface junction and therefore increasing photogenerated rate for the charge carries and then separated and collected easily. At the same time the recombination current as well as the leakage current will be reduced. These factors will enhance the the Voc value for band gap less than 1.45 eV as previously discussed as in Eq. (3)37. On the other hand the Voc value increase with thickness increasing and therefore improvement of the charge collection length and consequently increasing of electron hole pairs generation through the junction43. Moreover, the alignment of bandgaps plays important role to improve the Voc value where with small band gap for ZrS2 than 1.45 eV more confinement take place and therefore the intra-band tunneling for carriers at the interface voltage barrier increases and more current generated46. The same description could be applied to explain the behavior of the Jsc values especially for band gap less than 1.55 eV.

By increasing the ZrS2 band gap both the Voc and the Jsc values reduce and this could be attributed to increasing of recombination process as well as the leakage current especially with increasing of ZrS2 thickness2,38. In such case the mismatch between CuO band gap and ZrS2 band gap produce capture centers which increasing the carrier recombination38. The behavior of the FF could be explained where it is a function on the Voc values as shown in Eq. (4). The η values mainly followed the sum of the Voc, the Jsc, and the FF values as presented in Eq. (4)40.

From over results we decided that to have higher efficacies devices, the ZrS2 thickness and band gap would be in the range from 0.7 to 1 µm and 1.4 eV, respectively. So, JV curves with basic parameters of solar cell devices as function of ZrS2 thickness from 0.7 to 1 µm at fixed band gap of 1.4 eV are recorded as shown in Fig. 7. In this case, the Voc has value from 0.96 to 0.97 V, the Jsc has constant value of 34.5 mA/cm2, the FF has value from 70.28 to 71.7% and the η has value from 23.2 to 23.72% with increasing thickness from 0.7 to 1 µm, respectively.

Figure 7
figure 7

The simulated JV curves with basic parameters of solar cells as function on ZrS2 thickness from 0.7 to 1 µm.

Full size image

Figure 8 demonstrates the contour plot of the solar cell basic parameters as a function on the ZrS2 thin film thickness and the carrier concentration differ from 0.1 to 1 μm (the x-axis) and from 1 × 1014 to 1 × 1021 cm−3 (the y-axis), respectively.

Figure 8
figure 8

The simulated solar cells basic parameters including Voc (a), Jsc (b), FF (c), and η (d) as function on the window layer thickness (x-axis) and the carrier concentration (y-axis).

Full size image

It is evident from Fig. 8a that the Voc has different sectors depending mainly on the thickness of ZrS2. For carrier concentration less than 1020 cm−3, the Voc grows from about 0.944 V to about 0.955 V with thickness increasing from 0.1 till 0.5 μm where the Voc value is almost the same for each thickness. While for higher thickness, the Voc value remains nearly constant at about 0.957 V. For carrier concentration of 1020 and 1021 cm−3, the Voc continues almost constant. In general, the Voc value varies for different carrier concentration and thickness of ZrS2 with only small range of about 0.02 V.

The Jsc value stays constant at about 34.5 mA/cm2 for all different carrier concentration and thickness of ZrS2 as presented in Fig. 8b. Only for carrier concentration of 1020 and 1021 cm−3 and with higher thickness than 0.5 μm, the Jsc decreasing from about 34.5 mA/cm2 to 31.5 mA/cm2.

Figure 8c implies that the FF increases in sectors from about 61.5 to about 72.5% with thickness increasing and its value remains constant for each thickness with varying of carrier concentration till 1020 cm−3. While for carrier concentration above 1020 cm−3, the FF increase from about 70% to about 76%.

Figure 8d realizes that the η has different values with different sectors where it increases mainly from about 20% to about 23.5% with thickness increasing from 0.1 to 1 µm especially for carrier concentration less 1020 cm−3 and remains constant for each thickness even with different carrier concentration. There is a curved path in which the η has the highest value from about 23.5% to 23.8%. This path located between thickness of 1 µm and from carrier concentration of 1014 cm−3 to carrier 1020 cm−3, then for higher carrier concentration above1020 cm−3 and with ZrS2 thickness in the range from 0.3 to 1 µm.

It is clear that the increasing of donor concentrations of ZrS2 thin film has no influence on the Voc value especially with lower than 1020 cm−3 with each individual thickness. This may be due to full formation of the depletion width (Wd) which affected on the generation rate of charge carriers and the diffusion length of minority carriers (holes) in n-ZrS2 and (electrons) in p-CuO2. So, the photogenerated current is completely related to depletion Wd and therefore full built-in voltage (Vbi) which mainly constructed on the side of the p-CuO thin film37. On the other hand, the Voc value increase with increasing of ZrS2 thickness for each individual carrier concentration that could be attributed to increase the life time and length of charge collection leading more photogenerated current, therefore leakage current and recombination rate will decline with growing of thin film thickness45.

Such suggestions are validated since the increasing of carrier concentration above 1020 cm−3 produce almost constant value of the Voc even with thickness increasing. Moreover, the constant value of the Jsc with increasing of both thickness and carrier concentration of ZrS2 thin films supported such explanations. Also, the constant Jsc value due to that the window layer does not perform a huge part in the solar spectrum absorbing where it is mainly managed as conducting path for electrons47.

The η values reflect the total behavior of the Voc, the Jsc, and FF where its value mainly follows the Voc, and FF. The photogenerated current is investigated where EQE is simulated as function on ZrS2 thickness, band gap, and the carrier concentration as stated in Fig. 9. It is certain that EQE value reduce from about 72% to around zero with increasing thickness from 0.1 to 1 µm at higher energy and from 100% to around 80% at lower energy. With raising of the band gap, the EQE value downward from 100 to 38% especially for higher wavelength. This reducing for EQE with increasing of thickness and band gap could be attributed to improving of the recombination rate and decreasing the charge carrier collection and therefore decline of the separation of the generated current46. The EQE has the same value and shape with different carrier concentration. EQE results are agreed and supported the obtained values of Jsc for ZrS2 thin thilm thickness, band gap, and carrier concentrations.

Figure 9
figure 9

The simulated external quantum efficiency as function on ZrS2 thickness (a), band gap (b), and the carrier concentration (c), respectively.

Full size image

Figure 10 describes the obtained JV curves with solar cell basic parameters with variation of ZrS2 thin film thickness and carrier concentration. From Fig. 10a, the η value increase from 23.53 to 23.8% with thickness increasing from 0.7 to 1 µm, while the carrier concentration for ZrS2 thin film is fixed at above1020 cm−3. On the other hand, from Fig. 10a and at constant ZrS2 thickness of 1 µm So, the η value increase from 23.67 to 23.8% with increasing of carrier concentration from 1014 to 1020 cm−3. Additionally, our simulations results indicate that to have higher efficiencies of inorganic ZrS2/CuO heterojunction solar cell devices, the CuO band gap, thickness, and carrier concentration would be about 1.35 eV, 5.5 µm, and above 1018 cm−3. While, the ZrS2 band gap, thickness, and carrier concentration would be about 1.4 eV, 1 µm, and less than 1020 cm−3 where the highest efficiency of about 23.8% was achieved with the Voc value of 0.96 V, the Jsc value of 34.2 mA/cm2, and the FF value of 72.2%. Our results indicate that ZrS2/CuO solar cell devices could be comparable with one based on In2S3. The optimum devices of Cu(In, Ga)Se2, CuIn(S,Se)2 and Cu2ZnSnS4 based solar cells, where In2S3 was the buffer layer (50–125 nm thickness), fluorine-doped tin oxide was window layer and gold (Au) was used for back contact, revealed highest efficiencies in the range of 16.94–22.50%49. Additionally, Reyes et al. developed FTO/TiO2/MASnI3/Cu2ZnSnS4/Au as a n-i-p heterojunction perovskite solar cell48. They reported that when the acceptor and defect densities were 1016 cm–3 and 1014 cm–3, respectively, the best values (Voc of 0.96 V, Jsc of 31.66 mA/cm2, FF of 67% and η of 20.28%), were obtained50.

Figure 10
figure 10

The simulated JV curves with basic parameters of solar cells as function on ZrS2 thickness (a) and carrier concentration (b).

Full size image

Impact of operation temperature on JV curves and the basic parameters of optimum ZrS2/CuO solar cell

In this section, the influence of operation temperature on JV curves and the basic parameters of the optimum ZrS2/CuO solar cell was investigated as presented in Fig. 11. It is apparent that increasing of operation temperature minimize the Voc and the Jsc and therefore the η where their values decreasing from 1.05 to 0.87 V, 34.5 to 33.6 mA/cm2, and 24.8 to 22.1%, respectively with rising temperature from 260 to 340 K.

Figure 11
figure 11

The simulated JV curves and the basic parameters of optimum ZrS2/CuO solar cell as function on operation temperature (K).

Full size image

Such results could be explained employing Eq. (3) where the reverse saturation current (Io) increases by temperature increasing as well as the growing of the recombination probability for the charge carriers, and therefore the Voc, the Jsc, and the η values reduce44. The results indicate small variation in the η value especially with the average temperature all over the world and consequently the applicable of ZrS2/CuO solar cell to fabricate higher performance photovoltaic devices.

The explanations for the effect of carrier concentration and bandgap on the fundamental parameters of inorganic ZrS2/CuO heterojunction solar cells could be cleared by the energy band diagram for the window and absorber layers as presented in Fig. 1251,52. The figure indicates that the valence band (VB) and conduction band (CB) energies of ZrS2 and CuO thin films are with good match together which increasing of the generation and separation rates of generated the electron‐hole pairs. In such case, when the heterojunction absorbing photons, the electron‐hole pairs generate and therefore electrons move from CB of CuO thin film to CB of ZrS2 thin film while holes move from VB of ZrS2 thin film to VB of CuO thin film then they are separated at the front and back contacts. By increasing the carrier concentration, the generation of electron‐hole pairs will increase as well as the photocurrent. Moreover, when the band gaps values are 1.35 and 1.4 eV for ZrS2 and CuO thin films, the alignment of band energies will increase and therefore the efficiency will greatly be enhanced.

Figure 12
figure 12

The schematic for the energy band diagram of inorganic ZrS2/CuO heterojunction.

Full size image

Conclusions

In conclusion, novel inorganic ZrS2/CuO heterojunction solar cells was simulated for the first time using SCAPS-1D software. After successfully simulation process, the optimum thickness, carrier concentration, and bandgap for CuO thin film were found to be 1.35 eV, 5.5 µm, and above 1018 cm−3, respectively, and for ZrS2 thin film to be 1.4 eV, 1 µm, and less than 1020 cm−3, respectively to have higher solar cell efficiency. Employing such parameters, the highest η of 23.8% was realized with the Voc value of 0.96 V, the Jsc value of 34.2 mA/cm2, and the FF value of 72.2%. The photogenerated current, the recombination rate, the collection charge carrier length, the minority carrier lifetime, width of the depletion layer, the built-in potential are the elements that manipulated the performance of solar cell basic parameters. Application of our simulation outcomes on the experimental area could help to obtain high-efficiency photovoltaic devices based on ZrS2/CuO heterojunctions.