1 Introduction

Lactic (2-hydroxypropanoic) acid (LA) is a valuable platform chemical with both traditional and modern applications. It was usually used in food and cosmetics, beverage, pharmaceutical, and other fields as a neutralizer, preservative, or acidulant [1]. Recently, LA is applied as the precursor for various biodegradable polymers or building-block for eco-friendly solvents [2]. Also, LA is a resource for polylactic acid (PLA) production, a biodegradable plastic used commercially [3]. PLA has emerged as a green alternative to petroleum-based plastics because of its properties, such as biodegradability, biocompatibility, transparency, and processability [4]. By using sugar substrates, LA can be chemically synthesized or generated via microbial fermentations. In contrast to optically pure l- or d-LA, which can only be generated via fermentation by unique microbial species, LA produced via catalytic reactions is a racemic dl-LA mixture [5]. The demand for PLA now represents 11.4% of the world’s total production of bioplastics or about 18 × 104 metric tons per year, and it is expected to rise by 28% a year through 2025. However, PLA production costs remain high, mostly due to high-cost fermentation media components. To overcome this problem, several waste resources have been in employment as raw materials [6,7,8,9,10]. The biorefinery idea permits the conversion of inexpensive, renewable substrates into added-value chemicals, fuels, and foods for the environmentally responsible and sustainable growth of various industries [11]. So production of LA from corn steep water [12], corn stover [13], pineapple wastes [14], date juice [15], hardwood-pulp hydrolysate [16], and brown rice [17] has been investigated.

The main by-product of the wet-milling industry is corn steep water [18, 19]. Wet milling uses extra sulfur dioxide and natural proteases to reduce soluble protein, soften the kernels, and loosen the starch in the endosperm [20]. Heat damage, brokers, extraneous elements, and shrunken kernels are all variables that affect starch yields and quality [21]. Taking these elements into account raises the amount of free sugars and starch in the steep-water effluent [22]. As a result, the corn-steep industry’s effluents include high levels of sugar and nutrient s(amino acids, nitrogen, vitamins, and trace elements) that support the growth of microbes in a range of fermentation techniques [23, 24]. According to our earlier research, corn steep water comprises sugars, water-soluble vitamins, fat-soluble vitamins, amino acids, non-protein nitrogenous compounds, and inorganic ions [12].

Also, contamination risk is one of the most significant challenges in the lactic acid fermentation field that would decrease fermentation efficiency. This contamination arises from the mesophilic and neutral conditions as well as several nutrients required by most reported LA-producing microorganisms [25, 26]. Therefore, the use of alkaliphilic and thermophilic strains for LA fermentation processes would greatly minimize the potential for contamination and the promotion of non-sterile fermentation [27].

Furthermore, optimization is a crucial method, particularly in large-scale production, to minimize production costs and time [28]. The classic “one-factor-at-a-time” optimization strategy is primarily based on adjusting one factor while keeping the others constant, ignoring the inter-relationships between all parameters, consuming time, and being expensive. However, statistical models such as response surface methodology (RSM) are more cost-effective, effort-reducing, time-saving, efficient, and effective in biochemical and biotechnological process optimization [29, 30].

The factorial experimental design, which requires changing all parameters from one experiment to the next, was chosen to calculate the influence of various variables [31]. Factorial designs are widely used to investigate the effects of experimental factors and the interactions between those factors, that is, how the effect of one factor varies with the level of the other factors in response [32]. The relatively cheap cost, the decreased number of trials, and the improved opportunities to assess interactions between the variables are all benefits of factorial experiments. The two-level full (or fractional) factorization is the most often used first-order model. Each variable is experimentally explored at just two levels, which are stated in coded form: 1 for the low level and + 1 for high level. While fractional models are usually often used when the issue includes a high number of factors, the complete factorial design, which consists of a 2 k experiment (k factors, each trial at two levels), is particularly beneficial for either exploratory research or in the beginning stages of optimization [33,34,35,36]. Our objective in this study was to use sequential optimization techniques for substrates, media, and fermentation conditions for enhancing bioconversion of corn steep water to lactic acid using a newly thermo-alkali tolerant LA bacterium, E. faecium WH51-1 for “free nutrients supply” and “cost-effective production” approaches of LA from corn steep water.

2 Experimental section

2.1 Bacterial strain, fermentative media, and culture conditions

Our research unit collection provided the E. faecium WH51-1 that was used in this investigation. This strain was isolated from dairy products under thermo-alkaline conditions (pH 9 and 50 °C) during our previous studies [12] and identified by 16S rRNA-gene sequencing, and its sequence was deposited in the NCBI GenBank under the accession code MZ093371. This strain was regarded as the most powerful isolate due to its improved stability when exposed to stressors and inhibitory substances that might be present in the waste materials [12]. Modified YE dextrose (mYD) agar medium was used for cultivation of this bacterial strain at optimal conditions (60 g/L of CSW sugar, inocula size 10% (v/v), 45 °C (static condition), and sodium hydroxide as a neutralizing agent for 96 h).

2.2 Materials and substrate collections

In our previous study [12], a corn steep water effluent was harvested from the outflow of a steeping container in a commercial wet milling plant company for maize products on the 10th of Ramadan, El Sharqia Governorate, Egypt, and all samples were kept at − 20 °C for further research. This CSW had analyzed in our previous study [12] for (i) physicochemical characterization (e.g., form, color, appearance, odor, pH, temperature, conductivity, total dissolved solids (TDS), dissolved oxygen, chemical oxygen demand (COD), biological oxygen demand (BOD), total sugars, lactic acid, total water-soluble vitamins, protein total, total fat-soluble vitamins, total amino acid, and total non-protein nitrogenous compounds), (ii) inorganic ion content (e.g. magnesium and manganese), (iii) amino acid content (e.g. threonine, glutamic acid, serine, proline, glycine, aspartic acid, methionine, alanine, cystine, valine, leucine, phenylalanine, isoleucine, tyrosine, arginine, histidine, and lysine), (iv) fat-soluble and water-soluble vitamins (e.g., nicotinic acid, pyridoxine HCL, riboflavin, and nicotinamide), (v) and non-protein nitrogenous components (ethanolamine, ornithine, citrulline, taurine, ɣ-aminobutyric acid).

2.3 Optimization of fermentation conditions using one factor at a time (OFAT)

All optimization experiments were conducted in 250 mL Erlenmeyer flasks containing 100 mL working volume. The effect of different YE concentrations (viz., 0, 1, 2, 3, and 5 g/L) and different pH values (viz., 8, 8.5, 9, and 9.5) were investigated.

2.4 Statistical optimization using the CCD model

The statistical optimization was conducted through RSM. The most common and highly effective RSM technique used for optimization is the CCD which describes the correlation between the factors and response (here were consumed sugar, LA acid concentration, LA yield, and LA productivity) using cube points to fit a linear (first-order) model to evaluate the main and interaction effects between factors, the axial points to estimate the quadratic (second-order) polynomial terms, and center points in the cube that contribute to detecting the degree of curvature (quadratic effects) between low and high levels of each factor and also evaluating the pure experimental error. The mathematical and graphical outputs of the CCD statistical data analysis allow the model to create optimization curves that predict the final optimal settings of the interacted factors that increase LA production and minimize the residual sugar content in culture media. A two-level-five-factor (25) full factorial CCD was used to estimate the effect of sugar concentrations, temperature, pH, inocula sizes, and YE (with and without). The CCD matrix, including the actual values of the experimental runs at the five levels within each factor, is given in Table 1. Each estimated response variable, obtained from the CCD results, was fitted on a full quadratic (second-order polynomial) multiple regression design as a function of four continuous factors (sugar concentrations, temperature, pH values, and inocula sizes) at each level of categorical factors YE (with and without). Analysis of variance (ANOVA) was utilized to determine the statistical significance of the linear, squared (quadratic), and interaction terms.

Table 1 Experimental design and results for optimization of 25 full factorial CCD of consumed sugar (g/L), LA production (g/L), lactic acid yield (g/g), and total LA productivity (g/L.h) in response to all combinations of low and high levels of interacted factors
Full size table

2.5 Design and setup of experiments

All experiments were conducted in 250-mL Erlenmeyer flasks containing 100 mL working volume. To identify the impact of CSW concentration on the generation of LA by strain WH51-1, sixty-two Erlenmeyer flasks were divided into 31 flasks with the YE (5 g/L) and 31 flasks without any supplementation of YE. Five levels of sugar concentrations (20, 40, 60, 80, and 100 g/L), five levels of temperatures (35, 40, 45, 50, and 55 °C), five levels of inocula sizes (5, 7.5, 10, 12.5, and 15%), and five levels of pH values (7.5, 8, 8.5, 9, and 9.5) were investigated. To control the pH during the 96 h fermentation, a neutralized substance NaOH 5 N was applied (Table 1).

2.6 Response surface methodology validation

The response optimizer, a tool included in the Minitab® DoE (Design of Experiments) statistical package, was used to generate the optimization curves to determine the final combination settings of the interacted factors that maximize LA productivity and LA yield. Individual (d) and composite (D) desirability were used to assess how well (from 0 to 1 scale) the predicted settings maximize the response. This stage was ended by additional confirmation experiments (n = 10 replicated runs) to validate the predicted settings resulting from the optimization curves.

2.7 Statistical and analytical analysis

All the experimental data of RSM models were generated and analyzed using Minitab® version 18 (2017) extended with statistical and graphical software packages. Then, the power of the model was assessed by evaluating the coefficient of determination (R2) obtained from the analysis of variance (ANOVA). Using the same software, the results expressed as a mean ± standard deviation were analyzed by the analysis of variance (ANOVA) test, followed by comparisons of the means between them by the Fisher test at the 0.05 probability threshold. Then, Sigma Plot v14.0 SPW was used for plotting the surface plots.

For fermentation experiments, consumed sugar was analyzed by a phenol sulfuric acid method using glucose as standard [37] where the phenol and hot sulphuric acid were added and incubated in a steam water bath and then measure at absorbance 490 nm. The concentration of residual sugars was calculated against standard glucose concentrations of 2– 20 g/L (Table 2). The concentration of sugar content was calculated using a calibration curve obtained with standard solutions (Fig. 1).

Table 2 A standard curve of glucose representing the relation between glucose concentration (g/L) and their corresponding OD at 490 nm using the phenol sulfuric acid method
Full size table
Fig. 1
figure 1

A standard curve for glucose by phenol sulphuric acid method. Note: dilution 1:100

Full size image

Lactic acid analysis was performed according to [38] where the acetaldehyde is released from lactic acid by hot sulfuric acid. The acetaldehyde is reacted with copper and p-phenyl phenol (pPP) for yielding a chromogen absorbs at 570 nm. 0.5 ml of the supernatant is mixed with concentrated sulphuric acid, CuSO4 reagent pPP reagent were added and mixed well. The concentration of lactic acid was calculated against standard LA concentrations of 2.2–22.0 g/L (Table 3). The concentration of lactic acid was calculated using a calibration curve obtained with standard solutions (Fig. 2). The result is expressed as lactic acid, and the yield (%) was calculated as the gradient of the curve obtained by plotting product concentration against substrate concentration.

Table 3 A standard curve of LA representing the relation between lactic acid concentration (g/L) and their corresponding O.D. at 570 nm
Full size table
Fig. 2
figure 2

A standard curve for lactic acid (g/L). Note: dilution 1:1000

Full size image

LA yield (g/g) based on consumed sugars was calculated as the ratio of LA (g/L) to CSW sugar (g/L). LA productivity (g/L.h) is the ratio of LA synthesized to the time of fermentation. Maximum LA productivity was determined by the difference between LA concentrations of two respective samples divided by the time difference. Maximum lactic acid synthesis (g/L.h) was calculated by dividing the difference into LA levels between two different samples by the time interval.

(Eq. 1 LA yield (g/g) calculation):

$$\mathrm{\% Yield}=\mathrm{Grams of LA produced}/\mathrm{Grams of total sugar consumed}\times 100$$
(1)

(Eq. 2 LA productivity (g/L/h) calculation):

$$\mathrm{LA productivity}=\mathrm{Grams of LA produced}/\mathrm{The time of fermentation}$$
(2)

3 Results and discussion

3.1 Determination of significant factors for LA production in batch fermentation

In our previous study [12], a lactic acid concentration of about 44.6 g/L with high yield (0.89 ± 0.02 g/g) was obtained using 60 g/L of CSW-sugar, inocula size 10% (v/v), 45 °C, and NaOH as a neutralizing substance. So, we studied the effect of other optimized factors for enhancements of lactic acid concentration.

3.1.1 Effect of different concentrations of YE on LA production

Different concentrations of YE ranged (0.0˗5.0, g/L) in mYD media at 45○C for 96 h with the addition of sodium hydroxide as a pH neutralizing agent. Data represented in Table 4 showed that the maximum total viable cell was decreased from 178.66 ± 1.5 × 1010 CFU/mL at YE of 5 g/L (v/v) reaching 169 ± 4.0 × 1010 CFU/mL at complete removal of YE. In contrast, the sugar consumption by WH 51–1 strain was slightly decreased from 53.7 ± 0.5 at 5 g/L to 52.2 ± 2.0 g/L at complete removal of YE. However, the final LA concentration was increased from 44.6 ± 0.78 g/L obtained in our previous study [12] to 46.56 ± 2.6 g/L using 5 g/L (v/v) YE with a slight decrease at 46.50 ± 1.0 g/L at complete removal of YE indicating that LA concentration is not affected with YE supplementation. Also, the lactic acid yield and productivity also achieved the highest value of 0.89 ± 0.01 g/g and 0.48 ± 0.00 g/L.h, respectively. The previous results described the acidity of CSW and its contents of total sugars, total sulfites, total free amino acids, total reducing sugars, and total nitrogen, showing the value of CSW as a substrate for fermentation [39]. CSW has been utilized as a source of additional nutrients in fermentation processes and growth media [40]. Maddipati et al. [41] reported claimed that CSW was chosen as an alternative to YE for syngas fermentation since it is rich in nutrients and less expensive than YE [42]. Moreover, different non-protein nitrogenous compounds such as citrulline, ethanolamine, taurine, ornithine, and ɣ-aminobutyric acid were present in CSW [12] that have biostimulant properties that have biostimulant properties [43], source of sulfur for the growth of aerobic microorganisms [44]. Additionally, many aerobic bacteria are believed to use it as their main source of energy [45]. Denger et al. [46] reported the growth of two Rhodococcus spp. using taurine as a sole nitrogen source. Finally, the complete removal of YE was a high challenge to be selected as a free nutrient supplementation for LA synthesis by E. faecium WH51-1.

Table 4 Effect of different concentrations of YE on the growth, sugar consumption, LA concentration, LA yield, LA productivity, and maximum LA productivity by E. faecium WH51-1
Full size table

3.1.2 Effect of pH values on LA production by E. faecium WH51-1

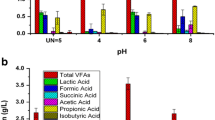
To determine the influence of initial pH values on LA production, fermentation processes were conducted at different pH values (8, 8.5, 9, and 9.5) at all previous optimal parameters. Data obtained in Table 5 summarized the fermentation parameters and profiles for LA production at different values of pH. The cell growth was increased from 171.3 ± 6.6 × 1010 CFU/mL at pH 8.0, reaching the maximum value of 178.0 ± 1.5 × 1010 CFU/mL at pH 8.5. The total viable cell was decreased from 171 ± 6.1 × 1010 CFU/mL at pH 9 and gave the lowest values of 167 ± 1.15 × 1010 CFU/mL at pH 9.5.

Table 5 Effect of different pH values on the growth, sugar consumption, LA concentration, LA yield, LA productivity, and maximum LA productivity by E. faecium WH51-1
Full size table

In contrast, the sugar consumption by WH 51–1 strain was increased from its minimal value of 52.3 ± 1.7 g/L at pH 8 to give the highest value of 53.7 ± 0.55 g/L at pH 8.5 while it decreased after that to reach 46.5 ± 1.3 g/L at pH 9.5 using at 100 g/L. A similar pattern was given for the LA production. The final LA concentration was increased from 46.5 ± 1.3 g/L at pH 8, achieving the highest value of 48.2 ± 2.7 g/L at pH 8.5, and decreased after that reaching its minimal value of 42.6 ± 1.1 g/L at higher pH value (9.5). On the other hand, LA yield showed a comparable range of 0.88–0.89 g/g of sugars consumed at pH 8 – 9.5. LA productivity was also increased at pH8.5 and reached 0.50 ± 0.03 g/L.h, while it decreased after that obtaining the minimal value of 0.44 ± 0.01 g/L.h at pH 9.5. The maximum LA productivity ranged from 1.12±0.05 to 1.55 ± 0.08 g/L.h giving the maximum value at 8.5 of pH value. pH plays a key role in the fermentation process, as it determines the final metabolites produced (that is, LA or the organic acid composition) and thus affects the final LA titer and yield based on consumed sugars [47].

3.2 Optimization of LA production by response surface methodology (RSM)

RSM was conducted to establish the optimum conditions (variables) to maximize the final LA concentration, consumed sugar, LA yield, LA productivity, and finally the maximum productivity of LA.

3.2.1 Response surface methodology for LA concentrations

Main and interaction effects (ANOVA)

A factorial analysis of variance (ANOVA) was used to determine variations in LA concentration. in response to different factors. The p values and correlation coefficient (r2) were used to determine the significance (p ≤ 0.05) of the model and how well the model fits the experimental results. Data represented in Table 4 showed the main and two-way interaction effects, coefficients of the model, and significance (p-value) for the full 25 full factorial CCD for LA production. Factor interaction is beneficial when the change in response from low to high levels of one factor is dependent on the level of another factor; the interaction effects were also investigated using the ANOVA model (Table 6). Our findings suggest that maximizing the five independent factors produces positive agreement with experimental findings (i.e., OFAT experiments). The greatest LA concentration (48.2 ± 2.7 g/L) was achieved by E. faecium WH51-1 at 60 g/L sugar CSW concentration, 45 °C, pH 8.5, inocula size (10%, (v/v), and NaOH as a neutralizing substance. The results of this study showed that the LA produced by the optimized fermentation conditions was 10% larger than that produced by OFAT optimization methods, and this statistical design model proved to be a good method for optimizing LA output. Alrefaey et al. [48] have shown that RSM is an effective tool for assessing the effect of variables on the generation of LA by E. faecium S6. De Lima et al. [49] have found that RSM is an excellent strategy for optimizing LA synthesis by Lactobacillus sp. from cheese whey with CSW as a substrate.

Table 6 Results of ANOVA model to test for differences in LA production from CSW by E. faecium WH51-1 in response to different factors. Significant differences are denoted in bold (r2 = 95.50%)
Full size table

Except for inocula sizes and pH, the interaction between all two-way terms was not significant. All the squared terms were significant, showing a curvature relationship between the factors and LA production. With a 95% confidence level, all other terms were significant. The produced LA might thus be stated using the following equation (Eq. 3 with uncoded factors and its effects):

With yeast extract

Lactic acid (g/L)

 = 

 − 1713 + 3.237 sugar conc. + 11.93 temp. + 0.49 inocula size

 + 328.1 pH − 0.023970 sugar conc. × sugar conc

 − 0.1189 temp. × temp. − 0.5575 inocula size × incula size

 − 19.82 pH × pH + 0.00070 sugar conc. × temp

 + 0.0072 sugar conc. × inocula size − 0.0405 sugar conc. × pH

 + 0.0085 temp. × inocula size − 0.119 temp. × pH

 + 1.312 inocula size × pH

Without yeast extract

Lactic acid (g/L)

 = 

 − 1717 + 3.219 sugar conc. + 11.93 temp. + 0.51 inocula size

 + 328.6 pH − 0.023970 sugar conc. × sugar conc

 − 0.1189 temp. × temp. − 0.5575 inocula size × inocula size

 − 19.82 pH × pH + 0.00070 sugar conc. × temp

 + 0.0072 sugar conc. × inocula size − 0.0405 sugar conc. × pH

 + 0.0085 temp. × inocula size − 0.119 temp. × pH

 + 1.312 inocula size × pH

In the previous equations, positive values indicated that increasing the parameters boosted LA production. Similarly, increasing the negative values reduced LA production. The amount of LA produced as a function of initial pH, temperature, inocula size, and initial CSW concentrations in the absence and presence of YE, in addition to their interactions, can be estimated using Eq. (3).

The main effect plots (Fig. 3) were designed to represent the prediction analysis results by showing average deviations between high and low levels within each factor. The results revealed that sugar concentration, temperature, inocula sizes, and pH values had a significant difference between low and high levels while the YE had no significant effect on LA concentrations.

Fig. 3
figure 3

Main effects plots explain the changes in lactic acid production from CSW by E. faecium WH51-1 between low and high levels of each factor

Full size image

3.3 The Pareto charts and normal probability plots

The Pareto chart was used to determine the relative importance and significance of the main and interaction effects (Fig. 4A). Factors that influence the LA fermentation were evaluated by using the Pareto chart plot after 96 h.

Fig. 4
figure 4

Pareto chart (A) and normal probability plot (B) of standardized effects lactic acid production from CSW by E. faecium WH51-1

Full size image

Pareto chart of the standardized effects for cell count (Fig. 2A) revealed that the main effect of sugar concentrations (A), temperature (B), inocula sizes (C), and pH values (D) and the interaction between them (AA, BB, CC, DD, CD) are extended beyond the reference line and indicating a significant effect of these terms at level of p ≤ 0.05, while the relative importance of each term is represented by the column length.

The normal probability plot determines the real (actual) effect of each term; therefore, it is indicating if the results occurred by chance (random) or not. Furthermore, normal probability plots determine whether the term has a negative or positive effect on the response, with a positive effect indicating that an increase in the factor causes an increase in the response and vice versa for a negative effect. Each effect is represented by a single point on the plot, and points close to a fitted line (refers to the position where the effects were zero) represent estimated factors that have no significant effect on the response, whereas points far away from the fitted line represent the actual (real) term effect. The main terms of inocula size (C), sugar concentration (A), temperature (B), and YE (E), followed by the interaction of pH and inocula size (CD), are far from the fitted straight line, indicating a strong significant impact on LA; additionally, their contribution had a positive effect because it is located on the right side of the graph (Fig. 2B). On the other hand, pH (D), the interaction between sugar concentrations (AA), the interaction between pH (DD), and the interaction between temperatures (BB) are all located to the left of the fitted line, indicating a significant negative effect on LA production (Fig. 4B). Our findings indicated that the main term specially sugar concentration was significantly affected in the production of lactic acid. Similarly, several scientists noted that, up to a certain point, initial sugar concentrations increased the LA concentration [15, 50, 51]. Sugar is one of the major factors in the economic production of lactic acid [52].

Contour plots of lactic acid production (g/L)

Based on the importance of the main and two-way interaction effects, contour plots were created to visually fit the increasing LA production of each two-factor while keeping the third factor that is not included in the plot constant. The contour plot is a two-dimensional graph in which all points, one from each plotted factor, with the same response value are connected to form a zonation (i.e., contour lines) from minimum to maximum response (count) values.

Surface plots for lactic acid production (g/L)

A surface-wireframe plot is a three-dimensional graph that depicts the relationship between the response and each of the two interdependent process factors. A 3D grid (wireframe) plot of the relationship shows the optimum peaks of the highest response values. Bingol et al. [40] reported that the function response surface plots are useful for understanding both the main and interaction factor effects.

A typical simple maximum pattern occurred in the contour and surface plots of LA production between the same interactions (Figs. 5 and 6) where the lactic acid was increased to 48 g/L at sugar concentrations ranging from 50 to 65 g/L and pH values ranging from 7.9 to 8.9 (Figs. 5A and 6A). On the other hand, the lactic acid was increased to 50 g/L at inocula size ranging from 8 to 13% and pH values ranging from 8 to 8.5 (Figs. 5B and 6B). Also, the LA concentration was increased to 50 g/L at a temperature of about 47 °C and inocula sizes ranging from 9 to 13% (Figs. 5C and 6C). In the case of temperatures, about ≈ 46 °C and pH values ranging from 8 to 8.5 the LA maximized to 50 g/L (Figs. 5D and 6D). Otherwise, LA concentration reached 50 g/L at a sugar concentration of ~ 60 g/L and inocula sizes ranging from 9 to 13% (Figs. 5E and 6E) and temperature ranging from 43 to 53 °C (Figs. 5F and 6F).

Fig. 5
figure 5

a The main and two-way interaction effects on LA concentrations between the two factors (inocula size and sugar concentrations), while keeping other factors that were not included in the plot constant. b The main and two-way interaction effects on LA concentrations between the two factors (pH and sugar concentrations), while keeping other factors. c The main and two-way interaction effects on LA concentrations between the two factors (temperature and sugar concentrations), while keeping other factors. d The main and two-way interaction effects on LA concentrations between the two factors (pH and inocula size), while keeping other factors. e The main and two-way interaction effects on LA concentrations between the two factors (pH and temperature), while keeping other factors. f The main and two-way interaction effects on LA concentrations between the two factors (inocula size and temperature), while keeping other factors.

Full size image
Fig. 6
figure 6

A The relationship between LA concentrations and each of the two interdependent process factors (sugar concentrations and pH). B The relationship between LA concentrations and the two interdependent process factors (inocula size and pH). C The relationship between LA concentrations and each of the two interdependent process factors (temperature and inocula size). D The relationship between LA concentrations and each of the two interdependent process factors (temperature and pH). E The relationship between LA concentrations and each of the two interdependent process factors (sugar concentrations and inocula size). F The relationship between LA concentrations and each of the two interdependent process factors (sugar concentrations and temperature)

Full size image

3.3.1 Response surface methodology for LA yield (g/g)

Main and Interaction effects (ANOVA)

ANOVA was used to detect the differences in LA yield in response to different conditions. Table 7 explains the main, square, two-way interaction effects and significance (p value) for the full 25 full factorial CCD. Data obtained in Table 7 and represented graphically in Fig. 7 summarized that all squared terms are significant, indicating that the relationship between the factors and the consumed sugar follows a curved line except YE. All other effects were significant with a 95% confidence level. In this way, the consumed sugar content in CSW could be expressed using the following equation (Eq. (4), regression equation in uncoded units):

Table 7 Results of ANOVA model to test for differences in LA yield (g/g) of CSW by E. faecium WH51-1 in response to different factors. Significant differences are denoted in bold (r2 = 89.39%)
Full size table
Fig. 7
figure 7

Main effects plots explain the changes in LA yield (g/g) of CSW by E. faecium WH51-1 between low and high levels of each factor

Full size image

With yeast

extract

LA yield (g/g)

 = 

 − 3.577 + 0.00158 sugar conc. + 0.04994 temp

 + 0.0843 inocula size + 0.6781 pH

 − 0.000041 sugar conc. × sugar conc. − 0.000260 temp. × temp

 − 0.001142 inocula size × inocula size − 0.03604 pH × pH

 − 0.000041 sugar conc. × temp. + 0.000081 sugar conc. × inocula size

 + 0.000531 sugar conc. × pH − 0.000925 temp. × inocula size

 − 0.001625 Temp. × pH − 0.00275 inocula size × pH

Without yeast

extract

LA yield (g/g)

 = 

 − 3.426 + 0.00085 sugar conc. + 0.04785 temp

 + 0.0848 inocula size + 0.6756 pH

 − 0.000041 sugar conc. × sugar conc. − 0.000260 temp. × temp

 − 0.001142 inocula size × inocula size − 0.03604 pH × pH

 − 0.000041 sugar conc. × temp. + 0.000081 sugar conc. × inocula size

 + 0.000531 sugar conc. × pH − 0.000925 temp. × inocula size

 − 0.001625 temp. × pH − 0.00275 inocula size × pH

The main effect plots (Fig. 7) were designed to represent the prediction analysis results by showing average deviations between high and low levels within each factor. The results revealed that temperature, sugar concentration, pH values, and inocula sizes had a significant difference between low and high levels, while the YE had no significant effect on LA yield.

The Pareto charts and normal probability plots

The dashed line in Fig. 8A represented the smallest statistically significant effect, where the values before that line have no significant effects [53]. The t test was performed to assess whether the estimated effects differed from zero.

Fig. 8
figure 8

Pareto chart (A) and normal probability plot (B) of standardized effects in LA yield (g/g) of CSW by E. faecium WH51-1

Full size image

Pareto chart of the standardized effects for LA yield (Fig. 8A) revealed that the main effect of sugar concentrations (A) and inocula sizes (C) and the interaction between them (AA, DD, BC, CC, BB, BE AE, AD, AC, AB, BD) are extended beyond the reference line, indicating a significant effect of these terms at level of p ≤ 0.05, while the relative importance of each term is represented by the column length. The main terms of the interaction of sugar concentration and YE (AE), temperature and YE (BE), sugar concentration and inocula size (AD), and sugar concentration and inocula sizes (AC) are far from the fitted straight line, indicating a highly significant impact on LA yield; also, their contribution had a positive effect because it is located on the right side of the graph (Fig. 8B). Additionally, the interaction between sugar concentrations (AA), the interaction between temperatures (BB), the interaction between pH (DD), the interaction between inocula sizes (CC), sugar concentrations (A), and the interaction between them (AB, BD, BC) are all located to the left of the fitted line, indicating a significant negative effect on LA production (Fig. 8B). Our results indicated that the interaction between sugar concentration was significantly increase the LA yield.

Contour and surface plots of LA yield (g/g)

The surface plots of the response functions are useful in understanding both the main and interaction effects of the factors [54]. Figure 9 and 10 represent the contour and surface plots of LA yield between the same interactions with a similar pattern where the LA yield increased to more than 0.90 g/g at sugar concentrations ranging from 50 to 70 g/L and wide range temperature ranging from 40 to 46 °C (Figs. 9A and 10A). Otherwise, LA yield increased to more than 0.91 g/g at inocula size ranging from 10 to 12.5% and pH values ranging from 8 to 8.5 (Figs. 9F and 10F). Additionally, LA yield increased to more than 0.91 g/g at the temperature of about 45 °C, and inocula sizes ranged from 7.5 to 12.5% (Figs. 9D and 10D). In the case of temperatures about ≈ 46 °C and pH values ranging from 8 to 8.5, LA yield maximized to more than 0.91 g/g (Figs. 9E and 10E). On the other hand, LA yield reached to more than 0.90 g/g at a sugar concentration of ~ 60 g/L and inocula sizes ranging from 7.5 to 12.5% (Fig. 9B and 10B) and temperature ranging from 43 to 53 °C (Figs. 9A and 10A). The results in this study indicated that the maximum lactic acid yield was observed at thermo-alkaline conditions. Production in thermo-alkaline temperatures would be very helpful in reducing contamination risk and facilitating non-sterile fermentation, which uses less energy during production [27].

Fig. 9
figure 9

a The main and two-way interaction effects on LA yield (g/g) between the two factors (temperature and sugar concentrations), while keeping other factors that were not included in the plot constant. b The main and two-way interaction effects on LA yield (g/g) between the two factors (inocula size and sugar concentrations), while keeping other factors. c The main and two-way interaction effects on LA yield (g/g) between the two factors (pH and sugar concentrations), while keeping other factors. d The main and two-way interaction effects on LA yield (g/g) between the two factors (inocula size and temperature), while keeping other factors. e The main and two-way interaction effects on LA yield (g/g) between the two factors (pH and temperature), while keeping other factors. f The main and two-way interaction effects on LA yield (g/g) between the two factors (pH and inocula size), while keeping other factors

Full size image
Fig. 10
figure 10

A The relationship between LA yield and each of the two interdependent process factors (sugar concentrations and temperature). B The relationship between LA yield and the two interdependent process factors (sugar concentrations and inocula size). C The relationship between LA yield and each of the two interdependent process factors (sugar concentration and pH). D The relationship between LA yield and each of the two interdependent process factors (temperature and inocula size). E The relationship between LA yield and each of the two interdependent process factors (temperature and pH). F The relationship between LA yield and each of the two interdependent process factors (inocula size and pH)

Full size image

3.3.2 Response surface methodology for lactic acid productivity (g/L.h)

Main and interaction effects (ANOVA)

The main and interaction effects were presented in Table 8. All main and square effects were highly significant, with R2 of 95.50%.

Table 8 Results of ANOVA model to test for differences in lactic acid productivity (g/L.h) from CSW by E. faecium WH51-1 in response to different factors. Significant differences are denoted in bold (r2 = 95.50%)
Full size table

In this way, the LA productivity could be expressed using the following equation (Eq. (5), regression equation in uncoded units):

With yeast

extract

Total productivity (g/L.h)

 = 

 − 17.84 + 0.03372 sugar conc. + 0.1243 temp

 + 0.0051 inocula size + 3.418 pH

 − 0.000250 sugar conc. × sugar conc

 − 0.001238 temp. × temp

 − 0.005807 inocula size × inocula size − 0.2065 pH × pH

 + 0.000007 sugar conc. × temp

 + 0.000075 sugar conc. × inocula size

 − 0.000422 sugar conc. × pH + 0.000089 temp. × inocula size

 − 0.00123 temp. × pH + 0.01366 inocula size × pH

Without yeast

extract

Total productivity (g/L.h)

 = 

 − 17.88 + 0.03354 sugar conc. + 0.1242 temp

 + 0.0053 inocula size + 3.423 pH

 − 0.000250 sugar conc. × sugar conc

 − 0.001238 temp. × temp

 − 0.005807 inocula size × inocula size − 0.2065 pH × pH

 + 0.000007 sugar conc. × temp

 + 0.000075 sugar conc. × inocula size

 − 0.000422 sugar conc. × pH + 0.000089 temp. × inocula size

 − 0.00123 temp. × pH + 0.01366 inocula size × pH

The main effect plots (Fig. 11) were created to represent the results of the prediction analysis by displaying the average deviations between high and low levels within each factor. Temperature, sugar concentration, pH values, and inocula sizes were found to be significantly different between low and high levels, while YE did not affect LA productivity.

Fig. 11
figure 11

Main effects plots explain the changes in lactic acid productivity (g/L.h) of CSW by E. faecium WH51-1 between low and high levels of each factor

Full size image

The Pareto charts and normal probability plots

The main effect of sugar concentrations (A), temperature (B), inocula sizes (C), and pH values (D) and the interaction between them (AA, BB, CC, DD, CD) are extended beyond the reference line, indicating a significant effect of these terms at the level of p ≤ 0.05, while the relative importance of each term is represented by the column length (Fig. 12A).

Fig. 12
figure 12

Pareto chart (A) and normal probability plot (B) of standardized effects in lactic acid productivity (g/L.h) of CSW by E. faecium WH51-1

Full size image

The main terms of the interaction of pH and inocula size (CD), inocula size (C), sugar concentration (A), temperature (B), and YE (E) are far from the fitted straight line, indicating a highly significant impact on consumed sugar; additionally, their contribution was positive because it is located on the right side of the graph (Fig. 6B). Furthermore, the interactions between sugar concentrations (AA), temperatures (BB), pH (DD), and pH (D) are all located to the left of the fitted line, indicating a significant negative effect on LA productivity (Fig. 12B). From previous observation, the inocula size was increase the LA productivity significantly. According to Aboseidah et al. [55], the best inocula size for E. faecalis KY072975’s LA fermentation was 5 percent (v/v), and this resulted in a progressive increase in LA productivity. Vishnu et al. [56] reported that the best inoculum concentration for Lactobacillus amylophilus GV6 to produce LA was 10% (v/v). According to Panesar et al. [57], Lacticaseibacillus casei NBIMCC 1013 was able to produce the most LA at a rate of 33.72 g/L with an inocula size of 2–4% (v/v).

Contour and surface plots of lactic acid productivity (g/L.h)

Figures 13 and 14 show the contour and surface plots of total LA productivity between the same interactions with a similar pattern, where the LA productivity increased to 0.5 g/L.h at sugar concentrations ranging from 50 to 65 g/L and pH values ranging from 7.9 to 8.9 (Figs. 13A and 14A). Otherwise, at inocula sizes ranging from 8 to 13% and pH values ranging from 7.9 to 9, the LA productivity increased to 0.5 g/L.h (Figs. 13B and 14B). Furthermore, at a temperature of about 45 °C and inocula sizes ranging from 9 to 13%, the LA productivity increased to 0.5 g/L.h (Figs. 13C and 14C). When the temperature was around 46 °C and the pH value ranged from 8 to 8.5, the LA productivity increased to 0.5 g/L.h (Figs. 13D and 14D). Otherwise, at sugar concentrations of 60 g/L and inocula sizes ranging from 9 to 13% (Figs. 13E and 14E) and temperatures ranging from 43 to 53 °C, LA productivity reached 0.5 g/L (Figs. 13F and 14F). Our results indicated that all main effects such as sugar concentrations, inocula size, temperature, pH, and the interaction between some of them except yeast extract. Although the yeast extract (YE) leads to the highest lactic acid concentrations in a variety of nitrogen sources due to the purine and pyrimidine bases and B vitamins [58, 59], we have been successful in eliminating the extra supplementation of any nutrient to the CSW and using it as the sole media. The cost of yeast extract alone formed about 38% of the total production costs [60].

Fig. 13
figure 13

a The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (temperature and sugar concentrations), while keeping other factors that were not included in the plot constant. b The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (inocula size and sugar concentrations), while keeping other factors. c The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (pH and sugar concentrations), while keeping other factors. d The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (inocula size and temperature), while keeping other factors. e The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (pH and temperature), while keeping other factors. f The main and two-way interaction effects on LA productivity (g/L.h) between the two factors (pH and inocula size), while keeping other factors

Full size image
Fig. 14
figure 14

A The relationship between LA productivity (g/L.h) and each of the two interdependent process factors (sugar concentrations and pH). B The relationship between LA productivity (g/L.h) and the two interdependent process factors (inocula size and pH). C The relationship between LA productivity (g/L.h) and each of the two interdependent process factors (temperature and inocula size). D The relationship between LA productivity (g/L.h) and each of the two interdependent process factors (temperature and pH). E The relationship between LA productivity (g/L.h) and each of the two interdependent process factors (sugar concentration and inocula size). F The relationship between LA productivity (g/L.h) and each of the two interdependent process factors (sugar concentrations and temperature)

Full size image

Alternative, less expensive nitrogen sources are therefore highly desired. In reality, it has been reported that YE has been partially and completely replaced with low-cost nitrogen supplies from inorganic nitrogen sources and agricultural byproducts. Even when several of these inexpensive nitrogen sources were mixed with YE, only a few of them produced lactic acid concentrations as high as those attained with YE by itself. The media that produced the same levels of lactic acid either required longer fermentation times or more expensive ingredients like peptone and vitamins [61,62,63,64]. The amount of YE in the medium must therefore be replaced with less expensive components to maintain good productivity and lactic acid yield. CSW, a by-product of the corn wet-milling industry, might be able to aid with this problem. CSW is rich in amino acids, polypeptides, and significant levels of B-complex vitamins, making it an excellent supply of nitrogen for the majority of bacteria [12]. So, our study is the first study that not only removing the extra supplementation of any nutrient to the CSW and using it as the sole media, but also maximizing the sugar utilization and LA production from CSW as raw material and the feasibly of the CSW effluent as a cheap alternative substrate for a biorefinery to lactic acid using potential strain as WH51-1 capable to grow and convert sugars in CSW to LA based on a specific screening protocol.

3.4 The optimization curves

The optimization curves (Fig. 15) were generated using the response optimizer tool to determine the final optimal settings of the factors that maximize LA concentration, consumed sugar, and LA productivity. Ten replicated confirmatory runs were prepared and incubated under the optimal conditions of initial sugar concentration 62.8 g/L, temperature 46.5 °C, and pH 8 to achieve the best results, which included maximizing lactic acid production to 53.0 g/L (individual desirability = 100 percent), increasing consumed sugar to 58.34 g/L (individual desirability = 100 percent), and maximizing LA productivity to 0.55 g/L.h. The confirmatory run results were plotted to compare the actual values (mean ± standard deviation) with the predicted values by the model (Fig. 16). The results revealed that the mean actual LA concentration was 53.5 ± 0.14 g/L, consumed sugar was 58.1 ± 0.48 g/L, and LA productivity was 0.55 ± 0.00 g/L.h.

Fig. 15
figure 15

The optimization curves show how the factors affect the predicted responses (y) including maximum LA production, maximum LA yield and maximum LA productivity, at low and high levels. The optimum factor settings (Cur) were predicted with a composite desirability (D) = 97.78%., 96.52%, and 97.78%, respectively

Full size image
Fig. 16
figure 16

Scatter plot, comparing the actual (n = 10) and predicted (Pred.) values of LA concentration (A), LA yield (B), and LA productivity (C). Error bars represent standard deviations

Full size image

4 Conclusion

Fermentation conditions were optimized using the “One-Factor-At-a-Time” optimization strategy for lactic acid production from corn steep water that achieved LA at 48.2 ± 2.7 g/L. The fermentation process was further optimized using the RSM strategy, which resulted in LA of 53.5 ± 0.14 g/L from a sugar CSW content of 60.0 g/L after 96 h. Our results investigated that LA synthesized of the optimized-fermentation conditions was 10% greater than classical optimization methods. Also, Complete removal of YE besides the utilization of waste materials was a high challenge to be selected as a “free nutrient supplementation” and “cost-effective” approach for LA production by E. faecium WH51-1. So, our study thought that the first study that not only removing the extra supplementation of any nutrient to the CSW and using it as the sole media, but also maximizing the sugar utilization and LA production from CSW as raw material and the feasibly of the CSW effluent as a cheap alternative substrate for a biorefinery to lactic acid using potential strain as WH51-1 capable to grow and convert sugars in CSW to LA based on a specific screening protocol.