Introduction

In the upstream oil and gas industry, geomechanical parameters are generally derived from petrophysical logs obtained by deploying a sonde down the well. As it is costly and time-intensive, this acquisition is usually limited to the reservoir part of the well (Maleki et al. 2014). Drilling problems may occur in the upper layers of the reservoir; thus, knowledge of these layers’ geomechanical parameters would help prevent these problems and reduce the associated costs. Acquiring continuous drilling data from the ground surface to the reservoir and using these data to develop a model for estimating geomechanical parameters would, therefore, be a valuable approach for solving drilling problems in the reservoir’s upper layers. The energy consumed for rock drilling is proportional to the geomechanical properties of the rock. The denser the rock and the higher the strength, the greater the energy required for drilling it (Anemangely et al. 2019). Therefore, the energy consumed for rock drilling can be used to estimate the geomechanical parameters of the rock.

Teale (1965) introduced the concept of rock mechanical specific energy (MSE) as a parameter determining the mechanical efficiency of rock grinding tools. Rock MSE, defined as the amount of energy required to grind unit volume of a rock, has been broadly applied to evaluate the performance of rock drilling machines in studies and projects focused on rock drillability.

Ersoy and Atıcı (2004) concluded that MSE can be employed for assessing the productivity of a wide range of grinding applications. An increase in the rate of penetration (ROP) or depth cutting can result in decreased MSE.

In a 2005 pilot project, Weis, Du Priest and Koederlitz used data collected from drilling operations to estimate the MSE, alternatively modifying drilling parameters and checking well log records to maximize the ROP (Dupriest and Koederitz 2005; Koederitz and Weis 2005). Their study demonstrated that proper monitoring of MSE substantially improved drilling efficiency and contributed to establish MSE surveillance as a standard for monitoring drilling operation data. However, the MSE model proposed by Teale did not consider the effect of hydraulics. Armenta (2008) argued that hydraulics considerably impact the drilling specific energy (DSE). Indeed, the hydraulics of a drill bit can increase the bit’s ROP, enhancing drilling performance. Mechanical action grinds rocks while a hydraulic agent removes the drilled cuttings from the bit face. Faster cuttings removal prevents redrilling and lowers the energy requirements (Armenta 2008). The DSE is calculated as follows:

$${\text{DSE}}=\frac{\text{WOB}}{{A}_{\mathrm{B}}}+\frac{120\times \pi \times {\text{RPM}}\times {\text{Torq}}}{{A}_{\mathrm{B}}\times {\text{ROP}}}-\frac{1980000\times {\text{HF}}\times {\text{HP}}}{{\text{ROP}}\times {A}_{\mathrm{B}}}$$
(1)

where WOB is the weight-on-bit (lb), ROP is the bit rate of penetration (ft/h), RPM is the drill string’s rotational speed (rpm), AB is the area of the bit involved in grinding (in2), T is the torque (lb-ft), while HP and HF are the bit hydraulic horsepower and hydraulic factor, respectively.

In the past two decades, MSE has been widely used to optimize drilling operations in the oil and gas industry. In these studies, empirical models or regression methods were applied to achieve the goals of the studies using the concept of specific energy. Hamrick (2011) conducted numerous experimental tests, optimizing the controllable parameters to minimize MSE and, thus, maximize the ROP. Laosripaiboon et al. (2015) used a combination of well logging data and down-hole specific energy to identify perforated zones of high production potential. Pinto and Lima (2016) performed a real-time geomechanical analysis based on MSE to prevent nonproductive time while drilling through evaporite layers. By defining the confined compressive strength (CCS) as the lower limit of MSE, they showed that whenever the MSE exceeds the value of CCS, it leads to drilling problems. Majidi et al. (2017) proposed a technique to determine pore pressure by applying the concepts of MSE and drilling efficiency. Mohammadi Behboud et al. (2017) devised a mathematical equation associated with geomechanical parameters and DSE in an oil field based in southwestern Iran. By evaluating the relationships of each geomechanical parameter with DSE, they showed that the DSE could be obtained with a nonlinear relationship between porosity, drilling fluid flow, and uniaxial compressive strength (UCS). Alsubaih et al. (2018) increased drilling rates by combining MSE with a statistical analysis approach (SAA). They developed a relationship with SAA to predict the drilling rate from drilling parameters. In their study, the nonproductive drilling time in areas associated with drilling problems was reduced by maximizing the drilling rate and bringing the MSE value closer to the UCS.

Rock mechanics is predominantly based on experimentation. For most part, completely accurate theoretical formulae do not exist, and most formulae commonly used to calculate critical parameters are empirical correlations. Due to the complexity of rock structures, rock behavior prediction depends on numerous factors. Therefore, examining the interactions between any pair of parameters using empirical relations and library data is nearly impossible. Mathematical modeling approaches are time-intensive and frequently fail to give adequately accurate estimations. Artificial intelligence-based approaches have served as good alternatives to mathematical modeling, providing adequately satisfying results. Artificial intelligence has been employed to estimate shear velocity (Anemangely et al. 2017; Mehrad et al. 2022), or predict pore pressure (Matinkia et al. 2022), drilling rate (Anemangely et al. 2018; Sabah et al. 2019a, b; Mehrad et al. 2020; Sobhi et al. 2022), and estimating the hydrogen absorption on porous carbon materials (Vo Thanh and Lee 2022; Vo-Thanh et al. 2022; Davoodi et al. 2023a), carbon dioxide geological trapping indexes prediction (Davoodi et al. 2023b), and lost circulation (Sabah et al. 2021). These studies have established that artificial intelligence-based methods are superior to analytical and regression methods in these applications.

Anemangely et al. (2019) used the concept of MSE to estimate the geomechanical parameters of rock, including CCS, UCS, internal friction angle (\(\varphi\)), and Poisson's ratio (\(\nu\)). They first identified and removed the outlier data and then used MSE, drilling fluid flow, and drill tooth wear rate as inputs to a hybrid multilayer perceptron neural network with cuckoo and particle optimization algorithms. Their results showed that contrary to the low accuracy of models in the estimation of \(\nu\); CCS, UCS, and \(\varphi\) parameters can be estimated with high accuracy. However, using neural networks due to being a black box can be considered as one of the weaknesses of that study, whereas conducting appropriate data pre-processing and applying hybrid algorithms were its strong points, leading to high-accuracy predictions. Gamal et al. (2021) estimated the UCS using the random forest and functional network algorithms from the drilling parameters of weight on the drill bit (WOB), drilling rate (ROP), rotational speed (RPM), torque (Torq), and stand pipe pressure. The study’s outcome revealed that the UCS could be estimated from drilling parameters with promising accuracy. However, their study lacks a logical understanding of the relationship between the used drilling parameters and the UCS of the rock. In some other studies, drilling parameters were employed as input variables to standalone machine learning algorithms to predict \(\nu\) (Ahmed et al. 2021; Siddig et al. 2021, 2022a), Young modulus (Siddig et al. 2022b), UCS (Gowida et al. 2021; Hiba et al. 2022), and rock density (Ahmed et al. 2022a, b).

Using fuzzy logic, fuzzy inference systems can model qualitative aspects of human knowledge and reasoning processes without incorporating qualitative analysis. First investigated by Takagi and Sugeno (1985), fuzzy modeling and identification have found numerous applications in control, identification, and prediction (Jang 1993). Combining fuzzy structures with artificial neural networks, fuzzy-neuro networks are used for system identification and time series prediction among many other applications. In the current study, we present a model using mud logging data and DSE to determine mechanical rock characteristics by means of a fuzzy-neuro network combined with a particle swarm optimization (PSO) algorithm. Since the DSE of a rock is dependent on its geomechanical characteristics, DSE can serve as an acceptable parameter to relate drilling parameters to mechanical rock characteristics. Therefore, the present study aimed at developing a hybrid machine-learning model to predict the mechanical parameters of rock using DSE as input.

Research methodology

To develop rock properties estimator models based on drilling data, we first calculated the DSE using Eq. (1). The approximation and detail coefficients of DSE were subsequently extracted using wavelet transformation. Approximation and detail coefficients contain low frequency and high frequency information, respectively. These coefficients were used as input for adaptive network-based fuzzy inference system (ANFIS) models with genetic algorithm (GA) and particle swarm optimization (PSO) algorithm. The ANFIS-GA and ANFIS-PSO algorithms’ targets were the rocks’ mechanical properties, namely the static Young's modulus E, the uniaxial compressive strength (UCS), the internal friction angle \(\phi\), the cohesion C, and the Poisson’s ratio \(\nu\) of the rock formation. These mechanical properties were estimated from petrophysical logs taken in the studied depth range using empirical correlations developed from laboratory tests' results. The drilling data was recorded meter by meter and the petrophysical logs were acquired every 0.1524 m. Therefore, the petrophysical log data were upscaled to match the resolution of the drilling data as a prerequisite to presenting the geomechanical parameters as target parameters for the predictor algorithms. The root mean square error (RMSE) was calculated using the algorithms’ output and the mechanical properties calculated from the petrophysical logs. Based on the RMSE, the algorithms iteratively improved their solutions. This general process is illustrated in Fig. 1, and each step is detailed in the following sections.

Fig. 1
figure 1

General steps for estimating the geomechanical properties of reservoir rock

Full size image

Drilling data

The drilling data used in the present research were collected from two vertical wells drilled in the Marun oilfield in southwestern Iran, located in the Dezful depression of the Zagros belt. The Aghajari formation outcrops at the surface of the Marun oilfield, which consists of three main reservoirs: the Bangistan and Khami groups, and the Asmari formation. The primary reservoir rock of this field, the Asmari formation, is divided into five reservoir layers. The top three reservoir layers (zones 1, 2, and 3) are mainly composed of dolomite carbonates, resulting in a high density of fractures, especially in zone 1, with a dolomite content reaching 90%. With a higher shale and marl content, the lower layers (zones 4 and 5) are less fragile. Therefore, fractures are less widespread, and microscopic fractures are prevalent (Arian and Mohammadian 2009).

Measurements were taken in well A and well B, both situated in the Asmari formation, at depth ranges of 2700–3232 m and 3506.47–3875.35 m, respectively. The data sets associated with well A and well B consisted of 533 and 370 data points, respectively. In model training, a larger volume and variety of input data results in a model with better generalization capability and higher accuracy; therefore, the data sets of wells A and B were combined. The ranges of the geomechanical characteristics and drilling parameters are presented in Tables 1 and 2, respectively. A total of 25 data points falling outside the standard deviation of the DSE were eliminated.

Table 1 Range of geomechanical rock characteristics in well A and B
Full size table
Table 2 Range of drilling parameters in well A and B
Full size table

Applying the operational parameters presented in Figs. 2 and 3 into Eq. (1), the DSE of the studied range was calculated. The DSE features were subsequently extracted via wavelet transform, using a db1 wavelet function. For this purpose, the DSE signal was decomposed to the fourth level. Figures 4 and 5 report the details of each decomposition level together with the fourth level approximation. The detail coefficients (d1, d2, d3, and d4) and approximation coefficient (a4) were derived from the extracted DSE features by wavelet and subsequently used as inputs for the ANFIS model. To determine optimized parameters for the membership function, 80% of the dataset was used for model training, and the remaining 20% was used for model testing.

Fig. 2
figure 2

Drilling parameter variations in well A

Full size image
Fig. 3
figure 3

Drilling parameter variations in well B

Full size image
Fig. 4
figure 4

DSE decomposition to the 4th level using db1 wavelet function in well A. a detail of 1st level; b detail of 2nd level; c detail of 3rd level; d detail of 4th level; and e approximation of 4th level

Full size image
Fig. 5
figure 5

DSE decomposition to the 4th level using db1 wavelet function in well B. a detail of 1st level; b detail of 2nd level; c detail of 3rd level; d detail of 4th level; and e approximation of 4th level

Full size image

Determination of the geomechanical parameters

Elastic rock characteristics, such as the Young’s modulus, shear modulus, volumetric modulus, and Poisson ratio, can be estimated using density logs, p-wave and s-wave seismic records (Boitsov et al. 2011). The dynamic Young’s Modulus can be obtained via Eq. (2). The rock’s dynamic Young’s Modulus given by Eq. (2) is generally higher than the static Young’s Modulus (Zoback 2007; Boitsov et al. 2011). In this equation, the density ρ and seismic wave velocities Vp and Vs are expressed in kg/m3 and m/s, respectively:

$${E}_{\mathrm{dyn}}=\rho {V}_{\mathrm{s}}^{2}\left(\frac{3{V}_{p}^{2}-4{V}_{\mathrm{s}}^{2}}{{V}_{p}^{2}-{V}_{\mathrm{s}}^{2}}\right)$$
(2)

The difference between the static and dynamic states stems from the physical structure and heterogeneous texture of rocks. As accessing cores directly is often difficult, the determination of static rock characteristics is typically associated with numerous constraints. Multiple formulae exist to transform dynamic elastic rock characteristics into static ones; the validity of each relation depends on the geographical region.

Najibi et al. (2015) used the following equation to estimate the static Young’s Modulus (expressed in GPa) of the Asmari and Sarvak Limestones, two main oil reservoirs in Iran:

$$E=0\text{.}169{V}_{p}^{3\text{.}324}$$
(3)

Estimation of the uniaxial compressive strength based on Young’s modulus

Young’s modulus of elasticity represents a significant rock characteristic directly related to rock strength and can therefore be utilized to estimate rock strength. This parameter can be measured statically or dynamically. As it is typically lower than the dynamic modulus, the static modulus is commonly employed for estimating the uniaxial compressive strength (UCS) of the rock. Archer and Rasouli (2013) define the USC as shown in Eq. (4):

$$\mathrm{UCS}=2.28+4\text{.}1089E$$
(4)

where Young’s modulus Esta and the USC are expressed in GPa and Mpa, respectively.

Estimation of the inherent cohesion and internal friction angle

Sonic log data were incorporated into Eq. (5) to estimate the internal friction angle ϕ. In this equation, the porosity NPHI and shale volume Vshale are expressed as fractions. The shale volume percentage is obtained using Eq. (6), which incorporates gamma ray (GR) data (Hudson et al. 2002):

$$\varphi =26.5-37.4\left(1-\mathrm{NPHI}-{V}_{\mathrm{Shale}}\right)+62.1{\left(1-\mathrm{NPHI}-{V}_{\mathrm{Shale}}\right)}^{2},$$
(5)
$${V}_{\mathrm{Shale}}=\frac{\mathrm{GR}-{\mathrm{GR}}_{\mathrm{min}}}{{\mathrm{GR}}_{\mathrm{max}}-{\mathrm{GR}}_{\mathrm{min}}}$$
(6)

Inherent rock cohesion can be defined as the rock’s shear strength when the normal stresses are null (Hudson et al. 2002). The inherent rock cohesion is given in Eq. (7), wherein the sine and cosine arguments are in radians:

$$C=\mathrm{UCS}\times \frac{1-\mathrm{sin}\left(\varphi \right)}{2\times \mathrm{cos}\left(\varphi \right)}$$
(7)

Wavelet transformation

Wavelet transforms belong to a group of mathematical functions used to decompose a continuous signal into its spectral components, with each component’s resolution equal to its scale. Wavelet transformation is the decomposition of a function into a set of wavelet functions. Having a strong damping nature and a finite length, wavelets are transformed, scaled models of a function (Mother wavelet). Numerous wavelet transformations exist; the present study uses a stationary wavelet transform whose main characteristic is time-invariance (Pesquet et al. 1996). This method resembles the discrete wavelet transform, but the signal subsampling step commonly used in discrete wavelet transforms is absent; instead, this method employs super sampling filters (Pesquet et al. 1996).

Hybrid predictor algorithms

In this section, we will describe each algorithm separately before discussing their hybridization.

ANFIS

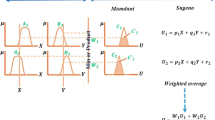
Introduced in 1993, ANFIS combines adaptive neural networks with fuzzy logic principles. Model parameters can be set via a hybrid learning process to model systems based on existing input–output data (Jang 1993). ANFIS is an integrated system employing a neural network to improve the fuzzy inference system. ANFIS’ structure consists of a series of fuzzy if–then rules with associated membership functions, selected according to the problem’s conditions to generate the stipulated input–output pairs. Based on the number and type of membership functions, ANFIS determines the fuzzy rules, aiming to minimize the estimation error. To describe the infinite structure, we consider the two following fuzzy if–then rules:

$$\text{Rule 1: if }\left(X\text{ is }{A}_{1}\right)\text{ and }\left(Y\text{ is }B1\right)\text{ then }{Z}_{1}={p}_{1}X+{q}_{1}Y+{r}_{1},$$
(8)
$$\text{Rule 2: if }\left(X\text{ is }{A}_{2}\right)\text{ and }\left(Y\text{ is }{B}_{2}\right)\text{ then }{Z}_{2}={p}_{2}X+{q}_{1}Y+{r}_{2},$$
(9)

where X and Y are inputs, Ai and Bi are fuzzy sets, Zi are outputs in the fuzzy domain determined by fuzzy rules, and pi, qi, and ri are parameters determined in the training process. To implement these rules, the ANFIS model is structured in five layers; these rules are described below and illustrated in Fig. 6.

Fig. 6
figure 6

ANFIS structure with two inputs (X and Y) and one output (Z). Squares denote adaptive nodes, and circles denote fixed nodes (Adaptive nodes have parameters that are assigned appropriate values for them by the training process; Meanwhile, fixed nodes do not require any adjustment)

Full size image

Layer 1: The first layer consists of membership functions responsible for fuzzificating the inputs. As seen in Fig. 6, this layer consists of adaptive nodes. The output \({o}_{i}\) of this layer corresponds to the degree of membership of each input:

$${o}_{i}^{1}={\mu }_{{A}_{i}}\left(X\right)\text{, }i=1\text{, }2$$
(10)
$${o}_{i}^{1}={\mu }_{{B}_{i-2}}\left(Y\right)\text{,} i=3\text{, }4.$$
(11)

In these equations, \({\mu }_{{A}_{i}}(X)\) and \({\mu }_{{B}_{i}}(Y)\) are membership functions, which are typically Gaussian functions. A Gaussian membership function using a mean c and a standard deviation \(\sigma\) can be expressed as follows:

$$\mu \left(x\right)={e}^{-\frac{{\left(x-c\right)}^{2}}{2{\sigma }^{2}}}.$$
(12)

Layer 2: This layer, shown in Fig. 6 with the circled letter M representing the fixed node associated with the membership function, acts as a multiplier. These nodes’ outputs are the fuzzy weights \({w}_{i}\) of each rule, determined by Eq. (13):

$${{w}_{i}=o}_{i}^{2}={\mu }_{{A}_{i}}\left(X\right){\mu }_{{B}_{i}}\left(Y\right)\text{,} i=1\text{, }2.$$
(13)

Layer 3: In this layer, which consists of fixed nodes, the normalized fuzzy weights are calculated by dividing the weight by the sum of the weights obtained from the previous layer (Eq. 14):

$${\overline{w} }_{i}={o}_{i}^{3}=\frac{{w}_{i}}{\sum_{i=1}^{2}{w}_{i}} .$$
(14)

Layer 4: Consisting of two adaptive nodes, this layer provides the output of the membership functions, as shown in Eq. 15:

$${o}_{i}^{4}={\overline{w} }_{i}{Z}_{i}={\overline{w} }_{i}\left({p}_{i}X+{q}_{i}Y+{r}_{i}\right)\text{, }i=1\text{, }2,$$
(15)

where p, q, and r are constant parameters associated with the membership functions.

Layer 5: This layer’s fixed node is responsible for summing the input signals as follows:

$${z=o}_{i}^{5}=\sum_{i=1}^{2}{\overline{w} }_{i}{z}_{i}=\frac{\sum_{i=1}^{2}{w}_{i}{Z}_{i}}{\sum_{i=1}^{2}{w}_{i}}.$$
(16)

Particle swarm optimization (PSO) algorithm

The PSO algorithm features fast convergence due to the sharing of information between particles and is easy to understand and implement (Ma et al. 2011), which has contributed to its widespread use. Each particle, representing an individual and a potential optimal solution, moves through the problem space following individual and social patterns. Solutions are generated based on the particles’ position in the problem space. PSO uses the best solution explored by each individual as well as the best solution explored by the swarm in each iteration to improve the global optimal solution. Using the best individual increases the diversity in the solutions’ quality, which is advantageous for solving highly nonlinear and multi-state problems.

To apply this algorithm, we started by randomly assigning the initial position x and velocity V for each particle i. In the next step, the random positions assigned to each particle were evaluated with an objective function. For each particle, the current position and the cost corresponding to that position were recorded as the best position \({P}_{\text{best}}\) and cost of that particle. The particle with the lowest cost was identified, and its position and cost were logged as the best current position \({g}_{\text{best}}\) and cost of the entire swarm. In the next step, a new velocity for each particle was calculated based on the particle’s current velocity, its distance from its best position, and its distance from the particle swarm's best position. This calculation is formulated in Eq. (17). The new position for each particle was obtained by summing the new velocity with the current position, as shown in Eq. (18):

$${V}_{i}\left({\text{new}}\right)=\,w{V}_{i}\left({\text{current}}\right)+{c}_{1}{r}_{1}\left({P}_{\text{besti}}\left({\text{current}}\right)-{x}_{i}\left({\text{current}}\right)\right)+{c}_{2}{r}_{2}\left({g}_{\text{best}}\left({\text{current}}\right)-{x}_{i}\left({\text{current}}\right)\right)$$
(17)
$${x}_{i}\left({\text{new}}\right)={x}_{i}\left({\text{current}}\right)+{V}_{i}\left({\text{new}}\right),$$
(18)

where i represents the index of each particle (a natural number between 1 and the total number of particles); \(w\) is the inertial weight controlling the particle velocity; c1 and c2 are the individual and social learning coefficients, respectively; and r1 and r2 are random numbers in the range of [0,1]. The new positions were evaluated again with the objective function. For each particle, the values of the best position \({P}_{\mathrm{best}}\) and cost were updated if the new positions' cost was lower than the best recorded cost. Likewise, the values of the best position \({g}_{\mathrm{best}}\) and cost of the entire swarm were updated if the lowest updated cost was lower than the cost associated with the current \({g}_{\mathrm{best}}\). This process was iterated until a predetermined termination condition was reached. A visual illustration of the PSO algorithm is presented in Fig. 7.

Fig. 7
figure 7

PSO algorithm flowchart (Rajabi et al. 2022)

Full size image

Genetic algorithm (GA) optimization

Inspired by the Darwinian theory of evolution and the concept of survival of the fittest, the GA is one of the most used algorithms. GA utilizes processes similar to genetic recombination and mutation to promote population evolution that satisfies a predetermined goal. In a crossover process, also known as selective reproduction, suitable individuals are preferably selected over individuals with less fitness to produce offspring. This creates a clear tendency toward harmonizing the population and enhancing the average result with each iteration of the algorithm. Subsequently, offspring mutations return diversity to the population and explore new regions of the parameter search space. Figure 8 gives a visual representation of the GA.

Fig. 8
figure 8

GA optimization flowchart (Sheykhinasab et al. 2022)

Full size image

In this technique, we began the optimization process by generating a randomly initialized population of candidate answers. A fitness score was attributed to each individual in the population based on its efficiency. The best scoring individuals were then selected as parents; a process referred to as elitism in the chart below. Crossover between the selected individuals, equivalent to the recombination of the parents’ genetic material, was subsequently performed to create new offspring. This offspring was then randomly altered or mutated to form the next generation, diversifying the population. At the next iteration, the fitness score of each individual in the child population was evaluated and the individuals with the best score were chosen as the next generation’s parents. This cycle continued until a preset termination condition was satisfied, and an appropriate solution was obtained (Okwu and Tartibu 2021).

ANFIS with hybrid optimization algorithms

The design of an ANFIS model with hybrid metaheuristic algorithms started by determining the type and number of membership functions. The ANFIS model was subsequently trained using the training data subset and a backpropagation optimization algorithm. During the training process, the values of the membership functions’ parameters for each input and output parameter were extracted. Next, we introduced the extracted values as the best current values of each individual in the PSO algorithm and one of the solutions in the GA. Based on their respective performance mechanisms, the optimization algorithms improved the values of the membership functions’ parameters, minimizing the error of the ANFIS model created with these values. By determining the optimal values of the membership functions’ parameters after satisfying the termination condition for the optimization algorithms, the optimized ANFIS model was created, and its performance was assessed using the testing data subset. This process is illustrated in Fig. 9.

Fig. 9
figure 9

ANFIS-PSO/GA Hybrid model flowchart

Full size image

Results and discussion

The relationships between the DSE and each of the geomechanical parameters were investigated in the form of a cross-plot. Results are presented in Fig. 10 for well A and in Fig. 11 for well B. As can be seen in Fig. 10, the geomechanical parameters in well A are directly related to the DSE: an increase in the parameters’ value leads to an increase in the energy required for drilling rock. However, there is no apparent relationship between the Poisson’s ratio \(\nu\) and the DSE in well A. This result is consistent as the energy needed to drill is proportional to the rock’s resistance, and E, C, \(\phi\), and UCS are parameters characterizing the rock resistance. In well B, the geomechanical parameters exhibit an even stronger relationship with the DSE, as can be seen in Fig. 11. The Poisson’s ratio \(\nu\) shows a weak relationship to the DSE. The UCS and E present a particularly strong relationship with the DSE in well A and B.

Fig. 10
figure 10

Cross-plot of DSE and geomechanical parameters in well A. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image
Fig. 11
figure 11

Cross-plot of the DSE and geomechanical parameters in well B. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image

To achieve a model with high accuracy and good generalization ability, a subset of the data set was used to train the hybrid ANFIS algorithms. To this end, we selected suitable values for controllable parameters, such as the number and type of membership functions. Triangular, Gaussian, generalized bell-shaped, and trapezoidal membership functions were applied to the ANFIS algorithm to model geomechanical parameters. The model generated using Gaussian membership functions exhibited higher accuracy; therefore, we selected Gaussian membership functions for use with the metaheuristic ANFIS-PSO and ANFIS-GA optimization algorithms. Sensitivity analysis conducted on the number of membership functions revealed that the modeling error decreases as the number of membership functions increases, as shown in Fig. 12. However, model overfitting occurred when the number of membership functions exceeded five. Therefore, the number of membership functions was set to five in ANFIS-PSO and ANFIS-GA.

Fig. 12
figure 12

The RMSE as a function of the number of membership functions in the modeling of a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image

Sensitivity analysis was employed to adjust the control parameters in the optimization algorithms. We identified the optimal value for the controllable parameters by evaluating the accuracy of the model obtained from the training data for different parameter values. Table 3 presents the optimal values for the controllable parameters in GA and PSO. These values were obtained using 200 iterations for each algorithm.

Table 3 The controllable parameters’ optimal values for the metaheuristic optimization algorithms
Full size table

Figures 13 and 14 show the cross-plots of the geomechanical parameters’ measured and predicted values generated from ANFIS-GA and ANFIS-PSO, respectively. In both models, the geomechanical parameters are overestimated at low values (the line of best fit is under the Y = T line), and underestimated at high values (the line of best fit is over the Y = T line). This pattern of over- and underestimation is most pronounced for the Poisson's ratio with both algorithms. Therefore, using the present method to predict \(\nu\) warrants caution. This result was expected, given the weak relationship between \(\nu\) and DSE in both wells. The Y = T line deviates less from the line of best fit in the \(\phi\) prediction model than in the \(\nu\) prediction model. Nevertheless, both algorithms predict \(\phi\) with relatively low accuracy. Both ANFIS-GA and ANFIS-PSO models are highly accurate in predicting E, UCS and C. This result was anticipated considering the strong relationship between these three parameters and the DSE (Figs. 10 and 11). Graphs of the membership functions resulted from the training process of ANFIS algorithm in the prediction of geomechanical properties of formation are presented in the appendix section.

Fig. 13
figure 13

Cross-plots of geomechanical parameters calculated from log data and predicted with ANFIS-GA using the training data subset. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image
Fig. 14
figure 14

Cross-plots of geomechanical parameters calculated from log data and predicted with ANFIS-PSO using the training data subset. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image

The cross-plots of the geomechanical parameters’ measured and predicted values for the testing data subset are shown in Figs. 15 and 16. They reveal a pattern of overestimation at low parameter values and underestimation at high parameter values. This pattern is similar to the pattern identified for the training data subset and was, therefore, anticipated. Both ANFIS-GA and ANFIS-PSO models predict \(\nu\) and \(\phi\) poorly for the testing data subset; this strongly confirms that using these algorithms to predict \(\nu\) and \(\phi\) warrants caution. Conversely, ANFIS-GA and ANFIS-PSO used with the testing data subset predict E, UCS and C with high accuracy. Therefore, we are confident that the proposed method can also predict these three geomechanical parameters with high accuracy for other wells in the studied oilfield.

Fig. 15
figure 15

Cross-plots of geomechanical parameters calculated from log data and predicted with ANFIS-GA using the testing data subset. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image
Fig. 16
figure 16

Cross-plots of geomechanical parameters calculated from log data and predicted with ANFIS-PSO using the testing data subset. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image

Tables 4 and 5 present the error criteria and coefficients associated with the ANFIS-PSO and ANFIS-GA algorithms in the training and test phases, respectively. These results suggest that the ANFIS-PSO algorithm predicts each of the five geomechanical parameters with higher accuracy than the ANFIS-GA algorithm. The RMSE of the ANFIS-PSO model is lower than that of the ANFIS-GA model in the training and test phases, indicating that the ANFIS-PSO model is highly generalizable in this application and could be employed for predicting geomechanical parameters for other wells in the Marun oilfield.

Table 4 Model error criteria of the ANFIS-GA and ANFIS-PSO models when used with the training data subset
Full size table
Table 5 Model error criteria of the ANFIS-GA and ANFIS-PSO models when used with the testing data subset
Full size table

Evaluating input parameters to determine the effect of each input on the target parameter is a valuable method for detecting anomalies. We performed sensitivity analysis on the approximation and detail coefficients (d1, d2, d3, d4, and a4) derived from the DSE to determine their respective influence on the geomechanical parameters. The results of this analysis are presented in Fig. 17. Results indicate that the first-level detail coefficient affects the Young’s modulus most strongly, and the fourth-level detail coefficient has the greatest impact on the UCS. The cohesion and internal friction angle are most influenced by the third-level detail coefficient, while the Poisson’s ratio is most affected by the third-level detail coefficient.

Fig. 17
figure 17

Influence of the input parameters in predicting the geomechanical parameters using the ANFIS-PSO model. a Young’s modulus E, b UCS, c rock cohesion C, d internal friction angle \(\phi\), and e Poisson’s ratio \(\nu\)

Full size image

Conclusions

In the present study, data collected in two vertical wells drilled in the Marun oilfield of southwestern Iran were used to develop predictive models of geomechanical parameters based on the drilling specific energy (DSE). We first calculated the DSE from the drilling parameters using the method proposed in Armenta (2008). Next, the DSE features were extracted using a stationary wavelet transform and used as input for two hybrid adaptive neural fuzzy inference system (ANFIS) models using a genetic algorithm (GA) and a particle swarm optimization (PSO) to predict the rocks’ geomechanical parameters. The ANFIS-GA and ANFIS-PSO model outputs were compared to the geomechanical parameters obtained from petrophysical logs using laboratory-developed empirical relationships. The results of this research are as follows:

  • The DSE-based numerical prediction of the geomechanical parameters revealed that the Young’s modulus and uniaxial compressive strength (UCS) are strongly correlated to the DSE. Conversely, the Poisson’s ratio \(\nu\) has a weak relationship with the DSE.

  • ANFIS models using Gaussian membership functions are more accurate than models using triangular, generalized bell-shaped, or trapezoidal membership functions.

  • The model’s error value decreases as the number of membership functions increases; however, the number of membership functions used in the ANFIS model was limited to five to avoid overfitting.

  • The technique proposed in this study predicts the UCS, the Young’s modulus, and the rock’s cohesion with high accuracy.

  • The ANFIS-PSO model exhibits higher accuracy and better generalization capability than the ANFIS-GA model. The low root mean square error (RMSE) values achieved for the Young’s modulus, UCS, and cohesion associated with the ANFIS-PSO indicate that this model is highly generalizable in its current application.

  • The ANFIS-PSO model output’s sensitivity to the input parameters revealed that first level details significantly affect the Young’s modulus, fourth level details have the greatest impact on the UCS, the fourth level approximation greatly influences the cohesion and internal friction angle, and third level details affect the Poisson’s ratio the most.

  • This study demonstrates that the ANFIS-PSO model could be employed for predicting certain geomechanical parameters for other wells in the Marun oilfield.

Future studies

Some events that occur during well drilling, such as loss, borehole collapse or pore pressure changes, influence the DSE. Loss or borehole collapse results in an increase in the DSE and a decrease in the energy required to drill. When pore pressure exceeds mud pressure (overpressure), rock cuttings are removed more efficiently, which lowers the drilling energy requirements. These conditions affecting the DSE were not considered in the present study. In future studies, we intend to further investigate the effects of the above parameters on the DSE and the rock’s geomechanical parameters.