Prediction and analysis of penetration rate in drilling operation using deterministic and metaheuristic optimization methods

Abstract

The rate of penetration (ROP) optimization is one of the most important factors in improving drilling efficiency, especially in the downturn time of oil prices. This process is crucial in the well planning and exploration phases, where the selection of the drilling bits and parameters has a significant impact on the total cost and time of the drilling operation. Thus, the optimization and best selection of the drilling parameters are critical. Optimization of ROP is difficult due to the complexity of the relationship between the drilling variables and the ROP. For this reason, the development of high-performance computer systems, predictive models, and algorithms will be the best solution. In this study, a new investigation approach for ROP optimization has been done regarding different ROP models (Maurer, Bingham, Bourgoyne and Young models), algorithms (Multiple regression, ant colony optimization (ACO), fminunc, fminsearch, fsolve, lsqcurvefit, lsqnonlin), and different objective functions. The well-known data from the Louisiana field in an offshore well have been used to compare the used parameter estimation approach with other techniques. Indeed, datasets from an onshore well in the Hassi Messaoud Algerian field are explored. The results confirmed the superiority and the effectiveness of B&Y models compared to Bingham and Maurer models. Fminsearch, lsqcurvefit, ACO, and Excel (GRG) algorithms give the best results in ROP prediction while the application of the MNLR approach. Using the mean squared error (MSE) and the determination coefficient (R$^{2}$) as objective functions significantly increases the accuracy prediction where the results given are ($R=0.9522$, $RMSE=2.85$) and ($R= 0.9811$, $RMSE=4.08$) for Wells 1 and 2, respectively. This study validates the application of B&Y model in both onshore and offshore wells. The findings reveal to deal with data limitation problems in ROP prediction. Simple and effective optimization techniques that require less memory space and computational time have been provided.

Introduction

One of the main goals of drilling optimization is to reduce the total time, maintain the risks as low as possible, save costs, and increase efficiency, especially in the early stage of the drilling project (planning and exploration phases). Drilling optimization is directly related to maximizing the rate of penetration (ROP). According to the field experience, there are several methods to reduce the drilling cost of the future well. One of these methods is the optimization of drilling parameters to obtain the maximum ROP in each bit run. The rate of penetration (ROP) refers to the improvement or progression speed of the drill bit when the formation rock breaks (Bourgoyne et al. 1986). It is determined by evaluating the required amount of time to drill one foot of depth, and it is usually reported in ft/h (field units) or m/h (SI units). ROP depends on many factors including mud properties, mechanical and hydraulic drilling parameters (Bourgoyne and Young 1974). We can classify these parameters into two separate groups: controllable and uncontrollable factors. The controllable drilling factors are the operational drilling parameters that can be changed by the driller from the surface such as revolutions per minute (RPM), weight on bit (WOB), the flow rate (Q), and standpipe pressure (SPP), whereas the uncontrollable factors are the ones that nothing can be done to change them because of technological or formation factors, for example, rock strength, pore pressure, mud weight, and wellbore trajectory (Youcefi et al. 2020).

Among all the preceding factors, RPM, WOB, and Q are known as the crucial controllable operational drilling parameters because they can affect ROP (Edalatkhah et al. 2010).

ROP modeling has been always the primary concern of researchers and companies in the industry since it is directly related to the drilling cost; over the past few decades, many authors have studied the effect of different parameters on the ROP; initially, they focused on creating empirical models based on experience results. Graham and Muench (1959) introduced the first attempts optimizing drilling parameters; the authors have established an empirical mathematical expression for the bit life and ROP as a function of WOB, depth, and RPM. Maurer (1962) suggested an equation for roller-cone bits to predict ROP, the bottom hole assumed to be perfectly cleaned.

Galle et al. (1963) have developed a method using a series of graphs and diagrams to determine the best combination of WOB and RPM for roller cone bits. Bingham (1965) has proposed a simple and experimental model which is a modification from the Maurer model; it is limited to low WOB and RPM; however, it does not consider the depth of drilling.

Teale (1965) developed the mechanical specific energy (MSE) model which determines the amount of energy required to remove a definite rock volume (ft-lb/ft3) and concluded that the MSE value is as close to the rock uniaxial compressive strength (UCS) in psi.

Eckel (1967) performed numerous micro-bit experiments, which showed that reducing the overbalance pressure can enhance the efficiency of the formation drillability, thus increasing ROP.

Bourgoyne and Young (1974) established one of the most important drilling optimization studies and developed an empirical model to predict the rate of penetration based on several drilling parameters. This model is widely used in the oil industry and is considered the best approach to optimize drilling parameters in real time (Eren and Ozbayoglu 2011). The model describes the effect of different drilling parameters on ROP, and they have proposed the multiple regression analysis to extract eight unknown parameters using well drilling datasets.

Warren (1987) presented a perfect cleaning ROP model for soft formation, and this model relates ROP to the WOB, RPM, UCS, and bit size. To offer comprehensive information regarding the interaction between rock and the bit, he employed experimental response curves and dimensional experiments. Later, Warren has adjusted his model by adding a wear function (Wf) to reflect the impact of bit wear.

Al-Betairi et al. (1988) have proposed a new ROP model using controllable and uncontrollable drilling variables toward predicting the optimum penetration rate and examined the correlational coefficients determined by multiple regression and evaluated the sensitivity of each drilling parameter on ROP.

Maidla and Ohara (1991) developed an optimization software for roller-cone bits toward the best selection of WOB, RPM, bit type, and bit wearing to minimize the drilling costs. They concluded that the drilling model performances depend on the quality of the data used to calculate the model’s coefficient.

Hareland and Rampersad (1994) introduced a model for drag bits that relates UCS, WOB, RPM, bit geometry, and Wf. Motahhari et al. (2010) developed a PDC model that considers the wear function and confined compressive strength (CCS) instead of UCS besides RPM, WOB, and bit size. The physics-based models mentioned above use empirical coefficients, which are highly dependent on the lithology and continuously varied due to calibration, such that constraining their functional forms. Hareland et al. (2010) has created a new simple model for roller cone bits and used laboratory data to estimate the UCS. Alum and Egbon (2011) used the original model of Bourgoyne and Young in series of studies, and the results have shown that the equivalent circulation density has a great influence on ROP because of the annular pressure losses; as a result, they proposed an analytical model to estimate ROP.

Recently, some researchers have tried to apply the inspired nature algorithms called metaheuristic techniques in the oil and gas industry.

Moazzeni and Khamehchi (2020) found that the rain optimization algorithm (ROA) outperformed the genetic algorithm (GA) and particle swarm optimization (PSO) in terms of time and accuracy prediction.

There have been several attempts to predict ROP in drilling using artificial intelligent (AI) and hybrids approaches, which give a good result in ROP prediction.

Jahanbakhshi et al. (2012) considered several drilling parameters to predict ROP, and the study included the use of multilayer perceptron in the data-driven model.

Bataee et al. (2014) used shuffled frog leaping algorithm as a function of WOB, RPM, and flow rate. They developed an ANN model using about 1810 data-point to train the model and to predict ROP.

Kahraman (2016) found that the use of Neural network models is more accurate than the use of regression techniques in the prediction of ROP.

Hegde et al. (2017) identified that the data-driven approach model for ROP predictions was more precise and accurate compared to those based on physical experiments.

In recent years, researchers have tended to apply hybrid models combining several techniques to predict ROP accurately.

Two hybrid ANNs were created by Anemangely et al. (2018) using PSO and cuckoo optimization algorithm (COA) as training functions for providing precise ROP prediction.

Elkatatny (2019) build a new ROP model using hybrid algorithm self-adaptive differential evolution artificial neural network, the model considers five drilling parameters (2223 data points) as input parameters and ROP as an output of the model, and the result was very promising by getting R = 0.98.

Indeed, using AI and hybrid models effectively increases the ROP accuracy prediction; however, the model requires an enormous amount of data and time to train and test the model. In addition, the use of the model is limited to a local area; moreover, the process requires high-performance computer systems and machine learning skills. So, the use of conventional models with the application of metaheuristics and regression techniques to optimize ROP is more appropriate.

In this context, this work starts by investigating different ROP models where Bingham, Maurer, B&Y models have been explored and described in sect. 3. Regression and metaheuristic algorithms have been used to extract the unknown parameters of the ROP model. Thus, Sect. 4 describes the optimization methods and several objective functions, while both linear and nonlinear objective functions have been evaluated to determine the most feasible one. Following that, various metrics have been utilized to assess the performances of the proposed optimization techniques and the objective functions. Various well data sets from onshore and offshore have been applied in this study. Section 5 deals with the data description and results. Finally, the conclusions are given in Sect. 6.

ROP modeling

In the literature, there are many ROP models have be

en developed in the last decade as we mentioned in the previous section. In this paper, we used only: Maurer, Bingham, and B&Y models.

Maurer

In 1962, Maurer stated that ROP can be calculated as a function of WOB, RPM, drillability strength of the rock (UCS), bit diameter (Db), and the drillability constant (K), the equation is based on ‘perfect cleaning’ condition where all of the rock debris has been removed, and Maurer’s model is described by Eq. 1 as follows:

$$\begin{aligned} ROP= K\times \frac{RPM\times WOB^2}{Db^2\times UCS^2} \end{aligned}$$

(1)

Bingham

Bingham’s 1965 paper suggested a model that predicted ROP by considering it as simply function of rotary speed, weight on bit, and bit diameter; however, it is known to be limited to low WOB, and RPM (Niknam 2008). Bingham’s equation is as follows:

$$\begin{aligned} ROP= \alpha \times RPM\times \left (\frac{WOB}{Db}\right)^\beta \end{aligned}$$

(2)

where ROP (ft/hr), WOB (klb), RPM (revolutions/min), Db is the bit diameter (in), and $\alpha$ and $\beta$ are constants determined for a given rock formation.

Bourgoyne and Young

The authors have developed a mathematical model in 1974 that simplified the rotary drilling process into one single model. They introduced ROP as a function of various drilling variables that are considered to affect the ROP. The model is mathematically given by:

$$\begin{aligned} ROP = \frac{{dD}}{{dt}}= Exp({a_1} + \sum \limits _{j = 2}^8 {{a_j}{x_j}} ) \end{aligned}$$

(3)

where ROP is the rate of penetration (ft./h), $a_j$ are the model coefficients, and $x_j$ are the eight drilling parameters.

The model can also be reformulated by equation 4 as follows:

$$\begin{aligned} ROP = ({f_{_1}}) + ({f_{_2}}) + ({f_3})\dots ({f_8}) \end{aligned}$$

(4)

where $f_1, f_2, ..., f_8$ represents the functional relations between penetration rate and various drilling variables. Each of these functions contains constants, which are shown as $a_1$ through $a_8$, while $f_{n = 1}^8$ represents the various normalized effects on ROP (Hareland and Rampersad 1994), where $f_1$ is the effect of rock drill ability, $f_{2}$ is the depth effect, $f_3$ is pore pressure effect on ROP, $f_4$ is the differential pressure effect, $f_5$ is the effect of changing the weight on ROP, $f_6$ is the effect of rotary speed, $f_7$ is the effect of bit wear on ROP, and $f_8$ is the effect of bit hydraulics. Equation 3 can be broken down into 7 sub-equations as follows:

$$\begin{aligned}&{\mathrm{{x}}_\mathrm{{2}}}\mathrm{{ = 10000 - D}} \end{aligned}$$

(5)

$$\begin{aligned}&{\mathrm{{x}}_\mathrm{{3}}}\mathrm{{ = }}{\mathrm{{D}}^{\mathrm{{0}}\mathrm{{.69}}}}\mathrm{{(}}{\mathrm{{g}}_\mathrm{{p}}}\mathrm{{ - 12}}\mathrm{{.5)}} \end{aligned}$$

(6)

$$\begin{aligned}&{\mathrm{{x}}_\mathrm{{4}}}\mathrm{{ = D(}}{\mathrm{{g}}_\mathrm{{p}}}\mathrm{{ - ECD)}}\ \end{aligned}$$

(7)

$$\begin{aligned}&{\mathrm{{x}}_5} = \ln \left[ {\frac{{\left( {\frac{w}{b}} \right) - {{\left( {\frac{w}{b}} \right) }_t}}}{{4 - {{\left( {\frac{w}{b}} \right) }_t}}}} \right] \end{aligned}$$

(8)

$$\begin{aligned}&{\mathrm{{x}}_6} = \ln \left[ {\frac{N}{{100}}} \right] \end{aligned}$$

(9)

$$\begin{aligned}&{\mathrm{{x}}_\mathrm{{7}}}\mathrm{{ = - h}} \end{aligned}$$

(10)

$$\begin{aligned}&{\mathrm{{x}}_8} = \frac{{\rho q}}{{350\mu {d_n}}} \end{aligned}$$

(11)

where D = well depth (ft), g$_p$ = pore pressure gradient (lb/gal), ECD = equivalent circulation mud density (lb/gal), w/d = weight on bit per inch of bit diameter (1,000 lb/in), (w/d)$_t$ = threshold bit weight per inch of bit diameter (1,000 lb/in), N = rotary speed (rpm), $\rho$ = mud density (lb/gal), q = flow rate (gal/min), $\mu$ = the apparent viscosity at 10,000 s−1 (cp), d$_n$ = bit nozzle diameter (in), and h = fractional tooth wear . Figure 1 represents the functional relationship of penetration rate. The model predicts the effect of the included eight drilling variables ($x_j$) on the ROP. In a given formation, the modeling is done by determining the eight constants ($a_j$). This model is considered as the most suitable model for real-time drilling optimization (Hareland and Rampersad 1994).

Fig. 1

Functional relationship of penetration rate

Problem formulation

In this study, the B&Y model is compared to the Maurer and Bingham models to determine its effectiveness. This is done through the use of a variety of objective function categories. In addition, the optimization techniques applied to identify the unknown parameters of the selected model are represented below.

Optimization methods

The optimization problem is becoming increasingly important in decision-making processes, there are several techniques to solve this problem, and these based-model extraction techniques could be divided into two broad approaches. One of these approaches is called deterministic, in which the search algorithms always use the same routing to arrive at the desired solution, and multiple linear regression (MLR) and multiple non-linear regression (MNLR) are the main techniques in the deterministic approaches. The other approach is the random or non-deterministic approach, in which the algorithm will not necessarily follow the same routing to the final solution and may even propose different solutions following the initial conditions proposed, and this approach is subdivided into heuristic and metaheuristic techniques. The analytical ROP models used in this paper are continuous smooth functions. In this study, both optimization approaches are checked to reach an accurate ROP prediction.

Multiple regression

Regression analysis is a method for estimating the relationships between one dependent variable and two or more independent variables. This data analysis technique is beneficial while comparing a quantitative variable to other variables. The multivariate analysis describes an observation factor by having several variables and taking into consideration all changes in properties that may happen simultaneously. There are two types of multiple regression analysis: linear regression and nonlinear regression.

Multiple linear regression

The model assumes that the relationship between the dependent variable $Y_i$ and the p vector of regressors $X_i$ is linear. The following represents a MLR equation (Pedhazur 1982):

$$\begin{aligned} Y\mathrm{{ }}\left( i \right) = \mathrm{{ }}\beta \mathrm{{ }} + \mathrm{{ }}{\alpha _1}{X_1} + \mathrm{{ }}{\alpha _2}{X_2} + \mathrm{{ }}{\alpha _3}{X_3} + \ldots \end{aligned}$$

(12)

where $\beta$ is the intercept, $\alpha$ are slopes or coefficients, and (i) is the number of observations. The simple linear regression model is used to find the straight line that best fits the data, while the multiple linear regression used to find the best plan that fits the data. In our case, equations (Eq.2 through Eq.11 ) define the general functional relations between penetration rate and other drilling variables; for example, Bourgoyne’s equation has eight constants. Before these equations can be used, $a_1$ through $a_8$ must be determined. These constants are obtained by performing a multiple regression analysis of detailed drilling data taken over short depth intervals. The model represent in Eq.3. Taking the logarithm of both sides of the above equation yields:

$$\begin{aligned} ln ROP = \ln \left(\frac{{dD}}{{dt}}\right) = \left({a_1} + \sum \limits _{j = 2}^8 {{a_j}{x_j}} \right) \end{aligned}$$

(13)

The residual error of the ith data point, ${\varepsilon _i}$,  is defined by:

$$\begin{aligned} {\varepsilon _i}\ = \left({a_1} + \sum \limits _{j = 2}^8 {{a_j}{x_j}} \right) - \ln \left(\frac{{dD}}{{dt}}\right) \end{aligned}$$

(14)

Multiple linear regression-analysis is used to determine the constants $a_1$ to $a_8$, so that the square of the residuals should be reduced. The following linear equation system can be produced using matrix:

$$\begin{aligned} \left[ {\;\begin{array}{*{20}{c}} n&{}{\sum \limits _{i = 1}^n {{x_{i2}}} }&{} \cdots &{}{\sum \limits _{i = 1}^n {{x_{i8}}} }\\ {\sum \limits _{i = 1}^n {{x_{i2}}} }&{}{\sum \limits _{i = 1}^n {{x_{i2}}^2} }&{} \cdots &{}{\sum \limits _{i = 1}^n {{x_{i2}}{x_{i8}}} }\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ {\sum \limits _{i = 1}^n {{x_{i8}}} }&{}{\sum \limits _{i = 1}^n {{x_{i8}}{x_{i2}}} }&{} \cdots &{}{\sum \limits _{i = 1}^n {{x_{i8}}^2} } \end{array}\;} \right] \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ {{a_3}}\\ \vdots \\ {{a_8}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sum \limits _{i = 1}^n {\ln \frac{{dD}}{{dt}}} }\\ {\sum \limits _{i = 1}^n {{x_{i2}}\ln \frac{{dD}}{{dt}}} }\\ {\sum \limits _{i = 1}^n {{x_{i3}}\ln \frac{{dD}}{{dt}}} }\\ \vdots \\ {\sum \limits _{i = 1}^n {{x_{i8}}\ln \frac{{dD}}{{dt}}} } \end{array}} \right] \end{aligned}$$

(15)

Multiple nonlinear regression

MNLR models assume that the relationship between the dependent variable $Y_i$ and the p vector of regressors $X_i$ is nonlinear, so the B&Y model represented in Eq.3 is employed without introducing the logarithm, while the residual error, ri, for the nonlinear regression, is defined by:

$$\begin{aligned} {\varepsilon _i}\ = \left(\frac{{dD}}{{dt}}\right) - Exp\left({a_1} + \sum \limits _{j = 2}^8 {{a_j}{x_j}}\right ) \end{aligned}$$

(16)

The square of the residuals should be reduced, and the constants $a_1$ to $a_8$ are determined using MNLR.

Ant colony optimization algorithm

Metaheuristics are a set of optimization algorithms to solve difficult optimization problems. They are often inspired by natural systems, whether taken in physics (if simulated annealing) in evolutionary biology (genetic algorithms cases), in ethology (case algorithms ant colony), or particle swarm optimization. In this study, we will use ACO to optimize the rate of penetration.

Ant colony optimization algorithm is a nature-inspired metaheuristic optimization method for solving complex combinatorial optimization problems, which is mimicking the ants’ foraging behavior proposed by Dorigo and Blum (2005). The real ant’s behavior follows the pheromone trail. Initially, real ants in a colony start searching for a food source at random. Once an ant finds a food source, it deposits a chemical substance called pheromone on its path back to the colony. Ants decide their path based on the concentration of the pheromone on the path. The higher concentration of pheromone on a path, the more likely that path will be followed (Deneubourg et al. 1990). ACO has been firstly used to solve discrete optimization problems. The algorithm uses a pheromone model to move ants toward the promising areas in the search space. The main components of ACO are the solution construction and pheromones update.

As it is illustrated in Fig. 2, after initialization, the ACO algorithm is set to search for solutions and update the pheromone. The first strategy is achieved by finding a target and selecting a solution from the ants’ investigation based on weights ($w_l$) and the selected probabilities ($p_l$) through Eqs.17 and 18, consecutively. While l is the possible solution index, NP is the size of the archived solutions (ant size) and q is a parameter for adjusting the standard deviation:

$$\begin{aligned}&\begin{aligned} {w_l} = \frac{1}{{qNP\sqrt{2\pi } }}{e^{ - \left( {{{(l - 1)}^2}/2{q^2}N{P^2}} \right) }}\ \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned}&\begin{aligned} p_{l}=\frac{w_{l}}{\sum _{l=1}^{N P} w_{l}} \end{aligned} \end{aligned}$$

(18)

The decision depends on the pheromone level and heuristic information, while $s_l^k$ is the amount of pheromone of l possible solution and k-dimensional index (Fig. 3).

The pheromone update can be formulated by using Eq.19 as follows:

$$\begin{aligned} \begin{gathered} \tau _{l, k}^{t}=s_{l}^{k}+\Delta \sigma _{l}^{k} \\ \end{gathered} \end{aligned}$$

(19)

where $\sigma _l^i$ is given by Eq.20 :

$$\begin{aligned} \begin{gathered} \sigma _{l}^{i}=\xi \sum _{r=1}^{N P} \frac{\left| s_{r}^{k}-s_{l}^{k}\right| }{N P-1} \end{gathered} \end{aligned}$$

(20)

Fig. 2

ACO algorithm

While $\Delta$ is a random number by using randn function of MATLAB, l is sorted out through the roulette selection method, where t is the index of m samples, and $\xi$ is the pheromone evaporation rate which influences the convergence speed. On account of the pheromone reflects on the solutions archive, an update-pheromone operation is established by renewing the archive of the possible solutions. After completing the construction of the solutions by ants, there will be m + NP solutions. To maintain the archive, all solutions are sorted according to the objective function. In the subsequent step, the worst solutions are removed, and the others remain in the archive. After that, the algorithm tests termination conditions (base on the maximum number of function evaluations). If the termination condition is not satisfied, the optimization procedure will repeat the searching strategies mentioned above until the condition is met. Otherwise, the NFE should be broken up, and the optimization results are returned as output, which are the optimal unknown parameters and the corresponding objective function. The ACO setting parameters are selected as follows: q = 0.5; m = 500; $\xi$ = 0.8. This is realized with limitation criteria of 50000 maximum number of function evaluations (NFE). In addition, the search boundaries of B&Y model unknown parameters are ranged from -2 to 5.

Fig. 3

Flowchart of ACO-based parameter estimation approach

Objective functions

Model fitting is an optimization problem in itself. Model coefficients are computed in this process to minimize the difference between data observed on the field and values calculated by the model (residual). We will examine many different statistical metrics as an objective function to predict ROP in this paper, including root mean squared error (RMSE), the sum of squares error (SSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and Coefficient of Determination ($R^{2}$).

Root mean squared error

$$\begin{aligned} RMSE = \sqrt{\frac{{\sum \limits _{i = 1}^N {{{(RO{P_i} - RO{P_{i predicted}})}^2}} }}{N}} \end{aligned}$$

(21)

Sum of squares error

$$\begin{aligned} SSE = \sum \limits _{i = 1}^N {{{(RO{P_i} - RO{P_{i predicted}})}^2}} \end{aligned}$$

(22)

Table 1 Statistical parameters data of Well 1 (30 points)

Table 2 Statistical parameters data of Well 2 (30 points)

Table 3 Regression result of different tools for Well 1

Table 4 Regression result of different tools for Well 2

Mean absolute error

$$\begin{aligned} MAE = \frac{1}{N}\sum \limits _{i = 1}^N {\left| {RO{P_i} - RO{P_{i predicted}}} \right| } \end{aligned}$$

(23)

Mean absolute percentage error

$$\begin{aligned} MAPE = \frac{1}{N}\sum \limits _{i = 1}^N {\left| {\frac{{RO{P_i} - RO{P_{i predicted}}}}{{RO{P_i}}}} \right| } \end{aligned}$$

(24)

Coefficient of determination ($R^{2}$)

$R^{2}$ is a measure of the perfectness of the fitted curve, which can be described as equation 25.

$$\begin{aligned} {R^2} = \frac{{RSS}}{{SST}} = \frac{{\sum \limits _{i = 1}^N {{{(RO{P_i} - RO{P_{i predicted}})}^2}} }}{{\sum \limits _{i = 1}^N {{{(RO{P_i} - RO{P_{mean}})}^2}} }} \end{aligned}$$

(25)

$R^{2}$ is calculated by the sum of squared of prediction error (RSS) divided by the total sum of square (TSS), which replaces the calculated prediction with mean. R Square ranges from 0 to 1, with a higher value indicating a better fit between the predicted and the actual curves. In the above equations, ROP$_i$ and ROP$_{i predicted}$ are the observations and predictions rate of penetration, respectively, and N is the total number of samples.

Data description and results discussion

The datasets are from two wells: Well 1 is an offshore well from the Louisiana field (Bourgoyne & Young data 1974), and Well 2 is an onshore drilled well from the Algerian field (2020). Table 1 summarizes the statistical parameter data for Well 1, where depth ranges from 350 to 11870 ft, ROP ranges from 2 to 100 ft/h, RPM ranges from 49 to 1638, WOB ranges from 0.55 to 3 klb/in, and ECD ranges from 9 to 17 ppg. This case study enables us to evaluate the proposed techniques’ ability to estimate the most accurate unknown parameters for ROP prediction.

For Well 2, the statistical parameters data are represented in Table 2, where depth ranged from 9515 to 20265 ft, ROP ranged from 6 to 43 ft/h, RPM ranged from 58 to 129, WOB ranged from 0.8 to 3 klb/in, and ECD ranged from 9.5 to 17.9 ppg. With a deeper level than the first well, this well allows the validation and efficiency of the suggested techniques while also verifying the accuracy of the adopted approach to predict the ROP. These apply to onshore and offshore wells with limited datasets of a maximum of 30 points.

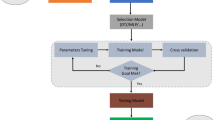
The application for both wells uses B&Y as the main model to evaluate its effectiveness compared with two other models. First, the parameters $x_2$ through $x_8$ must be calculated for each data entry using Eq.5 through Eq. 11, supported by the best value soft model constants $a_1$ through $a_8$. We use two different approaches: MLR and MNLR. To obtain the best optimum solution while applying different algorithms and objective functions, in this context, we apply multiple optimization tools and algorithms developed in both the MATLAB and Excel environments.

The following algorithms are listed:

• For Excel environment: we used data tool analysis for MLR and GRG algorithm for MNLR.

• For MATLAB environment: we used different algorithms: fminunc, fminsearch, fsolve, lsqcurvefit, lsqnonlin, ACO. In addition, we will compare the results by using different statistical metrics (R and RMSE).

Model comparison

To assess the obtained results of both wells, a comparison of three ROP models is performed. In this section, we will focus on results obtained from well 2. For the Maurer model, the formation drillability constant K is found using regression to be 1721.51, while for the Bingham model, two constants $\alpha$ and $\beta$ (WOB constant) are calculated using regression to be 0.01349 and 2.34 consecutively. The final ROP model is B&Y, for which the best correlation of eight exponents, $a_1$ to $a_8$, are found to be 0,089, 7,11E-05, 7,22E-04, 1,68E-04, -0,894, -0,386, -2,023, 0,298 and 0,981, respectively. Figure 5 shows the high accuracy of B&Y model in ROP prediction which gets an R-value of 0.98. The Maurer model underestimated the ROP values which yielded an R-value of -0.40 as it is illustrated in Fig. 5, and the Bingham model neglected the threshold WOB and UCS required for the penetration which resulted in a very low accuracy for ROP predicting (Fig. 5). The results yielded an R value of -0.39. In terms of RMSE, the B&Y model yielded the lowest RMSE, which was 4.08, while the Maurer and Bingham models yielded an RMSE of 27.31 and 27.19, respectively. Based on these results, we concluded that the best model to predict ROP is B&Y model for the Algerian fields which can be used as a robust and precise equation to predict ROP in future wells by means of this employed approach and objective functions, and the results can be applied in the same field while the coefficient equation can be tuned for wells in other fields.

Fig. 4

The best correlation results for Well 1

Fig. 5

The best correlation results for Well 2

Case study results

As it is illustrated in Tables 3 and 4, and after several tests, we have deduced the following points:

• 1. Case study 1: Well 1 (The Louisiana offshore well). Table 3 summarizes the best regression results of different objective functions and algorithms we find:

  • Seven algorithms have been applied, with the use of two approaches, MLR and MNLR. According to the findings, MNLR outperforms MLR by 5% in terms of RMSE value, resulting in high ROP prediction accuracy.

  • After 27 tests of various objective functions, fminsearch, Lsqcurvefit, ACO, and Excel algorithms rated top among other algorithms while using MNLR approach. Figure 4 represents the best correlation coefficient obtained by B&Y model using these techniques; they also came in second when using MLR approach.

  • Fminunc algorithm gives a moderate result and high convergence with MLR rather than the MNLR.

  • Lsqnonlin and fsolve algorithms give the same results and ranked 6 and 7 of the overall test, which means the worst ones compared with the other algorithms.

  • The best results are obtained using MSE and R$^{2}$ as an objective function, and both R and RMSE values are 0.95 and 2.80 for respectively.

  • B&Y model proves his superiority in ROP prediction using data of well 1 compared to the Bingham and Maurer model. Figure 4 shows that Bingham and Maurer models underestimated the ROP values.

• 2. Case study 2: Well 2 (The Algerian onshore well).

Table 4 shows the statistical regression results of the competing algorithms when different objective functions are used. As demonstrated, the ACO, fminsearch, and Excel optimizers while employing the MNLR technique produce the best fitting results compared to the others. They achieve 0.981 and 4.089 for the R and RMSE metrics consecutively. MNLR enhances the fitness function value by more than 2.14% compared to MLR with the same execution time. In addition, R$^{2}$ and MSE offer the best accuracy. They may be considered as the most suitable objective functions for ROP prediction. In terms of convergence quality assessment, MNLR Excel’s optimizer gives the best CPU run time with less than 10 s, whereas ACO is the worst since it does not reach the best results before 40 s, followed by Lsqnonlin and Fsolve which give similar results with the same objective functions. Meanwhile, Fminunc tool shows the worst fitting results of 0.898 in terms of R-value.

Summary and conclusions

The multiple regression and metaheuristic techniques have been successfully used to predict the downhole environment and improve the future of drilling operations, particularly as they offer the ability to optimize complex drilling operations, while the number of data used is limited, which leads to a complex and challenging solution search process. In the present work, an investigation for ROP optimization has been done regarding different ROP models (Bingham, Maurer, and B&Y model). Furthermore, regression analysis and ACO techniques with various approaches (MLR, MNLR) and objective functions (MSE, RMSE, MAE, MAPE, R2) have been examined. Two different wells (from onshore and& offshore) with only 30 data points for each well have been utilized. The following conclusions can be drawn:

• ROP modeling: we found that the B&Y model outperforms the published ROP models (Bingham and Maurer) with the highest correlation coefficient and the lowest RMSE (R=0.9522, RMSE=2.85) and (R= 0.9811, RMSE=4.08) for well 1 and 2 respectively.

• Techniques: Regression and metaheuristic techniques have been tested for ROP prediction using two different approaches, MLR and MNLR. The results reveal that MNLR is the most effective strategy for both techniques. This may be explained by the interaction between the applied drilling parameters and the formation, which leads to a nonlinear pattern.

• Objective function: After 27 tests of 5 different objective functions (MSE, RMSE, MAE, MAPE, and R$^{2}$), it has been found that the best results are obtained by MSE and R$^{2}$ as objective functions, for both well 1 and 2.

• Algorithms: Fminsearch, Lsqcurvefit, ACO, and Excel (GRG) algorithms give the most accurate results and high response to ROP prediction.

• Fminunc algorithm gives a moderate result and high convergence with MLR rather than the MNLR.

• Lsqnonlin and fsolve algorithms give the same results. However, they are the worst ones compared with other algorithms.

• Regression (Fminsearch, Lsqcurvefit, and Excel (GRG) algorithms) and ACO algorithms perform the best result in the application of MNLR approach with the use of MSE and R$^{2}$ as objective functions.

  This study validates the application of B&Y model in both onshore and offshore wells. The findings of this paper could be a strong candidate by providing a new approach deals with data limitation problems. Significantly the method can reduce the non-productive time and develop a fitness function during real-time optimization, yielding the lowest drilling cost in well planning and exploration phases. However, the selected models do not take all the drilling variables under consideration, such as vibration, torque, and formation characteristics; even so, due to the complexity of the problem, currently there is no perfect model that covers all the drilling parameters.