Introduction

Rainfall is considered one of the major water supply sources, representing the most important component of the water cycle. Population expansion and community socioeconomic development will exacerbate their requirements in the future (Benzater et al. 2019). Droughts and floods are intimately linked to the variability of precipitation. Both extreme meteorological events can endanger water supply, irrigation, and industry and change a country’s strategy by triggering catastrophic material and human damage. Climate change is the greatest threat to the water supply. These changes are due to either external variability (human activity) or internal variability (Zhao et al. 2019). Climate change has an increasingly negative influence on the environment, water resources, agricultural operations, industrial output, and human life due to global warming (Shi and Xu 2008). Because of its critical significance in developing future water supply and inducing flooding, detecting changes in precipitation is a significant and complex problem that is gaining more attention. According to the third assessment report of the Intergovernmental Panel on Climate Change (IPCC), global land rainfall increased by around 2% on average in the twentieth century (Ramaswamy et al. 2021; Beck and Oomen 2021; Sharek and Shah 2021; Molina and Abadal 2021). Annual global precipitation increased gradually from 1900 to the late 1950s, decreased until 1970, increased in the 1970s, and decreased after 1980. According to previous evaluations, the rainfall patterns study and investigation have become a more active research issue for better regional water resources and hazards management in recent years (Zerouali et al. 2022).

Numerous analyses and studies have been carried out to assess if rainfall observation shows patterns at the local level. Using least squares regression (LSR) and the t-test, Hamilton et al. (2001) found that precipitation amount revealed rising trends in the Kejimkujik, Canada. Cannarozzo et al. (2006) used the Mann–Kendall (MK) rank correlation test to confirm the presence of a trend at various rainfall time scales and the rainfall distribution. The results revealed a negative trend for the entire region. Using the cumulative sum method and rank-sum tests, Kampata et al. (2008) revealed no significant changes in the annual rainfall within the Zambezi River basin. Moreover, by applying the simple linear regression method, Millett et al. (2009) found that average rainfall has increased over the past century, despite reducing rainfall in Canada’s western prairies. Furthermore, using the empirical orthogonal function and continuous wavelet transform (CWT) techniques, Zhong and Li (2009) observed that annual rainfall in Mianyang (China) also exhibited a declining trend. Using the Mann–Kendall (MK) test, Kumar and Jain (2010) assessed annual and seasonal rainfall at five sites to understand rainfall trends throughout Kashmir (India). The results documented that all rainfall stations revealed a downward trend in winter and monsoon rainy days. In the Tarim River basin, Xu et al. (2010), using the MK test, concluded that mean annual rainfall increased from 1960 to 2007. Using the RClimdex 1.0 program, dos Santos et al. (2011) discovered that rainfall varied greatly over Utah (United States) from 1930 to 2006. At 12 selected meteorological stations, Ali et al. (2021), using Innovative Trend Methodology (ITM), revealed significant rising trends over the summer, with trend values ranging from 0.22 to 2.46. Furthermore, at a specific significance level, the ITM’s performance was shown to be compatible with both MK and Sen’s slope estimator tests. As well, climate change impacts have a direct effect on rainfall variability. Yun et al. (2021) proposed a mechanism that linked the rise in mean sea surface temperature (SST) to rainfall variability. They found that, under a warmer climate, the slope of the rainfall function over the Niño3 area gets steeper, with a 42.1% increase in 2050–2099 compared to 1950–1999, attributable to increases in the moisture sensitivity (16.2%) and the dynamic supports (25.9%). Azari et al. (2021) used R-factor regression models to calculate future rainfall erosivity and clarified that it would decrease in the dry zones of Iran’s Southeast, Center, and East, according to the Representative Concentration Pathways (RCP) 4.5 projections; but, in RCP 8.5, an increase in precipitation would induce a rise in rainfall erosivity in most regions of Iran. In addition, there are also some change point detection methods, such as hybrid methods like ITM (Nourani et al. 2015; Zerouali et al. 2020) and Innovative Triangular Trend Analysis (ITTM) (Zerouali et al. 2021a, b).

DWT and CWT wavelet transform techniques have been used successfully in many applications, including transient image and signal analysis and processing and communication systems (Chandrasekhar and Eswara Rao 2012; Galiana-Merino et al. 2013; Hill and Uvarova 2018). Wavelet transform is an excellent way to analyze nonstationary signals in nature (Zerouali et al. 2022; Sang et al. 2013). CWT and DWT are two procedures of wavelet transform (Brassarote et al. 2018; Rhif et al. 2019; Adhikari et al. 2020). For example, wavelet analysis was used on seismic data by Chakraborty and Okaya (1995), who emphasized the benefits of frequency-time decomposition for improved signal study. Wavelet analysis was utilized based on well-logging data by Prokoph et al. (2000) to determine the sedimentary cycles of oil source rocks. Additionally, the Hilbert Huang transform (HHT), designed by Huang et al. (1998), was used in this study as the second method for partial rainfall trend detection. The empirical mode decomposition (EMD) approach and the Hilbert spectral analysis (HSA) techniques are two different techniques used in HHT (Huang et al. 1998). The HSA may be used to identify each instantaneous frequency and amplitudes of the intrinsic mode functions (IMFs). In contrast, the EMD method decomposes the time series into oscillatory signals of various frequencies by a sifting process. As a result, the HHT methodology outperforms other spectrum decomposition methods to detect the signal’s space-frequency characteristics. HHT method has been implemented in several studies, such as distinguishing variations in geophysical well-log signals (Gairola and Chandrasekhar 2017; Subhakar and Chandrasekhar 2016), identifying surface and subsurface expressions of gas seepage (Schroot et al. 2005), performing fault diagnosis in a rotor system (Ji and Wang 2018), extracting infrasound generated by an earthquake (Zhu et al. 2017), diagnosing bearing fault (Kabla and Mokrani 2016), and processing ultrasonic echo signal of composites (Gao et al. 2019). Therefore, this work aims to improve the total annual rainfall trend visualization using combined ITM and their inspired approaches with time frequency-based methods, i.e., DWT versus HHT. Thus, new HHT-based hybrid methods (i.e., ITM-HHT, D-ITM-HHT, and T-ITM-HHT) are proposed and compared to the DWT-based methods suggested by Zerouali et al. (2020), and finally the best method is recommend.

Description of study area and database

In this research paper, three rainfall time series from 1920 to 2011 were selected from three different hydrological basins located in humid and semiarid regions of Northern Algeria (Fig. 1) to get a glimpse into the climate variability of Northern Algeria. In addition, this selected geographical region has a limited research focus.

Fig. 1
figure 1

Digital elevation model of Northern Algeria and the main selected rainfall stations used in this study

Full size image

Algeria has a climate that differs noticeably from south to north. The close part of the Mediterranean Sea is characterized by a Mediterranean climate, whereas the highlands (southern part) are characterized by cold winters and hot summers with little rain. The temperature difference between day and night is considerable. Further south, at the start of the Sahara Desert, the temperature difference between day and night is even more extreme. The rainfalls are discreet and vary according to the zones between 1 000 mm in the east (Grande Kabylie, Petite Kabylie, and Djebel Edough) and 400 mm in the west (Chelif Valley, the mountains of Aurès, and El-Amour).

Materials and methods

Empirical mode decomposition

In Zerouali et al. (2020), the DWT was used in conjunction with an ITM and its Double (D-ITM) and Triple (T-ITM) inspired approaches for rainfall trend analysis. This paper was proposed as a comparative study with the results obtained by Zerouali et al. (2020) using Hilbert Huang transform based on empirical mode decomposition (EMD) in conjunction with ITM, D-ITM, and T-ITM for rainfall trend detection.

Empirical Mode Decomposition (EMD) constitutes the first phase of an approach algorithm known as the Hilbert Huang transform (Tsolis and Xenos 2011). It is a multi-resolution decomposition of signals into IMFs. The team of Norden E. Huang of NASA first proposed it in 1998 (Huang 1998), intending to study climate-atmospheric data. The basic idea is to offer a flexible spectral approach, facilitate the reading, and extract data information (Abda and Chettih 2018). EMD is a nonlinear method of data analysis, where the stationarity assumptions are not required. Finally, it is a fully adaptive method that uses the sifting process of building the construction space directly from the time series (signal).

The sifting process permits a temporal decomposition of a signal into a sum of fundamental contributions (oscillating components) called IMFs or Empirical Modes, which are signals of AM-FM type with a mono-component, each of zero mean (Huang 1998). In practice, IMFs are almost orthogonal and mutually uncorrelated. Two conditions define the IMFs:

  • The extrema number and the zero crossings must be either equal or differ at most by one in the data set.

  • The envelope mean values defined by the local minima and maxima must be equal to zero at any point.

The following equation gives the decomposition of a signal by EMD:

$$x(t) = r_{n} (t) + \sum\limits_{j = 1}^{n} {C_{j} (t)}$$
(1)

where x(t) is the time series, rn(t) is the final residue, and Cj(t) represents a modal function intrinsic to phase j (Flandrin and Gonçalvès 2004).

Şen’s innovative trend methodology or analysis

Şen’s innovative trend methodology or analysis (ITM) is a simple and effective statistical approach, first proposed by Zekai Şen (2012) to partial trend detection in hydroclimatic and earth science series. In ITM, the time series is separated into two equal time intervals. The first interval is positioned on the abscissa (x-axis), and the second is positioned on the ordinate (y-axis) in ascending order.

The interpretation of the partial trend detected or the period that has the trend would be according to the positions of data points around the 45° line (x = y). Figure 2 illustrates categories of each partial trend according to subgroup for high, medium, and low rainfall. The reader is cordially invited to consult the papers of Şen (2012) and Kişi (2018) to understand ITM implantation better.

Fig. 2
figure 2

Şen’s innovative trend methodology template

Full size image

Multiple Şen’s innovative trend methodology

Several approaches were inspired and proposed from the basic concept of the innovative trend methodology, where “Multiple Şen-innovative trend analysis” is one of these approaches. It was first proposed by Yavuz Selim Güçlü (Güçlü 2018) in the framework of improving ITM for partial rainfall trend detection. Two methods were proposed in Güçlü (2018), the first one is the Double-ITM (D-ITM), and the second one is the Triple-ITM (T-ITM). D-ITM and T-ITM are robust in assessing the trend constancy in a rainfall time series (Zerouali et al. 2020).

For D-ITM, the rainfall series is divided into three sub-periods, wherein T-ITM is divided into four sub-periods before introducing them into the Şen’s method template. In D-ITM, the first sub-period is compared with the second and the third sub-periods. In addition to this comparison, the third sub-period is compared to the fourth sub-period in the T-ITM. As ITM, the sub-periods ranked ascending on the x- and y-axes. In this paper, for the D-ITM, the rainfall series were divided into sub-intervals as follows: (1920–1950), (1951–1981), and (1982–2010), whereas for the T-ITM, the time series were divided as (1920–1942), (1943–1965), (1966–1988), and (1989–2011).

The flowchart proposed in Fig. 3 was used for preprocessing the selected rainfall time series by combining the innovative trend methodology (ITM, D-ITM, and T-ITM) with DWT, which was discussed by Zerouali et al. (2020). The second part of the flowchart shows the combining of Hilbert Huang transform (HHT) with ITM, D-ITM, and T-ITM, i.e., hybrid approaches (ITM–HHT, D-ITM–HHT, and T-ITM–HHT), which is explained in the following stages:

  1. 1.

    Pretreatment process of the input signal x(t).

  2. 2.

    Use of the cubic spline to localize the maximum and minimum values in the signal to build the maxima and minima envelopes.

  3. 3.

    Construct the mean envelope mj(t) based on the local mean of both maxima emax(t) and minima emin(t) envelopes.

    $$m_{j} (t) = \frac{{e_{\max } (t) + e_{\min } (t)}}{2}$$
    (2)
  4. 4.

    Subtract the mean by a difference between the original signal and the average envelope, as follows:

    $$h_{j} (t) = x(t) - m_{j} (t)$$
    (3)

    if mj (t) ≡ 0, the function \(h_{j} (t)\) would be an IMF; if not, the process would continue and iterate until the criteria are obtained. Please consult Abda and Chettih (2018) for more detail about this stage.

  5. 5.

    After step 4, the IMF is obtained.

  6. 6.

    From the IMF and residues, 24 input combinations can be proposed (Table 1).

  7. 7.

    Apply the spectral and correlation analyses to perform the filtering and assess the periodicity.

  8. 8.

    Extract statistical features from the 24 proposed models and use them as input time series into the ITM, D-ITM, and T-ITM.

Fig. 3
figure 3

Flowchart methodology proposed for this study

Full size image
Table 1 Geographic location and statistical characteristics of the studied rainfall series and their DWT and HHT models
Full size table

Correlation and spectral analysis

Correlation and spectral analysis (CSA) describes the change in covariance at diverse frequency scales for the input–output relationship. The correlation technique assesses the inter-relationship of sequential time-series observations according to obtained autocorrelation coefficients rk (k = 0, 1, 2, 3, …, m) (Larocque et al. 1998; Mangin 1984). Based on the CSA concept of Box and Jenkins (1976), the truncation (m) that can be used for a signals analysis of N observation is obtained as m = 2 N/3, m = N/3, or m = N/2, where rk is given by the following expression:

$$r_{k} = \frac{{C_{k} (k)}}{{C_{k} (0)}}$$
(4)
$$C_{k} (0) = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left( {x_{t} - \overline{x}} \right)^{2} } \quad {\tt{and} \space} C_{k} (k) = \frac{1}{N}\sum\limits_{t = 1}^{N - k} {\left( {x_{t} - \overline{x}} \right)\;\left( {x_{t + k} - \overline{x}} \right)}$$
(5)

where the autocovariance and the time lag are represented by Cx(k) and k, respectively. In addition, the power spectral density function \(\Gamma_{x} \left( f \right)\) is given by Padilla and Pulido-Bosch (1995), which explains the unbiased approach of the Fourier transform:

$$\Gamma_{x} (f) = 2{\kern 1pt} \;\left[ {1 + 2\sum\limits_{x = 1}^{m} {D_{k} r_{k} {\kern 1pt} \cos {\kern 1pt} {\kern 1pt} (2\pi fk)} } \right]$$
(6)

where f and Dk are the frequency and the weighting function, respectively. The Tukey filters were used in this study.

Results and discussion

Empirical mode decomposition for trend rainfall analysis

Many uncertain and random factors contribute to increasing the noise, which contaminates the primary information contained in the hydrological signals (Sang et al. 2013). These noises can correspond to classic errors and inaccuracies in the measurement (physical noise), estimation modeling, and multi-annual fluctuations (Vaseghi 2008). According to Sang et al. (2013), noise should be paid much attention to and considered in hydrologic time series analysis. Several time-scale analysis techniques have been used to denoise the time series to distinguish trends from periodicities. One of these techniques is the wavelet transform, which increases the accuracy of statistical analysis approaches and improves the trend visualization (Zerouali et al. 2021a, b; Rashid et al. 2015).

In this part, the EMD was applied as a denoising approach for rainfall signals, where five models (IMF1, IMF2, IMF3, IMF4, and IMF 5) were applied without adding the residual component to avoid increasing the intercorrelation between the observations and residues (R) (Zerouali et al. 2021a, b). In addition, 18 other models are suggested (Table 1) based on the combinations developed (IMF and R) to straightforwardly obtain the best combinations that clarify nonlinear trends and climatic responses present in the rainfall series, and they were compared with the results obtained in previous research. The proposed models (combinations), as presented in Table 1, are suggested for the first time in this research. However, such proposed combinations (models) do not play a fundamental role in the decision-making regarding the existence/no existence of significant trends. Figure 4 illustrates the 24 combinations resulting from the DWT (Fig. 4a and Table 1) that have been proposed by Zerouali et al. (2020, 2021a, b) and the proposed combinations resulting from the HHT (Fig. 4b and Table 1) for the Oued Taria station. The correlation coefficient between each pair series model, resulting from DWT and HHT of the Oued Taria station, revealed that the high correlation coefficient between the models exceeds 0.8: M1, M11, M15, M16, M18, M19, M20, M21, M22, and M24, which the behavior similarity may explain. These models are followed by the M7, M12, M13, M14, and M23 models with correlation coefficient ranging between 0.7 and 0.78. The other models (i.e., M2, M3, M4, M5, M8, M9, and M10) are characterized by a correlation coefficient of less than 0.5, which explains less behavior similarity between each pair (Fig. 5).

Fig. 4
figure 4

The 24 proposed models resulting from the a discrete wavelet transform and b Hilbert Huang transform for the Oued Taria station

Full size image
Fig. 5
figure 5

Correlation coefficient between each pair series model resulting from discrete wavelet transform and Hilbert Huang transform for the Oued Taria station

Full size image

The HHT combined models were proposed in this paper for aided rainfall trend detection because they have proven their efficiency in science and engineering fields as Computer-Aided Diagnosis (CAD) images to explore Parkinson’s Disease (Rojas et al. 2013) and Spatial Pattern for Motor Imagery Brain-Computer Interface (He et al. 2012).

The largest amplitude and highest frequency characterize the first IMF1. As the order number of the mode increased, the amplitude and frequency of the IMFs decreased (Liu et al. 2020). The differences between the original time series and the sums of all four IMFs represent the trend (M6) (Fig. 4b). Each IMF represents a periodic component. Table 2 explains each combination or model with quasi-period. In this case, the minimum variance period was mentioned; in another case, Liu et al. (2020) described that the IMF1 might characterize periods ranging from 2 (1/0.47) to 8 years (1/0.12). It is evident for DWT, where each detail represents only one variance period (Table 2). On the other hand, the correlation coefficients between each proposed HHT model and the original rainfall series are presented in Fig. 6. The figure indicates that high correlation values are observed for the models, especially for the IMF1 (M1) and IMF5 (M5) components, which indicate a significant contribution to total variance equal to 34.7% and 40.3%, respectively. A low correlation was observed between the models M3, M4, and the original series (Fig. 6 and Table 1), especially for the Ain Beida station linked to the low contribution in total cumulative variance or energy (> 13%) (dissimilarity behavior). The distribution of the correlation values between HHT models and their original series (Fig. 6) is similar to that obtained by Zerouali et al. (2020, 2021a, b) between DWT models and the original rainfall series for the same stations with slight high values of correlation for HHT models and rainfall (Fig. 6).

Table 2 The variance with its periodic component for each combined model based on DWT and HHT
Full size table
Fig. 6
figure 6

Correlation coefficient between each proposed model resulting from Hilbert Huang transform and the original rainfall series

Full size image

The analysis showed an inverse relationship; the temporal variability decreases as the scale increases (from M1 to M6) (Fig. 5). This observation was also observed in the DWT decomposition (Zerouali et al. 2020), making the time–frequency-based method a good tool for trend and anomaly detection in hydrological and earth science time series. The EMD coefficients for IMF1 (M1) and IMF2 (M2) correspond to the intra-annual modes of variability of 2 and 4 years, respectively, indicating a uniform temporal distribution across the scales, with a similar magnitude to DWT coefficients for some scales (Fig. 4b). For the multi-annual to multi-decade components of HHT coefficients (IMF3, IMF4, and IMF5 corresponding to 8-years, 16-years, and 32-years modes of variability, respectively), the analysis revealed successive and dominant periodic phenomena, explaining dry and wet periods through the period of study. The residue (R) component indicates important information regarding trend direction towards the driest conditions, which explains that the R component contributes to the largest part of trend production of the original series. However, the components of IMF4 to IMF5 did not add or contribute considerably to the trend components observed in the three rainfall series (Fig. 5b).

Previous insights from ITM, D-ITM, and T-ITM

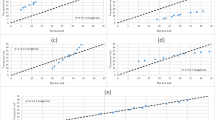
In the previous work of Zerouali et al. (2020), the Innovative Trend Methodology (Sen 2012) and their inspired approaches proposed by Güçlü (2018), under the term “Multiple Şen-innovative” or D-ITM and T-ITM, have been used and applied for partial rainfall trend identification. For ITM, the three rainfall time series were divided into two equal periods to compare the 1920–1965 period (x-axis) with the 1966–2011 period (y-axis) (Fig. 7). In D-ITM, the rainfall series were divided into three periods: 1920–1950, 1951–1981, and 1982–2010 (Fig. 8), whereas for the T-ITM, the time series were divided into four consecutive periods, i.e., 1920–1942, 1943–1965, 1966–1988, and 1989–2011 (Fig. 9). As can be seen, Fig. 7 shows a significant decrease in rainfall (monotonic trend) for the Oued Taria station at various amounts (medium and low), wherever the high amounts reveal a distribution of black points around the ITM scatterplot (Fig. 7a). However, Ain Beida and Azazga rainfall stations revealed a nonsignificant trend with data points close to the no-trend line, represented by the 45° line (Fig. 7b, c). The same observation has been marked by applying the D-ITM and T-ITM, as illustrated in Figs. 8a and 9a. This may be explained by the inhomogeneous nature of rainfall variability and nonlinear behavior. According to Xoplaki et al. (2004), at a regional scale, the rainfall trends in the Mediterranean are not statistically significant because of the high variability. Furthermore, Peña-Angulo et al. (2020) noted that the predominance of interannual and interdecadal modes of variability that characterize the rainfall mechanism can play a great role in hiding statistically significant trends, except for generally significant trends identified for shorter periods. In addition, Peña-Angulo et al. (2019) observed that the Mediterranean rainfall became irregular, extreme, and with erratic drier climatic conditions.

Fig. 7
figure 7

Representations and comparison of the results of the application of the innovative trend method (ITM) on original series (black points), some proposed models using DWT (red points), and HHT (blue points) (hybrid approach) at a Oued Taria, b Azazga, and c Ain Beida stations

Full size image
Fig. 8
figure 8

Representations and comparison of the results of the application of the Double-innovative trend method (D-ITM) on the original series (left side) and some proposed models using HHT (hybrid approach) at a Oued Taria, b Azazga, and c Ain Beida stations

Full size image
Fig. 9
figure 9

Representations and comparison of the results of the application of the Triple-innovative trend method (T-ITM) on the original series (left side) and some proposed models using HHT (hybrid approach) at a Oued Taria, b Azazga, and c Ain Beida stations

Full size image

According to Zerouali et al. (2020, 2021a, b), the results obtained using the ITM, D-ITM, T-ITM, and ITTM on the original series indicate that the high temporal variability of the studied rainfall series makes the detection of partial trends more complex, requiring a different approach that increases the accuracy of ITM, D-ITM, T-ITM, and ITTM to identify any changes and hidden trends in the time series. The discrete wavelet transform (DWT) was proposed as a preprocessing tool that allows for generating a high amount of information and captures the nonlinear variation of the signal at different scales (Zerouali et al. 2020, 2021a, b). The results revealed that the ITM-DWT, D-ITM-DWT, T-ITM-DWT, and ITTM-DWT methods outperformed the ITM, D-ITM, T-ITM, and ITTM methods for visible partial identification of trends, proving that DWT can improve the analysis accuracy.

In the next part, a relatively new hybrid method for trend detection on rainfall series is proposed and assessed, combining ITM, D-ITM, and T-ITM with EMD based on HHT.

New insights from the proposed hybrid methods

According to the literature review, the ITM approach proposed by Şen (2012) proved its effectiveness and success for partial trend identification on hydrology and earth science time series and has been used in hundred research papers for trend detection in various types of time series, such as rainfall (e.g., Achite and Caloiero 2021; Benzater et al. 2021; Boudiaf et al. 2021; Harkat and Kisi 2021;), streamflow (Ashraf et al. 2021; Yilmaz and Tosunoglu 2019; Kişi et 2018), temperature (Dabanli et al. 2021; Serencam 2019; Şen 2017a), drought (Mehr and Vaheddoost 2020; Tosunoglu et al. 2017), and water and air quality (Kisi and Ay 2014; Güçlü et al. 2019).

The success of ITM is the result of several scientific and technical advances that improve its performance, especially in enhancing the graphical visualization of significant trends. Under different autoregressive (AR) process magnitude, Şen (2014) concluded that ITM does not require assumptions or hypotheses. It can be applied in small sample lengths, non-normal data distribution, and serial dependence. According to a significance level, Kisi (2015) and Şen (2017b) developed a new contribution for ITM results interpretation. Şen (2017c) proposed a new procedure based on the pre-whitening (P-W) process to decrease the effect of serial correlation on trend analysis approach as MK and ITM. The results revealed that the P-W could reliably determine trends transported even in the serially dependent signals, especially in the original observations, which improve the accuracy of trends detection with periodic characteristics. Using some magnitude percentages, bootstraps, and variance correction based on Monte Carlo simulation for some rainfall England regions, Alashan (2020) concludes that the improved version ITM_R gives successful results compared with Mann–Kendall (MK) test. In addition, Nourani et al. (2015) combined ITM with DWT. The obtained results showed that the ITM-DWT method successfully identified partial trends. Alashan (2018) has improved trend visualization based on the change box approach and ITM method. The results showed that the proposed method has successfully improved the numerical illustration of the ITM scatterplot changes.

Recently, time–frequency-based methods such as HHT and DWT are among the most valuable stationary and nonstationary series analysis techniques. Their development made a scientific revolution in several sciences and engineering fields (e.g., medical sciences and electrical sciences). It has made very significant progress compared in the area of hydrology. The application in the hydrology field has shown its success since the beginning of the last decade, in particular in the hydrological time series analysis and forecasting (e.g., Chen et al. 2021; Zhang et al. 2021; Shi et al. 2021; Saraiva et al. 2021; Abda et al. 2021; Freire et al. 2019; Abda and Chettih 2018; Reddy and Adarsh 2016; Huang et al. 2014; Wang et al. 2018). It is worth highlighting that although CWT could give information and solution for our requirements, DWT and HHT are more flexible.

In this section, ITM-HHT, D-ITM-HHT, and T-ITM-HHT were developed and proposed to enhance the visualization of trends and their localization at time scales in the studied rainfall series. Furthermore, the proposed hybrid methods will be compared with the ITM applied in the original (rainfall) series (ITM-OS) and with the previous results obtained by Zerouali et al. (2020) based on ITM-DWT, D-ITM-DWT, and T-ITM-DWT.

For the Oued Taria station (Fig. 7a), the insert of selected models of the HHT (M6 and 10) (Table 1) in the ITM template illustrates that the data points are totally placed under the 45° straight line, especially for the M6 regardless the total of rainfall (i.e., low, medium, and high). A monotonic downward trend was visibly detected in the ITM template for the 1966–2011 period. The detected trend is very significant for ITM-DWT for medium rainfall at some models compared to the first 1920–1965 period. The application of ITM-HHT on the rainfall in Azazga and Ain Beida clearly indicates an improvement in the trend visualization and detection with model 6 (M6), especially for Azazga station (Fig. 7b, c). A monotonic downward trend was well noticeable in the 1966–2011 period for low and medium rainfalls. However, high rainfalls have shown an increasing trend at the scale of the two stations, using M6 and M4 models, and are well observed using ITM-HHT. The increasing trend of high rainfall can be considered a preliminary sign of the increase in future extreme rainfall events and their frequency that can produce flooding. This observation agrees with Elouissi et al. (2016), who studied precipitation records at 25 stations in the Macta basin (Northern Algeria).

The application of D-ITM-HHT to the studied rainfall series is shown in Fig. 8. The graphical results clearly indicate how D-ITM-HHT successively clearly detected the trends. For Oued Taria, the results indicate, by models 6 and 12, a positive trend for the 1951–1981 period compared to the first 1920–1950 period for medium and high rainfalls. Comparing the 1951–1981 and 1982–2010 periods, Fig. 8a shows that Oued Taria presents a monotonic upward trend during the 1982–2010 period with an increase in high rainfall amounts, as reported previously. In addition, similar results were also observed in the Azazga rainfall using the M6 and M11 models (Fig. 8b). The rainfall in Ain Beida clearly illustrates the importance of D-ITM-HHT in partial trend separation using M6 and M23 models, where two different and stable monotonic trends were identified, i.e., a downward trend was observed in the 1951–1981 period compared to the 1920–1950 period, easily identifying a negative trend starting in 1920 (blue points), whereas the red points indicated a positive partial trend in the 1982–2010 period compared to the 1951–1981 period. According to Ozer et al. (2003), the change-points towards wetter conditions identified African rainfall as statistically significant over a dozen years.

As the first observation on the T-ITM scatterplot (Fig. 9), the data points of rainfall observations near the no trend 45° line explain the high rainfall variability in Northern Algeria. This high variability hides the trends and makes them difficult to be seen clearly. By contrast, for T-ITM-HHT and D-ITM-HHT, the trends are clearly structured and well-observed at all studied rainfall stations (Fig. 9a, b, and c). Three remarkable and significant trends were observed for all stations using the T-HHT-DWT based on the combination model M6. Also, back to D-ITM-HHT and ITM-HHT with that T-ITM-HHT, the results indicate that the model M6 is marked as the typical model between the proposed approaches and can represent the climatic behavior of the rainfall over the study area. Model 6 represents the previously explained residue that transports most of the trend component. In comparison with ITM-DWT, T-ITM-DWT, and ITM-DWT, Zerouali et al. (2020) observed that the approximation component (A5) is the most representative of the climatic response of rainfall in the same study area and that A5 transports most of the trend component. According to the approximations, they are considered the trend production component (Zerouali et al. 2021a; Palizdan et al. 2017; Partal 2017; Adarsh and Reddy 2015; Nourani et al. 2015). Therefore, it can be concluded that approximation (A) and the residue (R) are some of the most recommended components that can be used for studies of climate variability assessment. Despite this, this information replicates that selecting an explicit model does not play any fundamental role in decision-making concerning the presence/no presence of significant hidden trends.

By using T-ITM-HHT, rainfall in Oued Taria shows that the second period (1943–1965) was wet compared to the first (1920–1942) and the third (1966–1988) and that the latter was wet compared to the fourth period (1989–2011), explained by the green data distribution under the no trend 45° line of the T-ITM-HHT scatterplot (Fig. 9a). Rainfall in Azazga showed that the 1943–1965 period has an upward trend compared to the 1920–1942 and 1966–1988 periods, and the 1989–2011 period is relatively wet compared to 1966–1989. This confirms the decrease in rainfall amount between 1980 and 2000, especially at the scale of Eastern Algeria (Habibi and Meddi 2021; Derdous et al. 2021; Zerouali et al. 2021b, Achour et al. 2020; Caloiero et al. 2019; Jemai et al. 2018; Piccarreta et al. 2013; Hamlaoui-Moulai et al. 2013; Philandras et al. 2011; Meddi et al. 2010).

Generally, the trends detected at the scale of the studied rainfall series are summarized as follows:

  1. (1)

    The 1930–1950 period has been known as probably dry episodes.

  2. (2)

    The 1950–1975 period has been known as probably wet episodes.

  3. (3)

    From 1975, a long-term drought was observed in the western region of Northern Algeria, which can be explained by the Moroccan Atlas Mountain that acts as a weather barrier stopping the wind influx from the Atlantic Ocean transport moisture into the region. Chbouki et al. (1995) revealed an oscillation of wet and dry periods, 1950–1970 and 1925–1950, respectively, in Morocco, with long-term drought starting from the mid of 1970. Meddi et al. (2010) detected in Northeastern Algeria a wet period between 1950 and 1970, with decreasing trends, and a drought period between the 1980s and 1990s. In Northern Central Algeria, Zerouali et al. (2021a, b) detected a long-term drought from the late 1980s, where more than half of the stations were influenced by moderate and severe dry events.

  4. (4)

    From 2001, a probably humid period of normal rainfall conditions was observed mainly in Northeastern Algeria. In the Tafna basin (Northwestern Algeria), Radia et al. (2021) observed deficient or dry decades in the 1980s, 1990s, and 2000s, with a remarkable rainfall amount trend between 2008 and 2014. In Northern Algeria, Nouaceur and Murărescu (2016) observed, during the 1970–1986 period, high rainfall variability with alternations of wet and dry years. They were followed by a long-term dry period (1987–2002), relatively wet between 2003 and 2013. Bougara et al. (2020) also observed in Northwestern Algeria a rainfall increase from the 2000s due to the rise of autumn rainfall amount. According to Hallouz et al. (2020), the dry sequence observed in the Cheliff watershed (northwest of Algeria), the 1971–1990 period, has been negatively correlated with SOI explained by El Niño. Zerouali et al. (2018) documented a significant link between the observed droughts of the 1980s and 1990s and the North Atlantic Oscillation (NAO) in Central Algeria. Mathbout et al. (2019) observed that a decrease in rainfall might be linked to the NAO positive phase (NAO +) in the Western Mediterranean, especially in Maghreb countries. In Mediterranean regions, López-Moreno et al. (2011) reported that the NAO could modulate the winter rainfall, especially in the mountain areas, producing more dry and warm events. In the Abruzzo region (Italy), Vergni et al. (2016) documented that the negative trends in rainfall were significantly linked to the positive phase (NOA +), while the negative phase (NAO −) acted in the opposite way.

Figures 10 and 11 show the correlogram and the spectrum analysis for the studied three rainfall series, respectively. The results of the original series revealed remarkable peaks at different frequencies, i.e., 0.048 (20 years), 0.1 (10 years), 0.18 (5 years), and 0.38 (2 years) (Figs. 10, 11). The analysis of the HHT models of this study and DWT models proposed by Zerouali et al. (2020) revealed similar behavior responses of models 6 and 10 by the dominance of low-frequency events less than 0.1, describing multi-decadal and decadal phenomena. This illustrates the significant filtering process (removing) of phenomena less than the decadal periodicity. From the analysis, it can be said that less than the decadal periodicity of short- and medium-term processes can increase rainfall variability, which masks the partial trend and makes it difficult to be identified (Figs. 10, 11).

Fig. 10
figure 10

Correlogram analysis of rainfall series (blue line), and some proposed models (M6, M10, and M23) using DWT (green line) and HHT (red line) for a Oued Taria, b Azazga, and c Ain Beida rainfall

Full size image
Fig. 11
figure 11

Spectrum analysis of rainfall series (blue line) and some proposed models (M6, M10, and M23) using DWT (green line) and HHT (red line) for a Oued Taria, b Azazga, and c Ain Beida rainfall

Full size image

From this study, the relatively new combined approaches ITM-HHT, D-ITM-HHT, and T-ITM-HHT have been applied to improve the visualization of hidden trends in rainfall series with high variability. The new combined models successfully detected in a clearly visible manner hidden trends present in the signals, which proves that the elimination or removal of some variability modes (components) of the original rainfall signals can increase the accuracy of the approaches used. The observations provided by these hybrid methods agree with those obtained by ITM-DWT, D-ITM-DWT, and T-ITM-DWT that proven the importance of the information resulting from the preprocessing using methods based on a time–frequency approach in making decisions concerning hidden trends.

Conclusion

This study assessed ITM and their inspired methods (D-ITM and T-ITM) and unconventional combined approaches (ITM-HHT, D-ITM-HHT, and T-ITM-HHT) for trend detection in some representative rainfall time series situated in the north of Algeria during the 1920–2011 period. The main results are summarized as follows:

  • The analysis revealed that ITM-HHT, D-ITM-HHT, and T-ITM-HHT successfully improved the visualization of trends, which can be concluded that HHT is efficient a coupling method that can enhance ITM, D-ITM, and T-ITM accuracy for partial trend identification.

  • A dry period was observed between 1980 and 2000, whereas the wet periods were detected from 1950 to 1975 and the beginning of the 2000s.

  • The analysis indicated the effectiveness of the proposed methods for detecting extreme rainfall events based on the high amount direction.

  • The study revealed that the HHT could be used as a denoising and filtering method in climatic time series.

  • The results indicate that the component (R) represented by model 6 is the typical model that can be used in ITM, D-ITM, and T-ITM for a better understanding of the climatic behavior of the study area.

  • HHT method may be used to diagnose rainfall series behavior by removing some components, improving the analysis’s accuracy.

  • The ITM-HHT, D-ITM-HHT, T-ITM-HHT, and ITTM-HHT outperformed the ITM, D-ITM, and T-ITM applied in the original series for partial trend identification.

Finally, in addition to the efficiency of ITM, D-ITM, and T-ITM, the main strong point of this research is the success of the second time–frequency-based method represented by HHT as a combined approach with ITM and their inspired methods, where the first technique that used DWT provided promising results. The proposed hybrid methods (ITM-HHT, D-ITM-HHT, and T-ITM-HHT and ITM-DWT, D-ITM-DWT, and T-ITM-DWT) give more information to the experimenter to understand the most trends that are hidden by the high variability of the signal and make the good decision about the climatic system behavior, being able to provide better resource management and planning under changing climate. However, it should be noted that the main weakness of this research is the use of short time series, which prevented us from dividing them into long sub-time intervals. Long time series may include many partial trends, and the wavelet approach usually gives good results on stationary and nonstationary phenomena. Furthermore, these hybrid approaches were applied to rainfall series to assess their efficiency, which opens the door to other researchers to use those approaches in different fields such as water quality, runoff, temperature, air quality, and all earth sciences time series. Likewise, it would be good to elaborate on other comparison studies using other time-scale-energy-based methods.