Introduction

Until recent years, water pollution caused by various pollutants such as dyes, heavy metals and toxic anions has been increasing rapidly due to industrial wastes thrown into the environment without treatment (Rangabhashiyam and Balasubramanian 2019a, 2018; Alam, 2014; Selvakumar and Rangabhashiyam 2019; Periyasamy et al. 2020). Heavy metals are extremely durable, bioaccumulative and inherently the most toxic (Rangabhashiyam and Balasubramanian 2019b). Among them, chromium (Cr) is one of the common heavy metals used in several metal surface treatment, electroplating, industrial processes, mining, chrome plating, wood preservation, including metal processing and leather tanning (Wang et al. 2020; Rangabhashiyam and Balasubramanian 2018). The chromium mainly exits in the aquatic environment in two oxidation situations, that is, trivalent chromium Cr(III) and hexavalent chromium Cr(VI) with significant differences. Hexavalent chromium is more water soluble, less stable, easily enters living cell and more toxic than trivalent chromium (Huang et al. 2016). The harmful effects of Cr(VI) cause health problems in humans such as dermatitis, skin irritation, bleeding, epigastric pain, bronchitis, chronic ulcers, nasal septum perforation, lung cancer, pneumonia and liver inflammation (Rangabhashiyam and Balasubramanian 2019b).

The World Health Orgnization (WHO) and the US Environmental Protection Agency (USEPA) restricted their maximum contaminant level of total Cr(VI) in potable water as 0.05 and 0.1 mg/L, respectively (Rangabhashiyam and Balasubramanian 2018; Li et al. 2020). Consequently, it is an imperative aim to treat Cr-polluted wastewater previous to discharge so as to the environment (Liu et al. 2020). Various methods such as chemical precipitation, electrochemical treatment, biological methods, membrane separation, ion exchange and adsorptive methods have been used to separate heavy metals from wastewater (ALOthman et al. 2013; Sun et al. 2020; Deng et al. 2020; Qin et al. 2020; Liu et al. 2020). Adsorption among all the other methods studied, it has been one of the preferred methods for Cr(VI) removal due to its efficiency, operational simplicity and low cost (ALOthman et al. 2013). Conversely, other methods have many disadvantages, such as being uneconomical and incomplete removing Cr(VI), requiring high reactive and energy, and creating toxic sludge or other waste products that require disposal or treatment (ALOthman et al. 2013). However, the high cost of adsorbents is one of the biggest obstacles for industries to apply the adsorption process. The cheapness of adsorbents reduces the cost and increases the applicability of adsorption technology. Therefore, there is a need to develop low-cost and readily available adsorbents for the removal of Cr(VI) ions from aqueous media (ALOthman et al. 2013).

Recently, nFe0 has been used to remove heavy metal impurities. nFe0 has become one of the promising and effective technologies in the removal of substances in the environment due to its large surface area, high reactivity and very small particle size. nFe0 is also capable of converting toxic substances into their non-toxic forms (Simeonidis et al. 2016; Jiang et al. 2018; Zhang et al. 2019). nFe0 can also be used to promote the reduction and precipitation of toxic and carcinogenic metals such as Cr(VI) to more stable forms such as Cr(III) (Dalal and Reddy 2019). However, the reduction in reactivity and mechanical strength, as well as agglomeration, limited the application of nFe0 when used in conventional treatment systems (Shu et al. 2020; Zhu et al. 2018). Furthermore, another problem is the difficult separation from the aqueous medium resulting from the small size of nFe0. In recent years, this problem has been compensated by immobilization, fixation or confinement of nFe0 to supporting materials such as silica, zeolite, kaolinite, bentonite, activated carbon, zeolites or polymer membranes. Immobilization of such materials, apart from the immobilization of nFe0, also affected their physicochemical properties. Immobilization of nFe0 also affected its physicochemical properties (Xu et al. 2018; Luo et al. 2019; Wu et al. 2020; Zhang et al. 2019). More importantly, the removal of adsorbent from the aqueous medium to remove water impurities through magnetic separation was strikingly advantageous by nFe0. This method has significant advantages in terms of speed and time compared to other conventional methods (Li et al. 2017).

Pumice is a rock formed as a result of volcanic eruptions with a large surface area and a skeletal structure, including open channels that allow water and ions to enter and exit the crystal structure. It can also be easily processed in metal removal and can be used as a suitable material due to its low cost (Amin et al. 2018; Indah et al. 2018; Guler and Cebeci 2017). Pumice having basic and acidic character has a high silica content that makes a negatively charged surface. Reducing the negative charge on the surface of the pumice increases its adsorption capacity and therefore acidification is performed (Samarghandi et al. 2013; Derakhshan et al. 2013; Jonasi et al. 2017).

The main objectives of this study are structural analysis of NBP and NDP; synthesize and characterize NBP- and NDP-supported nFe0 (BP-nFe0, DP-nFe0); use of NBP, NDP, BP-nFe0 and DP-nFe0 in the removal of Cr(VI) and determine and evaluate the adsorption efficiency under different experimental conditions; the use of magnetic separation method to separate BP-nFe0 and DP-nFe0 from aqueous media; comparison of Cr(VI) removal efficiencies of NBP, NDP, BP-nFe0 and DP-nFe0 adsorbents.

Materials and methods

Materials

The following chemical reagents were used: 1,5-diphenylcarbazide, K2Cr2O7, FeCl3·6H2O, NaBH4, HCl, NaOH and ethanol, which are all analytical reagent grade (Fluka, Sigma-Aldrich ve Merck). All chemicals were applied as delivered without further purification. As for support layer, pumice was supplied from different regions of Turkey. Native Diyarbakir pumice from Southeast Turkey and native Bitlis pumice from East Turkey were obtained and analyzed by X-ray fluorescence spectrometry (XRF, Rigaku ZSX Primus II). Native Diyarbakir pumice consisted of SiO2—69.9%, Al2O3—12.6%, Fe2O3—5.29%, Na2O—4.21%, MnO—0.159%, K2O—6.48% and native Bitlis pumice consisted of SiO2—63.7%, Al2O3—16.5%, Fe2O3—4.03%, Na2O—0.933%, MnO—0.078%, K2O—6.23%. To obtain 1000 mg/L aqueous stock solution of Cr(VI) for later use, 2.829 g of potassium dichromate (K2Cr2O7) was dissolved in one thousand mL deionized water. In this study, the solutions with desired concentrations were attained by diluting with deionized water of the stock solution.

Preparation and characterization of DP-nFe0 ve BP-nFe0

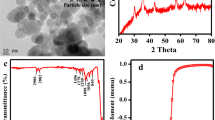
Native Diyarbakir pumice from Southeast Turkey and native Bitlis pumice from East Turkey were ground to 45 µM and acidified with 1% HCl for 24 h. It was washed several times with deionized water so as to remove impurities and until pH reached neutral levels. Acid activated native Diyarbakir pumice (NDP) and native Bitlis pumice (NBP) were dried at 65 °C in the oven and were prepared for nFe0 coating (Guler and Cebeci 2017). The coating process was performed according to Liu et al. (2014). The NDP- and NBP-supported nFe0 (DP-nFe0 and BP-nFe0) were produced according to conventional liquid phase method in which the pumice was used as a support layer and borohydride (NaBH4) was used as a reduction agent for iron ions (FeCl3) (Shi et al. 2011; Üzüm et al. 2009; Liu et al. 2014; Ponder et al. 2000). After 3.36 g of NDP and NBP was introduced into the three-necked flask, the iron solution obtained by dissolving 1.35 g of FeCl3.6H2O in 100 mL of ethanol/water (8:1 ratio) was added and stirred under argon gas for 1 h. Then, NaBH4 solution prepared by dissolving 0.95 g of NaBH4 in 100 mL of purified water was added to the mixture at a drop rate of 60 drops per minute. The mixture was stirred in the sonicator for 2 min every 10 min. After the addition of NaBH4 is complete, stirring was continued for one hour (Liu et al. 2014; Qasim et al. 2018). The synthesized composite is separated with a magnet and dried at lyophilizer (CHRIST, Alpha 2–4 LDplus). The theoretical mass fraction of the synthesized nFe0 is 7.7% of pumice-supported nFe0 adsorbents (Liu et al. 2014). The micro-morphology features were observed by scanning electron microscopy (SEM, Quanta 400F). Elemental mapping was obtained by energy-dispersive X-ray spectroscopy (EDX, Jeol 2100F microscope). The surface areas of NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents were measured using the BET-N2 adsorption method (Brunauer–Emmett–Teller isotherm) using the Accelerated Surface Area and Porosimetry Analyzer (Micromeritics-TriStar II Plus 3030, USA).

Batch experiments

Batch experiment for Cr(VI) removal was carried out in 50 mL flasks at room temperature using the mechanical agitation (IKA@KS 4000i) at 200 rpm. Various experimental parameters such as adsorbent dose (2, 4, 6, 8, 10 g/L), initial pH (1–9), initial Cr(VI) concentration (25, 50, 75 mg/L) and contact time (1–90 min) were studied. All experiments were repeated three times. The solid and liquid phases are separated by a magnet. The determination of Cr(VI) in the supernatant was performed with a UV–Vis spectrophotometer (Agilent Cary 60) using a 1,5-diphenylcarbazide spectrophotometric method at 545 nm.

Results and discussion

Characterization

The results of the chemical composition of NBP, BP-nFe0, NDP and DP-nFe0 obtained from EDX (energy-dispersive X-ray spectrophotometer) analysis are shown in Table 1. When the native pumice taken from different regions of Turkey was used as support material, although the synthesis method and conditions were the same, the amount of nFe0 formed on the surfaces of the NDP and NBP was affected. Iron content, which was 1.99% in NBP, increased 1.9-fold after synthesis to 3.83%. The iron content of NDP and DP-nFe0 is 2.08% and 60%, respectively, that is, the iron content increased 29 times after synthesis of DP-nFe0. Harman and Ibrahim (2018) used the Isparta pumice with 2.03% iron content as a support material, and after the synthesis of P-nZVI, the iron content increased to 41.98%, that is, 21 times with the same synthesis method.

Table 1 Elementary composition of NBP, BP-nFe0, NDP and DP-nFe0 from EDX characterization
Full size table

SEM images of NBP, BP-nFe0, NDP and DP-nFe0 are shown in Fig. 1. As seen in Fig. 1, NDP has an irregular or oval-shaped mesh of internal cavities/pores or vesicles, some of which are interconnected and open to the outer surface that provides suitable sites for adsorption compared to NBP. The images of DP-nFe0 and BP-nFe0 revealed that the prepared Fe0 nanoparticles showed heterogeneous distribution on the pumice surface. The Fe0 nanoparticles appear to be spherical in shape and do not have a single size. In the images of DP-nFe0 and BP-nFe0, when NDP was used as a support material, Fe0 nanoparticles were formed much more on the surface. This is probably due to the morphological differences between NDP and NBP.

Fig. 1
figure 1

SEM image of NBP, BP-nFe0, NDP and DP-nFe0

Full size image

The specific surface area of adsorbents was measured using a BET-N2 surface area analyzer. The average specific surface area of NDP and NBP natural pumice was measured as 6.3 and 1.3 m2/g, respectively. The specific surface areas of DP-nFe0 and BP-nFe0 obtained by covering the surfaces of two native pumice with nFe0 were measured as 40.5 and 6.8 m2/g, respectively. nFe0 coating of NDP, which has a larger surface area than NBP, has increased the surface area much more.

Influence of pH

The control of surface load in removing adsorbate from solution is significant, and the pH of the solution determines the surface charge. Due to the important role of pH in adsorption, the pH effect was examined in the range of 1–9 (Fig. 2). Maximum Cr(VI) removal effectiveness was obtained in acidic medium (pH 1–3) for NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents. As illustrated in Fig. 2, while pH increased from 1 to 9, adsorption yields of NDP, NBP, DP-nFe0 and BP-nFe0 dropped from 54 to 48%, from 57 to 54%, from 95 to 72% and from 74 to 60%, respectively. Both the adsorption and reduction processes of adsorbents were affected by the solution pH value. On the one hand, the adsorption process, caused by electrostatic, hydrophobic and hydrogen bond interactions, is strongly dependent on the solution pH value. On the other hand, pH value determines the current form of Cr(VI). Below pH 6, HCrO4− is the dominant species. If the pH rises to above 6, the form shifts to CrO42− and Cr2O72−, and when pH > 7.5, CrO42− is the only existence of chromate (Lv et al. 2012). On the other hand, pH value determines the surface charge of adsorbents. The adsorbent surface is highly protonated in an acidic solution medium. It increases the attraction force between positively charged adsorbent surface and negatively charged anionic species HCrO4− (Zhang et al. 2012; Xu et al. 2018). In addition, the reduction process of Cr(VI) (expressed as Eqs.(1)) by nFe0 was also affected by pH value. From this equation, it was easier to find out that H+ is strongly needed and consumed all along the reaction (Lv et al. 2012). That explained why an acidic environment is preferred by the removal of Cr(VI) in aqueous solution by nFe0.

$$2{\text{HCrO}}_{4}^{ - } + 3{\text{Fe}}^{0} + 14{\text{H}}^{ + } \to 3{\text{Fe}}^{{2 + }} + 2{\text{Cr}}^{{3 + }} + 8{\text{H}}_{2} {\text{O}}$$
(1)
Fig. 2
figure 2

Effect of pH on Cr(VI) removal yield NDP, NBP, DP-nFe0 and BP-nFe0 (C0: 50 mg/L; Dose: 0.05 g/10 mL; Temperature: 25 °C; mixing speed: 250 rpm; Time: 30 min). Error bars represent the standard deviation of the measurements

Full size image

This phenomenon can be seen as another reason for the low Cr(VI) ions concentration found by 1,5-diphenylcarbazide method during analysis. Increasing the pH of the solution reduces the degree of positive charge on the adsorbent and leads to poor attachment of negative species to the adsorbent surface. The other negative ion OH− in the basic medium can contend with the main anion CrO42− ions for adsorption on the adsorbents (Qin et al. 2020; Wu et al. 2020). Since the highest Cr(VI) removal is obtained at acidic pH and the real Cr(VI) solutions are also acidic, pH correction is not required in the practical applications of NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents. Similar results of various adsorbents have been reported to remove chromium using pumice. Sepehr et al. (Sepehr et al. 2014) examined the effect of pH in the range of 1–9 for the removal of chromium ions with native pumice (NP) and modified pumice (MGMP). They have shown that chromium sorption is pH dependent using NP and MGMP and higher extraction efficiency is observed at pH 2.

Initial Cr(VI) concentration-contact time profile modeling

Figure 3a–d shows the effect of initial Cr(VI) ion concentration and contact time on the removal effectiveness of Cr(VI) onto NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents. As can be seen, the intake of Cr(VI) in initial phase was high for each of the four adsorbents with a higher adsorption rate. An interesting feature of an adsorbent is that it adsorbs the solute rapidly in the first stage. Removal of Cr(VI) ions increased as the contact time increased until reaching equilibrium, because after about 20 min, the removal of chromium did not change significantly and was therefore taken into account thereafter. After 20 min contact time, 3.8, 4.9, 6.2 mg Cr(VI)/g NDP, 3.1, 5.2, 7.2 mg Cr(VI)/g NBP, 4.8, 8.1, 12.8 mg Cr(VI)/g DP-nFe0 and 3.7, 6.9, 9.4 mg Cr(VI)/g BP-nFe0 have been removed for 25, 50, 75 mgL−1 initial Cr (VI) concentrations, respectively. In the current study, as the chromium concentration increases, the removal efficiency of the chromium increases in certain adsorbent mass (Zhou et al. 2020; Yu et al. 2020).

Fig. 3
figure 3

Influence of contact time and initial chromium concentration on the removal efficiency of a NDP, b NBP, c DP-NFe0, d BP-nFe0 (pH: 2, adsorbent: 0.05 g/L, 25 °C temperature and 250 rpm agitation speed). Error bars represent the standard deviation of the measurements

Full size image

Effect of adsorbent dosage

Figure 4 demonstrates the effect of adsorbent’s dosage on the removal efficacy of Cr(VI) onto NDP, NBP, DP-nFe0 and BP-nFe0 at the room temperature. From the curves in Fig. 2, you can easily see that the adsorption capacity (qe) decreases as the amount of adsorbent increases. This is due to the fact that the active areas on the absorbent surface are not saturated by Cr(VI) ions. As the Cr(VI) concentration is constant and the amount of adsorbent increases, the Cr(VI) concentration decreases compared to the amount of adsorbent in the aqueous medium. Hence, the adsorbent is contacted with less Cr(VI) ions, that is, its active sites in the adsorbent remain unsaturated, meaning that the active sites remain unsaturated in the adsorbent. Thus, there has been a decrease in the adsorption value. In addition, as the amount of adsorbent increases, it increases in stacking and aggregation. This phenomenon increases the total amount of surface overlap of the absorbent material, and the active specific surface areas are reduced for absorption. This restricts the absorption capacity. Active specific surface sites for adsorption were found to be unsaturated with adsorption (Gupta and Babu 2009; Jain et al. 2010; Sepehr et al. 2014).

Fig. 4
figure 4

Effect of NDP, NBP, DP-nFe0 and BP-nFe0 mass on chromium removal (Cr(VI) concentration = 50 mg/L, contact time 60 min, pH 2, 25 °C temperature and 250 rpm agitation speed)

Full size image

Measurement of adsorption isotherm

The adsorption isotherms of the of NDP, NBP, DP-nFe0 and BP-nFe0 were investigated by 1,5-diphenylcarbazide spectrophotometric method. In our experiment, 50 mg of NDP, NBP, DP-nFe0 and BP-nFe0 was incubated with solutions of different Cr(VI) concentrations (from 20 to 100 mg/L, pH = 2) at 25 °C. Langmuir, Freundlich, Dubinin–Radushkevich (DR), Temkin and Jovanoic (Rangabhashiyam et al. 2014) were utilized to describe Cr(VI) adsorption isotherms to detect adsorbent surface properties and adsorption capacity of NDP, NBP, DP-nFe0 and BP-nFe0. The Langmuir isotherm model was established using the following equation (Langmuir 1918; Tural et al. 2017):

$$q_{e} = \frac{{q_{{\max }} K_{L} C_{e} }}{{1 + K_{L} C_{e} }}$$
(2)

where qe (mg/g), Ce (mg/L) and qmax (mg/g) are the amounts of Cr(VI) bound to the NBP, BP-nFe0, NDP and DP-nFe0 adsorbents, the free concentration of Cr(VI) at adsorption equilibrium and the maximal adsorption capacity of the adsorbents, respectively. KL is the Langmuir constant related to the adsorption capacity (L/mg). The equilibrium constants for these models were determined using linear regression analysis. The necessary properties of the Langmuir isotherm model are expressed as the equilibrium parameter, the dimensionless constant RL is referred as the separation/equilibrium parameter. RL is the separation factor expressed as

$$R_{L} = \frac{1}{{1 + K_{L} C_{0} }}$$
(3)

if RL > 1, the adsorption is unfavorable; if RL = 1, linear; if 0 < RL < 1, favorable; if RL = 0, irreversible. The Cr(VI) adsorption equilibrium data of NBP, BP-nFe0, NDP and DP-nFe0 adsorbents are compatible with the Langmuir model and results are shown in Table 2. The maximum adsorption capacity qm values of NBP, BP-nFe0, NDP and DP-nFe0 were 10.82 mg/g, 14.30 mg/g, 17.39 mg/g and 161.29 mg/g for, respectively (Table 3). DP-nFe0 adsorbent offered superior adsorption capacity compared to NBP, BP-nFe0 and NDP adsorbents. The experimental data fitting the Langmuir model give a linear plot of NBP, BP-nFe0, NDP and DP-nFe0 adsorbents. Coefficient of determination (R2) was in range of 0.981, 0.959, 0.991, 0.994 for NBP, BP-nFe0, NDP and DP-nFe0 adsorbents, respectively. The RL values decreased with increasing Cr(VI) concentration from 0.021 to 0.361 for NDP and NBP adsorbents, and BP-nFe0 and DP-nFe0 adsorbents range between 0.125 and 0.907 results (Table 2) Using the adsorbents studied, the Cr(VI) supported. The RL values were found decreasing with increasing Cr(VI) concentration for NDP and NBP adsorbents range from 0.021 to 0.361, and BP-nFe0 and DP-nFe0 adsorbents range between 0.125 and 0.907. As can be seen from Table 2, the results obtained from Cr(VI) removal with NBP, BP-nFe0, NDP and DP-nFe0 adsorbents favored the adsorption process.

Table 2 Langmuir separation factor for NBP, BP-nFe0, NDP, DP-nFe0
Full size table
Table 3 Adsorption isotherm parameters for chromium ions on to NBP, BP-nFe0, NDP ve DP-nFe0
Full size table

Freundlich isotherm model expression proposing multilayer adsorption is an empirical equation based on the heterogeneous surface area of adsorption (Freundlich and Helle 1939; Freundlich 1907). The Freundlich isotherm model is established using the following equation:

$$q_{e} = K_{F} C_{e}^{{1/n_F}}$$
(4)

where qe (mg/g) and Ce (mg/L) are the amounts of Cr(VI) bound to the NBP, BP-nFe0, NDP and DP-nFe0 at adsorption equilibrium and the free concentration of Cr(VI) at adsorption equilibrium, respectively. KF and nF are the Freundlich constants related to the adsorption capacity and intensity, respectively. The equilibrium constants for these models were determined using linear regression analysis. If the value of nF ranges between 1 and 10, indicate favorable adsorption. The value of nF for NBP, BP-nFe0, NDP and DP-nFe0 was 8.08, 1.84, 1.23 and 1.01, respectively. This reveals that 1/nF less than 1 signifies that use of adsorbents favored Cr(VI) adsorption. The coefficient of determination value of NBP (0.939) is lower compared to the BP-nFe0 (0.962), NDP (0.968) and DP-nFe0 (0.967) adsorbents.

Dubinin–Radushkevich isotherm model defines the porous structure of NBP, BP-nFe0, NDP and DP-nFe0 adsorbents. This model is based on adsorption potential theory, based on the assumption that adsorption is related to microporous filled adsorbate into the adsorbent, and not the layer-by-layer on pore walls (Dubinin and Radushkevich 1947). The linear presentation of the D-R isotherm equation is expressed by

$$q_{e} = q_{{\max }}\,^{{\exp \left( { - \beta \varepsilon ^{2} } \right)}}$$
(5)
$$\varepsilon = RT\ln \left( {1 + \frac{1}{{C_{e} }}} \right)$$
(6)

where qe is the amount of Cr(VI) adsorbed on per unit weight of materials (mg/g), qmax is the maximum adsorption capacity (mg/g), β is the activity coefficient related to the mean free energy of adsorption (mol2/J2) and ε is the Polanyi potential. R is universal gas constant (8.314 J/mol K), T is kelvin temperature (K) and mean adsorption energy E (kJ/mol).

$$E = \frac{1}{{\sqrt {2\beta } }}$$
(7)

Mean adsorption energy E (kJ/mol) displays important information about the nature of adsorption process. The E values in the range from 8 to 16 kJ/mol indicate chemical mechanism. If the E value is less than 8 kJ/mol, it indicates physical adsorption. The values of qmax and β given in Table 3 were obtained from the graph of log qe versus ε2 for the NBP, BP-nFe0, NDP and DP-nFe0 adsorbents. Great difference in adsorption capacity qmax (mg/g) was observed between the NDP and DP-nFe0 adsorbents. The DP-nFe0 adsorbent presented maximum adsorption capacity of 12.86 mg/g. Coefficient of determination R2 from D-R model is below 0.92 for all adsorbents. Compared to the Langmuir and Freundlich models, the values of R2 in D-R model were found low. Adsorption energy E (kJ/mol) less than 0.5 for all adsorbents revealed that the Cr(VI) adsorption is driven by physical mechanism (Zaheer et al. 2019).

Temkin isotherm model depends upon temperature, related to Cr(VI) and NBP, BP-nFe0, NDP and DP-nFe0 adsorbents surface interaction with all the molecules in the layer of adsorption. Liquid phase adsorption is a complex event, since adsorbed molecules are not organized in identical packed structure (Tempkin and Pyzhev 1940). The nonlinear equation of the Temkin isotherm model is shown as follows:

$$q_{e} = \frac{{RT}}{{b_{T} }}\ln (A_{T} C_{e} )$$
(8)

where qe (mg/g) and Ce (mg/L) were the amount of Cr(VI) bound to the NBP, BP-nFe0, NDP and DP-nFe0 and the free concentration of Cr(VI) at adsorption equilibrium. AT is the equilibrium bond constant related to the maximum energy of bond, bT (kJ/mol) is the Temkin constant concerned with the adsorption heat. R (8.314 kJ/mol K) is the universal gas constant, and T is the Kelvin temperature. The determined values of the Temkin isotherm model constants are shown in Table 3. The bT constant of Temkin model was obtained within range of 2.77–7.58 kJ/mol, and AT Temkin constant 0.10–0.60 L/mg, for adsorbents. Coefficient of determination R2 ≥ 0.868 is found for all adsorbents.

Jovanovic isotherm model assumptions are similar to the Langmuir model, which is used to predict monolayer localized adsorption without lateral interaction. This model applies to mobilized and localized phase adsorption during high solute concentrations reaching the saturation level (Jovanovic 1969). The nonlinear equation of the Jovanovic isotherm model is shown as follows:

$$q_{e} = q_{{\max }} (1 - e^{{K_{j} C_{e} }} )$$
(9)

where Kj (L/g) and qmax (mg/g) are the Jovanovic isotherm constant and the maximum adsorption capacity, respectively, in Jovanovic model. The calculated constants from the linear equation of the Jovanovic isotherm model are shown in Table 3. When the adsorption capacities of the isotherm models are compared, it was seen that adsorption capacity of The Jovanovic model is lower than that of the other isotherm models. R2 value of NDP (0.967) and DP-nFe0 (0.965) is greater than that of NBP (0.905) and BP-nFe0 (0.822).

Measurement of adsorption kinetics

The kinetic model data help to evaluate the rate determining step of Cr(VI) adsorption by NBP, BP-nFe0, NDP and DP-nFe0 adsorbents. Four kinetic models, pseudo-first-order, pseudo-second-order, Elovich model and intraparticle diffusion models, were used to analyze the experimental data and examine the adsorption kinetics (Alberti et al. 2012).

The pseudo-first-order equation was given by Lagergren and this model applicable during the initial stage of the adsorption process (Lagergren 1898). The equation of the nonlinear pseudo-first-order model is presented as follows:

$$\log (q_{e} - q_{t} ) = \log q_{e} - \frac{{k_{1} t}}{{2.303}}$$
(10)

where qe and qt (mg/g) represent the adsorption capacities at equilibrium time and time t (min), and k1 (1/min) is adsorption rate constant of nonlinear pseudo-first-order model. The results of the pseudo-first-order kinetic model parameter of adsorbents such as NBP, BP-nFe0, NDP and DP-nFe0 toward the removal of Cr(VI) are presented in Table 4. The pseudo-first-order rate constant is obtained from the slope of plot between log (qe−qt) against time, t.

Table 4 Pseudo-first-order and pseudo-second-order kinetic modeling constants of NBP, BP-nFe0, NDP and DP-nFe0
Full size table

The equation of the nonlinear pseudo-second-order model (Ho and McKay 1999) is presented as follows:

$$\frac{t}{{q_{t} }} = \frac{1}{{k_{2} q_{e}^{2} }} + \frac{1}{{q_{e} }}t$$
(11)

where qe and qt (mg/g) represent the adsorption capacity at equilibrium time and time t (min), respectively, and k2 (g/mg min) is the adsorption rate constant of the nonlinear pseudo-second-order model. The experimental data analysis of Cr(VI) adsorption using NBP, BP-nFe0, NDP and DP-nFe0 adsorbents showed better fitness with the pseudo-second-order kinetic model. The values of k2 and qe calculated from the pseudo-second-order equation are shown in Table 4. The values of R2 showed that the pseudo-second-order model best fitted the Cr(VI) adsorption behavior of NBP, BP-nFe0, NDP and DP-nFe0 adsorbents, indicating that the adsorption is the rate-controlling step. R2 values obtained from the pseudo-second-order kinetics model are found higher compared to the pseudo-first-order isotherm model.

The intraparticle diffusion model was used to determine the diffusion mechanism (Weber and Morris 1962). The kinetic expression of the model was established using the following equation:

$$q_{t} = k_{{\text{int} }} t^{{0.5}} + C$$
(12)

where kint (mg/g min0.5) and C (mg/g) are the rate constant and the intercept, respectively. Informative information about the boundary layer thickness of the diffusion mechanism of adsorption is obtained by the expression of the intraparticle diffusion model. The values of kint and C calculated from the intraparticle diffusion equation are shown in Table 4.

It is understood from the the R2 values that the experimental data are not well defined according to the intraparticle diffusion model. The value of intercept C was observed in the range of 1.401–26.839 for all adsorbents.

The Elovich model (Wu et al. 2009) explains that adsorption performance is related to chemical adsorption and heterogeneous systems. The kinetic model is established using the following equation (Wu et al. 2009)

$$q_{t} = \frac{1}{\beta }\ln (\alpha \beta ) + \frac{1}{\beta }\ln (t)$$
(13)

The constant α (mg/g min) is related to the rate of chemisorption, and the constant β (g/mg) is related to the surface coverage. Elovich kinetic model parameters are obtained from the plot of qt versus ln(t) via slope and intercept. The values of R2 showed that the experimental data are not well described by Elovich model (Table 4).

Mechanism of Cr(VI) removal

A two-step interaction mechanism is proposed (Fu et al. 2016; Lv et al. 2012; Ullah et al. 2020). In the beginning, Cr(VI) in aqueous solution was absorbed on the BP-nFe0 and DP-nFe0 surface (Fu et al. 2016; Lv et al. 2012; Ullah et al. 2020). Then, Cr(VI) was reduced by nFe0 and coprecipitated or precipitated on the surface of BP-nFe0 and DP-nFe0 material. The removal of Cr(VI) using BP-nFe0 and DP-nFe0 adsorbents was extremely rapid at the first 5 min, indicating an initial adsorption in this reaction. Moreover, from the kinetic study data using the so-called second-order adsorption model, it can be concluded that the rate control step is most likely adsorption rather than reduction. In addition, the adsorption ability and stability of pumice were crucial for improving Cr(VI) removal. The pumice surface provided numerous reactive sites to capture Cr(VI), and the adsorbed Cr(VI) enhanced the transfer of floating electrons on the pumice surface, which accelerated the electron transfer from nFe0 to Cr(VI) (Fu et al. 2016; Lv et al. 2012; Ullah et al. 2020).

Conclusion

In this study, pumice from different regions in Turkey (Diyarbakir; NDP and Bitlis; NBP) structurally was characterized by BET, XRF, SEM and EDX. Synthesis of nFe0 was performed under the same conditions using both NDP and NBP as support materials. Iron content of NBP, NDP, DP-nFe0 and BP-nFe0 was obtained from EDX analysis. According to the EDX results, the percentage of zero-valent iron is affected when pumice obtained from different regions of Turkey was used as support material. Iron content, which was 1.99% in NBP, increased 1.9-fold after synthesis to 3.83%. However, iron content of NDP (2.08%) increased approximately 29 times after synthesis (60%). NDP, NBP, DP-nFe0 and BP-nFe0 have been used to remove Cr(VI). In order to optimize reaction parameters, it was aimed to find the most effective conditions by changing the initial Cr(VI) concentration, contact time, adsorbent amount and pH values. The removal of Cr(VI) on this system was strongly pH dependent, and the reaction between Cr(VI) and NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents followed pseudo-second-order kinetics. The adsorption isotherm results fitted well with Langmuir models, and the maximum adsorption capacity of Cr(VI) was 10.82, 14.30, 161.29 and 17.39 mg/g for NDP, NBP, DP-nFe0 and BP-nFe0 adsorbents, respectively, at pH 2.0 and 25 °C. The results showed that NDP is a much better support material for nano-zero-valent iron when compared to NBP pumice.