Effect of slip velocity on Newtonian fluid flow induced by a stretching surface within a porous medium

Abstract

This article aims to examine an unsteady 2-D laminar flow of magnetohydrodynamic fluid caused by an elastic surface immersed in a permeable medium under the influence of thermal radiation and extended heat flux. Thermal conductivity and viscosity both are supposed to vary with temperature. This flow model also includes velocity slip, heat source, and joule heating. The governing equations of the fluid, including momentum and energy equations, of the proposed problem are transfigured into a system of interconnected non-linear ordinary differential equations through similarity transformations. The resultant equations are solved efficiently by employing the shooting technique in combination with the fourth-order Runge-Kutta method. Numerical values and the effect of numerous governing factors on the flow field, temperature distribution, local skin friction coefficient, and Nusselt number are showcased via graphs and tables. The investigation reveals that velocity slip, heat source, and porosity parameters enhance the temperature field while diminishing the velocity field. Furthermore, the velocity slip parameter notably reduces both the coefficient of skin friction and the Nusselt number.

Introduction

The analysis of the magnetohydrodynamic (MHD) flow of Newtonian fluid owing to stretching sheets has been a prominent area of research because of its significance in various industrial processes, energy systems, and environmental applications. These investigations are preferred due to their applications in paper production, continuous casting of metals, wire and fiber coatings, hot rolling, metallic bed cooling, polymer processes, condensation processes, drawing of plastic films, glass gusting, and reactor fluidization [1,2,3]. The idea of boundary layer flow on a moving solid sheet was initially introduced by Sakiadis [4]. He examined the boundary layer flow problem on continuously moving surfaces and compared the obtained results with those on moving sheets of finite length. This idea was further developed by Crane [5]. He employed a stretching surface where the velocity varies proportionally with the distance from the slit, a phenomenon commonly observed in the process of drawing plastic films. The fluid flow induced by stretching surfaces with heat transfer has wide-ranging applications in geophysics, biotechnology, and aeronautical engineering as well as in the fabrication of rubber molds, space vehicles, and polymer products. Therefore, a significant amount of work has been reported in this area using various stretching velocities [6, 7], different flow models [8], and different conditions [9, 10].

The majority of the previously mentioned research primarily focuses on steady flow. The investigation of fluid characteristics in a thin liquid film owing to a time-varying stretching surface was initially undertaken by Wang [11]. He found both numerical and analytical solutions to the problems. Later, Anderson et al. [12] introduced heat transfer phenomena in Wang’s problem and obtained that the higher values of unsteadiness parameter reduce the surface temperature. Elbashbeshy and Bazid [13] made a significant finding regarding the impact of the unsteadiness parameter (S) in their investigation of laminar boundary layer flow above a stretching surface. They witnessed a decline in both momentum and thermal boundary layer thickness for rising values of (S). Many researchers investigated the steady or unsteady flow for various fluid models due to stretching sheets under different conditions [14,15,16].

The presence of thermal radiation is crucial in high-temperature systems and space technology like advanced rockets, spacecraft, and jet engines where radiative heat transfer mechanisms become prominent. Thermal radiation affects the boundary layer. Therefore, in the field of polymer processing and glass production, thermal radiation significantly impacts heat transfer regulation [17]. Thermal radiation plays a critical role in designing equipment for various high-temperature applications like furnaces, combustion engines, and nuclear power plants, where its influence on heat transfer must be carefully considered [18]. El-Aziz [19] conducted a comprehensive investigation on the impact of thermal radiation on heat and fluid flow in the context of an unsteady stretching sheet. He concluded that the rate of heat transfer increased with an increase in the radiation parameter. In a separate study, Gnaneswara [20] examined the impact of thermal radiation on magnetohydrodynamic convective flow across a vertically extended surface in the existence of Hall current. He found that the temperature distribution increases as the radiation parameter increases. The exploration of heat flux has captured the interest of researchers owing to its broad utility in fields like heat exchangers, renewable energy systems, materials processing, and environmental engineering. Ishak et al. [21] analyzed the effect of variable heat flux in micropolar fluids over an extended sheet. He noticed that the heat transfer rate improves in the presence of variable heat flux. The flow behavior of MHD fluid induced by a stretching surface was investigated by Megahed [22], with a specific focus on the impact of varying heat flux and thermal radiation. He observed that the temperature profile increased with the intensity of heat flux, while the rate of heat transfer decreased.

The phenomenon of Joule heating occurs when electrical energy is transformed into heat within a conducting fluid, driven by the influence of an externally exerted magnetic field. The inclusion of joule heating is crucial in understanding the temperature distribution and heat transfer rates in MHD systems and has significant applications in many industries like food production, iron processing, electric coffee makers, and sterilization [23]. Maripala and Naikoti [24] conducted a study to explore the effect of the joule heating parameter on the unsteady magnetohydrodynamic flow over a stretched sheet in the appearance of a heat source. Additionally, Swain et al. [25] examined the influences of both viscous dissipation and joule heating on MHD and heat transfer over a stretched surface within a porous medium.

Fluid flow via porous media is a prevalent feature observed across different domains, including chemical engineering, geophysics, geothermal energy, and astrophysics. A comprehensive understanding of the mechanisms governing the transfer of mass, energy, and momentum within a permeable medium holds immense importance for various applications, including nuclear reactors, nuclear waste management, the functioning of petroleum reservoirs, insulation of buildings, and various manufacturing processes [26]. Representative work including these effects has been reported by Mukhopadhyay et al. [27], Swain et al. [28], and Seth et al. [29]. The phenomenon of heat source or sink holds significant importance in biomedical and various engineering applications, such as radial diffusers, thrust bearing design, and crude oil recovery. Kumar [30] conducted a study on the influence of a non-uniform heat source/sink on MHD micropolar fluid flow over a stretching sheet near the stagnation point, incorporating the variability of thermal conductivity. Mahmoud and Megahed [31] explored the influence of varying dynamic viscosity ($\mu$) and thermal conductivity ($\kappa$) on the behavior of a non-Newtonian liquid film as it flowed over an unsteadily moving sheet. This investigation took into account the existence of a magnetic field. They found that the Nusselt number decreases with an increase in both variable viscosity and thermal conductivity.

The behavior of real-world fluids is often characterized by variations in thermal conductivity and viscosity with temperature. Accounting for these variable fluid properties is essential for accurately predicting fluid flow and heat transfer phenomena. Several flow models proposed in existing studies [32,33,34] have incorporated an exponential relationship between viscosity and temperature, along with a linear relationship between thermal conductivity and temperature. Megahed [35] investigated the impact of slip velocity on the behavior of a Casson thin film over an extended sheet subjected to varying heat flux conditions. Velocity slip at the fluid-solid interface indicates the difference in velocity between the fluid and the solid surface. It is an important phenomenon that affects the boundary layer thickness and flow characteristics. Slips at fluid-solid boundaries play a pivotal role in tribology, influencing friction and reducing wear in various mechanical systems such as engines and bearings. In biomedical engineering, it assumes critical importance in facilitating the flow of blood within capillaries and artificial heart valves. Additionally, in the realm of heat exchangers, it significantly enhances heat transfer efficiency across various industrial processes, while in manufacturing, it serves to precisely control material deposition in techniques like inkjet and 3D printing. Mukhopadhyay [36] extensively explored the ramifications of slip mechanisms on the behavior of boundary layers and heat transfer in magnetohydrodynamic (MHD) fluid flows adjacent to an exponentially stretching surface. The study specifically accounted for thermal radiation and integrated the influences of suction/injection. The effect of velocity slip for various flow models and under different conditions has been presented by Megahed and co-authors [37,38,39].

Heat transfer over a stretching surface plays a significant role in manufacturing, contributing to the design of reliable apparatuses, gas turbines, and various impulsion devices such as cruise missiles and satellite launch vehicles. Due to its immense importance, numerous researchers have recently conducted studies on heat transfer and boundary layer flow over stretching surfaces, considering various effects such as thermal radiation, heat source/sink, joule heating, viscous dissipation, velocity slip, and porous medium effects. For instance, Saravana et al. [40] investigated the impact of thermal radiation on MHD Casson and Williamson fluid flow over a stretching sheet, taking into account velocity and thermal slip. Similarly, Konwar et al. [41] explored MHD boundary layer flow and heat transfer over an exponentially stretching surface within a porous medium, considering variable fluid properties. Sharma et al. [42] conducted a heat transfer analysis of MHD micropolar fluid flow past a stretching sheet with a slip effect, considering a permeable stretching surface and non-uniform heat source. Indeed, a considerable amount of research has been dedicated to exploring these phenomena, encompassing various effects in refs. [43,44,45].

In light of the existing literature, which primarily focuses on the analysis of MHD boundary layer flow over stretching surfaces using various heat flux models under different effects [1, 46, 47], there is a notable gap in research regarding the comprehensive investigation of the combined effect of variable heat flux, velocity slip, heat source/sink, and Joule heating on flow and heat transfer over unsteady stretching surfaces with variable fluid properties in a porous medium. Motivated by this identified research gap, we aim to provide a more thorough understanding of the intricate interplay between flow patterns and heat transfer behaviors by incorporating these complex factors. The insights gained from this comprehensive analysis hold significance for both academic advancement and practical applications in areas like microfluidic devices, blood flow analysis, and even improving industrial processes like polymer extrusion. It can also help us understand heat transfer in renewable energy systems.

Mathematical formulation

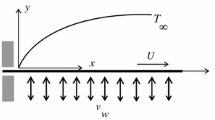
Consider the dynamics of a time-dependent 2-D laminar flow of a non-compressible Newtonian fluid due to a continuously stretching surface characterized by slip conditions. The stretching sheet is situated within a porous medium, and its permeability exhibits time-dependent behavior described by $k_p (t)=k_0 (1-at)$, where $k_0$ denotes the initial permeability [27]. Additionally, the system incorporates a heat source/sink coefficient given as $Q(t)=Q_0/(1-at)$. The physical properties of the fluid including density ($\rho$), specific heat ($c_p$), and electrical conductivity ($\sigma$) remain constant throughout the analysis. However, the viscosity ($\mu$) and thermal conductivity ($\kappa$) are regarded as variables that exhibit variations with changes in fluid temperature. The coordinate system chosen for this analysis involves aligning the x-axis parallel to the surface, while the y-axis is perpendicular to it. The flow is induced by the stretching of the sheet whose velocity is

$$\begin{aligned} U_w(x, t) = \frac{bx}{(1-at)} \end{aligned}$$

(1)

which depends upon x and t. A visual depiction of the flow model can be viewed in Fig. 1.

Fig. 1

Flow model of the problem

In our study, the existence of variable heat flux affects the temperature field. Liu and Megahed [48] were the first to propose a novel expression for variable heat flux, as follows:

$$\begin{aligned} q(x,t) = -{\kappa }{\frac{\partial {T}}{\partial {y}}} = T_0 {\frac{dx^r}{(1-at)^{m+{\frac{1}{2}}}}} \end{aligned}$$

(2)

where $T_0$ represents the reference temperature.

Under the Boussineq’s approximation [49], MHD Newtonian time-dependent flow and heat transfer equations are formulated, considering the impact of Joule heating, heat source/sink, thermal radiation, viscous dissipation with temperature-dependent conductivity, and viscosity within a porous medium, as follows [1, 24, 28]:

$$\begin{aligned} \frac{\partial {\grave{u}}}{\partial {x}} + \frac{\partial {\grave{v}}}{\partial {y}} = 0 \end{aligned}$$

(3)

$$\begin{aligned} {\rho _\infty }{\left( \frac{\partial \grave{u}}{\partial {t}} + \grave{u}{\frac{\partial \grave{u}}{\partial {x}}} + \grave{v}{\frac{\partial \grave{u}}{\partial {y}}}\right) } = {\frac{\partial }{\partial {y}}}{\left( \mu (T){\frac{\partial \grave{u}}{\partial {y}}}\right) }- {\frac{\mu }{k_p}}\grave{u}-{{\sigma {B^2}}}\grave{u} \end{aligned}$$

(4)

$$\begin{aligned} {\rho _\infty {c_p}}{\left( \frac{\partial {T}}{\partial {t}}+\grave{u}{\frac{\partial {T}}{\partial {x}}} + \grave{v}{\frac{\partial {T}}{\partial {y}}}\right) } = {\frac{\partial }{\partial {y}}}{\left( \kappa (T){\frac{\partial {T}}{\partial {y}}}\right) }+{\mu }\left( {\frac{\partial \grave{u}}{\partial {y}}}\right) ^2-{\frac{\partial {q_r}}{\partial {y}}}+{\sigma {B^2}}\grave{u}^2+ & \nonumber \\ {Q}{(T-T_\infty )} & \end{aligned}$$

(5)

Here, $\grave{u}$ and $\grave{v}$ are the velocities along the x and y axes, respectively, and t denotes the time. The variable $q_r$ quantifies the radiative heat flux, while B symbolizes the uniform magnetic field, oriented perpendicular to the sheet as follows:

$$\begin{aligned} B = B_0{(1-at)}^{-\frac{1}{2}} \end{aligned}$$

(6)

By incorporating the Rosseland approximation for radiative heat flux $q_r$, the non-linear term $T^4$ in the formulation of $q_r$ is linearized around $T_\infty$. After this, the combination of the conduction term and the radiation flux term within the energy equation results in the formulation of the effective conduction-radiation flux denoted as $q_{eff}$, and described as [50]:

$$\begin{aligned} q_{eff} = -{\left( \kappa (T)+{\frac{16{\sigma }^*{T_\infty }^3}{3{k}^*}}\right) }{\frac{\partial {T}}{\partial {y}}} \end{aligned}$$

(7)

Here, $\kappa _{eff}$ signifies the effective thermal conductivity, defined as:

$$\begin{aligned} \kappa _{eff} = \kappa (T)+{\frac{16{\sigma }^*{T_\infty }^3}{3{k}^*}} \end{aligned}$$

(8)

Consequently, Eq. (5) can be reformulated into its definitive form:

$$\begin{aligned} {\rho _\infty {c_p}} {\left( \frac{\partial {T}}{\partial {t}}+\grave{u}{\frac{\partial {T}}{\partial {x}}} + \grave{v}{\frac{\partial {T}}{\partial {y}}}\right) } = {\frac{\partial }{\partial {y}}}{\left( \kappa _{eff}{\frac{\partial {T}}{\partial {y}}}\right) }+{\mu }\left( {\frac{\partial \grave{u}}{\partial {y}}}\right) ^2+{\sigma {B^2}}\grave{u}^2+{Q}{(T-T_\infty )} \end{aligned}$$

(9)

The appropriate boundary conditions with velocity slip and effective variable heat flux are presented by [34, 51]

$$\begin{aligned} \begin{array}{ccccc} at&y=0,&\grave{u}= U_w + {\frac{\mu }{L}}{\frac{\partial \grave{u}}{\partial {y}}},&\grave{v}=o,&-{\kappa _{eff}}{\frac{\partial {T}}{\partial {y}}}= q_w(x,t) \end{array} \end{aligned}$$

(10)

$$\begin{aligned} \begin{array}{cccc} as&y \rightarrow \infty ,&\grave{u} \rightarrow 0,&T \rightarrow T_\infty \end{array} \end{aligned}$$

(11)

Here, L is the slip length coefficient. The third part of Eq. (10) represents the values of effective variable heat flux.

Now, we proceed by introducing a dimensionless variable $\zeta$ and functions $f(\zeta )$ and $\theta (\zeta )$, enabling us to transform the governing PDEs into a set of coupled ODEs, presented as follows [1]:

$$\begin{aligned} \begin{array}{cc} \zeta = y{{\left( \frac{b}{\nu _\infty {(1-at)}}\right) }^{\frac{1}{2}}},&\psi (x,y)= {\left( {\frac{{\nu _\infty }b}{(1-at)}}\right) ^{\frac{1}{2}}}{x{f(\zeta )}} \end{array} \end{aligned}$$

(12)

$$\begin{aligned} T =T_\infty + {{\frac{q_w(x,t)}{\kappa _\infty }{\sqrt{\frac{\nu _\infty }{b}}}{(1-at)}^{\frac{1}{2}}}}{\theta (\zeta )} \end{aligned}$$

(13)

where $\psi (x,y)$ is a dimensional stream function that identically satisfies the equation of continuity with $\grave{u}={\frac{\partial \psi }{\partial y}}$, $\grave{v}=-{\frac{\partial \psi }{\partial x}}$. Furthermore, variation in $\mu$ and $\kappa$ with temperature is taken into account, following the expressions presented by Megahed [37]

$$\begin{aligned} \mu = {\mu _\infty } exp({-\alpha \theta }) \end{aligned}$$

(14)

$$\begin{aligned} \kappa = {\kappa _\infty }{(1+\epsilon {\theta })} \end{aligned}$$

(15)

Here, $\alpha$ and $\epsilon$ are the dimensionless viscosity and thermal conductivity parameters.

Using the similarity transformations given in Eqs. (12)-(13) into Eqs. (4), (9)-(11), we obtain following non-dimensional equations:

$$\begin{aligned} exp({-\alpha \theta }){\left( f^{\prime \prime \prime }-\alpha {\theta }^{\prime }f^{\prime \prime }-kf^{\prime }\right) }+ ff^{\prime \prime }-S\left( \frac{\zeta }{2}f^{\prime \prime }+f^{\prime }\right) -Mf^{\prime }-{f^{\prime }}^2 = 0 \end{aligned}$$

(16)

$$\begin{aligned} {\frac{1}{Pr}}{\left[ \left( 1+R+\epsilon \theta \right) {\theta }^{\prime \prime }+\epsilon {\theta ^{\prime }}^2\right] }+ f{\theta }^{\prime }-rf^{\prime }\theta -S{\left( m\theta +\frac{1}{2}\zeta {\theta }^{\prime }\right) }+ Ec.{exp({-\alpha \theta })}{f^{\prime \prime }}^2 + M.Ec{f^{\prime }}^2 + \gamma \theta = 0 \end{aligned}$$

(17)

And the boundary conditions:

$$\begin{aligned} \begin{array}{ccccc} at&\zeta = 0,&f(0) = 0,&f^{\prime }(0) = 1+\lambda e^{-\alpha \theta }f^{\prime \prime }(0),&{\theta ^{\prime }(0)} = \frac{-1}{1+R+\epsilon \theta (0)} \end{array} \end{aligned}$$

(18)

$$\begin{aligned} \begin{array}{cccc} as&\zeta \rightarrow \infty ,&f^{\prime }\rightarrow 0,&\theta \rightarrow 0 \end{array} \end{aligned}$$

(19)

To achieve a similarity solution, we opt for $r=m=2$, leading to the definition of several dimensionless parameters that hold significant importance. The unsteadiness parameter, denoted as $S=\frac{a}{b}$, governs the temporal behavior of the system. The magnetic number, represented by $M=\frac{\sigma {B_0}^2}{b \rho _\infty }$, quantifies the effect of an external magnetic field. The radiation parameter, $R=\frac{16{\sigma }^*{T_\infty }^3}{3\kappa _\infty {k}^*}$, characterizes the role of radiative heat flux. $Pr={\frac{\mu _\infty c_p}{\kappa _\infty }}$ is the Prandtl number. The porosity parameter, $k={\frac{\nu _\infty }{k_0 b}}$, provides insight into the permeability of the porous medium. The Eckert number, defined as $Ec={\frac{\kappa _\infty {b}^{5/2}}{d \sqrt{\nu _\infty }c_p T_0}}$, encapsulates the significance of heat transfer due to viscous dissipation. Further influence on energy transfer is encapsulated by the heat source/sink parameter, $\gamma =\frac{Q_0}{\rho _\infty c_p b}$. Lastly, the velocity slip parameter, $\lambda ={\frac{\mu _\infty }{L}}\sqrt{\frac{b}{\nu _\infty {(1-at)}}}$, encapsulates the fluid-surface interaction at the boundary. Remarkably, the governing Eqs. (16) and (17) elucidate an intrinsic interdependency between velocity and temperature.

Our attention is now directed towards the examination of vital physical quantities, specifically the skin-friction coefficient $(Cf_x)$ and the Nusselt number $(Nu_x)$. These paramount parameters play a fundamental role in deciphering the flow dynamics and heat transfer attributes. Their explicit formulations are presented below:

$$\begin{aligned} \begin{array}{ccc} Cf_x = \frac{\tau _w}{{\frac{1}{2} \rho _\infty {U_w}^2}},&\,&Nu_x = \frac{x q_w(x,t)}{\kappa _\infty (T_w-T_\infty )} \end{array} \end{aligned}$$

(20)

where $\tau _w = -\left( \mu \frac{\partial \grave{u}}{\partial {y}}\right) _{y=o}$ and $q_w(x,t) = -\kappa _{eff}\left( \frac{\partial {T}}{\partial {y}}\right) _{y=0}$.

Subsequently, the formulation for $Cf_x$ and $Nu_x$ associated with this particular problem is given as:

$$\begin{aligned} \begin{array}{ccc} \frac{1}{2}Cf_x {Re_x}^{1/2} = -e^{-\alpha \theta (0)}f^{\prime \prime }(0),&\,&Nu_x {Re_x}^{-1/2} = \frac{1}{\theta (0)} \end{array} \end{aligned}$$

(21)

where $Re_x = \frac{U_w x}{\nu _\infty }$ (Reynolds number)

Methods

The initial step is to convert the set of higher-order nonlinear coupled ODEs provided in Eqs. (16)-(17) and the associated boundary conditions in (18)-(19) into an initial value problem through a first-order system:

$$\begin{aligned} \begin{array}{ccccc} Z_1 = f(\zeta ),&Z_2 = Z_1^{\prime },&Z_3 = Z_2^{\prime },&Z_4 = \theta (\zeta ),&Z_5 = Z_4^{\prime } \end{array} \end{aligned}$$

(22)

Subsequently, Eqs. (16)-(17) with endpoint conditions (18)-(19) are converted into a system of five first-order simultaneous equations written as:

$$\begin{aligned} Z_1^{\prime } = Z_2, \qquad \quad Z_1(0)= 0 \end{aligned}$$

$$\begin{aligned} Z_2^{\prime } = Z_3, \qquad \quad Z_2 (0) = 1+\lambda e^{-\alpha Z_4(0)}Z_3(0) \end{aligned}$$

$$\begin{aligned}&Z_3^{\prime } = e^{\alpha Z_4}\left[ {Z_2}^2-Z_1 Z_3 + S\left( \frac{1}{2} {\zeta } Z_3+ Z_2\right) +M Z_2\right]&\nonumber \\&+{\alpha } Z_5 Z_3 + k Z_2, \qquad \quad Z_3(0)=S_{01}&\end{aligned}$$

(23)

$$\begin{aligned} Z_4^{\prime } = Z_5, \qquad \quad Z_4(0) = S_{02} \end{aligned}$$

$$\begin{aligned} Z_5^{\prime } = \frac{1}{(1+R+\epsilon Z_4)}\left[ Pr\left( r Z_2 Z_4 - Z_1 Z_5 + S\left( m Z_4 + \frac{\zeta }{2} Z_5\right) - Ec e^{-\alpha Z_4}{Z_3}^2 - M Ec {Z_2}^2 - \gamma Z_4 \right) \right. & \\ \left. - \epsilon {Z_5}^2 \right] ,\qquad \quad Z_5(0) = -\frac{1}{1+R+\epsilon Z_4(0)} & \end{aligned}$$

To solve the system of initial value problems (23), we employ a numerical technique combining the $4^{th}$-order Runge-Kutta method with the shooting technique. The shooting method, a trial-and-error approach, is utilized to iteratively determine suitable initial guess values $S_{01}$ (representing $f^{\prime \prime }(0)$) and $S_{02}$ (denoting $\theta (0)$) until the boundary condition is met. Once the appropriate initial values are determined, integration of the system proceeds using the $4^{th}$-order Runge-Kutta method. Furthermore, to enhance accuracy, the initial estimations are iteratively refined using the Newton-Raphson method until the desired accuracy level of $10^{-6}$ is achieved.

Validation of numerical method

In this section, to evaluate the precision of the proposed numerical technique, our results are compared with the outcomes achieved by Prasad et al. [52] (in Newtonian case n = 1) who used the Keller-Box method and Megahed et al. [1] who employed shooting technique in conjunction with R-K method of $4^{th}$ order in their published work. The values of $-f^{\prime \prime }(0)$ are compared in Table 1 for various M in the absence of S, $\alpha$, $\lambda$, and k parameters. Also, the values of $-{Cf_x Re_x^{1/2}}/{2}$ and $Nu_xRe_x^{-1/2}$ are compared with the work of Megahed et al. [1] for various M and Ec ignoring the parameters k, $\lambda$, and $\gamma$ shown in Table 2. The outcomes from both tables exhibit good agreement, validating the accuracy of the numerical method.

Table 1 Comparative analysis of skin-friction [$-f^{\prime \prime }(0)$] values for $S=\alpha =\lambda =k=0$ with published work

Table 2 Comparative analysis of the values of $-{Cf_x Re_x^{1/2}}/{2}$ and $Nu_xRe_x^{-1/2}$ with Megahed et al. [1] when $r = m = 2$, $Pr = 1$, $k = \lambda = \gamma =0$, $R = \alpha = \epsilon = 0.2$ and $S = 0.8$

Results and discussion

Numerical computations have been conducted to investigate theoretical aspects of the physical model, considering a range of values for various physical parameters M, Ec, S, R, $\alpha$, $\epsilon$, k, $\lambda$, and $\gamma$. An analysis has been made to determine the impact of these parameters on flow and heat transfer properties, providing insights into the system’s behavior under different conditions. The results obtained from the numerical simulations are presented through figures displaying velocity $f^{\prime }(\zeta )$ and temperature distribution $\theta (\zeta )$. Figure 2a and b represent $f^{\prime }(\zeta )$ and $\theta (\zeta )$ for several values of M. The graphical representation of the data visually shows that increasing M reduces $f^{\prime }(\zeta )$ (Fig. 2a) while increases $\theta (\zeta )$ (Fig. 2b). The existence of a transverse magnetic field in an electrically conducting fluid induces a resisting force named Lorentz force that slows the fluid’s motion. For greater values of M, the Lorentz force becomes more pronounced, leading to a reduction in $f^{\prime }(\zeta )$. Conversely, lower values of M result in a significant increase in $f^{\prime }(\zeta )$. Hence, by adjusting the strength of the magnetic field, one can achieve the desired flow rate, which may be crucial for clinical or mechanical reasons when controlling fluid flow [25]. Additionally, the Lorentz force also generates heat energy in the flow. Thus, the width of the thermal boundary layer increases for rising values of M.

Fig. 2

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, \alpha =0.2, k=0.2, \lambda =0.2, R=0.2, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different M

Figure 3a and b depict the variation in dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$ for several values of R within boundary layer region, respectively. From Fig. 3a, a slight increase in velocity has been observed for rising values of R. From Fig. 3b, we can see that inside the boundary layer region, $\theta (\zeta )$ increases with the increase in R while surface temperature $\theta (0)$ decreases. Physically, increasing values of R enhance the heat transfer performance from the sheet to the fluid. Therefore, more heat is transmitted into the fluid for higher values of R. As a result, the surface temperature decreases, but the thermal boundary layer thickens.

Fig. 3

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, \alpha =0.2, k=0.2, \lambda =0.2, M=0.5, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different R

Figure 4a and b provide valuable insights into impact of the Ec on $f^{\prime }(\zeta )$ and $\theta (\zeta )$, respectively. As depicted in Fig. 4b, the temperature distribution experiences an increase with an increment in the viscous dissipation parameter, represented by Ec. The existence of viscous dissipation causes the conversion of kinetic energy into internal energy, as the fluid performs work against viscous forces. Consequently, this leads to rise in $\theta (0)$ as well as $\theta (\zeta )$. Notably, this is the additional heat energy stored in the fluid and the heat generation along the sheet is more substantial. Furthermore, the velocity field demonstrates a slight reduction with rising values of Ec [26].

Fig. 4

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, \alpha =0.2, k=0.2, \lambda =0.2, R=0.2, M=0.5, \epsilon =0.2, \gamma =0.2$ and different Ec

The impact of $\alpha$ on $f^{\prime }(\zeta )$ and $\theta (\zeta )$ are displayed in Fig. 5a and b respectively. Significantly, rising values of $\alpha$ lead to a reduction in the dimensionless velocity $f^{\prime }(\zeta )$ as well as in the momentum boundary layer thickness but alters the surface velocity $f^{\prime }(0)$ as depicted in Fig. 5a. This phenomenon occurs because increasing values of $\alpha$ lead to a reduction in viscosity near the surface. Consequently, the viscosity near the surface becomes smaller than the ambient viscosity. Therefore, the velocity near the surface increases, but $f^{\prime }(\zeta )$ decreases with increasing values of $\alpha$, thereby thickening the momentum boundary layer. Likewise, Fig. 5b illustrates that an increment in the value of $\alpha$ leads to an elevation in both $\theta (\zeta )$ and $\theta (0)$. However, this increase in temperature is accompanied by a decrease in the heat transfer rate from sheet to the fluid.

Fig. 5

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, M=0.5, k=0.2, \lambda =0.8, R=0.2, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different $\alpha$

Figure 6a and b visually showcase the influence of S on dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$ respectively. Increasing the unsteadiness parameter S yields significant changes. Along the sheet, the velocity diminishes, leading to a corresponding decrease in the momentum boundary layer thickness. Conversely, at a distance from the sheet, the velocity exhibits a reverse trend (Fig. 6a). Additionally, Fig. 6b reveals that increasing values of S lead to a reduction in both $\theta (\zeta )$ and $\theta (0)$ regardless of the distance $\zeta$ from the surface. Interestingly, the effect of S on the temperature $\theta (\zeta )$ is more pronounced compared to its effect on the velocity $f^{\prime }(\zeta )$. Moreover, the heat transfer rate intensifies with higher values of S, highlighting the essential fact that higher values of S lead to a faster rate of cooling, while lower values result in longer cooling times [53].

Fig. 6

Variance in a velocity and b temperature against $\zeta$ for $M=0.5, \alpha =0.2, k=0.2, \lambda =0.2, R=0.2, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different S

Furthermore, the variations in thermal conductivity parameter ($\epsilon$) significantly affect the dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$, as displayed in Fig. 7a and b respectively. Notably, a substantial impact of $\epsilon$ on $\theta (\zeta )$ is observed. Specifically, for higher values of $\epsilon$, temperature along the sheet decreases, while it increases away from the surface, as depicted in Fig. 7b. But the velocity experiences a slight enhancement as $\epsilon$ rises (Fig. 7a).

Fig. 7

Variance in a velocity and b temperature against $\zeta$ for $M=0.5, S=0.8, \alpha =0.2, k=0.2, \lambda =0.2, R=0.2, Ec=0.2, \gamma =0.2$ and different $\epsilon$s

The impact of k on dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$ is visually represented in Fig. 8a and b respectively. It should be noticed that larger values of k suggest a porous medium with low permeability and high dynamic viscosity as $k= \frac{\nu _\infty }{k_0 b}$ which produces a higher fluid flow resistance. As seen in Fig. 8a, rising values of k result in a drop in $f^{\prime }(\zeta )$ but improve $\theta (\zeta )$ over the boundary layer as shown in Fig. 8b. Thus, the existence of a porous medium contributes to a decrease in flow velocity while concurrently enhancing the temperature distribution.

Fig. 8

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, \alpha =0.2, M=0.5, \lambda =0.2, R=0.2, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different k

Furthermore, Fig. 9a and b visually demonstrate the considerable influence of $\lambda$ on the dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$ respectively. Figure 9a shows that the velocity is found to be at its maximum when there is no velocity slip, and it falls when the slip parameter is increased. This phenomenon arises due to the impact of slip conditions, where the flow velocity near the surface deviates from the stretching velocity of the surface. This deviation occurred because, under the slip condition, the pulling of the stretching sheet can only be partly transmitted to the fluid, leading to a reduction in velocity. This influence on the velocity field subsequently affects the temperature distribution and contributes to an increase in $\theta (\zeta )$ for increasing values of $\lambda$, as illustrated in Fig. 9b.

Fig. 9

Variance in a velocity and b temperature against $\zeta$ for $M=0.5, S=0.8, \alpha =0.2, k=0.2, R=0.2, Ec=0.2, \epsilon =0.2, \gamma =0.2$ and different $\lambda$

Figure 10a and b depict the variations in dimensionless profiles $f^{\prime }(\zeta )$ and $\theta (\zeta )$ for several values of $\gamma$, respectively. A slight change in velocity profile has occurred for $\gamma$. The velocity $f^{\prime }(\zeta )$ decreases for rising values of $\gamma$($>0$) while it increases with the increment in $\gamma$($<0$) (Fig. 10a). Furthermore, Fig. 10b indicates that temperature distribution rises with higher values of $\gamma$ ($>0$), but it falls in case of $\gamma$ ($<0$). Consequently, the thermal boundary layer expands for greater values of $\gamma$ ($>0$), while it contracts in the case of $\gamma$ ($<0$). This phenomenon occurs because an increase in the heat source parameter amplifies the heat energy in the flow regime, thereby thickening the thermal boundary layer, while heat energy is released in the case of the heat sink parameter, hence leading to a decline in the boundary layer thickness. It is also noted that increasing $\gamma$ ($>0$) causes a reduction in the heat transfer rate, while the opposite effect is observed in the case of $\gamma$ ($<0$).

Fig. 10

Variance in a velocity and b temperature against $\zeta$ for $S=0.8, M=0.5, \alpha =0.2, k=0.2, \lambda =0.2, R=0.2, Ec=0.2, \epsilon =0.2$, and different $\gamma$

To comprehensively characterize the dynamics of flow and heat transfer, vital dimensionless physical quantities $Cf_x$ and $Nu_x$ are meticulously examined for different governing parameters M, R, Ec, $\alpha$, S, $\epsilon$, k, $\lambda$, and $\gamma$. A comprehensive summary of these interactions is presented in Table 3. After meticulous analysis of the tabulated outcomes, discernible trends come to light. The skin-friction coefficient undergoes a notable escalation for increasing values of $\epsilon$, M, S, k, R, and $\gamma (<0)$. However, a reduction in $Cf_x$ is observed for increasing values of Ec, $\alpha$, and $\lambda$. Significantly, among these parameters, M, k, and $\lambda$ exhibit a more pronounced impact on the values of $Cf_x$. Simultaneously, the Nusselt number $(Nu_x)$, another crucial parameter, exhibits distinct patterns. It witnesses an increment under the influence of R, S, $\epsilon$, and $\gamma (<0)$. But an adverse effect is noted for rising values of M, Ec, $\alpha$, k, $\lambda$, and $\gamma (>0)$. Remarkably, a more significant impact on Nusselt number $(Nu_x)$ is observed for parameters M, R, Ec, S, $\epsilon$, and $\gamma$.

Table 3 Effect of parameters M, R, Ec, $\alpha$, S, $\epsilon$, k, $\lambda$ and $\gamma$ on the value of $-{Cf_x Re_x^{1/2}}/{2}$ and $Nu_xRe_x^{-1/2}$ while keeping $r=2, m=2$, and $Pr=1$

Conclusions

Within the confines of this research, a comprehensive analysis is undertaken to unveil the intricacies of flow and heat transfer. The present work centers on an MHD boundary layer, where an incompressible Newtonian fluid interacts with a dynamically evolving slippery stretching sheet. The investigation becomes more complex due to the presence of a porous medium, in conjunction with variable fluid properties and heat flux. Moreover, the interplay of heat source/sink, thermal radiation, and Joule heating further enriches the analytical landscape. Following a meticulous exploration of this intricate physical scenario, the research yields a set of compelling findings, outlined below:

• 1. The slip parameter ($\lambda$) suppresses both velocity field $f^{\prime }(\zeta )$ and surface velocity $f^{\prime }(0)$, leading to a significant decrease in $Cf_x$.

• 2. The influence of k, S, and M reduces $f^{\prime }(\zeta )$ as well as momentum boundary layer thickness.

• 3. A significant increase in thermal boundary layer thickness and $\theta (\zeta )$ is obtained with increment in Ec and $\gamma (>0)$, while an adverse result is obtained for S and $\gamma (<0)$.

• 4. Increment in $\alpha$ enhances the sheet velocity $f^{\prime }(0)$ but reduces the momentum boundary layer thickness.

• 5. Thickness of the thermal boundary layer is slightly enhanced for greater values of M, k, and $\lambda$.

• 6. $Cf_x$ highly depends on M, S, and k and it increases with the effect of these parameters.

• 7. Increment in R, S and $\epsilon$ enhances the heat transfer rate but reduces the sheet temperature $\theta (0)$ which can be used for fast cooling

• 8. $Nu_x$ decreases significantly with higher values of Ec, M, and $\gamma (>0)$, but increases with escalating values of S and $\gamma (<0)$.

Nomenclature

 

a:

Positive constant ($s^{-1}$)

$\rho$:

Fluid density

r, m:

Space and time index

B:

Magnetic field

$\mu$:

Fluid viscosity

$k_p$:

Permeability of porous medium

$c_p$:

Specific heat

$\grave{u}, \grave{v}$:

Velocity components

$\sigma ^*$:

Stefan-Boltzmann constant

$q_r$:

Radiative heat flux

$\epsilon$:

Thermal conductivity parameter

$T_\infty$:

Ambient temperature

q(x, t):

Heat flux

$U_w(x,t)$:

Sheet velocity

$k^*$:

Absorption coefficient

$k_0$:

Constant

$\rho _\infty$:

Ambient density

f:

Dimensionless stream function

$\nu _\infty$:

Ambient kinematic viscosity

$\sigma$:

Electrical conductivity

$\mu _\infty$:

Ambient viscosity

b:

Stretching rate ($s^{-1}$)

$B_0$:

Constant (Tesla)

d:

Constant

T:

Fluid temperature

$Cf_x$:

Skin-friction coefficient

$\nu$:

Kinematic viscosity

L:

Slip length coefficient

$\zeta$:

Dimensionless variable

$\theta$:

Dimensionless temperature

$\kappa$:

Thermal conductivity

$\alpha$:

Viscosity parameter

$\gamma$:

Heat source/sink parameter

Pr:

Prandtl number

M:

Magnetic number

R:

Radiation parameter

S:

Unsteadiness parameter

$Re_x$:

Local Reynolds number

Ec:

Eckert number

$\kappa _\infty$:

Ambient thermal conductivity

$T_0$:

Reference temperature

k:

Porosity parameter

$\lambda$:

Velocity slip parameter

$Nu_x$:

Nusselt number