Seismic reflection and transmission coefficients of a single layer sandwiched between two dissimilar poroelastic solids

Abstract

The seismic reflection and transmission characteristics of a single layer sandwiched between two dissimilar poroelastic solids saturated with two immiscible viscous fluids are investigated. The sandwiched layer is modeled as a porous solid with finite thickness. The propagation of waves is represented with potential functions. The displacements of particles in different phases of the aggregate are defined in terms of these potential functions. Due to the presence of viscosity in pore fluids, the reflected and transmitted waves are inhomogeneous in nature, i.e., with different directions of propagation and attenuation. The closed-form analytical expressions for reflection and transmission coefficients are derived theoretically for appropriate boundary conditions. These expressions are calculated as a non-singular system of linear algebraic equations and depend on the various parameters involved in this non-singular system. Hence, numerical examples are studied to determine the effects of various properties of the sandwich layer on reflection and transmission coefficients. The essential features of layer thickness, incident direction, wave frequency, liquid saturation and capillary pressure of the porous layer on reflection and transmission coefficients are depicted graphically and discussed. The analysis shows that reflection and transmission coefficients are strongly associated with incident direction and various properties of the porous layer.

1 Introduction

In general, earth is a layered structure with different elastic properties. Thus, propagation of seismic waves through such a layered structure is influenced very much by these elastic properties. The nature of these layers present in the interior of earth’s crust has not yet been addressed completely. Therefore, it is necessary to consider the various studies to determine the actual internal structure of earth and the various phases such as oil, gases and hydrocarbons embedded in the earth. The problem of reflection and transmission of seismic waves at a sandwiched layer is an important phenomenon due to its practical applications in earthquake engineering, geophysics, seismology, petroleum engineering and hydrology. During the past several decades, most of the studies on reflection and transmission phenomena have preferred to use a single interface, for example Pride et al. (1992), Kaynia and Banerjee (1993), Gurevich and Schoenberg (1999), Denneman et al. (2002), Sharma (2008, 2013), Tomar and Arora (2006), Arora and Tomar (2007), Yeh et al. (2010), Sharma and Kumar (2011), Chen et al. (2012), Kumar and Saini (2012, 2016), Kumar and Sharma (2013), Kumar and Kumari (2014). The latest book by Carcione (2014) is also recommended for relevant references and detailed procedures. However, to the best of our knowledge, in view the importance of the transition layer, only a few limited efforts have been made to study the phenomenon of reflection and transmission of plane waves at a layer sandwiched between two dissimilar media. Some of the recent studies on reflection and transmission of seismic waves through a transition layer have been carried out by various authors including Sinha (1964), Cerveny and Vanek (1974), Kuo (1992), Ainslie (1996), Wang et al. (2013), Lyu et al. (2014), Sahu et al. (2015) and Paswan et al. (2016). Recently, Corredor et al. (2014) studied the effects of layer thickness on reflection and transmission coefficients of a single layer sandwiched between two dissimilar poroelastic media. They also discussed several special cases. Chen et al. (2015) studied the reflection of acoustic waves from the elastic seabed with an overlying gassy poroelastic layer. They studied the influences of poroelastic layer thickness, wave frequency, incident direction and liquid saturation on reflection characteristics.

To the best of our knowledge, until now the problem of reflection and transmission of plane waves at the surface of a layer sandwiched between two dissimilar porous solids saturated with two immiscible viscous fluids has not been investigated. Generally, it is observed that natural rocks are composed of multi-fluid porous solids. The phenomenon of wave propagation is generally affected by the nature of such rocks. In the present work, the complete reflection–transmission phenomenon across a poroelastic layer sandwiched between two dissimilar porous solids saturated with two immiscible viscous fluids is investigated. This type of study is motivated by the problems faced by the oil industry, where the desired product is usually found in the form of multiple fluids. The mathematical model presented in this article is based on the continuum mixture theory of Tuncay and Corapcioglu (1997). Corredor et al. (2014) studied the reflection and transmission coefficients of a single layer embedded between two dissimilar porous solid saturated with a single fluid. It is based on the poroelastic theory of Biot. The present work generalizes reflection/transmission phenomenon studied by Corredor et al. (2014) to the reflection/transmission phenomena across a poroelastic layer sandwiched between two dissimilar porous solids saturated with two immiscible viscous fluids.

In this study, the propagation of waves is represented with potential functions. The displacement of particles in different phases of the aggregate is defined in terms of these potential functions. All the poroelastic media are dissipative due to the presence of viscosity in pore fluids. Hence, the propagation of plane waves in such media is represented by inhomogeneous waves, i.e., different directions of propagation and attenuation. Thus, the incident wave is an inhomogeneous wave specified by two angles, one for the propagation direction and the other for its deviation from the attenuation direction. The closed-form expressions for reflection and transmission coefficients are derived theoretically for appropriate boundary conditions. These expressions are calculated as a non-singular system of linear algebraic equations and depend on various parameters involved in this non-singular system. Hence, numerical examples are studied to determine the effects of various properties of the sandwich layer on reflection and transmission coefficients. The influences of layer thickness, liquid saturation and capillary pressure of the porous layer, incident direction and wave frequency on reflection and transmission coefficients are depicted graphically and discussed.

2 Basics equations

Following Tuncay and Corapcioglu (1997), the equations of motion for two-phase immiscible viscous fluid flows in deformable porous media, in the absence of body forces, are defined as follows

$$ \delta_{0} \tau_{ij,j} = \delta_{0} \rho_{0} \ddot{u}_{i} + d_{1} \left( {\dot{u}_{i} - \dot{v}_{i} } \right) + d_{2} \left( {\dot{u}_{i} - \dot{w}_{i} } \right), $$

(1)

$$ - \;\delta_{1} p_{,i}^{(1)} = \delta_{1} \rho_{1} \ddot{v}_{i} + d_{1} \left( {\dot{v}_{i} - \dot{u}_{i} } \right), $$

(2)

$$ - \;\delta_{2} p_{,i}^{(2)} = \delta_{2} \rho_{2} \ddot{w}_{i} + d_{2} \left( {\dot{w}_{i} - \dot{u}_{i} } \right), $$

(3)

where $u_{i} ,v_{i}$ and $w_{i}$ denote the components of displacements of solid, first fluid and second fluid particles, respectively. $p^{\left( 1 \right)} ,\,p^{\left( 2 \right)}$ are pressures in fluid phases, and $\tau_{ij}$ is the stress tensor for the drained porous frame. $\rho^{\prime } s$ are intrinsic densities of constituents. Dots over these vectors denote partial time derivatives. A comma before an index implies partial differentiation in space. $\delta_{0} ,\delta_{1}$ and $\delta_{2}$ are the volume fractions of the solid, first and second fluid phases, respectively. $\delta_{0} = 1 - f,\;\delta_{1} = (1 - \sigma )f,\;\delta_{2} = f\sigma$ with $\delta_{0} + \delta_{1} + \delta_{2} = 1,$ where $\sigma$ is the fraction of second fluid saturation in connected pore space and $f$ is porosity. $d_{1} ( = \eta_{1} \delta_{1}^{2} /\chi_{0} k_{r1} )$ and $d_{2} ( = \eta_{2} \delta_{2}^{2} /\chi_{0} k_{r2} )$ are the dissipation coefficients of first and second fluid phases, respectively. These coefficients involve relative permeabilities $(k_{r1} ,k_{r2} )$ and viscosities $(\nu_{1} ,\nu_{2} )$ of the corresponding phases and the intrinsic permeability of the composite medium $\chi_{0}$. The relative permeabilities $(k_{r1} ,k_{r2} )$ for current model are given as follows (Lo et al. 2005): $k_{r1} = (1 - \sigma )^{\chi } \left[ {1 - \sigma^{{\frac{n}{n - 1}}} } \right]^{{\frac{2(n - 1)}{n}}} ,\;\;k_{r2} = \sigma^{\chi } \left[ {1 - \{ 1 - \sigma^{{\frac{n}{n - 1}}} \}^{{\frac{n - 1}{n}}} } \right]^{2} ,$ where $n$ and $\chi$ are fitting parameters. Following Tuncay and Corapcioglu (1997), the constitutive relations for stresses in the porous matrix and fluid pressures in the pore space are given by

$$ \delta_{0} \tau_{ij} = \left( {a_{11} \nabla .\vec{u} + a_{12} \nabla .\vec{v} + a_{13} \nabla .\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {w} } \right)\delta_{ij} + G\left( {u_{i,j} + u_{j,i} - \frac{2}{3}u_{k,k} \delta_{ij} } \right), $$

(4)

$$ - \;\delta_{1} p^{(1)} = (a_{21} \nabla .\vec{u} + a_{22} \nabla .\vec{v} + a_{23} \nabla .\vec{w})\delta_{ij} , $$

(5)

$$ - \;\delta_{2} p^{(2)} = (a_{31} \nabla .\vec{u} + a_{32} \nabla .\vec{v} + a_{33} \nabla .\vec{w})\delta_{ij} , $$

(6)

where $\delta_{ij}$ is the Kronecker symbol. The coefficients $a_{ij} ( = a_{ji} )$ denote the elastic constants and are given by

$$ a_{11} = K_{0} ,\,\,a_{12} = K_{1} \delta_{0} (1 - \sigma )(K_{c} + K_{2} )/K,\,a_{13} = K_{2} \delta_{0} \sigma (K_{c} + K_{1} )/K, $$

$$ a_{22} = K_{1} \delta_{1} ((1 - \sigma )K_{2} + K_{c} )/K,\,\,a_{23} = K_{1} K_{2} (1 - \sigma )\delta_{2} /K, $$

$$ a_{33} = K_{2} \delta_{2} (K_{1} \sigma + K_{c} )/K,\,\,K = K_{1} \sigma + K_{c} + K_{2} (1 - \sigma ), $$

where $K_{1}$ and $K_{2}$ are the bulk moduli of first and second fluid phases, respectively, whereas $K_{0}$ is bulk modulus of the porous frame or drained matrix. $G$ is the shear modulus of the porous solid. $K_{c} = \sigma K_{\text{cap}} ,$ where $K_{\text{cap}}$ is the equivalent bulk modulus (Garg and Nayfeh 1986) for macroscopic capillary pressure between wetting and non-wetting fluids.

Following Kumar and Saini (2012), the displacement potentials $\varphi_{i} ,(i = 1,2,3,4),$ represent the propagation of $P_{1} ,P_{2} ,P_{3} ,SV$ waves with velocities $V_{1} ,V_{2} ,V_{3} ,V_{4} ,$ respectively. The velocities $(V_{1} ,V_{2} ,V_{3} )$ of longitudinal waves are derived from the three roots of a cubic equation in $V^{2} ,$ given by

$$ DV^{6} + CV^{4} + BV^{2} + A = 0. $$

(7)

The various coefficients in this cubic equation are given by

$$ \begin{aligned} A = a_{11}^{*} A_{3} + a_{12} A_{1} + a_{13} A_{2} ,\;\;B = a_{11}^{*} B_{3} + \varLambda_{s} A_{3} + a_{12} B_{1} \,+ a_{13} B_{2} - \chi_{1} A_{1} - \chi_{2} A_{2} , \\ C = a_{11}^{*} C_{3} + \varLambda_{s} B_{3} + a_{12} C_{1} + a_{13} C_{2} - \chi_{1} B_{1} - \chi_{2} B_{2} ,\;\;D = \varLambda_{s} C_{3} - \chi_{1} C_{1} - \chi_{2} C_{2} , \\ \end{aligned} $$

where

$$ \begin{aligned} & A_{1} = a_{23} a_{13} - a_{12} a_{33} ,\,\,A_{2} = a_{12} a_{23} - a_{13} a_{22} ,\,\,A_{3} = a_{22} a_{33} - a_{23} a_{23} , \\ & B_{1} = a_{33} \chi_{1} - a_{12} \varLambda_{2} - a_{23} \chi_{2} ,\,\,B_{2} = a_{22} \chi_{2} - a_{13} \varLambda_{1} - a_{23} \chi_{1} ,\,\,B_{3} = a_{22} \varLambda_{2} + a_{33} \varLambda_{1} , \\ & C_{1} = \varLambda_{2} \chi_{1} ,\,\,C_{2} = \varLambda_{1} \chi_{2} ,\;\;C_{3} = \varLambda_{1} \varLambda_{2} ,\,\,a_{11}^{*} = a_{11} + \frac{4}{3}G, \\ \end{aligned} $$

and

$$ \chi_{1} = \frac{\iota }{\omega }d_{1} ,\;\;\chi_{2} = \frac{\iota }{\omega }d_{2} ,\;\;\varLambda_{1} = \delta_{1} \rho_{1} + \chi_{1} ,\;\;\varLambda_{2} = \delta_{2} \rho_{2} + \chi_{2} , $$

where $\iota = \sqrt { - 1}$ and $\omega$ is angular frequency. The coupling coefficients between the potentials of longitudinal waves are given by

$$ \mu_{j} = \frac{{A_{1} - B_{1} V_{j}^{2} + C_{1} V_{j}^{4} }}{{A_{3} - B_{3} V_{j}^{2} + C_{3} V_{j}^{4} }},\;\;\;\lambda_{j} = \frac{{A_{2} - B_{2} V_{j}^{2} + C_{2} V_{j}^{4} }}{{A_{3} - B_{3} V_{j}^{2} + C_{3} V_{j}^{4} }},\;\;\;(j = 1,2,3). $$

The shear wave velocity $V_{4}$ and coupling coefficients $(\varGamma_{1} ,\;\varGamma_{2} )$ are given by

$$ V_{4}^{2} = \frac{G}{{\varLambda_{0} - \chi_{1} \varGamma_{1} - \chi_{2} \varGamma_{2} }},\,\,\,\varGamma_{1} = \frac{{\chi_{1} }}{{\varLambda_{1} }},\,\,\,\varGamma_{2} = \frac{{\chi_{2} }}{{\varLambda_{2} }},\;\;\;\;\varLambda_{0} = \delta_{0} \rho_{0} + \chi_{1} + \chi_{2} . $$

3 Displacements

For two-dimensional motion in the $x - z$ plane, the displacement components of solid and fluid phases are given by

$$ u_{x} = \sum\limits_{j = 1}^{3} {\frac{{\partial \varphi_{j} }}{\partial x} - \frac{{\partial \varphi_{4} }}{\partial z}} ,\;\;\;u_{z} = \sum\limits_{j = 1}^{3} {\frac{{\partial \varphi_{j} }}{\partial z} + \frac{{\partial \varphi_{4} }}{\partial x}} , $$

(8)

$$ v_{x} = \sum\limits_{j = 1}^{3} {\mu_{j} \frac{{\partial \varphi_{j} }}{\partial x} - \varGamma_{1} \frac{{\partial \varphi_{4} }}{\partial z}} ,\;\;\;v_{z} = \sum\limits_{j = 1}^{3} {\mu_{j} \frac{{\partial \varphi_{j} }}{\partial z} + \varGamma_{1} \frac{{\partial \varphi_{4} }}{\partial x}} , $$

(9)

$$ w_{x} = \sum\limits_{j = 1}^{3} {\lambda_{j} \frac{{\partial \varphi_{j} }}{\partial x} - \varGamma_{2} \frac{{\partial \varphi_{4} }}{\partial z}} ,\;\;\;w_{z} = \sum\limits_{j = 1}^{3} {\lambda_{j} \frac{{\partial \varphi_{j} }}{\partial z} + \varGamma_{2} \frac{{\partial \varphi_{4} }}{\partial x}} . $$

(10)

4 Formulation of the problem

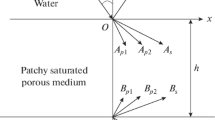
We consider a poroelastic layer sandwiched between two dissimilar poroelastic solids saturated with two immiscible viscous fluids. This poroelastic layer is considered as solid matrix (or skeleton) whose pores are filled with two immiscible viscous fluids. Hence, this system consists of three dissimilar poroelastic media designated by $\varOmega_{j} ,(j = 1,2,3)$ as shown in Fig. 1. A rectangular Cartesian coordinate system $(x,\,y,\,z)$ is chosen with the $z$-axis directed vertically downwards and the $x$-axis considered as the horizontal direction. Let $z = 0$ and $z = h$ represent two plane interfaces separating the media $\varOmega_{1} ,$ $\varOmega_{2}$ and $\varOmega_{3} ,$ respectively. Hence, the poroelastic solid $\varOmega_{1}$ occupies the region $- \infty < z < 0,$ poroelastic layer $\varOmega_{2}$ occupies the region $0< {\text{z}} < {\text{h}}$, and poroelastic solid $\varOmega_{3}$ occupies the region $h < z < \infty$.

Fig. 1

Geometry of the problem

5 Boundary conditions

Boundary conditions are considered to determine the unknown complex amplitudes of various reflected and transmitted waves. These boundary conditions concerning the displacements of solid and fluid particles, normal and shear stresses, and fluids pressure need to ensure continuity at the interfaces located at $z = 0$ and $z = h$. Therefore, the boundary conditions at the interfaces (Dutta and Ode 1983; Santos et al. 2004; Corredor et al. 2014), in the present formulations, are given by

$$ \begin{aligned} & (\delta_{0} \tau_{zz} )^{(m)} = (\delta_{0} \tau_{zz} )^{(m + 1)} ,\;\;\;(\delta_{0} \tau_{zx} )^{(m)} = (\delta_{0} \tau_{zx} )^{(m + 1)} , \\ & ( - \delta_{1} p^{(1)} )^{(m)} = ( - \delta_{1} p^{(1)} )^{(m + 1)} ,\;\;\quad ( - \delta_{2} p^{(2)} )^{(m)} = ( - \delta_{2} p^{(2)} )^{(m + 1)} , \\ & u_{x}^{(m)} = u_{x}^{(m + 1)} ,\;\;\;u_{z}^{(m)} = u_{z}^{(m + 1)} ,\;\;\;v_{z}^{(m)} = v_{z}^{(m + 1)} ,\;\;\;w_{z}^{(m)} = w_{z}^{(m + 1)} ,\;\;\;m = 1,2. \\ \end{aligned} $$

(11)

The super-index $(m)$ denotes the any variable associated with the medium $\varOmega_{m}$.

6 Reflection and transmission coefficients

In the present study, our goal is to analyze the reflection and transmission coefficients of a poroelastic layer sandwiched between two dissimilar poroelastic solids saturated with two immiscible fluids. A plane wave, either $P_{1}$ or $SV$, is incident on the plane interface $z = 0$ with an angular frequency $\omega$ and an angle of incidence $\theta_{0}$ with respect to vertical $z$-axis. This incidence results in four reflected waves generated in the poroelastic medium $\varOmega_{1}$. Furthermore, four waves from the upper interface (i.e., $z = 0$) and four reflected waves from the lower interface (i.e., $z = h$) are generated in the poroelastic layer $\varOmega_{2}$ and four transmitted waves exist in the poroelastic medium $\varOmega_{3} ,$ as shown in Fig. 1. Hence, as a result of multiple reflections at the boundaries of the layer, eight resulting waves with different directions of propagation and attenuation are developed. The procedure used in the present work to determine the reflection and transmission coefficients of plane waves is illustrated by Brekhovskikh (1960), p. 45. This recursive approach is used by various authors including Carcione (2001), Wang et al. (2013), Lyu et al. (2014), Corredor et al. (2014), Chen et al. (2015, 2017), Sahu et al. (2015), Bai et al. (2015, 2016), Paswan et al. (2016), Feng et al. (2016). All the poroelastic media are dissipative due to the presence of viscosity in pore fluids. Hence, the propagation of plane waves in such a medium is represented by inhomogeneous waves, i.e., with different directions of propagation and attenuation. Thus, the incidence of an inhomogeneous wave at the boundary $z = 0$ is specified through its propagation direction $\theta_{0}$ and attenuation angle $\gamma_{0}$. In the $x$-$z$ plane, $\theta_{0}$ is the angle that propagation vector $\vec{P}_{0}$ of the incident wave makes with the $z$-axis and $\gamma_{0}$ is the angle between propagation vector $(\vec{P}_{0} )$ and attenuation vector $(\vec{A}_{0} ).$

In terms of these angles, the complex wave number $k$ is written as (Borcherdt 1982),

$$ k = \left| {\vec{P}_{0} } \right|\sin \theta_{0} - \iota \left| {\vec{A}_{0} } \right|\sin (\theta_{0} - \gamma_{0} ), $$

(12)

where for incident wave of velocity $V_{0}$, we have

$$ \left| {\vec{P}_{0} } \right|^{2} = \frac{1}{2}\left[ {\Re \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right) + \sqrt {\left\{ {\left( {\Re \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} + {{\left( {\Im \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\Im \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} } {\cos^{2} \gamma_{0} }}} \right. \kern-0pt} {\cos^{2} \gamma_{0} }}} \right\}} } \right], $$

(13)

$$ \left| {\vec{A}_{0} } \right|^{2} = \frac{1}{2}\left[ { - \Re \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right) + \sqrt {\left\{ {\left( {\Re \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} + {{\left( {\Im \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\Im \left( {\frac{{\omega^{2} }}{{V_{0}^{2} }}} \right)} \right)^{2} } {\cos^{2} \gamma_{0} }}} \right. \kern-0pt} {\cos^{2} \gamma_{0} }}} \right\}} } \right]. $$

(14)

Then, the displacement potential for the incident wave is defined as

$$ \phi_{0} = F_{0} \exp (\vec{A}_{0} \cdot \vec{r})\exp (\iota \vec{P}_{0} \cdot \vec{r} - \omega t), $$

(15)

The propagation vector $\vec{P}_{0}$ and attenuation vector $\vec{A}_{0}$ are defined as

$$ \vec{P}_{0} = k_{R} \hat{x} + d_{0R} \hat{z},\;\;\vec{A}_{0} = - \;k_{I} \hat{x} - d_{0I} \hat{z},\;\;d_{0} = \pm \;p.v.\left[ {\left( {\frac{\omega }{{V_{0} }}} \right)^{2} - \left( {k^{(1)} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\;\;\;\vec{r} = x\hat{x} + z\hat{z}, $$

where $\hat{x}$ and $\hat{z}$ denote unit (or coordinate) vectors along $x$-axis and $z$-axis, respectively. $F_{0}$ is the amplitude of the incident wave. Subscripts $R$ and $I$ denote the real and imaginary parts of the corresponding complex quantities.

Following Borcherdt (1982), the displacement potential functions of reflected and transmitted waves can be expressed as

• (1) In the poroelastic solid $\varOmega_{1} \,( - \infty < z < 0)$

$$ \varphi_{j}^{(1)} = F_{rj}^{(1)} \exp (\vec{A}_{rj}^{(1)} \cdot \vec{r})\exp \{ \iota (\vec{P}_{rj}^{(1)} \cdot \vec{r} - \omega t)\} ,\quad (j = 1,2,3,4), $$

(16)

where arbitrary constants $F_{rj}^{(1)} ,(j = 1,2,3,4),$ represent the amplitudes of reflected $P_{1} ,P_{2} ,P_{3} ,SV$ waves, respectively.

The propagation vectors $\vec{P}_{rj}^{(1)}$ and attenuation vectors $\vec{A}_{rj}^{(1)}$ are defined as

$$ \vec{P}_{rj}^{(1)} = k_{R}^{(1)} \hat{x} - d_{rjR}^{(1)} \hat{z},\,\,\,\,\vec{A}_{rj}^{(1)} = - \;k_{I}^{(1)} \hat{x} + d_{rjI}^{(1)} \hat{z},\,\,\,d_{rj}^{(1)} = \pm \,p.v.\left[ {\left( {\frac{\omega }{{V_{j}^{(1)} }}} \right)^{2} - \left( {k^{(1)} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} , $$

where $p.v.$ denotes the principal value of the complex quantity derived from the square root. The sign of $d_{rj}^{(1)}$ is chosen to ensure the decay of associated reflected wave along negative $z$-direction, i.e., a positive value for imaginary part of $d_{rj}^{(1)}$. Wave number $k^{(1)} \,( = k_{R}^{(1)} + \iota k_{I}^{(1)} )$ is a complex quantity such that $k_{R}^{(1)} \ge 0$ defines the propagation in positive $x$-direction.

• (2) In the poroelastic layer $\varOmega_{2} \,(0 < z < h)$

$$ \begin{aligned} \varphi_{j}^{(2)} & = F_{tj}^{(2)} \exp (\vec{A}_{tj}^{(2)} \cdot \vec{r})\exp \{ \iota (\vec{P}_{tj}^{(2)} \cdot \vec{r} - \omega t)\} \\ & + F_{rj}^{(2)} \exp (\vec{A}_{rj}^{(2)} \cdot \vec{r})\exp \{ \iota (\vec{P}_{rj}^{(2)} \cdot \vec{r} - \omega t)\} ,\,\,\,\,(j = 1,\,2,\,3,\,4),\, \\ \end{aligned} $$

(17)

where arbitrary constants $F_{rj}^{(2)} \,(F_{tj}^{(2)} ),\,(j = 1,\,2,\,3,\,4),$ represent the amplitudes of reflected (transmitted) $P_{1} ,\,P_{2} ,\,P_{3} ,\,SV$ waves, respectively.

The propagation vectors $(\vec{P}_{rj}^{(2)} ,\vec{P}_{tj}^{(2)} )$ and attenuation vectors $(\vec{A}_{rj}^{(2)} ,\,\vec{A}_{tj}^{(2)} )$ are defined as

$$ \begin{aligned} & \vec{P}_{rj}^{(2)} = k_{R}^{(2)} \hat{x} - d_{rjR}^{(2)} \hat{z},\;\;\;\;\;\vec{P}_{tj}^{(2)} = k_{R}^{(2)} \hat{x} + d_{tjR}^{(2)} \hat{z},\,\,\, \\ & \vec{A}_{rj}^{(2)} = - \;k_{I}^{(2)} \hat{x} + d_{rjI}^{(2)} \hat{z},\;\;\;\;\;\vec{A}_{tj}^{(2)} = - \;k_{I}^{(2)} \hat{x} - d_{tjI}^{(2)} \hat{z},\,\, \\ & d_{rj}^{(2)} = \pm \;p.v.\left[ {\left( {\frac{\omega }{{V_{j}^{(2)} }}} \right)^{2} - \left( {k^{(2)} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} , \\ & d_{tj}^{(2)} = \pm \;p.v.\left[ {\left( {\frac{\omega }{{V_{j}^{(2)} }}} \right)^{2} - \left( {k^{(2)} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\;\;\;\;\;(j = 1,\,2,\,3,\,4). \\ \end{aligned} $$

• (3) In the poroelastic solid $\varOmega_{3} \,(h < z < \infty )$

$$ \varphi_{j}^{(3)} = F_{tj}^{(3)} \exp (\vec{A}_{tj}^{(3)} \cdot \vec{r})\exp \{ \iota (\vec{P}_{tj}^{(3)} \cdot \vec{r} - \omega t)\} ,\;\;\;(j = 1,\,2,\,3,\,4), $$

(18)

where arbitrary constants $F_{tj}^{(3)} ,\,(j = 1,\,2,\,3,\,4),$ represent the amplitudes of transmitted $P_{1} ,\,P_{2} ,\,P_{3} ,\,SV$ waves, respectively.

The propagation vectors $\vec{P}_{tj}^{(3)}$ and attenuation vectors $\vec{A}_{tj}^{(3)}$ are defined as

$$ \begin{aligned} & \vec{P}_{tj}^{(3)} = k_{R}^{(3)} \hat{x} + d_{tjR}^{(3)} \hat{z},\,\,\,\,\vec{A}_{tj}^{(3)} = - k_{I}^{(3)} \hat{x} - d_{tjI}^{(3)} \hat{z},\,\,\, \\ & d_{tj}^{(3)} = \pm\;p.v.\left[ {\left( {\frac{\omega }{{V_{j}^{(3)} }}} \right)^{2} - \left( {k^{(3)} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ,\;\;\;\;\;(j = 1,\,2,\,3,\,4). \\ \end{aligned} $$

Sign of $d_{tj}^{(3)}$ is chosen to ensure the decay of the associated transmitted wave along the positive $z$-direction, i.e., a positive value for the imaginary part of $d_{tj}^{(3)}$. The subscripts $t,r$ indicate the transmitted and reflected waves, respectively.

To satisfy the system of boundary conditions defined by (11), the potentials given by (15), (16), (17) and (18) are used to calculate the displacements and stresses in the media $\varOmega_{j} ,\,(j = 1,\,2,\,3)$. The continuity requirements along the interfaces $z = 0$ and $z = h$ are satisfied with the identical phase for all the waves on either side of the interfaces. This provides that Snell’s law for reflection/transmission phenomenon is considered. This translates further into the same wave number for all the waves across interfaces, i.e., $k = k^{(1)} = k^{(2)} = k^{(3)}$. Then, for an incident wave specified with $V_{0} ,\,\theta_{0} ,\,\gamma_{0}$ and $\omega ,$ $k$ is calculated from (12). This $k$ is used further to calculate $d_{rj}^{(m)} ,\,d_{tj}^{(m)} ,\,(m = 1,\,2,\,3),$ for reflected and transmitted waves, respectively. Applying boundary conditions (11) and considering Snell’s law at the interfaces $z = 0$ and $z = h,$, we get two systems of simultaneous linear equations (see Appendix 1). These two systems of equations are combined by using matrix notations of Carcione (2007, Section 6.4) to relate the fields at $z = 0$ and $z = h$. Hence, these two systems are translated into a system of eight simultaneous linear equations given by

$$ {\mathbf{(M}} - {\mathbf{N}} * {\mathbf{O)Q}} = {\mathbf{R,}} $$

(19)

where ${\mathbf{Q}} = [C_{r1}^{(1)} ,\,C_{r2}^{(1)} ,\,C_{r3}^{(1)} ,\,C_{r4}^{(1)} ,\,C_{t1}^{(3)} ,\,C_{t2}^{(3)} ,\,C_{t3}^{(3)} ,\,C_{t4}^{(3)} ]^{\text{T}} ,\,$ and ${\mathbf{N}} = {\mathbf{T}}(0) * {\mathbf{T}}(h)^{ - 1}$.

The matrices ${\mathbf{M,}}\,{\mathbf{O}}$ and ${\mathbf{T}}$ are given in Appendix 2. The matrix ${\mathbf{R}}$ in the system (19) is written as follows.

• (1) For incident $P$-waves

  $$ {\mathbf{R}} = [ - \;m_{1j} ,\,m_{2j} ,\, -\, m_{3j} ,\, -\, m_{4j} ,\, -\, m_{5j} ,\,m_{6j} ,\,m_{7j} ,\,m_{8j} ]^{\text{T}} ,\,\,\,(j = 1,\,2,\,3). $$

• (2) For incident $SV$-wave

  $$ {\mathbf{R}} = [m_{14} ,\, -\, m_{24} ,\,m_{34} ,\,m_{44} ,\,m_{54} ,\, -\, m_{64} ,\, -\, m_{74} ,\, -\, m_{84} ]^{\text{T}} . $$

7 Numerical results and discussion

7.1 Numerical example

The expressions for velocities, reflection and transmission coefficients involve a large number of parameters. Hence, to study the dependence of reflection and transmission coefficients on layer thickness, wave frequency, liquid saturation, capillary pressure of the porous layer, propagation and attenuation direction of the incident wave, we restrict our numerical work to a particular model. In this model, medium $\varOmega_{1}$ is taken to be Columbia fine sandy loam saturated by an air–water mixture, medium $\varOmega_{2}$ is taken to be sandstone saturated by water, and ${\text{CO}}_{ 2} ,$ medium $\varOmega_{3}$ is taken to be Columbia fine sandy loam saturated by an oil–water mixture.

Following Lo et al. (2005), the values of elastic and dynamic constants chosen for Columbia fine sandy loam (medium $\varOmega_{1}$) saturated by an air–water mixture are as follows. The skeletal frame of sandstone with bulk modulus K ₀ = 8.33 MPa, rigidity modulus G = 3.83 MPa and density ρ ₀ = 2650 kg/m³ supports the porosity f = 0.45. The pore space is filled with air of bulk modulus K ₁ = 0.145 MPa, density ρ ₁ = 1.1 kg/m³ and viscosity $\eta_{1} = 18 \times 10^{ - 6}$ Ns/m² mixed with water of bulk modulus $K_{2} = 2.25$ GPa, density $\rho_{2} = 997$ kg/m³ and viscosity $\eta_{2} = 0.001$ Ns/m². The fitting parameters $n = 2.145$, $\chi = 0.5$ along with intrinsic permeability $\chi_{0} = 5.3 \times 10^{ - 13}$ m² of composite. The value of $K_{\text{cap}} = 0.005K_{2}$ and $\sigma = 0.5.$

A reservoir rock (sandstone) saturated with water and CO₂ (medium $\varOmega_{2}$) is chosen for the numerical model of the poroelastic layer (Garg and Nayfeh 1986). The skeletal frame of sandstone with bulk modulus $K_{0} = 12$ GPa, rigidity modulus $G = 9$ GPa and density $\rho_{0} = 2650$  kg/m³ supports the porosity $f = 0.45$. The pore space is filled with gas of bulk modulus $K_{1} = 3.7$ MPa and density $\rho_{1} = 103$ kg/m³ mixed with water of bulk modulus $K_{2} = 2.25$ GPa and density $\rho_{2} = 990$ kg/m³. Viscous dissipation in pores is defined with coefficient $d_{1} = 0.04$ MPa s m⁻² for gas and $d_{2} = 1$ MPa s m⁻² for water.

Following Lo et al. (2005), the values of elastic and dynamic constants chosen for Columbia fine sandy loam (medium $\varOmega_{3}$) saturated by an oil–water mixture are: the skeletal frame of sandstone with bulk modulus $K_{0} = 8.33$ MPa, rigidity modulus $G = 3.85$ MPa and density $\rho_{0} = 2650$ kg/m³ supports the porosity $f = 0.45$. The pore space is filled with oil of bulk modulus $K_{1} = 0.57$ GPa, density $\rho_{1} = 762$ kg/m³ and viscosity $\eta_{1} = 0.00144$ Ns/m² mixed with water of bulk modulus $K_{2} = 2.25$ GPa, density $\rho_{2} = 997$ kg/m³ and viscosity $\eta_{2} = 0.001$ Ns/m². The fitting parameters are $n = 2.037$, $\chi = 0.5$ along with intrinsic permeability $\chi_{0} = 8 \times 10^{ - 13}$ m² of composite. The value of $K_{\text{cap}} = 0.005K_{2}$ and $\sigma = 0.5.$

7.2 Numerical discussion

The reflection and transmission coefficients defined in Sect. 6 are calculated for incident direction $\theta_{0} \in (0,\,90^{0} ).$ In this article, the incidence of two main waves (i.e., $P_{1} \,$ and $SV$) is considered. The variations of reflection and transmission coefficients with incident direction ($\theta_{0}$) are shown in Figs. 2–6 (for incident $P_{1} \,$ wave) and in Figs. 7–11 (for incident $SV$ wave). The detailed discussion on figures is as follows.

Fig. 2

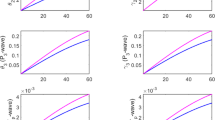
Reflection and transmission coefficients as a function of incident direction $(\theta_{0} )$ for four different layer thickness: $h = 0,\,1,\,10{\text m}$ and $h \to \infty$; $\omega = 2\pi \times 100{\text {Hz}}$; $\sigma = 0.2$; $K_{\text{cap}} = 0.005K_{2}$; incident $P_{1}$ wave

Figure 2 displays the variation of reflection and transmission coefficients as a function of incident direction ($\theta_{0}$) for four different values of $h$: 0, 1, 10 m and $h \to \infty$. The reflected and transmitted $SV$ waves get stronger with an increase in layer thickness. It is clear that at normal incidence reflected and transmitted $SV$ waves do not survive quantitatively for any value of layer thickness ($h$). The transmission coefficients of $P_{1} ,\,P_{2} ,\,P_{3}$ waves behave differently to reflection coefficients in regards to layer thickness. A critical angle is observed between $8^{0}$ and $15^{0}$. In both cases (i.e., $h = 0$ and $h \to \infty$), the poroelastic layer is eliminated from the system and represents the reflection and transmission of waves at the boundary between two dissimilar poroelastic solids saturated with two immiscible fluids. In case of $h = 0$, the variations in reflection and transmission coefficients with incident direction are different from that in the case of $h \to \infty$. This variation in reflection and transmission coefficients occurs due to the difference in the numerical values of elastic/dynamical constants of the two media. The effect of the saturating fluid on the variation of reflection and transmission coefficients is shown in Fig. 3. It is observed that the transmission coefficients of $P_{3}$ and $SV$ waves behave almost like reflection coefficients, for any value of $\sigma$.

Fig. 3

Reflection and transmission coefficients as a function of incident direction $(\theta_{0} )$ for three different liquid saturations: $\sigma = 0.01,\,0.5,\,0.99$; $\omega = 2\pi \times 1000{\text{Hz}}$; $h = 1{\text m}$; $K_{\text{cap}} = 0.02K_{2}$; incident $P_{1}$ wave

However, with the change in $\sigma$, the transmission coefficients of $P_{1}$ and $P_{2}$ waves behave opposite to reflection coefficients. The effect of wave frequency on reflection and transmission coefficients is displayed in Fig. 4. It is noticed that the reflection and transmission coefficients of $P_{2} ,\,P_{3}$ and $SV$ waves increase with an increase in wave frequency $\omega$. The effect of frequency on the transmission coefficient of the $P_{1}$ wave is insignificant. However, beyond $10^{0}$ incidence, the reflection coefficient of the $P_{1}$ wave decreases with an increase in frequency. Further, the behavior of the transmission coefficient of $P_{1}$ is opposite to the corresponding reflection coefficient for $\theta_{0} \in (50^{0} ,\,90^{0} ).$ The effect of capillary pressure on the reflection and transmission coefficients is displayed in Fig. 5. For $\theta_{0} \in (0,\,90^{0} )$, the transmission coefficients of $P_{3}$ and $SV$ waves behave like their corresponding reflection coefficients. However, the transmission coefficients of $P_{1}$ and $P_{2}$ waves behave opposite to the reflection coefficients with the change in capillary pressure. The effect of viscosity of pore fluids on reflection and transmission coefficients is shown in Fig. 6. The viscosity of pore fluids may have considerable effect on all the reflected and transmitted waves for $\theta_{0} \in (20^{0} ,\,85^{0} )$ except for the transmitted $P_{1}$ wave. The reflection coefficient of the $P_{1}$ wave increases due to the presence of viscosity in pore fluids, while all the other reflection and transmission coefficients decrease due to the presence of viscosity in pore fluids.

Fig. 4

Reflection and transmission coefficients as a function of incident direction $(\theta_{0} )$ for three different frequencies: $\omega = 2\pi \times 0.1{\text{kHz}},\,2\pi \times 0.5{\text{kHz}},\,\,2\pi \times 1{\text{kHz}}$; $h = 1{\text m}$; $\sigma = 0.5$; $K_{\text{cap}} = 0.005K_{2}$; incident $P_{1}$ wave

Fig. 5

Reflection and transmission coefficients as a function of incident direction $(\theta_{0} )$ for three different values of capillary pressure: $K_{\text{cap}} = 0.1K_{2} ,\,0.02K_{2} ,\,\,0.005K_{2}$; $\omega = 2\pi \times 1000{\text {Hz}}$; $\sigma = 0.5$; $h = 1{\text m}$; incident $P_{1}$ wave

Fig. 6

Effect of viscosity of pore fluids on reflection and transmission coefficients; $h = 1{\text m}$; $K_{\text{cap}} = 0.005K_{2}$; $\omega = 2\pi \times 100{\text {Hz}}$; $\sigma = 0.8$; incident $P_{1}$ wave

For the incidence of the $SV$ wave, the reflection and transmission coefficients as a function of incident direction ($\theta_{0}$) are shown in Fig. 7 for four different values of $h$: 0, 1, 10 m and $h \to \infty$. In Fig. 7, a significant effect of variations in layer thickness is observed on the reflection and transmission coefficients. It is clear that at normal incidence only reflected $SV$ waves survive quantitatively for any value of layer thickness ($h$). In the absence of a sandwiched layer (i.e., $h = 0$), a critical angle is not observed for both reflected and transmitted $SV$ waves, while critical angles are observed for all the other reflected and transmitted waves. The effect of saturation ($\sigma$) on reflection and transmission coefficients is shown in Fig. 8. A significant effect of saturation is observed on the reflection and transmission coefficients of $P_{2}$ and $P_{3}$ waves, while $P_{1}$ and $SV$ waves are only slightly influenced by a change in liquid saturation. The transmission coefficients of $P_{2}$ waves behave nearly opposite to their corresponding reflection coefficient with respect to saturation. In Fig. 9, a significant effect of variations in frequency is visible on all the reflected and transmitted waves. Hence, all the waves are dispersive in nature. In Fig. 10, a small effect of capillary pressure is observed on the two main waves (i.e., $P_{1} ,\,SV$), but a significant effect of capillary pressure is observed on the two slower waves (i.e., $P_{2} ,\,P_{3}$). The effect of viscosity of pore fluids on reflection and transmission coefficients is shown in Fig. 11. Similar to the case of incident $P_{1}$ wave, the presence of viscosity in pore fluids may have considerable effect on the reflection and transmission coefficients for $\theta_{0} \in (20^{0} ,\,80^{0} )$. The variational pattern of transmission coefficients is nearly similar to reflection coefficients except for the $SV$ wave.

Fig. 7

Same as Fig. 2 but for incident $SV$ wave

Fig. 8

Same as Fig. 3 but for incident $SV$ wave

Fig. 9

Same as Fig. 4 but for incident $SV$ wave

Fig. 10

Same as Fig. 5 but for incident $SV$ wave

Fig. 11

Same as Fig. 6 but for incident $SV$ wave

8 Conclusions

In the present study, a theoretical procedure is used to analyze the effects of layer thickness, liquid saturation, capillary pressure of the porous layer, incident direction and wave frequency on the reflection and transmission characteristics. This mathematical model can be used in many practical applications such as to predict the seismic response of fractures in sandstones. Some interesting consequences of the present study are explained as follows.

• (1) At the normal incidence of $P_{1}$ wave, reflected and transmitted $SV$ waves do not survive quantitatively, while at the normal incidence of $SV$ wave, only transmitted $SV$ waves survive.

• (2) All the reflected and transmitted waves are strongly influenced by variations in frequency for both incidence (i.e., $P_{1}$ and $SV$). Therefore, all the reflected and transmitted waves are frequency dependent in nature.

• (3) For the incidence of $SV$ wave, in the absence of a sandwiched layer (i.e., $h = 0$ and $h \to \infty$), a critical angle is not observed for either reflected or transmitted $SV$ waves.

• (4) All the reflected and transmitted waves are significantly influenced by the presence of viscosity in pore fluids for both incidences.

• (5) For both incidences, all reflected and transmitted waves are strongly associated with layer thickness, liquid saturation, capillary pressure of the sandwiched layer and incident direction.

The study of reservoir characteristics such as layer thickness, capillary pressure and saturation through seismic (reflection and transmission) methods is helpful in detecting hydrocarbons and minerals present beneath the Earth’s surface. Hence, the various issues resolved in this study are relevant to many of the practical problems of hydrology, geophysics, petroleum engineering and seismology.

Appendices

Appendix 1: Linear systems

The first system of simultaneous linear equations at the interface $z = 0$ is given by

$$ \sum\limits_{j = 1}^{4} {x_{i,j} C_{rj}^{(1)} + } \sum\limits_{j = 5}^{8} {x_{i,j} C_{tl}^{(2)} + } \sum\limits_{j = 9}^{12} {x_{i,j} C_{rq}^{(2)} = b_{i} ,\,\,\,\,l = j - 4,} \,\,\,\,q = j - 8,\,\,\,i = 1,\,2,\,3,\,4,\,5,\,6,\,7,\,8. $$

(20)

where

$$ \begin{aligned} & x_{1,j} = - \;[\alpha_{j}^{(1)} + (\alpha_{j}^{(1)} + 2G^{(1)} )(d_{rj}^{(1)} /k)^{2} ],\\ & x_{1,4} = 2G^{(1)} (d_{r4}^{(1)} /k), \,\, x_{2,j} = \,2G^{(1)} (d_{rj}^{(1)} /k)\,,\\ & x_{2,4} = \,G^{(1)} ((d_{r4}^{(1)} /k)^{2} - 1), \,\, x_{3,j} = - \;\beta_{j}^{(1)} (1 + (d_{rj}^{(1)} /k)^{2} ),\\ & x_{3,4} = 0,\,\,x_{4,j} = - \;\gamma_{j}^{(1)} (1 + (d_{rj}^{(1)} /k)^{2} ),\,\,\,\,x_{4,4} = 0. \\ \end{aligned} $$

For $(j = 1,\,2,\,3),$ we have

$$ \begin{aligned} & x_{5,j} = 1,\,\,\,x_{5,4} = d_{r4}^{(1)} /k,\,\,\,x_{6,j} = - \;d_{rj}^{(1)} /k,\,\,\,\,x_{6,4} = 1, \\ & x_{7,j} = - \;\mu_{j}^{(1)} (d_{rj}^{(1)} /k),\,\,\,x_{7,4} = \varGamma_{1}^{(1)} ,\,\,x_{8,j} = - \;\gamma_{j}^{(1)} (d_{rj}^{(1)} /k),\,\,\,x_{8,4} = \varGamma_{2}^{(1)} . \\ \end{aligned} $$

For $(j = 5,\,6,\,7;\,l = j - 4),$ we have

$$ \begin{aligned} & x_{1,j} = [\alpha_{l}^{(2)} + (\alpha_{l}^{(2)} + 2G^{(2)} )(d_{tl}^{(2)} /k)^{2} ],\,\,\,\,x_{1,8} = 2G^{(2)} (d_{t4}^{(2)} /k), \\ & x_{2,j} = \,2G^{(2)} (d_{tl}^{(2)} /k)\,,\,\,x_{2,8} = \, - G^{(2)} ((d_{t4}^{(2)} /k)^{2} - 1), \\ & x_{3,j} = \beta_{l}^{(2)} (1 + (d_{tl}^{(2)} /k)^{2} ),\,\,\,\,x_{3,8} = 0,\,\,x_{4,j} = \gamma_{l}^{(2)} (1 + (d_{tl}^{(2)} /k)^{2} ),\,\,\,\,x_{4,8} = 0, \\ & x_{5,j} = - \;1,\,\,\,x_{5,8} = d_{t4}^{(2)} /k,\,\,\,x_{6,j} = - \;d_{tl}^{(2)} /k,\,\,\,\,x_{6,8} = - \;1, \\ & x_{7,j} = - \;\mu_{l}^{(2)} (d_{tl}^{(2)} /k),\,\,\,x_{7,8} = - \;\varGamma_{1}^{(2)} ,\,\,x_{8,j} = - \;\gamma_{l}^{(2)} (d_{tl}^{(2)} /k),\,\,\,x_{8,4} = - \;\varGamma_{2}^{(2)} . \\ \end{aligned} $$

For $(j = 9,\,10,\,11;\,q = j - 8),$ we have

$$ \begin{aligned} & x_{1,j} = [\alpha_{q}^{(2)} + (\alpha_{q}^{(2)} + 2G^{(2)} )(d_{rq}^{(2)} /k)^{2} ],\,\,\,\,x_{1,12} = 2G^{(2)} (d_{r4}^{(2)} /k), \\ & x_{2,j} = \, - 2G^{(2)} (d_{rq}^{(2)} /k)\,,\,\,x_{2,12} = \, - G^{(2)} ((d_{r4}^{(2)} /k)^{2} - 1), \\ & x_{3,j} = \beta_{q}^{(2)} (1 + (d_{rq}^{(2)} /k)^{2} ),\,\,\,\,x_{3,12} = 0,\,\,x_{4,j} = \gamma_{q}^{(2)} (1 + (d_{rq}^{(2)} /k)^{2} ),\,\,\,\,x_{4,12} = 0, \\ & x_{5,j} = - \;1,\,\,\,x_{5,12} = - \;d_{r4}^{(2)} /k,\,\,\,x_{6,j} = d_{rq}^{(2)} /k,\,\,\,\,x_{6,12} = - \;1, \\ & x_{7,j} = \mu_{q}^{(2)} (d_{rq}^{(2)} /k),\,\,\,x_{7,12} = - \;\varGamma_{1}^{(2)} ,\,\,x_{8,j} = \gamma_{q}^{(2)} (d_{rq}^{(2)} /k),\,\,\,x_{8,12} = - \;\varGamma_{2}^{(2)} . \\ \end{aligned} $$

The second system of simultaneous linear equations at the interface $z = h,$ is given by

$$ \sum\limits_{j = 1}^{4} {y_{i,j} e^{{\iota d_{j}^{(2)} h}} C_{tj}^{(2)} + } \sum\limits_{j = 5}^{8} {y_{i,j} e^{{ - \iota d_{j}^{(2)} h}} C_{rq}^{(2)} = \sum\limits_{j = 1}^{4} {z_{i,j} e^{{\iota d_{j}^{(2)} h}} C_{tj}^{(3)} ,} } \,\,\,q = j - 8,\,\,\,i = 1,\,2,\,3,\,4,\,5,\,6,\,7,\,8. $$

(21)

For $(j = 1,\,2,\,3),$ we have

$$ y_{1,j} = - \;[\alpha_{j}^{(2)} + (\alpha_{j}^{(2)} + 2G^{(2)} )(d_{tj}^{(2)} /k)^{2} ],\,\,\,\,y_{1,4} = - \;2G^{(2)} (d_{t4}^{(2)} /k), $$

$$ y_{2,j} = \, - 2G^{(2)} (d_{tj}^{(2)} /k)\,,\,\,y_{2,4} = \,G^{(2)} ((d_{t4}^{(2)} /k)^{2} - 1), $$

$$ y_{3,j} = - \;\beta_{j}^{(2)} (1 + (d_{tj}^{(2)} /k)^{2} ),\,\,\,\,y_{3,4} = 0,\,\quad y_{4,j} = - \;\gamma_{j}^{(2)} (1 + (d_{tj}^{(2)} /k)^{2} ),\,\,\,\,y_{4,4} = 0, $$

$$ y_{5,j} = 1,\,\,\,y_{5,4} = - \;d_{t4}^{(2)} /k,\,\,\,y_{6,j} = d_{tj}^{(2)} /k,\,\,\,\,y_{6,4} = 1, $$

$$ y_{7,j} = \mu_{j}^{(2)} (d_{tj}^{(2)} /k),\,\,\,y_{7,4} = \varGamma_{1}^{(2)} ,\,\,y_{8,j} = \gamma_{j}^{(2)} (d_{tj}^{(2)} /k),\,\,\,y_{8,4} = \varGamma_{2}^{(2)} . $$

For $(j = 5,\,6,\,7;\,q = j - 4),$ we have

$$ \begin{aligned} & y_{1,j} = - \;[\alpha_{q}^{(2)} + (\alpha_{q}^{(2)} + 2G^{(2)} )(d_{rq}^{(2)} /k)^{2} ],\,\,\,\,y_{1,8} = 2G^{(2)} (d_{r4}^{(2)} /k), \,\,\,\, y_{2,j} = \,2G^{(2)} (d_{rq}^{(2)} /k)\,,\,\,y_{2,8} = \, - G^{(2)} ((d_{r4}^{(2)} /k)^{2} - 1), \,\,\,\, y_{3,j} = - \;\beta_{q}^{(2)} (1 + (d_{rq}^{(2)} /k)^{2} ),\,\,\,\quad y_{3,8} = 0,\,\,y_{4,j} = - \;\gamma_{q}^{(2)} (1 + (d_{rq}^{(2)} /k)^{2} ),\,\,\,\,y_{4,8} = 0, \\ & y_{5,j} = 1,\,\,\,y_{5,8} = d_{r4}^{(2)} /k,\,\,\,y_{6,j} = - \;d_{rq}^{(2)} /k,\,\,\,\,y_{6,8} = 1, \\ & y_{7,j} = - \;\mu_{q}^{(2)} (d_{rq}^{(2)} /k),\,\,\,y_{7,8} = \varGamma_{1}^{(2)} ,\,\,y_{8,j} = - \;\gamma_{q}^{(2)} (d_{rq}^{(2)} /k),\,\,\,y_{8,4} = \varGamma_{2}^{(2)} . \\ \end{aligned} $$

For $(j = 1,\,2,\,3),$ we have

$$ z_{1,j} = - \;[\alpha_{j}^{(3)} + (\alpha_{j}^{(3)} + 2G^{(3)} )(d_{tj}^{(3)} /k)^{2} ]e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,\quad z_{1,4} = - \;2G^{(3)} (d_{t4}^{(3)} /k)e^{{\iota d_{j4}^{(3)} h}} , $$

$$ z_{2,j} = - \;2G^{(3)} (d_{tj}^{(3)} /k)\,e^{{\iota d_{tj}^{(3)} h}} ,\,\quad z_{2,4} = G^{(3)} ((d_{t4}^{(3)} /k)^{2} - 1)e^{{\iota d_{t4}^{(3)} h}} , $$

$$ z_{3,j} = - \;\beta_{j}^{(3)} (1 + (d_{tj}^{(3)} /k)^{2} )e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,\,z_{3,4} = 0,\,\quad z_{4,j} = - \;\gamma_{j}^{(3)} (1 + (d_{tj}^{(3)} /k)^{2} )e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,\,z_{4,4} = 0, $$

$$ z_{5,j} = e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,z_{5,4} = - \;(d_{t4}^{(3)} /k)e^{{\iota d_{t4}^{(3)} h}} ,\,\,\quad z_{6,j} = (d_{tj}^{(3)} /k)e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,\,z_{6,4} = e^{{\iota d_{t4}^{(3)} h}} , $$

$$ z_{7,j} = \mu_{j}^{(3)} (d_{tj}^{(3)} /k)e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,z_{7,4} = \varGamma_{1}^{(3)} e^{{\iota d_{t4}^{(3)} h}} ,\,\quad z_{8,j} = \gamma_{j}^{(3)} (d_{tj}^{(3)} /k)e^{{\iota d_{tj}^{(3)} h}} ,\,\,\,z_{8,4} = \varGamma_{2}^{(3)} e^{{\iota d_{t4}^{(3)} h}} . $$

Appendix 2: Linear systems

The final system of linear equations. The matrices given in system (19) are defined as

$$ M = \left[ {\begin{array}{*{20}c} {x_{1,1} } & {x_{1,2} } & {x_{1,3} } & {x_{1,4} } & 0 & 0 & 0 & 0 \\ {x_{2,1} } & {x_{2,2} } & {x_{2,3} } & {x_{2,4} } & 0 & 0 & 0 & 0 \\ {x_{3,1} } & {x_{3,2} } & {x_{3,3} } & {x_{3,4} } & 0 & 0 & 0 & 0 \\ {x_{4,1} } & {x_{4,2} } & {x_{4,3} } & {x_{4,4} } & 0 & 0 & 0 & 0 \\ {x_{5,1} } & {x_{5,2} } & {x_{5,3} } & {x_{5,4} } & 0 & 0 & 0 & 0 \\ {x_{6,1} } & {x_{6,2} } & {x_{6,3} } & {x_{6,4} } & 0 & 0 & 0 & 0 \\ {x_{7,1} } & {x_{7,2} } & {x_{7,3} } & {x_{7,4} } & 0 & 0 & 0 & 0 \\ {x_{8,1} } & {x_{8,2} } & {x_{8,3} } & {x_{8,4} } & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

and

$$ {\mathbf{O}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {z_{1,1} } & {z_{1,2} } & {z_{1,3} } & {z_{1,4} } \\ 0 & 0 & 0 & 0 & {z_{2,1} } & {z_{2,2} } & {z_{2,3} } & {z_{2,4} } \\ 0 & 0 & 0 & 0 & {z_{3,1} } & {z_{3,2} } & {z_{3,3} } & {z_{3,4} } \\ 0 & 0 & 0 & 0 & {z_{4,1} } & {z_{4,2} } & {z_{4,3} } & {z_{4,4} } \\ 0 & 0 & 0 & 0 & {z_{5,1} } & {z_{5,2} } & {z_{5,3} } & {z_{5,4} } \\ 0 & 0 & 0 & 0 & {z_{6,1} } & {z_{6,2} } & {z_{6,3} } & {z_{6,4} } \\ 0 & 0 & 0 & 0 & {z_{7,1} } & {z_{7,2} } & {z_{7,3} } & {z_{7,4} } \\ 0 & 0 & 0 & 0 & {z_{8,1} } & {z_{8,2} } & {z_{8,3} } & {z_{8,4} } \\ \end{array} } \right] $$

Finally, ${\mathbf{N}} = {\mathbf{T}}(0) * [{\mathbf{T}}(h)]^{ - 1}$ and ${\mathbf{T}}(z) = {\mathbf{S}}_{1} * {\mathbf{S}}_{2} (z)$ being

$$ {\mathbf{S}}_{1} = \left[ {\begin{array}{*{20}c} {y_{1,1} } & {y_{1,2} } & {y_{1,3} } & {y_{1,4} } & {y_{1,5} } & {y_{1,6} } & {y_{1,7} } & {y_{1,8} } \\ {y_{2,1} } & {y_{2,2} } & {y_{2,3} } & {y_{2,4} } & {y_{2,5} } & {y_{2,6} } & {y_{2,7} } & {y_{2,8} } \\ {y_{3,1} } & {y_{3,2} } & {y_{3,3} } & {y_{3,4} } & {y_{3,5} } & {y_{3,6} } & {y_{3,7} } & {y_{3,8} } \\ {y_{4,1} } & {y_{4,2} } & {y_{4,3} } & {y_{4,4} } & {y_{4,5} } & {y_{4,6} } & {y_{4,7} } & {y_{4,8} } \\ {y_{5,1} } & {y_{5,2} } & {y_{5,3} } & {y_{5,4} } & {y_{5,5} } & {y_{5,6} } & {y_{5,7} } & {y_{5,8} } \\ {y_{6,1} } & {y_{6,2} } & {y_{6,3} } & {y_{6,4} } & {y_{6,5} } & {y_{6,6} } & {y_{6,7} } & {y_{6,8} } \\ {y_{7,1} } & {y_{7,2} } & {y_{7,3} } & {y_{7,4} } & {y_{7,5} } & {y_{7,6} } & {y_{7,7} } & {y_{7,8} } \\ {y_{8,1} } & {y_{8,2} } & {y_{8,3} } & {y_{8,4} } & {y_{8,5} } & {y_{8,6} } & {y_{8,7} } & {y_{8,8} } \\ \end{array} } \right] $$

and

$$ {\mathbf{S}}_{2} = \left[ {\begin{array}{*{20}c} {e^{{\iota d_{t1} z}} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {e^{{\iota d_{t2} z}} } & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {e^{{\iota d_{t3} z}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {e^{{\iota d_{t4} z}} } & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & {e^{{ - \iota d_{r1} z}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {e^{{ - \iota d_{r2} z}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {e^{{ - \iota d_{r3} z}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {e^{{ - \iota d_{r4} z}} } \\ \end{array} } \right] $$