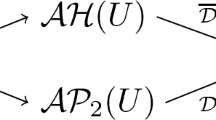Abstract
The Fueter-Sce-Qian mapping theorem gives a constructive way to extend holomorphic functions of one complex variable to slice hyperholomorphic functions. By means of the Cauchy formula for slice hyperholomorphic functions it is possible to have a Fueter-Sce-Qian mapping theorem in integral form for n odd. On this theorem it is based the \( \mathcal {F}\)-functional calculus for n-tuples of commuting operators. It is a functional calculus based on the commutative version of the S spectrum. Furthermore, it is a monogenic functional calculus in the spirit of McIntosh and collaborators. In this paper, inspired by the quaternionic case and some particular Clifford algebras cases, we show a general resolvent equation for the \( \mathcal {F}\)-functional calculus in the Clifford algebra setting. Moreover, we prove that the \( \mathcal {F}\)-resolvent equation is the suitable equation to study the Riesz projectors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the deepest and important result in hypercomplex analysis is the Fueter-Sce-Qian mapping theorem. This gives a two step procedure to construct a monogenic function, i.e., null solutions of the generalized Cauchy Riemann operator in \( \mathbb {R}^{n+1}\), starting from a holomorphic function of one complex variable. In the first step the class of holomorphic functions is extended to the one of slice hyperholomorphic functions. In the second step the class of monogenic functions is generated by applying the so-called Fueter-Sce-Qian map, namely \( \Delta ^{\frac{n-1}{2}}\) (where \( \Delta \) is the Laplace operator), to the class of slice hyperholomorphic functions. For more details see [27].
Nowadays both slice hyperholomorphic and monogenic functions are widely studied. See, for example, the books, [25, 26, 33, 34], and the references therein, for further information about slice hyperholomorphic functions. Recently, this theory of functions has generated the following research directions: quaternionic integral transforms see [30, 31], quaternionic perturbation theory and invariant subspaces [8], the characteristic operator functions and applications to linear system theory [5], Schur analysis [4], fractional powers of quaternionic linear operators [14]. Based on these there are new classes of fractional diffusion problems [9, 10, 20].
For further information about the theory of monogenic functions see, for instance, [7, 24, 28, 35] and references therein. Some applications of this function theory are related to the functional calculus, see [36], peculiar integral transforms [29], singular integrals [38].
A Cauchy formula holds for slice hyperholomorphic functions and it is the heart of the S-functional calculus. In order to give further information about this we need some preliminary material.
Let \(\mathbb {R}_n\) be the real Clifford algebra over n imaginary units \(e_1,\ldots ,e_n\) satisfying the relations \(e_\ell e_m+e_me_\ell =0\), \(\ell \not = m\), \(e_\ell ^2=-1.\) An element in the Clifford algebra will be denoted by \(\sum _A e_Ax_A\) where \(A=\{ \ell _1\ldots \ell _r\}\in \mathcal {P}\{1,2,\ldots , n\}, \ell _1<\ldots <\ell _r\) is a multi-index and \(e_A=e_{\ell _1} e_{\ell _2}\ldots e_{\ell _r}\), \(e_\emptyset =1\). A point \((x_0,x_1,\ldots ,x_n)\in \mathbb {R}^{n+1}\) will be identified with the element \( x=x_0+{\underline{x}}=x_0+ \sum _{j=1}^n x_j e_j\in \mathbb {R}_n \) called paravector and the real part \(x_0\) of x will also be denoted by \(\textrm{Re}(x)\). The vector part of x is defined by \({\underline{x}}=x_1e_1+\cdots +x_ne_n\). The conjugate of x is denoted by \({\overline{x}}=x_0-{\underline{x}}\) and the Euclidean modulus of x is given by \(|x|^2=x_0^2+\cdots +x_n^2\).
In this paper we work in a Clifford algebra setting, and in the sequel we denote by \(\mathcal {B}(V_n)\) the Banach space of all bounded right linear operators acting on a two sided Clifford Banach module \(V_n=V\otimes \mathbb {R}_n\), where V is a real Banach space.
Let \(T:V_n \rightarrow V_n\) be a bounded right linear operator. The formulation of a quaternionic quantum mechanic given by G.Birkhoff and J.Von Neumann in the paper [6] suggests the existence of an appropriate quaternionic spectrum. The notion of S-spectrum was discovered in 2006 by F.Colombo and I.Sabadini, see [15, 26].
The S-spectrum is defined in an unconventional way because the square of the linear operator T is involved, it is given by:
and the resolvent set is defined as its complementary set, namely:
The left and the right S-resolvent operators are defined as
and
respectively. The left S-resolvent operator satisfies the equation
and the right S-resolvent operator satisfies
By combining in a suitable way formulas (1.1) and (1.2) it is possible to get the so-called S-resolvent equation, see [1]:
for s, \(p \in \rho _S(T)\). The peculiarity of this equation is that both the left and the right resolvent operators are involved. Moreover it preserves the right slice hyperholomorphicity in s and the left slice hyperholomorphicity in p.
Remark 1.1
In the S-resolvent equation the product \(S_L^{-1}(p,T) S_R^{-1}(s,T)\) cannot be used, because it destroys the slice hyperholomorphicity.
We observe that in this setting the spectral mapping theorem plays a very important role, see the quaternionic case [2], the particular cases [3] and the extension to fully Clifford algebras, see [17]. For recent contributions on the S-functional calculus, see for example [16, 18].
In [22] a commutative version of the S-functional calculus is studied. To introduce this we need some preliminary notations.
In the sequel, we will consider bounded paravector operators T, with commuting components \(T_\ell \in \mathcal {B}(V)\) for \(\ell =0,1,\ldots ,n\), n odd. By \(\mathcal{B}\mathcal{C}(V_n)\) we will denote the subset of \({\mathcal {B}(V_n)}\) consisting of Clifford operators with commuting components, i.e., operators of the type \(\sum _A e_AT_A\) where \(A=\{ \ell _1\ldots \ell _r\}\in \mathcal {P}\{1,2,\ldots , n\},\ \ \ell _1<\cdots <\ell _r\) is a multi-index, \(T_{\emptyset }=T_0\), and the operators \(T_A\) commute among themselves.
Let us consider the paravector operator \(T=T_0+e_1T_1+\cdots +e_nT_n\) in \(\mathcal{B}\mathcal{C}(V_n)\), the \( \mathcal {F}\)-spectrum of T is defined as
where we have set \({\overline{T}}:=T_0-e_1T_1-\ldots -e_nT_n\), and the \(\mathcal {F}\)-resolvent set
In [23] it is showed that the \(\mathcal {F}\)-spectrum is the commutative version of the S-spectrum, i.e., we have
The definition of \( \mathcal {F}\)-spectrum comes from the shape of the commutative S-resolvent operators. Let us consider an operator \(T \in \mathcal{B}\mathcal{C}(V_n)\), the commutative version of the left S-resolvent operator is defined as
and the commutative version of the right S-resolvent operator is
For the sake of simplicity we have still denoted the commutative version of the S-resolvent operators with the same symbols as for the noncommutative ones. The operator
is called the commutative pseudo S-resolvent operator (for short, it is called pseudo resolvent operator).
In the sequel, when we mention the S-resolvent operators we intend their commutative versions.
By applying the Fueter-Sce map, namely \( \Delta ^{\frac{n-1}{2}}\) with n odd, to the slice hyperholomorphic Cauchy formulas it is possible to get a Fueter-Sce mapping theorem in integral form, see [23]. This result is crucial to define the \( \mathcal {F}\)-functional calculus, which is a monogenic functional calculus in the spirit of A.McIntosh and collaborators, see [36]. For more information about the \( \mathcal {F}\)-functional see Sect. 2 of this paper and the papers [11, 13, 21], here we are only interested to recall the definitions of \( \mathcal {F}\)-resolvent operators. Let us consider \(T \in \mathcal{B}\mathcal{C}(X)\) and \(s \in \rho _\mathcal {F}(T)\), for n being an odd number we define the left \( \mathcal {F}\)-resolvent operator as
and the right \(\mathcal {F}\)-resolvent operator as
where the constant \(\gamma _n\) is defined by
In [13] a resolvent equation for the \(\mathcal {F}\)-functional calculus in the quaternionic case (which coincides with the case \(n=3\)) was obtained, and it is given by
for \(T\in \mathcal{B}\mathcal{C}(V_3)\) and for any \(p,s\in \rho _{\mathcal {F}}(T)\), with \(s\not \in [p]\).
The \( \mathcal {F}\)-functional calculus depends crucially on the powers of the \( \Delta ^{\frac{n-1}{2}}\). This means that when we increase the dimension of the algebra we have to increase the power of the Laplacian and this generates more involved computations.
The \( \mathcal {F}\)-resolvent equation when \(n=5\) is written in terms of the S-resolvent operators and of the commutative pseudo S-resolvent operators, it is given by
for \(p, s \in \rho _{\mathcal {F}}(T)\) and where \(\gamma _5\) is given by (1.8) for \(n=5\). In [11] is showed that this equation can be still written in terms of \( \mathcal {F}\)-resolvent operators.
For the case \(n=7\) we have the following resolvent equation
Nevertheless, in this case it is too much complicated to write the equation (1.11) in terms of the \( \mathcal {F}\)-resolvent operators.
This last case shows that the general case of n-tuples of operators can be treated only in terms of S-resolvent operators and commutative pseudo S-resolvent operators. In this paper we show, with all the details, the proof of the following formula
where \(h= \frac{n-1}{2}\), n is odd, \(T \in \mathcal{B}\mathcal{C}(V_n)\) and \(p,s \in \rho _{\mathcal {F}}(T)\).
In the introduction of the paper [11] a comparison between all the properties of the resolvent equations of the holomorphic functional calculus, the S-functional calculus and the \( \mathcal {F}\)-functional calculus, is done.
Moreover, we prove that this equation is fundamental to study the Riesz projectors that are defined by
where \(\gamma _{n}\) is given in (1.8) and the sets \(G_1\) and \(G_2\) contain part of the \( \mathcal {F}\)-spectrum.
Outline of the paper: Besides of this introduction the paper consist of 4 sections. In Section 2 we recall basic results of the theories of slice hyperholomorphic and monogenic functions. Moreover, we recall also the notions of S-functional functional calculus and \(\mathcal {F}\)-functional calculus. In Section 3 we provide an expression of the \( \mathcal {F}\)-resolvent equation for any n odd. Finally in Section 4 we study the Riesz projectors for the \(\mathcal {F}\)-functional calculus by using the \(\mathcal {F}\)-resolvent equation.
2 Preliminary Material
Keeping in mind the notations about the real Clifford algebra \( \mathbb {R}_n\), given in the Introduction, we recall the main notions for the slice hyperholomorphic and monogenic functions. These two classes of functions are the ones that appear in the Fueter-Sce-Qian construction and they extend holomorphic functions to quaternionic or Clifford algebra valued-functions.
2.1 Function Theories
We start by recalling the concept of slice hyperholomorphic function. To introduce this notion we need to fix some notations. We denote by \(\mathbb {S}\) the sphere of purely imaginary vectors with modulus 1, which is defined by
We observe that if \(I \in \mathbb {S}\), then \(I^2=-1\). This means that I behaves like an imaginary unit, and we denote by
an isomorphic copy of the complex numbers. Given a non-real paravector \(x=x_0+{\underline{x}}=x_0+J_x |{\underline{x}}|\), we set \(J_x:={\underline{x}}/|{\underline{x}}|\in \mathbb {S}\), and we associate to x the sphere defined by
Definition 2.1
Let \(U \subseteq {\mathbb {R}}^{n+1}\). We say that U is axially symmetric if, for every \(u+Iv \in U\), all the elements \(u+Jv\) for \(J\in \mathbb {S}\) are contained in U.
Definition 2.2
Let \(U\subseteq \mathbb {R}^{n+1}\) be an axially symmetric open set and let \(\mathcal {U}\subseteq \mathbb {R}\times \mathbb {R}\) be such that \(x=u+J v\in U\) for all \((u,v)\in \mathcal {U}\). We say that a function \(f:U \rightarrow \mathbb {R}_n\) of the form
is left slice hyperholomorphic if \(f_0\), \(f_1\) are \(\mathbb {R}_n\)-valued differentiable functions such that
and if \(f_0\) and \(f_1\) satisfy the Cauchy-Riemann system
We recall that right slice hyperholomorphic functions are of the form
where \(f_0\), \(f_1\) satisfy the above conditions.
Remark 2.3
There are other different notions of slice hyperholomorphic functions. However, the previous definition is the most appropriate for the operator theory see [14, 15].
The set of left (resp. right) slice hyperholomorphic function on U is denoted with the symbol \({SH}_L(U)\) (resp. \({SH}_R(U)\)). The subset of intrinsic functions consist of those slice hyperholomorphic functions such that \(f_0\), \(f_1\) are real-valued and is denoted by N(U).
Now, we recall the slice hyperholomorphic Cauchy formulas, that are crucial to develop the hyperholomorphic spectral theory on the S-spectrum.
Definition 2.4
Let \(x\not \in [s]\). We define and
We say that (2.1) is the left Cauchy kernel in form I, while (2.2) is in the form II.
Analogously, we say that the right Cauchy kernel in form I, while (2.4) is in the form II.
Lemma 2.5
Let \(s\notin [x]\).
-
The left slice hyperholomorphic Cauchy kernel \(S_L^{-1}(s,x)\) is left slice hyperholomorphic in x and right slice hyperholomorphic in s.
-
The right slice hyperholomorphic Cauchy kernel \(S_R^{-1}(s,x)\) is left slice hyperholomorphic in s and right slice hyperholomorphic in x.
Theorem 2.6
(The Cauchy formulas for slice monogenic functions) Let \(U\subset \mathbb {R}^{n+1}\) be a bounded slice Cauchy domain, let \(J\in \mathbb {S}\) and set \(ds_J=ds (-J)\). If f is a (left) slice monogenic function on a set that contains \({\overline{U}}\) then
If f is a right slice hyperholomorphic function on a set that contains \({\overline{U}}\), then
These integrals depend neither on U nor on the imaginary unit \(J\in \mathbb {S}\).
Now, we recall the definition of monogenic functions
Definition 2.7
Let U be an open set in \(\mathbb {R}^{n+1}\). A real differentiable function \(f: U\rightarrow \mathbb {R}_n\) is left monogenic if
It is right monogenic if
Also for this class of functions it is possible to have a Cauchy formula, that is the heart of the functional calculus developed by A. McIntosh and collaborators see [36].
A bridge between the theory of slice hyperholomorphic and monogenic functions is the Fueter-Sce theorem. This was proved by R. Fueter in 1934, see [32] for quaternions. More than 20 years later M. Sce, see [39], extended this result to Clifford algebras in a very general way; see [27] for an English translation of Sce works in hypercomplex analysis.
In the original paper of R. Fueter, [32], holomorphic functions are defined on open sets of the complex upper half plane. However, this condition can be relaxed if one consider functions of the following type
defined in a set \(D\subseteq {\mathbb {C}}\), symmetric with respect to the real axis such that the functions \(g_0\) and \(g_1\) satisfy the so-called even-odd conditions, namely
Furthermore \(g_0\) and \(g_1\) satisfy the Cauchy-Riemann system. The same conditions are required by Sce for higher dimensions.
Theorem 2.8
(Sce [39]) Consider the Euclidean space \(\mathbb {R}^{n+1}\), n odd, whose elements are identified with paravectors \(x=x_0+{\underline{x}}\). Let \({\tilde{f}}(z) = f_0(u,v)+if_1(u,v)\) be a holomorphic function defined in a domain (open and connected) D in the upper-half complex plane and let
be the open set induced by D in \(\mathbb {R}^{n+1}\). The map
takes the holomorphic functions \({\tilde{f}}(z)\) and gives the Clifford-valued function f(x). Then the function
where \(T_{FS2}:=\Delta _{n+1}^{\frac{n-1}{2}}\) and \(\Delta _{n+1}\) is the Laplacian in \(n+1\) dimensions, is a monogenic function.
We observe that the operator \(T_{FS2}\) is a differential operator when n is odd. On the other side when n is even the operator \(T_{FS2}\) is a fractional operator, and it is possible to define \(T_{FS2}\) by means of the Fourier multipliers, as Tao Qian did in in [37].
Moreover, we note that a different method to connect slice hyperholomorphic and monogenic functions is the Radon and dual Radon transform, see [19].
In [23] the Fueter-Sce theorem is written in integral form. The main advantage of this approach is that one can obtain a monogenic function by integrating suitable slice hyperholomorphic functions. We recall what happens when we apply the Fueter-Sce map \( T_{FS2}= \Delta ^{\frac{n-1}{2}}_{n+1}\) to the slice hyperholomorphic Cauchy kernels written in the second form.
Theorem 2.9
Let n be an odd number and let x, \(s\in \mathbb {R}^{n+1}\). For \(s\not \in [x]\), we have
and
where the constants \(\gamma _n\) are defined in (1.8).
Remark 2.10
The previous result has been generalized for all the dimensions in [12].
Proposition 2.11
Let n be an odd number and let x, \(s\in \mathbb {R}^{n+1}\) be such that \(x\not \in [s]\). Let \(S_L^{-1}(s,x)\) and \(S_R^{-1}(s,x)\) be the slice hyperholomorphic Cauchy kernels in form II. Then:
-
The function \(\Delta ^{\frac{n-1}{2}}S_L^{-1}(s,x)\) is a left monogenic function in the variable x and right slice hyperholomorphic in s.
-
The function \(\Delta ^{\frac{n-1}{2}}S_R^{-1}(s,x)\) is a right monogenic function in the variable x and left slice hyperholomorphic in s.
Definition 2.12
(The \(\mathcal {F}\)-kernels) Let n be an odd number and let x, \(s\in \mathbb {R}^{n+1}\). We define, for \(s\not \in [x]\), the \(\mathcal {F}_n^L\)-kernel as
and the \(\mathcal {F}_n^R\)-kernel as
where the constant \(\gamma _n\) are defined in (1.8).
Theorem 2.13
(The Fueter-Sce mapping theorem in integral form) Let \(U\subset \mathbb {R}^{n+1}\) be a bounded slice Cauchy domain, let \(J\in \mathbb {S}\) and set \(ds_J=ds (-J)\).
-
(a)
If f is a (left) slice monogenic function on a set that contains \({\overline{U}}\), then the left monogenic function \(\breve{f}(x)=\Delta ^{\frac{n-1}{2}}f(x)\) admits the integral representation
$$\begin{aligned} \breve{f}(x)=\frac{1}{2 \pi }\int _{\partial (U\cap \mathbb {C}_J)} \mathcal {F}_n^L(s,x)ds_J f(s). \end{aligned}$$(2.7) -
(b)
If f is a right slice monogenic function on a set that contains \({\overline{U}}\), then the right monogenic function \(\breve{f}(x)=\Delta ^{\frac{n-1}{2}}f(x)\) admits the integral representation
$$\begin{aligned} \breve{f}(x)=\frac{1}{2 \pi }\int _{\partial (U\cap \mathbb {C}_J)} f(s)ds_J \mathcal {F}_n^R(s,x). \end{aligned}$$(2.8)
The integrals depend neither on U and nor on the imaginary unit \(J\in \mathbb {S}\).
2.2 Functional Calculi on the S-Spectrum
In the sequel, we will consider bounded paravector operators \(T=e_1T_1+\cdots +e_nT_n\), with commuting components \(T_\ell \) acting on a real vector space V, i.e. \(T_\ell \in \mathcal {B}(V)\) for \(\ell =0,1,\ldots ,n\). The set of bounded paravector operators is denoted by \(\mathcal{B}\mathcal{C}^{0,1}(V_n)\) where \(V_n=V\otimes \mathbb {R}_n\). The subset of \({\mathcal {B}(V_n)}\) given by the operators T with commuting components \(T_\ell \) will be denoted by \(\mathcal{B}\mathcal{C}(V_n)\).
Let \(T\in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). We denote by \(\mathcal{S}\mathcal{M}_L(\sigma _{S}(T))\), \(\mathcal{S}\mathcal{M}_R(\sigma _{S}(T))\) the set of all left (or right) slice hyperholomorphic functions f with \(\sigma _{S}(T)\subset {\text {dom}}(f)\). We now recall the following definition:
Definition 2.14
(The S-functional calculus for n-tuples of operators) Let \(V_n\) be a two sided Banach module and \(T\in \mathcal {B}^{0,1}(V_n)\). Let \(U\subset \mathbb {R}^{n+1}\) be a bounded slice Cauchy domain that contains \(\sigma _{S}(T)\) and set \(ds_J=- ds J\). We define
and
The definition of the S-functional calculus is well posed since the integrals in (2.9) and (2.10) depend neither on U and nor on the imaginary unit \(J\in \mathbb {S}\).
Remark 2.15
The S-functional calculus has been generalized for fully Clifford operators with non commuting components in [18].
The \(\mathcal {F}\)-functional calculus is based on the Fueter-Sce theorem in integral form. Since this result is obtained by means of the second form of the slice hyperholomorphic Cauchy kernels the \(\mathcal {F}\)-functional calculus is limited to paravector operators with commuting components. Moreover, it is based on the commutative version of the S-spectrum, the so-called \(\mathcal {F}\)-spectrum.
Definition 2.16
(The \(\mathcal {F}\)-functional calculus for bounded operators) Let n be an odd number, let \(T= e_1T_1 + \cdots + e_n T_n\in \mathcal{B}\mathcal{C}(V_n)\), assume that the operators \(T_{\ell }\), \(\ell =1,..,n\) have real spectrum and set \(ds_J=ds/J\). For any function \(f\in \mathcal{S}\mathcal{M}_L(\sigma _S(T))\), we define
For any \(f\in \mathcal{S}\mathcal{M}_R(\sigma _S(T))\), we define
where \(J\in \mathbb {S}\) and U is a slice Cauchy domain U.
The definition of the \(\mathcal {F}\)-functional calculus is well posed since the integrals in (2.11) and (2.12) depend neither on U and nor on the imaginary unit \(J\in \mathbb {S}\).
We can write the left \(\mathcal {F}\)-resolvent operator in terms of the pseudo S-resolvent operators as follows.
Definition 2.17
(\(\mathcal {F}\)-resolvent operators) Let n be an odd number. Let us consider \(T=T_0+ T_1e_1 + \cdots + T_n e_n \in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). For \(s \in \rho _\mathcal {F}(T)\), we define the left \( \mathcal {F}\)- resolvent operator as
and the right \( \mathcal {F}\)-resolvent operator as
where \(\gamma _n\) are defined in (1.8).
For these operators hold the following relations, proved in [13, Thm. 5.1]
Theorem 2.18
(The left and right \(\mathcal {F}\)-resolvent equations) Let n be an odd number and let \(T \in \mathcal {B}^{0,1}(V_n)\). Let \(s \in \rho _{\mathcal {F}}(T)\). Then the \( \mathcal {F}\)-resolvent operators satisfy the equations
and
where the constants \(\gamma _n\) are given by (1.8).
In [11] a series expansions of the \( \mathcal {F}\)-resolvent operators is proved in terms of T and \( {\bar{T}}\). To state this result we need to introduce the following notation
Theorem 2.19
Let \(s \in \mathbb {R}^{n+1}\). For \(\Vert T\Vert < |s|\), we have
and
where \(\gamma _n\) are as in (1.8).
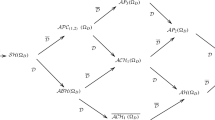
The following diagram sums up all the constructions exposed

Remark 2.20
Observe that in the above diagram the arrow from the space of axially monogenic function AM(U) is missing because the \(\mathcal {F}\)-functional calculus is deduced from the slice hyperholomorphic Cauchy formula.
3 The \(\mathcal {F}\)-Resolvent Equation for n Odd
Inspired from the \( \mathcal {F}\)-resolvent equations in the cases \(n=3\),5,7 studied in [11], we get a general \( \mathcal {F}\)-resolvent equation for any n odd. From the case \(n=7\), see (1.11), it is clear that writing the \( \mathcal {F}\)-resolvent equation only in terms of \( \mathcal {F}\)-resolvent operators is too much complicated. For generic n odd we write the \( \mathcal {F}\)-resolvent equation in terms of S-resolvent operators and pseudo S-resolvent operators. We start by showing a technical result.
Lemma 3.1
(The general structure of the \(\mathcal {F}\)-resolvent equation with the pseudo S-resolvent operators) Let \(n>3\) be an odd number, and let \( h= \frac{n-1}{2}\) be the Sce exponent. Let us consider \(T \in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). Then for \(p,s \in \rho _{\mathcal {F}}(T)\) the following equation holds
Proof
We left multiply the S-resolvent equation (1.3) by \( \gamma _n \mathcal {Q}_s^{h}(T)\)
and we right multiply it by \( \gamma _n \mathcal {Q}_p^h(T)\), so we get
We now multiply S-resolvent equation on the left and on the right by \( \mathcal {Q}_s^{h-1-i}(T)\) and \( \mathcal {Q}_p^{i+1}(T)\), respectively. Then, we sum on the index \(0 \le i \le h-2\) and we obtain
Now we sum (3.2), (3.3) and (3.4) multiplied by \( \gamma _n\), and we get
Putting in order the terms in the right hand side of the previous equation we get
Now, using the definition of left and right S-resolvent operators we get
Then we compute
Hence
Finally, by substituting (3.8) in (3.6) we get (3.1).
Remark 3.2
The proof of the previous lemma shows that the structure of the resolvent equations of the hyperholomorphic functional calculi is crucial. In fact the term
involves the difference of the \(\mathcal {F}\)-resolvent operators entangled with the Cauchy kernel of slice monogenic functions. This term is equal to a function involving the products of the F-resolvent operators and of the S-resolvent operators that appear in the term
and of a more complicated part that involves the S-resolvent operators and the pseudo S-resolvent operators, namely
Remark 3.3
If in equation (3.1) we consider \(n=5\), then \(h=2\), and \(n=7\), then \(h=3\), we get the equation (1.10) and (1.11).
In order to find a pseudo \( \mathcal {F}\)-resolvent equation we divide into two cases according to the parity of the Sce exponent \(h= \dfrac{n-1}{2}\). To state the following result we introduce this notations
and
3.1 The General Structure of the Pseudo \(\mathcal {F}\)-Resolvent Equation for h Odd
The main result of this subsection is the following theorem.
Theorem 3.4
(The general structure of the pseudo \(\mathcal {F}\)-resolvent equation for h odd number) Let \(n>3\) be an odd number as well as h. Let \(T \in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). Then for \(p,s \in \rho _{\mathcal {F}}(T)\) the following equation holds
where the three terms \(\mathcal {A}_0(s,p,T)\), \(\mathcal {B}_0(s,p,T)\) and \(\mathcal {C}_0(s,p,T)\) are defined above.
Proof
We start by rewriting formula (3.1) as
Now, we focus on the term \(\mathcal {Q}_s^{\frac{h+1}{2}}(T) \mathcal {Q}_p^{\frac{h+1}{2}}(T)\) and with some manipulations we obtain
By the binomial formula we get
Now, we use the left and right \( \mathcal {F}\)-resolvent equations, (see Theorem 2.18)
and
We go through the computations term by term
Then we consider
Then we compute the term
We have also
Finally by using the definition of left and right S-resolvent operators we get
and this concludes the proof. \(\square \)
3.2 The General Structure of the Pseudo \(\mathcal {F}\)-Resolvent Equation for h Even Number
In this last subsection we consider the case in which \(h=(n-1)/2\) is an even number. To state the following result we need these notations
and
and
Theorem 3.5
(The general structure of the pseudo \(\mathcal {F}\)-resolvent equation for h even number) Let \(n>3\) be an odd number and h be even. Let \(T \in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). Then for \(p,s \in \rho _{\mathcal {F}}(T)\) the following equation holds
where the three terms \(\mathcal {A}_1(s,p,T)\), \(\mathcal {B}_1(s,p,T)\) and \(\mathcal {C}_1(s,p,T)\) are defined above.
Proof
Let us begin by writing formula (3.1) as
Now, we focus on the \(\mathcal {Q}_s^{\frac{h}{2}}(T) S^{-1}_R(s,T)S^{-1}_L(p,T) \mathcal {Q}_p^{\frac{h}{2}}(T)\). By definition of left and right S-resolvent operators we get
We continue the calculations only on the term \(s\mathcal {Q}_s^{\frac{h+2}{2}}(T)\mathcal {Q}_p^{\frac{h+2}{2}}(T)p\). By the binomial formula we get
Now, we use the left and right \( \mathcal {F}\)-resolvent equations in Theorem 2.18 and we go through the computations term by term
and
then we consider the term
and the other term
Finally by using the definition of left and right S-resolvent operators we obtain
and this concludes the proof. \(\square \)
4 The Riesz Projectors for the \(\mathcal {F}\)-Functional Calculus: The General Case of n Odd
In the monogenic functional calculus developed by McIntosh and collaborators, [36], the resolvent equation is missing. They are able to study the Riesz projectors by using another functional calculus: the Weyl calculus. For the \( \mathcal {F}\)-functional calculus, which is a monogenic functional calculus, the interesting symmetries that appear in the equations of Theorem 3.4 and Theorem 3.5 allow to study the Riesz projectors.
Next result follows as in the case \(n=5\), see [11, Lemma 5.4].
Lemma 4.1
Let \( T \in \mathcal{B}\mathcal{C}(V_n)\) and \( h= \frac{n-1}{2}\). Suppose that G contains just some points of the \( \mathcal {F}\)-spectrum of T and assume that the closed smooth curve \( \partial (G \cap \mathbb {C}_I)\) belongs to the \( \mathcal {F}\)-resolvent set of T, for every \(I \in \mathbb {S}\). Then
for all \(m \le 2h-1\).
In order to study the Riesz Projectors for the \(\mathcal {F}\)-functional calculus we now state the following results.
Lemma 4.2
Let f and g be left slice monogenic and right slice monogenic functions, respectively, defined on an open set U. For any \(I \in \mathbb {S}\) and any open bounded set \(D_I\) in \(U \cap \mathbb {C}_I\) whose boundary is a finite union of continuously differentiable Jordan curves, we have
Lemma 4.3
Let \(B \in \mathcal {B}(V_n)\). Let G be a bounded slice Cauchy domain and let f be an intrinsic slice monogenic function whose domain contains G. Then for \(p \in G\), and for any \(I\in {\mathbb {S}}\) we have
Theorem 4.4
Let \(n>3\) be an odd number and let \( T=\sum _{i=1}^{n} e_i T_i \in \mathcal{B}\mathcal{C}^{0,1}(V_n)\). Let \( \sigma _{\mathcal {F}}(T)= \sigma _{\mathcal {F},1}(T) \cup \sigma _{\mathcal {F},2}(T)\) with
and
Let \(G_1\), \(G_2\) be two admissible sets for T such that \( \sigma _{\mathcal {F},1}(T) \subset G_1\) and \( {\bar{G}}_1 \subset G_2\) and such that \(dist \left( G_2, \sigma _{\mathcal {F},2}(T) \right) >0\). Then the operator
is a projector.
Proof
We divide the proof in two cases, according to the parity of \(h= \frac{n-1}{2}\).
CASE I: The Sce exponent h is odd.
We start by multiplying the equation of Theorem 3.4 by \(s^h\) on the left and \(p^h\) on the right, and since \(T_0=0\) we get
Now, we multiply equation (4.2) by \(ds_I\) on the left, integrate it over \( \partial (G_2 \cap \mathbb {C}_I)\) with respect to \(ds_I\) and then we multiply it by \( dp_I\) on the right and integrate over \( \partial (G_1 \cap \mathbb {C}_I)\) with respect to \(dp_I\). We obtain
Recalling the definition of \( \mathcal {A}_0\), \(\mathcal {B}_0\), \(\mathcal {C}_0\) and the fact that \(T_0=0\) we have
Now, since \(h \le 2h-1\) by Lemma 4.1 we get
Moreover, since \(2h-2k \le 2h-1\) and \(2h-1-2k \le 2h-1\) we obtain
Now, we focus on the term
First of all we split the sum in two parts and write
where \( \lfloor . \rfloor \) is the floor of a number. In the first sum the powers of \( \mathcal {Q}_s(T)\) are more than the powers of \( \mathcal {Q}_p(T)\), and conversely in the second sum.
Since \(T_0=0\), by the binomial formula we get
Consider the first sum. By the \( \mathcal {F}\)- resolvent equation, see (2.16) we get
Hence we have to compute the following integrals
Now, since h is odd then we can write \(h=2N+1\), with \(N \in \mathbb {N}\). This implies that
Similarly we get
Therefore by Lemma 4.1 we get
Now, we focus on the second sum. By the \( \mathcal {F}\)- resolvent equation, see (2.15), we get
Hence we have to compute the following integrals
Since \(h=2N+1\), with \(N \in \mathbb {N}\) we get
and similarly
together with Lemma 4.1 we get
Similar arguments applied to the other members of (4.3) lead to
Since \(h= \frac{n-1}{2}\), by formula (4.1) we get
Now, we work on the integral on the right hand side. As \( {\bar{G}}_1 \subset G_2\), for any \(s \in \partial (G_2 \cap \mathbb {C}_I)\) the functions
are slice monogenic on \( \bar{G_1}\). By Lemma 4.2 we have
This implies that
and
Then we have
From Lemma 4.3 with \(B=:\mathcal {F}_n^L(p,T)\) and \(f(s):=s^h\) we get
CASE II: The Sce exponent h is even.
We multiply the equation of Theorem 3.5 by \(s^h\) left and \(p^h\) on the right, and since \(T_0=0\) we get
Now, we multiply by \(ds_I\) on the left, integrate it over \( \partial (G_2 \cap \mathbb {C}_I)\) with respect to \(ds_I\) and then we multiply it by \( dp_I\) on the right and integrate over \( \partial (G_1 \cap \mathbb {C}_I)\) with respect to \(dp_I\), and we obtain
From the definition of \( \mathcal {A}_1\), \( \mathcal {B}_1\), \(\mathcal {C}_1\) and recalling that \(T_0=0\) we have
Now we observe that since \(h \le 2h-1\) by Lemma 4.1 we have
Moreover, since \(2h-2k \le 2h-1\) and \(2h-1-2k \le 2h-1\) we get
Now, we focus on computing the integral
By the binomial formula and recalling that \(T_0=0\) we get
By the \( \mathcal {F}\)-resolvent, see (2.15), we deduce that
We observe that
similarly we have \(h+2k \le 2h-1\), so formula (4.13) together with Lemma 4.1 imply that
Using similar arguments, we obtain
By similar computations made when h is odd we get
By formula (4.1) we get
Finally, by following exactly the same steps done when h is odd we get
\(\square \)
Data Availability
There are no data involved in the research in this manuscript.
References
Alpay, D., Colombo, F., Gantner, J., Sabadini, I.: A new resolvent equation for the S-functional calculus. J. Geom. Anal. 25(3), 1939–1968 (2015)
Alpay, D., Colombo, F., Kimsey, D.P.: The spectral theorem for quaternionic unbounded normal operators based on the \(S\)-spectrum. J. Math. Phys. 57(2), 023503, 27 (2016)
Alpay, D., Colombo, F., Kimsey, D.P., Sabadini, I.: The spectral theorem for unitary operators based on the S-spectrum. Milan J. Math. 84(1), 41–61 (2016)
Alpay, D., Colombo, F., Sabadini, I.: Slice Hyperholomorphic Schur Analysis, Operator Theory: Advances and Applications, 256. Birkhäuser/Springer, Cham, . xii+362 pp (2016)
Alpay, D., Colombo, F., Sabadini, I.: Quaternionic de Branges spaces and characteristic operator function, Springer Briefs in Mathematics, Springer, Cham (2020/21)
Birkhoff, G., Von Neumann, J.: The logic of quantum mechanics. Ann. Math. 37, 823–843 (1936)
Brackx, F., Delanghe, R., Sommen, F.: Clifford analysis, Research Notes in Mathematics, 76. Pitman (Advanced Publishing Program), Boston, MA, x+308 pp (1982)
Cerejeiras, P., Colombo, F., Kähler, U., Sabadini, I.: Perturbation of normal quaternionic operators. Trans. Am. Math. Soc. 372(5), 3257–3281 (2019)
Colombo, F., Deniz-Gonzales, D., Pinton, S.: Fractional powers of vector operators with first order boundary conditions. J. Geom. Phys., 151, 103618, 18 pp (2020)
Colombo, F., Deniz-Gonzales, D., Pinton, S.: Non commutative fractional Fourier law in bounded and unbounded domains. Complex Anal. Oper. Theory (2021)
Colombo, F., De Martino, A., Sabadini, I.: Towards a general \(\cal{F} \)-resolvent equation and Riesz projectors. J. Math. Anal. Appl. 517(2), 126652 (2023)
Colombo, F., De Martino, A., Qian, T., Sabadini, I.: The Poisson kernel and the Fourier transform of the slice monogenic Cauchy kernels. J. Math. Anal. Appl. 512(1), 126115 (2022)
Colombo, F., Gantner, J.: Formulations of the \( \cal{F}\)- functional calculus and some consequences. Proc. R. Soc. Edinb. 146 A, 509–545 (2016)
Colombo, F., Gantner, J.: Quaternionic Closed Operators, Fractional Powers and Fractional Diffusion Processes, Operator Theory: Advances and Applications, 274. Birkhäuser/Springer, Cham, viii+322 pp (2019)
Colombo, F., Gantner, J., Kimsey, D.P.: Spectral Theory on the S-Spectrum for Quaternionic Operators, Operator Theory: Advances and Applications, 270. Birkhäuser/Springer, Cham, ix+356 pp (2018)
Colombo, F., Gantner, J., Kimsey, D.P., Sabadini, I.: Universality property of the \(S\)-functional calculus, noncommuting matrix variables and Clifford operators. Preprint (2020)
Colombo, F., Kimsey, D.P.: The spectral theorem for normal operators on a Clifford module. Preprint (2020)
Colombo, F., Kimsey, D.P., Pinton, S., Sabadini, I.: Slice monogenic functions of a Clifford variable. Proc. Am. Math. Soc. Ser. B 8, 281–296 (2021)
Colombo, F., Lavicka, R., Sabadini, I., Soucek, V.: The Radon transform between monogenic and generalized slice monogenic functions. Math. Ann. 363(3–4), 733–752 (2015)
Colombo, F., Peloso, M., Pinton, S.: The structure of the fractional powers of the noncommutative Fourier law. Math. Methods Appl. Sci. 42, 6259–6276 (2019)
Colombo, F., Sabadini, I.: The F-functional calculus for unbounded operators. J. Geom. Phys. 86, 392–407 (2014)
Colombo, F., Sabadini, I.: The F-spectrum and the SC-functional calculus. Proc. R. Soc. Edinb. Sect. A 142(3), 479–500 (2012)
Colombo, F., Sabadini, I., Sommen, F.: The Fueter mapping theorem in integral form and the F-functional calculus. Math. Methods Appl. Sci. 33, 2050–2066 (2010)
Colombo, F., Sabadini, I., Sommen, F., Struppa, D.C.: Analysis of Dirac systems and computational algebra, Progress in Mathematical Physics, 39. Birkhäuser Boston, Inc., Boston, MA, xiv+332 pp (2004)
Colombo, F., Sabadini, I., Struppa, D.C.: Entire slice regular functions, Springer Briefs in Mathematics. Springer, Cham, v+118 pp (2016)
Colombo, F., Sabadini, I., Struppa, D.C.: Noncommutative Functional Calculus. Theory and Applications of Slice Hyperholomorphic Functions, Progress in Mathematics, 289. Birkhäuser/Springer Basel AG, Basel (2011)
Colombo, F., Sabadini, I., Struppa, D.C.: Michele Sce’s works in hypercomplex analysis, p. 122. Birkhäuser/Springer, Cham, A translation with commentaries (2020)
Delanghe, R., Sommen, F., Soucek, V.: Clifford algebra and spinor-valued functions. A function theory for the Dirac operator, Related REDUCE software by F. Brackx and D. Constales. With 1 IBM-PC floppy disk (3.5 inch). Mathematics and its Applications, 53. Kluwer Academic Publishers Group, Dordrecht (1992)
De Martino, A.: On the Clifford short-time Fourier transform and its properties. Appl. Math. Comput. 418, 126812 (2022)
De Martino, A., Diki, K.: On the quaternionic short-time Fourier and Segal–Bargmann transforms. Mediterr. J. Math. 18(3) (2021)
De Martino, A., Diki, K.: On the polyanalytic short-time Fourier transform in the quaternionic setting. Commun. Pure Appl. Anal 21(11), 3629–3665 (2022)
Fueter, R.: Die Funktionentheorie der Differentialgleichungen \(\Delta u=0\) und \(\Delta \Delta u=0\) mit vier reellen Variablen. Comment. Math. Helv., 7, 307–330 (1934-35)
Gal, S., Sabadini, I.: Quaternionic approximation. With application to slice regular functions, Frontiers in Mathematics. Birkhäuser/Springer, Cham, x+221 pp (2019)
Gentili, G., Stoppato, C., Struppa, D.C.: Regular functions of a quaternionic variable, Springer Monographs in Mathematics. Springer, Heidelberg, x+185 pp (2013)
Gürlebeck, K., Habetha, K., Sprößig, W.: Application of holomorphic functions in two and higher dimensions, Birkhääuser/Springer, [Cham], xv+390 pp (2016)
Jefferies, B.: Spectral properties of noncommuting operators. Lecture Notes in Mathematics, vol. 1843. Springer-Verlag, Berlin (2004)
Qian, T.: Generalization of Fueter’s result to \(R^{n+1}\). Rend. Mat. Acc. Lincei 9, 111–117 (1997)
Qian, T., Li, P.: Singular integrals and Fourier theory on Lipschitz boundaries, Science Press Beijing, Beijing; Springer, Singapore, xv+306 pp (2019)
Sce, M.: Osservazioni sulle serie di potenze nei moduli quadratici. Atti Accad. Naz. Lincei. Rend. Cl. Sci. Fis. Mat. Nat. (8) 23, 220–225 (1957)
Acknowledgements
The first author is partially supported by the PRIN project Direct and inverse problems for partial differential equations: theoretical aspects and applications.
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement. None.
Author information
Authors and Affiliations
Contributions
The authors declare that their contributions in the research results and in the writing is equally shared.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Daniel Alpay.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Higher Dimensional Geometric Function Theory and Hypercomplex Analysis” edited by Irene Sabadini, Michael Shapiro and Daniele Struppa
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Colombo, F., De Martino, A. & Sabadini, I. The \(\mathcal {F}\)-Resolvent Equation and Riesz Projectors for the \(\mathcal {F}\)-Functional Calculus. Complex Anal. Oper. Theory 17, 26 (2023). https://doi.org/10.1007/s11785-022-01323-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11785-022-01323-7
Keywords
- Spectral theory on the S-spectrum
- \(\mathcal {F}\)-Resolvent operators
- \(\mathcal {F}\)-Resolvent equation
- Riesz projectors for the \(\mathcal {F}\)-functional calculus