Mathematical Modeling and Experimental Validation of the Warm Spray (Two-Stage HVOF) Process

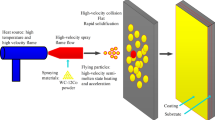
The warm spray (WS) gun was developed to make an oxidation-free coating of temperature-sensitive material, such as titanium and copper, on a substrate. The gun has a combustion chamber followed by a mixing chamber, in which the combustion gas is mixed with the nitrogen gas at room temperature. The temperature of the mixed gas can be controlled in the range of about 1000-2500 K by adjusting the mass flow rate of nitrogen gas. The gas in the mixing chamber is accelerated to supersonic speed through a converging-diverging nozzle followed by a straight barrel. This paper shows how to construct the mathematical model of the gas flow and particle velocity/temperature of the WS process. The model consists of four parts: (a) thermodynamic and gas-dynamic calculations of combustion and mixing chambers, (b) quasi-one-dimensional calculation of the internal gas flow of the gun, (c) semiempirical calculation of the jet flow from the gun exit, and (d) calculation of particle velocity and temperature traveling in the gas flow. The validity of the mathematical model is confirmed by the experimental results of the aluminum particle sprayed by the WS gun.

Introduction

In the history of the recently developed thermal spray processes from the 1980s, the larger kinetic energy of the process gas, that is the supersonic thermal spray process, rather than the larger thermal energy, has been used to accelerate the spray particle. This is because the higher gas velocity is advantageous in obtaining the higher particle velocity, resulting in higher bond strength and denser coating. In order to obtain the supersonic gas flow, the stagnation pressure of twice the atmospheric pressure or above is necessary. The stagnation temperature, on the other hand, does not work to accelerate the stagnant gas to the supersonic speed. Therefore, a wide range of gas temperature from room temperature to over several thousand K can be employed in the supersonic thermal spray processes.

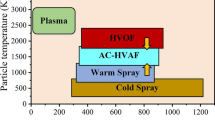
Figure 1 summarizes the comparison of the gas temperature and the particle velocity in supersonic thermal spray processes operated in the atmosphere. The vertical axis of the figure shows the temperature of the gas in which the spray particle travels in the spray gun, and the horizontal axis shows the particle velocity in the thermal spray gun. The high-velocity oxyfuel (HVOF) thermal spray gun (Ref 1) was developed in the 1980s to provide a wear-resistant coating of WC powder. In the HVOF process, the liquid or gaseous fuel is combusted by oxygen to generate the combustion (process) gas. The HVOF process can suppress the thermal degradation of the spray particle because of its much lower gas temperature compared to the plasma spray process. However, the gas temperature of the HVOF gun is still too high in some applications to obtain satisfactory coating properties. The high-velocity air-fuel (HVAF) thermal spray process (Ref 2, 3) uses air instead of oxygen to burn the fuel, causing the gas temperature to be around 1000 K lower than the HVOF process. In the HVOF and HVAF processes, the gas temperature can be controlled in a narrow range of around 300 K by changing the equivalence ratio in the combustion chamber. The latest thermal spray process, cold spray (Ref 4), developed in the 1990s, employs an electrically heated inert gas as a process gas. Recently, researchers have been trying to elevate the gas temperature in the cold spray process above the conventional upper limit of 1000 K to obtain a higher mechanical strength of the coatings (Ref 5) or to successfully spray cermet powder (Ref 6). The gap of the gas temperature between the HVOF and the cold spray was covered by the warm spray (WS) process recently developed by the authors (Ref 7-10).

Fig. 1

Comparison of gas temperature and particle velocity for supersonic thermal spray processes

The WS process can adjust the gas temperature in the range of around 1000-2500 K at an optimum value varying with the powder material, while keeping the particle velocity comparable to the HVOF process. The WS gun is a modified Praxair-Tafa JP-5000 (Ref 11), which is used to control the gas temperature. Schematic diagrams of the conventional HVOF gun and the WS gun are shown in Fig. 2. The WS gun has a combustion chamber (CC) followed by a mixing chamber (MC), in which the combustion gas is mixed with the nitrogen gas at room temperature. Therefore, the gun is also called two-stage HVOF thermal spray gun because of its configuration. The stagnation temperature in the MC can be controlled by adjusting the mass flow rate of the nitrogen gas supplied to the MC. The combustion gas mixed with the nitrogen gas is accelerated to supersonic speed through a converging-diverging (C-D) nozzle; then, the gas is discharged into the atmosphere at a supersonic speed after passing through a barrel. The solid particles are injected into the supersonic flow in the upstream part of the barrel. Then, the particles are accelerated and heated by the supersonic flow in the downstream direction, and after traveling in the jet flow, the particles impact against the substrate to form a coating. The idea of mixing the nitrogen gas with the combustion gas is not new; Browning has this type of U.S. patent (Ref 12) regarding the HVOF thermal spray gun. However, the relationship between the mass flow rate of the nitrogen gas and the performance of such a gun has not been studied in open literature.

Fig. 2

Schematic diagram of (a) HVOF gun and (b) WS gun

It is well known that the coating quality heavily depends on the impact velocity and temperature of the spray particle on the substrate. Numerical calculation of the particle conditions at the substrate is quite helpful and cost effective in the estimation of the effects of many spray parameters on the particle velocity and temperature. In order to calculate the particle velocity and temperature of the WS gun accurately, the precise prediction of the gas condition in CC, MC, barrel, and jet flow is necessary. The purpose of this paper is to construct a mathematical model of the WS gun in order to well understand the relationship between a wide variety of spray parameters and the particle temperature and velocity. The model consists of four parts: (a) thermodynamic and gas-dynamic calculations of CC and MC, (b) quasi-one-dimensional calculation of the internal gas flow of the gun, (c) semiempirical calculation of the jet flow from the gun exit, and (d) calculation of particle velocity and temperature traveling in the gas flow. In addition to constructing the mathematical model, two types of experiments were carried out in this study; the first one is to adjust or determine free parameters used in the mathematical model, and the second one is to validate the model of the WS gun.

Mathematical Model

Since the WS gun is water cooled, the cooling rate of the CC largely affects the gas temperature and pressure in the CC. This is also true for the MC and barrel. However, it is difficult to experimentally measure the cooling rate of these three parts separately. This section mainly explains the mathematical model of the cooling rate of the CC, MC, and barrel. At the same time, how to calculate the stagnation condition of the gas in the MC is described. In addition to that, the method of how to calculate the supersonic gas flow in the nozzle, barrel, and jet flow, as well as the particle behavior traveling in the gas flow, are also summarized briefly.

Combustion and Mixing Chambers

A schematic diagram of the CC followed by the MC is shown in Fig. 3. The following assumptions are used to simplify the mathematical model of the CC and MC:

Fig. 3

Analytical model of the combustion and mixing chambers

• The gas in the CC consists of eight gas species: CO, CO₂, H₂O, H₂, H, OH, O₂, and O (Ref 13).

• Each gas species follows the equation of state of the ideal gas.

• The gases in CC and MC are stagnant and are in the chemical equilibrium condition (Ref 13).

• The static pressures at the exit of the nozzles of the CC and that of the N₂ injection chamber are equal to the stagnation pressure in the MC.

• The combustion gas mixes with the nitrogen gas uniformly at the moment of entering the MC.

Under the normal operating conditions of the WS gun investigated in this paper, it was found by the present calculation that the combustion gas and nitrogen gas enter the MC at subsonic speed smaller than Mach number of 0.54 and 0.24, respectively.

Cooling Rate of Combustion Chamber

The WS gun has the same CC as the JP-5000. It means that the cooling rate of the CC in the WS gun can be estimated by the experiment of JP-5000. The following equation, a modified equation of the mass flow rate of gas-dynamic theory, is used to determine the cooling rate of the CC from the experimental data of the pressure in the CC and the mass flow rate of the combustion gas of the HVOF gun, which is choked at the throat of the C-D nozzle.

$$ \frac{{p_{01} A_{{1{\text{t}}}} }}{{\dot{m}_{1} }} = \frac{{\sqrt {R_{1} T_{{{\text{g}}01}} } }}{{\sqrt {\upgamma_{1} [2/(\upgamma_{1} + 1)]^{{(\upgamma_{1} + 1)/(\upgamma_{1} - 1)}} } }}\quad\left( {\text{HVOF gun}} \right) $$

(1)

where $\dot{m}$ shows the mass flow rate of the gas, T is the gas temperature, γ is the specific heat ratio, R is the gas constant, and A is the cross-sectional area, respectively. The subscripts 0, 1, g, and t in Eq 1 show the stagnant condition, CC, gas, and nozzle throat, respectively. The mass flow rate of combustion gas $\dot{m}_{1}$ is the summation of the mass flow rates of kerosene and oxygen. The gas properties in the CC, T _g01, R ₁, and γ₁, in the right side of Eq 1 are calculated by a software called chemical equilibrium with applications (CEA) (Ref 14) for the given enthalpy of reaction and pressure. In this paper, the enthalpy of reaction is related to the cooling rate of CC, σ_ce1, which is defined as;

$$ \upsigma_{{{\text{ce}}1}} = \frac{{q_{{{\text{ce}}1}} \dot{m}_{1} }}{{H_{\text{l}} \dot{m}_{\text{f}} }} $$

(2)

where q _ce1 is the quantity of heat removed from the gas of unit mass in CC under the chemical equilibrium condition, $\dot{m}_{\text{f}}$ is the mass flow rate of kerosene, and H _l is the lower heating value of kerosene (45.4 MJ/kg). The kerosene is assumed to have a molecular formula of C₁₀H₂₁. Equation 2 shows the theoretical heat removed from the combustion gas in the CC per unit time under the chemical equilibrium condition, $q_{{{\text{ce}}1}} \dot{m}_{1}$, against the maximum theoretical heat generated in the CC per unit time, $H_{\text{l}} \dot{m}_{\text{f}}$. The difference of heat removed from the CC and MC between the chemical equilibrium condition and the actual situation is discussed in Sect 4.1. By modifying Eq 2,

$$ q_{{{\text{ce}}1}} = \upsigma_{{{\text{ce}}1}} H_{\text{l}} \frac{{\dot{m}_{\text{f}} }}{{\dot{m}_{1} }} $$

(3)

The value of q _ce1 multiplied by −1 is the enthalpy of reaction and is used in the CEA calculation of the CC. By assuming the overall coefficient of heat transfer of the CC to be constant, the heating value transferred from the combustion gas to the cooling water is proportional to the temperature difference in the combustion gas and cooling water. In this situation, σ_ce1 in Eq 3 is considered to be given by the form:

$$ \upsigma_{{{\text{ce}}1}} = \upsigma_{{{\text{ce}}1,{\text{r}}}} \cdot \frac{{T_{{{\text{g}}01}} - T_{\text{c}} }}{{T_{{{\text{g}}01,{\text{r}}}} - T_{\text{c}} }} $$

(4)

where T _c is the representative temperature of the cooling water of the WS gun and is set at 333 K. The value of T _c was found to have a negligible effect on the calculated results at least within the range of 323 < T _c < 343 K. The subscript r in Eq 4 shows the reference condition, which was selected to be the equivalence ratio $\upphi=1$ for the CC. In Eq 4, σ_ce1,r and T _g01,r are constants, and their proper values were found to be σ_ce1,r = 0.28 and T _g01,r = 3110 K by CEA calculation for the reference condition to best correlate with the experimental data, as is shown in Sect 4.1. The values of T _g01, R ₁, and γ₁, which are needed to calculate the right side of Eq 1, are obtained by iterative calculations using the CEA program along with Eq 3 and 4. The comparison is made in Sect 4.1 between the calculated results of the right side of Eq 1 and the experimental results of the left side of Eq 1 to derive the formula of the cooling rate of CC.

Cooling Rate of Mixing Chamber

Based on the assumptions mentioned previously, the following equations hold for the MC from the theory of gas dynamics when the C-D nozzle attached to the exit of the MC is choked:

$$ \dot{m}_{1} + \dot{m}_{2} = \dot{m}_{3} $$

(5)

$$ \dot{m}_{1} = \frac{{p_{01} A_{{1{\text{t}}}} }}{{\sqrt {R_{1} T_{{{\text{g}}01}} } }}\Upgamma_{1} \sqrt {\upgamma_{1} [2/(\upgamma_{1} + 1)]^{{(\upgamma_{1} + 1)/(\upgamma_{1} - 1)}} } $$

(6)

$$ \dot{m}_{2} = \frac{{p_{02} A_{{2{\text{t}}}} }}{{\sqrt {R_{2} T_{{{\text{g}}02}} } }}\Upgamma_{2} \sqrt {\upgamma_{2} [2/(\upgamma_{2} + 1)]^{{(\upgamma_{2} + 1)/(\upgamma_{2} - 1)}} } $$

(7)

$$ \dot{m}_{3} = \frac{{p_{03} A_{{3{\text{t}}}} }}{{\sqrt {R_{3} T_{{{\text{g}}03}} } }}\sqrt {\upgamma_{3} [2/(\upgamma_{3} + 1)]^{{(\upgamma_{3} + 1)/(\upgamma_{3} - 1)}} } $$

(8)

$$ \frac{{p_{01} }}{{p_{{1{\text{t}}}} }} = \frac{{p_{01} }}{{p_{03} }} = \left( {1 + \frac{{\upgamma_{1} - 1}}{2}M_{{{\text{g}}1{\text{t}}}}^{2} } \right)^{{\upgamma_{1} /(\upgamma_{1} - 1)}} $$

(9)

$$ \frac{{p_{02} }}{{p_{{2{\text{t}}}} }} = \frac{{p_{02} }}{{p_{03} }} = \left( {1 + \frac{{\upgamma_{2} - 1}}{2}M_{{{\text{g}}2{\text{t}}}}^{2} } \right)^{{^{{\upgamma_{2} /(\upgamma_{2} - 1)}} }} $$

(10)

In Eq 5-10, M shows the Mach number and Γ is the gas-dynamic function defined as:

$$ \Upgamma_{i} = M_{\text{git}} \left[ {\frac{{2 + \left( {\upgamma_{i} - 1} \right)M_{\text{git}}^{2} }}{{\upgamma_{i} + 1}}} \right]^{{ - (\upgamma_{i} + 1)/2\left( {\upgamma_{i} - 1} \right)}} \quad\left( {i = 1, 2} \right) $$

(11)

The subscripts 2 and 3 in Eq 5-11 show N₂ injection chamber and MC, respectively. By giving $\dot{m}_{1}$ and $\dot{m}_{2}$ from the experimental conditions, the six unknown physical values, p ₀₁, p ₀₂, p ₀₃, M _g1t, M _g2t, and $\dot{m}_{3}$, can be obtained by solving Eq 5-10. The temperature of the nitrogen gas T _g02 was set at 300 K. The gas properties in the MC, T _g03, R ₃, and γ₃ are calculated by the CEA program for the specific value of cooling rate of MC. Equation 12, a modification of Eq 6, is used to determine the cooling rate of the MC from the experimental data of the pressure in the CC and the mass flow rate of the combustion gas of the WS gun,

$$ \frac{{p_{01} A_{{1{\text{t}}}} }}{{\dot{m}_{1} }} = \frac{{\sqrt {R_{1} T_{{{\text{g}}01}} } }}{{\Upgamma_{1} \sqrt {\upgamma_{1} [2/(\upgamma_{1} + 1)]^{{(\upgamma_{1} + 1)/(\upgamma_{1} - 1)}} } }}\quad\left( {\text{WS gun}} \right) $$

(12)

The same forms of Eq 3 and 4 for CC are also applied to MC as,

$$ q_{{{\text{ce}}3}} = \upsigma_{{{\text{ce}}3}} H_{\text{l}} \frac{{\dot{m}_{\text{f}} }}{{\dot{m}_{3} }} $$

(13)

$$ \upsigma_{{{\text{ce}}3}} = \upsigma_{{{\text{ce}}3,{\text{r}}}} \cdot \frac{{T_{{{\text{g}}03}} - T_{\text{c}} }}{{T_{{{\text{g}}03,{\text{r}}}} - T_{\text{c}} }} $$

(14)

The reference condition for MC was selected as $\upphi=1$ and $\dot{m}_{2}$ = 0.021 kg/s (1000 sLm). In Eq 14, σ_ce3,r and T _g03,r are constants, and their proper values were found to be σ_ce3,r = 0.18 and T _g03,r = 2204 K for the reference condition of MC to best correlate with the experimental data, as is shown in Sect 4.1. The values of T _g01, R ₁, γ₁, and M _g1t, which are needed to calculate the right side of Eq 12, are obtained by iterative calculations by using the CEA program along with the cooling rate of the CC and the solution of Eq 5-10. The comparison is made in Sect 4.1 between the calculated results of the right side of Eq 12 and the experimental results of the left side of Eq 12 to derive the formula of the cooling rate of the MC.

Quasi-One-Dimensional Flow in Nozzle and Barrel

The assumptions to model the internal gas flow through the C-D nozzle and the barrel of the WS gun are:

• (a) The gas flow is steady, quasi-one-dimensional (Ref 15), and chemically frozen (Ref 16).

• (b) The gas flow in the converging nozzle from the CC to the MC, and that from the N₂ injection chamber to the MC are adiabatic and frictionless.

• (c) The gas flow leaving the mixing chamber chokes at the throat of the C-D nozzle.

• (d) The gas flow in the barrel is uniformly cooled in the flow direction.

• (e) The velocity and temperature of the gas flow are not affected by the particle flow.

The gas flow from the nozzle throat to the barrel exit was calculated by numerically integrating the conservation equations of mass, momentum, and energy for the quasi-one-dimensional flow, including the effects of the wall friction and heat transfer (Ref 17). The value of δq/dx (Ref 17) of the barrel must be specified in order to numerically integrate the quasi-one-dimensional equations, where x is the axial distance along the centerline of the gun and δq is the heat removed from the unit mass of the gas during the distance of dx. Based on the assumption (c) mentioned in this section, δq/dx can be modified as:

$$ \frac{\updelta q}{dx} = \frac{{\upsigma_{\text{b}} H_{\text{l}} \dot{m}_{\text{f}} /\dot{m}_{3} }}{{L_{\text{b}} }} = \upsigma^{\prime}_{\text{b}} H_{\text{l}} \frac{{\dot{m}_{\text{f}} }}{{\dot{m}_{3} }} $$

(15)

where L _b is the barrel length, σ_b is the cooling rate of the barrel, and $\upsigma^{\prime}_{\text{b}}$ is the cooling rate of the barrel per unit length defined by Eq 16.

$$ \upsigma^{\prime}_{\text{b}} = \frac{\Updelta Q}{{H_{\text{l}} \dot{m}_{\text{f}} }}\frac{1}{{\Updelta L_{\text{b}} }} $$

(16)

The right side of Eq 16 can be experimentally calculated as follows. When the total amount of heat removed by the cooling water per unit time is Q for the WS gun with the barrel length of L _b, and Q + ΔQ with longer barrel length of L _b + ΔL _b while keeping the gas conditions unchanged, then $\upsigma^{\prime}_{\text{b}}$ can be calculated by Eq 16. In this study, L _b = ΔL _b = 0.2 m as can be seen in Table 1 which is explained in Sect 3.

Table 1 Experimental conditions of the HVOF and WS guns

Jet Flow from the Barrel Exit

Since the spray particle is assumed to travel along the centerline of the gas flow in the present model, as is described in the next section, the gas velocity, density, and temperature along the centerline of the jet flow, in addition to those inside the gun, must be specified to calculate the particle behavior. In this model, the gas temperature as well as the gas velocity from the barrel exit is assumed to be kept constant in the range of the potential-core length, which can be calculated by the empirical formula proposed by (Ref 18). Beyond the potential-core length, the decaying distributions of the velocity and temperature of the jet flow were calculated using the semiempirical formulas proposed by (Ref 19) and (Ref 20). The density of the gas jet along the centerline was calculated by the equation of state of the ideal gas under the assumption of the static pressure in the jet to be equal to the ambient pressure. The overexpansion or underexpansion of the jet flow is also modeled such that the gas flow at the barrel exit expands or compresses isentropically to the atmospheric pressure, resulting in a discontinuous change in velocity, temperature, density, and pressure at the barrel exit. The detail of the modeling of the jet flow can be found in (Ref 21).

Particle Flow

The following assumptions are used for the particle traveling in the gas flow to simplify the mathematical model:

• The particles are spherical in shape.

• The particles travel along the nozzle axis.

• The interaction between the particles is negligible.

• The acceleration of particles in the gas flow is caused by gas-dynamic drag force.

• The particle is heated by the gas flow through heat transfer and heat radiation.

• The temperature distribution inside of a particle is uniform.

• The material properties of the particle are constant.

Then, the equation of particle motion is written as:

$$ m_{\text{p}} u_{\text{p}} \frac{{du_{\text{p}} }}{dx} = \frac{1}{2}c_{\text{d}} \uprho_{\text{g}} \left( {u_{\text{g}} - u_{\text{p}} } \right) \cdot \left| {u_{\text{g}} - u_{\text{p}} } \right|A{}_{\text{p}}^{{}} $$

(17)

where m _p is the mass of the particle, u _p is the particle velocity, A _p is the projected area of the particle, and c _d is the drag coefficient of the particle, respectively. The particle temperature can be calculated by:

$$ m_{\text{p}} Cu_{\text{p}} \frac{{dT_{\text{p}} }}{dx} = \upalpha \left( {T_{\text{g}} - T_{\text{p}} } \right)A_{\text{s}} + \upvarepsilon \upsigma_{\text{SB}} \left( {T_{\infty }^{4} - T_{\text{p}}^{4} } \right)A_{\text{s}} $$

(18)

where C is the specific heat of the particle, α is the heat-transfer coefficient, A _s is the surface area of the particle, T _p is the particle temperature, T _∞ is the gas temperature far away from the particle (T _∞ = T _g in the gun, whereas T _∞ = 300 K, atmospheric temperature, in the jet), σ_SB is the Stefan-Boltzmann constant, respectively. The surface emissivity ε was set at 0.5. The detail of the modeling of the particle behavior can be found in (Ref 17).

Experiment

Two types of experiments were carried out in this study; the first one was to adjust or determine free parameters used in the mathematical model, and the second one was to validate the model of the WS gun. During the experiment of this study, the volume flow rate of fuel (kerosene), oxygen, nitrogen, and the gas pressure in the CC were recorded. In addition, the temperatures of cooling water at its inlet and outlet positions of the WS gun were also measured using thermocouples to calculate the total heat loss Q of the WS gun. The volume flow rate of the cooling water was set at 40 sLm. The experimental conditions of the WS and HVOF guns in this study are summarized in Table 1. The WS gun is a modification from the Praxair-Tafa JP-5000; a removable MC is inserted between the CC and the supersonic nozzle. In the present study, the WS gun was also operated as a conventional HVOF gun by removing the MC. The experiments of the HVOF gun were conducted in order to obtain the cooling rate of the CC, as is shown in Sect 4.1. The equivalence ratio $\upphi$ in the CC was set at 1.0 in most cases for both the WS and HVOF guns, and in the other cases $\upphi=0.834\;\text{or }1.25$. The barrel of 0.2 and 0.4 m length were used for the WS gun to calculate the cooling rate of the barrel per unit length, as is described in Sect 2.2.

The validity of the mathematical model was confirmed by the wipe testing of aluminum (Al) particles: the WS gun was traversed very rapidly over the steel substrate in order to (a) isolate the individual impacts from each other and (b) minimize the heat input from the warm jet to the deposited particle during the coating process. The diameter of Al particle used in the model-validation experiment was in the narrow range of 25-32 μm. The splat shapes of Al particle on the substrate were observed in order to see the validity of the calculated particle temperature and the melting fraction of particle (MFP) (Ref 17).

Results and Discussion

Estimation of Cooling Rates

Combustion Chamber

The comparison between the experimental values of p ₀₁ A _1t/$\dot{m}_{1}$ and calculated results by Eq 1, along with Eq 3 and 4, is shown in Fig. 4 as a function of $\upphi.$ In the calculations, the values of σ_ce1,r and T _g01,r in Eq 4 were determined using the method of least squares to fit the experimental values of p ₀₁ A _1t/$\dot{m}_{1}$ and were found to be σ_ce1,r = 0.28 and T _g01,r = 3110 K. As can be seen in Fig. 4, the analytical curve coincides well with the experimental values. It means that the cooling rate of the CC is successfully described by Eq 4 with σ_ce1,r = 0.28 and T _g01,r = 3110 K.

Fig. 4

Comparison between the measured and calculated results of Eq 1

The calculated result of σ_ce1 obtained during the computation of the solid curve in Fig. 4 is shown in Fig. 5 as a function of $\upphi.$ Figure 5 shows that the cooling rate σ_ce1 is slightly dependent on $\upphi$ and varies between 0.26 and 0.28 for $\upphi=0.6{\text{-}}1.3.$ The curve in Fig. 5 was found to be well fitted by:

$$ \upsigma_{{{\text{ce}}1}} = 0.175 + 0.216 \upphi - 0.111 \upphi^{2} $$

(19)

Equation 19 is more convenient than Eq 4 when calculating the performance of the WS gun. Although the fitting formula, Eq 19, can be used only for the present WS gun, as well as JP-5000, the procedure to derive Eq 19 can be applicable to any WS gun with similar structure.

Fig. 5

Calculated cooling rate of the combustion chamber under the chemical equilibrium condition

Mixing Chamber

The comparison between the experimental values of p ₀₁ A _1t/$\dot{m}_{1}$ for the WS gun and the calculated results by Eq 12, along with Eq 13 and 14, is shown in Fig. 6 as a function of nitrogen mass-flow ratio ψ₂₁ ≡ $\dot{m}_{2} /\dot{m}_{1}$. The values of σ_ce3,r and T _g03,r in Eq 14 were determined by the method of least squares to fit the experimental values of p ₀₁ A _1t/$\dot{m}_{1}$ for the WS gun with $\upphi=1$ and were found to be σ_ce3,r = 0.18 and T _g03,r = 2204 K. Although these values were determined using the experimental data of p ₀₁ A _1t/$\dot{m}_{1}$ of the WS gun only for $\upphi=1$ to draw the solid curve in Fig. 6, the experimental data of p ₀₁ A _1t/$\dot{m}_{1}$ for $\upphi$ ≠ 1 also locate close to the analytical solid curve in Fig. 6. In fact, the addition of the experimental data of $\upphi$ ≠ 1 to that of $\upphi=1$ did not change the values of σ_ce3,r and T _g03,r. It roughly means that the cooling rate of MC, σ_ce3, simply depends on ψ₂₁, but not on $\upphi .$

Fig. 6

Comparison between the measured and calculated results of Eq 12

The calculated result of σ_ce3 obtained during the computation of the solid curve in Fig. 6 is shown in Fig. 7 as a function of ψ₂₁. Figure 7 shows that the cooling rate σ_ce3 almost linearly decreases by the increase in ψ₂₁. Using the least squares method, the curve in Fig. 7 was found to be well fitted by:

$$ \upsigma_{{{\text{ce}}3}} = 0.226 - 0.0441\uppsi_{21} $$

(20)

Equation 20 is more useful than Eq 14 when calculating the performance of the WS gun.

Fig. 7

Calculated cooling rate of the mixing chamber under the chemical equilibrium condition

The actual total heat loss through the CC and MC, Q ₁₊₃, against the theoretical maximum heat generated in the CC is a concern when considering the thermodynamic efficiency of the WS gun. For this purpose, the following cooling rate σ₁₊₃ is introduced:

$$ \upsigma_{1 + 3} = \frac{{Q_{1 + 3} }}{{\dot{m}_{\text{f}} H_{\text{l}} }} $$

(21)

The numerator of Eq 21 can be calculated by subtracting the heat loss during the barrel calculated by Eq 24, which is shown later, from the amount of heat loss from the entire WS gun, Q. In addition, another concern in this model is of how close the chemical reaction in the CC and MC is to the chemical equilibrium condition, which is assumed in Sect 2.1. The comparison of the actual heat loss Q ₁₊₃ with the heat loss obtained by the CEA calculation of the CC and MC provides us with the information on how close the chemical reaction in the CC and MC is to the chemical equilibrium condition, from the viewpoint of the heat removed from the product gases. For this purpose, the parameter η, called the chemical equilibrium parameter in this paper, is introduced as:

$$ \upeta = \frac{{Q_{1 + 3} }}{{\dot{m}_{1} q_{{{\text{ce}}1}} + \dot{m}_{3} q_{{{\text{ce}}3}} }} = \frac{{\upsigma_{1 + 3} }}{{\upsigma_{{{\text{ce}}1}} + \upsigma_{{{\text{ce}}3}} }} $$

(22)

Experimentally obtained values of σ₁₊₃ and η are shown in Fig. 8 as a function of ψ₂₁. The data of σ₁₊₃ in Fig. 8 show that the summation of the actual heat removed from the combustion and mixing chambers is in the range of 33-43% against the theoretical maximum heat generated in the CC. In addition, it is also shown in Fig. 8 from the data of η that the actual total heat loss in the CC and MC is 68-100% against the total heat loss in the CC and MC under the assumption of chemical equilibrium condition. In the range of ψ₂₁ < 1.0, η is below 75% which may mean that the gas is away from the chemical equilibrium condition. However, the calculated values of gas temperature, gas constant, and specific heat ratio in the CC and MC are expected to be in an acceptable limit when considering the coincidence of the calculated results with the experimental data in Fig. 4 for the CC and those in Fig. 6 for the MC.

Fig. 8

Experimentally determined cooling rate of the combustion and mixing chambers and the chemical equilibrium parameter

Barrel

The experimental results of the cooling rate of the barrel per unit length for the WS gun, obtained by Eq 16, are plotted in Fig. 9 as a function of ψ₂₁. In the figure, solid circles show the present experimental data, and the open circle was obtained from (Ref 22) for JP-5000. The experimental data in Fig. 9 is well fitted by:

$$ \upsigma^{\prime}_{\text{b}} = 0.654 + 0.173\uppsi_{21} - 0.218\uppsi_{21}^{2} $$

(23)

From Fig. 9, $\upsigma^{\prime}_{\text{b}}$ decreases with the increase in ψ₂₁ as a whole due to the decrease in the gas temperature. The cooling rate of the barrel σ_b for the length L _b can be obtained by:

$$ \upsigma_{\text{b}} = \upsigma^{\prime}_{\text{b}} L_{\text{b}} $$

(24)

Fig. 9

Experimentally determined cooling rate of barrel per unit length

Trend of Gas Temperature in the WS Gun

The gas temperatures of the WS process were calculated for ψ₂₁ = 0.27, 1.0, and 1.7 to see the effect of the mass flow rate of nitrogen on the gas temperature. The calculated results downstream of the throat of the C-D nozzle are shown in Fig. 10. The cooling rate of the CC, MC, and barrel were calculated by Eq 18, 20, and 24, respectively. In the figure, the barrel is located at x = −0.22 to 0 m, and the jet region is x > 0. For ψ₂₁ = 0.27 (300 sLm of N₂), the gas temperature T _g at the powder injection port x = −0.21 m is 1800 K, which is highest among three cases at the same axial location. Then, T _g decreases to 1300 K at the barrel exit due to the heat loss in the barrel. The decrease in T _g through the barrel means that the acceleration effect by cooling (Rayleigh flow) excels the deceleration effect by the pipe friction (Fanno flow). The slight abrupt increase in T _g at the barrel exit shows a weak overexpansion of the jet flow. The potential-core length for ψ₂₁ = 0.27 was calculated as 0.08 m by the empirical equation proposed by (Ref 18). After exiting the barrel, therefore, T _g is kept constant for x = 0-0.08 m in the potential-core region, beyond which T _g gradually decreases. As for ψ₂₁ = 1.7 (1500 sLm of N₂), T _g is as low as 1250 K at the powder injection port. Then, T _g increases toward the barrel exit due to the smaller amount of cooling compared to the case of ψ₂₁ = 0.27, while the effect of deceleration by the wall friction is comparable to the case of ψ₂₁ = 0.27. The large amount of abrupt decrease in T _g at the barrel exit shows a strong underexpansion of the jet flow. The static temperature of the jet flow at the barrel exit is around 1300 K regardless of ψ₂₁, because of the balance between the gas temperature leaving the MC, the effects of cooling/pipe friction in the barrel, and the extent of expansion of the gas at the barrel exit.

Fig. 10

Calculated gas temperatures downstream of the throat of C-D nozzle

Validation of the Mathematical Model

The histories of Al particle sprayed by the WS gun were calculated for ψ₂₁ = 0.45 (500 sLm of N₂) and 1.7 (1500 sLm of N₂) to compare the calculated results with the wipe tests. Figure 11(a) shows the calculated results of the gas and particle temperatures, and MFP for ψ₂₁ = 0.45. The MFP, shown as two convex curves in the lower part in Fig. 11(a), means the mass fraction of molten part of a single particle. Figure 11(a) shows that the Al particles reach the melting point of 905 K while they travel in the barrel, then the particle temperatures are kept constant at the melting point until x = 0.3 m. The MFP takes the maximum value of 0.83 and 0.44 for the particle diameter d _p = 25 and 32 μm, respectively, at x = 0.15 m. Therefore, it is roughly expected from the calculated results of MFP that more than 50 vol% of a single Al particle is in a molten condition on average in the jet region.

Fig. 11

Calculated gas and Al particle temperatures for (a) ψ₂₁ = 0.45 and (b) ψ₂₁ = 1.7

Figure 11(b) shows the calculated results for ψ₂₁ = 1.7. The Al particle of d _p = 25 μm reaches the melting point just after exiting the barrel. Although T _p of d _p = 25 μm particle is equal to the melting point in the jet flow region, the maximum MFP is as low as 0.14. Furthermore, T _p of d _p  = 32 μm particle does not reach the melting point during the WS process. Therefore, it is roughly expected that less than 10 vol% of a single Al particle is in a molten condition on average in the jet flow region.

Figure 12(a) shows the morphologies of Al particles deposited on the steel substrate by the wipe testing of the WS process at ψ₂₁ = 0.45 and the standoff distance of 0.1 m, to be compared with Fig. 11(a). As can be seen in the figure, each splat has widely spread on the substrate along with a dark-colored core at the center of each splat. This observation means that a large amount of volume of each particle is in a molten condition, but there still exists a solid core in each Al particle before impact. This experimental result is well explained by the calculated results shown in Fig. 11(a), showing the validity of the mathematical model.

Fig. 12

Morphology of the Al particle sprayed at (a) ψ₂₁ = 0.45 and (b) ψ₂₁ = 1.7

Figure 12(b) shows the morphologies of the Al particles deposited on the steel substrate by the wipe testing of the WS process at ψ₂₁ = 1.7 and the standoff distance of 0.1 m, to be compared with Fig. 11(b). In the Fig. 12(b), the diameters of the impacts are roughly comparable to that of the feedstock powder of 25-32 μm, and less splashing can be seen in the figure. This result shows that the Al particles impact on the substrate mostly in a solid condition. This experimental result is well explained by the calculated results shown in Fig. 11(b), again showing the validity of the mathematical model.

Concluding Remarks

The mathematical model of the water-cooled WS gun was constructed based on the thermodynamic and gas-dynamic theories. The model consists of four parts: (a) thermodynamic and gas-dynamic calculations of CC and MC, (b) quasi-one-dimensional calculation of the internal gas flow of the gun, (c) semiempirical calculation of the jet flow from the gun exit, and (d) calculation of particle velocity and temperature traveling in the gas flow. The free parameters used in the model were adjusted or decided by using the experimental data, such as the inlet and outlet temperatures of the cooling water, gas pressure in the CC, and mass flow rate of the combustion and nitrogen gases. In order to validate the mathematical model, the wipe testing of the WS gun was conducted using the Al powder. The comparison was made between the calculated particle temperature and the experimental observation of the splats formed on the steel substrate. The results are summarized as:

• The cooling rates of the CC, MC, and barrel, which cannot be experimentally measured separately, can be estimated by the present mathematical model by acquiring the experimental data of the inlet and outlet temperatures of the cooling water, gas pressure in the CC, and mass flow rate of the combustion and nitrogen gases.

• The cooling rate of the CC slightly depends on the equivalence ratio and has a maximum value of 0.28 at the equivalence ratio of around 1. The cooling rates of the MC and the barrel decrease by the increase in the mass flow rate of the nitrogen gas.

• The mathematical model predicts that the gas temperature at the powder injection port decreases from 1800 to 1250 K by increasing the nitrogen mass flow ratio from 0.27 to 1.7. However, the static temperature at the barrel exit is around 1300 K regardless of the value of the nitrogen mass flow ratio, because of the balance between the gas temperature leaving the MC, the effects of cooling/pipe friction in the barrel, and the extent of expansion of the gas at the barrel exit.

• The experimentally obtained splat formations of the Al particle obtained by the wipe testing of the WS gun were reasonably well explained by the calculated results of the particle temperature and MFP, demonstrating the validity of the present mathematical model.