Introduction

Electromagnetic stirring (EMS) has been used in the continuous casting of steel[1] since as early as the 1970s as a way to control solidification structures, thereby increasing yield and productivity. In tandem, mathematical modeling has played an important role in the implementation of EMS, as regards providing understanding of exactly what effect stirring has.

A cornerstone of the modeling literature in this area is a sequence of papers by Schwerdtfeger and co-workers[2,3,4,5,6,7] which explore, both experimentally and theoretically, the effect of stirring in the round billet, rectangular bloom, and slab geometries that are characteristic for the continuous casting of steel. The models in question consist of the Navier–Stokes equations for the velocity field of the molten metal and Maxwell’s equations for the induced magnetic flux density; in principle, these are two-way coupled, since the alternating magnetic field gives rise to a Lorentz force which drives the velocity field, which can in turn affect the magnetic field. Moreover, the frequency of the magnetic field is typically great enough to allow the use of the time average of the Lorentz force as input to the Navier–Stokes equations.

In calculating the induced magnetic field, an assumption is necessary as regards the applied oscillating field surrounding the domain of interest, typically the steel strand. To obtain adequate data for this, it may in practice mean using a Hall probe magnetometer to make measurements of the magnetic field at a point or points in the space between the outer surface of the steel strand and the periodic winding of the inductor on an iron comb,[2,3,7] or a Gauss meter[8,9]; indeed, measurements acquired in the former way were used as the basis for prescribing the normal component of the magnetic flux density at the surface of the strand. However, some time later, and in a mathematically related problem, McKee et al.[10] prescribed the tangential component in their model for particle tracking within a turbulent cylindrical electromagnetically driven steel melt. Consequently, there appears to be some uncertainty as to what should be the correct boundary condition in this situation: indeed, McKee et al.[10] followed Moffatt[11] in initially assuming that both the normal and tangential components of the magnetic flux density are required as boundary conditions, only to ultimately just use the latter. Moreover, the fact that the expressions for the components of the Lorentz force for round billets[2,7] and for rectangular strands[3] have been cited and used on numerous occasions since, even up to the present day,[9,12,13,14,15,16,17,18,19] suggests that a resolution of the issue is timely.

Here, we focus on the analytically simpler case of the round billet. In particular, we demonstrate that prescribing the normal component of the magnetic flux density at the boundary leads to a solution that is not unique; however, prescribing the tangential component leads to a solution that is unique. It is also found that the expressions for the spatial distributions of the time-averaged radial and cylindrical components of the Lorentz force obtained via the two routes turn out to be the same as each other, to within a multiplicative factor that depends on a single dimensionless parameter, although only when the magnetic Reynolds number is small. Otherwise, it is possible to reconcile only the tangential and normal components at the boundary from the two routes, although this time via a multiplicative factor that depends on two dimensionless parameters, one of which is the magnetic Reynolds number; this factor can only be computed numerically by solving the full model equations. Lastly, remedies are suggested for avoiding the problems mentioned above, as is the significance of these results for further work.

Model Equations

Governing Equations and Boundary Conditions

Fig. 1
figure 1

Schematic of the arrangement of an inductor around a circular steel strand for inducing rotating fields

Full size image

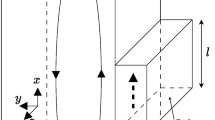
We consider, as shown in Figure 1, a rotary EMS stirrer operating with an electric current having angular velocity \(\omega ,\) related to the frequency of the coil current f by \(f=\omega /2\pi ,\) acting on a melt region of radius \(r_{b}\); a horizontal cross-section of Figure 1 is shown in Figure 2.

The continuity equation for the region in \(0<r<r_{b}\) is given in cylindrical (\(r,\theta ,z\)) coordinates by

$$\frac{1}{r}\frac{\partial }{\partial r}\left( rv_{r}\right) +\frac{1}{r} \frac{\partial v_{\theta }}{\partial \theta }+\frac{\partial v_{z}}{\partial z}=0, $$
(1)

where \(v_{r},v_{\theta },\) and \(v_{z}\) denote the r-, \(\theta \)-, and z-components of velocity, respectively. The conservation of momentum for \(0<r<r_{b}\) is given by

$$\rho \left\{ v_{r}\frac{\partial v_{r}}{\partial r}+\frac{v_{\theta }}{r} \frac{\partial v_{r}}{\partial \theta }+v_{z}\frac{\partial v_{r}}{\partial z}-\frac{v_{\theta }^{2}}{r}\right\} = -\frac{\partial p}{\partial r}+\frac{1}{r}\frac{\partial }{\partial r}\left( r\tau _{rr}\right) +\frac{1}{r}\frac{\partial \tau _{\theta r}}{\partial \theta }-\frac{\tau _{\theta \theta }}{r}+\frac{\partial \tau _{zr}}{\partial z}+\bar{F}_{r},$$
(2)
$$\rho \left\{ v_{r}\frac{\partial v_{\theta }}{\partial r}+\frac{v_{\theta }}{r}\frac{\partial v_{\theta }}{\partial \theta }+v_{z}\frac{\partial v_{\theta } }{\partial z}+\frac{v_{r}v_{\theta }}{r}\right\} = -\frac{1}{r}\frac{\partial p}{\partial \theta }+\frac{1}{r^{2}}\frac{\partial }{\partial r}\left( r^{2}\tau _{r\theta }\right) +\frac{1}{r}\frac{\partial \tau _{\theta \theta }}{\partial \theta }+\frac{\partial \tau _{z\theta } }{\partial z}+\bar{F}_{\theta }, $$
(3)
$$\rho \left\{ v_{r}\frac{\partial v_{z}}{\partial r}+\frac{v_{\theta }}{r} \frac{\partial v_{z}}{\partial \theta }+v_{z}\frac{\partial v_{z}}{\partial z}\right\} =-\frac{\partial p}{\partial z}+\frac{1}{r}\frac{\partial }{\partial r}\left( r\tau _{zr}\right) +\frac{1}{r}\frac{\partial \tau _{\theta z}}{\partial \theta }+\frac{\partial \tau _{zz}}{\partial z}+\bar{F}_{z}, $$
(4)

where \(\rho \) is the density of the melt and p is the pressure. Also, in Eqs. [2] through [4], \(\tau _{rr},\tau _{\theta \theta },\tau _{zz},\tau _{rz},\tau _{zr},\tau _{\theta r} ,\tau _{r\theta },\tau _{\theta z},\) and \(\tau _{z\theta }\) denote the components of the stress tensor and are given, respectively, by

$$\tau _{rr}=2\frac{\partial v_{r}}{\partial r},$$
(5)
$$\tau _{\theta \theta }=\frac{2\left( \mu +\mu _{\mathrm{T}}\right) }{r}\left( \frac{\partial v_{\theta }}{\partial \theta }+v_{r}\right) ,$$
(6)
$$\tau _{zz}=2\left( \mu +\mu _{\mathrm{T}}\right) \frac{\partial v_{z}}{\partial z},$$
(7)
$$\tau _{rz}=\tau _{zr}=\left( \mu +\mu _{\mathrm{T}}\right) \left( \frac{\partial v_{z}}{\partial r}+\frac{\partial v_{r}}{\partial z}\right) ,$$
(8)
$$\tau _{\theta r}=\tau _{r\theta }=\left( \mu +\mu _{\mathrm{T}}\right) \left( r\frac{\partial }{\partial r}\left( \frac{v_{\theta }}{r}\right) +\frac{1}{r}\frac{\partial v_{r}}{\partial \theta }\right),$$
(9)
$$\tau _{\theta z}=\tau _{z\theta }=\left( \mu +\mu _{\mathrm{T}}\right) \left( \frac{\partial v_{\theta }}{\partial z}+\frac{1}{r}\frac{\partial v_{z} }{\partial \theta }\right),$$
(10)

with \(\mu\) being the dynamic viscosity and \(\mu _{\mathrm{T}}\), the turbulent viscosity. Furthermore, in Eqs. [2] through [4], \(\bar{F}_{r},\bar{F}_{\theta },\) and \(\bar{F}_{z}\) denote the time-averaged components of the Lorentz force, which we write as \(F_{r},F_{\theta },\) and \(F_{z}\) and which are given by

$$F_{r}=J_{\theta }B_{z}-J_{z}B_{\theta },\quad F_{\theta }=J_{z}B_{r}-J_{r} B_{z},\quad F_{z}=J_{r}B_{\theta }-J_{\theta }B_{r}, $$

respectively, where \(\left( J_{r},J_{\theta },J_{z}\right) \) is the electrical current density vector, \({\mathbf{J}}\), and \(\left( B_{r},B_{\theta },B_{z}\right) \) is the magnetic flux density vector, \({\mathbf{B}}\); moreover, \(F_{r},F_{\theta }, \) and \(F_{z}\) are related to \(\bar{F}_{r},\bar{F}_{\theta }, \) and \(\bar{F}_{z}\) by

$$\bar{F}_{r}=\frac{1}{2\pi /\omega }\int _{0}^{2\pi /\omega }F_{r}{\mathrm{d}} t^{\prime },\quad \bar{F}_{\theta }=\frac{1}{2\pi /\omega }\int _{0}^{2\pi /\omega }F_{\theta }{\mathrm{d}}t^{\prime },\quad \bar{F}_{z}=\frac{1}{2\pi /\omega }\int _{0}^{2\pi /\omega }F_{z}{\mathrm{d}}t^{\prime },$$

where the integrals are taken with respect to time over one oscillation period, \(2\pi /\omega .\) At this point, it may appear that \(\bar{F}_{r},\bar{F}_{\theta },\) and \(\bar{F}_{z}\) should all be functions of \(r,\theta, \) and z,  but, as a consequence of the boundary conditions to be specified later, they will only be functions of r.

Fig. 2
figure 2

Horizontal cross-section of the geometry in Fig. 1

Full size image

To determine \({\mathbf{J}}\) and \({\mathbf{B}},\) we must solve Maxwell’s equations in the magnetohydrodynamic (MHD) approximation, which consist of the following:

  • the magnetic field constraint,

    $$\nabla \cdot {\mathbf{B}}=0; $$
    (11)

  • Ampere’s law,

    $${\mathbf{J}} =\nabla \times {\mathbf{H}}, $$
    (12)

    where \({\mathbf{H}}\) is the magnetic field strength, which is related to \({\mathbf{B}}\) by \({\mathbf{B}}=\eta {\mathbf{H}}\), where \(\eta \) is the magnetic permeability;

  • Faraday’s law,

    $$\nabla \times {\mathbf{E}}=-\frac{\partial {\mathbf{B}}}{\partial t}, $$
    (13)

    where t is the time and \({\mathbf{E}}\) is the electric field;

  • Ohm’s law,

    $${\mathbf{J}}=\sigma \left( {\mathbf{E}}+{\mathbf{v}}\times {\mathbf{B}}\right), $$
    (14)

    where \(\sigma \) is the metal electrical conductivity, which we take to be constant, and \({\mathbf{v}}\) is the velocity vector, \(\left( v_{r},v_{\theta },v_{z}\right) .\)

Manipulating [12] through [14], we arrive at

$$\sigma \eta \frac{\partial {\mathbf{B}}}{\partial t}=\nabla ^{2}{\mathbf{B}} +\sigma \eta \left\{ \left( \nabla \cdot {\mathbf{B}}+{\mathbf{B}}\cdot \nabla \right) {\mathbf{v}}-\left( \nabla \cdot {\mathbf{v}} +{\mathbf{v}}\cdot \nabla \right) {\mathbf{B}}\right\},$$
(15)

whence, on using Eqs. [1] and [11], we obtain

$$\sigma \eta \frac{\partial {\mathbf{B}}}{\partial t}=\nabla ^{2}{\mathbf{B}} +\sigma \eta \left\{ \left( {\mathbf{B}}\cdot \nabla \right) {\mathbf{v}} -\left( {\mathbf{v}}\cdot \nabla \right) {\mathbf{B}}\right\};$$
(16)

note, however, that this must still be solved together with Eq. [11].

The above may be simplified in a self-consistent way by taking \(v_{r} \equiv 0,v_{z}\equiv 0,v_{\theta }=v_{\theta }\left( r\right) ,p=p\left( r\right) ,\) \(B_{z}=0, \) and \(\partial /\partial z=0\) in Eqs. [1] through [4], [11], and [16]. We find that [1] and [4] are satisfied automatically, whereas [2] and [3] become

$$-\frac{\rho v_{\theta }^{2}}{r}=-\frac{{\mathrm{d}}p}{{\mathrm{d}}r}+\bar{F}_{r},$$
(17)
$$0=\frac{1}{r^{2}}\frac{{\mathrm{d}}}{{\mathrm{d}}r}\left\{ \left( \mu +\mu _{\mathrm{T}}\right) r^{2}\left( \frac{{\mathrm{d}}v_{\theta }}{{\mathrm{d}}r} -\frac{v_{\theta }}{r}\right) \right\} +\bar{F}_{\theta }, $$
(18)

respectively, with \(\bar{F}_{r}\) and \(\bar{F}_{\theta }\) being determined using

$$F_{r}=-\frac{B_{\theta }}{r}\left( \frac{\partial }{\partial r}\left( rB_{\theta }\right) -\frac{\partial B_{r}}{\partial \theta }\right) ,\quad F_{\theta }=\frac{B_{r}}{r}\left( \frac{\partial }{\partial r}\left( rB_{\theta }\right) -\frac{\partial B_{r}}{\partial \theta }\right). $$
(19)

Equation [18] is the same as that given by Tacke and Schwerdtfeger,[7] which can be solved first for \(v_{\theta },\) after which [17] it can be solved for p. Also, \(B_{r}\) and \(B_{\theta }\) satisfy

$$\frac{1}{r}\frac{\partial }{\partial r}\left( rB_{r}\right) +\frac{1}{r} \frac{\partial B_{\theta }}{\partial \theta }=0,$$
(20)
$$\sigma \eta \frac{\partial B_{r}}{\partial t}={{\frac{\partial ^{2}B_{r} }{\partial r^{2}}+}}\frac{1}{r}\frac{\partial B_{r}}{\partial r}+{\frac{1}{{r}^{2}}}\frac{\partial ^{2}B_{{r}}}{\partial {\theta }^{2}}-\frac{B_{r}}{r^{2} }-{\frac{2}{{r}^{2}}}\frac{\partial B_{{\theta }}}{\partial \theta }-\sigma \eta \frac{v_{\theta }}{r}\frac{\partial B_{{r}}}{\partial \theta },$$
(21)
$$ \sigma \eta \frac{\partial B_{{\theta }}}{\partial t}={{\frac{\partial ^{2}B_{{\theta }}}{\partial {r}^{2}}+\frac{1}{r}{\frac{\partial B_{{\theta }} }{\partial r}}+{\frac{1}{{r}^{2}}}\frac{\partial ^{2}B_{{\theta }}}{\partial {\theta }^{2}}}-\frac{B_{{\theta }}}{r^{2}}+\frac{2}{r^{2}} {\frac{\partial B_{{r}}}{\partial \theta }}}+\sigma \eta \left( B_{r}\frac{\partial v_{{\theta }}}{\partial r} -\frac{v_{\theta }}{r}\frac{\partial B_{{\theta }}}{\partial \theta }\right).$$
(22)

The boundary conditions for \(v_{\theta }\) are then just

$$ v_{\theta }=0\quad {\text{at}}\;r=r_{b},$$
(23)
$$v_{\theta }=0\quad {\text{at}}\;r=0, $$
(24)

Also, the only boundary condition prescribed on the magnetic field quantities is that for \(B_{r}\) at the edge of the melt,[2,7]

$$B_{r}=B_{0}\cos \left( \omega t-n\theta \right) \quad {\text{at}}\;r=r_{b}, $$
(25)

where n is the number of poles. In addition, however, we require

$$B_{r}\quad {\text{finite}}\quad {\text{at}}\;r=0. $$
(26)

Note that no conditions are set for \(B_{\theta }.\)

Nondimensionalization

It is ultimately more instructive to nondimensionalize the equations, and we do this through

$$R=\frac{r}{r_{b}},\quad V_{\theta }=\frac{v_{\theta }}{V},\quad P=\frac{p}{\rho V^{2}},\quad \bar{\mu }_{\mathrm{T}}=\frac{\mu _{\mathrm{T}}}{\mu },\quad B_{R}=\frac{B_{r}}{B_{0}},\quad B_{\theta }=\frac{B_{\theta }}{B_{0}}, \tau=\frac{\omega t}{2\pi },\quad \bar{F}_{R}=\frac{\bar{F}_{r}}{B_{0} ^{2}/r_{b}\eta },\quad \bar{F}_{\Theta }=\frac{\bar{F}_{\theta }}{B_{0}^{2} /r_{b}\eta }, $$
(27)

where V is a velocity scale that has to be determined. Equations [17] and [18] become

$$-\frac{V_{\theta }^{2}}{R}=-\frac{{\mathrm{d}}P}{{\mathrm{d}}R}+\left( \frac{\mathrm{Ha}^{2}}{{\mathrm{Re}}_{\mathrm{m}}{\mathrm{Re}}}\right) \bar{F}_{R}, $$
(28)

with

$$0=\frac{1}{R^{2}}\frac{{\mathrm{d}}}{{\mathrm{d}}R}\left\{ \left( 1+\bar{\mu }_{\mathrm{T}}\right) R^{2}\left( \frac{\partial V_{\theta }}{\partial R} -\frac{V_{\theta }}{R}\right) \right\} +\frac{\mathrm{Ha}^{2}}{{\mathrm{Re}}_{\mathrm{m}}}\bar{F}_{\Theta }, $$
(29)

where \(\mathrm{Ha,Re},\) and \({\mathrm{Re}}_{\mathrm{m}}\) denote the Hartmann, Reynolds, and magnetic Reynolds numbers, respectively, and are given by

$$\mathrm{Ha}=B_{0}r_{b}\sqrt{\frac{\sigma }{\mu }},\quad {\mathrm{Re}}=\frac{\rho Vr_{b}}{\mu },\quad {\mathrm{Re}}_{\mathrm{m}}=Vr_{b}\eta \sigma ; $$
(30)

for completeness, we show in the Appendix how V can be determined. On the other hand, Eqs. [20] through [22] become

$$\frac{1}{R}\frac{\partial }{\partial R}\left( RB_{R}\right) +\frac{1}{R} \frac{\partial B_{\theta }}{\partial \theta }=0, $$
(31)
$$\Omega \frac{\partial B_{R}}{\partial \tau }={{\frac{\partial ^{2}B_{R}}{\partial R^{2}}+}}\frac{1}{R}\frac{\partial B_{R}}{\partial R}+{\frac{1}{{R}^{2}}} \frac{\partial ^{2}B_{{R}}}{\partial {\theta }^{2}}-\frac{B_{R}}{R^{2}}-{\frac{2}{{R}^{2}}}\frac{\partial B_{{\theta }}}{\partial \theta }-{\mathrm{Re}}_{\mathrm{m}} \frac{V_{\theta }}{R}\frac{\partial B_{{R}}}{\partial \theta }, $$
(32)
$$\Omega \frac{\partial B_{{\theta }}}{\partial \tau }={{\frac{\partial ^{2}B_{{\theta }}}{\partial {R}^{2}}+\frac{1}{R}{\frac{\partial B_{{\theta }} }{\partial R}}+{\frac{1}{{R}^{2}}}\frac{\partial ^{2}B_{{\theta }}}{\partial {\theta }^{2}}}-\frac{B_{{\theta }}}{R^{2}}+\frac{2}{R^{2}} {\frac{\partial B_{{R}}}{\partial \theta }}}+{\mathrm{Re}}_{\mathrm{m}}\left( B_{R}\frac{\partial V_{{\theta }}}{\partial R}-\frac{V_{\theta }}{R}\frac{\partial B_{{\theta }}}{\partial \theta }\right) , $$
(33)

where \(\Omega =f\sigma \eta r_{b}^{2}.\) Note here that the related quantity \(\omega \sigma \eta r_{b}^{2}\) was defined by Tacke and Schwerdtfeger[7] as the magnetic Reynolds number \({\mathrm{Re}}_{\mathrm{m}}\), but that the latter is generally defined as in Eq. [30].[10,11] We note also that, although magnetohydrodynamic flows are in general characterized by \(\mathrm{Ha}\) and \({\mathrm{Re}},\) and in particular by the combination \(\mathrm{Ha}^{2}/{\mathrm{Re}},\) \({\mathrm{Re}}\) plays a secondary role in this particular configuration and serves only to adjust the radial pressure gradient after \(V_{\theta }\) has already been determined.

Boundary conditions [23] through [26] are now

$$V_{\theta }=0\quad {\text{at}}\;R=1,$$
(34)
$$V_{\theta }=0\quad {\text{at}}\;R=0,$$
(35)
$$B_{R}=\cos \left( 2\pi \tau -n\theta \right) \quad {\text{at}}\; R=1,$$
(36)
$$B_{R}\quad {\text{finite}}\quad {\text{at}}\;R=0, $$
(37)

respectively.

Analysis

Earlier Solution[2,7]

We first consider what happens when \({\mathrm{Re}}_{\mathrm{m}}\ll 1,\) so that, on using [31], Eq. [32] can be rewritten as

$$\Omega \frac{\partial }{\partial \tau }\left( RB_{R}\right) =\frac{1}{R} {{\frac{\partial }{\partial R}}}\left( RB_{R}\right) +{{\frac{\partial ^{2} }{\partial R^{2}}}}\left( RB_{R}\right) +\frac{1}{R^{2}}{{\frac{\partial ^{2}}{\partial \theta ^{2}}\left( RB_{R}\right) .}} $$
(38)

Setting

$$RB_{R}=-{{\text{{Re}}}}\left( {\mathrm{i}}na{{\mathrm{e}}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) , $$
(39)

where \(i=\sqrt{-1}\) and Re denotes the real part,  we have

$$\frac{{\mathrm{d}}^{2}a}{{\mathrm{d}}R^{2}}+\frac{1}{R}\frac{{\mathrm{d}} a}{{\mathrm{d}}R}-\left( \frac{n^{2}}{R^{2}}+2\pi \Omega {\text{i}}\right) a=0, $$
(40)

subject to

$$a=\frac{{\mathrm{i}}}{n}\quad {\text{at}}\;R=1,$$
(41)
$$a=0\quad {\text{at}}\;R=0. $$
(42)

The second condition is necessary; otherwise, \(B_{R}\) will not be finite at \(R=0.\)

Thence, solving Eq. [40], subject to [41] and [42], gives

$$a\left( R\right) = \frac{{\mathrm{i}}J_{n}\left( R\sqrt{2\pi \Omega } {{\mathrm{e}}}^{3\pi {\mathrm{i}}/4}\right) }{nJ_{n}\left( \sqrt{2\pi \Omega }{{\mathrm{e}}}^{3\pi {\mathrm{i}}/4}\right) }, $$
(43)

where \(J_{n}\left( R\right) \) is a Bessel function of the first kind, satisfying

$$R^{2}{{\frac{{\mathrm{d}}^{2}J_{n}}{{\mathrm{d}}R^{2}}+}}R{{\frac{{\mathrm{d}}J_{n} }{{\mathrm{d}}R}}}+\left( R^{2}-n^{2}\right) J_{n}=0. $$
(44)

Anomaly

Now,

$$\frac{\partial B_{{\theta }}}{\partial \theta }={{\text{{Re}}}}\left( {\mathrm{i}}n{{\mathrm{e}}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\frac{{\mathrm{d}} a}{{\mathrm{d}}R}\right) , $$
(45)

so that

$$B_{{\theta }}=-{{\text{{Re}}}}\left( {{\mathrm{e}}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\frac{{\mathrm{d}}a}{{\mathrm{d}}R}\right) +\phi \left( R,\tau \right) , $$
(46)

where \(\phi \) is a function of R and \(\tau ,\) which was omitted entirely in earlier work[2,7]; hence, since

$$J_{Z}=\frac{1}{R}\left( \frac{\partial }{\partial R}\left( RB_{\theta }\right) -\frac{\partial B_{R}}{\partial \theta }\right) , $$
(47)

using Eqs. [39] and [46] to simplify the resulting expression, we have

$$J_{Z}=\frac{1}{R}\frac{\partial }{\partial R}\left( R\phi \right) -2\pi \Omega {{\text{{Re}}}}\left( {\mathrm{i}}a{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) , $$
(48)

and thus

$$F_{R}=-2\pi \Omega {{\text{Re}}}\left( {\mathrm{i}}a{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) {{\text{Re}}}\left( {\mathrm{e}}^{{\mathrm{i}} \left( 2\pi \tau -n\theta \right) }\frac{{\mathrm{d}}a}{{\mathrm{d}}R}\right) +{\mathcal{F}}_{R},$$
(49)
$$F_{\Theta }=\frac{2\pi \Omega }{R}{{\text{Re}}}\left( {\mathrm{i}} a{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) {{\text{Re}}} \left( {\mathrm{i}}na{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) +{\mathcal{F}}_{\Theta }, $$
(50)

where

$${\mathcal{F}}_{R}=-\left( \frac{1}{R}\frac{\partial }{\partial R}\left( R\phi \right) -2\pi \Omega {{\text{Re}}}\left( {\mathrm{i}}a{\mathrm{e}}^{{\mathrm{i}} \left( 2\pi \tau -n\theta \right) }\right) \right) \phi +\frac{1}{R}\frac{\partial }{\partial R}\left( R\phi \right) {{\text{Re}}}\left( {\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) } \frac{{\mathrm{d}}a}{{\mathrm{d}}R}\right) ,$$
(51)
$${\mathcal{F}}_{\Theta }=-\frac{1}{R^{2}}\frac{\partial }{\partial R}\left( R\phi \right) {{\text{Re}}}\left( {\mathrm{i}}na{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) , $$
(52)

leading to

$$\bar{F}_{R}=\Omega \pi \left( {{\text{Re}}}\left( a\right) {{\text{Im}}}\left( \frac{{\mathrm{d}}a}{{\mathrm{d}}R}\right) -{{\text{Im}}}\left( a\right) {{\text{Re}}}\left( \frac{{\mathrm{d}}a}{{\mathrm{d}}R}\right) \right) +{\bar{\mathcal{F}}}_{R} ,$$
(53)
$$\bar{F}_{\Theta }=\frac{\Omega \pi n}{R}\left( {{\text{Re}}}\left( a\right) ^{2}+{{\text{Im}}}\left( a\right) ^{2}\right) +{\bar{\mathcal{F}}}_{\Theta }, $$
(54)

where Im denotes the imaginary part and

$${\bar{\mathcal{F}}}_{R}=\int _{0}^{1}{\mathcal{F}}_{R}{\mathrm{d}}\tau ^{\prime } ,\quad {\bar{\mathcal{F}}}_{\Theta }=\int _{0}^{1}{\mathcal{F}}_{\Theta } {\mathrm{d}}\tau ^{\prime }. $$
(55)

A further point omitted in earlier work[2,7] was whether [46], even without \(\phi \left( R,\tau \right) ,\) would satisfy [33]. Substituting [39] and [46] into [33], we obtain

$$\Omega \frac{\partial \phi }{\partial \tau }-\frac{\partial ^{2}\phi }{\partial R^{2}}-\frac{1}{R}\frac{\partial \phi }{\partial R}+\frac{\phi }{R^{2} }=-{{\text{Re}}}\left\{ \frac{{\mathrm{d}}}{{\mathrm{d}}R}\left( \frac{{\mathrm{d}}^{2}a}{{\mathrm{d}}R^{2}}+\frac{1}{R}\frac{{\mathrm{d}} a}{{\mathrm{d}}R}-\left( \frac{n^{2}}{R^{2}}+2\pi \Omega {\text{i}}\right) a\right) \right\} . $$
(56)

Thus, if \(\phi =0,\) [33] would be satisfied as a consequence of [40]; otherwise, we are left with

$$\Omega \frac{\partial \phi }{\partial \tau }=\frac{\partial ^{2}\phi }{\partial R^{2}}+\frac{1}{R}\frac{\partial \phi }{\partial R}-\frac{\phi }{R^{2}}, $$
(57)

and there appears to be no more information available to determine \(\phi .\)

To gain further insight, consider a formulation in terms of a magnetic vector potential, \({\varvec{A}}=\left( 0,0,A\right) .\) To cut down on the algebra, we revert briefly to Cartesian (X, Y) coordinates, so that \(\left( B_{X},B_{Y},0\right) ={{\text{curl}}}{\varvec{A}}\) and \(A=A\left( X,Y\right) \) with

$$X=R\cos \theta ,\quad Y=R\sin \theta ; $$
(58)

however, for later use, we note that

$$B_{R}=\frac{1}{R}\frac{\partial A}{\partial \theta },\quad B_{\theta } =-\frac{\partial A}{\partial R}. $$
(59)

The nondimensionalized versions of the X- and Y-components of Eq. [16] give, in the small \({\mathrm{Re}}_{\mathrm{m}}\) limit,

$$\frac{\partial }{\partial Y}\left( \Omega \frac{\partial A}{\partial \tau } -\frac{\partial ^{2}A}{\partial X^{2}}-\frac{\partial ^{2}A}{\partial Y^{2} }\right)=0,$$
(60)
$$\frac{\partial }{\partial X}\left( \Omega \frac{\partial A}{\partial \tau } -\frac{\partial ^{2}A}{\partial X^{2}}-\frac{\partial ^{2}A}{\partial Y^{2} }\right)=0, $$
(61)

leading, on integrating with respect to Y and X, respectively, to

$$\Omega \frac{\partial A}{\partial \tau }=\frac{\partial ^{2}A}{\partial X^{2}}+\frac{\partial ^{2}A}{\partial Y^{2}}+\gamma _{1}\left( X,\tau \right) ,$$
(62)
$$\Omega \frac{\partial A}{\partial \tau }=\frac{\partial ^{2}A}{\partial X^{2}}+\frac{\partial ^{2}A}{\partial Y^{2}}+\gamma _{2}\left( Y,\tau \right) , $$
(63)

where \(\gamma _{1}\) and \(\gamma _{2}\) are functions to be determined; however, since X and Y are independent variables, clearly \(\gamma _{1}\) and \(\gamma _{2}\) can only be functions of \(\tau \) with \(\gamma _{1}=\gamma _{2}\left( =\gamma \right) .\) We can write \(A=\bar{A}+\frac{1}{\Omega } \int ^{\tau }\gamma \left( t^{\prime }\right) {\mathrm{d}}t^{\prime },\) so that [62] and [63] both give

$$\Omega \frac{\partial \bar{A}}{\partial \tau }=\frac{\partial ^{2}\bar{A}}{\partial X^{2}}+\frac{\partial ^{2}\bar{A}}{\partial Y^{2}}. $$
(64)

Reverting back to (\(R,\theta \)) coordinates, this becomes

$$\Omega \frac{\partial \bar{A}}{\partial \tau }=\frac{1}{R}\frac{\partial }{\partial R}\left( R\frac{\partial \bar{A}}{\partial R}\right) +\frac{1}{R^{2}} \frac{\partial ^{2}\bar{A}}{\partial \theta ^{2}} $$
(65)

with [36] now being given by

$$\frac{\partial \bar{A}}{\partial \theta }=\cos \left( 2\pi \tau -n\theta \right) \quad {\text{at}}\;R=1, $$
(66)

which can be integrated with respect to \(\theta \) to give

$$\bar{A}=-\frac{1}{n}\sin \left( 2\pi \tau -n\theta \right) +A^{*}\left( \tau \right) \quad {\text{at}}\;R=1, $$
(67)

where \(A^{*}\left( \tau \right) \) is a function of \(\tau \) that would need to be determined. We should also expect that

$$\bar{A}\quad {\text{finite}}\quad {\text{at}}\;R=0. $$

Setting \(\bar{A}=\bar{A}_{1}+\bar{A}_{2},\) the original problem for \(\bar{A}\) is broken up into two problems, one for \(\bar{A}_{1}\) and one for \(\bar{A} _{2}.\) The problem for \(\bar{A}_{1}\) is given by

$$\Omega \frac{\partial \bar{A}_{1}}{\partial \tau }=\frac{1}{R}\frac{\partial }{\partial R}\left( R\frac{\partial \bar{A}_{1}}{\partial R}\right) +\frac{1}{R^{2}}\frac{\partial ^{2}\bar{A}_{1}}{\partial \theta ^{2}}, $$
(68)

subject to

$$\bar{A}_{1}=-\frac{1}{n}\sin \left( 2\pi \tau -n\theta \right) \quad {\text{at}}\;R=1, $$
(69)

while the problem for \(\bar{A}_{2}\) is given by

$$\Omega \frac{\partial \bar{A}_{2}}{\partial \tau }=\frac{1}{R}\frac{\partial }{\partial R}\left( R\frac{\partial \bar{A}_{2}}{\partial R}\right) +\frac{1}{R^{2}}\frac{\partial ^{2}\bar{A}_{2}}{\partial \theta ^{2}}, $$
(70)

subject to

$$\bar{A}_{2}=A^{*}\left( \tau \right) \quad {\text{at}}\;R=1. $$
(71)

It is worth pointing out that the decomposition of a problem for the function of interest, in this case \(\bar{A},\) into a sequence of simpler subproblems in this way is an established mathematical procedure; see, for example, the book by Carslaw and Jaeger.[20] In the current context, we can note also that boundary condition [69] for \(\bar{A}_{1}\) can be set without knowing details about \(\bar{A}_{2}.\)

For the \(\bar{A}_{1}\)-problem, setting

$$\bar{A}_{1}=\frac{1}{n}{{\text{Re}}}\left( {\mathrm{i}}\bar{a} {\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) , $$
(72)

we have

$$\frac{1}{R}\frac{{\mathrm{d}}}{{\mathrm{d}}R}\left( R\frac{{\mathrm{d}}\bar{a} }{{\mathrm{d}}R}\right) -\left( \frac{n^{2}}{R^{2}}+2\pi \Omega {\mathrm{i}} \right) \bar{a}=0, $$
(73)

subject to

$$\bar{a}=1\quad {\text{at}}\;R=1 $$
(74)

and

$$\bar{a}\quad {\text{finite}}\quad {\text{at}}\;R=0. $$
(75)

Notice also that \(\bar{a}\) satisfies the same differential equation as a,  i.e., [40], although the boundary condition at \(R=0\) is less constrained. Nevertheless, although \(Y_{n},\) the Bessel function of the second kind, would also satisfy [40], it is unbounded at \(R=0,\) which is why it was omitted earlier. Nevertheless, Eq. [75], although less constraining than [42], does not permit \(Y_{n}\) as a viable solution either, and the solution for \(\bar{a}\) is in effect the same as that for a earlier.

However, we are still left with the \(\bar{A}_{2}\)-problem, consisting of Eqs. [70] and [71]. Note that even if \(\gamma \ne 0,\) \(B_{R}\) can still satisfy [40]. Moreover, it is still possible that \(\bar{A}_{2}\ne 0,\) which will ultimately mean that \(B_{\theta }\) is not uniquely determined.

New Solution

Now consider what happens if we replace [25] by a boundary condition on the tangential component of \({\mathbf{B}},\) \(B_{\theta },\) instead; we can easily demonstrate that there will be a unique solution for \(\bar{A}\) and hence for \(B_{R}\) and \(B_{\theta }.\) To see this, we replace [25] by

$$B_{\theta }=\cos \left( 2\pi \tau -n\theta \right) \quad {\text{at}}\;R=1, $$
(76)

which leads to [66] being replaced by

$$\frac{\partial \bar{A}}{\partial R}=-\cos \left( 2\pi \tau -n\theta \right) \quad {\text{at}}\;R=1; $$
(77)

we will relate this new problem to the original problem shortly, although it is a natural replacement: if \(B_{R}\) exhibits periodic behavior at \(R=1,\) we would expect \(B_{\theta }\) also to have periodic behavior. Note that built into Eq. [76] is the assumption that the maximum value for \(B_{\theta }\) at the edge of the domain is the same as the maximum value for \(B_{R};\) this is not an unreasonable starting point, since it corresponds to using the characteristic value, \(B_{0},\) that has presumably been obtained from an experiment. Furthermore, from a mathematical point of view, it is also well established that with [77] as a boundary condition for [65], there will be a unique solution for \(\bar{A}\), provided that an initial condition for \(\bar{A}\) is prescribed; see, for example, the book by Protter and Weinberger.[21] In the present case, where we seek periodic solutions for \(\bar{A},\) we do not set an initial condition for \(\bar{A},\) but use an ansatz for \(\bar{A}\) of the type used in Eq. [72]; although the resulting solution is only unique up to a constant, this is still enough to give unique solutions for \(B_{R}\) and \(B_{\theta },\) since these are obtained by taking the spatial derivatives of \(\bar{A}.\)

To demonstrate these ideas more concretely, we set about solving [65] subject to [77] directly. First of all, note that if \(\bar{A}\) is a solution of these equations, then so is \(\bar{A}+C^{*},\) where \(C^{*}\) is an arbitrary constant; this is the constant mentioned in the previous paragraph, and henceforth we set it to zero, as it does not affect the analysis. Then, setting

$$\bar{A}={{\text{Re}}}\left( a{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) , $$
(78)

where once again \(a=a\left( R\right) ,\) Eq. [65] gives

$$\frac{{\mathrm{d}}^{2}a}{{\mathrm{d}}R^{2}}+\frac{1}{R}\frac{{\mathrm{d}} a}{{\mathrm{d}}R}-\left( \frac{n^{2}}{R^{2}}+2\pi \Omega {\text{i}}\right) a=0, $$
(79)

subject to

$$\frac{{\mathrm{d}}a}{{\mathrm{d}}R}=-1\quad {\text{at}}\;R=1,$$
(80)
$$a=0\quad {\text{at}}\;R=0. $$
(81)

The first of these comes from [77], whereas the second comes from the requirement that \(B_{R}\) is finite at \(R=0;\) from [59] and [78], it is quickly evident that [81] must hold.

The solution for a is now given by

$$a=\frac{J_{n}\left( R\sqrt{2\pi \Omega }{\mathrm{e}}^{3\pi {\mathrm{i}}/4}\right) }{\sqrt{2\pi \Omega }{\mathrm{e}}^{3\pi {\mathrm{i}}/4}J_{n}^{\prime }\left( \sqrt{2\pi \Omega }{\mathrm{e}}^{3\pi {\mathrm{i}}/4}\right) }, $$
(82)

with the prime denoting differentiation with respect to R,  and, having found a,  we obtain

$$B_{R}=-\frac{1}{R}{{\text{Re}}}\left( n{\mathrm{i}}a{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) ,\quad B_{\theta }=-{{\text{Re}}}\left( \frac{{\mathrm{d}}a}{{\mathrm{d}}R}{\mathrm{e}}^{{\mathrm{i}}\left( 2\pi \tau -n\theta \right) }\right) . $$
(83)

This time, it is clear that the solutions for \(B_{R}\) and \(B_{\theta }\) are unique.

Table I Model Parameters
Full size table

By this stage, it has become evident that using [76] is certainly sufficient in order to obtain \(B_{r}\) and \(B_{\theta }\) uniquely. However, it is certainly not a necessary condition: applying the result from Protter and Weinberger,[21] it is evident that a unique solution for \(\bar{A},\) and hence \(B_{r}\) and \(B_{\theta },\) can be obtained if \(\bar{A}\) satisfies a boundary condition of the form

$$\alpha \left( \theta ,\tau \right) \bar{A}+\beta \left( \theta ,\tau \right) \frac{\partial \bar{A}}{\partial R}=\delta \left( \theta ,\tau \right) $$
(84)

at \(R=1,\) for functions \(\alpha ,\beta ,\delta .\) In particular, if \(\alpha \equiv 0,\) this simply reduces to a condition on \(B_{\theta }\) once again. However, one motivation for using [76] as an alternative boundary condition for the problem was that it permitted instructive analysis that contrasts starkly with that which results when prescribing a boundary condition on \(B_{r}.\) Secondly, as we see next, it permits the original solution from earlier work[2,7] to be recovered in a time-averaged sense.

Results

It is of interest to compare this new solution with the one from earlier work,[2,7] although this needs to be done carefully for the comparison to be meaningful; we have, after all, replaced one boundary condition with another. In order to fix ideas, we use input data from earlier work[7]; this is given in Table I.

Fig. 3
figure 3

\({{\text{Re}}}\left( a\right) \) as a function of R :  (a) earlier solution[2,7] and (b) new solution

Full size image
Fig. 4
figure 4

\({{\text{Im}}}\left( a\right) \) as a function of R:  (a) earlier solution[2,7] and (b) new solution

Full size image
Fig. 5
figure 5

\(\bar{F}_{R}\) as a function of R:  (a) earlier solution[2,7] and (b) new solution

Full size image
Fig. 6
figure 6

\(\bar{F}_{\Theta }\) as a function of R:  (a) earlier solution[2,7] and (b) new solution

Full size image

First of all, it makes sense to compare \(a\left( R\right) \) and this is done in Figures 3 and 4 for \({{\text{Re}}}\left( a\right) \) and \({{\text{Im}}}\left( a\right) ,\) respectively, for three different values of \(\Omega ;\) these values correspond to \(f=10,30,50\) Hz, which covers the range considered by Tacke and Schwerdtfeger.[7] Not surprisingly, in view of the differing boundary conditions at \(R=1,\) the profiles are entirely different.

Noting now that the functional forms of expressions for \(\bar{F}_{R}\) and \(\bar{F}_{\Theta }\) are the same as before, i.e., [53] and [54] with \({\bar{\mathcal{F}}}_{R}={\bar{\mathcal{F}}}_{\Theta }=0\), Figures 5 and 6 show \(\bar{F}_{R}\) and \(\bar{F}_{\Theta }\) as the functions of R for the same three values as shown in Figures 3 and 4. It is readily apparent that the earlier and new solutions for a lead to profiles for \(\bar{F}_{R}\) and \(\bar{F}_{\Theta }\) that each differ simply by a multiplicative constant; however, the constant is different for each value of \(\Omega .\)

Fig. 7
figure 7

\(\psi \) as a function of f

Full size image
Fig. 8
figure 8

\(n{\mathcal{R}}_{a}\) as a function of f

Full size image
Fig. 9
figure 9

\(\lambda \) as a function of \({\mathrm{Re}}_{\mathrm{m}}\) for different values of \(\Omega \)

Full size image

To understand this, we express \(a\left( 1\right) \) for the new solution as

$$a\left( 1\right) ={\mathcal{R}}_{a}{\mathrm{e}}^{{\text{i}}\psi }, $$
(85)

where

$${\mathcal{R}}_{a}=\sqrt{{{\text{Re}}}^{2}\left( a\left( 1\right) \right) +{{\text{Im}}}^{2}\left( a\left( 1\right) \right) },\quad \psi =\tan ^{-1}\left( \frac{{{\text{Im}}}\left( a\left( 1\right) \right) }{{{\text{Re}}}\left( a\left( 1\right) \right) }\right) . $$
(86)

Thence, we find

$$\left( B_{R}\right) _{R=1}=n{\mathcal{R}}_{a}\cos \left( 2\pi \tau -n\theta -\frac{\pi }{2}+\psi \right) , $$
(87)

which implies that the new solution has a phase shift of \(\psi -\frac{\pi }{2},\) as compared to the earlier solution, and that \(\left( B_{R}\right) _{R=1}\) will have a maximum value of \(n{\mathcal{R}}_{a};\) however, both \(\psi \) and \(n{\mathcal{R}}_{a}\) will depend on \(\Omega ,\) and these dependencies are shown in Figures 7 and 8, respectively. This means that if the value of \(B_{0}\) in the earlier solution is replaced by \(B_{0}/n{\mathcal{R}}_{a}\) for the new solution, the two solutions would have identical behavior at \(R=1\), save for the shift in \(\psi -\pi /2;\) however, this shift is without consequence as regards \(\bar{F}_{R}\) and \(\bar{F}_{\Theta },\) since these are calculated as time averages over one period of oscillation. Thus, a comparison of the profiles in Figures 5(a) and 6(a) with those in Figures 5(b) and 6(b), divided by \(\left( n{\mathcal{R}}_{a}\right) ^{2},\) would yield identical results.

Discussion

Thus, so far, we have found that the expressions for \(\bar{F}_{R}\) and \(\bar{F}_{\Theta }\) are the same as those found in earlier work when \({\mathrm{Re}}_{\mathrm{m}}=0;\) this might have been expected from the discussion given after Eq. [77] concerning the identical spatial and temporal periodicity of \(B_{R}\) and \(B_{\theta },\) and the same scaling with the imposed magnetic flux density \(B_{0}.\) In this sense, it might be argued that the original assumption that \(\phi \left( R,\tau \right) =0\) was in fact correct; however, it needs to be remembered that this is not the case if \({\mathrm{Re}}_{\mathrm{m}}\ne 0,\) and even if \({\mathrm{Re}}_{\mathrm{m}}=0\) the actual expressions for \(B_{r}\) and \(B_{\theta }\) are different to those in earlier work, as seen in the differences in a shown in Figures 3 and 4.

Now, if \({\mathrm{Re}}_{\mathrm{m}}\ne 0,\) the equations for a and \(V_{\theta }\) will be coupled, and in the form

$$0=\frac{1}{R^{2}}\frac{{\mathrm{d}}}{{\mathrm{d}}R}\left\{ \left( 1+\bar{\mu }_{\mathrm{T}}\right) R^{2}\left( \frac{{\mathrm{d}}V_{\theta }}{{\mathrm{d}}R} -\frac{V_{\theta }}{R}\right) \right\} +\left( \frac{\mathrm{Ha}^{2}}{{\mathrm{Re}}_{\mathrm{m}}}\right) \frac{\Omega \pi n}{R}\left( {{\text{Re}}}\left( a\right) ^{2} +{{\text{Im}}}\left( a\right) ^{2}\right) , $$
(88)
$$\frac{{\mathrm{d}}^{2}a}{{\mathrm{d}}R^{2}}+\frac{1}{R}\frac{{\mathrm{d}} a}{{\mathrm{d}}R}-\left( {\text{i}}\left( 2\pi \Omega -{\mathrm{Re}}_{\mathrm{m}}n\frac{V_{\theta }}{R}\right) +\frac{n^{2}}{R^{2}}\right) a=0. $$
(89)

This time, we have a coupled nonlinear system of ordinary differential equations, and there is no reason to expect our modified problem to give the same expressions for \(\bar{F}_{R}\) and \(\bar{F}_{\Theta }\) as the original one. This leads to a wider issue: if it is only \(\left( B_{r}\right) _{r=r_{b}}\) that can be used as input data from an experiment, how can these data be used to obtain a unique solution? Solving [88] and [89], subject to [34], [35], [80], and [81], would once again give \(a\left( 1\right) ,\) and thence \({\mathcal{R}}_{a},\) with the maximum value of \(\left( B_{R}\right) _{R=1}\) being \(n{\mathcal{R}}_{a}.\) However, instead of replacing the original value of \(B_{0}\) by \(B_{0}/n{\mathcal{R}}_{a}\) this time, we should modify Eq. [80] to give

$$\frac{{\mathrm{d}}a}{{\mathrm{d}}R}=-\lambda \quad {\text{at}}\;R=1, $$
(90)

where \(\lambda \) is a real constant to be determined, and iterate for \(\lambda \) until \(n{\mathcal{R}}_{a}=1.\) In general, \(\lambda \) will depend on \({\mathrm{Re}}_{\mathrm{m}},\) as well as \(\Omega .\) This is a fairly straightforward numerical task and we omit the details. Instead, we show in Figure 9 the obtained values of \(\lambda \) as a function of \({\mathrm{Re}}_{\mathrm{m}}\) for the three values of \(\Omega \) used earlier. Note that, on using Figure 8, we find that \(\lambda =1/n{\mathcal{R}}_{a}\) when \({\mathrm{Re}}_{\mathrm{m}}=0,\) as expected. Furthermore, we see that \(\lambda \) takes its greatest value when \({\mathrm{Re}}_{\mathrm{m}}=0\) and then decreases, before starting to increase again at around \({\mathrm{Re}}_{\mathrm{m}}=40.\)

Conclusions

This paper has revisited some early, yet still often-cited, mathematical models for electromagnetic stirring in continuous casting[2,3,4,5,6,7] and has found that the solutions obtained originally were not unique. Detailed analysis for the case of a round billet under rotary EMS shows how to avoid this behavior, whilst still making use of the experimental data that motivated the original models. Moreover, although the current results are for a round billet, they are of relevance for rectangular strands, in that they indicate that it is the tangential component of the magnetic flux density that must be prescribed at the boundary of the melt region, not the normal one. The issue seems to be linked to the fact that it was easier to measure the normal component of the field experimentally, and that it was therefore used as a boundary condition in the models[2,3,7]; however, the theory requires the tangential component for a unique solution. There are therefore, at least, two remedies:

  • to measure the tangential component, if possible;

  • to set an unknown tangential component in the model and iterate on it to find the experimentally obtained normal component.

For a round billet, we have shown how the second option can be implemented. However, the simplicity of this advice depends on the axisymmetric geometry, and new results will be needed for rectangular billet and bloom geometries undergoing either rotary EMS or linear traveling EMS. Nevertheless, it should be noted that the theorem from Protter and Weinberger[21] that was used in discussing possible necessary and sufficient conditions for the round billet case is actually valid for more general boundaries. Indeed, if [64] holds on a domain \(\Gamma \) which is bounded by a curve \(\partial \Gamma \) on which \(\bar{A}\) satisfies

$$\alpha \left( s,\tau \right) \bar{A}+\beta \left( s,\tau \right) \frac{\partial \bar{A}}{\partial \nu }=\delta \left( s,\tau \right) , $$
(91)

where s is the arc length around \(\partial \Gamma \) and \(\partial /\partial \nu \) is any directional derivative in an outward direction on \(\partial \Gamma ,\) then the solution for \(\bar{A},\) and hence \(B_{X}\) and \(B_{Y},\) will be unique. Furthermore, if \(\alpha \equiv 0,\) then [91] reduces simply to a condition on the tangential component of the magnetic field at \(\partial \Gamma \). In addition, if \(\partial \Gamma \) is a square or a rectangle, then it is clear that a billet or bloom geometry is being considered. At this stage, it is evident that the analysis is limited to the case of rotary EMS leading to a planar magnetic field that can be expressed in terms of a single function \(\bar{A}.\) Further work is needed to consider the situation when linear traveling EMS is used, as is the case for slabs, but also for blooms and billets; in this case, all three components of the magnetic vector potential may be nonzero.

The results obtained are of significance for a number of reasons. First, as detailed in the analysis, correct use of the experimentally measured normal component at the boundary in the model leads to a phase shift in time, as compared to the way that this component was originally used. As we have seen, this difference does not alter the time-averaged Lorentz force when the magnetic Reynolds is small enough and only one inductor frequency is used. However, in modulated EMS,[22,23,24] magnetic fields of different frequencies are applied and it is the intention that the resulting Lorentz force should have a constant time-averaged and a time-varying component; in this case, posing the correct boundary conditions for the magnetic field is vital for obtaining meaningful results from modeling.

Furthermore, although current-day software packages are in principle able to couple the fluid dynamics and electromagnetics and solve numerically for both the strand and the surrounding core, so that the issue regarding this boundary condition appears less relevant, it is nevertheless important if one is seeking to develop more fundamental models for understanding the effects of EMS on the mushy zone, for example dendrite fragmentation[25,26] and white band formation.[6,27,28,29,30] In this context, having to include a model for the surrounding core in order just to avoid this issue is clearly an inconvenience.