Phase-Field Simulation of Orowan Strengthening by Coherent Precipitate Plates in an Aluminum Alloy

Abstract

The density-functional theory and phase-field dislocation model have been used to compute and simulate the strength of θ′ plates and precipitate-dislocation interactions in an Al-4Cu-0.05Sn (wt pct) alloy that is strengthened exclusively by coherent θ′ precipitate plates. The density-functional theory computation indicates that a 1.06 GPa applied stress is required for a dislocation to shear through a θ′ plate, which is far larger than the critical resolved shear stress increment (ΔCRSS) of the peak-aged sample of the alloy. The ΔCRSS values of the alloy aged for 0.5, 3, 48, and 168 hours at 473 K (200 °C) are computed by the phase-field dislocation model, and they agree well with experimental data. The phase-field simulations suggest that the ΔCRSS value increases with an increase in plate aspect ratio and number density, and that the change of ΔCRSS is not sensitive to the variation of the distribution of θ′ plate diameters when the average diameter of θ′ plates is fixed, and that the coherency strain of θ′ plates does not contribute much to ΔCRSS of the alloy when the θ′ number density and aspect ratio are below certain values. The simulations further suggest that, when the volume fraction of θ′ is constant, the ΔCRSS value for a random spatial distribution of the θ′ plates is 0.78 times of that for a regular spatial distribution.

Appendices

Appendix A

To test whether the change of ΔCRSS is related to the distribution of planar diameters of precipitates, different types of planar diameter distributions are selected:

1.1 Degenerate distribution

In this case, the planar diameters of all precipitates are the same and equal to $\bar{d}$ _p, and $\bar{d}$ _p = 47.35 nm. Thus, f(d _p) has the following form:

$$ f\left( {d_{\text{p}} } \right) = \left\{ {\begin{array}{*{20}c} {1 \quad d_{\text{p}} = 47.35} \\ { 0 \quad d_{\text{p}} \ne 47.35} \\ \end{array} } \right. . $$

1.2 Bernoulli Distribution

Two arbitrary values are assumed for the planar diameters of precipitates: d _p1 = 10.0 nm and d _p2 = 84.7 nm. To make $\bar{d}$ _p equal to 47.35 nm, the number of precipitates of each size is equal. Thus, f(d _p) can be expressed as

$$ f\left( {d_{\text{p}} } \right) = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {0.5 \quad d_{\text{p}} = 10.0} \\ {0.5 \quad d_{\text{p}} = 84.7} \\ \end{array} } \\ {0 \qquad {\text{other}}} \\ \end{array} } \right. . $$

1.3 Uniform Distribution

The d _p values are uniformly distributed between 10 and 84.7 nm, i.e., the probability for a precipitate to have a planar diameter of any value between 10 and 84.7 nm is equal. Thus, f(d _p) has the following form:

$$ f\left( {d_{\text{p}} } \right) = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\frac{1}{84.7 - 10} \quad 10 < d_{\text{p}} < 84.7} \\ {0 \qquad \quad d_{\text{p}} < 10 \;{\text{or}} \quad d_{\text{p}} > 84.7} \\ \end{array} } \\ \end{array} } \right. . $$

Appendix B

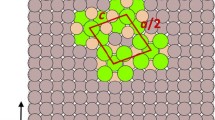
The α-Al matrix has a face-centered cubic structure with a = 0.404 nm, while θ′ has a tetragonal structure, with a = 0.404 nm and c = 0.58 nm.[39] As described in Section I, the orientation relationship between θ′ and α-Al phases is such that (100) _θ′ //(100) _α and [001] _θ′ //[001] _α . For the given lattice parameters, transformation strains are zero along the [100] _α and [010] _α directions. Along the [001] _α direction, the 2c _θ′ :3c _Al matching configuration is used,[59] and the corresponding transformation strain is 0.043. Therefore, if the [100] _α , [010] _α , and [001] _α directions are set as the x ₀, y ₀, and z ₀ directions, respectively, then the transformation matrices $T_{i}^{0}$ of the three θ′ variants are

$$ T_{1}^{0} = \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & {0.9570} \\ \end{array} } \right) , $$

$$ T_{2}^{0} = \left( {\begin{array}{*{20}c} {0.9570} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right) , $$

$$ T_{3}^{0} = \left( {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {0.9570} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right) . $$

$T_{i}^{0}$ needs to be transformed into the xyz coordinate system that is used in the current study, i.e., x: [11${\bar{\text{2}}}$] _α , y: [${\bar{\text{1}}}$10] _α, and z: [111] _α . For the x ₀ y ₀ z ₀ to xyz transformation, the transformation matrix R is

$$ R = \left( {\begin{array}{*{20}c} {0.4082} & {0.4082} & { - 0.8165} \\ { - 0.7071} & {0.7071} & 0 \\ {0.5774} & {0.5774} & {0.5774} \\ \end{array} } \right) . $$

After the change of the coordinate system, the transformation matrices become

$$ T_{1} = \left( {\begin{array}{*{20}c} {0.9713} & 0 & {0.0203} \\ 0 & 1 & 0 \\ {0.0203} & 0 & {0.9857} \\ \end{array} } \right) , $$

$$ T_{2} = \left( {\begin{array}{*{20}c} {0.9928} & {0.0124} & { - 0.0101} \\ {0.0124} & {0.9785} & {0.0176} \\ { - 0.0101} & {0.0176} & {0.9857} \\ \end{array} } \right) , $$

$$ T_{3} = \left( {\begin{array}{*{20}c} {0.9928} & { - 0.0124} & { - 0.0101} \\ { - 0.0124} & {0.9785} & { - 0.0176} \\ { - 0.0101} & { - 0.0176} & {0.9857} \\ \end{array} } \right) . $$

The SFTS of the α-Al to θ′ transformation can be obtained from the transformation matrice according to the following relationship:

$$ \varepsilon \left( p \right) = \frac{{T_{p}^{\prime} T_{p} - I}}{2}, \quad p = 1, 2, 3. $$