1 Introduction

In most practical control systems, unexpected faults or failures are often unknown and occur at uncertain time in most cases. These malfunctions may lead to degradation of performance and even to system instability. To improve the reliability of such systems, research on faults detection and isolation has received considerable attention in the past two decades (see [1 – 4]). Specially, several researches have exploited the fuzzy modeling approach for control and diagnosis of nonlinear systems (see [5 – 9]). Indeed, the main feature of a Takagi-Sugeno (T-S) fuzzy model is based on the interpolation of linear sub-models by nonlinear weighting functions satisfying the convex sum property. These sub-models represent local behaviors of the nonlinear system. Therefore, the T-S fuzzy model has proven to be a powerful tool in the analysis and identification of nonlinear and complex system[10–12].

Very interesting approaches were proposed for diagnosis of T-S fuzzy systems subject to sensor and actuator faults by using different techniques. These techniques include sliding mode observer, piecewise Lyapunov functions, linear matrix inequality (LMI) approach, fuzzy descriptor approach, adaptive thresh-old technique and bounded-error approach (BEA algorithm) (see [13 – 17]). Special attention was given to the diagnosis of T-S fuzzy systems with H ∞performance[4,18]. In [14], a robust observer was presented and applied to electro-mechanical pitch drive systems of wind. The synthesis of this observer is based on faults detection approach combined with the sliding mode for T-S fuzzy systems. The problem of H ∞ fuzzy observer based nonparallel distributed compensation (Non-PDC) controller design for uncertain T-S fuzzy systems with external disturbances was proposed in [19]. This is done using a fuzzy Lya-punov function and the descriptor redundancy approach. The authors in [20] developed a singular approach to design an observer for T-S fuzzy systems with unknown output disturbance and its application to estimate sensor faults. The singular approach was also developed in [18] to investigate H_/H ∞ faults estimation and detection for T-S fuzzy systems with unknown bounded disturbance. The problem is solved with a sufficient conditions based on an iterative LMI procedure[21]. In [22] a fuzzy adaptive backstepping output feedback control was constructed for a class of nonlinear systems with unknown time-delay based on a fuzzy observer to estimate unmeasured states. The authors in [23] proposed a robust fault detection approach for nonlinear systems using Lyapunov techniques and provided a sufficient condition for the existence of a robust observer.

In this study, motivated by the work in [24], we use the fuzzy descriptor approach to investigate sensor faults estimation with unmeasurable premise variables of T-S fuzzy system affected by unknown bounded disturbance. By considering the sensor faults term as an auxiliary state vector, an augmented descriptor system is constructed. A suitable Lyapunov matrix in the form of LMI is used to find out the gains of the fuzzy observer with H ∞ performance without recourse to the hard calculation of block matrix inversion which gives nonlinear and complex terms like in [24].

The outline of this paper is as follows. In Section 2, the class of studied systems and a background results are given. Robust fault detection based-observer design with unmeasurable premise variables is given in Section 3. Section 4 presents an example to illustrate the effectiveness of the proposed method. Concluding remarks are given in Section 5.

Notation. X T and X −1 are the transpose and the inverse of matrix X, respectively. Sym(X) = X + X T. I is the identity matrix with appropriate dimension.

2 System description and background results

Consider the nonlinear system described by the following fuzzy IF-THEN rules:

Rule i:

IF ξ 1(t) is M 1i and, ⋯ , and ξ g (t) is M si , THEN

$$\begin{array}{*{20}{l}} {\dot x(t) = {A_i}x(t) + {B_i}u(t)} \\ {y(t) = Cx(t)} \end{array}$$
(1)

where x(t) ∈ R n is the state vector, u(t) ∈ R m is the input vector and y(t) ∈ R p is the output vector. A i , B i and C are constant real matrices with appropriate dimensions. ξ j (j = 1, ⋯ , s) are the fuzzy sets and r is the number of rules.

By fuzzy blending, the overall fuzzy model with sensor faults f s(t) and affected by unknown bounded disturbance d(t) is inferred as follows:

$$\begin{array}{*{20}{l}} {\dot x(t) = \sum\limits_{i = 1}^r {{\mu _i}} \left( {{A_i}x(t) + {B_i}u(t) + {B_d}d(t)} \right)} \\ {y(t) = Cx(t) + {D_s}{f_s}(t)} \end{array}$$
(2)

where

$$\begin{array}{*{20}{l}} {{\mu _i}(\xi (t)) = \frac{{{\omega _i}(\xi (t))}}{{\sum\limits_{i = 1}^r {{\omega _i}(\xi (t))} }}} \\ {{\omega _i}(\xi (t)) = \prod\limits_{j = 1}^r {{M_{ij}}(\xi (t)).} } \end{array}$$

Hence, µ i (ξ(t)) satisfies

$$\sum\limits_{i = 1}^r {{\mu _i}(\xi (t))} = 1\quad \operatorname{and} \quad {\mu _i}(\xi ) > 0\quad \operatorname{for} \quad i = 1, \cdots r$$

where B d and D s are matrices with appropriate dimensions. For sake of simplicity, the time variable (t) is omitted in the followings.

In order to estimate state vector x and sensor fault f s , an augmented system is constructed using the descriptor technique. Then the T-S fuzzy system (2) can be written as follows:

$$\begin{array}{*{20}{l}} {\bar E\dot \bar x = \sum\limits_{i = 1}^r {{\mu _i}(\xi )} \left( {({{\bar A}_i}\bar x + {{\bar B}_i}u) + N{x_s} + {{\bar B}_d}d} \right)} \\ {y = \bar C\bar x = {C_0}\bar x + {x_s}} \end{array}$$
(3)

where

$$\begin{array}{*{20}{c}} {{x_s} = {D_s}{f_s},\bar x = \left[ {\begin{array}{*{20}{l}} x \\ {{x_s}} \end{array}} \right]} \\ {\bar E = \left[ {\begin{array}{*{20}{c}} {{I_n}}&0 \\ 0&0 \end{array}} \right],\;{{\bar A}_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ 0&{ - {I_p}} \end{array}} \right],\;{{\bar B}_i} = \left[ {\begin{array}{*{20}{c}} {{B_i}} \\ 0 \end{array}} \right]} \\ {N = \left[ {\begin{array}{*{20}{c}} 0 \\ {{I_p}} \end{array}} \right],\;{{\bar B}_d} = \left[ {\begin{array}{*{20}{c}} {{B_d}} \\ 0 \end{array}} \right],\;{C_0} = \left[ {C\quad 0} \right],\;\bar C = \left[ {C\quad {I_p}} \right].} \end{array}$$

Vector x s is considered as an auxiliary state of the augmented system (3). So if the state estimation of the augmented system (3) exists, then the state estimation of the original system (3) and the fault estimation exist too.

Based on this model, the following fuzzy observer structure is adopted

$$\begin{array}{*{20}{l}} {E\dot z = \sum\limits_{i = 1}^r {{\mu _i}(\xi )} \left( {{F_i}z + {{\bar B}_i}u} \right)} \\ {\hat \bar x = z + Ly} \end{array}$$
(4)

where z ∈ R n+p is an auxiliary state vector of the observer and \(\hat \bar x \in {{\mathbf{R}}^{n + p}}\) is the state estimation of (3).

Lemma 1[24]. If there exist positive definite symmetric matrices P 1 and P 2, matrix R, non singular matrix M and scalar γ > 0 such that the following LMI is satisfied for i = 1, ⋯ ,r,

(5)

then there exist a fuzzy observer in the form (4) to asymptotically estimate the state and fault sensor for fuzzy system (2). The observer parameters are given by

$${F_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ { - C}&{ - {I_p}} \end{array}} \right]$$
(6)
$$L = \left[ {\begin{array}{*{20}{c}} 0 \\ {{I_p}} \end{array}} \right]$$
(7)
$$E = \left[ {\begin{array}{*{20}{c}} {{I_n} + RC}&R \\ {MC}&M \end{array}} \right]$$
(8)

where

$$M = {(P_2^{ - 1}{Z_2} - CP_1^{ - 1}{Z_1})^{ - 1}}$$
(9)
$$R = P_1^{ - 1}{Z_1}M.$$
(10)

Remark 1. Conditions (5)–(10) in Lemma 1 were obtained by using Lyapunov techniques. This approach requires the calculation of the inverse of matrix E which yields nonlinear and complex terms. Moreover, the approach uses a diagonal Lyapunov matrix in the form P = diag(P 1,P 2) which is too restrictive.

Remark 2. The T-S model representation is very interesting since it allows to simplify the stability analysis of nonlinear systems. In [18,20,24], the authors used the tools inspired directly by the study of linear systems. In [25,26] the authors worked on the problem of state estimation and application for diagnosis of T-S fuzzy systems. However, they assumed that the premise variable ξ(t) is measurable, i.e., ξ(t) = u(t) or ξ(t) = y(t). In the diagnosis problem, this hypothesis imposes to conceive a bank of observers based on multiple models whose weighting functions depend on the input u(t), for the detection and isolation of the sensor faults, or on the output y(t) for the detection and isolation of the actuator fault. This requires the elaboration of two different T-S models for the same nonlinear system. Hence, it is interesting to develop only one T-S model which considers the system state as premise variable. This is the case of the present paper. Thus, in the next section we develop an observer to estimate the system state and the sensor fault for the system with weighting functions depending on the system state. The observer weighting functions will depend on the measurements.

3 Design of robust descriptor observer with unmeasurable premise variables

In this section, we assume that the weighting functions that depend on the system state, then system (2) becomes

$$\begin{array}{*{20}{l}} {\dot x = \sum\limits_{i = 1}^r {{\mu _i}(x)({A_i}x + {B_i}u) + {B_d}d} } \\ {y = Cx + {D_s}{f_s}.} \end{array}$$
(11)

Adding and subtracting the term \(\sum {_{i = 1}^r\left( {{\mu _i}(\hat x)} \right)\left( {{A_i}x + {B_i}u} \right)} \), we obtain the following equivalent system with the weighting functions depending on the estimated state.

$$\begin{array}{*{20}{l}} {\dot x = \sum\limits_{i = 1}^r {{\mu _i}(\hat x)({A_i}x + {B_i}u) + {B_d}d} + \omega } \\ {y = Cx + {D_s}{f_s}} \end{array}$$
(12)

where

$$\omega = \sum\limits_{i = 1}^r {({\mu _i}(x) - {\mu _i}(\hat x))\left( {{A_i}x + {B_i}u} \right)} .$$

The global system (12) can be rewritten as follows

$$\begin{array}{*{20}{l}} {\dot x = \sum\limits_{i = 1}^r {{\mu _i}(\hat x)({A_i}x + {B_i}u) + {{\tilde B}_d}v} } \\ {y = Cx + {D_s}{f_s}} \end{array}$$
(13)

where

In the augmented form, model (13) becomes

$$\begin{array}{*{20}{l}} {\bar E\dot \bar x = \sum\limits_{i = 1}^r {{\mu _i}(\hat x)({{\bar A}_i}\bar x + {{\bar B}_i}u) + N{x_s} + {{\bar \tilde B}_d}v} } \\ {y = \bar C\bar x = {C_0}\bar x + {x_s}} \end{array}$$
(14)

where

$$\begin{array}{*{20}{c}} {{x_s} = {D_s}{f_s},\bar x = \left[ {\begin{array}{*{20}{c}} x \\ {{x_s}} \end{array}} \right]} \\ {\bar E = \left[ {\begin{array}{*{20}{c}} {{I_n}}&0 \\ 0&0 \end{array}} \right],\;{{\bar A}_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ 0&{ - {I_p}} \end{array}} \right],\;{{\bar B}_i} = \left[ {\begin{array}{*{20}{c}} {{B_i}} \\ 0 \end{array}} \right],} \\ {N = \left[ {\begin{array}{*{20}{c}} 0 \\ {{I_p}} \end{array}} \right],\;{{\bar \tilde B}_d} = \left[ {\begin{array}{*{20}{c}} {{{\tilde B}_d}} \\ 0 \end{array}} \right],\;{C_0} = \left[ {C\quad 0} \right],\;\bar C = \left[ {C\quad {I_p}} \right].} \end{array}$$

Let us consider the following fuzzy observer with unmea-surable premise variables

$$\begin{array}{*{20}{l}} {E\dot z = \sum\limits_{i = 1}^r {{\mu _i}} (\hat x)({F_i}z + {{\bar B}_i}u)} \\ {\;\,\hat \bar x = z + Ly} \end{array}$$
(15)

where z ∈ R n +p is an auxiliary state vector of the observer and \(\hat \bar x \in {{\mathbf{R}}^{n + p}}\) is the state estimation of (3). By substituting \(z = \hat \bar x - L\bar C\bar x = \hat \bar x - L{C_0}\bar x - L{x_s}\) into the differential algebraic equation of (4), we obtain

$$E\dot \hat \bar x - EL\bar C\dot \bar x = \sum\limits_{i = 1}^r {{\mu _i}(\xi )} \left( {{F_i}(\hat \bar x - L{C_0}\bar x - L{x_s}) + {{\bar B}_i}u} \right).$$
(16)

Subtracting (16) from (3) yields

$$(\bar E + EL\bar C)\dot \bar x - E\dot \hat \bar x = {\bar \tilde B_d}v + \sum\limits_{i = 1}^r {{\mu _i}(\xi )} \times \left( {({{\bar A}_i} + {F_i}L{C_0})\bar x - {F_i}\hat \bar x + (N + {F_i}L){x_s}} \right).$$
(17)

Let the error estimation be defined by \(\bar e = \bar x - \hat \bar x\), and suppose that

$$E = \bar E + EL\bar C,$$
(18)
$${F_i} = {\bar A_i} + {F_i}L{C_0},$$
(19)
$$N = - {F_i}L.$$
(20)

The error dynamic can then be written as follows

$$E\dot \bar e = \sum\limits_{i = 1}^r {{\mu _i}(\xi ){F_i}\bar e + {{\bar \tilde B}_d}v.} $$
(21)

Notice that substituting (20) into (19) one gets

$${F_i} = \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ { - C}&{ - {I_p}} \end{array}} \right].$$
(22)

Considering (19) and taking account of the expression of Ā i above we get

$$\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ { - C}&{ - {I_p}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ 0&{ - {I_p}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ { - C}&{ - {I_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{L_1}} \\ {{L_2}} \end{array}} \right]\left[ {C\quad 0} \right] = } \\ {\quad \quad \quad \quad \quad \;\;\left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ 0&{ - {I_p}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{A_i}}&0 \\ { - C}&{ - {I_p}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{L_1}C}&0 \\ {{L_2}C}&0 \end{array}} \right] = } \\ {\quad \quad \quad \quad \quad \;\;\left[ {\begin{array}{*{20}{c}} {{A_i} + {A_i}{L_1}C}&0 \\ { - C{L_1}C - {L_2}C}&{ - {I_p}} \end{array}} \right]} \end{array}$$

from which a unique choice of L follows as L 1 = 0 and L 2 = I p or

$$L = \left[ {\begin{array}{*{20}{c}} 0 \\ {{I_p}} \end{array}} \right].$$
(23)

Therefore, condition (18) becomes

$$\begin{array}{*{20}{l}} {E = \left[ {\begin{array}{*{20}{c}} {{I_n}}&0 \\ 0&0 \end{array}} \right] + E\left[ {\begin{array}{*{20}{c}} 0&0 \\ C&{{I_p}} \end{array}} \right] = } \\ {\quad \;\;\;\left[ {\begin{array}{*{20}{c}} {{I_n}}&0 \\ 0&0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{E_{12}}C}&{{E_{12}}} \\ {{E_{22}}C}&{{E_{22}}} \end{array}} \right]} \end{array}$$

from which we get

$$\begin{array}{*{20}{l}} {{E_{11}} = {I_n} + {E_{12}}C} \\ {{E_{12}} = {E_{12}}} \\ {{E_{21}} = {E_{22}}C} \\ {{E_{22}} = {E_{22}}.} \end{array}$$

Let R = E 12 and M = E 22 ; then E becomes

$$E = \left[ {\begin{array}{*{20}{c}} {{I_n} + RC}&R \\ {MC}&M \end{array}} \right] = \bar E + K\bar C$$
(24)

with .

Matrices R and M can be chosen in such a way that E is invertible.

Then, the error dynamic (21) becomes

$$\dot \bar e = \sum\limits_{i = 1}^r {{\mu _i}(\hat x){S_i}\bar e + \tilde Gv} $$
(25)

where

$${S_i} = {E^{ - 1}}{F_i},\quad \tilde G = {E^{ - 1}}{\bar \tilde B_d}.$$
(26)

The following definition is borrowed from [27] with some adaptation concerning the initial conditions.

Definition 1 (H ∞ Problem). Given a real positive scalar γ, find the observer parameters such that the estimation error \(\bar e = \bar x - \hat \bar x\) is asymptotically stable with v(t) = 0 and the L 2 gain between v(t) and ē satisfies

(27)

where Φ(0) is a positive scalar depending on the initial conditions.

Notice that when Φ(0) = 0, that is, the case of null initial condition we get the standard expression used for the L 2 gain approach.

To satisfy the stabilization conditions of system (25), we propose Theorem 1 below.

Theorem 1. The T-S fuzzy system (25) is asymptotically stable and satisfies the H ∞ performances, if there exist a positive definite symmetric matrix X and a matrix Y such that the following LMI is satisfied, for i = 1, ⋯ , r

(28)

The observer parameters R and M are then given by

Proof. Consider the following Lyapunov function V(ē) = ē T Pē with P > 0 and a positive scalar γ such the following condition

(29)

holds.

Therefore, integrating the inequality above from zero to +∞, we get

from which we get

and since V(·) is positive it comes that (27) is satisfied and the system achieves an H ∞ bound less than γ.

Therefore, to satisfy (29) we have

from which we deduce that

(30)

is a sufficient condition to satisfy (29).

From (26), we can write

(31)

Note that matrix E depends on the unknown matrices R and M and to make the computation easier we have to get rid of the term E −1 and get as a consequence an LMI where R and M will be the decision variables. For this purpose, we rewrite (31) as follows:

(32)

and we proceed to a change of variable X = E – T PE −1 to get

(33)

Using (24), it comes then that condition (33) becomes

(34)

Since E is invertible and P > 0 so X is a positive definite and symmetric matrix.

Unfortunately, condition (28) is still not an LMI with respect to K. Therefore, to get an LMI condition we have to consider the change of variable Y = XK. Then, condition (28) becomes

(35)

To compute the observer parameters, the following procedure is proposed.

  1. 1)

    For a given γ, compute matrices X and Y by solving LMI (28).

  2. 2)

    Compute matrix K = X −1 Y.

  3. 3)

    Deduce the observer gains F i , L and E from (22), (23), and (24), respectively.

The sensor faults estimation is defined by

(36)

Remark 3. Comparing the obtained result with [24], we can see that in the present work a systematic method is provided in order to compute the observer parameters. The proposed method introduces more degrees of freedom by means of two additional variables, which may lead to less conservatism.

4 Numerical example

In order to illustrate the effectiveness of the proposed approach, we consider an academic T-S system in the form of (2) with the following matrices:

$$\begin{array}{*{20}{l}} {{A_1} = \left[ {\begin{array}{*{20}{c}} { - 2}&1&1 \\ { - 1}&{ - 3}&0 \\ { - 2}&1&{ - 8} \end{array}} \right],\;{A_2} = \left[ {\begin{array}{*{20}{c}} { - 3}&2&2 \\ { - 1}&{ - 3}&{0.2} \\ {0.5}&2&{ - 5} \end{array}} \right],\;{B_1} = \left[ {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ { - 2} \end{array}} \right]} \\ {{B_2} = \left[ {\begin{array}{*{20}{c}} 1 \\ { - 1} \\ {0.5} \end{array}} \right],\;C = \left[ {\begin{array}{*{20}{l}} 1&0&1 \\ 0&1&0 \end{array}} \right],\;{D_s} = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right],\;{B_d} = \left[ {\begin{array}{*{20}{c}} 1 \\ {0.5} \\ {0.8} \end{array}} \right].} \end{array}$$

The membership functions for rules 1 and 2 are

$${\mu _1} = \frac{{1 - \tanh ({x_1})}}{2},\quad {\mu _2} = \frac{{1 + \tanh ({x_1})}}{2} = 1 - {\mu _1}.$$

For a given γ = 0.68, we apply Theorem 1 and we get a feasible solution for LMI (28) as follows:

$$\begin{array}{*{20}{l}} {X = \left[ {\begin{array}{*{20}{c}} {0.44}&{0.32}&{ - 0.12}&{ - 0.42}&{ - 0.009} \\ {0.32}&{2.31}&{ - 1.41}&{1.76}&{ - 2.63} \\ { - 0.12}&{ - 1.41}&{3.79}&{ - 4.74}&{2.49} \\ { - 0.42}&{1.76}&{ - 4.74}&{236174.30}&{ - 2.91} \\ { - 0.09}&{ - 2.63}&{2.49}&{ - 2.91}&{236171.61} \end{array}} \right]} \\ {\;Y = \left[ {\begin{array}{*{20}{c}} {0.13}&{ - 0.05} \\ {0.21}&{ - 1.05} \\ { - 1.16}&{0.55} \\ {19682.75}&{ - 2328.38} \\ {2327.09}&{29522.69} \end{array}} \right],\;K = \left[ {\begin{array}{*{20}{c}} {0.44}&{0.15} \\ { - 0.18}&{ - 0.37} \\ { - 0.26}&{ - 0.08} \\ {0.08}&{ - 0.01} \\ {0.01}&{0.13} \end{array}} \right].} \end{array}$$

Matrices M and R are deduced from the equality K T = [R T M T] . The observer parameters are then computed from (22), (23) and (24) as follows:

We suppose the sensor fault in the following form:

$${f_s} = \left[ {\begin{array}{*{20}{c}} {{f_{s1}}} \\ {{f_{s2}}} \end{array}} \right]$$
(37)

where

$${f_{s2}} = \left\{ {\begin{array}{*{20}{l}} {0,}&{0 \leqslant t \leqslant 6} \\ {0.1( - 0.25t + 3.5)}&{6 \leqslant t < 8} \\ {0,}&{8 \leqslant t < 10} \\ { - 0.15}&{10 \leqslant t < 12} \\ {0,}&{12 \leqslant t < 14} \\ {0.15}&{14 \leqslant t < 16} \\ {0,}&{t \geqslant 16} \end{array}} \right.$$

and the input u = 0.1sin(t).

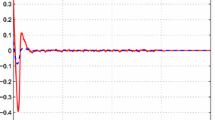
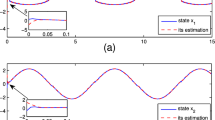
By applying Theorem 1, we obtain a set of feasible solutions. The descriptor observer provides the estimated states and faults. Figs. 1–3 show the state variables and their estimation. The sensor fault estimation is presented in Figs. 4 and 5. Fig. 6 shows the estimation of the weighting functions. By examining the different curves, we can say that the estimation quality of the system states and the sensors faults provides a satisfying result despite the presence of unknown bounded disturbance given by Fig. 7.

Fig. 1
figure 1

Variable state x 1 and its estimate

Full size image
Fig. 2
figure 2

Variable state x 2 and its estimate

Full size image
Fig. 3
figure 3

Variable state x 3 and its estimate

Full size image
Fig. 4
figure 4

Sensor fault f s1 and its estimate

Full size image
Fig. 5
figure 5

Sensor fault f s 2 and its estimate

Full size image
Fig. 6
figure 6

Weighting functions µ 1 (\({\mu _1}(\hat x)\)) and µ 2 (\({\mu _1}(\hat x)\))

Full size image
Fig. 7
figure 7

Disturbance d

Full size image

5 Conclusions

This paper presents a robust observer with unmeasurable premise variables for the T-S fuzzy model affected by sensor faults and bounded input disturbances using descriptor technique. In order to decouple the sensor faults, an augmented descriptor model has been constructed by assuming the sensor faults as an auxiliary state variable and the simultaneous estimates of the original state and sensor faults are thus obtained. The convergence of the proposed observer has been performed by the search of suitable Lyapunov matrices. The main results are formulated in the form of LMI with the H ∞ criterion. Finally, simulation results are presented to verify the effectiveness of the proposed method. The proposed observer can be extended to a technique for actuator fault estimation and fault tolerant control.