Introduction

The optimal recovery of hydrocarbon reserves necessitates a thorough understanding of reservoir quality and its lateral variations, which are crucial for accurate development planning (Nazemi et al. 2018; Bashir et al. 2021; Radwan et al. 2022; Derafshi et al. 2023; Mohsin et al. 2023). Building a reservoir model relies heavily on accurately describing lateral changes in reservoir heterogeneity (Lake and Jensen 1991; Wang 2021; Yazynina et al. 2021; Venieri et al. 2022). Lithology, porosity, permeability, and properties of porous fluids are among the key parameters used to describe reservoirs (Qu et al. 2019; Wang et al. 2022; Saberi et al. 2023; Taheri et al. 2022), as they significantly influence the seismic characteristics of a reservoir. Therefore, establishing a correlation between these parameters and seismic measurements is essential for predicting reservoir properties.

While drilling provides direct access to reservoir properties, the limited distribution of wells compared to the field's heterogeneity restricts the ability to obtain a comprehensive and continuous description of reservoir properties. To address this challenge, previous studies have proposed hybrid algorithms that utilize conventional well logs and flow zone index (FZI) to estimate open fracture permeability (Bagheri and Falahat 2021). However, seismic data remains the primary source of information for describing reservoirs within the field range. In recent years, the integration of seismic data with well-logging data has gained attention as an efficient tool for reservoir characterization (Makarian et al. 2023a, b; Mirhashemi et al. 2022). The utilization of the quality factor has proven particularly favorable due to advancements in vertical seismic profile (VSP) tools and processing software development. Studies by Ekanem et al. (2015) and Deng et al. (2023) have reported acceptable correlations between anisotropy, absorption coefficient in seismic data, and fluid viscosity. Additionally, investigations into seismic wave absorption centered on markers for fluids, fractures, and structural properties have been conducted in the Abu Dhabi oil field (Bouchaala et al. 2016; Abd Al-Aali et al. 2022).

Recent research has emphasized the significance of lithofacies identification and sand quality discrimination in illuminating reservoir properties and reducing uncertainties in hydrocarbon reservoir characterization. In an Iranian oilfield study, prestack Poisson impedance inversion (PI) and Poisson dampening factor (PDF) attributes were employed to identify lithofacies and discriminate zones with varying sand qualities (Ghanbarnejad Moghanloo and Riahi 2022). Additionally, a model for studying carbonate rocks with high heterogeneity was presented, comparing laboratory results of core and petrophysical evaluations and analyzing the absorption coefficient of VSP downgoing waves. Makarian et al. (2023a, b) conducted an analysis of longitudinal and transverse wave velocities and the numerical value of the quality factor to examine reservoir quality. Their findings indicated a decrease in the quality factor at lower values of the longitudinal-to-transverse wave velocity ratio.

Despite the growing attention paid to seismic absorption coefficients and quality factors in recent studies, the direct relationship between these parameters and reservoir properties has received limited attention, particularly in carbonate reservoirs (Raji and Rietbrock 2013; Wandycz et al. 2019; Larki et al. 2021; Olya and Mohebian 2023; Shuai et al. 2023). This study aims to investigate the impact and correlation between the quality factor and independent petrophysical and reservoir parameters, such as permeability, fracture density, and the amount of free gas per unit volume of porous space in a gas field. By utilizing multiple linear regression statistical analysis, we intend to extract reservoir quality conditions based on the quality factor, even in situations where sufficient reservoir data from logs and cores is not available.

In previous studies, image logs and sonic logs have played crucial roles in geological feature analysis, fracture detection, lithological variations, determination of rock properties, and geomechanical assessments (Elyasi et al. 2016; Larki et al. 2022; Roshan et al. 2023). However, in this research, we specifically focus on the utility of the quality factor as an independent indicator of reservoir quality, demonstrating its relatively accurate estimation capabilities even in the absence of other reservoir parameters. The integration of the quality factor with seismic data presents a promising approach to reservoir characterization and evaluation.

Overall, this study aims to enhance our understanding of carbonate reservoirs with high heterogeneity by investigating the correlation between the quality factor and key reservoir parameters. The results obtained will contribute to the extraction of reservoir quality conditions using quality factor data, providing valuable insights for reservoir characterization and management.

Geological setting

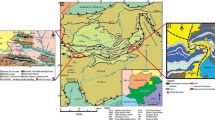
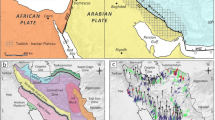
This study has been carried out in the Zagros sedimentary basin (ZSB) in the south of Iran and the north and northeastern parts of the Arabian Plate. To be more accurate, this independent plate extends over the Arabian Peninsula, along with Jordan, Syria, Iraq, and the Zagros Mountains of southwest Iran (Delchiaro et al. 2023). A tectonostratigraphic study shows that different sediment covers of the Arabian Plate lie on the crystalline Precambrian basement, which is exposed in the western parts of the plate. Extensive research shows that ZSB was formed of a thick layer of terrigenous (more sandstone and shale) carbonate and evaporate formations, which play an important role as source, reservoir, and cap rock in the huge hydrocarbon system in the area (Sun et al. 2023). The interested intervals, including carbonate-evaporate formations, belong to the Lower Permian and Triassic periods. Investigations show that, in terms of lithology, a part of the researched zone includes medium- to thick-bedded oolitic to micritic shallow-marine carbonates, locally reefed, with intercalations of evaporites (Zarei et al. 2023). Another part consists of bioclastic limestone at the basal part, which is overlain by an alternation of dolomitic limestone, dolomite, and occasional anhydrite layers toward the top. Tectonically, the area is currently not affected by faulting or special fracture settings (Karimian Torghabeh et al. 2023).

Methodology

In this study, first, with the help of petrophysical logs, including sonic logs, neutron logs, and density logs, velocity deviation logs are obtained. The quantitative fracture density is calculated using the electrical image log interpretation information. This method defines and calculates the number of fractures along the good axis per meter. The amount of free gas per porous volume obtained from the petrophysical interpretation and the permeability from the core analysis is used to validate the results of this study. Figure 1 shows a schematic of the step-by-step process of this research.

Fig. 1
figure 1

Step-by-step schematic of the research outline

Full size image

This study collected data from two appraisal wells in a gas field, including petrophysical logs, electrical image logs (in two wells), vertical seismic profiles, and core data. In the next step, after quality control of the data in reservoir formations, the fracture density was quantitatively calculated while determining natural fractures using imaging logs. Then, with the help of porosity logs, velocity deviation logs were calculated for each of the wells. The quality factor was calculated after processing and reducing the true amplitude recovery for the downgoing waves in the VSP data. The quality factor and the velocity deviation log in the reservoir areas were compared in the next step. Then, using core data, the correlation between reservoir parameters and quality factors was evaluated by the multiple linear regression statistical method. Finally, the quality of the reservoir was evaluated by cluster analysis.

The amount of quality factor for the total well distances is calculated using the downgoing waves of the vertical seismic profile data processed by the spectral ratio method. In each formation, the value of the correlation between the quality factor and velocity deviation index is examined and validated. Then, in one of the studied wells where core information is available, the correlation between key reservoir parameters such as permeability and the amount of free gas with the quality factor is investigated by statistical analysis of multiple linear regression. In the following, the quality of the reservoir interval will be quantified using the K-Means cluster analysis.

Results and discussion

Velocity deviation log

Separation of different types of pores, as well as separation of sedimentary and diagenetic environments, can be done in common petrophysical logs, including sonic logs (DT), neutron logs (NPHI), and density logs (RHOB). The velocity deviation log is a synthetic log calculated from a combination of porosity logs using the Wiley equation (Wyllie et al. 1956). Numerous studies have been conducted in this regard (Anselmetti and Eberli 1999; Anselmetti and Eberli 1993; Hirmohamadi et al. 2017, Salih et al. 2023). The velocity deviation log can provide information about the main porosity types of carbonates, the distribution of diagenetic voids, and the permeability of the reservoir. This log is the difference between the values of real compressional wave velocity (Vpreal) and synthetic compressional wave velocity (Vpsyn). The real compressional wave velocity is determined according to Eq. 1:

$$Vp_{{{\text{real}}}} = \frac{304.8}{{{\text{DT}}_{\log } }},$$
(1)

DTlog، sonic log reading is in microseconds per foot.

The synthetic compressional wave velocity can also be obtained according to Eq. 2:

$$V{\text{p}}_{{{\text{syn}}}} = \frac{304.8}{{{\text{DT}}_{{{\text{syn}}}} }}.$$
(2)

Porosity relations are used to obtain the synthetic sonic log (DTsyn). The porosity obtained from the sonic log is obtained through Eq. 3. In this relation, neutron-density porosity is placed instead of sonic porosity, and the DTsyn log is calculated through this relation. Given

The fluid type is saline, and the DTfl is 189.5 microseconds per foot (Serra 2004; Ali et al. 2023).

$$Q = \frac{{ - \pi f\delta t_{2 - 1} }}{{\ln \left( {A_{2} /A_{1} } \right)}}.$$
(3)

Thus, the velocity deviation log can be calculated from the difference in velocity between Eq. 1 (real velocity) and Eq. 2 (synthetic velocity):

$$\Delta Vp = Vp_{{{\text{real}}}} - Vp_{{{\text{syn}}}}.$$
(4)

After calculating the velocity deviation log, based on the answers obtained from this log, three zones will be recognizable in terms of the type of porosity (Anselmett and Eberli 1993, 1999):

  1. 1.

    Zones with positive deviation (VP>+500). These intervals, which show relatively high values of velocity, represent porosities such as intra-particle or melodic porosity, and their permeability is usually low. In melodic porosity, positive deviation indicates severe diagenetic processes, such as dissolution, grain displacement, or re-deposition in rock. The cavities are usually in a cemented and dense matrix in these zones. Due to the lack of communication between most of these cavities, the permeability of the rock is low.

  2. 2.

    Zones with zero deviation (− 500<VP<+500). These zones, with small deviations and velocities close to zero, represent areas with various microporosities, intercrystalline and interparticle porosities. In these areas, unlike high-velocity zones, the diagenetic processes are mild. Due to the formation of pores after sediment deposition, there is generally a good correlation between the voids, which leads to high permeability, except for micropores, which reduce permeability.

  3. 3.

    Zones with negative deviation (VP<− 500). Despite the high permeability, the low velocity in these zones indicates that factors other than lithology can change velocity along the log. Three main factors can be mentioned to explain this phenomenon:

(A) Borehole washouts: The presence of rugosity in the borehole occurs at negative velocities on the sonic log. (B) Natural fractures: Although porosity caused by fractures is known as secondary porosity, and it is expected that the velocity of the sound wave is high and cause a positive deviation, several studies have shown that fractures in both small and large scales reduce velocity (Li et al. 2022). The waves are falling. (C) Free gas content: High free gas content can also cause negative velocity deviation because the presence of gas effectively reduces the velocity of the sonic log. In addition, reducing the hydrogen content in the fluid phase reduces the porosity reading of the neutron log.

In this study, electrical image logs were used to confirm the existence of a fracture and its type (negative deviation of the velocity deviation log). The log of the calculated velocity deviation in the reservoir distances of wells A and B in the studied field, along with the gamma-ray log, is shown in Fig. 2(a, b).

Fig. 2
figure 2

Log of velocity deviation calculated in wells A and B a with gamma-ray log b. The velocity deviation log shows the positive deviation from zero in blue and the negative deviation in red

Full size image

Fractures and velocity deviation log

Fractures play a significant role in altering the elastic behavior and geomechanical response of reservoir rocks by introducing discontinuities that disrupt stress fields and rock behavior (Elyasi et al. 2015). The empirical concept of the Wyllie equation further reinforces this understanding, stating that no rock can exhibit a velocity lower than the predicted velocity (Wyllie et al. 1956). In fractured rocks, the actual velocity experiences a sharp decrease, while the synthetic velocity remains relatively unaffected due to the limited porosity within fractured zones. Consequently, this leads to a negative difference between the synthetic velocity and the actual velocity, as indicated by the velocity deviation relationship.

Figure 3a presents the calculated fracture density and its impact on the numerical reduction of velocity deviation in the vicinity of the lithological column within the high-density fractured portion of the K4 reservoir layer. In contrast, Fig. 3b illustrates a depth interval within a segment of the K3 reservoir layer that is free from natural fractures, allowing for a comparison of the effect of fracture presence or absence on the velocity deviation log. Notably, the absence of fractures does not influence the reduction rate of the velocity deviation log.

Fig. 3
figure 3

a Comparison between the image log and the numerical value of velocity deviation in non-fracture areas in the K3 reservoir layer. In general, there are two types of wave amplitude reduction in seismic data: a intrinsic amplitude reduction, which is related to the geometric expansion of the wave and is independent of the wave passage medium, and b amplitude reduction due to the passage of porous and fractured formations. b Show the presence of fractures and their effect on the numerical value of velocity deviation in fractured areas in the K4 reservoir layer

Full size image

VSP data

This section briefly reviews the borehole seismic data required to determine the quality factor. Figure 4 shows the processing flowchart and calculation of the quality factor. After loading and geometric allocation of seismic data, the first-time receipts are marked, and then the velocity model is calculated to achieve the velocity model. This velocity model, the square velocity of the mean squares (Fig. 5), is used to regenerate a domain that has been reduced by geometric expansion.

Fig. 4
figure 4

Processing flowchart and the process of calculating the quality factor

Full size image
Fig. 5
figure 5

The average velocity of P-squares is from a depth of 400 to 3500 m

Full size image

The energy released at the source is propagated in waves and distributed over the surface of larger spheres over time. As a result, the amount of energy per unit area decreases as a function of the inverse square of the distance, and the amplitude of the waves increases as a function of the inverse of the distance traveled. In addition, some energy is absorbed and lost in the layers, which in turn causes a further drop in amplitude.

In the processing steps, minimizing the amplitude reduction effect is necessary due to the wave's geometric propagation on the seismic rejection. Therefore, by reducing the amplitude of the waves exponentially with the help of mathematical tools, seismic events related to the impact of the earth on the data can be investigated more accurately. The distance traveled (average velocity-to-velocity ratio) must be multiplied by the amplitudes obtained to correct the effect of spherical divergence (Fig. 5). The correction of the adsorption effect is also done using Eq. 5 by selecting the appropriate geometric absorption coefficient β:

$$A = A_{2} e^{{ - \beta \left( {r - r_{0} } \right)}}.$$
(5)

In this research, the numerical value of the absorption coefficient of 1.7 has been selected by performing various tests.

The reduction in wavelength relative to the distance traveled by spherical distribution, including absorption, can be calculated from Eq. 6:

$$A = A_{0} \frac{{r_{0} }}{r}e^{{ - \beta \left( {r - r_{0} } \right)}}.$$
(6)

In seismic data processing, upcoming and downgoing waves must be separated. For this purpose, there are several methods, the most common of which is the F-K filter conversion tool. In this research, the same method has been used to separate upcoming and downgoing waves. It should be noted that upcoming waves have less amplitude and energy than downgoing waves due to their longer wavelengths. Therefore, downgoing waves are preferable to upcoming waves to examine the quality factor. After removing the upcoming waves, the downgoing waves become flattened with the help of the time distances of the first receipts (Fig. 6).

Fig. 6
figure 6

Display of separated and flatten down-going waves with the help of the first-time receipts

Full size image

As can be seen, the process of domain distribution varies at different depths. For a closer look, a time window is selected from the flattening seismic data between 50 and 180 ms.

Quality factor (QC)

Wave attenuation means the loss of wave amplitude in environmental conditions by increasing the propagation field. Wave attenuation is defined by the ratio of the two amplitudes of a wave and is usually expressed in neper or decibels.

$$\begin{gathered} {\text{L }}\left[ {{\text{Neper}}} \right] = \ln \left( {{\text{A}}_{0} /{\text{A}}} \right) \hfill \\ {\text{L }}\left[ {{\text{dB}}} \right] = 20\log \left( {{\text{A}}_{0} /{\text{A}}} \right). \hfill \\ \end{gathered}$$
(7)

In this regard, L, A0, and A are the amplitude, the attenuated amplitude, and the attenuated amplitude, respectively.

Loss can occur due to the collision of a wave with the discontinuity boundary of two materials. Still, when attenuation is discussed, it means energy loss regarding propagation distance. Loss is generally expressed as follows:

$$L = \alpha d,$$
(8)

where d is the propagation distance, and α is the attenuation coefficient.

Seismic waves on the ground are attenuated so that higher-frequency waves are absorbed faster than lower-frequency waves. Quantities such as environmental absorption coefficient (α) and quality factor (Q) are commonly used to calculate environmental attenuation. It is important to estimate the rate of weakening of seismic waves in the earth because, first, the amplitude and content of the frequency of the waves change as they pass through the earth.

Second, attenuation parameters can provide important information about the type of rock and its saturated fluid content (Soleimani et al. 2018).

The absorption coefficient (α) is one of the important parameters in determining the attenuation, which is related to the amplitude as follows:

$$A_{1} = A_{0} e^{ - \alpha r},$$
(9)

where A1 is the domain at distance r from the source, and A0 is the initial value of the domain. At two points that are at a distance of one wavelength (λ) from each other, we can write:

$$A_{2} = A_{1} e^{{ - \alpha \left( {r + \lambda } \right)}},$$
(10)
$$A_{1} /A_{2} = e^{ - \alpha r} /e^{{ - \alpha \left( {r + \lambda } \right)}},$$
(11)
$$A_{1} = A_{2} e^{\alpha \lambda },$$
(12)

where α is obtained as follows:

$$\alpha = \frac{1}{\lambda }\ln \frac{{A_{1} }}{{A_{2} }}.$$
(13)

The relationship between α and Q is as follows (Schön 1996):

$$Q = \left( {\frac{\pi }{\alpha \lambda }} \right).$$
(14)

The ability of a rock to weaken seismic waves is usually expressed by a dimensionless quantity called the quality factor (Q). Physically, Q is the ratio of energy to energy lost in an oscillation cycle. The rocks have a Q range between 10 and 400.

There are different methods for determining the quality factor: the spectral ratio method, the synchronization method, the analytical signal method, the dispersion equation method, the delay time correction method, and the experimental equation method. In this research, the spectral ratio method has been used. In this method, spectral changes at several different depths are considered, and Q is calculated. The relationship between Q and the frequency band, the amplitude of the seismic signal, and the amplitude of the source is as follows (Shaw et al. 2004):

$$A = A_{0} \exp \left( { - \frac{\pi fZ}{{QV}}} \right),$$
(15)

where A is the amplitude at the desired depth Z, A0 is the amplitude at the source, f is the wave frequency at depth Z, Q is the quality factor, and V is the seismic wave propagation velocity. For a particular frequency, we can write seismic maps at two different depths:

$$A_{2} /A_{1} = A_{02} \exp \left( { - \pi fZ_{1} /QV} \right),$$
(16)

where A1 and A2 are the spectrum amplitudes at two depths, Z1 and Z2.

$$\ln \left( {A_{2} /A_{1} } \right) - \ln \left( {A_{02} /A_{01} } \right) = - \pi f\delta t_{2 - 1} /.$$
(17)

The expression ln (A02/A01) is called the correction coefficient of a seismic source, the natural logarithm of the ratio of the amplitudes of waves from two different seismic sources at different depths. If the waves come from the same source, no seismicity is considered. Equation 17 can be written as follows:

$$Q = \frac{{ - \pi f\delta t_{2 - 1} }}{{\ln \left( {A_{2} /A_{1} } \right)}},$$
(18)

where the Q factor is calculated for a given wave at a constant frequency, δt 2–1 is the difference in transit time at two depths.

It should be noted that for the ratios 0.85 < A2 / A1 < 1.15, the value of Q changes from large negative values (physical meaninglessness) to large positive values. Thus, this method can only provide a meaningful and stable estimate of Q when the amount of damping is large (more than 10% amplitude reduction), or Q is small (De et al. 1994). In addition, this method does not have high accuracy in thin films.

Figure 7 compares the frequency analysis of two down going waves at depths of 3100 and 3160 m within the selected time window range. As can be seen, the frequency content has generally decreased. This decrease in frequency content can be considered a seismic indicator.

Fig. 7
figure 7

Comparison between absorption coefficient and frequency content of aftershocks at two depths of 3100 and 3160 m

Full size image

The numerical value of the quality factor is obtained by placing the numerical values of amplitude and frequency in Eq. 18. Figure 8a shows the thermal amplitude thermal log in frequency and depth for all aftershocks.

Fig. 8
figure 8

a Frequency distribution of earthquakes for different depths and low-frequency areas. b Comparison between absorption coefficient and frequency content of aftershocks at depths with unusual damping

Full size image

In the two areas marked in Fig. 8, which correspond to two different depth distances, the energy amplitude shows smaller values (colder color spectrum) than its upper and lower depths, indicating the phenomenon of energy absorption at these distances.

As can be seen in Fig. 8b, in the range specified, the numerical value of the absorption coefficient is relatively high, so it is expected that the amount of energy attenuation in terms of frequency and amplitude in this range is reduced. Finally, using the expressed mathematical relations, the numerical value of the quality factor was calculated. Figure 9 shows the numerical value of the calculated quality factor t in terms of depth.

Fig. 9
figure 9

Quality factor calculated in terms of different depths

Full size image

Numerical comparison of quality factors and velocity deviation

This section discusses the numerical comparison of quality factors and velocity deviation. For examining this process's impact in more detail, this study was limited to reservoir layers (K1, K2, K3, and K4). For this purpose, two evaluation wells, A and B, were surveyed from the studied gas field, and VSP logs were taken. Figure 10 shows the quality factor and velocity deviations calculated for these two wells, along with the results of the petrophysical evaluation. The quality factor is observed to be lower in areas with negative velocity deviation, which is more likely to indicate gas-rich distances or the presence of fractures. The numerical values ​​of velocity deviation and the quality factor values for these four reservoir layers were plotted and analyzed to investigate the frequency distribution better.

Fig. 10
figure 10

Quality factor log, velocity deviation, and petrophysical evaluation results for wells A and B

Full size image

Figure 11a and b shows the frequency distribution of the numerical velocity deviation values in wells A and B reservoir formations. To better analyze and separate reservoir events, four numerical categories for velocity deviation values were determined: category 1(C1) (green) includes velocity values less than − 500, category 2 (C2) (blue) includes velocity values between − 500 and 500, category 3 (C3) (blue-green color) includes velocity deviation values ​​between 500 and 7500, and category 4 (C4) (pink color) includes velocity deviation values ​​between 700 and 1500. Due to the nature of the velocity deviation log, category 1 includes a high-quality reservoir area, category 2 includes a low-quality reservoir area, and Categories 3 and 4 include low to medium-quality reservoirs.

Fig. 11
figure 11

a Frequency distribution of velocity deviation in four reservoirs of well A. b Frequency distribution of velocity deviation in four reservoir layers of well B

Full size image

The frequency distribution of quality factors with the desired classification for the four reservoir formations in the two wells studied is shown in Fig. 12a and b. As can be seen, the value of the quality factor in the green areas, which indicates the high quality of the reservoir, is almost all less than 100. In other words, generally, in areas with high reservoir quality, the numerical value of the quality factor is low.

Fig. 12
figure 12

a Frequency distribution of quality factor in four reservoirs of well A. b Quality factor frequency distribution in four reservoirs of well B

Full size image

To increase the accuracy of the studies, a cross-plot of velocity deviation and quality factor was drawn concerning each other. A cross-plot of velocity deviation and quality factor for four reservoir layers in wells A and B are drawn in Fig. 13a and b. As can be seen for the K2 and K4 layers in the two wells studied, in the method presented in this study, the high-quality reservoir areas and the fracture areas cover a range of cross-plot logs. In other words, this cross-plot log can be used to study high-quality reservoir areas.

Fig. 13
figure 13

a Cross-plot quality factor and velocity deviation log in four reservoir layers of well A. b Cross-plot of quality factor and velocity deviation in four reservoir layers of well B

Full size image

Comparison of quality factor and fracture density

According to rock physics, there is a direct relationship between fracture rate and permeability (Ekanem et al. 2015; Deng et al. 2023). Due to the geometric conditions and granulation of the geological layer structure as well as the wave scattering in the fracture-containing regions, which reduces the numerical value of the quality factor, there is expected to be a logical relationship between the quality factor data and fracture density. In a study using R statistical software, the detection coefficient (R2) between the quality factor and the density of fractures was equal to 0.83 (Fig. 14 a). In this figure, it is observed that for each unit of fracture density decrease, the quality factor increases by about ten units. For a better understanding, the variations in velocity deviation for different quality factors and fracture density values are shown as a thermal log in Fig. 14b. It is observed that in the blue areas (low values of velocity deviation), the amount of quality factor is low, and the fracture density is high.

Fig. 14
figure 14

a Correlation between quality factor and fracture density. b Thermal representation of numerical values of velocity deviation in terms of quality factor and fracture density

Full size image

Comparison of a quality factor with petrophysical parameters of the reservoir

One of the most important objectives of this study is to investigate the relationship between reservoir parameters such as the amount of free gas per unit volume of porous and permeability. This research calculates the amount of gas volume by evaluating common petrophysical logs using the mathematical method of solving possible simultaneous equations (Multimin Method). Permeability data were also obtained from the core analysis. It was observed that there is a relatively good detection coefficient (0.82) between permeability data and quality factor (Fig. 15 a). Figure 15b shows a thermal log of changes in velocity deviation regarding the quality factor. This figure also shows that small values of velocity deviation, indicated by the cold color spectrum, are seen in the range where the quality factor value is low and the permeability value is relatively high.

Fig. 15
figure 15

a Correlation between quality factor and core permeability. b Thermal representation of numerical values of velocity deviation regarding quality factor and core permeability

Full size image

Since the amount of gas volume is derived from theoretical relations, for accuracy, the coefficient of detection (R2) between the volume of gas and permeability, which is obtained from direct analysis of the core, is calculated. As shown in Fig. 16a, the detection coefficient is 0.74, representing an acceptable correlation between core permeability and gas content per unit of porous volume. Therefore, the calculated amount of gas can be trusted, and it can be considered as one of the indicators affecting the trend of quality factor changes. In addition, the calculation shows that the value of the coefficient of detection between the quality factor and the amount of gas calculated per unit volume of porous material is equal to 0.68 (Fig. 16b).

Fig. 16
figure 16

a Correlation between permeability and gas content. b Correlation between quality factor and gas volume

Full size image

Figure 17 shows the thermal log of velocity deviations regarding quality factor and gas content per unit of porous volume. It is observed that the high values of the quality factor (range 110–140) and the values of positive velocity deviation correspond to a small volume of gas (range 0–0.05 per porous volume).

Fig. 17
figure 17

Thermal representation of numerical values of velocity deviation in terms of quality factor and amount of gas in porous volume

Full size image

Investigation of clustering and reservoir quality areas

The Stepwise Multiple Linear Regression method achieved the best relationship between the quality factor and the studied parameters. In this analysis, a p-value less than 0.05 was considered statistically significant. Regression analysis showed that fracture density had the highest correlation with the quality factor. In other words, the follow-up of fracture density changes from the trend of quality factor changes is more evident than other parameters.

Using the K-Means Clustering method, permeability data clustering, velocity deviation log, fracture density, gas volume, and quality factor were performed. Figure 18 shows the distribution of the data related to these parameters concerning each other. After review, four clusters were selected as the most optimal ones, representing good, medium, poor, and very poor reservoir qualities. Table 1 shows the Mode values ​​of each studied parameter in the four clusters.

Fig. 18
figure 18

Dispersion distribution of quality factor parameters, gas volume, permeability, fracture density, and velocity deviation concerning each other

Full size image
Table 1 Mode value of the parameters in the defined clusters
Full size table

Table 2 shows the amount of data in each cluster. Accordingly, 18% of the studied reservoir area is evaluated as good quality, 33% moderate, 36% poor, and 12% hydrocarbon-free.

Table 2 Frequency of data in each cluster
Full size table

Figure 19 shows the lithological logs, velocity deviation, amount of free gas, fracture density, permeability, and quality factor in the whole reservoir area of ​​the studied well. The left column of Fig. 19 (depth) distinguishes different clusters by color. Cluster 1 (good) is shown in green, Cluster 2 (medium) in turquoise blue, Cluster 3 (weak) in dark blue, and Cluster 4 (very weak) in pink. As can be seen, in cluster 1 (green), which indicates the presence of a high-quality reservoir, fracture density, permeability, and gas content have the highest values ​​, and the quality factor and velocity deviation value are low. In contrast, in cluster 4 (pink), which represents hydrocarbon-free distances, the lowest fracture density, permeability, and free gas and the highest quality factor and velocity deviation is observed. Interval values ​​of these parameters can also be seen in clusters 2 and 3.

Fig. 19
figure 19

Comparative graph of lithology, velocity deviation, free gas volume, fracture density, permeability obtained from core analysis and quality factor for depth and clustering (green: cluster 1; turquoise blue: cluster 2; dark blue: cluster 3; pink: Cluster 4)

Full size image

After evaluating the reservoir quality in the whole studied section, to identify the utilization zones in each of the reservoir layers (K1 to K4), separately the permeability cross-plot (Fig. 20 a), fracture density (Fig. 20b), and the amount of free gas (Fig. 20c) were drawn according to the quality factor. In general, from Fig. 20a–20c, it can be inferred that the K4 reservoir layer has the greenest dots (representative of cluster one), which indicates the good reservoir quality of this layer and, consequently, the greater exploitation potential. After this layer, layers K2 and K3, and finally, layer K1, are placed in the tank quality rating.

Fig. 20
figure 20

Cross-plot log of a quality and permeability factor in four reservoir layers. b quality factor and fracture density in four reservoir layers. c Quality factor and amount of free gas in four reservoir layers

Full size image

Conclusions

The analysis conducted using multiple linear regression highlighted fracture density as the most influential parameter affecting changes in the quality factor. Fractured areas exhibited a more significant decrease in the quality factor compared to fracture-free areas. Additionally, a positive correlation was observed between the quality factor and core data permeability. During periods of maximum permeability, the quality factor exhibited lower values.

Cluster analysis results revealed that reservoir layers with higher gas volumes, specifically K4 and K2, exhibited lower quality factor values and higher permeability. This indicates that the quality factor can serve as an indicator of reservoir quality in these layers.

The validity of the research hypotheses was supported by core information and image log data from well B, establishing an acceptable correlation between the quality factor and reservoir parameters. This finding suggests that the quality factor can be utilized to estimate reservoir quality in other wells within the gas field, even in the absence of well logs or VSP data. It was also observed that by having VSP data from one or more wells in each carbonate gas field, reservoir quality can be examined with satisfactory accuracy, eliminating the need for petrophysical logs, cores, and other reservoir tests.

Analysis of well B (control well) data demonstrated a strong correlation between velocity deviation values and quality factors in high-quality reservoir areas. Good-quality reservoir intervals were characterized by quality factor values ranging from 80 to 100. The K-Means clustering analysis categorized the studied reservoir interval into four categories: 18% as good quality, 33% as medium quality, 36% as poor quality, and 12% as hydrocarbon-free. On the other hand, comparative analysis of velocity and quality factor logs revealed distinct patterns. Gas-rich and fractured areas exhibited quality factor values below 100 and velocity logs below − 500.

Based on the study's findings, it is recommended to employ this approach in modeling reservoir heterogeneity and evaluating 2D and 3D seismic data to forecast reservoir quality in gas fields prior to well drilling.