Numerical modeling of seismic wave propagation in loosely deposited partially saturated sands: an application to a mine dump monitoring case

Abstract

Extensive mine dumps consisting of loosely deposited sands have been created as a result of open-pit lignite mining, with a risk of soil liquefaction under high water saturation and a corresponding initiating event. Soil compaction is one of the feasible methods for reducing the probability of liquefaction. For the monitoring of liquefaction events and the evaluation of compaction work, seismic survey methods with sensitivity to changes in soil saturation and structure may thus complement other methods. Compared to exploration methods for deep systems, the shallow subsurface presents some unique challenges. To this end, an open-source, customizable code based on Biot’s theory was developed in the FEniCS library, which takes into account partial saturation and porosity dependence of stiffness, permeability, and other quantities. Following code verification, a comprehensive investigation of parameter studies is conducted, from which the effects of different factors on wave propagation characteristics were obtained. The numerical model was applied to simulate the expected changes in seismic response following soil compaction. Furthermore, the position of the high saturation area could be detected from the reflection and refraction P waves. The goal of this work is to provide an analysis framework for the assessment of compaction works and monitoring liquefiable soils in mine dumps under conditions of variable saturation due to rising groundwater tables.

Introduction

Loosely deposited sands in former mining areas or deposited as part of marine sedimentation are problematic from a geotechnical perspective. Marine sediments are regularly used as the foundation soil for various ocean engineering applications. Anthropogenic dynamic loads or natural seismicity can have a detrimental impact on the stability of such foundations. Likewise, large areas of sandy soil deposited as part of open-pit mines are attractive as landscapes for renewable energies, such as solar and wind energy, but likewise, require careful foundation engineering and soil mechanical insights. These landscapes are prone to liquefaction following groundwater rise after the cessation of mining activities. Soil compaction is one of the feasible treatments for the utilization and reclamation of loosely deposited sands. It is therefore necessary to investigate how to monitor the liquefaction events as well as how to assess the success of compaction works.

Seismic wave characteristics lead us to understand the physical properties of the medium and can help addressing challenging geotechnical problems, e.g, seismic site investigation for landslide risk assessment (Zakaria et al 2022) and dam construction (Takamte et al 2022). Forward seismic modeling is an effective tool to determine the seismic fingerprint of expected geological features. Geotechnical materials are usually three-phase composites composed of solid, liquid, and gas phases. However, it is common in seismic analyses to model geotechnical materials as single-phase elastic solids in many cases. Although this modeling approach is valid at typical seismic frequencies, no direct correlation between seismic characteristics and soil properties, e.g., saturation, porosity, permeability, and other factors, can be established with are essential in soil engineering (Carcione 2015). Biot’s theory (Biot 1956a, b) provided a fundamental framework for the analysis of wave propagation in porous media and predicted the existence of two types of compressional waves with different velocities, which are called the fast P wave (PI wave), similar to the elastic P wave, and the slow P wave (PII wave), first confirmed by Plona’s experiment (Plona 1980). Afterward, numerous authors modified and simplified Biot’s theory, e.g. Boer and Didwania (2001), and provided formulations, which are easier to solve numerically.

Seismic wave propagation and attenuation in porous geotechnical materials differ owing to various solid matrix structures, like the existence of fractures and heterogeneous pore distribution. To address this problem, Guo et al. have adopted the Chapman effective medium model and carried out numerical experiments to assess the variation in P-wave velocity and attenuation, and the shear-wave splitting anisotropy with the frequency and azimuth of the incident wave (Guo et al 2018). Moradi et al. have focused on the prediction of dynamic permeability and dynamic tortuosity of granular media at different frequencies from porosity and average grain size data, utilizing numerical simulations (Moradi and Kantzas 2018). To approximate seismic wave propagation in double-porosity media, Liu et al. have used the effective Biot theory, which can explain the high level of attenuation observed at seismic frequencies, but which is unaccounted for with classic Biot theory (Liu and Greenhalgh 2019). Ding et al. have measured the scale-dependent velocity and anisotropy effects through laboratory experiments on porous and non-porous artificial rocks containing aligned fractures (Ding et al 2020). In accordance with the wave features in porous and fractured media, Lahcen and Pascale have investigated the hydrogeophysical characterization of a chalk aquifer in Beauvais, France (Zouhri and Lutz 2016). Moreover, a pressure gradient leading to fluid flow accompanied by energy dissipation, known as wave-induced fluid flow can be induced when a seismic wave passes through the porous media (Anthony and Vedanti 2020). This characteristic has been further applied in oil or gas exploration (Gao et al 2021) and $\mathrm {CO_2}$ sequestration (Goodarzi et al 2011; Boxberg et al 2015) or hydrogen storage (Pfeiffer et al 2016) monitoring.

In view of the above study, the soil structure as well as the fluid properties can contribute to changes in wave propagation features. In geotechnical engineering, the localization and characterization of soil heterogeneities and events by seismic monitoring requires knowledge of the frequency, depth and saturation dependency of dynamic soil properties. Previous studies have shown that the seismic velocity in geotechnical material basically shows the following variation pattern (Mikhaltsevitch et al 2016): almost no change or only a slight decrease in the range of most water saturation, and a sudden and significant increase when approaching full saturation. It provides the possibility to identify highly saturated areas, e.g. the groundwater table, employing seismic survey method. Furthermore, there is a significant change of the pore structure during the compaction process, which will also affect the seismic wave propagation and impact the detection results. However, most compaction assessment methods, like dynamic cone penetration test, are local in nature, which is problematic especially for characterization at the large scale. To date, studies that employ seismic survey method for monitoring liquefaction events and assessment compaction works are still limited.

Meanwhile, the interpretation of seismic data from shallow loose media is different from deep systems analysis due to the complexity of the environmental conditions (Crane 2013). For example, stiffness and saturation vary strongly with depth in typical soils. The common methods and tools of interpreting seismic field data for deep exploration are not directly transferable to environmental or geotechnical applications with shallow depth and loose material (Prasad et al 2012). In this regard, numerous scholars have investigated the effect of relevant properties of shallow loose media on wave propagation characteristics at the laboratory scale and developed theoretical models, e.g. Williams et al (2002); Zimmer et al (2007); Barrière et al (2012); Gu et al (2021). However, there is generally a different between acoustic (field scale) and ultrasonic (lab scale) frequency ranges in terms of wave propagation characterizes (Shukla 2019). This requires indirect parameter adjustments not directly related to soil state variables, composition or direct laboratory testing at higher frequencies. In addition, some researchers have developed modified interpretative tools based on equivalent elastic modeling, e.g., Shen et al (2013). The studies of poroelastic modeling for complex shallow loose media, especially considering its property variations with depth, remains limited, e.g, Asfour (2021). There is a lack of open-source, customizable codes for the dynamics of partially saturated media with features relevant for shallow subsurface applications, hindering the transfer of more advanced interpretation tools into geotechnical practice. Existing tools resting on elastic assumptions are only partially applicable, and often fall short when transferring lab to field-scale data due to a lack of physically based frequency and composition dependence. To facilitate these types of analyses, this work establishes a basic flexible and accessible analysis framework that can later be extended towards inelastic soil behaviour due to existing interfaces to non-linear constitutive integrators (Helfer et al 2020).

This paper is outlined as follows: first, an extended Biot’s model with two fluid phases is proposed and developed in FEniCS Python library (Sect. 2); secondly, a set of analytical solutions is used to verify the numerical implementation and parameter studies demonstrate the rich physical features of the model in Sect. 3; thirdly, the numerical model is applied for the application of seismic monitoring in mine dumps compaction in Sect. 4; finally, the conclusions are presented in Sect. 5.

Table 1 List of symbols used throughout the paper

Mathematical model

Governing equations

To model the wave propagation in loosely deposited sands, a fully coupled u-p-w formulations is presented based on Biot’s theory (Biot 1956a, b), which describes the mixture balance of momentum, fluid balance of momentum and fluid mass conservation in terms of the solid skeleton displacement ${\mathbf{{u}}}$, relative fluid displacement ${\mathbf{{w}}}$ and pore pressure p as follows:

$$\begin{aligned}{} & {} \rho \ddot{{\mathbf{{u}}}} + \rho _\textrm{f} \ddot{\mathbf{{w}}} = \textrm{div} \, (\varvec{\sigma }{'} - \alpha p {\varvec{I}}) \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \rho _\textrm{f} \ddot{{\mathbf{{u}}}} + \frac{\rho _\textrm{f}\tau }{\phi } \ddot{\mathbf{{w}}} + \frac{\mu _\textrm{f}}{k_\textrm{f}} \dot{\mathbf{{w}}} = - \textrm{grad} \, p \end{aligned}$$

(2)

$$\begin{aligned}{} & {} S {\dot{p}} + \alpha \, \textrm{div} \, \dot{{\mathbf{{u}}}} + \textrm{div} \, \dot{\mathbf{{w}}} = 0 \end{aligned}$$

(3)

where, the relative displacement of fluid is defined as ${\mathbf{{w}}} = \phi ({\mathbf{{u}}}^{{\rm f}} - {\mathbf{{u}}})$. The Biot coefficient represents the ratio of changes in the fluid volume to the total bulk volume for deformation on the drained condition (Biot and Willis 1957; Zienkiewicz 1982), defined as $\alpha = 1 - K/K_\textrm{s}$. The storativity coefficient represents the increase of the amount of fluid (per unit volume of solid) as a result of a unit increase of pore pressure (Chang and Yoon 2018), given by $S = \phi /K_\textrm{f} + (\alpha - \phi )/K_\textrm{s}$. Moreover, the tortuosity, which is a parameter describing the geometry of the pore space, can be approximated by $\tau = 1+ 0.5(1/\phi - 1)$ (Carcione 2015). The effective density of porous media is determined by the density of solid grain and fluid, defined as $\rho = \phi \rho _\textrm{f} + (1 - \phi ) \rho _\textrm{s}$. Table 1 give notations used throughout the paper.

In Biot’s theory, the flow mode of pore fluid is frequency-dependent, and there is a critical frequency, given by:

$$\begin{aligned} f_\textrm{c} = \frac{\phi \mu _\textrm{f}}{2 \pi k_\textrm{f} \tau \rho _\textrm{f}} \end{aligned}$$

(4)

When $f/f_\textrm{c} \ll 1$, the viscous interaction forces become dominant in fluid motion. This describes a low-frequency regime, whereas high-frequency wave propagation occurs if $f/f_\textrm{c} \gg 1$ where inertial forces dominate. However, for approximately $0.1 \geqslant f/f_\textrm{c} \geqslant 10$ both the inertial and the viscous forces contribute to fluid motion. This frequency range describes an intermediate regime with attenuated waves (Han et al 2016). It should be pointed out that a relaxation function is required in the high-frequency regime to better characterize the fluid flow, which is further discussed in the subsequent work.

The deformation of the solid skeleton is governed by the effective stress. According to the generalized form of Hooke’s law, the constitutive equation of the elastic solid skeleton is written as

$$\begin{aligned} \varvec{\sigma }{'} = 2 G \varvec{\epsilon } + \left( K-\frac{2}{3}G\right) \textrm{tr}(\varvec{\epsilon }) {\textbf{I}} \end{aligned}$$

(5)

where K and G can be considered as linearized stiffness values around an initial state characterized by strong non-linearity.

The relationship between strain and displacement in the poroelastic model is given by

$$\begin{aligned} \varvec{\epsilon } = \frac{1}{2} (\textrm{grad} \, {\mathbf{{u}}} + (\textrm{grad} \, {\mathbf{{u}}})^\textrm{T}). \end{aligned}$$

(6)

Effective fluid model

In the previous section, we have discussed the classic Biot theory of single-phase fluid. Now a simple manner to include two-phase effects is discussed. According to Berryman (Berryman et al 1988), two-phase fluid in porous media can be represented by a single-multiphase fluid, which is only valid when the fluid phases are mixed at a sufficiently fine scale with respect to the wavelength, coinciding with the low-frequency condition. Thereby, the effective bulk modulus of fluid can be calculated according to the Wood’s work (Wood 2021):

$$\begin{aligned} \frac{1}{K_\textrm{f}} = \frac{1 - S_\textrm{w}}{K_\textrm{g}} + \frac{S_\textrm{w}}{K_\textrm{w}}. \end{aligned}$$

(7)

An effective viscosity can be obtained from water and gas viscosity following (Teja and Rice 1981):

$$\begin{aligned} \mu _\textrm{f} = \mu _\textrm{g} \left( \frac{\mu _\textrm{w}}{\mu _\textrm{g}}\right) ^{S_\textrm{w}}. \end{aligned}$$

(8)

Considering the interaction between the pore gas and water, the relative permeability functions depend on saturation (Barrière et al 2012), specifically

$$\begin{aligned} k_{\mathrm {r \xi }} = S_{\mathrm {e \xi }} ^{1/2}\bigg [ 1 - \left( 1 - S_\mathrm {e \xi }^{1/m_\mathrm {\xi }} \right) ^{m_\mathrm {\xi }} \bigg ]^2 \end{aligned}$$

(9)

was chosen here.

The effective saturation of gas and water is defined as:

$$\begin{aligned} S_{\mathrm {e\xi }} = \frac{S_\xi - S_\xi ^{\mathrm {{min}}}}{S_\xi ^{\textrm{max}} - S_\xi ^{\textrm{min}}} \end{aligned}$$

(10)

where, the $\xi$ represent either gas or water; the maximum and minimum saturation are linked via $S_\textrm{w} ^\textrm{max} = 1 - S_\textrm{g} ^\textrm{min}$ and $S_\textrm{g} ^\textrm{max} = 1 - S_\textrm{w} ^\textrm{min}$.

The effective permeability is defined consisting of gas and water relative permeability:

$$\begin{aligned} k_\textrm{f} = k_\textrm{f0} (k_{\textrm{rw}} + k_{\textrm{rg}}). \end{aligned}$$

(11)

According to the Kozeny–Carman equation (Costa 2006; Mohammadi et al 2020), the permeability-porosity relationship

$$\begin{aligned} k_\textrm{f0} = k_{0} \left( \frac{\phi }{\phi _0}\right) ^3\left( \frac{1 - \phi _0}{1 - \phi }\right) ^2 \end{aligned}$$

(12)

can be used to estimate the effect of a variable packing density, e.g. with depth, on the permeability. Meanwhile, for the mixture of two-phase fluid, the fluid density is a linear average of each component, given by

$$\begin{aligned} \rho _\textrm{f} = \rho _\textrm{g}(1 - S_\textrm{w}) + \rho _\textrm{w}S_\textrm{w} \end{aligned}$$

(13)

.

Boundary condition

Along the far-field boundaries, the classic first-order viscous absorbing boundary is employed to improve computational efficiency and avoid artificial reflection. The traction vectors on boundaries with unit outward normal ${\mathbf{{n}}}$ are given by (Morency and Tromp 2008):

$$\begin{aligned} \overline{{\mathbf{t}}} = \rho v_\textrm{pI}(\dot{{\mathbf{{u}}}} \cdot {\mathbf{{n}}}){\mathbf{{n}}} + \rho _\textrm{f}v_\textrm{pII} (\dot{\mathbf{{w}}} \cdot {\mathbf{{n}}}) {\mathbf{{n}}} + (\rho - \phi \rho _\textrm{f}/\tau ) v_\textrm{s}({\mathbf{I}} - {\mathbf{{n}}}\otimes {\mathbf{{n}}}) \cdot \dot{{\mathbf{{u}}}} \end{aligned}$$

(14)

and

$$\begin{aligned} \overline{{\mathbf{t}}}_\textrm{f} = \rho _\textrm{f}v_\textrm{pII} \tau / \phi (\dot{\mathbf{{w}}} \cdot {\mathbf{{n}}}) {\mathbf{{n}}} + \rho _\textrm{f} v_\textrm{pI}(\dot{{\mathbf{{u}}}} \cdot {\mathbf{{n}}}) {\mathbf{{n}}}. \end{aligned}$$

(15)

The mathematical model is numerically formulated via the finite element method, and programmed using the open-source finite element library FEniCS (Langtangen and Logg 2017). Detailed information on the implementation can be found in Appendix A.

Verification and parameter studies

Model verification against analytical solution

To verify the numerical model, a 2D homogeneous saturated poroelastic media is excited with a Ricker wavelet source with a frequency of 30Hz. Since the physical quantities associated with the saturation are constants once the saturation is determined, only the case of $S_\textrm{w}=1.0$, i.e, full saturation, is studied in this section for principal code verification. Partial saturation in particular will be acressed in the next section.

It should be pointed out that the source can be introduced as a moment tensor which only generates P waves. In the case of an inviscid fluid ($\mu _\textrm{f} = 0$), the numerical result is compared with the analytical solution derived by Dai et al (1995). In the case of a viscous fluid ($\mu _\textrm{f} = 0.001$ Pa s), the analytical solution employed was derived by Carcione and Ouiroga-Goode (1996).

Table 2 Input parameters for verification simulations

The model setup is displayed in Fig. 1(a) and Table 2 lists the input parameters. Figure 1(b) and Fig. 1(c) show snapshots of the total solid displacement at 0.15s of the inviscid model and viscous model, respectively. It can be clearly found that there are two types of P waves in the inviscid model, whereas only one exists in the viscous model.

From Fig. 1(e) and Fig. 1(f), there is a good agreement of the vertical solid skeleton displacement at receivers between the simulation result and analytical solution. The agreement between these two solutions illustrates the capability of the numerical model to capture seismic waves in porous media. Furthermore, the vertical solid skeleton displacement obtained with inviscid model and viscous model are compared in Fig. 1(d). The difference between two results coincides with the velocities summarized in Table 2 and shows that seismic wave in viscous model exhibits a strong attenuation.

Fig. 1

The results of 2D simulation for wave propagation in a homogeneous saturated porous media. The four edges are absorbing boundaries. (a) The geometry, the position of source and receivers. (b) Snapshot of the total solid skeleton displacement of inviscid model at t = 0.15s. The fast P wave and slow P wave can be observed. (c) Snapshot of the total solid skeleton displacement of viscous model at t = 0.15s. Only fast P wave could be observed. (d) Comparison of the vertical solid displacement seismograms between inviscid model and viscous model. (e) Comparison of the vertical solid displacement seismograms to the analytical solution for inviscid model. (f) Comparison of the vertical solid displacement seismograms to the analytical solution for viscous model

Parameter studies

The flow mode of fluid in porous media is frequency-dependent. Thus, it is necessary to study the effect of frequency on wave propagation in loosely deposited sands and to stay within the validity limits of a chosen modeling approach. According to the numerous experimental data shown in the literature review, the P wave velocity suddenly increases as full saturation is approached. This is an important feature in applications with variable groundwater tables, such as mine deposits. We therefore demonstrate the model’s capability to capture this effect in this section.

A second important feature for this type of application scenario is the dependence of several hydraulic and mechanical properties on the packing density. In the process of compaction, the pore structure becomes dense, which means that the porosity is reduced. It is essential to perform a parametric study of the effect of porosity on seismic wave propagation to provide a basis for the interpretation of seismograms. In the low-frequency range, the stiffness of the soil depends only on the microscopic pore structure and the minerals making up the grains (Pride 2005). Under this assumption, a theoretical model was proposed for predicting the stiffness module of loosely deposited sands of an open-pit mine dumps based on experimental data by (Wegener and Hering 2018):

$$\begin{aligned} G = 323 \frac{(2.97 - e)^2}{1 + e} \cdot p_\textrm{a} \cdot \left( \frac{p'}{p_\textrm{a}}\right) ^{0.5} \end{aligned}$$

(16)

where the e is the void ratio, given by $e = \phi / (1 - \phi )$; $p_\textrm{a}$ is the atmospheric pressure, ${1 \times {10^{5}}}\hbox {Pa}$; $p'$ is the effective pressure. Here, the Poisson’s ratio $\nu$ was set to 0.3.

Table 3 The physical properties for parameter studies

To demonstrate the physical features of the model, three sets of simulations were conducted to study the impact of frequency, porosity, and saturation on wave propagation. The input parameters are listed in Table 3. The analytical solution of different wave velocities could be obtained by monochromatic wave analysis, which will be applied to compare with numerical outcomes. Figure 2 presents the comparison between the analytical solution and the numerical results of wave velocities and attenuation. The results of the two methods are in agreement, which further verifies the correctness of the numerical model in terms of parameter dependence.

The effect of frequency on the wave propagation is demonstrated in Fig. 2(a)-(c). From those figures, it can be seen that the velocity of the fast P wave and shear wave are almost independent of the frequency in the low-frequency regime, where the viscous shearing dominates, and in the high-frequency regime, where the inertia force dominates. But in the intermediate regime, there are significant velocity changes since both forces contribute on a comparable magnitude. For the slow P wave in the diffusive and intermediate regimes, the velocity increases due to the increasing interaction between the solid and the fluid and reaches a constant value in the high-frequency regime. Moreover, it is also found that the attenuation of the fast P wave and shear wave are independent of the frequency in the low-frequency and high-frequency regimes. There is a peak in the intermediate regime because this is the result of a combination of inertia force and viscous shearing. Furthermore, it can be seen that the attenuation of slow P wave has a strong frequency dependence and tends to zero in high frequency regime. This is explained by the fact that this wave is diffusive in the low-frequency regime whereas it propagates in the high-frequency regime.

Figure 2(d)-(f) display the effect of porosity on the wave propagation. It can be found that the velocities of the fast P wave and shear wave have an apparent reduction with increasing porosity. This is mainly because the increase in porosity leads to a reduction in the stiffness of the soil skeleton. Otherwise, the velocity of the slow P wave becomes larger due to the enhanced relative motion of solid–fluid with the increase of porosity. It should be stated that the slow P wave can’t be observed in these simulation results owing to a strong attenuation in the low-frequency regime.

Figure 2(g)-(i) illustrate the results of the saturation effect on the wave propagation. From those figures, it can be noted that the velocity of the fast P wave has a sudden increase in the highly saturated area coinciding with the literature review whereas shear wave velocity undergoes a slight decrease due to the increase in the effective density of the porous media as the saturation increases. Meantime, the slow P wave will not be discussed as it is difficult to capture in field measurements. Two different porosity cases are presented to reveal the variation of velocity due to compaction. The compaction effect reduces the porosity of the soil, and the velocities of waves increases which is well explained in the porosity variation sets.

The frequency- and saturation-dependent behaviour observed here is supported by previously published data (Boxberg et al 2015; Xiong et al 2021).

Fig. 2

Parameter studies in terms of frequency, porosity and saturation

Application example: seismic monitoring in mine dumps compaction

Motivation

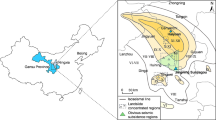
The following model refers to the practical aspects of landscape recultivation after open-pit mining south of Berlin and west of the city of Cottbus in the region of Lower Lusatia/Germany. The landscape in this region is shaped by large open pit mines with tertiary lignite seams covered by Pleistocene sands, silt and clay. The overburden sediments ahead of the mining zone are continuously removed and used to fill the remaining pits after the extraction of the lignite. These fillings consist of a mixture of unconsolidated sediments with a high porosity. In particular the unconsolidated sands cause unexpected problems after the closure of the mines and the rerise of the groundwater to its natural level. The reduced stability of these sands causes soil liquefaction, which poses a safety issue not only to the immediate location where liquefaction occurs but also to the surroundings of the former mines because of possible flood waves in the numerous lakes in Lower Lusatia. Such a flood wave event occurred for example on the embankment of Lake Knappensee near the town of Hoyerswerda on March 11 in 2021 during recultivation works (Oberbergamt 2021). A land area of approximately 400m to 500m times 200m flowed into the lake and caused a flood wave with a height of 1.5m destroying some of the infrastructure on the shore of the lake. As a consequence, the lake and its surroundings were closed for public use by the mining authority.

An aim of the ongoing recultivation is to compact and stabilize the soil in endangered areas. Soil compaction is mainly used for this purpose. For instance, as part of the Trans-European Railway Corridor CE 30, the railway line Wegliniec-Horka-Roßlau on the German/Polish border is above the dumping area of the former open pit mine in the region of Lusatia. To eliminate the risk of settlements and liquefaction, as so to ensure the safe operation of the railroad, vibratory compaction of the mine dumps was carried out (Wegener and Hering 2018). To evaluate the need for and the success of this procedure and to distinguish between areas with sufficient compaction and areas with a remaining high porosity in the subsurface prone to soil liquefaction, seismic surveys might be used to characterize the state of the subsurface.

Model description

The parameter studies showed the capability of the model to capture effects related to changing saturation, soil density and other parameters in a homogeneous setting. Now its behaviour in a heterogeneous setting is studied, where depth-dependent stress states and water content given by the soil’s retention curve are provided as input. The developed axisymmetric model is thus used to detect reflectors related to state variable gradients and to quantify changes due to compaction works of mine dumps of loosely deposited sands. The model is presented in Fig. 3. The seismic point source is always situated in the center of the receiver line and acts as a vertical force. The source signature is a Gaussian wavelet with a source center frequency of 50Hz. The receivers record the vertical component of the particle velocity, including the surface receivers and well receivers. The surface of the model is characterized by a free surface boundary condition, i.e. the stress vanishes on the surface whereas other edges are absorbing boundaries. This top boundary condition together with the source on the surface will generate a Rayleigh wave that is close to the shear wave velocity, although we are not concerned with it in this paper. The changes of porosity is utilized to describe the compaction process, i.e. $\phi =0.42$ represents the state of pre-compaction and $\phi =0.3$ indicates the state of post-compaction. The parameters are summarized in Table 3.

Fig. 3

Model geometry for a seismic survey

As the Eq. 16, the stiffness is dependent on the effective pressure in addition to the pore structure. An effective pressure model considering capillary pressure in the vadose zone can be employed (Romero-Ruiz et al 2021), defined as:

$$\begin{aligned} p' = \sigma _z - S_\textrm{ew} p_\textrm{g} - S_\textrm{ew} (p_\textrm{c} - p_\textrm{g}) \end{aligned}$$

(17)

where $\sigma _z = \rho g z$ is the overburden stress; $p_\mathrm {\xi } = \rho _\mathrm {\xi } g z$ is the gas or water pore fluid pressure; $p_\textrm{c}$ is the capillary pressure, fulfilling the van Genuchten’s constitutive model (Van Genuchten 1980) as shown in Eq. 18.

$$\begin{aligned} p_\textrm{c} = p_\textrm{vg} \left[ (S_\textrm{ew})^{-1/m_\textrm{c}} - 1 \right] ^{1/n_\textrm{c}} \end{aligned}$$

(18)

where $p_\textrm{vg}$ is a pressure scaling parameter, $p_\textrm{vg} = {677}\hbox {Pa}$; $m_\textrm{c}$ and $n_\textrm{c}$ are the exponent parameters, $n_\textrm{c} = 2.68$ and $m_\textrm{c} = 1 - 1/n_\textrm{c}$. These parameters of van Genuchten’s model for loosely deposited sands are obtained from Carsel and Parrish (1998). The saturation is taken in the range of 0.085 to 1, and the range of capillary pressure can be calculated.

A saturation distribution given by a retention curve is considered in this application, which also determines the position of the groundwater table. It is found that the capillary pressure varies linearly with depth applying van Genuchten constitutive model to 1D isotropic Richards’ equation (Solazzi et al 2021). If the saturation at groundwater table is set as 1.0 and the saturation at Earth’s surface is set as 0.085, the saturation function of depth could be obtained as:

$$\begin{aligned} S_\textrm{ew} = {\left\{ \begin{array}{ll} \left\{ 1 + \left[ \frac{\rho _\textrm{w}g}{p_\textrm{vg}}\left( z_\textrm{w} - z\right) \right] ^{n_\textrm{c}}\right\} ^{-m_\textrm{c}} &{} \text {for} \ \ z < z_\textrm{w}\\ 1 &{} \text {for} \ \ z \ge z_\textrm{w} \end{array}\right. } \end{aligned}$$

(19)

where, $p_\textrm{c} ^\textrm{max}$ is the maximum capillary pressure; $z_\textrm{w}$ is the depth of water table, $z_\textrm{w} = {15}{\rm m}$.

Results and discussion

Compaction works of loosely deposited sands change soil properties such as the porosity, permeability and the stiffness which in turn will change the wave propagation. A rising ground water table will cause changing saturation profiles. Considering the saturation and stiffness distribution along the depth, the simulations were conducted to detect the location of the groundwater table and assess the influence of porosity variations as they would occur in compaction works. Settlement after compaction is not regarded in this paper.

Figure 4 shows the snapshots of the solid skeleton displacement at 0.10s for states of pre-compaction and post-compaction. It can be clearly noticed that the fast P waves are reflected and refracted near the water table which can be used to recognize high-saturation areas. The waves propagate farther in the state of post-compaction by comparing the two snapshots. This is because compaction works resulted in a smaller porosity, which in turn led to a larger wave velocity. This has been well explained in parameter studies.

Fig. 4

Snapshot of solid skeleton of total displacement at t = 0.10s

In practice, seismograms are an important results obtained by geophysicists through seismic survey methods, which indicates the changes in the subsurface structure. The seismograms of the vertical solid skeleton velocity at surface receivers are presented in Fig. 5 for pre-compaction and post-compaction states above the water level. From those figures, direct P wave, shear wave, reflection P wave and refraction P wave can all be observed. However, it is difficult to distinguish the reflected P wave from the direct P wave after 0.10s or beyond a distance of 50m from the source (for the chosen parameters). This demonstrates that the seismic refraction method may be more applicable to shallow exploration. Moreover, after compaction works, the reflection P wave and the refraction P wave can be received earlier as shown in Fig. 5(c). This observation illustrates that compaction effects increase wave velocities in the soil to a degree that can be picked up by seismic methods with the aim of compaction assessment.

Fig. 5

Seismograms of vertical solid skeleton displacement at surface receivers

In general, well survey data can be supplemented to the surface survey to obtain high-resolution seismograms and to better see below the ground water table. Besides, for the compaction assessment, well survey or cross-hole survey can more accurately distinguish between areas with sufficient compaction and areas with a remaining high porosity in the subsurface prone to soil liquefaction. Figure 6 shows the seismograms of the vertical solid skeleton velocity at well receivers. It can be noticed that the different wave types can be well distinguished from each other, i.e. well data can provide a better inversion of physical information than the seismic surface survey in the local assessment of the subsurface structure, e.g., through cross-hole tomography imaging. The comparison between the pre-compaction and post-compaction at well receivers below the water level are presented in Fig. 6(c). It can again be seen that the wave velocities pre- and post-compaction differ sufficiently for signal analysis to aid with compaction assessment.

Fig. 6

Seismograms of vertical solid skeleton displacement at well receivers

Conclusions

This study presents a poroelastic dynamic model for partially saturated media with features relevant for the shallow subsurface. A series of parameter studies centered around the effects of frequency, porosity and saturation was carried out. The numerical model was applied to a mine dump monitoring application and picks up a range of relevant wave phenomena in fluid-filled porous media with gradients in saturation, effective stress and stiffness (fast P wave, shear wave, reflection, refraction, etc.). The following conclusions can be drawn:

• 1. Given the complex characteristics of loosely deposited sands, a poroelastic dynamic model should integrate porosity and effective stress-dependent properties due to their effect on wave velocities. This includes retention curve-based saturation profiles particularly in soils with higher suction.

• 2. Parametric studies can help in linking lab-scale material characterization with in-situ applications, which often rely on very different testing frequencies. Models such as this one are naturally frequency-dependent due to different phase properties (e.g. density) and have multiphasic dissipation mechanisms explicitly represented.

• 3. Starting from retention curves and well-defined property-composition relationships, the position of the high saturation area (water table) can be detected from the reflected and refracted P waves.

• 4. Comparing the effects of different soil densities pre- and post-compaction, signal shifts sufficient for interpreting soil compaction improvements were observed both for surface surveys and cross-hole surveys.

This paper can provide useful information for the design and utilization of seismic methods employed in mine dump monitoring applications. Although this study attempts to develop a numerical model for describing the wave propagation in complex loosely deposited sands, lab and field tests are still needed to further validate the developed model. Future work will isolate the effects of dynamic drainage-imbibition effects, as for example present in the model by Boxberg et al (2015), on the predictions under practically relevant conditions. Moreover, soil compaction is not a homogeneous process but induces heterogeneous structures with porosity gradients towards each primary compaction point. Furthermore, the pre-compaction state is already characterized by heterogeneities itself due to mine dump and in-situ soil genesis. This heterogeneity will lead to more complex wave signals and is also the topic of future work.

Appendix A

A.1 Weak form for equations system

The space of square integrable functions over the domain is denoted by $L^2(\Omega )$. The first-order Sobelov space function space over the domain is denoted by $H^1(\Omega )$. For the integrals in the computed domain, we choose an appropriate function space for ${\mathbf{{u}}}$, ${\mathbf{{w}}}$ and p, respectively.

$$\begin{aligned} \begin{aligned} P&= \{p \in L^2(\Omega )\}, \, p = {\bar{p}} \quad \text {on} \quad {\partial \Omega }_{p} \} \\ \\ W&= \{{\mathbf{{w}}} \in H^1(\Omega ),\, {\mathbf{{w}}} = \bar{\mathbf{{w}}} \quad \text {on} \quad {\partial \Omega }_{w} \} \\ \\ U&= \{{\mathbf{{u}}} \in H^1(\Omega ),\, {\mathbf{{u}}} = \bar{{\mathbf{{u}}}} \quad \text {on} \quad {\partial \Omega }_{u} \} \end{aligned} \end{aligned}$$

Additionally, following a Bubnov-Galerkin procedure, we introduce test functions for the three equations as $\delta {\mathbf{{u}}}$, $\delta {\mathbf{{w}}}$, $\delta p$. Suitable function spaces for the test functions are given by

$$\begin{aligned} \begin{aligned} \delta P&= \{\delta p \in L^2(\Omega )\}, \, \delta p = 0 \quad \text {on} \quad {\partial \Omega }_{p} \} \\ \\ \delta W&= \{\delta {\mathbf{{w}}} \in H^1(\Omega ),\, \delta {\mathbf{{w}}} = {\varvec{0}} \quad \text {on} \quad {\partial \Omega }_{w} \} \\ \\ \delta U&= \{\delta {\mathbf{{u}}} \in H^1(\Omega ),\, \delta {\mathbf{{u}}} = {\varvec{0}} \quad \text {on} \quad {\partial \Omega }_{u} \}. \end{aligned} \end{aligned}$$

The weak form is a scalar relation, which can be get by multiplying the equations with arbitrary function and integrating over the computational domain. To adopt the finite element method to solve the problem, it is necessary to derive the weak form of the system of equations, firstly. The principle of virtual work is a weak form of equations system, in which the arbitrary function which are called weighted function or test function for three equations are $\delta {\mathbf{{u}}}$, $\delta {\mathbf{{w}}}$, $\delta p$. The weak form are obtained using these functions as follows:

$$\begin{aligned} \begin{aligned}&\int _\Omega \delta {\mathbf{{u}}} \varvec{\cdot } \rho {\ddot{\mathbf{u}}} \, \textrm{d}\Omega + \int _\Omega \delta {\mathbf{{u}}} \varvec{\cdot } \rho _\textrm{f} {\ddot{\mathbf{w}}} \, \textrm{d}\Omega + \int _\Omega (\text {grad}\, \delta {\mathbf{{u}}}) \varvec{:}(\varvec{\sigma {'}}-\alpha p {\varvec{I}}) \, \textrm{d}\Omega \\&+ \int _{{\partial \Omega }} \delta {\mathbf{{u}}} \varvec{\cdot } \bar{{\mathbf{{t}}}} \, \textrm{d}{\partial \Omega } = 0 \\&\int _\Omega \delta {\mathbf{{w}}} \varvec{\cdot } \rho _\textrm{f} {\ddot{\mathbf{u}}} \, \textrm{d}\Omega + \int _\Omega \delta {\mathbf{{w}}} \varvec{\cdot } \frac{\mu _\textrm{f}}{k} \dot{{\mathbf{{w}}}} + \int _\Omega \delta {\mathbf{{w}}} \varvec{\cdot } \frac{ \rho _\textrm{f}\tau }{\phi } \ddot{\mathbf{{w}}} \, \textrm{d}\Omega -\int _\Omega (\text {grad}\, \delta {\mathbf{{w}}}) \varvec{:} (p{\varvec{I}}) \, \textrm{d}\Omega \\&+ \int _{{\partial \Omega }} \delta {\mathbf{{w}}} \varvec{\cdot } \bar{{\mathbf{{t}}}}_\textrm{f} \, \textrm{d}{\partial \Omega } = 0 \\&\int _{\Omega } \delta p \varvec{\cdot } \alpha \, \textrm{div} \, \dot{{\mathbf{{u}}}} \, \textrm{d}\Omega + \int _{\Omega } \delta p \cdot S {\dot{p}} \, \textrm{d}\Omega +\int _{\Omega } \delta p \varvec{\cdot } \textrm{div} \, \dot{{\mathbf{{w}}}} \, \textrm{d}\Omega = 0 \end{aligned} \end{aligned}$$

.

A.2 Spatial discretization

The computational domain is discrete using finite element mesh with $N_e$ cells. The solid displacement can be approximated by a sum such that:

$$\begin{aligned} {\mathbf{{u}}}({\mathbf{x}}, t) \approx \hat{{\mathbf{{u}}}}= \sum \limits _{b} N_b({\mathbf{x}}){\tilde{\mathbf{u}}}_b(t) = {\mathbf{{N}}}({\mathbf{x}}) {\tilde{\mathbf{u}}}(t) \end{aligned}$$

where $N_b$ is are the shape function(the quadratic piecewise polynomials), ${\tilde{\mathbf{u}}}_b(t)$ are the nodal solid displacement of the association time.

An approximation for the test function of solid displacement is specified by

$$\begin{aligned} \delta {\mathbf{{u}}}({\mathbf{x}}, t) \approx \delta {\hat{\mathbf{u}}} = \sum \limits _{a} N_a({\mathbf{x}})\delta {\tilde{\mathbf{u}}}_a = {\mathbf{{N}}}({\mathbf{x}})\delta {\tilde{\mathbf{u}}}(t) \end{aligned}$$

The fluid displacement can be approximated by the same method:

$$\begin{aligned} {\mathbf{{w}}}({\mathbf{x}}, t) \approx {\hat{\mathbf{w}}}= \sum \limits _{b} N_b({\mathbf{x}}){\tilde{\mathbf{w}}}_b(t) = {\mathbf{{N}}}({\mathbf{x}}) {\tilde{\mathbf{w}}}(t) \end{aligned}$$

where ${\tilde{\mathbf{w}}}_b(t)$ are time dependent nodal fluid displacement. The shape function of fluid displacement are same with the solid displacement as the same integral space is employed for them.

An approximation for the test function of fluid displacement is given by

$$\begin{aligned} \delta {\mathbf{{w}}}({\mathbf{x}}, t) \approx \delta {\hat{\mathbf{w}}} = \sum \limits _{a} N_a({\mathbf{x}}) \delta {\tilde{\mathbf{w}}}_a(t) = {\mathbf{{N}}}({\mathbf{x}})\delta {\tilde{\mathbf{w}}}(t) \end{aligned}$$

The pore pressure can be approximated as follows:

$$\begin{aligned} p({\mathbf{x}},t) \approx {\hat{p}} = \sum \limits _{b} H_b({\mathbf{x}}) \tilde{p}_b(t) = {\mathbf{H}}({\mathbf{x}})\tilde{\textrm{p}}(t) \end{aligned}$$

where $H_b$ are the shape functions(the linear piecewise polynomials) of pore pressure, ${\tilde{\mathbf{p}}}_b(t)$ are the nodal pore pressure of the association time.

The test function of pore pressure approximates as follows:

$$\begin{aligned} \delta p({\mathbf{x}}, t) \approx \delta {\hat{p}} = \sum \limits _{a} H_a({\mathbf{x}}) \tilde{p}_a = {\mathbf{H}}({\mathbf{x}})\delta \tilde{\textrm{p}}(t) \end{aligned}$$

Next by substituting the above approximations into weak form system, the equations are extended as:

$$\begin{array}{l} {{\rm M}_{\rm s}}\ddot {\tilde{\rm u}} + {{\rm M}_f}\mathop {\widetilde {\rm w}}\limits^{..} + {\rm K}\tilde {\rm u} - \alpha {\rm B}\widetilde {\rm p} = {{\rm T}_{\rm s}}\\ {{\rm M}_{{\rm sf}}}\mathop {\widetilde {\rm u}}\limits^{..} + {{\rm M}_{{\rm ff}}}\mathop {\widetilde {\rm w}}\limits^{..} + {\rm D}\mathop {\widetilde {\rm w}}\limits^. - {\rm B}\widetilde {\rm p} = {{\rm T}_{\rm f}}\\ \alpha {{\rm B}^{\rm T}}\mathop {\widetilde {\rm u}}\limits^. + {{\rm B}^{\rm T}}\mathop {\widetilde {\rm w}}\limits^. + {\rm Q}\mathop {\widetilde {\rm p}}\limits^. = 0 \end{array}$$

where:

$$\begin{aligned} {{{\mathbf M}}}_s&= \int _\Omega {{{\mathbf N}}}^{{\rm T}} \rho {{{\mathbf N}}} \, \text {d}\Omega&{{{\mathbf M}}}_{\rm f}&= \int _\Omega {{{\mathbf N}}}^{{\rm T}} \rho_{\rm f} {{{\mathbf N}}} \, {\rm d}\Omega \\ {{{\mathbf K}}}&= \int _\Omega {{\mathbf S}}^{{\rm T}} {\varvec{{\mathcal{C}}}}{{{\mathbf S}}} \, \text{d}\Omega&{{{\mathbf{T}}_{\rm s}}}&= \int _{\Gamma } {{{\mathbf N}}}^{{\rm T}} {\bar{{\mathbf t}}} \, {\rm d}\Gamma \\ {{{\mathbf M}}}_{sf} &= \int _\Omega {{{\mathbf N}}}^{{\rm T}} \rho _{{\rm f}} {{{\mathbf N}}} \, {\rm d}\Omega&{{{\mathbf M}}}_{{\rm ff}}&= \int _\Omega {{{\mathbf N}}}^{{\rm T}} \frac{\tau \rho _{\rm f}}{\phi } {{{\mathbf N}}} \, {\rm d}\Omega \\ {{{\mathbf D}}}&= \int _\Omega {{{\mathbf N}}}^{{\rm T}} \frac{\mu _{\rm f}}{k} {{{\mathbf N}}} \, {\rm d}\Omega&{{{\mathbf B}}}&= \int _\Omega {{{\mathbf S}}}^{{\rm T}} {{\mathbf H}}{\varvec{I}} \,\text {d} \Omega \\ {{{\mathbf T}}}_f&= \int _{\Gamma } {{{\mathbf N}}}^{\rm T} {{\bar{{\mathbf t}}}}_{\rm f} \, {\rm d}\Gamma&{{{\mathbf Q}}}&= \int _\Omega S {{{\mathbf H}}} {{{\mathbf H}}} \, \text {d}\Omega{} & {} \end{aligned}$$

and the ${\mathbf{S}}$ is the strain–displacement matrix, $\varvec{{\mathcal {C}}}$ is the elasticity matrix.

A.3 Time discretization

The Newmark-$\beta$ method is a popular time integration method, which is widely used in dynamic finite element analysis. It yields the following expressions for the update of the wave field:

$$\begin{aligned} \begin{aligned} {\dot{\mathbf{u}}}_{n+1}&= {\dot{\mathbf{u}}}_n + \Delta t \left[ (1-\gamma ){\ddot{\mathbf{u}}}_{n} + \gamma {\ddot{\mathbf{u}}}_{n+1} \right] \\ {\ddot{\mathbf{u}}}_{n+1}&= \frac{1}{\beta \Delta t^2}({\mathbf{{u}}}_{n+1} -{\mathbf{{u}}}_{n} - \Delta t {\dot{\mathbf{u}}}_n) + \frac{1-2\beta }{2\beta }{\ddot{\mathbf{u}}}_n \end{aligned} \end{aligned}$$

where, $\gamma$ and $\beta$ are used to control the accuracy and stability of the time discretization method. The Newmark-$\beta$ method is unconditionally stable when $\gamma \geqslant \frac{1}{2}$ and $\beta \geqslant \frac{1}{4}(\gamma + \frac{1}{2})^2$ (Hughes 2012). The update expressions for the fluid velocity field follow analogously:

$$\begin{aligned} \begin{aligned} {\dot{\mathbf{w}}}_{n+1}&= {\dot{\mathbf{w}}}_n + \Delta t[(1-\gamma ){\ddot{\mathbf{w}}}_{n} + \gamma {\ddot{\mathbf{w}}}_{n+1} \\ {\ddot{\mathbf{w}}}_{n+1}&= \frac{1}{\beta \Delta t^2}({\mathbf{{w}}}_{n+1} -{\mathbf{{w}}}_{n} - \Delta t {\dot{\mathbf{w}}}_n) + \frac{1-2\beta }{2\beta }{\ddot{\mathbf{w}}}_n. \end{aligned} \end{aligned}$$

The expression for the update of the pressure rate ${\dot{p}}$ is given as (Zienkiewicz et al 1990):

$$\begin{aligned} {\dot{p}}_{n+1} = \frac{1}{\theta \Delta t}(p_{n+1} - p_n) - \frac{1 - \theta }{\theta } {\dot{p}}_n \end{aligned}$$

where, the parameter $\theta$ has to fulfill the stability condition $\theta \geqslant \frac{1}{2}$. In this paper, $\gamma = \frac{1}{2}, \beta = \frac{1}{4}, \theta = \frac{1}{2}$, to ensure numerical stable.

Expanding the time terms as the above approximation method, the following system to solve can be obtained:

$$\begin{aligned} \begin{bmatrix} {\mathbf{K}}_{11} &{} {\mathbf{K}}_{12} &{} {\mathbf{K}}_{13}\\ {\mathbf{K}}_{21} &{} {\mathbf{K}}_{22} &{} {\mathbf{K}}_{23}\\ {\mathbf{K}}_{31} &{} {\mathbf{K}}_{32} &{} {\mathbf{K}}_{33} \end{bmatrix} \begin{bmatrix} {\tilde{\mathbf{u}}}_{n+1}\\ {\tilde{\mathbf{w}}}_{n+1}\\ \tilde{p}_{n+1} \end{bmatrix}= \begin{bmatrix} {\overline{\mathbf{T}}_\textrm{s}}_{n+1}\\ {\overline{\mathbf{T}}_\textrm{f}}_{n+1}\\ {\overline{\mathbf{T}}_\textrm{p}}_{n+1} \end{bmatrix} \end{aligned}$$

where:

$$\begin{aligned} {{{\mathbf K}}}_{11}&= m_1 {{{\mathbf M}}_{\rm s}} + {{{\mathbf K}}}&{{{\mathbf K}}}_{12}&= m_1 {{{\mathbf M}}_{\rm f}} \\ {{\mathbf K}}_{13}&= -\alpha {{{\mathbf B}}}&{{{\mathbf K}}}_{21}&= m_1 {{{\mathbf M}}_{\rm sf}} \\ {{{\mathbf K}}}_{22}&= m_1{{{\mathbf M}}_{\rm ff}} +d_1{{{\mathbf D}}}&{{{\mathbf K}}}_{23}&= - {{{\mathbf B}}} \\ {{{\mathbf K}}}_{31}&= d_1 \alpha {{{\mathbf B}}}^{T}&{{{\mathbf K}}}_{32}&= d_1 {{{\mathbf B}}}^{{\rm T}} \\ {{{\mathbf K}}}_{33}&= d_4 {{{\mathbf Q}}}&m_1&= \frac{1}{\beta \Delta t^2} \\ m_2&= \frac{1}{\beta \Delta t}&m_3&= \frac{1-2\beta }{2\beta }\\ d_1&= \frac{\gamma }{\beta \Delta t}&d_2&= 1- \frac{\gamma }{\beta } \\ d_3&= \Delta t \left(1 - \gamma \frac{1-4\beta }{2\beta }\right)&d_4&= \frac{1}{\theta \Delta t} \\ d_5&= \frac{1 - \theta }{\theta }\\ {{\overline{{\mathbf T}}}_{\rm s}}_{n+1} =&{{{\mathbf T}}_{\rm s}}_{n} + {\mathbf {M_{\rm s}}}(m_1{{\tilde{{\mathbf u}}}}_n + m_2{{\dot{\tilde{{\mathbf u}}}}}_n + m_3{{\ddot{\tilde{{\mathbf u}}}}}_n) + { {\mathbf M}}_{\rm f}(m_1{{\tilde{{\mathbf w}}}}_n + m_2{{\dot{\tilde{{\mathbf w}}}}}_n + m_3{{\ddot{\tilde{{\mathbf w}}}}}_n)\\ \\ {{\overline{{\mathbf T}}}_{\rm f}}_{n+1} =&{{{\mathbf T}}_{\rm f}}_{n} + { {\mathbf M}}_{\rm sf}(m_1{\tilde{{\mathbf u}}}_n + m_2{{\dot{\tilde{{\mathbf u}}}}}_n + m_3{{\ddot{\tilde{{\mathbf u}}}}}_n) \\ &+ { {\mathbf M}}_{\rm ff}(m_1{{\tilde{{\mathbf w}}}}_n + m_2{{\dot{\tilde{{\mathbf w}}}}}_n + m_3{{\ddot{\tilde{{\mathbf w}}}}}_n) + {{{\mathbf D}}}(d_1{{\tilde{{\mathbf w}}}}_n + d_2{{\dot{\tilde{{\mathbf w}}}}}_n + d_3{{\ddot{\tilde{{\mathbf w}}}}}_n)\\ {{\overline{{\mathbf T}}}_{\rm p}}_{n+1} =&\Delta t \alpha {{{\rm B}}}^{{\mathbf T}} (d_1{{\tilde{{\mathbf u}}}}_n + d_2{{\dot{\tilde{{\mathbf u}}}}}_n + d_3{{\ddot{\tilde{{\mathbf u}}}}}_n) + {{{\mathbf B}}}^{{\rm T}} (d_1{{\tilde{{\varvec w}}}}_n + d_2{{\dot{\tilde{{\varvec w}}}}}_n + d_3{{\ddot{\tilde{{\varvec w}}}}}_n) \\&+{{{\varvec Q}}}(d_4\tilde{p}_n + d_5 {\dot{\tilde{p}}}_n) \end{aligned}$$

Meanwhile, the choice of element sizes and time step lengths influences the numerical dispersion (Tasiopoulou et al 2015). A sufficiently refined mesh is necessary to obtain accurate results, as the numerical dispersion increases with increasing element size. The mesh size should be less than a tenth of the minimum wavelength for application of the Galerkin finite element method (Hughes 2012):

$$\begin{aligned} \Delta x \le \frac{v_{\textrm{min}}}{10f} \end{aligned}$$

where $v_{\textrm{min}}$ is the minimum velocity in the porous medium.

Simultaneously, the time step size is constrained as follows:

$$\begin{aligned} \Delta t \le \frac{\Delta x}{v_{\textrm{max}}} \le \frac{v_{\textrm{min}}}{v_{\textrm{max}}} \cdot \frac{1}{10f} \end{aligned}$$

where $v_{\textrm{max}}$ is the maximum velocity in porous media, which is usually the velocity of the fast P wave in porous media.

After choosing a suitable element size and time increment, the developed model is programmed into the FEniCS python library (Langtangen and Logg 2017), which is a popular open-source finite element computing platform for solving partial differential equations. Moreover, the direct solver(SuperLU) or block-pre-conditioned solver(GMRES) are employed to solve linear systems of equations in FEniCS programs.