Mathematical analysis of a disease-resistant model with imperfect vaccine, quarantine and treatment

Abstract

In this paper, we develop a new disease-resistant mathematical model with a fraction of the susceptible class under imperfect vaccine and treatment of both the symptomatic and quarantine classes. With standard incidence when the associated reproduction threshold is less than unity, the model exhibits the phenomenon of backward bifurcation, where a stable disease-free equilibrium co-exists with a stable endemic equilibrium. It is then proved that this phenomenon vanishes either when the vaccine is assumed to be 100% potent and perfect or the Standard Incidence is replaced with a Mass Action Incidence in the model development. Furthermore, the model has a unique endemic and disease-free equilibria. Using a suitable Lyapunov function, the endemic equilibrium and disease free equilibrium are proved to be globally-asymptotically stable depending on whether the control reproduction number is less or greater than unity. Some numerical simulations are presented to validate the analytic results.

1 Introduction

Infectious diseases have been a major health hazard claiming lives of countless number of people around the globe. It is therefore imperative and expedient to research more in these global epidemics. The new contribution of this work is to provide a better and comprehensive understanding of some category of diseases such as influenza virus, HIV/AIDS etc where disease resistance plays an important role.

Disease resistance is the phenomenon where some exposed individuals appear uninfected after being exposed to diseases. In this case, they become susceptible and take no part in the disease transmission. In a more general term, it is the phenomenon whereby a person in the exposed or infected class returns back to the susceptible class without treatment. This phenomenon has been studied by just few researchers.

Quarantine as a preventive measure has also play important role in disease control mechanism. It simply means the isolation of infected and exposed individuals in a safe place to reduce disease transmission. This phenomenon has also been studied by some researchers like [1, 2] in recent years.

Since vaccination is one of the preventive measure against infectious disease, mass vaccination has been identified as one of the major ways of disease prevention. Lately, it was discovered that despite mass vaccination of susceptible individuals and millions of dollars spent, infectious diseases are still prevalent and endemic in almost everywhere in the world. Vaccines, biologically, are expected to elicit an immune response similar to what would be triggered by a natural infection without causing the actual infectious disease [3]. This type of vaccine that partially prevent disease spread by allowing some pathogen or disease or virus transmission is referred to as leaky or imperfect vaccine.

According to the study in [3], researchers therein opined that imperfect vaccines are of three types. The first is called leaky vaccine whereby vaccination reduces but does not eliminate the chances of infection after exposure to an infectious disease. The second is all-or-nothing vaccine which offers lifetime immunity for some people but no protection for others. And the third one is waning vaccine which works only for a short period of time. This is for us to grasp the effect of imperfect vaccine in literature which ensures its inclusion in this model and mostly because it has been studied only by few researchers [1, 4, 5] in mathematical modeling.

The stability analysis of a disease resistant SEIR model was studied by Jia and Xiao [6]. They used nonlinear incidence rate and later applied the model to influenza virus. But they only studied the basic SEIR which doesn’t give better insight on the dynamics of the disease.

In the work of [7], they also studied the basic SEIR model and transcritical bifurcation which is very much similar to the one studied by Jia and Xiao [6]. They also mentioned that very few work has been done on disease-resistant models.

Several researchers like [6, 8,9,10,11,12] and references therein have published commendable research output about transmission dynamics of infectious diseases. They have also studied control and prevention strategies of these notorious epidemic. In order to further extend, complement and contribute to the work of [6, 7], a new comprehensive model has been designed. We also picked insights in [2, 4] to improve the quality of this work. The model we present here is suitable for infectious diseases like influenza virus, severe acute respiratory syndrome (SARS) and others.

We hope this research helps policymakers and public health workers in the epidemic control.

The objectives of this current study are to

• 1. Incorporate the treatment class by administering a therapeutic vaccine which was not included in [9].

• 2. Include a separate compartment (E) for individuals that fail the therapeutic treatment. This wasn’t considered by Okosun et al. [8], Hussaini et al. [9] and Mastahun and Abdurahman [10]. To the best of our knowledge, it has not been considered before.

• 3. Include the influence of resistance to disease.

• 4. Examine the effect of disease-induced death rate, in the bifurcation analysis, of the individuals that fail treatment which wasn’t considered by Okosun et al. [8], Hussaini et al. [9] and Mastahun and Abdurahman [10].

• 5. Discuss the impact of imperfect vaccine in the susceptible class and in the bifurcation analysis.

• 6. Assess the impact of resistance in disease transmission.

The paper is organized as follows. Section 2 entails model formulation and assumptions. Basic model analysis, and local asymptotic stability of the disease-free equilibrium (DFE) of the model are discussed in Sect. 3. Bifurcation analysis of the model with both standard and mass action incidence rate is completely established with their respective condition of existence in Sect. 4. Section 5 discusses the global asymptotic stability of both the endemic equilibrium (EE) and disease-free equilibrium points. And finally, Sect. 6 contains the assessment of the resistance impact followed by conclusion in Sect. 7.

2 Model formulation and model assumptions

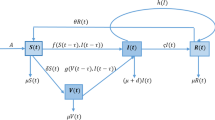
The model analyses the transmission dynamics of an infectious disease with fraction of susceptible vaccinated and treated individuals. It also qualitatively and quantitatively examined the combined effect of both vaccination and treatment. It is consequently designed by, first of all, incorporating standard-incidence rate by splitting the total human population at time t, denoted by N(t), into seven mutually-exclusive compartments of susceptible individuals on vaccination S(t),  vaccinated class P(t),  asymptomatic class $I_1(t),$ symptomatic class $I_2(t),$ quarantine class A(t),  treatment class T(t),  and individuals that fail treatment E(t) such that

$$\begin{aligned} N(t)=S(t)+P(t)+I_1(t)+I_2(t)+A(t)+T(t)+E(t). \end{aligned}$$

The treatment compartment T consists of infected individuals under treatment and are assumed not to participate in disease transmission.

Individuals are recruited into the susceptible population at a rate B. A fraction q, of the newly recruited individuals, are vaccinated. The susceptible individuals are vaccinated at the rate $\alpha _1$, $\epsilon _1$ is the vaccine potency while $\epsilon _2$ denotes the vaccine waning rate. The susceptible individuals that are not vaccinated acquire the disease through effective contact with an infectious individuals at the rate $\lambda$ given by

$$\begin{aligned} \lambda =\frac{\beta (I_1+c_1I_2+c_2A+c_3E)}{N}, \end{aligned}$$

(1)

where $\beta$ in (1) denotes the effective contact rate that is capable of leading to infection, $0< c_1< 1$ denotes the modification parameter that account for the assumed reduction in the transmission of disease by the symptomatic class $I_2$ in comparison to the asymptomatic individuals in $I_1$, $0< c_2,c_3< 1$ are the modification parameters for the A and E class respectively. We also need to understand that the compartment $I_1$ has the highest rate of transmission. This is because the asymptomatic individuals are those that doesn’t experience any symptom and assumed not to know their status. For this reason, they are not cautious of themselves and transmit the infection rapidly. This is followed by the symptomatic $I_2$ that are expected to be cautious of their actions. For this reason, we assume that $c_3<c_2<c_1<1$. We assumed that the vaccine is imperfect, so that individuals on vaccination acquire less infection at a reduced rate $(1-\epsilon _1)\lambda$, where $0 < \epsilon _1 \le 1$ denotes the potency or efficacy of the vaccine. According to the research in [6, 7], a fraction of both asymptomatic and symptomatic infected individuals who develop disease-resistant blood cells and immunity capable enough of protecting them against infections go back to the susceptible class at the rate $\sigma _1 m_1$ and $\sigma _2 m_2$ respectively. Those without the resistance are quarantined respectively at the rate $(1-m_1)\sigma _1$ and $(1-m_2)\sigma _2$ while natural death occur to anybody at the given rate z. Therefore, the rate of change of the total population of the susceptible and vaccinated classes is respectively given by

$$\begin{aligned} \dot{S}(t)=\,&(1-q)B-\lambda S-(\alpha _1+z)S+\sigma _1m_1I_1+\sigma _2m_2I_2+\epsilon _2P,\\ \dot{P}(t)=\,&qB-(1-\epsilon _1)\lambda P -(\epsilon _2+z)P+\alpha _1S, \end{aligned}$$

where $^\cdot$ represents derivative with respect to time.

The asymptomatic infected population is generated by the break-through infection of vaccinated individuals at the rate $(1-\epsilon _1)\lambda$ and the infection of susceptible individuals at the rate $\lambda$ and it’s decreased by the natural death rate z, symptom appearance rate $\alpha _2$ and progression rate leading to resistance $\sigma _1$ so that we have

$$\begin{aligned} \dot{I_1}(t)=[S +(1-\epsilon _1)P]\lambda -(\sigma _1+z+\alpha _2)I_1. \end{aligned}$$

Similarly, we compose the symptomatic infected population by the symptom appearance rate $\alpha _2$ and it’s being decreased by the natural death rate z, progression rate leading to resistance $\sigma _2$, treatment rate $\theta _1$ and the disease-induced death rate $\tau _1$ so that we have

$$\begin{aligned} \dot{I_2}(t)=\alpha _2I_1-(\sigma _2+z+\tau _1+\theta _1)I_2. \end{aligned}$$

Those that don’t have the resistance are quarantined at the rate $(1-m_1)\sigma _1$ and $(1-m_2)\sigma _2$ and this population is decreased by treatment rate $\theta _2$, disease-induced death rate $\tau _2$ and natural death rate z so that we have

$$\begin{aligned} \dot{A}(t)=(1-m_1)\sigma _1I_1+(1-m_2)\sigma _2I_2-(\theta _2+z+\tau _2)A. \end{aligned}$$

In the treatment class, treatment are given to both the symptomatic and quarantined classes at the rate $\theta _1$ and $\theta _2$ respectively and are decreased by natural death z, disease-induced death rate $\tau _3$ and treatment-failure $\gamma$. Thus

$$\begin{aligned} \dot{T}(t)=\theta _1I_2+\theta _2A-(z+\tau _3+\gamma )T. \end{aligned}$$

We didn’t bother to administer the treatment to the $I_1$ class because they are asymptomatic and assumed unaware of their status. And lastly, after the failure of treatment at the rate $\gamma$, we express the treatment-failure class by

$$\begin{aligned} \dot{E}(t)=\gamma T-(\tau _4+z)E, \end{aligned}$$

where $\tau _4$ is disease-induced death rate. The following are the model equations and the flowchart (Fig. 1):

$$\begin{aligned} \frac{dS}{dt}= & {} (1-q)B-\lambda S-(\alpha _1+z)S+\sigma _1m_1I_1+\sigma _2m_2I_2+\epsilon _2P,\end{aligned}$$

(2)

$$\begin{aligned} \frac{dP}{dt}= & {} qB-(1-\epsilon _1)\lambda P -(\epsilon _2+z)P+\alpha _1S,\end{aligned}$$

(3)

$$\begin{aligned} \frac{dI_1}{dt}= & {} [S +(1-\epsilon _1)P]\lambda -(\sigma _1+z+\alpha _2)I_1,\end{aligned}$$

(4)

$$\begin{aligned} \frac{dI_2}{dt}= & {} \alpha _2I_1-(\sigma _2+z+\tau _1+\theta _1)I_2,\end{aligned}$$

(5)

$$\begin{aligned} \frac{dA}{dt}= & {} (1-m_1)\sigma _1I_1+(1-m_2)\sigma _2I_2-(\theta _2+z+\tau _2)A,\end{aligned}$$

(6)

$$\begin{aligned} \frac{dT}{dt}= & {} \theta _1I_2+\theta _2A-(z+\tau _3+\gamma )T,\end{aligned}$$

(7)

$$\begin{aligned} \frac{dE}{dt}= & {} \gamma T-(\tau _4+z)E . \end{aligned}$$

(8)

Table 1 contains the value of the parameters that will be used in numerical simulations.

Fig. 1

Flowchart of the model

Table 1 Hypothetical value of parameters

3 Model analysis

3.1 Basic properties

Epidemiological meaningfulness of the model (234567)–(8) is one of the paramount analysis in this section since it describes human population. We establish as follows.

3.1.1 Positivity of solution

Theorem 3.1

Let the initial conditions

$$\begin{aligned} S(0)>0,P(0)>0, I_1(0)>0,I_2(0)>0,A(0)>0, T(0)>0,E(0)>0 \end{aligned}$$

(9)

exist in the interval $t\in [0,\infty )$ then the solutions $S(t),P(t),I_1(t),I_2(t),A(t)$, T(t), E(t) of the model (234567)–(8) are positive for all $t\ge 0.$

Proof

Obviously, since the right-hand side of (234567)–(8) is locally Liptschitzian, differentiable and continuous on the space of continuous function $C^{'},$ the solution of $S(t),P(t),I_1(t),I_2(t),A(t),T(t),E(t)$ with respect to (9) uniquely exist on $[0,\eta )$, where $0<\eta \le \infty$. Suppose that the solution components of the model equation are not positive, then $\exists$ a first time $\bar{t}>0$ defined as follows

$$\begin{aligned} \bar{t}= & {} \inf \left\{ t|S(t)=0 \;\text {or}\;P(t)=0 \;\text {or}\;I_1(t)=0 \;\text {or}\;I_2(t)=0 \;\text {or}\;A(t)=0\right. \\&\quad \left. \text {or}\; T(t)=0 \; \text {or}\; E(t)=0\right\} . \end{aligned}$$

Now if $S(\bar{t})=0,S(t)>0,P(t)>0,I_1(t)>0,I_2(t)>0,T(t)>0,A(t)>0,E(t)>0$ for $t\in (0,\bar{t})$ then $\dot{S}(\bar{t})<0.$ In Contradiction, from (234567)

$$\begin{aligned} \frac{dS(\bar{t})}{dt}=(1-q)B>0, \end{aligned}$$

which clearly shows that $S(t)>0$. Following the same format, we establish that all the solutions $S(t),P(t),I_1(t),I_2(t),T(t),A(t),E(t)$ are positive for all $t\ge 0$. $\square$

3.1.2 Feasible region

Lemma 3.2

The biological feasible region

$$\begin{aligned} \zeta =\left\{ (S,P,I_1,I_2,A,T,E)\in \mathbb {R}^7_+:S+P+I_1+I_2+T+A+E\le \frac{B}{z} \right\} \end{aligned}$$

is positively attracting and invariant for the model (234567)–(8).

Proof

Adding up all equations of (234567)–(8), we have

$$\begin{aligned} \frac{dN}{dt}=B-zN-(\tau _1I_2+\tau _2A+\tau _3T+\tau _4E)\le B-zN. \end{aligned}$$

(10)

From the provision of (10) and the Gronwall Inequality, we have that $N(t)\le N(0)e^{-zt}+\frac{B}{z}\left[ 1-e^{-zt}\right] .$ Basically, $N(t)\le \frac{B}{z}$ with respect to the condition $N(0)\le \frac{B}{z}.$ Therefore, we have $\zeta$ to be positively invariant and attracting which suffices that system (234567)–(8) can be considered in $\zeta$. Hence, the system is considered to be well-posed mathematically and epidemiologically. $\square$

3.2 Reproduction number and local stability of DFE

The disease-free equilibrium (DFE) of the model (234567)–(8) is given by

$$\begin{aligned} \xi _o=(S^*,P^*,I_1^*,I_2^*,A^*,T^*,E^*)=\left( \frac{Q_1\epsilon _2+Q_of_3}{f_1f_3-\alpha _1\epsilon _2},\frac{Q_1f_1+\alpha _1Q_o}{f_1f_3-\alpha _1\epsilon _2},0,0,0,0,0 \right) . \end{aligned}$$

(11)

The local stability of $\xi _o$ will be established using the next generation operator method [13, 14]. The new infection term denoted by non-negative matrix $\mathcal {F}$ and the transition term denoted by the non-negative matrix $\mathcal {V}$ of the model (234567)–(8) are given respectively by the M-matrices

$$\begin{aligned} \mathcal {F}=\left( \begin{array}{ccccc} \frac{\beta z(S^*+f_2P^*)}{B}&{}\frac{\beta c_1 z(S^*+f_2P^*)}{B}&{}\frac{\beta c_2 z(S^*+f_2P^*)}{B}&{}0&{}\frac{\beta c_3 z(S^*+f_2P^*)}{B}\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ \end{array}\right) , \end{aligned}$$

and

$$\begin{aligned} \mathcal {V}=\left( \begin{array}{ccccc} f_4&{}0&{}0&{}0&{}0\\ -\alpha _2&{}f_5&{}0&{}0&{}0\\ -g_3&{}-g_4&{}f_6&{}0&{}0\\ 0&{}-\theta _1&{}-\theta _2&{}f_7&{}0\\ 0&{}0&{}0&{}-\gamma &{}f_8 \end{array}\right) . \end{aligned}$$

Hence, taking $\rho$ as the spectral radius, the control reproduction number denoted by $\mathcal {R}_o=\rho (\mathcal {F}\mathcal {V}^{-1})$ is given by

$$\begin{aligned} \mathcal {R}_o= & {} \frac{\beta z(\epsilon _2 Q_1+Q_of_3)[f_6f_7f_8(f_5+c_1\alpha _2)+c_3\gamma H_2+c_2f_7f_8H_1]}{B\prod \limits _{i=4}^{8} f_{i}(f_1f_3-\alpha _1\epsilon _2)}\nonumber \\&\quad +\frac{\beta zf_2(\alpha _1Q_o+Q_1f_1)[f_6f_7f_8(f_5+c_1\alpha _2)+c_3\gamma H_2+c_2f_7f_8H_1]}{B\prod \limits _{i=4}^{8} f_{i}(f_1f_3-\alpha _1\epsilon _2)},\nonumber \\ \end{aligned}$$

(12)

where

$$\begin{aligned} Q_o= & {} (1-q)B, f_1=\alpha _1+z, f_2=1-\epsilon _1, f_3=\epsilon _2+z, f_4=\sigma _1+z+\alpha _2,\nonumber \\ f_8= & {} \tau _4+z, g_1=\sigma _1m_1,g_2=\sigma _2 m_2, g_3=(1-m_1)\sigma _1, g_4=(1-m_2)\sigma _2, Q_1=qB,\nonumber \\ H_1= & {} \alpha _2g_4+g_3f_5,H_2=\alpha _2f_6\theta _1+\alpha _2g_4\theta _2+g_3f_5\theta _2=\alpha _2f_6\theta _1+\theta _2H_1, \nonumber \\ H_4= & {} \epsilon _2Q_1+Q_of_3+f_2(\alpha _1Q_o+Q_1f_1),H_5=f_7f_8(\alpha _2\tau _1f_6+\tau _2H_1)+H_2(\tau _3f_8+\gamma \tau _4),\nonumber \\ H_6= & {} f_2(f_4f_5-f_5g_1-g_2\alpha _2), Q_2=1-q,f_6=\theta _2+z+\tau _2,f_7=z+\tau _3+\gamma ,\nonumber \\ Q_3= & {} z+\alpha _1+\epsilon _2,f_5=\sigma _2+z+\tau _1+\theta _1,H_3=f_6f_7f_8(f_5+c_1\alpha _2)+c_3\gamma H_2+c_2f_7f_8 H_1,\nonumber \\ H_7= & {} f_2(f_1f_4f_5-f_5g_1\alpha _1-g_2\alpha _1\alpha _2)+f_3f_5(f_4-g_1)-f_3g_2\alpha _2. \end{aligned}$$

(13)

Using (12), we establish the following result.

Lemma 3.3

The DFE of the model (234567)–(8), given by (11), is locally asymptotically stable (LAS) if $\mathcal {R}_{o}<1$, and unstable if $\mathcal {R}_{o}>1$.

The threshold quantity $\mathcal {R}_o$ signifies the average number of new disease infection generated by a single infection introduced in to a community of totally susceptible individuals where a fraction of them are vaccinated. The result in Lemma 3.3 shows that the disease can be eliminated in the community when the control reproduction number $\mathcal {R}_o<1$ if the initial size of the population is under the basin of attraction of the DFE $\xi _o.$ The proof of Lemma 3.3 is elementary and can be established using Theorem 2 of [14].

4 Backward bifurcation analysis

In the following lines, we establish the endemic equilibria (EE) of the model (234567)–(8). These are the equilibria where at least one of the disease-infected compartments is nonzero. Let

$$\begin{aligned} \xi ^*=(S^{**},P^{**},I_1^{**},I_2^{**},A^{**},T^{**},E^{**}) \end{aligned}$$

represents the endemic equilibrium points EEP of the model (234567)–(8). We further define the force of infection as

$$\begin{aligned} \lambda ^{**}=\frac{\beta (I_1^{**}+c_1I_2^{**}+c_2A^{**}+c_3E^{**})}{N^{**}}. \end{aligned}$$

(14)

Solving (234567)–(8) at steady states, we obtain the following expressions

$$\begin{aligned} S^{**}+P^{**}f_2= & {} \dfrac{f_4f_5[\lambda ^{**}f_2(Q_o+Q_1)+H_4]}{H_6\lambda ^{**2}+H_7\lambda ^{**}+f_4f_5(f_1f_3-\alpha _1\epsilon _2)}, I_1^{**}=\frac{\lambda ^{**}(S^{**}+f_2P^{**})}{f_4},\nonumber \\ T^{**}= & {} \frac{H_2\lambda ^{**}(S^{**}+f_2P^{**})}{f_4f_5f_6f_7}, E^{**}=\frac{\gamma H_2\lambda ^{**}(S^{**}+f_2P^{**})}{f_4f_5f_6f_7 f_8}\nonumber \\ I_2^{**}= & {} \frac{\alpha _2 \lambda ^{**}(S^{**}+f_2P^{**})}{f_4f_5},N^{**}=\frac{Bf_4f_5f_6f_7f_8-H_5 \lambda ^{**}(S^{**}+f_2P^{**})}{zf_4f_5f_6f_7 f_8},\nonumber \\ A^{**}= & {} \frac{H_1 \lambda ^{**}(S^{**}+f_2P^{**})}{f_4f_5f_6}. \end{aligned}$$

(15)

Substituting all the equations in (15) into (14), it can be shown that the non-zero equibria of the model satisfy the below quadratic equation in terms of $\lambda ^{**}$:

$$\begin{aligned}&a_o\lambda ^{**2}+a_1\lambda ^{**}+a_2=0,\end{aligned}$$

(16)

$$\begin{aligned} a_o= & {} Bf_6f_7f_8H_6-H_5f_2(Q_o+Q_1),\nonumber \\ a_1= & {} Bf_6f_7f_8H_7-z\beta H_3f_2(Q_o+Q_1)-H_4H_5,\nonumber \\ a_2= & {} B\displaystyle \prod _{i=4}^{8}f_{i}(f_1f_3-\alpha _1\epsilon _2)[1-\mathcal {R}_o]. \end{aligned}$$

(17)

The proof of positiveness of $a_o$ can be established as follows: $g_1+g_3=\sigma _1, g_2+g_4=\sigma _2$. Substituting these into expressions in (13) and the results are substituted in to $a_o$, the full expansion is positive but cumbersome and thus omitted.

Clearly, $a_o$ is positive and $a_2\ge 0$ if and only if $\mathcal {R}_o \le 1$. To obtain the endemic equilibria of model (234567)–(8), we solve for $\lambda ^{**}$ in (16) and substitute its positive values in to expressions in (15). We then obtain endemic equilibria when $\mathcal {R}_o>1$. Hence, the unique endemic equilibria can be analyzed in the following theorem.

Theorem 4.1

The model (234567)–(8) has

• i a unique endemic equilibrium if $a_2<0 \iff \mathcal {R}_o>1$;

• ii a unique endemic equilibrium if $a_1<0$ and $a_2=0$ or $a_1^2-4a_oa_2=0$;

• iii two endemic equilibria if $a_2>0,a_1<0$ and $a_1^2-4a_oa_2>0$;

• iv no endemic equilibrium otherwise.

In the above theorem, case i shows that $\exists$ a unique endemic equilibrium $\xi ^*$ whenever $\mathcal {R}_o>1.$ Particularly, case iii shows the possibility of backward bifurcation. This is the phenomenon where an asymptotically stable DFE coexists with an asymptotically stable endemic equilibrium whenever $\mathcal {R}_o<1$ [2, 4]. To prove this fact, a critical value of $\mathcal {R}_o$ denoted by $\mathcal {R}^c_o$ can be obtained by solving the discriminant $a_1^2-4a_oa_2=0$ to obtain

$$\begin{aligned}&a_1^2-4a_oa_2=0\implies a_1^2=4a_oa_2\implies 4a_oa_2\left( 1-\frac{a_1^2}{4a_oa_2} \right) =0\\&\implies 1-\frac{a_1^2}{4a_oa_2}=0\implies \mathcal {R}_o^c=1-\frac{a_1^2}{4a_o\left[ B\prod \limits _{i=4}^{8}f_{i}(f_1f_3-\alpha _1\epsilon _2)(1-\mathcal {R}_o)\right] }. \end{aligned}$$

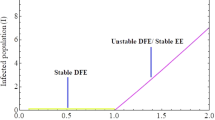
Thus, possibility of backward bifurcation would occur for values of $\mathcal {R}_o^c<\mathcal {R}_o<1.$ This can be illustrated by the bifurcation diagram presented in Fig. 2.

Fig. 2

Bifurcation diagram

Brief explanation of the figure

In the bifurcation curve, we plotted the force of infection $\lambda ^{**}$ (this is because the equation in (16) was expressed in terms of $\lambda ^{**}$) against the reproduction number using the values in Table 1. For values of $\mathcal {R}_o$ less than unity, the DFE is locally asymptotically stable but unstable for values of $\mathcal {R}_o$ greater than unity which supports the provision of Lemma 3.3. On the other-hand, for values of $\mathcal {R}_o$ less than unity, the EE becomes unstable but stable for values of $\mathcal {R}_o$ greater than unity. Since equation (16) was expressed in terms of $\lambda ^{**}$ whose expression in (14) can only be positive if $\mathcal {R}_o>1$ (since $I_1^{**},I_2^{**},A^{**},T^{**},E^{**}$ only exist for values of $\mathcal {R}_o>1$) and coefficients of equation (17) which shows the existence of EE can only be positive for values of $\mathcal {R}_o<1$, this shows the coexistence of both DFE and EE whenever $\mathcal {R}_o^c<\mathcal {R}_o<1$ confirming that the model equation undergoes the phenomenon of backward bifurcation as depicted in the bifurcation curve. We also have $\mathcal {R}_o=0.9458<1$ and $\mathcal {R}_o^c=0.8683<1$ so that ($\mathcal {R}_o^c<\mathcal {R}_o<1$). This vividly shows that there is coexistence of two equilibria when $\mathcal {R}_o^c<\mathcal {R}_o<1$, and it consequently confirms the existence of backward bifurcation [2, 4, 5].

The epidemiological implication of this is that the classical condition of $\mathcal {R}_o<1$ is only necessary but not sufficient enough to ensure complete eradication of the infectious disease.

4.1 Non-existence of Backward Bifurcation

Since bifurcation is an unfortunate phenomenon that hinder the elimination of infection in the community and our aim is to facilitate the effective elimination or reduction of the disease spread, it is therefore imperative to examine scenarios that will ensure the removal of the bifurcation property of the model.

In this section, we shall examine two scenarios listed and proved below.

Case 1: Use of Perfect Vaccine.

A perfect vaccine is a vaccine with 100% efficacy and potency. We shall consider the model equation (234567)–(8) with a perfect vaccine (i.e. when $\epsilon _1=1$). This will make the endemic equilibrium to be non-existing whenever $\mathcal {R}_o<1$. It is worth noting that bifurcation only occur when there is multiple endemic equilibria whenever $\mathcal {R}_o<1$.

Firstly, when $\epsilon _1 =1$ the control reproduction number in (12) reduces to

$$\begin{aligned} \mathcal {R}_p=\mathcal {R}_o|_{\epsilon _1 =1}&=\frac{\beta z(\epsilon _2 Q_1+Q_of_3)[f_6f_7f_8(f_5+c_1\alpha _2)+c_3\gamma H_2+c_2f_7f_8H_1]}{B\prod \limits _{i=4}^{8} f_{i}(f_1f_3-\alpha _1\epsilon _2)}. \end{aligned}$$

(18)

We state and prove the following theorem.

Theorem 4.2

The disease-resistant model (234567)–(8) with perfect vaccine has no endemic equilibrium whenever $\mathcal {R}_p\le 1$ and has a unique endemic equlibrium otherwise.

Proof

Let $\epsilon _1=1$ i.e. $f_2=0$ in the model (234567)–(8) thereby reducing (16) to

$$\begin{aligned} \bar{a}_1\lambda ^{**}+\bar{a_2}=0 \end{aligned}$$

(19)

where

$$\begin{aligned} \bar{a}_1=\,&Bf_6f_7f_8[f_3f_5(f_4-g_1)-f_3g_2\alpha _2]-(\epsilon _2 Q_1+Q_of_3)\\&\times [f_7f_8(\alpha _2\tau _1f_6+\tau _2 H_1)+H_2(\tau _3f_8+\gamma \tau _4)]\\ \bar{a}_2&=B\displaystyle \prod _{i=4}^{8}f_{i}(f_1f_3-\alpha _1\epsilon _2) (1-\mathcal {R}_p). \end{aligned}$$

Clearly, $\bar{a}_1>0$ and $\bar{a_2}\ge 0$ whenever $\mathcal {R}_p\le 1$ so that $\lambda ^{**}=-\frac{\bar{a}_2}{\bar{a_1}}\le 0.$

Therefore, for this case, the linear equation in (19) has no positive solution and as such, has no positive endemic equilibrium whenever $\mathcal {R}_p\le 1$. Hence, Theorem 4.2 is proved.

The proof of the positiveness of $\bar{a_1}$ can be carried out using method similar to the one presented earlier. $\square$

In this case, possibility of backward bifurcation is consequently ruled out. This is because bifurcation only occur when at least two positive endemic equilibria exist whenever $\mathcal {R}_p\le 1$ [2, 4].

Furthermore, we assumed that the perfect vaccine has a negligible waning rate i.e. ($\epsilon _2=0$). This means $f_3=z$ and the new control reproduction number becomes

$$\begin{aligned} \hat{\mathcal {R}}_p=\mathcal {R}_o|_{\epsilon _1 =1,\epsilon _2=0}&=\frac{\beta zQ_o[f_6f_7f_8(f_5+c_1\alpha _2)+c_3\gamma H_2+c_2f_7f_8H_1]}{Bf_1\prod _{i=4}^{8} f_{i}}. \end{aligned}$$

(20)

Using the reproduction number in (20), the disease-resistant model (234567)–(8) with perfect vaccine and negligible waning rate has no endemic equilibrium whenever $\hat{\mathcal {R}}_p\le 1$ and has a unique endemic equlibrium otherwise. The proof can be established using similar method as in the proof of Theorem 4.2.

Case II The Mass-Action Model.

According to the work of [2], it was reported that some mathematical models for infectious disease undergo the phenomenon of backward bifurcation whenever the associated reproduction number is less than unity which usually hinder the reduction and elimination of the disease in the community. This phenomenon can be removed by replacing the standard incidence function with mass action function. In particular, [4] applied the technique to measles model while [5] applied the technique to dengue fever model. Here, we shall use the same technique to analyze the removal of backward bifurcation in a disease-resistant mathematical model. This shows that they have a negligible disease-induced mortality rate. We will now consider model (234567)–(8) with negligible disease-induced mortality rate i.e. $\tau _1=\tau _2=\tau _3=\tau _4=0$ as follows.

Substituting $\tau _1=\tau _2=\tau _3=\tau _4=0$ into (10), we have

$$\begin{aligned} \frac{dN}{dt}=B-zN\implies N\rightarrow \frac{B}{z}~\text {as}~t\rightarrow \infty . \end{aligned}$$

Therefore, $\frac{B}{z}$ is an upper bound for N(t) provided that $N(0)\le \frac{B}{z}.$ Using $N=\frac{B}{z}$ in (1), we have

$$\begin{aligned} \lambda _{mas}=\acute{\beta }(I_1+c_1I_2+c_2A+c_3E) \end{aligned}$$

(21)

as the force of infection for the mass-action model where $\acute{\beta }=\frac{z\beta }{B}$.

The mass-action model equation is given below

$$\begin{aligned} \frac{dS}{dt}= & {} Q_o-(\lambda _{mas} +f_1)S+g_1I_1+g_2I_2+\epsilon _2P, \end{aligned}$$

(22)

$$\begin{aligned} \frac{dP}{dt}= & {} Q_1-P(f_3+f_2\lambda _{mas} )+\alpha _1S, \end{aligned}$$

(23)

$$\begin{aligned} \frac{dI_1}{dt}= & {} [S +f_2P]\lambda _{mas}-f_4I_1, \end{aligned}$$

(24)

$$\begin{aligned} \frac{dI_2}{dt}= & {} \alpha _2I_1-\acute{f}_5I_2, \end{aligned}$$

(25)

$$\begin{aligned} \frac{dA}{dt}= & {} g_3I_1+g_4I_2-\acute{f}_6A, \end{aligned}$$

(26)

$$\begin{aligned} \frac{dT}{dt}= & {} \theta _1I_2+\theta _2A-\acute{f}_7T, \end{aligned}$$

(27)

$$\begin{aligned} \frac{dE}{dt}= & {} \gamma T-\acute{f}_8E, \end{aligned}$$

(28)

where

$$\begin{aligned} \acute{f}_5=\sigma _2+z+\theta _1, \acute{f}_6=\theta _2+z,\acute{f}_7=z+\gamma , \acute{f}_8=z. \end{aligned}$$

The DFE of (222324252627)–(28) is the same with the one presented in (11).

Using the same approach as in (12), we calculate the reproduction number of the mass-action model as follows:

$$\begin{aligned} \mathcal {F}=\left( \begin{array}{ccccc}\acute{\beta } (S^*+f_2P^*)&{}\acute{\beta } c_1(S^*+f_2P^*)&{}\acute{\beta }c_2 (S^*+f_2P^*)&{}0&{}\acute{\beta }c_3 (S^*+f_2P^*)\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ \end{array}\right) \end{aligned}$$

and

$$\begin{aligned} \mathcal {V}=\left( \begin{array}{ccccc}f_4&{}0&{}0&{}0&{}0\\ -\alpha _2&{}\acute{f}_5&{}0&{}0&{}0\\ -g_3&{}-g_4&{}\acute{f}_6&{}0&{}0\\ 0&{}-\theta _1&{}-\theta _2&{}\acute{f}_7&{}0\\ 0&{}0&{}0&{}-\gamma &{}\acute{f}_8 \end{array}\right) . \end{aligned}$$

Hence, taking $\rho$ as the spectral radius, the control reproduction number of the mass-action model denoted by $\mathcal {R}_{mas}=\rho (\mathcal {F}\mathcal {V}^{-1})$ is given by

$$\begin{aligned} \mathcal {R}_{mas}&=\frac{\acute{\beta }(\epsilon _2 Q_1+Q_of_3)[\acute{f}_6\acute{f}_7\acute{f}_8(\acute{f}_5+c_1\alpha _2)+c_3\gamma \acute{H}_2+c_2\acute{f}_7\acute{f}_8\acute{H}_1]}{f_4\prod _{i=5}^{8} \acute{f}_{i}(f_1f_3-\alpha _1\epsilon _2)}\nonumber \\&\quad +\frac{\acute{\beta } f_2(\alpha _1Q_o+Q_1f_1)[\acute{f}_6\acute{f}_7\acute{f}_8(\acute{f}_5+c_1\alpha _2)+c_3\gamma \acute{H}_2+c_2\acute{f}_7\acute{f}_8\acute{H}_1]}{f_4\prod _{i=5}^{8} \acute{f}_{i}(f_1f_3-\alpha _1\epsilon _2)} \end{aligned}$$

(29)

where

$$\begin{aligned} \acute{H}_2= & {} \alpha _2\acute{f}_6\theta _1+\alpha _2g_4\theta _2+g_3\acute{f}_5\theta _2=\alpha _2\acute{f}_6\theta _1+\theta _2\acute{H}_1,\nonumber \\ \acute{H}_1= & {} \alpha _2g_4+g_3\acute{f}_5,\acute{H}_4=\epsilon _2Q_1+Q_of_3+f_2(\alpha _1Q_o+Q_1f_1),\nonumber \\ \acute{H}_7= & {} f_2(f_1f_4\acute{f}_5-\acute{f}_5g_1\alpha _1-g_2\alpha _1\alpha _2)+f_3\acute{f}_5(f_4-g_1)-f_3g_2\alpha _2,\nonumber \\ \acute{H}_3= & {} \acute{f}_6\acute{f}_7\acute{f}_8(\acute{f}_5+c_1\alpha _2)+c_3\gamma H_2+c_2\acute{f}_7\acute{f}_8 \acute{H}_1,\acute{H}_6=f_2(f_4\acute{f}_5-\acute{f}_5g_1-g_2\alpha _2).\nonumber \\ \end{aligned}$$

(30)

We establish the local asymptotic stability of the mass-action model using the following lemma.

Lemma 4.3

The DFE of the mass-action model (222324252627)–(28), given by (11), is locally-asymptotically stable (LAS) if $\mathcal {R}_{mas}<1,$ and unstable if $\mathcal {R}_{mas}>1.$

The proof of this lemma is elementary and thus omitted.

4.1.1 Nonexistence of endemic equilibrium when $\mathcal {R}_{mas}\le 1$

Here, we will establish that the mass-action model does not have any positive endemic equilibrium when $\mathcal {R}_{mas}\le 1.$ We claim and prove the Theorem below.

Theorem 4.4

The mass-action model (222324252627)–(28) has no positive endemic equilibrium whenever $\mathcal {R}_{mas}\le 1$ and has a unique positive endemic equilibrium otherwise.

Proof

Let

$$\begin{aligned} \acute{\xi }^*=(S^{**},P^{**},I_1^{**},I_2^{**},A^{**},T^{**},E^{**}) \end{aligned}$$

represents the endemic equilibrium points EEP of the model (222324252627)–(222324252627). Solving (222324252627)–(28) at steady states, we obtain the following expressions

$$\begin{aligned} S^{**}+P^{**}f_2= & {} \dfrac{f_4\acute{f}_5[\lambda _{mas}^{**}f_2(Q_o+Q_1)+H_4]}{\acute{H}_6\lambda ^{**2}_{mas}+\acute{H}_7\lambda ^{**}_{mas}+f_4\acute{f}_5(f_1f_3-\alpha _1\epsilon _2)}, I_1^{**}=\frac{\lambda ^{**}_{mas}(S^{**}+f_2P^{**})}{f_4},\nonumber \\ I_2^{**}= & {} \frac{\alpha _2 \lambda ^{**}_{mas}(S^{**}+f_2P^{**})}{f_4\acute{f}_5},A^{**}=\frac{\acute{H}_1 \lambda ^{**}_{mas}(S^{**}+f_2P^{**})}{f_4\acute{f}_5\acute{f}_6},\nonumber \\ T^{**}= & {} \frac{\acute{H}_2\lambda ^{**}_{mas}(S^{**}+f_2P^{**})}{f_4\acute{f}_5\acute{f}_6\acute{f}_7}, E^{**}=\frac{\gamma \acute{H}_2\lambda ^{**}_{mas}(S^{**}+f_2P^{**})}{f_4\acute{f}_5\acute{f}_6\acute{f}_7 \acute{f}_8}. \end{aligned}$$

(31)

Substituting all the equations in (31) into (21), it can be shown that the non-zero equibria of the model satisfy the following quadratic equation in terms of $\lambda ^{**}_{mas}$:

$$\begin{aligned}&a_3\lambda ^{**2}_{mas}+a_4\lambda ^{**}_{mas}+a_5=0\end{aligned}$$

(32)

$$\begin{aligned} a_3= & {} \acute{f}_6\acute{f}_7\acute{f}_8\acute{H}_6>0\nonumber \\ a_4= & {} \acute{f}_6\acute{f}_7\acute{f}_8\acute{H}_7-\acute{\beta } \acute{H}_3f_2(Q_o+Q_1)\nonumber \\ a_5= & {} f_4\displaystyle \prod _{i=5}^{8}\acute{f}_{i}(f_1f_3-\alpha _1\epsilon _2)[1-\mathcal {R}_{mas}]. \end{aligned}$$

(33)

Hence, $a_4\ge 0$ whenever $\mathcal {R}_{mas}\le 1.$ Explicitly, all the coefficients $a_3,a_4,a_5$ are positive whenever $\mathcal {R}_{mas}\le 1$ (the proof of their positiveness can be found under the Appendix). Therefore, under the condition $\mathcal {R}_{mas}\le 1$, the quadratic equation (3233) has no positive root. Hence, the model equation (222324252627)–(28) has no positive endemic equilibrium whenever $\mathcal {R}_{mas}\le 1$. This consequently removes the bifurcation phenomenon.

5 Global asymptotic stability of the mass-action model

In this section, we shall establish the global asymptotic stability of both the DFE points and EE points of the mass-action model (222324252627)–(28). Using the approach of [15], we re-express (222324252627)–(28) in the following form.

$$\begin{aligned} \dot{X}= & {} L(X,Y)\end{aligned}$$

(34)

$$\begin{aligned} \dot{Y}= & {} M(X,Y), M(X,0)=0 \end{aligned}$$

(35)

where the vector $X=(S,P)$ denote the uninfected compartment of the system and $Y=(I_1,I_2,A,T,E)\in \mathbb {R}_+^5$ represents the infected compartments.

Using the provision of equation (11) to establish the stability analysis, the following two conditions must be satisfied:

$\mathbf{N} _1:$ For $\dot{X}(t)=L(X^{o},0)$, $X^o$ is globally asymptotically stable. $\mathbf{N} _2:$ $M(X,Y)=JY-\hat{M}(X,Y)$, $\hat{M}(X,Y)\ge 0$ for $X,Y\in \Omega _m$

where $J=\frac{\partial M}{\partial Y}(X^o,0)$.

From our model equation, we obtain the Jacobian matrix of only the infected compartment at DFE as follows:

$$\begin{aligned} JY= \left[ \begin{array}{ccccc}U_4\beta -f_4&{}U_4c_1\beta &{}U_4c_2\beta &{}0&{}U_4\beta c_3\\ \alpha _2&{}-\acute{f_5}&{}0&{}0&{}0\\ g_3&{}g_4&{}-\acute{f}_6&{}0&{}0\\ 0&{}\theta _1&{}\theta _2&{}-\acute{f}_7&{}0\\ 0&{}0&{}0&{}\gamma &{}-\acute{f}8 \end{array}\right] \left[ \begin{array}{c}I_1\\ I_2\\ A\\ T\\ E \end{array}\right] , \end{aligned}$$

where $U_4^*=(S^*+f_2P^*),U_4=(S+f_2P)$,

$$\begin{aligned}&\hat{M}(X,Y)=JY-M(X,Y)\\&=\left[ \begin{array}{c}\beta (I_1+c_1I_2+c_2A+c_3E)U_4^*-f_4I_1\\ \alpha _2I_1-\acute{f}_5I_2\\ g_3I_1+g_4I_2-\acute{f}_6A\\ \theta _1I_2+\theta _2A-\acute{f}_7T\\ \gamma T-\acute{f}_8E\end{array}\right] -\left[ \begin{array}{c}\beta (I_1+c_1I_2+c_2A+c_3E)U_4-f_4I_1\\ \alpha _2I_1-\acute{f}_5I_2\\ g_3I_1+g_4I_2-\acute{f}_6A\\ \theta _1I_2+\theta _2A-\acute{f}_7T\\ \gamma T-\acute{f}_8E\end{array}\right] ,\\&\hat{M}(X,Y)=\left[ \begin{array}{c}\beta (I_1+c_1I_2+c_2A+c_3E)(S^*+f_2P^*)\left( 1-\frac{S+f_2P}{S^*+f_2P^*}\right) \\ 0\\ 0\\ 0\\ 0\end{array}\right] ,\\ \end{aligned}$$

where $\hat{M}(X,Y)\ge 0$ if $\left( \frac{S+f_2P}{S^*+f_2P^*}\right) \le 1.$ It can be seen that $\lim _{t\longrightarrow \infty }X(t)=X^o$ and J is an M-matrix, thus $X^o$ is globally asymptotically stable, hence, $\mathbf{N} _1$ is satisfied. Also $\hat{M}(X,Y)>0$, for $(X,Y)\in \Omega _m$. Hence, $\mathbf{N} _2$ is satisfied and $\xi _o$ is globally asymptotically stable whenever $\mathcal {R}_{mas}<1.$

This shows that all solution of the mass action model with equation (21) and the initial conditions in $\zeta$, approaches the DFE $\xi _o$ as t tends to $\infty$ whenever $\mathcal {R}_{mas}<1.$ This result is expressed numerically in Fig. 3 (time series plot) after simulating the mass action model using parameter values in Table 1 (with $\acute{\beta }=0.0003$) when $\mathcal {R}_{mas}<1.$

Fig. 3

Time series plot of the mass action model for $\mathcal {R}_{mas}<1$

Brief explanation of Fig. 3

Figure 3 above depicts the behavior of the infected population of the mass action model for values of $\mathcal {R}_{mas}<1$. The initial population used is S=300, P=200, $I_1$=100, $I_2$=70, A=50, T=20, E=10 while other parameter values are in Table 1. When $\acute{\beta }=0.0003$, $\mathcal {R}_{mas}=0.00026$ which is less than unity. It can be noticed that when the reproduction number for the mass action model is less than unity, the infected population reduces significantly (but not equal to zero). This clearly shows that the DFE is stable asymptotically.

5.1 Global Stability analysis of the EEP For special case

We consider the special case where the vaccine doesn’t wane ($\epsilon _2=0$), no vaccination programme $(\alpha _1=0)$, both quarantined and treatment failure classes do not transmit the disease ie. $(c_2=c_3=0)$ and no resistance to the disease i.e. $m_1=m_2=0$ so that the model reduces to

$$\begin{aligned} \frac{dS}{dt}=\,&Q_o-(\acute{\lambda }_{mas} +z)S,\end{aligned}$$

(36)

$$\begin{aligned} \frac{dP}{dt}=\,&Q_1-P(z+f_2\acute{\lambda }_{mas} ),\end{aligned}$$

(37)

$$\begin{aligned} \frac{dI_1}{dt}=\,&(S +f_2P)\acute{\lambda }_{mas}-f_4I_1,\end{aligned}$$

(38)

$$\begin{aligned} \frac{dI_2}{dt}=\,&\alpha _2I_1-\acute{f}_5I_2,\end{aligned}$$

(39)

$$\begin{aligned} \frac{dA}{dt}=\,&\sigma _1I_1+\sigma _2I_2-\acute{f}_6A,\end{aligned}$$

(40)

$$\begin{aligned} \frac{dT}{dt}=\,&\theta _1I_2+\theta _2A-\acute{f}_7T,\end{aligned}$$

(41)

$$\begin{aligned} \frac{dE}{dt}=\,&\gamma T-zE, \end{aligned}$$

(42)

where $\acute{\lambda }_{mas}=\acute{\beta }(I_1+c_1I_2),~~\acute{\beta }=\frac{\beta z}{B}$. It can be established that the reproduction number for the reduced model is given by

$$\begin{aligned} \acute{\mathcal {R}}_{mas}=\frac{\acute{\beta }[(Q_o+f_2Q_1)(\alpha _2c_1+\acute{f}_5)]}{zf_4\acute{f}_5}. \end{aligned}$$

(43)

If $\acute{\mathcal {R}}_{mas}>1$, the endemic equilibrium is given by

$$\begin{aligned} \acute{\xi }^*_2=(S^{**},P^{**},I_1^{**},I_2^{**},A^{**},T^{**},E^{**}). \end{aligned}$$

Hence, we claim the following result without proof.

Lemma 5.1

The reduced model (36)–(42) with (43) has a unique positive endemic equilibrium $\acute{\xi }^*_2$ whenever $\acute{\mathcal {R}}_{mas}>1.$

We define the invariant region $\zeta _2$ as follows:

$$\begin{aligned} \zeta _2=\left\{ (S,P,I_1,I_2,A,T,E)\in \mathbb {R}_+^7:I_1=I_2=A=T=E=0\right\} \end{aligned}$$

(44)

Theorem 5.2

The unique positive endemic equilibrium $\acute{\xi }^*_2$ of the reduced model (36)–(42) with (43) is globally-asymptotically stable in $\acute{\xi }^*_2$ if $\acute{\mathcal {R}}_{mas}>1.$

Proof

Since Lemma 5.1 has already been established for the reduced model (36)–(42) with (43) whenever $\acute{\mathcal {R}}_{mas}>1$, we construct the following non-linear Lyapunov function for the subsystem consisting of the first four equations as follows:

$$\begin{aligned} J&=\frac{\acute{\beta }}{z}\left[ S-S^{**}-S^{**}\ln \left( \frac{S}{S^{**}}\right) \right] +\frac{\acute{\beta }}{z}\left[ P-P^{**}-P^{**}\ln \left( \frac{P}{P^{**}}\right) \right] \\&\qquad +\frac{\acute{\beta }}{\alpha _{{2}}}\left[ I_1-I_1^{**}-I_1^{**}\ln \left( \frac{I_1}{I_1^{**}}\right) \right] +\acute{\beta z}\left[ I_2-I_2^{**}-I_2^{**}\ln \left( \frac{I_2}{I_2^{**}}\right) \right] . \end{aligned}$$

The Lyapunov derivative with respect to t is given by

$$\begin{aligned} \dot{J}=\frac{\acute{\beta }}{z}\left[ \dot{S}-\dfrac{S^{**}}{S}\dot{S}\right] +\frac{\acute{\beta }}{z}\left[ \dot{P}-\dfrac{P^{**}}{P}\dot{P}\right] +\frac{\acute{\beta }}{\alpha _{{2}}}\left[ \dot{I_1}-\dfrac{I_1^{**}}{I_1}\dot{I_1}\right] +\acute{\beta }z\left[ \dot{I_2}-\dfrac{I_2^{**}}{I_2}\dot{I_2}\right] . \end{aligned}$$

Using (36)–(39), we have

$$\begin{aligned} \dot{J}&=\frac{\acute{\beta }}{z}\left[ Q_o-(z+\acute{\lambda }_{mas})S-\frac{S^{**}}{S}\left\{ Q_o-(z+\acute{\lambda }_{mas})S\right\} \right] \nonumber \\&\quad +\frac{\acute{\beta }}{z}\left[ Q_1-(z+f_2\acute{\lambda }_{mas})P-\frac{P^{**}}{P}\left\{ Q_1-(z+f_2\acute{\lambda }_{mas})P \right\} \right] \nonumber \\&\quad +\frac{\acute{\beta }}{\alpha _{2}}\left[ (S+f_2P)\acute{\lambda }_{mas}-f_4I_1-\frac{I_1^{**}}{I_1}\left\{ (S+f_2P)\acute{\lambda }_{mas}-f_4I_1\right\} \right] \nonumber \\&\quad +\acute{\beta } z\left[ \alpha _{{2}}I_1-\acute{f}_5I_2-\frac{I_2^{**}}{I_2}\left\{ \alpha _{{2}}I_1-\acute{f}_5I_2 \right\} \right] . \end{aligned}$$

(45)

From (36)–(39), it can be shown that

$$\begin{aligned}&Q_o=zS^{**}+\acute{\beta }(I_1^{**}+c_1I_2^{**})S^{**}, Q_1=P^{**}z+P^{**}f_2\acute{\beta }(I_1^{**}+c_1I_2^{**})\end{aligned}$$

(46)

$$\begin{aligned}&f_4=\frac{S^{**}\acute{\beta }(I_1^{**}+c_1I_2^{**})+f_2P^{**}(I_1^{**}+c_1I_2^{**})}{I_1^{**}}, f_5I_2^{**}=\frac{\acute{\beta }\alpha _2(I_1^{**}+c_1I_2^{**})(S^{**}+f_2P^{**})}{f_4} \end{aligned}$$

(47)

$$\begin{aligned}&\sigma _1I_1^{**}+\sigma _2I_2^{**}=f_6A^{**}, \theta _1I_2^{**}+\theta _2A^{**}=\acute{f}_7T^{**}, \gamma T^{**}=\acute{f}_8E^{**}. \end{aligned}$$

(48)

Substituting (46) and (47) in (45), we have

$$\begin{aligned} \dot{J}&=\frac{\acute{\beta }}{z}\left[ zS^{**}+\acute{\lambda }_{mas}^{**}S^{**}-\acute{\lambda }_{mas}S -zS-\frac{S^{**}}{S}[zS^{**}+\acute{\lambda }_{mas}^{**}S^{**}]+zS^{**}+\acute{\lambda }_{mas}^{**}S^{**}\right] \\&\quad +\frac{\acute{\beta }}{z}\left[ P^{**}z+f_2(P^{**}\acute{\lambda }_{mas}^{**}-P\acute{\lambda }_{mas})-Pz-\frac{P^{**}}{P}\left\{ P^{**}z+(P^{**}\acute{\lambda }_{mas}^{**} -P\acute{\lambda }_{mas})f_2-Pz\right\} \right] \\&\quad +\frac{\acute{\beta }}{\alpha _{2}}\left[ S\acute{\beta }(I_1+c_1I_2)+f_2P\acute{\beta }(I_1+c_1I_2)-\left( \frac{(S^{**}+f_2P^{**})\acute{\lambda }_{mas}^{**}}{I_1^{**}} \right) I_1 -\frac{I_1^{**}S\acute{\lambda }_{mas}}{I_1} \right] \\&\quad -\frac{\beta }{\alpha _2}\left[ \frac{I_1^{**}f_2P\acute{\beta }(I_1+c_1I_2)}{I_1}+\left( \frac{(S^{**}+f_2P^{**})\acute{\beta }(I_1^{**}+c_1I_2^{**})}{I_1^{**}} \right) I_1^{**}\right] \\&\quad +\frac{\acute{\beta f_4}z}{\alpha _2}\left[ \alpha _2I_1-\left( \frac{\acute{\beta }\alpha _2(S^{**}+f_2P^{**})\acute{\lambda }_{mas}^{**}}{f_4I_2^{**}} \right) I_2-\frac{\alpha _2I_2^{**}I_1}{I_2} -\left( \frac{\acute{\beta }\alpha _2(S^{**}+f_2P^{**})\acute{\lambda }_{mas}^{**}}{f_4I_2^{**}} \right) I_2^{**}\right] \end{aligned}$$

After some simplification and factorization, we have

$$\begin{aligned} \dot{J}&=\acute{\beta }S^{**}\left( 2-\frac{S^{**}}{S}-\frac{S}{S^{**}} \right) +\frac{\acute{\beta }}{z}\left[ S^{**}\acute{\beta }(I_1^{**}+c_1I_2^{**})-\acute{\lambda }_{mas} S-\frac{\acute{\lambda }_{mas}^{**}{S^{**}}^2}{S}+\acute{\lambda }_{mas}S^{**}\right] \\&\quad +\acute{\beta }P^{**}\left( 2-\frac{P^{**}}{P}-\frac{P}{P^{**}} \right) +\frac{\acute{\beta }}{z}\left[ P^{**}f_2 \acute{\beta } (I_1^{**}+c_1I_2^{**})+\acute{\beta } (I_1+c_1I_2)(P^{**}f_2-Pf_2)\right] \\&\quad +I_2P^{**}c_1f_2\left( 3-\frac{S}{S^{**}}-\frac{PI_2}{P^{**}I_2^{**}}-\frac{I_2}{I_2^{**}} \right) +I_2Pc_1\left( 3-\frac{I_2}{I_2^{**}}-\frac{I_2^{**}P}{I_2P^{**}}-\frac{I_2^{**}P^{**}}{I_2P} \right) \\&\quad +PI_2^{**}f_2I_1\left( 4-\frac{P}{P^{**}}-\frac{I_2}{I_2^{**}}-\frac{I_1I_2^{**}}{I_1^{**}I_2}-\frac{SI_1^{**}I_2}{S^{**}I_1I_2^{**}} \right) . \end{aligned}$$

which gives

$$\begin{aligned} \dot{J}&\le \acute{\beta }S^{**}\left( 2-\frac{S^{**}}{S}-\frac{S}{S^{**}} \right) +\acute{\beta }P^{**}\left( 2-\frac{P^{**}}{P}-\frac{P}{P^{**}} \right) \\&\quad +\frac{\acute{\beta }^2(I_1^{**}+c_1I_2^{**})S^{**}}{z}\left[ 2-\frac{(I_1+c_1I_2)S}{(I_1^{**}+c_1I_2^{**})S^{**}} -\frac{S^{**}}{S}\right] \\&\quad +I_2P^{**}c_1f_2\left( 3-\frac{S}{S^{**}}-\frac{PI_2}{P^{**}I_2^{**}}-\frac{I_2}{I_2^{**}} \right) +I_2Pc_1\left( 3-\frac{I_2}{I_2^{**}}-\frac{I_2^{**}P}{I_2P^{**}}-\frac{I_2^{**}P^{**}}{I_2P} \right) \\&\quad +PI_2^{**}f_2I_1\left( 4-\frac{P}{P^{**}}-\frac{I_2}{I_2^{**}}-\frac{I_1I_2^{**}}{I_1^{**}I_2}-\frac{SI_1^{**}I_2}{S^{**}I_1I_2^{**}} \right) . \end{aligned}$$

Consequently, since the arithmetic mean exceeds the geometric mean, then we have

$$\begin{aligned}&\left( 2-\frac{S^{**}}{S}-\frac{S}{S^{**}} \right) \le 0, \left( 2-\frac{P^{**}}{P}-\frac{P}{P^{**}} \right) \le 0,\left( 3-\frac{I_2}{I_2^{**}}-\frac{I_2^{**}P}{I_2P^{**}}-\frac{I_2^{**}P^{**}}{I_2P} \right) \le 0,\\&\frac{\acute{\beta }^2(I_1^{**}+c_1I_2^{**})S^{**}}{z}\left[ 2-\frac{(I_1+c_1I_2)S}{(I_1^{**}+c_1I_2^{**})S^{**}} -\frac{S^{**}}{S}\right] \le 0,\left( 3-\frac{S}{S^{**}}-\frac{PI_2}{P^{**}I_2^{**}}-\frac{I_2}{I_2^{**}} \right) \le 0 \\&\left( 4-\frac{P}{P^{**}}-\frac{I_2}{I_2^{**}}-\frac{I_1I_2^{**}}{I_1^{**}I_2}-\frac{SI_1^{**}I_2}{S^{**}I_1I_2^{**}} \right) \le 0. \end{aligned}$$

Since $S\ge 0,P\ge 0,I_1\ge 0,I_2\ge 0,A\ge 0,T\ge 0,E\ge 0$ and Lemma 5.1 is satisfied, it follows that $\dot{J}\le 0$ since all other model parameters are non-negative. Furthermore, $\dot{J}=0$ if and only if $S=S^{**},P=P^{**},I_1=I_1^{**},I_2=I_2^{**}.$ Thus, $\dot{J}$ is a Lyapunov function of the subsystem (36)–(39) on $\zeta _2.$ It therefore follow by LaSalle’s Invariance Principle [16] that

$$\begin{aligned} \lim _{t\longrightarrow \infty }S(t)=S^{**},\lim _{t\longrightarrow \infty }P(t)=P^{**},\lim _{t\longrightarrow \infty }I_1(t)=I_1^{**},\lim _{t\longrightarrow \infty }I_1(t)=I_1^{**}, \end{aligned}$$

$\lim _{t\longrightarrow \infty }I_2(t)=I_2^{**}.$ It also follows that

$$\begin{aligned}&\lim _{t\longrightarrow \infty }\inf S(t) =\lim _{t\longrightarrow \infty }\sup S(t)=S^{**},\lim _{t\longrightarrow \infty }\inf P(t) =\lim _{t\longrightarrow \infty }\sup P(t)=P^{**},\\&\lim _{t\longrightarrow \infty }\inf I_1(t) =\lim _{t\longrightarrow \infty }\sup I_1(t)=I_1^{**},\lim _{t\longrightarrow \infty }\inf I_2(t) =\lim _{t\longrightarrow \infty }\sup I_2(t)=I_2^{**}. \end{aligned}$$

Therefore, for sufficiently small $\delta >0$, $\exists$ $t^*>0$ such that

$$\begin{aligned}&\lim _{t\longrightarrow \infty }\sup S(t)\le S^{**}+\delta ,~\lim _{t\longrightarrow \infty } \sup P(t)\le P^{**}+\delta ,\\&\lim _{t\longrightarrow \infty }\sup I_1(t)\le I_1^{**}+\delta , \lim _{t\longrightarrow \infty } \sup I_2(t)\le I_2^{**}+\delta . \end{aligned}$$

for all $t>t^*.$

Now from (42), we have

$$\begin{aligned} \frac{dE}{dt}=\gamma T -zE\implies \frac{dE}{dt}\le \gamma (T^{**}+\delta ) -zE \end{aligned}$$

By comparison [17], we have

$$\begin{aligned} \lim _{t\longrightarrow \infty } E(t)\le \frac{\gamma (T^{**}+\delta )}{z} \end{aligned}$$

For sufficiently small $\delta$, we have

$$\begin{aligned} \lim _{t\longrightarrow \infty } E(t)\le \frac{\gamma T^{**}}{z} \end{aligned}$$

(49)

Similarly, for sufficiently small $\delta$, we have

$$\begin{aligned} \lim _{t\longrightarrow \infty } E(t)\ge \frac{\gamma T^{**}}{z}. \end{aligned}$$

(50)

It is concluded from (49) and (50) that

$$\begin{aligned} \lim _{t\rightarrow \infty }E(t)=E^{**} \end{aligned}$$

where

$$\begin{aligned} E^{**}=\frac{\gamma T^{**}}{z}. \end{aligned}$$

The same approach can be used for $T\rightarrow T^{**}$ and $A\rightarrow A^{**}$. Therefore all solutions of the model (36)–(42) with condition (9) approaches the endemic equilibrium $\acute{\xi }^*_2$ as $t\rightarrow \infty$ for $\acute{\mathcal {R}}_{mas}>1.$ Hence, the endemic equilibrium of the reduced model (36)–(42) is globally asymptotically stable. $\square$

The numerical simulation of the reduced model (36)–(42) with (43) such that $\acute{\mathcal {R}}_{mas}>1$ using parameter values on Table 1 is presented in Fig. 4 confirming Theorem 5.2.

Fig. 4

Time series plot of the reduced model for $\acute{\mathcal {R}}_{mas}>1$

Brief explanation of Fig. 4

Figure 4 above depicts the behavior of the infected population of the reduced model for values of $\mathcal {R}_{mas}>1$. The initial population used is $S=30{,}000$, $P=20{,}000$, $I_1=10{,}000$, $I_2=5000$, $A=1000$, $T=500$, $E=20$ while other parameter values are in Table 1. When $\acute{\beta }=1.9000$, $\mathcal {R}_{mas}=1.5918$ which is greater than unity. It can be noticed that when the reproduction number for the mass action model is greater than unity, the infected population grows significantly. This clearly shows that the EE is stable asymptotically confirming the provision of Theorem 5.2.

6 Assesment of the resistance impact

In this section, we perform the numerical simulation of the system of the model to validate the points highlighted in the analytical results and to understand the impact of the resistance. The numerical simulation will help to understand the projected benefit of virus resistance blood cells in disease transmission. All other parameters used are properly referenced in Table 1.

Figure 5 represents the effect of resistance level (0–95%) for $m_1$ and (0–98%) for $m_2$ on appearance of new infection. Using Python Programming Language, we present the potential impact of disease resistance on the appearance of new infections in the population. We vary the resistance $0\%\le m_1\le 95\%$ and $0\%\le m_2\le 98\%$ with reference to the initial condition. The simulation results are presented in Fig. 6. It can be easily seen that as the resistance increases in the blood cells, the transmission of the disease becomes reduced. This result emphasizes the potential benefit of resistance when the cells developed it at higher level. We also note that the highest peak of the new infection ie. 1.4 million is reached when the cells gain no resistance to infection and the lowest level is reached i.e 200,000 when the resistance is as high as $95\%$ and $98\%$ respectively.

Fig. 5

Effect of resistance on the appearance of new infected population

Fig. 6

Effect of resistance on the appearance of new susceptible uninfected population

Figure 6 represents the effect of resistance on appearance of new susceptible uninfected population.

We can easily observe that an increase in resistance translates to increase in uninfected individuals. It’s not that the resistance is curing the infected population but only increasing the uninfected susceptible population by reducing the rate at which the disease is been contacted and transmitted. This result emphasizes the potential benefit of resistance when the cells developed it at a higher level. We also note that the highest peak of the new uninfected population ie. 1.6 million is reached when the cells gain the highest resistance to infection and the lowest level is reached i.e 700,000 when the resistance is at the lowest level.

7 Conclusion

In this study, a new model representing the dynamics of disease resistance using an autonomous nonlinear system of ordinary differential equations incorporating quarantine, treatment and imperfect vaccine was developed and analyzed. The fundamental properties of the model including positivity solution, feasible region, analysis of the control reproduction number and its bifurcation analysis, equilibria points and its stability were thoroughly discussed. The model exhibits both disease-free and endemic equilibrium points. The analysis shows that there is bifurcation which can be removed either when the vaccine is perfect or when the standard incidence is replaced with mass action incidence.

The global stability analysis of the DFE was carried out using the approach of [15] while the global stability analysis of the endemic equilibrium points was carried out using a suitable Lyapunov function.

The model analysis vividly shows that all effort should be made so that individuals can develop resistance to the disease under suitable quarantine condition.

The model can be modified to include other dynamics that can influence the spread of the disease. We can particularly relax some assumptions of the model or include other measures so that the disease can be reduced or eradicated. Optimal control and cost-effectiveness among others can also be carried out to gain more knowledge about the dynamics of the model. The model can be modified and applied to HIV/AIDS which is our future study.

Appendix

Computation of the positiveness of $a_3$, $a_4$ and $a_5$

$$\begin{aligned} \acute{H}_6=f_2(f_4\acute{f}_5-\acute{f}_5g_1-g_2\alpha _2)= & {} f_2[(\sigma _1+z+\alpha _2)U_1-U_1\sigma _1m_1-\alpha _2\sigma _2m_2]\\= & {} f_2[(1-m_1)(\sigma _1U_1+\alpha _2\sigma _2)+\alpha _2(z+\theta _1)]\\&+z\acute{f}_5f_2+f_2[\sigma _2\alpha _2(1-m_2)]\\= & {} f_2[(g_3+z)(g_2+g_4+z+\theta _1)+\alpha _2 U_2]>0\\&0\le m_1\le 1, 0\le m_2\le 1. \end{aligned}$$

where $U_1=\sigma _2+z+\theta _1,U_2=g_4+z+\theta _1.$

Hence, $a_3$ is positive.

$$\begin{aligned} \acute{H}_7&=f_2(f_1f_4\acute{f}_5-\acute{f}_5g_1\alpha _1-g_2\alpha _1\alpha _2)+f_3\acute{f}_5(f_4-g_1)-f_3g_2\alpha _2\\&=f_2[-\alpha _1\alpha _2g_2-\alpha _1g_1U_3+f_1(g_1+g_3+z+\alpha _2)U_3]\\&\quad +(z+\epsilon _2)(g_2+g_4+z+\theta _1)(g_3+z+\alpha _2)-(z+\epsilon _2)g_2\alpha _2 \end{aligned}$$

where $U_3=g_2+g_4+z+\theta _1$, after some simplifications, we arrive at

$$\begin{aligned} \acute{H}_7&=f_1f_2[z^2+H_9z+H_8]+\epsilon _2(z^2+H_9z+H_8)+z^3+H_9z^2\\&\quad +H_8z+zf_2[g_1(z+K)+\alpha _2g_2]>0 \end{aligned}$$

where

$$\begin{aligned} H_8= & {} \alpha _2(g_4+\theta _1)+g_3(g_2+g_4+\theta _1), H_9=\alpha _2+g_2+g_3+g_4+\theta _1, f_1=\alpha _1+z,\\ K= & {} g_1+g_2+\theta _1. \end{aligned}$$

To show that $a_4$ is positive, it is sufficient for us to show that $\frac{\acute{\beta } \acute{H}_3f_2B}{\acute{f}_6\acute{f}_7\acute{f}_8\acute{H}_7}\le 1$ whenever $\mathcal {R}_{mas}\le 1.$ Equation (29) can be re-expressed as

$$\begin{aligned}&\mathcal {R}_{mas}=\frac{\acute{\beta }\acute{H}_3 Q_3}{f_4\acute{f}_5\acute{f}_6\acute{f}_7\acute{f}_8}+\frac{\acute{\beta }\acute{H}_3 Q_4f_2}{f_4\acute{f}_5\acute{f}_6\acute{f}_7\acute{f}_8},~~\mathcal {R}_{mas}\le 1\implies \frac{\acute{\beta }\acute{H}_3 Q_3}{f_4\acute{f}_5\acute{f}_6\acute{f}_7\acute{f}_8}+\frac{\acute{\beta }\acute{H}_3 Q_4f_2}{f_4\acute{f}_5\acute{f}_6\acute{f}_7\acute{f}_8}\le 1\nonumber \\&\qquad \acute{\beta }\acute{H}_3\le \frac{f_4\acute{f}_5\acute{f}_6\acute{f}_7\acute{f}_8}{ Q_3+Q_4f_2}, \end{aligned}$$

(51)

where $Q_3=\frac{\epsilon _2 Q_1+Q_of_3}{f_1f_3-\alpha _1\epsilon _2}>0,~ Q_4=\frac{\alpha _1Q_o+Q_1f_1}{f_1f_3-\alpha _1\epsilon _2}>0.$

Hence,

$$\begin{aligned} \dfrac{\acute{\beta } \acute{H}_3f_2B}{\acute{f}_6\acute{f}_7\acute{f}_8\acute{H}_7}\le \frac{f_2Bf_4\acute{f}_5}{( Q_3+Q_4f_2)\acute{H}_7} . \end{aligned}$$

It is also sufficient to show that

$$\begin{aligned} f_2Bf_4\acute{f}_5-( Q_3+Q_4f_2)\acute{H}_7=\,&Bf_2K_1U_3[-\alpha _1\epsilon _2-(\alpha _1+z)(\epsilon _2+z)]\\&-[\epsilon _2qB+(1-q)B(\epsilon _2+z)+f_2B(\alpha _1+zq)]\\&[f_2[(\alpha _1+z)K_1 U_3-U_3g_1\alpha _1-g_2\alpha _1\alpha _2] \\&+(\epsilon _2+z)(g_2+g_4+z+\theta _1)(g_3+z+\alpha _2)]< 0, \end{aligned}$$

where $K_1=g_1+g_3+z+\alpha _2,$

so that $\frac{\acute{\beta } \acute{H}_3f_2B}{\acute{f}_6\acute{f}_7\acute{f}_8\acute{H}_7}\le 1$.