1 Introduction

There are lots of people dying because of infectious diseases every day. From an epidemiological viewpoint, it is important to study the global stability of disease transmission. Mathematical models describing the infectious disease dynamics have played an important role and provided the preventive strategies in a period. The SEIRS epidemic model is an important model. It shows that the total population is divided into four classes: the susceptible S, the exposed E, the infectious I and the removed R. This model has been studied by many authors [1–11]; however, many literature works did not consider disease resistance in humans. With the development and progress of society, people begin to understand the importance of health and exercise. In other words, people’s resistance has improved greatly. So, disease resistance has become an indispensable factor in the study of infectious disease models. Nguyen Huu Khanh considered the disease resistance and formulated a mathematical model [3]. In the model, a person in the exposed group or infected group can return to the susceptible group without treatment.

In fact, the disease incidence plays an important role in the study of mathematical epidemiological model. The general form of incidence rate is written as \(\beta U(N)\frac{S}{N}I\), where \(U(N)\) is usually called the contact rate. In many articles, the adequate contact rate takes two forms frequently, the corresponding disease incidence is the bilinear incidence rate \(\beta SI\) (\(U(N)=N\)) and the standard incidence rate \(\beta\frac{S}{N}I\) (\(U(N)=1\)). Between the two contact rates, there is a more realistic saturated contact rate \(U(N)=\frac{\alpha N}{1+\omega N}\) [12]. Heesterbeek et al. considered the saturated contact rate forming \(U(N)=\frac{\alpha N}{1+b N+\sqrt{1+2bN}}\) [13]. The above specific contact rates have the following common characteristic:

$$U(0)=0,\qquad U'(N)\geq0,\qquad\biggl(\frac{U(N)}{N} \biggr)'\leq0. $$

Based on this characteristic, more general incidence rates have also been proposed, for example, \(\beta I^{p} S^{q} \) [14, 15], \(\beta Sg(I)\) [16], \(f(S,N,I)\) [17], \(f(S,I)\) [4, 18]. Moreover, Qi and Cui established a new SEIRS epidemic model including a general incidence forming \(\beta h(S)I\) [6], and it also satisfied the above characteristics.

In real life, many infectious diseases are transmitted through both exposed individuals and infected individuals, for example, HIV, HBV and influenza. For the convenience of mathematical research, we assume that the exposed and infected individuals have the same infection rate. It is assumed that the nonlinear incidence is to be of the form \(\beta h(S)(E+I)\), where h satisfies

(\(A_{1}\)):

for \(x\geq0\), \(h(x)\geq0\), with equality if and only if \(x=0\), \(h'(x)>0\) and \(h''(x)\leq0\) (where ′ represents differentiation with respect to x).

Our paper is organized as follows. In Section 2, we formulate an SEIRS mathematical model and obtain the basic reproductive number \(\Re_{0}\). Furthermore, the existence of equilibria is given. In Section 3, we prove the global stability of the disease-free equilibrium. Section 4 is devoted to the stability analysis of the endemic equilibria of the model. In Section 5, some numerical simulations are given to justify the theoretical analysis. Finally, we summarize this work.

2 The model and its basic properties

2.1 The structure of the model

We consider the transmission of influenza virus with disease resistance in humans. The total population is divided into four classes of individuals which are the susceptible (S), the exposed (E), the infected (I) and the recovered (R). The model is given by a system of ordinary differential equations

$$ \textstyle\begin{cases} \frac{\mathrm{d} S}{\mathrm{d} t} = A-\beta h(S)(E+I)+cE+bI+\alpha R-\mu S,\\ \frac{\mathrm{d} E}{\mathrm{d} t} = \beta h(S)(E+I)-(c+\varepsilon+\mu )E,\\ \frac{\mathrm{d} I}{\mathrm{d} t} = \varepsilon E-(\gamma+b+\mu)I,\\ \frac{\mathrm{d} R}{\mathrm{d} t} = \gamma I-(\alpha+\mu)R, \end{cases} $$
(2.1)

where A is the recruitment of susceptible, c, b are the rates at which the exposed and infectious individuals become susceptible individuals without treatment, respectively, ε is the constant rate for the exposed population becoming infectious, α is the rate at which the recovered individuals become susceptible individuals again, γ is the constant rate for recovery, and μ is the natural death rate of the human population. All parameters are assumed to be positive. Consider the epidemiological implications, we assume that \(b< c\).

Let \(N(t)=S(t)+E(t)+I(t)+R(t)\). The rate of change of \(N(t)\), which can be obtained by adding all the equations in model (2.1), is given by

$$\frac{\mathrm{d} N}{\mathrm{d} t}\leq A-\mu N. $$

Therefore, from biological consideration, we study (2.1) in the closed set

$$\Omega=\biggl\{ (S,E,I,R) \Big\vert S,E,I,R\ge0,S+E+I+R\leq\frac{A}{\mu}\biggr\} . $$

It is easy to see that the set Ω is a positively invariant set for (2.1).

2.2 Basic reproduction number

The basic reproduction number, denoted by \(\Re_{0}\), is ‘the expected number of secondary cases produced, in a completely susceptible population, by a typical infective individual’ [19]. We use the method of next generating matrix to determinate the expression for \(\Re_{0}\) [20]. Let \(x=(E,I,S,R)^{T}\), we rewrite system (2.1) in the matrix form

$$\frac{\mathrm{d} x}{\mathrm{d} t}=\mathcal{F}(x)-\mathcal{V}(x), $$

where

$$\mathcal{F}(x)=\left ( \begin{matrix} \beta h(S)(E+I)\\ 0\\ 0\\ 0 \end{matrix} \right ),\qquad \mathcal{V}(x)=\left ( \begin{matrix} (c+\varepsilon+\mu)E\\ -\varepsilon E+(\gamma+b+\mu)I\\ -A+\beta h(S)(E+I)-cE-bI-\alpha R+\mu S\\ -\gamma I+(\alpha+\mu)R \end{matrix} \right ). $$

We can get

$$F=\left ( \begin{matrix} \beta h(S_{0}) & \beta h(S_{0})\\ 0 & 0 \end{matrix} \right ),\qquad V=\left ( \begin{matrix} c+\varepsilon+\mu& 0\\ -\varepsilon & \gamma+b+\mu \end{matrix} \right ), $$

where \(S_{0}=\frac{A}{\mu}\). The next generation matrix for model (2.1) is

$$FV^{-1}= \begin{matrix} {\frac{\beta h(S_{0})(b+\gamma+\mu+\varepsilon)}{(\gamma+b+\mu )(c+\varepsilon+\mu)}} & {\frac{\beta h(S_{0})}{\gamma+b+\mu}}\\ 0 & 0 \end{matrix} . $$

The spectral radius \(\rho(FV^{-1})\) is \(\frac{\beta h(S_{0})(b+\gamma+\mu +\varepsilon)}{(\gamma+b+\mu)(c+\varepsilon+\mu)}\). According to Theorem 2 in [20], the basic reproduction number of system (2.1) is \(\Re_{0}=\frac{\beta h(S_{0})(b+\gamma+\mu+\varepsilon)}{(\gamma+b+\mu )(c+\varepsilon+\mu)}\).

2.3 Existence of equilibria

Theorem 2.1

There exist at most two equilibria in Ω.

  1. (i)

    System (2.1) has the disease-free equilibrium \(E_{0}=(S_{0},0,0,0)=(\frac{A}{\mu},0,0,0)\).

  2. (ii)

    If \(\Re_{0}>1\), system (2.1) has two equilibria, the disease-free equilibrium \(E_{0}\) and the unique endemic equilibrium \(E_{c}=(S^{*},E^{*},I^{*},R^{*})\).

Proof

It is easy to see that the disease-free equilibrium \(E_{0}\) always exists.

From the second and third equations of (2.1), let their right-hand side be equal to zero, we have

$$ F(S)=:\beta h(S) (\gamma+b+\varepsilon+\mu)-(c+\varepsilon+\mu) (\gamma +b+ \mu)=0. $$
(2.2)

It is easy to see that

$$\begin{gathered} F(0)=-(c+\varepsilon+\mu) (\gamma+b+\mu)< 0, \qquad F'(S)=\beta h'(S) (\gamma+b+\mu)>0, \\ F(S_{0})=\beta h(S_{0}) (\gamma+b+\varepsilon+\mu) \biggl(1-\frac{1}{\Re_{0}}\biggr). \end{gathered} $$

If \(\Re_{0}>1\), \(F(S_{0})>0\), then Eq. (2.2) has a unique root \(S^{*}>0\). Hence, if \(\Re_{0}>1\), system (2.1) has a unique endemic equilibrium \(E_{c}=(S^{*},E^{*},I^{*},R^{*})\), where

$$I^{*}=\frac{A-\mu S^{*}}{\frac{(\varepsilon+\mu)(\gamma+b+\mu)}{\varepsilon }-b-\frac{\alpha\gamma}{\alpha+\mu}}, \qquad E^{*}=\frac{\gamma+b+\mu}{\varepsilon}I^{*}, \qquad R^{*}= \frac{\gamma}{\alpha+\mu}I^{*}. $$

The proof of Theorem 2.1 is completed. □

3 The stability of the disease-free equilibrium

In this section, we analyze the stability of the disease-free equilibrium.

Theorem 3.1

\(E_{0}\) is locally asymptotically stable if \(\Re_{0}<1\), whereas \(E_{0}\) is unstable if \(\Re_{0}>1\).

Proof

The Jacobian matrix at \(E_{0}\) is given by

$$ J_{E_{0}}=\left ( \begin{matrix} -\mu & c-\beta h(S_{0}) & b-\beta h(S_{0}) & \alpha\\ 0 & \beta h(S_{0})-(c+\varepsilon+\mu) & \beta h(S_{0}) & 0\\ 0 & \varepsilon & -(\gamma+b+\mu) & 0\\ 0 & 0 & \gamma & -(\alpha+\mu) \end{matrix} \right ). $$
(3.1)

We can obtain that the characteristic roots are \(\lambda_{1}=-\mu\), \(\lambda _{2}=-(\alpha+\mu)\) and the other two roots \(\lambda_{3}\) and \(\lambda_{4}\) are the roots of the following equation:

$$ \lambda^{2}+a_{1}\lambda+a_{2}=0, $$
(3.2)

where

$$\begin{aligned} &a_{1}=-\beta h(S_{0})+c+\varepsilon+\mu+\gamma+b+\mu, \\ & a_{2}=-\beta h(S_{0}) (\gamma+b+\mu+\varepsilon)+(c+ \varepsilon+\mu) (\gamma+b+\mu). \end{aligned} $$

When \(\Re_{0}<1\), we have \(\beta h(S_{0})(\gamma+b+\mu+\varepsilon )<(c+\varepsilon+\mu)(\gamma+b+\mu)\) and \(\beta h(S_{0})< c+\varepsilon+\mu\). It is clear that \(a_{i}>0\); \(i=1,2\). By Vieta’s theorem, all roots of (3.2) are negative. Hence, \(E_{0}\) is locally asymptotically stable.

When \(\Re_{0}>1\), we have \(a_{2}<0\), (3.2) has a positive root, so \(E_{0}\) is unstable. □

In the following, applying LaSalle’s invariance principle and the Lyapunov direct method, we prove the global stability of the disease-free equilibrium.

Theorem 3.2

The disease-free equilibrium \(E_{0}\) is globally asymptotically stable if \(\Re_{0}<1\).

Proof

Define a Lyapunov function

$$ V(t)=\varepsilon E-\bigl[\beta h(S_{0})-(c+\varepsilon+\mu)\bigr]I. $$
(3.3)

When \(\Re_{0}<1\), we have \(\beta h(S_{0})< c+\varepsilon+\mu\), then \(V(t)\geq0\). The total derivative of V along the solutions of (2.1) is

$$\begin{aligned}[b] V'(t)&= \varepsilon\bigl[\beta h(S) (E+I)-(c+\varepsilon+\mu)E\bigr]-\bigl[\beta h(S_{0})-(c+\varepsilon+ \mu)\bigr] \bigl[\varepsilon E-(\gamma+b+\mu)I\bigr] \\ &= \bigl[\beta h(S)-\beta h(S_{0})\bigr]\varepsilon E+\beta h(S) \varepsilon I+\bigl[\beta h(S_{0})-(c+\varepsilon+\mu)\bigr](\gamma+b+ \mu)I. \end{aligned} $$

From \(h'(S)>0\) and \(0< S< S_{0}\), we have \(h(S)< h(S_{0})\), and then

$$ \begin{aligned}[b] V'(t)&\leq\beta h(S_{0}) \varepsilon I+\bigl[\beta h(S_{0})-(c+\varepsilon+\mu )\bigr](\gamma+b+ \mu)I \\ &= \biggl[\beta h(S_{0}) (\gamma+b+\mu+\varepsilon)- \frac{\beta h(S_{0})(\gamma +b+\mu+\varepsilon)}{\Re_{0}}\biggr]I \\ &= \beta h(S_{0}) (\gamma+b+\mu+\varepsilon) \biggl(1- \frac{1}{\Re_{0}}\biggr)I. \end{aligned} $$
(3.4)

It is easy to see that \(V'(t)\leq0\) and \(V'(t)=0\) if and only if \(I(t)=0\). It follows from (2.1) that \(E(t)\rightarrow0\), \(R(t)\rightarrow0\), \(S(t)\rightarrow S_{0}\) as \(t\rightarrow+\infty\), and then \(E_{0}\) is the largest invariant subset of the invariant set \(\{(S,E,I,R)\in\Omega: V'(t)=0\}\). Therefore, by the LaSalle’s invariance principle, \(E_{0}\) is globally attractive in Ω. This, combined with the local stability of \(E_{0}\), completes the proof. □

4 The stability of the endemic equilibrium

In this section, we analyze the stability of the endemic equilibrium.

Theorem 4.1

If \(\Re_{0}>1\), \(\beta h(S^{*})\leq c+\varepsilon\) and \(\beta h'(S^{*})I^{*}\geq\frac {b+\gamma+\mu-\varepsilon}{b+\gamma+\mu+\varepsilon}-(\mu+b)\), then the endemic equilibrium \(E_{c}\) is locally asymptotically stable.

Proof

The Jacobian matrix at \(E_{c}\) is given by

$$ J_{E_{c}}=\left ( \begin{matrix} -\beta h'(S^{*})(E^{*}+I^{*})-\mu&c-\beta h(S^{*}) & b-\beta h(S^{*}) & \alpha\\ \beta h'(S^{*})(E^{*}+I^{*}) & \beta h(S^{*})-(c+\varepsilon+\mu) & \beta h(S^{*})&0\\ 0 & \varepsilon&-(\gamma+b+\mu) & 0\\ 0 & 0 & \gamma&-(\alpha+\mu) \end{matrix} \right ). $$
(4.1)

The characteristic equation is

$$ \lambda^{4}+a_{1}\lambda^{3}+a_{2} \lambda^{2}+a_{3}\lambda+a_{4}=0, $$
(4.2)

where

$$\begin{aligned}& a_{1} = G+2\mu+\alpha+B+F, \\& a_{2} = (G+\mu) (\alpha+\mu)+M+(G+2\mu+\alpha) (B+F)+G\bigl(\beta h \bigl(S^{*}\bigr)-c\bigr), \\& \begin{aligned} a_{3} &= (G+2\mu+\alpha)M+(G+\mu) (\alpha+ \mu) (B+F)+G\bigl(\beta h\bigl(S^{*}\bigr)-c\bigr) (B+\alpha+\mu) \\ &\quad{}+\varepsilon G\bigl(\beta h\bigl(S^{*}\bigr)-b\bigr), \end{aligned} \\& a_{4} = (G+\mu) (\alpha+\mu)M+GB\bigl(\beta h\bigl(S^{*} \bigr)-c\bigr) (\alpha+\mu )+\varepsilon G\bigl(\beta h\bigl(S^{*} \bigr)-b\bigr) (\alpha+\mu)-\varepsilon G\gamma\alpha, \end{aligned}$$

and

$$\begin{gathered} G=\beta h'\bigl(S^{*}\bigr) \biggl(\frac{\gamma+b+\mu+\varepsilon}{\varepsilon }\biggr)I^{*},\qquad B=\gamma+b+\mu, \\ F=c+\varepsilon+\mu-\beta h\bigl(S^{*}\bigr), \qquad M=(\gamma+b+\mu ) \bigl(c+\varepsilon+\mu-\beta h\bigl(S^{*}\bigr)\bigr)-\varepsilon \beta h\bigl(S^{*}\bigr). \end{gathered} $$

From Eq. (2.2), we have \((\gamma+b+\mu)(c+\varepsilon+\mu)-\beta h(S^{*})(b+\gamma+\mu+\varepsilon)=0\) and \(\beta h(S^{*})< c+\varepsilon+\mu\), so we get \(M=0\), \(F>0\).

When \(\beta h(S^{*})\geq c+\varepsilon\) and \(b< c\), we have \(\beta h(S^{*})>b+\varepsilon\). Take notice of condition \(\beta h'(S^{*})I^{*}\geq\frac{b+\gamma+\mu-\varepsilon}{b+\gamma+\mu +\varepsilon}-(\mu+b)\). It is easy to see that \(a_{i}>0\); \(i=1,2,3,4\), \(a_{1}a_{2}-a_{3}>0\) and \(a_{4}(a_{3}(a_{1}a_{2}-a_{3})-a_{1}^{2}a_{4})>0\). By the Routh-Hurwitz criterion, all roots of (4.2) have negative real parts. Hence, the endemic equilibrium \(E_{c}\) of system (2.1) is locally asymptotically stable.

The proof of Theorem 4.1 is completed. □

In the following, we use the geometric approach to discuss the global stability of the endemic equilibrium. We will expand its application to four-dimensional systems, which can also be seen in [21].

Firstly, we present some preliminaries on the geometric approach to prove global stability [22].

Definition 4.1

System (2.1) is said to be uniformly persistent in Ω if there exists a constant \(k > 0\) such that any solution \((S(t),E(t),I(t),R(t))\) of system (2.1) with the initial value \((S(0),E(0),I(0),R(0)) \in\operatorname{int}\Omega\) satisfies

$$\min\Bigl\{ \liminf_{t \rightarrow\infty}S(t),\liminf_{t \rightarrow\infty}E(t), \liminf_{t \rightarrow\infty}I(t),\liminf_{t \rightarrow\infty }R(t)\Bigr\} \geq k. $$

Similar to [7], we can get the following.

Theorem 4.2

System (2.1) is uniformly persistent in Ω if and only if \(\Re_{0}>1\).

Remark 4.1

The uniform persistence of system (2.1) in the bounded set Ω is equivalent to the existence of a compact \(K\subset\Omega\) that is absorbing for (2.1) (see [23]). Denote

$$K=\bigl\{ (S,E,I,R) \vert\delta_{S} \leq S\leq M_{S}, \delta_{E} \leq E\leq M_{E}, \delta_{I} \leq I \leq M_{I}, \delta_{R} \leq R\leq M_{R}\bigr\} \subset\Omega, $$

where \(\delta_{i}>0\), \(i=S,E,I,R\).

Consider the autonomous dynamical system

$$ \frac{\mathrm{d} x}{\mathrm{d} t}=f(x), $$
(4.3)

where \(x\rightarrow f(x)\in R^{n}\) is a \(C^{1}\) function about x in \(\Omega_{1}\subset R^{n}\).

Assume that the following hypotheses hold:

(H1):

There is a compact absorbing set \(K\subset\Omega_{1}\);

(H2):

Differential equation (4.3) has a unique equilibrium \(x^{*}\) in \(\Omega_{1}\).

Let \(x \rightarrow P(x)\) be a \(\bigl({\scriptsize\begin{matrix}{} n\cr 2 \end{matrix}} \bigr)\times \bigl({\scriptsize\begin{matrix}{} n\cr 2 \end{matrix}} \bigr)\) matrix-valued function that is \(C^{1}\) for \(x \in\Omega_{1}\). Assume that \(P^{-1}(x)\) exists and is continuous for \(x \in K\) and consider

$$B=P_{f}P^{-1}+PJ^{[2]}P^{-1}, $$

where the matrix \(P_{f}\) is \((p_{ij}(x))_{f}=(\frac{\partial p_{ij}(x)}{\partial x})^{T}\cdot f(x)=\nabla p_{ij}(x)\cdot f(x)\), \(J^{[2]}\) is the second additive compound matrix of the Jacobian matrix J, i.e., \(J(x)=Df(x)\). Consider the Lozinskiĭ measure μ of Q with respect to a vector norm \(\Vert\cdot\Vert\) in \(R^{ \bigl({\scriptsize\begin{matrix}{}n\cr 2 \end{matrix}} \bigr)}\) (see [24]), that is,

$$\mu(B)=\lim_{h \to0^{+}}\frac{ \Vert I+hB \Vert -1}{h}. $$

A quantity q is defined as follows:

$$q=\limsup_{t \to\infty} \sup_{x\in K}\frac{1}{t} \int_{0}^{t} \mu \bigl(B\bigl(x(s,x_{0}) \bigr)\bigr)\,\mathrm{d}s. $$

The following global stable result is proved in Theorem 3.5 of [22].

Lemma 4.1

([22])

Suppose that \(\Omega_{1}\) is simply connected and that assumptions (H1) and (H2) hold, then the unique equilibrium \(x^{*}\) of system (4.3) is globally stable in \(\Omega _{1}\) if \(q < 0\).

Now we apply Lemma 4.1 to prove the global stability of \(E_{c}\).

Theorem 4.3

If \(\Re_{0}>1\), then the endemic equilibrium \(E_{c}\) of system (2.1) is globally asymptotically stable provided that

$$ \begin{aligned}[b] 2\mu&>\max\bigl\{ 3\beta h(M_{S})-\beta h'(M_{S}) (\delta_{E}+\delta _{I})-c-\varepsilon-b, \\ &\quad {}\varepsilon+c-d-\beta h(\delta_{S})-\beta h'(M_{S}) (\delta_{E}+\delta_{I}), \\ &\quad {}\beta h'(\delta_{S}) (M_{E}+M_{I})+2 \beta h(M_{S})-c-d-\varepsilon, \varepsilon -\alpha-b-\gamma\bigr\} , \end{aligned} $$
(4.4)

where \(d=\min\{b,\alpha\}\).

Proof

The Jacobian matrix of system (2.1) is given by

$$ J=\left ( \begin{matrix} -\beta h'(S)(E+I)-\mu &c-\beta h(S) &b-\beta h(S) &\alpha\\ \beta h'(S)(E+I) &\beta h(S)-(c+\varepsilon+\mu) &\beta h(S) &0\\ 0 &\varepsilon &-(\gamma+b+\mu) &0\\ 0 &0 &\gamma &-(\alpha+\mu) \end{matrix} \right ). $$
(4.5)

Hence, the second additive compound matrix \(J^{[2]}\) [21] of J is given by

$$J^{[2]}=\left ( \begin{matrix} M_{11} &\beta h(S) &0 &\beta h(S)-b &-\alpha &0\\ \varepsilon &M_{22} &0 &c-\beta h(S) &0 &-\alpha\\ 0 &\gamma &M_{33} &0 &c-\beta h(S) &b-\beta h(S)\\ 0 &\beta h'(S)(E+I) &0 &M_{44} &0 &0\\ 0 &0 &\beta h'(S)(E+I) &\gamma &M_{55} &\beta h(S)\\ 0 &0 &0 &0 &\varepsilon &M_{66} \end{matrix} \right ), $$

where

$$\begin{gathered} M_{11}=-\beta h'(S) (E+I)- \mu+\beta h(S)-(c+\varepsilon+\mu), \\ M_{22}=-\beta h'(S) (E+I)-\mu-(\gamma+b+\mu), \\ M_{33}=-\beta h'(S) (E+I)-\mu-(\alpha+\mu), \qquad M_{44}=\beta h(S)-(c+\varepsilon+\mu)-(\gamma+b+\mu), \\ M_{55}=\beta h(S)-(c+\varepsilon+\mu)-(\alpha+\mu),\qquad M_{66}=-(\gamma+b+\mu)-(\alpha+\mu). \end{gathered} $$

Let

$$P=P(S,E,I,R)=\operatorname{diag}\biggl(\frac{1}{I},\frac{1}{I}, \frac {1}{I},\frac{1}{I},\frac{1}{I},\frac{1}{I} \biggr), $$

then

$$P_{f}P^{-1}=\operatorname{diag}\biggl(-\frac{I'}{I},- \frac{I'}{I},-\frac {I'}{I},-\frac{I'}{I},-\frac{I'}{I},- \frac{I'}{I}\biggr). $$

Let

$$\begin{aligned}&Q(S,E,I,R)\\ &\quad =P_{f}P^{-1}+PJ^{[2]}P^{-1} \\ &\quad =\left ( \begin{matrix} M_{11}-\frac{I'}{I} &\beta h(S) &0 &\beta h(S)-b &-\alpha &0\\ \varepsilon &M_{22}-\frac{I'}{I} &0 &c-\beta h(S) &0 &-\alpha\\ 0 &\gamma &M_{33}-\frac{I'}{I} &0 &c-\beta h(S) &b-\beta h(S)\\ 0 &\beta h'(S)(E+I) &0 &M_{44}-\frac{I'}{I} &0 &0\\ 0 &0 &\beta h'(S)(E+I) &\gamma &M_{55}-\frac{I'}{I} &\beta h(S)\\ 0 &0 &0 &0 &\varepsilon &M_{66}-\frac{I'}{I} \end{matrix} \right ). \end{aligned} $$

The matrix \(Q(S,E,I,R)\) can be written in the block form

$$Q(S,E,I,R)=\left ( \begin{matrix} Q_{11}&Q_{12}&Q_{13}&Q_{14}\\ Q_{21}&Q_{22}&Q_{23}&Q_{24}\\ Q_{31}&Q_{32}&Q_{33}&Q_{34}\\ Q_{41}&Q_{42}&Q_{43}&Q_{44} \end{matrix} \right ), $$

where

$$\begin{aligned}& Q_{11}=M_{11}-\frac{I'}{I},\qquad Q_{12}= \left ( \begin{matrix}\beta h(S)&0 \end{matrix} \right ),\qquad Q_{13}=\left ( \begin{matrix}\beta h(S)-b&-\alpha \end{matrix} \right ), \\& Q_{14}=0,\qquad Q_{21}=\left ( \begin{matrix}\varepsilon&0 \end{matrix} \right )^{T}, \\& Q_{22}=\left ( \begin{matrix} M_{22}-\frac{I'}{I}&0\\ \gamma &M_{33}-\frac{I'}{I} \end{matrix} \right ),\qquad Q_{23}=\left ( \begin{matrix} c-\beta h(S)&0\\ 0&c- \beta h(S) \end{matrix} \right ), \\& Q_{24}= \left ( \begin{matrix} -\alpha&b-\beta h(S) \end{matrix} \right )^{T},\qquad Q_{31}=0, \\& Q_{32}=\left ( \begin{matrix} \beta h'(S)(E+I)&0\\ 0&\beta h'(S)(E+I) \end{matrix} \right ), \qquad Q_{33}=\left ( \begin{matrix} M_{44}-\frac{I'}{I}&0\\ \gamma&M_{55}-\frac{I'}{I} \end{matrix} \right ), \\& Q_{34}=\left ( \begin{matrix}0&\beta h(S) \end{matrix} \right )^{T},\qquad Q_{41}=0, \qquad Q_{42}=0, \qquad Q_{43}=\varepsilon, \qquad Q_{44}= M_{66}- \frac{I'}{I}. \end{aligned}$$

Let \(z=(z_{1},z_{2},z_{3},z_{4},z_{5},z_{6})\) denote a vector in \(R^{6} \simeq R^{ \bigl({\scriptsize\begin{matrix}{} 4\cr2\end{matrix}} \bigr)}\), we select a norm in \(R^{6}\) as

$$\bigl\Vert (z_{1},z_{2},z_{3},z_{4},z_{5},z_{6}) \bigr\Vert =\max\bigl\{ \vert z_{1} \vert , \vert z_{2} \vert + \vert z_{3} \vert , \vert z_{4} \vert + \vert z_{5} \vert , \vert z_{6} \vert \bigr\} . $$

Let \(\sigma(Q)\) be the Lozinskiĭ measure of Q with respect to the induced matrix norm \(\Vert\cdot\Vert\) in \(R^{6}\), defined by

$$\sigma(Q)=\lim_{h \to0^{+}}\frac{ \Vert I+hQ \Vert -1}{h}. $$

We have the following estimate:

$$\sigma\bigl(Q(S,E,I,R)\bigr)\leq\sup\{g_{1},g_{2},g_{3},g_{4} \}, $$

where

$$\begin{gathered} g_{1}=\sigma_{1}(Q_{11})+ \vert Q_{12} \vert + \vert Q_{13} \vert + \vert Q_{14} \vert , \qquad g_{2}=\sigma _{1}(Q_{22})+ \vert Q_{21} \vert + \vert Q_{23} \vert + \vert Q_{24} \vert , \\ g_{3}=\sigma_{1}(Q_{33})+ \vert Q_{31} \vert + \vert Q_{32} \vert + \vert Q_{34} \vert , \qquad g_{4}=\sigma _{1}(Q_{44})+ \vert Q_{41} \vert + \vert Q_{42} \vert + \vert Q_{43} \vert . \end{gathered} $$

\(|Q_{ij}|\) (\(i\neq j\), \(i,j =1,2,3,4\)) are matrix norms with respect to the \(l_{1}\) vector norm, and \(\sigma_{1}\) denotes the Lozinskiĭ measure with respect to the \(l_{1}\) norm.

From the first equations of (2.1), we have

$$ S'= A-\bigl(\beta h(S)-c\bigr)E-\bigl(\beta h(S)-b\bigr)I+\alpha R- \mu S. $$
(4.6)

From equation (4.6), it easy to prove that there is \(t^{*}\), when \(t>t^{*}\), we have \(\beta h(S)-b>0\). In fact, if \(\beta h(S)\leq b\), from equation (4.6) and \(b< c\), we have \(S'\geq A-\mu S=\mu(\frac{A}{\mu}-S)>0\), which means that each solution starting from K must have crossed the curve \(\beta h(S)=b\) in a limited time; this is contradiction to \(\beta h(S)\leq b\). To calculate the values of \(g_{i}\), we firstly obtain that

$$\begin{aligned}& \sigma_{1}(Q_{11})=\beta h(S)- \beta h'(S) (E+I)-\mu-(c+\varepsilon+\mu )-\frac{I'}{I}, \\& \sigma_{1}(Q_{22})\leq-d-2\mu-\beta h'(S) (E+I)-\frac{I'}{I}, \\& \begin{gathered} \sigma_{1}(Q_{33})\leq\beta h(S)-c-\varepsilon-2\mu-d- \frac{I'}{I}, \\ \sigma_{1}(Q_{44})=-\alpha-b-\gamma-2\mu-\frac{I'}{I}, \end{gathered} \end{aligned}$$

and

$$\begin{gathered} \vert Q_{12} \vert =\beta h(S),\qquad \vert Q_{13} \vert =\beta h(S)-b,\qquad \vert Q_{14} \vert =0, \\ \vert Q_{21} \vert =\varepsilon,\qquad \vert Q_{23} \vert =c-\beta h(S),\qquad \vert Q_{24} \vert \leq 0, \\ \vert Q_{31} \vert =0, \qquad \vert Q_{32} \vert = \beta h'(S) (E+I), \qquad \vert Q_{34} \vert =\beta h(S), \\ \vert Q_{41} \vert =0, \qquad \vert Q_{42} \vert =0, \qquad \vert Q_{43} \vert =\varepsilon, \end{gathered} $$

where \(d=\min\{\alpha,b\}\). From \(h''(S)<0\), we have \(h'(M_{S})< h'(S)< h'(\delta_{S})\). Then we further have

$$\begin{aligned}& \begin{aligned} g_{1}&= 3\beta h(S)-\beta h'(S) (E+I)-\mu-(c+\varepsilon+\mu)-b-\frac {I'}{I} \\ &\leq-\frac{I'}{I}+3\beta h(M_{S})-\beta h'(M_{S}) (\delta_{E}+\delta_{I})-2\mu -c-\varepsilon-b, \end{aligned} \\& \begin{aligned} g_{2}&= \varepsilon+c-\beta h(S)-d-2\mu- \beta h'(S) (E+I)-\frac{I'}{I} \\ &\leq-\frac{I'}{I}+\varepsilon+c-2\mu-d-\beta h(\delta_{S})- \beta h'(M_{S}) (\delta_{E}+ \delta_{I}), \end{aligned} \\& \begin{aligned} g_{3}&= \beta h'(S) (E+I)+2 \beta h(S)-c-d-\varepsilon-2\mu-\frac{I'}{I} \\ &\leq-\frac{I'}{I}+\beta h'(\delta_{S}) (M_{E}+M_{I})+2\beta h(M_{S})-c-d-\varepsilon-2 \mu, \end{aligned} \\& g_{4}= -\frac{I'}{I}+\varepsilon-\alpha-b-\gamma-2\mu. \end{aligned}$$

Let

$$\begin{aligned} \bar{b}&=\min\bigl\{ 2\mu+\beta h'(M_{S}) (\delta_{E}+\delta_{I})+c+\varepsilon +b-3\beta h(M_{S}), \\ &\quad {}2\mu-\varepsilon-c+d+\beta h(\delta_{S})+\beta h'(M_{S}) (\delta_{E}+\delta _{I}), \\ &\quad {}2\mu+c+d+\varepsilon-\beta h'(\delta_{S}) (M_{E}+M_{I})-2\beta h(M_{S}),2\mu +\alpha+b+ \gamma-\varepsilon\bigr\} . \end{aligned} $$

From condition (4.4), we have \(\bar{b}>0\) and

$$g_{1}\leq-\frac{I'}{I}-\bar{b},\qquad g_{2}\leq- \frac{I'}{I}-\bar{b},\qquad g_{3}\leq-\frac{I'}{I}-\bar{b}, \qquad g_{4}\leq-\frac{I'}{I}-\bar{b}. $$

Along each solution \((S(t),I(t),R(t),I(t))\) of system (2.1) with the initial value \((S(0),I(0), R(0),I(0))\in K\), when \(t>t^{*}\), we have

$$\begin{aligned}& \frac{1}{t} \int_{0}^{t} g_{1}\,\mathrm{d}s \leq \frac{1}{t} \int_{0}^{t^{*}} g_{1}\,\mathrm{d}s- \frac{1}{t}\ln\frac {I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}, \\& \frac{1}{t} \int_{0}^{t} g_{2}\,\mathrm{d}s \leq \frac{1}{t} \int_{0}^{t^{*}} g_{2}\,\mathrm{d}s- \frac{1}{t}\ln\frac {I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}, \\& \frac{1}{t} \int_{0}^{t} g_{3}\,\mathrm{d}s \leq \frac{1}{t} \int_{0}^{t^{*}} g_{2}\,\mathrm{d}s- \frac{1}{t}\ln\frac {I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}, \\& \frac{1}{t} \int_{0}^{t} g_{4}\,\mathrm{d}s \leq \frac{1}{t} \int_{0}^{t^{*}} g_{3}\,\mathrm{d}s- \frac{1}{t}\ln\frac {I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}. \end{aligned}$$

Furthermore, we have

$$\begin{aligned}& \frac{1}{t} \int_{0}^{t} \sigma\bigl(Q(S,E,I,R)\bigr)) \,\mathrm{d}s \\& \quad \leq \sup\biggl\{ \frac{1}{t} \int_{0}^{t^{*}} g_{1}\,\mathrm{d}s- \frac{1}{t}\ln \frac{I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}, \frac{1}{t} \int _{0}^{t^{*}} g_{2}\,\mathrm{d}s- \frac{1}{t}\ln\frac{I(t)}{I(t^{*})}-\bar{b}\frac {t-t^{*}}{t}, \\& \qquad {}\frac{1}{t} \int_{0}^{t^{*}} g_{3}\,\mathrm{d}s- \frac{1}{t}\ln\frac {I(t)}{I(t^{*})}-\bar{b}\frac{t-t^{*}}{t}, \frac{1}{t} \int_{0}^{t^{*}} g_{4}\,\mathrm{d}s- \frac{1}{t}\ln\frac{I(t)}{I(t^{*})}-\bar{b}\frac {t-t^{*}}{t}\biggr\} . \end{aligned}$$

Therefore,

$$q=\limsup_{t \to\infty} \sup_{x\in K}\frac{1}{t} \int_{0}^{t} \sigma \bigl(Q(S,E,I,R)\bigr) \,\mathrm{d}s\leq-\overline{b}< 0. $$

The proof of Theorem 4.1 is completed. □

5 Numerical simulation

To support our main results, we perform some numerical simulations. We choose \(h(S)=\frac{S}{1+gS}\) and consider the set of parameters:

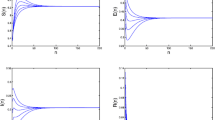
(1) \(\beta= 0.025\), \(\alpha= 0.25\), \(c = 0.15\), \(\mu= 0.15\), \(A = 0.1\), \(\gamma= 0.4\), \(g=0.8\), \(\varepsilon=0.25\), with the initial condition \((S(0),E(0),I(0),R(0))=(0.15,0.15,0.15,0.15)\), we have \(\Re _{0}=0.3403<1\). In this case, according to Theorem 3.2, the disease-free equilibrium \(E_{0}\) of system (2.1) is globally asymptotically stable (see Figure 1).

Figure 1
figure 1

The disease-free equilibrium \(\pmb{E_{0}}\) is globally asymptotically stable.

Full size image

(2) \(\beta=0.35\), \(\alpha= 0.04\), \(b = 0.04\), \(c = 0.05\), \(\mu= 0.23\), \(A = 0.23\), \(\gamma=0.008\), \(g = 0.1\), \(\varepsilon= 0.25\), with the initial condition \((S(0),E(0),I(0),R(0))=(0.5,0.1,0.1,0.1)\), we have \(\Re_{0}=1.1402>1\), and \(3\beta h(M_{S})-\beta h'(M_{S})(\delta_{E}+\delta_{I})-c-\varepsilon -b=0.4529\), \(\varepsilon+c-d-\beta h(\delta_{S})-\beta h'(M_{S})(\delta _{E}+\delta_{I})=0.0948\), \(\beta h'(\delta_{S})(M_{E}+M_{I})+2\beta h(M_{S})-c-d-\varepsilon=0.2778\), \(\varepsilon-\alpha-b-\gamma=0.1620\), so condition (4.4) is satisfied. According to Theorem 4.3, the endemic equilibrium \(E_{c}\) of system (2.1) is globally asymptotically stable (see Figure 2).

Figure 2
figure 2

The endemic equilibrium \(\pmb{E_{c}}\) of system ( 2.1 ) is globally asymptotically stable.

Full size image

6 Conclusions

In this paper, we have proposed a nonlinear mathematical model for influenza virus transmission with disease resistance; nonlinear incidence has a more general form. Through mathematical analysis we obtain the dynamic behaviors of the model. The basic reproduction number \(\Re_{0}\) is obtained. If \(\Re_{0}<1\), the disease-free equilibrium is globally asymptotically stable. It implies that the disease dies out eventually. When \(\Re_{0}>1\), the endemic equilibrium is globally asymptotically stable under some conditions. It implies that the disease persists in the population. All of these results imply that the disease resistance and nonlinear incidence can influence the dynamic behaviors of the SEIRS model. From the expression of \(\Re_{0}\), it is easy to see that when β is increased, b, c decrease and then \(\Re_{0}\) increases. \(\Re_{0}>1\) leads to the stability of the endemic equilibrium and then the prevalence of the disease. So we can get some effective strategies for controlling the disease such as reducing the contact rate β and increasing the b, c. That is to say, by taking proper isolation of the population and increasing the resistance of people, we can avoid the development of infectious diseases into endemic diseases. In reality, the exposed and infected individuals have different infection rates, which will be the focus of our future research.