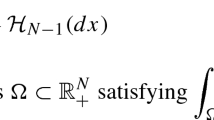An isoperimetric inequality in the plane with a log-convex density

Abstract

Given a positive lower semi-continuous density f on $\mathbb {R}^2$ the weighted volume $V_f:=f\mathscr {L}^2$ is defined on the $\mathscr {L}^2$-measurable sets in $\mathbb {R}^2$. The f-weighted perimeter of a set of finite perimeter E in $\mathbb {R}^2$ is written $P_f(E)$. We study minimisers for the weighted isoperimetric problem

$$\begin{aligned} I_f(v):=\inf \Big \{ P_f(E):E\text { is a set of finite perimeter in }\mathbb {R}^2\text { and }V_f(E)=v\Big \} \end{aligned}$$

for $v>0$. Suppose f takes the form $f:\mathbb {R}^2\rightarrow (0,+\infty );x\mapsto e^{h(|x|)}$ where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Let $v>0$ and B a centred ball in $\mathbb {R}^2$ with $V_f(B)=v$. We show that B is a minimiser for the above variational problem and obtain a uniqueness result.

1 Introduction

Let f be a positive lower semi-continuous density on $\mathbb {R}^2$. The weighted volume $V_f:=f\mathscr {L}^2$ is defined on the $\mathscr {L}^2$-measurable sets in $\mathbb {R}^2$. Let E be a set of finite perimeter in $\mathbb {R}^2$. The weighted perimeter of E is defined by

$$\begin{aligned} P_f(E):=\int _{\mathbb {R}^2}f\,d|D\chi _E|\in [0,+\infty ]. \end{aligned}$$

(1.1)

We study minimisers for the weighted isoperimetric problem

$$\begin{aligned} I_f(v):=\inf \Big \{ P_f(E):E\text { is a set of finite perimeter in }\mathbb {R}^2\text { and }V_f(E)=v\Big \} \end{aligned}$$

(1.2)

for $v>0$. To be more specific we suppose that f takes the form

$$\begin{aligned} f:\mathbb {R}^2\rightarrow (0,+\infty );x\mapsto e^{h(|x|)} \end{aligned}$$

(1.3)

where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Our first main result is the following. It contains the classical isoperimetric inequality (cf. [9, 12]) as a special case; namely, when h is constant on $[0,+\infty )$.

Theorem 1.1

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Let $v>0$ and B a centred ball in $\mathbb {R}^2$ with $V_f(B)=v$. Then B is a minimiser for (1.2).

For $x\ge 0$ and $v\ge 0$ define the directional derivative of h in direction v by

$$\begin{aligned} h^\prime _+(x,v):=\lim _{t\downarrow 0}\frac{h(x+tv)-h(x)}{t}\in \mathbb {R} \end{aligned}$$

and define $h^\prime _-(x,v)$ similarly for $x>0$ and $v\le 0$. We introduce the notation

$$\begin{aligned} \rho _+:=h^\prime _+(\cdot ,+1), \rho _-:=-h^\prime _+(\cdot ,-1) \text { and } \rho :=(1/2)(\rho _++\rho _-) \end{aligned}$$

on $(0,+\infty )$. The function h is locally of bounded variation and is differentiable a.e. with $h^\prime =\rho$ a.e. on $(0,+\infty )$. Our second main result is a uniqueness theorem.

Theorem 1.2

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Suppose that $R:=\inf \{\rho >0\}\in [0,+\infty )$ and set $v_0:=V(B(0,R))$. Let $v>0$ and E a minimiser for (1.2). The following hold:

• (i) if $v\le v_0$ then E is a.e. equivalent to a ball B in $\overline{B}(0,R)$ with $V(B)=V(E)$;

• (ii) if $v>v_0$ then E is a.e. equivalent to a centred ball B with $V(B)=V(E)$.

Theorem 1.1 is a generalisation of Conjecture 3.12 in [24] (due to K. Brakke) in the sense that less regularity is required of the density f: in the latter, h is supposed to be smooth on $(0,+\infty )$ as well as convex and non-decreasing. This conjecture springs in part from the observation that the weighted perimeter of a local volume-preserving perturbation of a centred ball is non-decreasing ([24] Theorem 3.10). In addition, the conjecture holds for log-convex Gaussian densities of the form $h:[0,+\infty )\rightarrow \mathbb {R};t\mapsto e^{ct^2}$ with $c>0$ ([3, 24] Theorem 5.2). In subsequent work partial forms of the conjecture were proved in the literature. In [19] it is shown to hold for large v provided that h is uniformly convex in the sense that $h^{\prime \prime }\ge 1$ on $(0,+\infty )$ (see [19] Corollary 6.8). A complemen tary result is contained in [11] Theorem 1.1 which establishes the conjecture for small v on condition that $h^{\prime \prime }$ is locally uniformly bounded away from zero on $[0,+\infty )$. The above-mentioned conjecture is proved in large part in [7] (see Theorem 1.1) in dimension $n\ge 2$ (see also [4]). There it is assumed that the function h is of class $C^3$ on $(0,+\infty )$ and is convex and even (meaning that h is the restriction of an even function on $\mathbb {R}$ to $[0,+\infty )$). A uniqueness result is also obtained ( [7] Theorem 1.2). We obtain these results under weaker hypotheses in the 2-dimensional case and our proofs proceed along different lines.

We give a brief outline of the article. In Sect. 2 we discuss some preliminary material. In Sect. 3 we show that (1.2) admits an open minimiser E with $C^1$ boundary M (Theorem 3.8). The argument draws upon the regularity theory for almost minimal sets (cf. [27]) and includes an adaptation of [21] Proposition 3.1. In Sect. 4 it is shown that the boundary M is of class $C^{1,1}$ (and has weakly bounded curvature). This result is contained in [21] Corollary 3.7 (see also [8]) but we include a proof for completeness. This Section also includes the result that E may be supposed to possess spherical cap symmetry (Theorem 4.5). Section 5 contains further results on spherical cap symmetric sets useful in the sequel. The main result of Sect. 6 is Theorem 6.5 which shows that the generalised (mean) curvature is conserved along M in a weak sense. In Sect. 7 it is shown that there exist convex minimisers of (1.2). Sections 8 and 9 comprise an analytic interlude and are devoted to the study of solutions of the first-order differential equation that appears in Theorem 6.6 subject to Dirichlet boundary conditions. Section 9 for example contains a comparison theorem for solutions to a Ricatti equation (Theorem 9.15 and Corollary 9.16). These are new as far as the author is aware. Section 10 concludes the proof of our main theorems.

2 Some preliminaries

Geometric measure theory. We use $|\cdot |$ to signify the Lebesgue measure on $\mathbb {R}^2$ (or occasionally $\mathscr {L}^2$). Let E be a $\mathscr {L}^2$-measurable set in $\mathbb {R}^2$. The set of points in E with density $t\in [0,1]$ is given by

$$\begin{aligned} E^t:=\left\{ x\in \mathbb {R}^2:\,\lim _{\rho \downarrow 0}\frac{|E\cap B(x,\rho )|}{|B(x,\rho )|}=t\right\} . \end{aligned}$$

As usual $B(x,\rho )$ denotes the open ball in $\mathbb {R}^2$ with centre $x\in \mathbb {R}^2$ and radius $\rho >0$. The set $E^1$ is the measure-theoretic interior of E while $E^0$ is the measure-theoretic exterior of E. The essential boundary of E is the set $\partial ^\star E:=\mathbb {R}^2{\setminus }(E^0\cup E^1)$.

Recall that an integrable function u on $\mathbb {R}^2$ is said to have bounded variation if the distributional derivative of u is representable by a finite Radon measure Du (cf. [1] Definition 3.1 for example) with total variation |Du|; in this case, we write $u\in \mathrm {BV}(\mathbb {R}^2)$. The set E has finite perimeter if $\chi _E$ belongs to $\mathrm {BV}_{\mathrm {loc}}(\mathbb {R}^2)$. The reduced boundary $\mathscr {F}E$ of E is defined by

$$\begin{aligned} \mathscr {F}E:= & {} \Big \{x\in \mathrm {supp}|D\chi _E|:\nu ^E(x):=\lim _{\rho \downarrow 0}\frac{D\chi _E(B(x,\rho ))}{|D\chi _E|(B(x,\rho ))}\\&\quad \text { exists in }\mathbb {R}^2\text { and }|\nu ^E(x)|=1\Big \} \end{aligned}$$

(cf. [1] Definition 3.54) and is a Borel set (cf. [1] Theorem 2.22 for example). We use $\mathscr {H}^k$ ($k\in [0,+\infty )$) to stand for k-dimensional Hausdorff measure. If E is a set of finite perimeter in $\mathbb {R}^2$ then

$$\begin{aligned} \mathscr {F}E\subset E^{1/2}\subset \partial ^* E \text { and } \mathscr {H}^1(\partial ^* E{\setminus }\mathscr {F}E)=0 \end{aligned}$$

(2.1)

by [1] Theorem 3.61.

Let f be a positive locally Lipschitz density on $\mathbb {R}^2$. Let E be a set of finite perimeter and U a bounded open set in $\mathbb {R}^2$. The weighted perimeter of E relative to U is defined by

$$\begin{aligned} P_f(E,U):=\sup \Big \{\int _U\mathrm {div}(fX)\,dx:X\in C^\infty _c(U,\mathbb {R}^2),\Vert X\Vert _\infty \le 1\Big \}. \end{aligned}$$

By the Gauss–Green formula ( [1] Theorem 3.36 for example) and a convolution argument,

$$\begin{aligned} P_f(E,U)&=\sup \Big \{\int _{\mathbb {R}^2}f\langle \nu ^E,X\rangle \,d|D\chi _E|: X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2),\nonumber \\&\qquad \qquad \mathrm {supp}[X]\subset U,\Vert X\Vert _\infty \le 1\Big \}\nonumber \\&=\sup \Big \{\int _{\mathbb {R}^2}f\langle \nu ^E,X\rangle \,d|D\chi _E|: X\in C_c(\mathbb {R}^2,\mathbb {R}^2),\nonumber \\&\qquad \qquad \mathrm {supp}[X]\subset U,\Vert X\Vert _\infty \le 1\Big \}\nonumber \\&=\int _U f\,d|D\chi _E| \end{aligned}$$

(2.2)

where we have also used [1] Propositions 1.47 and 1.23.

Lemma 2.1

Let $\varphi$ be a $C^1$ diffeomeorphism of $\mathbb {R}^2$ which coincides with the identity map on the complement of a compact set and $E\subset \mathbb {R}^2$ with $\chi _E\in \mathrm {BV}(\mathbb {R}^2)$. Then

• (i) $\chi _{\varphi (E)}\in \mathrm {BV}(\mathbb {R}^2)$;

• (ii) $\partial ^\star \varphi (E)=\varphi (\partial ^\star E)$;

• (iii) $\mathscr {H}^1(\mathscr {F}\varphi (E)\varDelta \varphi (\mathscr {F}E))=0$.

Proof

Part (i) follows from [1] Theorem 3.16 as $\varphi$ is a proper Lipschitz function. Given $x\in E^0$ we claim that $y:=\varphi (x)\in \varphi (E)^0$. Let M stand for the Lipschitz constant of $\varphi$ and L stand for the Lipschitz constant of $\varphi ^{-1}$. Note that $B(y,r)\subset \varphi (B(x,Lr))$ for each $r>0$. As $\varphi$ is a bijection and using [1] Proposition 2.49,

$$\begin{aligned} |\varphi (E)\cap B(y,r)|&\le |\varphi (E)\cap \varphi (B(x,Lr)|\\&=|\varphi (E\cap B(x,Lr))|\le M^2|E\cap B(x,Lr)|.\nonumber \end{aligned}$$

This means that

$$\begin{aligned} \frac{|\varphi (E)\cap B(y,r)|}{|B(y,r)|} \le (LM)^2 \frac{|E\cap B(x,Lr)|}{|B(x,Lr)|} \end{aligned}$$

for $r>0$ and this proves the claim. This entails that $\varphi (E^0)\subset [\varphi (E)]^0$. The reverse inclusion can be seen using the fact that $\varphi$ is a bijection. In summary $\varphi (E^0)=[\varphi (E)]^0$. The corresponding identity for $E^1$ can be seen in a similar way. These identities entail (ii). From (2.1) and (ii) we may write $\mathscr {F}\varphi (E)\cup N_1=\varphi (\mathscr {F}E)\cup \varphi (N_2)$ for $\mathscr {H}^1$-null sets $N_1,N_2$ in $\mathbb {R}^2$. Item (iii) follows. $\square$

Curves with weakly bounded curvature. Suppose the open set E in $\mathbb {R}^2$ has $C^1$ boundary M. Denote by $n:M\rightarrow \mathbb {S}^1$ the inner unit normal vector field. Given $p\in M$ we choose a tangent vector $t(p)\in \mathbb {S}^1$ in such a way that the pair $\{t(p),n(p)\}$ forms a positively oriented basis for $\mathbb {R}^2$. There exists a local parametrisation $\gamma _1:I\rightarrow M$ where $I=(-\delta ,\delta )$ for some $\delta >0$ of class $C^1$ with $\gamma _1(0)=p$. We always assume that $\gamma _1$ is parametrised by arc-length and that $\dot{\gamma _1}(0)=t(p)$ where the dot signifies differentiation with respect to arc-length. Let X be a vector field defined in some neighbourhood of p in M. Then

$$\begin{aligned} (D_{t}X)(p):=\frac{d}{ds}\Big |_{s=0}(X\circ \gamma _1)(s) \end{aligned}$$

(2.3)

if this limit exists and the divergence $\mathrm {div}^M X$ of X along M at p is defined by

$$\begin{aligned} \mathrm {div}^M X:=\langle D_{t}X,t\rangle \end{aligned}$$

(2.4)

evaluated at p. Suppose that X is a vector field in $C^1(U,\mathbb {R}^2)$ where U is an open neighbourhood of p in $\mathbb {R}^2$. Then

$$\begin{aligned} \mathrm {div}\,X=\mathrm {div}^M X+\langle D_nX,n\rangle \end{aligned}$$

(2.5)

at p. If $p\in M{\setminus }\{0\}$ let $\sigma (p)$ stand for the angle measured anti-clockwise from the position vector p to the tangent vector t(p); $\sigma (p)$ is uniquely determined up to integer multiples of $2\pi$.

Let E be an open set in $\mathbb {R}^2$ with $C^{1,1}$ boundary M. Let $x\in M$ and $\gamma _1:I\rightarrow M$ a local parametrisation of M in a neighbourhood of x. There exists a constant $c>0$ such that

$$\begin{aligned} |\dot{\gamma }_1(s_2)-\dot{\gamma }_1(s_1)|\le c|s_2-s_1| \end{aligned}$$

for $s_1,s_2\in I$; a constraint on average curvature (cf. [10, 18]). That is, $\dot{\gamma }_1$ is Lipschitz on I. So $\dot{\gamma }_1$ is absolutely continuous and differentiable a.e. on I with

$$\begin{aligned} \dot{\gamma }_1(s_2)-\dot{\gamma }_1(s_1)=\int _{s_1}^{s_2}\ddot{\gamma }_1\,ds \end{aligned}$$

(2.6)

for any $s_1,s_2\in I$ with $s_1<s_2$. Moreover, $|\ddot{\gamma }_1|\le c$ a.e. on I (cf. [1] Corollary 2.23). As $\langle \dot{\gamma }_1,\dot{\gamma }_1\rangle =1$ on I we see that $\langle \dot{\gamma }_1,\ddot{\gamma }_1\rangle =0$ a.e. on I. The (geodesic) curvature $k_1$ is then defined a.e. on I via the relation

$$\begin{aligned} \ddot{\gamma }_1=k_1n_1 \end{aligned}$$

(2.7)

as in [18]. The curvature k of M is defined $\mathscr {H}^1$-a.e. on M by

$$\begin{aligned} k(x):=k_1(s) \end{aligned}$$

(2.8)

whenever $x=\gamma _1(s)$ for some $s\in I$ and $k_1(s)$ exists. We sometimes write $H(\cdot ,E)=k$.

Let E be an open set in $\mathbb {R}^2$ with $C^{1}$ boundary M. Let $x\in M$ and $\gamma _1:I\rightarrow M$ a local parametrisation of M in a neighbourhood of x. In case $\gamma _1\ne 0$ let $\theta _1$ stand for the angle measured anti-clockwise from $e_1$ to the position vector $\gamma _1$ and $\sigma _1$ stand for the angle measured anti-clockwise from the position vector $\gamma _1$ to the tangent vector $t_1=\dot{\gamma }_1$. Put $r_1:=|\gamma _1|$ on I. Then $r_1,\theta _1\in C^1(I)$ and

$$\begin{aligned} \dot{r}_1&=\cos \sigma _1; \end{aligned}$$

(2.9)

$$\begin{aligned} r_1\dot{\theta }_1&=\sin \sigma _1; \end{aligned}$$

(2.10)

on I provided that $\gamma _1\ne 0$. Now suppose that M is of class $C^{1,1}$. Let $\alpha _1$ stand for the angle measured anti-clockwise from the fixed vector $e_1$ to the tangent vector $t_1$ (uniquely determined up to integer multiples of $2\pi$). Then $t_1=(\cos \alpha _1,\sin \alpha _1)$ on I so $\alpha _1$ is absolutely continuous on I. In particular, $\alpha _1$ is differentiable a.e. on I with $\dot{\alpha }_1=k_1$ a.e. on I. This means that $\alpha _1\in C^{0,1}(I)$. In virtue of the identities $r_1\cos \sigma _1=\langle \gamma _1,t_1\rangle$ and $r_1\sin \sigma _1=-\langle \gamma _1,n_1\rangle$ we see that $\sigma _1$ is absolutely continuous on I and $\sigma _1\in C^{0,1}(I)$. By choosing an appropriate branch we may assume that

$$\begin{aligned} \alpha _1&=\theta _1+\sigma _1 \end{aligned}$$

(2.11)

on I. We may choose $\sigma$ in such a way that $\sigma \circ \gamma _1=\sigma _1$ on I.

Flows. Recall that a diffeomorphism $\varphi :\mathbb {R}^2\rightarrow \mathbb {R}^2$ is said to be proper if $\varphi ^{-1}(K)$ is compact whenever $K\subset \mathbb {R}^2$ is compact. Given $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ there exists a 1-parameter group of proper $C^\infty$ diffeomorphisms $\varphi :\mathbb {R}\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ as in [20] Lemma 2.99 that satisfy

$$\begin{aligned} \left. \begin{array}{rl} \partial _t\varphi (t,x)&{}= X(\varphi (t,x))\text { for each }(t,x)\in \mathbb {R}\times \mathbb {R}^2;\\ \varphi (0,x) &{}= x \text { for each } x\in \mathbb {R}^2.\\ \end{array} \right. \end{aligned}$$

(2.12)

We often use $\varphi _t$ to refer to the diffeomorphism $\varphi (t,\cdot ):\mathbb {R}^2\rightarrow \mathbb {R}^2$.

Lemma 2.2

Let $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ and $\varphi$ be the corresponding flow as above. Then

• (i) there exists $R\in C^\infty (\mathbb {R}\times \mathbb {R}^2,\mathbb {R}^2)$ and $K>0$ such that

  $$\begin{aligned} \varphi (t,x)= \left\{ \begin{array}{ll} x+tX(x)+R(t,x) &{} \text { for }x\in \mathrm {supp}[X];\\ x &{} \text { for }x\not \in \mathrm {supp}[X];\\ \end{array} \right. \end{aligned}$$

  where $|R(t,x)|\le K t^2$ for $(t,x)\in \mathbb {R}\times \mathbb {R}^2$;

• (ii) there exists $R^{(1)}\in C^\infty (\mathbb {R}\times \mathbb {R}^2,M_2(\mathbb {R}))$ and $K_1>0$ such that

  $$\begin{aligned} d\varphi (t,x)= \left\{ \begin{array}{ll} I+tdX(x)+R^{(1)}(t,x) &{} \text { for }x\in \mathrm {supp}[X];\\ I &{} \text { for }x\not \in \mathrm {supp}[X];\\ \end{array} \right. \end{aligned}$$

  where $|R^{(1)}(t,x)|\le K_1 t^2$ for $(t,x)\in \mathbb {R}\times \mathbb {R}^2$;

• (iii) there exists $R^{(2)}\in C^\infty (\mathbb {R}\times \mathbb {R}^2,\mathbb {R})$ and $K_2>0$ such that

  $$\begin{aligned} J_2d\varphi (t,x)= \left\{ \begin{array}{ll} 1+t\,\mathrm {div}\,X(x)+R^{(2)}(t,x) &{} \text { for }x\in \mathrm {supp}[X];\\ 1 &{} \text { for }x\not \in \mathrm {supp}[X];\\ \end{array} \right. \end{aligned}$$

  where $|R^{(2)}(t,x)|\le K_2 t^2$ for $(t,x)\in \mathbb {R}\times \mathbb {R}^2$.

Let $x\in \mathbb {R}^2,v$ a unit vector in $\mathbb {R}^2$ and M the line though x perpendicular to v. Then

• (iv) there exists $R^{(3)}\in C^\infty (\mathbb {R}\times \mathbb {R}^2,\mathbb {R})$ and $K_3>0$ such that

  $$\begin{aligned} J_1d^{M}\varphi (t,x)= \left\{ \begin{array}{ll} 1+t(\mathrm {div}^{M}\,X)(x)+R^{(3)}(t,x) &{} \text { for }x\in \mathrm {supp}[X];\\ 1 &{} \text { for }x\not \in \mathrm {supp}[X];\\ \end{array} \right. \end{aligned}$$

  where $|R^{(3)}(t,x)|\le K_3 t^2$ for $(t,x)\in \mathbb {R}\times \mathbb {R}^2$.

Proof

(i) First notice that $\varphi \in C^\infty (\mathbb {R}\times \mathbb {R}^2)$ by [16] Theorem 3.3 and Exercise 3.4. The statement for $x\not \in \mathrm {supp}[X]$ follows by uniqueness (cf. [16] Theorem 3.1); the assertion for $x\in \mathrm {supp}[X]$ follows from Taylor’s theorem. (ii) follows likewise: note, for example, that

$$\begin{aligned}{}[\partial _{tt}d\varphi ]_{\alpha \beta }\vert _{t=0}=X^\alpha _{,\beta \delta }X^\delta +X^\alpha _{,\gamma }X^\gamma _{,\beta } \end{aligned}$$

where the subscript $_,$ signifies partial differentiation. (iii) follows from (ii) and the definition of the 2-dimensional Jacobian (cf. [1] Definition 2.68). (iv) Using [1] Definition 2.68 together with the Cauchy–Binet formula [1] Proposition 2.69, $J_1d^M\varphi (t,x)=|d\varphi (t,x)v|$ for $t\in \mathbb {R}$ and the result follows from (ii). $\square$

Let I be an open interval in $\mathbb {R}$ containing 0. Let $Z:I\times \mathbb {R}^2\rightarrow \mathbb {R}^2;(t,x)\mapsto Z(t,x)$ be a continuous time-dependent vector field on $\mathbb {R}^2$ with the properties

• (Z.1) $Z(t,\cdot )\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$ for each $t\in I$;

• (Z.2) $\mathrm {supp}[Z(t,\cdot )]\subset K$ for each $t\in I$ for some compact set $K\subset \mathbb {R}^2$.

By [16] Theorems I.1.1, I.2.1, I.3.1, I.3.3 there exists a unique flow $\varphi :I\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ such that

• (F.1) $\varphi :I\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ is of class $C^1$;

• (F.2) $\varphi (0,x)=x$ for each $x\in \mathbb {R}^2$;

• (F.3) $\partial _t\varphi (t,x)=Z(t,\varphi (x,t))$ for each $(t,x)\in I\times \mathbb {R}^2$;

• (F.4) $\varphi _t:=\varphi (t,\cdot ):\mathbb {R}^2\rightarrow \mathbb {R}^2$ is a proper diffeomorphism for each $t\in I$.

Lemma 2.3

Let Z be a time-dependent vector field with the properties (Z.1)–(Z.2) and $\varphi$ be the corresponding flow. Then

• (i) for $(t,x)\in I\times \mathbb {R}^2$,

  $$\begin{aligned} d\varphi (t,x)= \left\{ \begin{array}{ll} I+tdZ_0(x)+tR(t,x) &{} \text { for }x\in K;\\ I &{} \text { for }x\not \in K;\\ \end{array} \right. \end{aligned}$$

  where $\sup _K|R(t,\cdot )|\rightarrow 0$ as $t\rightarrow 0$.

Let $x\in \mathbb {R}^2,v$ a unit vector in $\mathbb {R}^2$ and M the line though x perpendicular to v. Then

• (ii) for $(t,x)\in I\times \mathbb {R}^2$,

  $$\begin{aligned} J_1d^M\varphi (t,x)= \left\{ \begin{array}{ll} 1+t(\mathrm {div}^{M}\,Z_0)(x)+tR^{(1)}(t,x) &{} \text { for }x\in K;\\ 1 &{} \text { for }x\not \in K.\\ \end{array} \right. \end{aligned}$$

  where $\sup _K|R^{(1)}(t,\cdot )|\rightarrow 0$ as $t\rightarrow 0$.

Proof

(i) We first remark that the flow $\varphi :I\times \mathbb {R}^2\rightarrow \mathbb {R}^2$ associated to Z is continuously differentiable in t, x in virtue of (Z.1) by [16] Theorem I.3.3. Put $y(t,x):=d\varphi (t,x)$ for $(t,x)\in I\times \mathbb {R}^2$. By [16] Theorem I.3.3,

$$\begin{aligned} \dot{y}(t,x)=dZ(t,\varphi (t,x))y(t,x) \end{aligned}$$

for each $(t,x)\in I\times \mathbb {R}^2$ and $y(0,x)=I$ for each $x\in \mathbb {R}^2$ where I stands for the $2\times 2$-identity matrix. For $x\in \ K$ and $t\in I$,

$$\begin{aligned} d\varphi (t,x)&=I+d\varphi (t,x)-d\varphi (0,x)\nonumber \\&=I+t\dot{y}(0,x)+t\Big \{\frac{d\varphi (t,x)-d\varphi (0,x)}{t}-\dot{y}(0,x)\Big \}\nonumber \\&=I+t dZ(0,x)+t\Big \{\frac{y(t,x)-y(0,x)}{t}-\dot{y}(0,x)\Big \}\nonumber \\&=I+t dZ_0(x)+t\Big \{\frac{y(t,x)-y(0,x)}{t}-\dot{y}(0,x)\Big \}.\nonumber \end{aligned}$$

Applying the mean-value theorem component-wise and using uniform continuity of the matrix $\dot{y}$ in its arguments we see that

$$\begin{aligned} \frac{y(t,\cdot )-y(0,\cdot )}{t}-\dot{y}(0,\cdot )\rightarrow 0 \end{aligned}$$

uniformly on K as $t\rightarrow 0$. This leads to (i). Part (ii) follows as in Lemma 2.2. $\square$

Let E be a set of finite perimeter in $\mathbb {R}^2$ with $V_f(E)<+\infty$. The first variation of weighted volume resp. perimeter along $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ is defined by

$$\begin{aligned} \delta V_f(X)&:=\frac{d}{dt}\Big \vert _{t=0}V_f(\varphi _t(E)),\end{aligned}$$

(2.13)

$$\begin{aligned} \delta P_f^+(X)&:=\lim _{t\downarrow 0}\frac{P_f(\varphi _t(E))-P_f(E)}{t}, \end{aligned}$$

(2.14)

whenever the limit exists. By Lemma 2.1 the f-perimeter in (2.14) is well-defined.

Convex functions. Suppose that $h:[0,+\infty )\rightarrow \mathbb {R}$ is a convex function. For $x\ge 0$ and $v\ge 0$ define

$$\begin{aligned} h^\prime _+(x,v):=\lim _{t\downarrow 0}\frac{h(x+tv)-h(x)}{t}\in \mathbb {R} \end{aligned}$$

and define $h^\prime _-(x,v)$ similarly for $x>0$ and $v\le 0$. For future use we introduce the notation

$$\begin{aligned} \rho _+:=h^\prime (\cdot ,+1), \rho _-:=-h^\prime (\cdot ,-1) \text { and } \rho :=(1/2)(\rho _++\rho _-) \end{aligned}$$

on $(0,+\infty )$. It holds that h is differentiable a.e. and $h^\prime =\rho$ a.e. on $(0,+\infty )$. Define $[\rho ]:=\rho _+-\rho _-$. Then $[\rho ]\ge 0$ and vanishes a.e. on $(0,+\infty )$.

Lemma 2.4

Suppose that the function f takes the form (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a convex function. Then

• (i) the directional derivative $f^\prime _+(x,v)$ exists in $\mathbb {R}$ for each $x\in \mathbb {R}^2$ and $v\in \mathbb {R}^2$;

• (ii) for $v\in \mathbb {R}^2$,

  $$\begin{aligned} f^\prime _+(x,v)= \left\{ \begin{array}{ll} f(x)h^\prime _+(|x|,\mathrm {sgn}\langle x,v\rangle )\frac{|\langle x,v\rangle |}{|x|} &{} \text { for }x\in \mathbb {R}^2{\setminus }\{0\};\\ f(0)h^\prime _+(0,+1)|v| &{} \text { for }x=0;\\ \end{array} \right. \end{aligned}$$

• (iii) if M is a $C^1$ hypersurface in $\mathbb {R}^2$ such that $\cos \sigma \ne 0$ on M then f is differentiable $\mathscr {H}^1$-a.e. on M and

  $$\begin{aligned} (\nabla f)(x)=f(x)\rho (|x|)\frac{\langle x,\cdot \rangle }{|x|} \end{aligned}$$

  for $\mathscr {H}^1$-a.e. $x\in M$.

Proof

The assertion in (i) follows from the monotonicity of chords property while (ii) is straightforward. (iii) Let $x\in M$ and $\gamma _1:I\rightarrow M$ be a $C^1$-parametrisation of M near x as above. Now $r_1\in C^1(I)$ and $\dot{r_1}(0)=\cos \sigma (x)\ne 0$ so we may assume that $r_1:I\rightarrow r_1(I)\subset (0,+\infty )$ is a $C^1$ diffeomorphism. The differentiability set D(h) of h has full Lebesgue measure in $[0,+\infty )$. It follows by [1] Proposition 2.49 that $r_1^{-1}(D(h))$ has full measure in I. This entails that f is differentiable $\mathscr {H}^1$-a.e. on $\gamma _1(I)\subset M$. $\square$

3 Existence and $C^1$ regularity

We start with an existence theorem.

Theorem 3.1

Assume that f is a positive radial lower-semicontinuous non-decreasing density on $\mathbb {R}^2$ which diverges to infinity. Then for each $v>0$,

• (i) (1.2) admits a minimiser;

• (ii) any minimiser of (1.2) is essentially bounded.

Proof

See [22] Theorems 3.3 and 5.9. $\square$

But the bulk of this section will be devoted to a discussion of $C^1$ regularity.

Proposition 3.2

Let f be a positive locally Lipschitz density on $\mathbb {R}^2$. Let $E\subset \mathbb {R}^2$ be a bounded set with finite perimeter. Let $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$. Then

$$\begin{aligned} \delta V_f(X) =\int _{E}\mathrm {div}(fX)\,dx =-\int _{\mathscr {F}E} f\,\langle \nu ^E, X\rangle \,d\mathscr {H}^1. \end{aligned}$$

Proof

Let $t\in \mathbb {R}$. By the area formula ( [1] Theorem 2.71 and (2.74)),

$$\begin{aligned} V_f(\varphi _t(E)) = \int _{\varphi _t(E)}f\,dx = \int _{E}(f\circ \varphi _t)\,J_2 d(\varphi _t)_x\,dx \end{aligned}$$

(3.1)

and

$$\begin{aligned} V_f(\varphi _t(E))-V_f(E)&=\int _E(f\circ \varphi _t)J_2 d\varphi _t - f\,dx\\&=\int _E(f\circ \varphi _t)(J_2 d\varphi _t-1)\,dx+\int _Ef\circ \varphi _t-f\,dx. \end{aligned}$$

The density f is locally Lipschitz and in particular differentiable a.e. on $\mathbb {R}^2$ (see [1] 2.3 for example). By the dominated convergence theorem and Lemma 2.2,

$$\begin{aligned} \delta V_f(X)&=\int _{E}\Big \{f\mathrm {div}(X)+\langle \nabla f,X\rangle \Big \}\,dx =\int _{E}\mathrm {div}(fX)\,dx\\&=-\int _{\mathscr {F}E} f\,\langle \nu ^E,X\rangle \,d\mathscr {H}^1 \end{aligned}$$

by the generalised Gauss–Green formula [1] Theorem 3.36. $\square$

Proposition 3.3

Let f be a positive locally Lipschitz density on $\mathbb {R}^2$. Let $E\subset \mathbb {R}^2$ be a bounded set with finite perimeter. Let $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$. Then there exist constants $C>0$ and $\delta >0$ such that

$$\begin{aligned} |P_f(\varphi _t(E))-P_f(E)|\le C|t| \end{aligned}$$

for $|t|<\delta$.

Proof

Let $t\in \mathbb {R}$. By Lemma 2.1 and [1] Theorem 3.59,

$$\begin{aligned} P_f(\varphi _t(E)) =\int _{\mathbb {R}^2}f\,d|D\chi _{\varphi _t(E)}| =\int _{\mathscr {F}\varphi _t(E)}f\,d\mathscr {H}^1 =\int _{\varphi _t(\mathscr {F}E)}f\,d\mathscr {H}^1. \end{aligned}$$

As $\mathscr {F}E$ is countably 1-rectifiable ( [1] Theorem 3.59) we may use the generalised area formula [1] Theorem 2.91 to write

$$\begin{aligned} P_f(\varphi _t(E))=\int _{\mathscr {F}E}(f\circ \varphi _t)J_1d^{\mathscr {F}E}(\varphi _t)_x\,d\mathscr {H}^1. \end{aligned}$$

For each $x\in \mathscr {F}E$ and any $t\in \mathbb {R}$,

$$\begin{aligned} |(f\circ \varphi _t)(x)-f(x)|\le K|\varphi (t,x)-x|\le K\Vert X\Vert _\infty |t| \end{aligned}$$

where K is the Lipschitz constant of f on $\mathrm {supp}[X]$. The result follows upon writing

$$\begin{aligned} P_f(\varphi _t(E))-P_f(E)&=\int _{\mathscr {F}E}(f\circ \varphi _t)(J_1d^{\mathscr {F}E}(\varphi _t)_x-1)\nonumber \\&\quad +\,[f\circ \varphi _t-f] \,d\mathscr {H}^1 \end{aligned}$$

(3.2)

and using Lemma 2.2. $\square$

Lemma 3.4

Let f be a positive locally Lipschitz density on $\mathbb {R}^2$. Let $E\subset \mathbb {R}^2$ be a bounded set with finite perimeter and $p\in \mathscr {F}E$. For any $r>0$ there exists $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X]\subset B(p,r)$ such that $\delta V_f(X)=1$.

Proof

By (2.2) and [1] Theorem 3.59 and (3.57) in particular,

$$\begin{aligned} P_f(E,B(p,r))=\int _{B(p,r)\cap \mathscr {F}E}f\,d\mathscr {H}^1>0 \end{aligned}$$

for any $r>0$. By the variational characterisation of the f-perimeter relative to B(p, r) we can find $Y\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[Y]\subset B(p,r)$ such that

$$\begin{aligned} 0<\int _{E\cap B(p,r)}\mathrm {div}(fY)\,dx=-\int _{\mathscr {F}E\cap B(p,r)}f\langle \nu ^E,Y\rangle \,d\mathscr {H}^1=:c \end{aligned}$$

where we make use of the generalised Gauss–Green formula (cf. [1] Theorem 3.36). Put $X:=(1/c)Y$. Then $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X]\subset B(p,r)$ and $\delta V_f(X)=1$ according to Proposition 3.2. $\square$

Proposition 3.5

Let f be a positive lower semi-continuous density on $\mathbb {R}^2$. Let U be a bounded open set in $\mathbb {R}^2$ with Lipschitz boundary. Let $E, F_1, F_2$ be bounded sets in $\mathbb {R}^2$ with finite perimeter. Assume that $E\varDelta F_1\subset \subset U$ and $E\varDelta F_2\subset \subset \mathbb {R}^2{\setminus }\overline{U}$. Define

$$\begin{aligned} F:=\Big [F_1\cap U\Big ]\cup \Big [F_2{\setminus } U\Big ]. \end{aligned}$$

Then F is a set of finite perimeter in $\mathbb {R}^2$ and

$$\begin{aligned} P_f(E)+P_f(F)= P_f(F_1)+P_f(F_2). \end{aligned}$$

Proof

The function $\chi _E\vert _U\in \mathrm {BV}(U)$ and $D(\chi _E\vert _U)=(D\chi _E)\vert _U$. We write $\chi _E^U$ for the boundary trace of $\chi _E\vert _U$ (see [1] Theorem 3.87); then $\chi _E^U\in L^1(\partial U,\mathscr {H}^1|\!\_\partial U)$ (cf. [1] Theorem 3.88). We use similar notation elsewhere. By [1] Corollary 3.89,

$$\begin{aligned} D\chi _E&=D\chi _E|\!\_U+(\chi _E^U-\chi _E^{\mathbb {R}^2{\setminus }\overline{U}})\nu ^U\mathscr {H}^1|\!\_{\partial U}+D\chi _E|\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ D\chi _F&=D\chi _{F_1}|\!\_U+(\chi _{F_1}^U-\chi _{F_2}^{\mathbb {R}^2{\setminus }\overline{U}})\nu ^U\mathscr {H}^1|\!\_{\partial U}+D\chi _{F_2}|\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ D\chi _{F_1}&=D\chi _{F_1}|\!\_U+(\chi _{F_1}^U-\chi _{E}^{\mathbb {R}^2{\setminus }\overline{U}})\nu ^U\mathscr {H}^1|\!\_{\partial U}+D\chi _{E}|\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ D\chi _{F_2}&=D\chi _{E}|\!\_U+(\chi _{E}^U-\chi _{F_2}^{\mathbb {R}^2{\setminus }\overline{U}})\nu ^U\mathscr {H}^1|\!\_{\partial U}+D\chi _{F_2}|\!\_(\mathbb {R}^2{\setminus }\overline{U}). \end{aligned}$$

From the definition of the total variation measure ([1] Definition 1.4),

$$\begin{aligned} |D\chi _E|&=|D\chi _E||\!\_U+|\chi _E^U-\chi _E^{\mathbb {R}^2{\setminus }\overline{U}}|\mathscr {H}^1|\!\_{\partial U}+|D\chi _E||\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ |D\chi _F|&=|D\chi _{F_1}||\!\_U+|\chi _E^U-\chi _E^{\mathbb {R}^2{\setminus }\overline{U}}|\mathscr {H}^1|\!\_{\partial U}+|D\chi _{F_2}||\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ |D\chi _{F_1}|&=|D\chi _{F_1}||\!\_U+|\chi _E^U-\chi _{E}^{\mathbb {R}^2{\setminus }\overline{U}}|\mathscr {H}^1|\!\_{\partial U}+|D\chi _{E}||\!\_(\mathbb {R}^2{\setminus }\overline{U});\nonumber \\ |D\chi _{F_2}|&=|D\chi _{E}||\!\_U+|\chi _{E}^U-\chi _E^{\mathbb {R}^2{\setminus }\overline{U}}|\mathscr {H}^1|\!\_{\partial U}+|D\chi _{F_2}||\!\_(\mathbb {R}^2{\setminus }\overline{U}); \end{aligned}$$

where we also use the fact that $\chi _{F_1}^U=\chi _E^U$ as $E\varDelta F_1\subset \subset U$ and similarly for $F_2$. The result now follows. $\square$

Proposition 3.6

Assume that f is a positive locally Lipschitz density on $\mathbb {R}^2$. Let $v>0$ and suppose that the set E is a bounded minimiser of (1.2). Let U be a bounded open set in $\mathbb {R}^2$. There exist constants $C>0$ and $\delta >0$ with the following property. For any $x\in U$ and $0<r<\delta$,

$$\begin{aligned} P_f(E)-P_f(F)\le C\big |V_f(E)-V_f(F)\big | \end{aligned}$$

(3.3)

where F is any set with finite perimeter in $\mathbb {R}^2$ such that $E\varDelta F\subset \subset B(x,r)$.

Proof

The proof follows that of [21] Proposition 3.1. We assume to the contrary that

$$\begin{aligned} (\forall \,C>0)(\forall \,\delta >0)(\exists \,x\in U)(\exists \,r\in (0,\delta ))(\exists \,F\subset \mathbb {R}^2) \end{aligned}$$

$$\begin{aligned} \Big [ F\varDelta E\subset \subset B(x,r) \wedge \varDelta P_f > C|\varDelta V_f| \Big ] \end{aligned}$$

(3.4)

in the language of quantifiers where we have taken some liberties with notation.

Choose $p_1,p_2\in \mathscr {F}E$ with $p_1\ne p_2$. Choose $r_0>0$ such that the open balls $B(p_1,r_0)$ and $B(p_2,r_0)$ are disjoint. Choose vector fields $X_j\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X_j]\subset B(p_j,r_0)$ such that

$$\begin{aligned} \delta V_f(X_j)=1 \text { and } |P_f(\varphi ^{(j)}_t(E))-P_f(E)|\le a_j|t|\text { for }|t|<\delta _j\text { and }j=1,2\nonumber \\ \end{aligned}$$

(3.5)

as in Lemma 3.4 and Proposition 3.3. Put $a:=\max \{a_1,a_2\}$. By (3.5),

$$\begin{aligned} V_f(\varphi ^{(j)}_t(E))-V_f(E)=t + o(t)\text { as }t\rightarrow 0\text { for }j=1,2. \end{aligned}$$

So there exist $\varepsilon >0$ and $1>\eta >0$ such that

$$\begin{aligned}&t-\eta |t|< V_f(\varphi ^{(j)}_t(E)) - V_f(E)< t + \eta |t|;\nonumber \\&|P_f(\varphi _t^{(j)}(E)) - P_f(E) |<(a+1)|t|; \end{aligned}$$

(3.6)

for $|t|<\varepsilon$ and $j=1,2$. In particular,

$$\begin{aligned}&|V_f(\varphi ^{(j)}_t(E)) - V_f(E)|>(1-\eta )|t|;\nonumber \\&|P_f(\varphi _t^{(j)}(E)) - P_f(E)|<\frac{1+a}{1-\eta }|V_f(\varphi ^{(j)}_t(E)) - V_f(E)| \text { for }|t|<\varepsilon ; \end{aligned}$$

(3.7)

for $|t|<\varepsilon$ and $j=1,2$.

In (3.4) choose $C=(1+a)/(1-\eta )$ and $\delta >0$ such that

• (a) $0<2\delta <\mathrm {dist}(B(p_1,r_0),B(p_2,r_0))$,

• (b) $\sup \{V_f(B(x,\delta )):\,x\in U\}<(1-\eta )\,\varepsilon$.

Choose x, r and $F_1$ as in (3.4). In light of (a) we may assume that $B(x,r)\cap B(p_1,r_0)=\emptyset$. By (b),

$$\begin{aligned} |V_f(F_1) - V_f(E)|\le V_f(B(x,r))\le V_f(B(x,\delta ))<(1-\eta )\,\varepsilon . \end{aligned}$$

(3.8)

From (3.6) and (3.8) we can find $t\in (-\varepsilon ,\varepsilon )$ such that with $F_2:=\varphi _t^{(1)}(E)$,

$$\begin{aligned} V_f(F_2) - V_f(E)=-\Big \{V_f(F_1) - V_f(E)\Big \} \end{aligned}$$

(3.9)

by the intermediate value theorem. From (3.4),

$$\begin{aligned} P_f(F_1) < P_f(E)-C|V_f(F_1) - V_f(E)| \end{aligned}$$

(3.10)

while from (3.7),

$$\begin{aligned} P_f(F_2) < P_f(E) + C|V_f(F_2) - V_f(E)|. \end{aligned}$$

(3.11)

Let F be the set

$$\begin{aligned} F:=\Big [F_1{\setminus } B(p_1,r_0))\Big ]\cup \Big [B(p_1,r_0)\cap F_2\Big ]. \end{aligned}$$

Note that $E\varDelta F_2\subset \subset B(p_1,r_0)$. By Proposition 3.5, F is a bounded set of finite perimeter in $\mathbb {R}^2$ and

$$\begin{aligned} P_f(E)+P_f(F)= P_f(F_1)+P_f(F_2). \end{aligned}$$

We then infer from (3.10), (3.11) and (3.9) that

$$\begin{aligned} P_f(F)&= P_f(F_1)+P_f(F_2)-P_f(E)\nonumber \\&<P_f(E)-C|V_f(F_1) - V_f(E)|+ P_f(E) \nonumber \\&\quad +\, C|V_f(F_2) - V_f(E)|-P_f(E)\ =P_f(E). \end{aligned}$$

On the other hand, $V_f(F)=V_f(F_1)+V_f(F_2)-V_f(E)=V_f(E)$ by (3.9). We therefore obtain a contradiction to the f-isoperimetric property of E. $\square$

Let E be a set of finite perimeter in $\mathbb {R}^2$ and U a bounded open set in $\mathbb {R}^2$. The minimality excess is the function $\psi$ defined by

$$\begin{aligned} \psi (E,U)&:=P(E,U)-\nu (E,U) \end{aligned}$$

(3.12)

where

$$\begin{aligned} \nu (E,U) :=\inf \{P(F,U):F\text { is a set of finite perimeter with }F\varDelta E\subset \subset U\} \end{aligned}$$

as in [27] (1.9). We recall that the boundary of E is said to be almost minimal in $\mathbb {R}^2$ if for each bounded open set U in $\mathbb {R}^2$ there exists $T>0$ and a positive constant K such that for every $x\in U$ and $r\in (0,T)$,

$$\begin{aligned} \psi (E,B(x,r))\le K r^2. \end{aligned}$$

(3.13)

This definition corresponds to [27] Definition 1.5.

Theorem 3.7

Assume that f is a positive locally Lipschitz density on $\mathbb {R}^2$. Let $v>0$ and assume that E is a bounded minimiser of (1.2). Then the boundary of E is almost minimal in $\mathbb {R}^2$.

Proof

Let U be a bounded open set in $\mathbb {R}^2$ and $C>0$ and $\delta >0$ as in Proposition 3.6. The open $\delta$-neighbourhood of U is denoted $I_\delta (U)$. Let $x\in U$ and $r\in (0,\delta )$. Put $V:=I_{2\delta }(U)$. For the sake of brevity write $m:=\inf _{B(x,r)}f$ and $M:=\sup _{B(x,r)}f$. Let F be a set of finite perimeter in $\mathbb {R}^2$ such that $F\varDelta E\subset \subset B(x,r)$. By Proposition 3.6,

$$\begin{aligned}&P(E,B(x,r))-P(F,B(x,r))\\&\quad \le \frac{1}{m}P_f(E,B(x,r))-\frac{1}{M}P_f(F,B(x,r))\nonumber \\&\quad =\frac{1}{m} \Big ( P_f(E,B(x,r))-P_f(F,B(x,r)) \Big )+ \Big (\frac{1}{m}-\frac{1}{M} \Big ) P_f(F,B(x,r))\nonumber \\&\quad \le \frac{1}{m} \Big ( P_f(E,B(x,r))-P_f(F,B(x,r)) \Big )+ \frac{M-m}{m^2} P_f(F,B(x,r))\nonumber \\&\quad \le \frac{C}{\inf _V f}|V_f(E)-V_f(F)| + (2Lr)\frac{\sup _V f}{(\inf _V f)^2}P(F,B(x,r))\nonumber \\&\quad \le C\pi r^2\frac{\sup _V f}{\inf _V f} + (2Lr)\frac{\sup _V f}{(\inf _V f)^2}P(F,B(x,r))\nonumber \end{aligned}$$

where L stands for the Lipschitz constant of the restriction of f to V. We then derive that

$$\begin{aligned} \psi (E,B(x,r))\le C\pi r^2\frac{\sup _V f}{\inf _V f} + (2Lr)\frac{\sup _V f}{(\inf _V f)^2} \nu (E,B(x,r)). \end{aligned}$$

By [13] (5.14), $\nu (E,B(x,r))\le \pi r$. The inequality in (3.13) now follows. $\square$

Theorem 3.8

Assume that f is a positive locally Lipschitz density on $\mathbb {R}^2$. Let $v>0$ and suppose that E is a bounded minimiser of (1.2). Then there exists a set $\widetilde{E}\subset \mathbb {R}^2$ such that

• (i) $\widetilde{E}$ is a bounded minimiser of (1.2);

• (ii) $\widetilde{E}$ is equivalent to E;

• (iii) $\widetilde{E}$ is open and $\partial \widetilde{E}$ is a $C^1$ hypersurface in $\mathbb {R}^2$.

Proof

By [13] Proposition 3.1 there exists a Borel set F equivalent to E with the property that

$$\begin{aligned} \partial F=\{x\in \mathbb {R}^2:0<|F\cap B(x,\rho )|<\pi \rho ^2\text { for each }\rho >0\}. \end{aligned}$$

By Theorem 3.7 and [27] Theorem 1.9, $\partial F$ is a $C^1$ hypersurface in $\mathbb {R}^2$ (taking note of differences in notation). The set

$$\begin{aligned} \widetilde{E}:=\{x\in \mathbb {R}^2:|F\cap B(x,\rho )|=\pi \rho ^2\text { for some }\rho >0\} \end{aligned}$$

satisfies (i)–(iii). $\square$

4 Weakly bounded curvature and spherical cap symmetry

Theorem 4.1

Assume that f is a positive locally Lipschitz density on $\mathbb {R}^2$. Let $v>0$ and suppose that E is a bounded minimiser of (1.2). Then there exists a set $\widetilde{E}\subset \mathbb {R}^2$ such that

• (i) $\widetilde{E}$ is a bounded minimiser of (1.2);

• (ii) $\widetilde{E}$ is equivalent to E;

• (iii) $\widetilde{E}$ is open and $\partial \widetilde{E}$ is a $C^{1,1}$ hypersurface in $\mathbb {R}^2$.

Proof

We may assume that E has the properties listed in Theorem 3.8. Put $M:=\partial E$. Let $x\in M$ and U a bounded open set containing x. Choose $C>0$ and $\delta >0$ as in Proposition 3.6. Let $0<r<\delta$ and $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X]\subset B(x,r)$. Then

$$\begin{aligned} P_f(E)-P_f(\varphi _t(E))\le C|V_f(E)-V_f(\varphi _t(E))| \end{aligned}$$

for each $t\in \mathbb {R}$. From the identity (3.2),

$$\begin{aligned}&-\int _M(f\circ \varphi _t)(J_1d^M(\varphi _t)_x-1)\,d\mathscr {H}^1\le C|V_f(E)-V_f(\varphi _t(E))| \\&\qquad +\,\int _M[f\circ \varphi _t-f]\,d\mathscr {H}^1 \nonumber \\&\quad \le \, C|V_f(E)-V_f(\varphi _t(E))| +\sqrt{2}K\Vert X\Vert _\infty \mathscr {H}^1(M\cap \mathrm {supp}[X])t \end{aligned}$$

where K stands for the Lipschitz constant of f restricted to U. On dividing by t and taking the limit $t\rightarrow 0$ we obtain

$$\begin{aligned} -\int _M f\mathrm {div}^M X\,d\mathscr {H}^1&\le C\Big |\int _M f\langle n,X\rangle \,d\mathscr {H}^1\Big |\\&\quad +\,\sqrt{2}K\Vert X\Vert _\infty \mathscr {H}^1(M\cap \mathrm {supp}[X]) \end{aligned}$$

upon using Lemma 2.2 and Proposition 3.2. Replacing X by $-X$ we derive that

$$\begin{aligned} \Big |\int _M f\mathrm {div}^M X\,d\mathscr {H}^1\Big |\le C_1\Vert X\Vert _\infty \mathscr {H}^1(M\cap \mathrm {supp}[X]) \end{aligned}$$

where $C_1=C\Vert f\Vert _{L^\infty (U)}+\sqrt{2}K$. Let $\gamma _1:I\rightarrow M$ be a local $C^1$ parametrisation of M near x. Suppose that $Y\in C^1_c(I,\mathbb {R}^2)$ with $\mathrm {supp}[Y]\subset I$ and that $\gamma _1(I)\subset M\cap B(x,r)$. Note that there exists $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X]\subset B(x,r)$ such that $X\circ \gamma _1=Y$ on I. The above estimate entails that

$$\begin{aligned} \Big |\int _I(f\circ \gamma _1)\langle \dot{Y},t\rangle \,ds\Big |\le C_1\Big |\mathrm {supp}[Y]\Big |\Vert Y\Vert _\infty . \end{aligned}$$

This means that the function $(f\circ \gamma _1)t$ belongs to $\mathrm {BV}(I)$ and this implies in turn that $t\in \mathrm {BV}(I)$. For $s_1,s_2\in I$ with $s_1<s_2$,

$$\begin{aligned} |t(s_2)-t(s_1)|&=|Dt((s_1,s_2))|\le |Dt|((s_1,s_2))\nonumber \\&=\sup \Big \{\int _{(s_1,s_2)}\langle t,\dot{Y}\rangle \,ds:Y\in C^1_c((s_1,s_2))\text { and }\Vert Y\Vert _\infty \le 1\Big \}\nonumber \\&\le c\sup \Big \{\int _{(s_1,s_2)}(f\circ \gamma _1)\langle t,\dot{Y}\rangle \,ds:Y\in C^1_c((s_1,s_2))\text { and }\Vert Y\Vert _\infty \le 1\Big \}\nonumber \\&\le cC_1|s_2-s_1|\nonumber \end{aligned}$$

where $1/c=\inf _{\overline{U}}f>0$. It follows that M is of class $C^{1,1}$. $\square$

We turn to the topic of spherical cap symmetrisation. Denote by $\mathbb {S}^1_\tau$ the centred circle in $\mathbb {R}^2$ with radius $\tau >0$. We sometimes write $\mathbb {S}^1$ for $\mathbb {S}^1_1$. Given $x\in \mathbb {R}^2,v\in \mathbb {S}^1$ and $\alpha \in (0,\pi ]$ the open cone with vertex x, axis v and opening angle $2\alpha$ is the set

$$\begin{aligned} C(x,v,\alpha ):=\Big \{y\in \mathbb {R}^2:\langle y-x,v\rangle >|y-x|\cos \alpha \Big \}. \end{aligned}$$

Let E be an $\mathscr {L}^2$-measurable set in $\mathbb {R}^2$ and $\tau >0$. The $\tau$-section $E_\tau$ of E is the set $E_\tau :=E\cap \mathbb {S}^1_\tau$. Put

$$\begin{aligned} L(\tau )=L_E(\tau ):=\mathscr {H}^1(E_\tau )\text { for }\tau >0 \end{aligned}$$

(4.1)

and $p(E) := \{\tau>0:L(\tau )>0\}$. The function L is $\mathscr {L}^1$-measurable by [1] Theorem 2.93. Given $\tau >0$ and $0<\alpha \le \pi$ the spherical cap $C(\tau ,\alpha )$ is the set

$$\begin{aligned} C(\tau ,\alpha ):= \left\{ \begin{array}{ll} \mathbb {S}^1_\tau \cap C(0,e_1,\alpha ) &{} \text { if }0<\alpha <\pi ;\\ \mathbb {S}^1_\tau &{} \text { if }\alpha =\pi ;\\ \end{array} \right. \end{aligned}$$

and has $\mathscr {H}^1$-measure $s(\tau ,\alpha ):=2\alpha \tau$. The spherical cap symmetral $E^{sc}$ of the set E is defined by

$$\begin{aligned} E^{sc}:=\bigcup _{\tau \in p(E)}C(\tau ,\alpha ) \end{aligned}$$

(4.2)

where $\alpha \in (0,\pi ]$ is determined by $s(\tau ,\,\alpha )=L(\tau )$. Observe that $E^{sc}$ is a $\mathscr {L}^2$-measurable set in $\mathbb {R}^2$ and $V_f(E^{sc})=V_f(E)$. Note also that if B is a centred open ball then $B^{sc}=B{\setminus }\{0\}$. We say that E is spherical cap symmetric if $\mathscr {H}^1((E\varDelta E^{sc})_\tau )=0$ for each $\tau >0$. This definition is broad but suits our purposes.

The result below is stated in [22] Theorem 6.2 and a sketch proof given. A proof along the lines of [2] Theorem 1.1 can be found in [23]. First, let B be a Borel set in $(0,+\infty )$; then the annulus A(B) over B is the set $A(B):=\{x\in \mathbb {R}^2:|x|\in B\}$.

Theorem 4.2

Let E be a set of finite perimeter in $\mathbb {R}^2$. Then $E^{sc}$ is a set of finite perimeter and

$$\begin{aligned} P(E^{sc},A(B))\le P(E,A(B)) \end{aligned}$$

(4.3)

for any Borel set $B\subset (0,\infty )$ and the same inequality holds with $E^{sc}$ replaced by any set F that is $\mathscr {L}^2$-equivalent to $E^{sc}$.

Corollary 4.3

Let f be a positive lower semi-continuous radial function on $\mathbb {R}^2$. Let E be a set of finite perimeter in $\mathbb {R}^2$. Then $P_f(E^{sc})\le P_f(E)$.

Proof

Assume that $P_f(E)<+\infty$. We remark that f is Borel measurable as f is lower semi-continuous. Let $(f_h)$ be a sequence of simple Borel measurable radial functions on $\mathbb {R}^2$ such that $0\le f_h\le f$ and $f_h\uparrow f$ on $\mathbb {R}^2$ as $h\rightarrow \infty$. By Theorem 4.2,

$$\begin{aligned} P_{f_h}(E^{sc})=\int _{\mathbb {R}^2}f_h\,d|D\chi _{E^{sc}}| \le \int _{\mathbb {R}^2}f_h\,d|D\chi _{E}|= P_{f_h}(E) \end{aligned}$$

for each h. Taking the limit $h\rightarrow \infty$ the monotone convergence theorem gives $P_f(E^{sc})\le P_f(E)$. $\square$

Lemma 4.4

Let E be an $\mathscr {L}^2$-measurable set in $\mathbb {R}^2$ such that $E{\setminus }\{0\}=E^{sc}$. Then there exists an $\mathscr {L}^2$-measurable set F equivalent to E such that

• (i) $\partial F=\{x\in \mathbb {R}^2:0<|F\cap B(x,\rho )|<|B(x,\rho )|\text { for any }\rho >0\}$;

• (ii) F is spherical cap symmetric.

Proof

Put

$$\begin{aligned} E_1&:=\{x\in \mathbb {R}^2:|E\cap B(x,\rho )|=|B(x,\rho )|\text { for some }\rho>0\};\nonumber \\ E_0&:=\{x\in \mathbb {R}^2:|E\cap B(x,\rho )|=0\text { for some }\rho >0\}.\nonumber \end{aligned}$$

We claim that $E_1$ is spherical cap symmetric. For take $x\in E_1$ with $\tau =|x|>0$ and $|\theta (x)|\in (0,\pi ]$. Now $|E\cap B(x,\rho )|=|B(x,\rho )|$ for some $\rho >0$. Let $y\in \mathbb {R}^2$ with $|y|=\tau$ and $|\theta (y)|<|\theta (x)|$. Choose a rotation $O\in \mathrm {SO}(2)$ such that $OB(x,\rho )=B(y,\rho )$. As $E{\setminus }\{0\}=E^{sc},|E\cap B(y,\rho )|=|O(E\cap B(x,\rho ))|=|E\cap B(x,\rho )|=|B(x,\rho )|=|B(y,\rho )|$. The claim follows. It follows in a similar way that $\mathbb {R}^2{\setminus } E_0$ is spherical cap symmetric. It can then be seen that the set $F:=(E_1\cup E){\setminus } E_0$ inherits this property. As in [13] Proposition 3.1 the set F is equivalent to E and enjoys the property in (i). $\square$

Theorem 4.5

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a bounded minimiser of (1.2). Then there exists an $\mathscr {L}^2$-measurable set $\widetilde{E}$ with the properties

• (i) $\widetilde{E}$ is a minimiser of (1.2);

• (ii) $L_{\widetilde{E}}=L$ a.e. on $(0,+\infty )$;

• (iii) $\widetilde{E}$ is open, bounded and has $C^{1,1}$ boundary;

• (iv) $\widetilde{E}{\setminus }\{0\}=\widetilde{E}^{sc}$.

Proof

Let E be a bounded minimiser for (1.2). Then $E_1:=E^{sc}$ is a bounded minimiser of (1.2) by Corollary 4.3 and $L_E=L_{E_1}$ on $(0,+\infty )$. Now put $E_2:=F$ with F as in Lemma 4.4. Then $L_{E_2}=L$ a.e. on $(0,+\infty )$ as $E_2$ is equivalent to $E_1,E_2$ is a bounded minimiser of (1.2) and $E_2$ is spherical cap symmetric. Moreover, $\partial E_2=\{x\in \mathbb {R}^2:0<|E_2\cap B(x,\rho )|<|B(x,\rho )|\text { for any }\rho >0\}$. As in the proof of Theorem 3.8, $\partial E_2$ is a $C^1$ hypersurface in $\mathbb {R}^2$. Put

$$\begin{aligned} \widetilde{E}:=\{x\in \mathbb {R}^2:|E_2\cap B(x,\rho )|=|B(x,\rho )|\text { for some }\rho >0\}. \end{aligned}$$

Then $\widetilde{E}$ is equivalent to $E_2$ so that (ii) holds, and is a bounded minimiser of (1.2); $\widetilde{E}$ is open and $\partial \widetilde{E}=\partial E_2$ is $C^1$. In fact, $\partial \widetilde{E}$ is of class $C^{1,1}$ by Theorem 4.1. As $E_2$ is spherical cap symmetric the same is true of $\widetilde{E}$. But $\widetilde{E}$ is open which entails that $\widetilde{E}{\setminus }\{0\}=\widetilde{E}^{sc}$. $\square$

5 More on spherical cap symmetry

Let

$$\begin{aligned} H:=\{x=(x_1,x_2)\in \mathbb {R}^2:x_2>0\} \end{aligned}$$

stand for the open upper half-plane in $\mathbb {R}^2$ and

$$\begin{aligned} S:\mathbb {R}^2\rightarrow \mathbb {R}^2;x=(x_1,x_2)\mapsto (x_1,-x_2) \end{aligned}$$

for reflection in the $x_1$-axis. Let $O\in \mathrm {SO}(2)$ represent rotation anti-clockwise through $\pi /2$.

Lemma 5.1

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$. Let $x\in M{\setminus }\{0\}$. Then

• (i) $Sx\in M{\setminus }\{0\}$;

• (ii) $n(Sx)=Sn(x)$;

• (iii) $\cos \sigma (Sx)=-\cos \sigma (x)$.

Proof

(i) The closure $\overline{E}$ of E is spherical cap symmetric. The spherical cap symmetral $\overline{E}$ is invariant under S from the representation (4.2). (ii) is a consequence of this last observation. (iii) Note that $t(Sx)=O^\star n(Sx)=O^\star Sn(x)$. Then

$$\begin{aligned} \cos \sigma (Sx)&=\langle Sx,t(Sx)\rangle =\langle Sx,O^\star Sn(x)\rangle =\langle x,SO^\star Sn(x)\rangle \nonumber \\&=\langle x,On(x)\rangle =-\langle x,O^\star n(x)\rangle =\cos \sigma (x)\nonumber \end{aligned}$$

as $SO^\star S=O$ and $O=-O^\star$. $\square$

We introduce the projection $\pi :\mathbb {R}^2\rightarrow [0,+\infty );x\mapsto |x|$.

Lemma 5.2

Let E be an open set in $\mathbb {R}^2$ with boundary M and assume that $E{\setminus }\{0\}=E^{sc}$.

• (i) Suppose $0\ne x\in \mathbb {R}^2{\setminus }\overline{E}$ and $\theta (x)\in (0,\pi ]$. Then there exists an open interval I in $(0,+\infty )$ containing $\tau$ and $\alpha \in (0,\theta (x))$ such that $A(I){\setminus }\overline{S}(\alpha )\subset \mathbb {R}^2{\setminus }\overline{E}$.

• (ii) Suppose $0\ne x\in E$ and $\theta (x)\in [0,\pi )$. Then there exists an open interval I in $(0,+\infty )$ containing $\tau$ and $\alpha \in (\theta (x),\pi )$ such that $A(I)\cap S(\alpha )\subset E$.

• (iii) For each $0<\tau \in \pi (M),M_\tau$ is the union of two closed spherical arcs in $\mathbb {S}^1_\tau$ symmetric about the $x_1$-axis.

Proof

(i) We can find $\alpha \in (0,\theta (x))$ such that $\mathbb {S}^1_\tau {\setminus } S(\alpha )\subset \mathbb {R}^2{\setminus }\overline{E}$ as can be seen from definition (4.2). This latter set is compact so $\mathrm {dist}(\mathbb {S}^1_\tau {\setminus } S(\alpha ),\overline{E})>0$. This means that the $\varepsilon$-neighbourhood of $\mathbb {S}^1_\tau {\setminus } S(\alpha )$ is contained in $\mathbb {R}^2{\setminus }\overline{E}$ for $\varepsilon >0$ small. The claim follows. (ii) Again from (4.2) we can find $\alpha \in (\theta (x),\pi )$ such that $\overline{\mathbb {S}^1_\tau \cap S(\alpha )}\subset E$ and the assertion follows as before.

(iii) Suppose $x_1,x_2$ are distinct points in $M_\tau$ with $0\le \theta (x_1)<\theta (x_2)\le \pi$. Suppose y lies in the interior of the spherical arc joining $x_1$ and $x_2$. If $y\in \mathbb {R}^2{\setminus }\overline{E}$ then $x_2\in \mathbb {R}^2{\setminus }\overline{E}$ by (i) and hence $x_2\not \in M$. If $y\in E$ we obtain the contradiction that $x_1\in E$ by (ii). Therefore $y\in M$. We infer that the closed spherical arc joining $x_1$ and $x_2$ lies in $M_\tau$. The claim follows noting that $M_\tau$ is closed. $\square$

Lemma 5.3

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M. Let $x\in M$. Then

$$\begin{aligned} \liminf _{\overline{E}\ni y\rightarrow x}\Big \langle \frac{y-x}{|y-x|},n(x)\Big \rangle \ge 0. \end{aligned}$$

Proof

Assume for a contradiction that

$$\begin{aligned} \liminf _{\overline{E}\ni y\rightarrow x}\Big \langle \frac{y-x}{|y-x|},n(x)\Big \rangle \in [-1,0). \end{aligned}$$

There exists $\eta \in (0,1)$ and a sequence $(y_h)$ in E such that $y_h\rightarrow x$ as $h\rightarrow \infty$ and

$$\begin{aligned} \Big \langle \frac{y_h-x}{|y_h-x|},n(x)\Big \rangle&<-\eta \end{aligned}$$

(5.1)

for each $h\in \mathbb {N}$. Choose $\alpha \in (0,\pi /2)$ such that $\cos \alpha =\eta$. As M is $C^1$ there exists $r>0$ such that

$$\begin{aligned} B(x,r)\cap C(x,-n(x),\alpha )\cap E=\emptyset . \end{aligned}$$

By choosing h sufficiently large we can find $y_h\in B(x,r)$ with the additional property that $y_h\in C(x,-n(x),\alpha )$ by (5.1). We are thus led to a contradiction. $\square$

Lemma 5.4

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$. For each $0<\tau \in \pi (M)$,

• (i) $|\cos \sigma |$ is constant on $M_\tau$;

• (ii) $\cos \sigma =0$ on $M_\tau \cap \{x_2=0\}$;

• (iii) $\langle Ox,n(x)\rangle \le 0$ for $x\in M_\tau \cap H$

• (iv) $\cos \sigma \le 0$ on $M_\tau \cap H$;

and if $\cos \sigma \not \equiv 0$ on $M_\tau$ then

• (v) $\tau \in p(E)$;

• (vi) $M_\tau$ consists of two disjoint singletons in $\mathbb {S}^1_\tau$ symmetric about the $x_1$-axis;

• (vii) $L(\tau )\in (0,2\pi \tau )$;

• (viii) $M_\tau =\{(\tau \cos (L(\tau )/2\tau ),\pm \tau \sin (L(\tau )/2\tau )\}$.

Proof

(i) By Lemma 5.2, $M_\tau$ is the union of two closed spherical arcs in $\mathbb {S}^1_\tau$ symmetric about the $x_1$-axis. In case $M_\tau \cap \overline{H}$ consists of a singleton the assertion follows from Lemma 5.1. Now suppose that $M_\tau \cap \overline{H}$ consists of a spherical arc in $\mathbb {S}^1_\tau$ with non-empty interior. It can be seen that $\cos \sigma$ vanishes on the interior of this arc as $0=r_1^\prime =\cos \sigma _1$ in a local parametrisation by (2.9). By continuity $\cos \sigma =0$ on $M_\tau$. (ii) follows from Lemma 5.1. (iii) Let $x\in M_\tau \cap H$ so $\theta (x)\in (0,\pi )$. Then $S(\theta (x))\cap \mathbb {S}^1_\tau \subset \overline{E}$ as $\overline{E}$ is spherical cap symmetric. Then

$$\begin{aligned} 0\le \lim _{S(\theta (x))\cap \mathbb {S}^1_\tau \ni y\rightarrow x}\Big \langle \frac{y-x}{|y-x|},n(x)\Big \rangle =-\langle Ox,n(x)\rangle \end{aligned}$$

by Lemma 5.3. (iv) The adjoint transformation $O^\star$ represents rotation clockwise through $\pi /2$. Let $x\in M_\tau \cap H$. By (iii),

$$\begin{aligned} 0\ge \langle Ox,n(x)\rangle =\langle x,O^\star n(x)\rangle =\langle x,t(x)\rangle =\tau \cos \sigma (x) \end{aligned}$$

and this leads to the result. (v) As $\cos \sigma \not \equiv 0$ on $M_\tau$ we can find $x\in M_\tau \cap H$. We claim that $\mathbb {S}^1_\tau \cap S(\theta (x))\subset E$. For suppose that $y\in \mathbb {S}^1_\tau \cap S(\theta (x))$ but $y\not \in E$. We may suppose that $0\le \theta (y)<\theta (x)<\pi$. If $y\in \mathbb {R}^2{\setminus }\overline{E}$ then $x\in \mathbb {R}^2{\setminus }\overline{E}$ by Lemma 5.2. On the other hand, if $y\in M$ then the spherical arc in H joining y to x is contained in M again by Lemma 5.2. This arc also has non-empty interior in $\mathbb {S}^1_\tau$. Now $\cos \sigma =0$ on its interior so $\cos (\sigma (x))=0$ by (i) contradicting the hypothesis. A similar argument deals with (vi) and this together with (v) in turn entails (vii) and (viii). $\square$

Lemma 5.5

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$. Suppose that $0\in M$. Then

• (i) $(\sin \sigma )(0+)=0$;

• (ii) $(\cos \sigma )(0+)=-1$.

Proof

(i) Let $\gamma _1$ be a $C^1$ parametrisation of M in a neighbourhood of 0 with $\gamma _1(0)=0$ as above. Then $n(0)=n_1(0)=e_1$ and hence $t(0)=t_1(0)=-e_2$. By Taylor’s Theorem $\gamma _1(s)=\gamma _1(0)+t_1(0)s+o(s)=-e_2s+o(s)$ for $s\in I$. This means that $r_1(s)=|\gamma _1(s)|=s+o(s)$ and

$$\begin{aligned} \cos \theta _1=\frac{\langle e_1,\gamma _1\rangle }{r_1}=\frac{\langle e_1,\gamma _1\rangle }{s}\frac{s}{r_1}\rightarrow 0 \end{aligned}$$

as $s\rightarrow 0$ which entails that $(\cos \theta _1)(0-)=0$. Now $t_1$ is continuous on I so $t_1=-e_2+o(1)$ and $\cos \alpha _1=\langle e_1,t_1\rangle =o(1)$. We infer that $(\cos \alpha _1)(0-)=0$. By (2.11), $\cos \alpha _1=\cos \sigma _1\cos \theta _1-\sin \sigma _1\sin \theta _1$ on I and hence $(\sin \sigma _1)(0-)=0$. We deduce that $(\sin \sigma )(0+)=0$. Item (ii) follows from (i) and Lemma 5.4. $\square$

The set

$$\begin{aligned} \varOmega :=\pi \Big [(M{\setminus }\{0\})\cap \{\cos \sigma \ne 0\}\Big ] \end{aligned}$$

(5.2)

plays an important rôle in the proof of Theorem 1.1.

Lemma 5.6

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$. Then $\varOmega$ is an open set in $(0,+\infty )$.

Proof

Suppose $0<\tau \in \varOmega$. Choose $x\in M_\tau \cap \{\cos \sigma \ne 0\}$. Let $\gamma _1:I\rightarrow M$ be a local $C^1$ parametrisation of M in a neighbourhood of x such that $\gamma _1(0)=x$ as before. By shrinking I if necessary we may assume that $r_1\ne 0$ and $\cos \sigma _1\ne 0$ on I. Then the set $\{r_1(s):s\in I\}\subset \varOmega$ is connected and so an interval in $\mathbb {R}$ (see for example [25] Theorems 6.A and 6.B). By (2.9), $r_1^\prime (0)=\cos \sigma _1(0)=\cos \sigma (p)\ne 0$. This means that the set $\{r_1(s):s\in I\}$ contains an open interval about $\tau$. $\square$

6 Generalised (mean) curvature

Given a set E of finite perimeter in $\mathbb {R}^2$ the first variation $\delta V_f(Z)$ resp. $\delta P_f^+(Z)$ of weighted volume and perimeter along a time-dependent vector field Z are defined as in (2.13) and (2.14).

Proposition 6.1

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Let E be a bounded open set in $\mathbb {R}^2$ with $C^1$ boundary M. Let Z be a time-dependent vector field. Then

$$\begin{aligned} \delta P_f^+(Z)=\int _M f^\prime _+(\cdot ,Z_0) + f\mathrm {div}^M Z_0\,d\mathscr {H}^1 \end{aligned}$$

where $Z_0:=Z(0,\cdot )\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$.

Proof

The identity (3.2) holds for each $t\in I$ with M in place of $\mathscr {F}E$. The assertion follows on appealing to Lemma 2.3 and Lemma 2.4 with the help of the dominated convergence theorem. $\square$

Given $X,Y\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ let $\psi$ resp. $\chi$ stand for the 1-parameter group of $C^\infty$ diffeomorphisms of $\mathbb {R}^2$ associated to the vector fields X resp. Y as in (2.12). Let I be an open interval in $\mathbb {R}$ containing the point 0. Suppose that the function $\sigma :I\rightarrow \mathbb {R}$ is $C^1$. Define a flow via

$$\begin{aligned} \varphi :I\times \mathbb {R}^2\rightarrow \mathbb {R}^2; (t,x)\mapsto \chi (\sigma (t),\psi (t,x)). \end{aligned}$$

Lemma 6.2

The time-dependent vector field Z associated with the flow $\varphi$ is given by

$$\begin{aligned} Z(t,x)=\sigma ^\prime (t)Y(\chi (\sigma (t),\psi (t,x)))+d\chi (\sigma (t),\psi (t,x))X(\psi (t,x)) \end{aligned}$$

(6.1)

for $(t,x)\in I\times \mathbb {R}^2$ and satisfies (Z.1) and (Z.2).

Proof

For $t\in I$ and $x\in \mathbb {R}^2$ we compute using (2.12),

$$\begin{aligned} \partial _t\varphi (t,x) =(\partial _t\chi )(\sigma (t),\psi (t,x))\sigma ^\prime (t)+d\chi (\sigma (t),\psi (t,x))\partial _t\psi (t,x) \end{aligned}$$

and this gives (6.1). Put $K_1:=\mathrm {supp}[X],K_2:=\mathrm {supp}[Y]$ and $K:=K_1\cup K_2$. Then (Z.2) holds with this choice of K. $\square$

Let E be a bounded open set in $\mathbb {R}^2$ with $C^1$ boundary M. Define $\varLambda :=(M{\setminus }\{0\})\cap \{\cos \sigma =0\}$ and

$$\begin{aligned} \varLambda _1&:=\{x\in M:\mathscr {H}^1(\varLambda \cap B(x,\rho ))=\mathscr {H}^1(M\cap B(x,\rho ))\text { for some }\rho >0\}. \end{aligned}$$

(6.2)

For future reference put $\varLambda _1^{\pm }:=\varLambda _1\cap \{x\in M:\pm \langle x,n\rangle >0\}$.

Lemma 6.3

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Let E be a bounded open set in $\mathbb {R}^2$ with $C^{1,1}$ boundary M and suppose that $E{\setminus }\{0\}=E^{sc}$. Then

• (i) $\varLambda _1$ is a countable disjoint union of well-separated open circular arcs centred at 0;

• (ii) $\mathscr {H}^1(\overline{\varLambda _1}{\setminus }\varLambda _1)=0$;

• (iii) f is differentiable $\mathscr {H}^1$-a.e. on $M{\setminus }\overline{\varLambda _1}$.

The term well-separated in (i) means the following: if $\varGamma$ is an open circular arc in $\varLambda _1$ with $\varGamma \cap (\varLambda _1{\setminus }\varGamma )=\emptyset$ then $d(\varGamma ,\varLambda _1{\setminus }\varGamma )>0$.

Proof

(i) Let $x\in \varLambda _1$ and $\gamma _1:I\rightarrow M$ a $C^{1,1}$ parametrisation of M near x. By shrinking I if necessary we may assume that $\gamma _1(I)\subset M\cap B(x,\rho )$ with $\rho$ as in (6.2). So $\cos \sigma =0$ $\mathscr {H}^1$-a.e. on $\gamma _1(I)$ and hence $\cos \sigma _1=0$ a.e. on I. This means that $\cos \sigma _1=0$ on I as $\sigma _1\in C^{0,1}(I)$ and that $r_1$ is constant on I by (2.9). Using (2.10) it can be seen that $\gamma _1(I)$ is an open circular arc centred at 0. By compactness of M it follows that $\varLambda _1$ is a countable disjoint union of open circular arcs centred on 0. The well-separated property flows from the fact that M is $C^1$. (ii) follows as a consequence of this property. (iii) Let $x\in M{\setminus }\overline{\varLambda _1}$ and $\gamma _1:I\rightarrow M$ a $C^{1,1}$ parametrisation of M near x with properties as before. We assume that x lies in the upper half-plane H. By shrinking I if necessary we may assume that $\gamma _1(I)\subset (M{\setminus }\overline{\varLambda _1})\cap H$. Let $s_1,s_2, s_3\in I$ with $s_1<s_2<s_3$. Then $y:=\gamma _1(s_2)\in M{\setminus }\overline{\varLambda _1}$. So $\mathscr {H}^1(M\cap \{\cos \sigma \ne 0\}\cap B(y,\rho ))>0$ for each $\rho >0$. This means that for small $\eta >0$ the set $\gamma _1((s_2-\eta ,s_2+\eta ))\cap \{\cos \sigma \ne 0\}$ has positive $\mathscr {H}^1$-measure. Consequently, $r_1(s_3)-r_1(s_1)=\int _{s_1}^{s_3}\cos \sigma _1\,ds<0$ bearing in mind Lemma 5.4. This shows that $r_1$ is strictly decreasing on I. So h is differentiable a.e. on $r_1(I)\subset (0,+\infty )$ in virtue of the fact that h is convex and hence locally Lipschitz. This entails (iii). $\square$

Proposition 6.4

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a minimiser of (1.2). Assume that E is a bounded open set in $\mathbb {R}^2$ with $C^1$ boundary M and suppose that $E{\setminus }\{0\}=E^{sc}$. Suppose that $M{\setminus }\overline{\varLambda _1}\ne \emptyset$. Then there exists $\lambda \in \mathbb {R}$ such that for any $X\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$,

$$\begin{aligned} 0\le \int _M\Big \{f^\prime _+(\cdot ,X) + f\,\mathrm {div}^M X-\lambda f\langle n, X\rangle \Big \} \,d\mathscr {H}^1. \end{aligned}$$

Proof

Let $X\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$. Let $x\in M$ and $r>0$ such that $M\cap B(x,r)\subset M{\setminus }\overline{\varLambda _1}$. Choose $Y\in C^\infty _c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[Y]\subset B(x,r)$ as in Lemma 3.4. Let $\psi$ resp. $\chi$ stand for the 1-parameter group of $C^\infty$ diffeomorphisms of $\mathbb {R}^2$ associated to the vector fields X resp. Y as in (2.12). For each $(s,t)\in \mathbb {R}^2$ the set $\chi _s(\psi _t(E))$ is an open set in $\mathbb {R}^2$ with $C^1$ boundary and $\partial (\chi _s\circ \psi _t)(E)=(\chi _s\circ \psi _t)(M)$ by Lemma 2.1. Define

$$\begin{aligned} V(s,t)&:=V_f(\chi _t(\psi _s(E)))-V_f(E),\nonumber \\ P(s,t)&:=P_f(\chi _t(\psi _s(E))),\nonumber \end{aligned}$$

for $(s,t)\in \mathbb {R}^2$. We write $F=(\chi _t\circ \psi _s)(E)$. Arguing as in Proposition 3.2,

$$\begin{aligned} \partial _t V(s,t)&=\lim _{h\rightarrow 0}(1/h)\{V_f(\chi _h(F))-V_f(F)\} =\int _F\mathrm {div}(fY)\,dx\nonumber \\&=\int _E(\mathrm {div}(fY)\circ \chi _t\circ \psi _s)\,J_2 d(\chi _t\circ \psi _s)_x\,dx\nonumber \end{aligned}$$

with an application of the area formula (cf. [1] Theorem 2.71). This last varies continuously in (s, t). The same holds for partial differentiation with respect to s. Indeed, put $\eta :=\chi _t\circ \psi _s$. Then noting that $J_2d(\eta \circ \psi _h)=(J_2d\eta )\circ \psi _h J_2d\psi _h$ and using the dominated convergence theorem,

$$\begin{aligned} \partial _s V(s,t)&=\lim _{h\rightarrow 0}(1/h) \Big \{ V_f(\eta (\psi _h(E)))-V_f(\eta (E)) \Big \}\nonumber \\&=\lim _{h\rightarrow 0}(1/h) \Big \{ \int _E(f\circ \eta \circ \psi _h)J_2d(\eta \circ \psi _h)_x\,dx-\int _E(f\circ \eta )J_2d\eta _x\,dx \Big \}\nonumber \\&=\lim _{h\rightarrow 0}(1/h) \Big \{ \int _E[(f\circ \eta \circ \psi _h)-(f\circ \eta )]J_2d(\eta \circ \psi _h)_x\,dx\nonumber \\&\quad +\int _E(f\circ \eta )[(J_2d\eta \circ \psi _h-J_2d\eta ]J_2d\psi _h\,dx\nonumber \\&\quad +\int _E(f\circ \eta )J_2d\eta [J_2d\psi _h-1]\,dx \Big \}\nonumber \\&=\int _E\langle \nabla (f\circ \eta ),X\rangle J_2d\eta _x\,dx +\int _E(f\circ \eta )\langle \nabla J_2d\eta ,X\rangle \,dx\nonumber \\&\quad +\int _E(f\circ \eta )J_2d\eta \,\mathrm {div}\,X\,dx\nonumber \end{aligned}$$

where the explanation for the last term can be found in the proof of Proposition 3.2. In this regard we note that $d(d\chi _t)$ (for example) is continuous on $I\times \mathbb {R}^2$ (cf. [1] Theorem 3.3 and Exercise 3.2) and in particular $\nabla J_2d\chi _t$ is continuous on $I\times \mathbb {R}^2$. The expression above also varies continuously in (s, t) as can be seen with the help of the dominated convergence theorem. This means that $V(\cdot ,\cdot )$ is continuously differentiable on $\mathbb {R}^2$. Note that

$$\begin{aligned} \partial _tV(0,0)=\int _E\mathrm {div}(fY)\,dx=1 \end{aligned}$$

by choice of Y. By the implicit function theorem there exists $\eta >0$ and a $C^1$ function $\sigma :(-\eta ,\eta )\rightarrow \mathbb {R}$ such that $\sigma (0)=0$ and $V(s,\sigma (s))=0$ for $s\in (-\eta ,\eta )$; moreover,

$$\begin{aligned} \sigma ^\prime (0)&=-\partial _s V(0,0) =-\int _E\Big \{\langle \nabla f,X\rangle +f\,\mathrm {div}\,X\Big \}\,dx\nonumber \\&=-\int _E\mathrm {div}(fX)\,dx =\int _M f\,\langle n, X\rangle \,d\mathscr {H}^1\nonumber \end{aligned}$$

by the Gauss–Green formula (cf. [1] Theorem 3.36).

The mapping

$$\begin{aligned} \varphi :(-\eta ,\eta )\times \mathbb {R}^2\rightarrow \mathbb {R}^2;t\mapsto \chi (\sigma (t),\psi (t,x)) \end{aligned}$$

satisfies conditions (F.1)–(F.4) above with $I=(-\eta ,\eta )$ where the associated time-dependent vector field Z is given as in (6.1) and satisfies (Z.1) and (Z.2); moreover, $Z_0=Z(0,\cdot )=\sigma ^\prime (0)Y+X$. Note that $Z_0=X$ on $M{\setminus } B(x,r)$.

The mapping $I\rightarrow \mathbb {R};t\mapsto P_f(\varphi _t(E))$ is right-differentiable at $t=0$ as can be seen from Proposition 6.1 and has non-negative right-derivative there. By Proposition 6.1 and Lemma 6.3,

$$\begin{aligned} 0\le \delta P_f^+(Z)&=\int _{M} f^\prime _+(\cdot , Z_0)+ f\,\mathrm {div}^M Z_0\,d\mathscr {H}^1\nonumber \\&=\int _{M{\setminus }\overline{\varLambda _1}} f^\prime _+(\cdot , Z_0) + f\,\mathrm {div}^M Z_0\,d\mathscr {H}^1 \nonumber \\&\quad +\,\int _{\overline{\varLambda _1}} f^\prime _+(\cdot , X) + f\,\mathrm {div}^M X\,d\mathscr {H}^1 \nonumber \\&=\int _{M{\setminus }\overline{\varLambda _1}}\sigma ^\prime (0)\langle \nabla f,Y\rangle +\langle \nabla f,X\rangle \nonumber \\&\quad +\,\sigma ^\prime (0)\,f\,\mathrm {div}^M Y+f\,\mathrm {div}^M X\,d\mathscr {H}^1\nonumber \\&\quad +\int _{\overline{\varLambda _1}} f^\prime _+(\cdot , X) + f\,\mathrm {div}^M X\,d\mathscr {H}^1\nonumber \\&=\int _{M}f^\prime _+(\cdot , X) + f\,\mathrm {div}^M X\,d\mathscr {H}^1\nonumber \\&\quad +\,\sigma ^\prime (0)\int _{M}f^\prime _+(\cdot , Y)+ f\,\mathrm {div}^M Y\,d\mathscr {H}^1. \end{aligned}$$

(6.3)

The identity then follows upon inserting the expression for $\sigma ^\prime (0)$ above with $\lambda =-\int _{M}f^\prime _+(\cdot ,Y) + f\,\mathrm {div}^M Y\,d\mathscr {H}^1$. The claim follows for $X\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$ by a density argument. $\square$

Theorem 6.5

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a minimiser of (1.2). Assume that E is a bounded open set in $\mathbb {R}^2$ with $C^{1,1}$ boundary M and suppose that $E{\setminus }\{0\}=E^{sc}$. Suppose that $M{\setminus }\overline{\varLambda _1}\ne \emptyset$. Then there exists $\lambda \in \mathbb {R}$ such that

• (i) $k+\rho \sin \sigma +\lambda =0$ $\mathscr {H}^1$-a.e. on $M{\setminus }\overline{\varLambda _1}$;

• (ii) $\rho _--\lambda \le k\le \rho _+-\lambda$ on $\varLambda _1^+$;

• (iii) $-\rho _+-\lambda \le k\le -\rho _--\lambda$ on $\varLambda _1^-$.

The expression $k+\rho \sin \sigma$ is called the generalised (mean) curvature of M.

Proof

(i) Let $x\in M$ and $r>0$ such that $M\cap B(x,r)\subset M{\setminus }\overline{\varLambda _1}$. Choose $X\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$ with $\mathrm {supp}[X]\subset B(x,r)$. We know from Lemma 6.3 that f is differentiable $\mathscr {H}^1$-a.e. on $\mathrm {supp}[X]$. Let $\lambda$ be as in Proposition 6.4. Replacing X by $-X$ we deduce from Proposition 6.4 that

$$\begin{aligned} 0=\int _M\Big \{\langle \nabla f,X\rangle + f\,\mathrm {div}^M X-\lambda f\langle n, X\rangle \Big \} \,d\mathscr {H}^1. \end{aligned}$$

The divergence theorem on manifolds (cf. [1] Theorem 7.34) holds also for $C^{1,1}$ manifolds. So

$$\begin{aligned} \int _M\langle \nabla f, X\rangle + f\,\mathrm {div}^MX\,d\mathscr {H}^1&=\int _M \partial _nf\,\langle n,\,X\rangle +\langle \nabla ^M f,\,X\rangle +f\,\mathrm {div}^M\,X \,d\mathscr {H}^1\nonumber \\&=\int _M \partial _n f\,\langle n,\,X\rangle +\mathrm {div}^M(fX) \,d\mathscr {H}^1\nonumber \\&=\int _M \partial _n f\,\langle n,\,X\rangle -Hf\langle n,\,X\rangle \,d\mathscr {H}^1\nonumber \\&=\int _M fu \left\{ \partial _n \log f-H \right\} \,d\mathscr {H}^1\nonumber \end{aligned}$$

where $u=\langle n,X\rangle$. Combining this with the equality above we see that

$$\begin{aligned} \int _M uf \left\{ \partial _n\log f-H-\lambda \right\} \,d\mathscr {H}^1=0 \end{aligned}$$

for all $X\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$. This leads to the result.

(ii) Let $x\in M$ and $r>0$ such that $M\cap B(x,r)\subset \varLambda _1^+$. Let $\phi \in C^1(\mathbb {S}^1_r)$ with support in $\mathbb {S}^1_r\cap B(x,r)$. We can construct $X\in C^1_c(\mathbb {R}^2,\mathbb {R}^2)$ with the property that $X=\phi n$ on $M\cap B(x,r)$. By Lemma 2.4,

$$\begin{aligned} f^\prime _+(\cdot ,X)=fh^\prime _+(|x|,\mathrm {sgn}\langle x,X\rangle )|\langle n,X\rangle | =fh^\prime _+(|x|,\mathrm {sgn}\,\phi \langle x,n\rangle )|\phi | \nonumber \end{aligned}$$

on $\varLambda _1$. Let us assume that $\phi \ge 0$. As $\langle \cdot ,n\rangle >0$ on $\varLambda _1^+$ we have that $f^\prime _+(\cdot ,X)=f\phi h^\prime _+(|x|,+1)=f\phi \rho _+$ so by Proposition 6.4,

$$\begin{aligned} 0&\le \int _M\Big \{f^\prime _+(\cdot ,X) + f\,\mathrm {div}^M X-\lambda f\langle n, X\rangle \Big \} d\mathscr {H}^1\nonumber \\&=\int _M f\phi \Big \{\rho _+-k-\lambda \Big \} \,d\mathscr {H}^1.\nonumber \end{aligned}$$

We conclude that $\rho _+-k-\lambda \ge 0$ on $M\cap B(x,r)$. Now assume that $\phi \le 0$. Then $f^\prime _+(\cdot ,X)=-f\phi h^\prime _+(|x|,-1)=f\phi \rho _-$ so

$$\begin{aligned} 0&\le \int _M f\phi \Big \{\rho _--k-\lambda \Big \} \,d\mathscr {H}^1\nonumber \end{aligned}$$

and hence $\rho _--k-\lambda \le 0$ on $M\cap B(x,r)$. This shows (ii).

(iii) The argument is similar. Assume in the first instance that $\phi \ge 0$. Then $f^\prime _+(\cdot ,X)=f\phi h^\prime _+(|x|,-1)=-f\phi \rho _-$ so

$$\begin{aligned} 0\le \int _M f\phi \Big \{-\rho _--k-\lambda \Big \} \,d\mathscr {H}^1.\nonumber \end{aligned}$$

We conclude that $-\rho _--k-\lambda \ge 0$ on $M\cap B(x,r)$. Next suppose that $\phi \le 0$. Then $f^\prime _+(\cdot ,X)=-f\phi h^\prime _+(|x|,+1)=-f\phi \rho _+$ so

$$\begin{aligned} 0\le \int _M f\phi \Big \{-\rho _+-k-\lambda \Big \} \,d\mathscr {H}^1\nonumber \end{aligned}$$

and $-\rho _+-k-\lambda \le 0$ on $M\cap B(x,r)$. $\square$

Let E be an open set in $\mathbb {R}^2$ with $C^1$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$ and that $\varOmega$ is as in (5.2). Bearing in mind Lemma 5.4 we may define

$$\begin{aligned}&\theta _2:\varOmega \rightarrow (0,\pi );\tau \mapsto L(\tau )/2\tau ; \end{aligned}$$

(6.4)

$$\begin{aligned}&\gamma :\varOmega \rightarrow M;\tau \mapsto (\tau \cos \theta _2(\tau ),\tau \sin \theta _2(\tau )). \end{aligned}$$

(6.5)

The function

$$\begin{aligned} u:\varOmega \rightarrow [-1,1];\tau \mapsto \sin (\sigma (\gamma (\tau ))). \end{aligned}$$

(6.6)

plays a key role.

Theorem 6.6

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open with $C^{1,1}$ boundary M and that $E{\setminus }\{0\}=E^{sc}$. Suppose that $M{\setminus }\overline{\varLambda _1}\ne \emptyset$ and let $\lambda$ be as in Theorem 6.5. Then $u\in C^{0,1}(\varOmega )$ and

$$\begin{aligned} u^\prime +(1/\tau +\rho )u+\lambda =0 \end{aligned}$$

a.e. on $\varOmega$.

Proof

Let $\tau \in \varOmega$ and x a point in the open upper half-plane such that $x\in M_\tau$. There exists a $C^{1,1}$ parametrisation $\gamma _1:I\rightarrow M$ of M in a neighbourhood of x with $\gamma _1(0)=x$ as above. Put $u_1:=\sin \sigma _1$ on I. By shrinking the open interval I if necessary we may assume that $r_1:I\rightarrow r_1(I)$ is a diffeomorphism and that $r_1(I)\subset \subset \varOmega$. Note that $\gamma =\gamma _1\circ r_1^{-1}$ and $u=u_1\circ r_1^{-1}$ on $r_1(I)$. It follows that $u\in C^{0,1}(\varOmega )$. By (2.9),

$$\begin{aligned} u^\prime =\frac{\dot{u}_1}{\dot{r}_1}\circ r_1^{-1} =\dot{\sigma }_1\circ r_1^{-1} \end{aligned}$$

a.e. on $r_1(I)$. As $\dot{\alpha }_1=k_1$ a.e. on I and using the identity (2.10) we see that $\dot{\sigma }_1=\dot{\alpha }_1-\dot{\theta }_1=k_1-(1/r_1)\sin \sigma _1$ a.e on I. Thus,

$$\begin{aligned} u^\prime =k-(1/\tau )\sin (\sigma \circ \gamma )=k-(1/\tau )u \end{aligned}$$

a.e. on $r_1(I)$. By Theorem 6.5 there exists $\lambda \in \mathbb {R}$ such that $k+\rho \sin \sigma +\lambda =0$ $\mathscr {H}^1$-a.e. on M. So

$$\begin{aligned} u^\prime =-\rho (\tau )u-\lambda -(1/\tau )u =-(1/\tau +\rho (\tau ))u-\lambda \end{aligned}$$

a.e. on $r_1(I)$. The result follows. $\square$

Lemma 6.7

Suppose that E is a bounded open set in $\mathbb {R}^2$ with $C^1$ boundary M and that $E{\setminus }\{0\}=E^{sc}$. Then

• (i) $\theta _2\in C^1(\varOmega )$;

• (ii) $\theta _2^\prime =-\frac{1}{\tau }\frac{u}{\sqrt{1-u^2}}$ on $\varOmega$.

Proof

Let $\tau \in \varOmega$ and x a point in the open upper half-plane such that $x\in M_\tau$. There exists a $C^1$ parametrisation $\gamma _1:I\rightarrow M$ of M in a neighbourhood of x with $\gamma _1(0)=x$ as above. By shrinking the open interval I if necessary we may assume that $r_1:I\rightarrow r_1(I)$ is a diffeomorphism and that $r_1(I)\subset \subset \varOmega$. It then holds that

$$\begin{aligned} \theta _2=\theta _1\circ r_1^{-1}\text { and }\sigma \circ \gamma =\sigma _1\circ r_1^{-1} \end{aligned}$$

on $r_1(I)$ by choosing an appropriate branch of $\theta _1$. It follows that $\theta _2\in C^1(\varOmega )$. By the chain-rule, (2.10) and (2.9),

$$\begin{aligned} \theta _2^\prime= & {} \frac{\dot{\theta }_1}{\dot{r}_1}\circ r_1^{-1} =\left( \frac{1}{r_1}\tan \sigma _1\right) \circ r_1^{-1}\\= & {} (1/\tau )\tan (\sigma \circ \gamma ) \end{aligned}$$

on $r_1(I)$. By Lemma 5.4, $\cos (\sigma \circ \gamma )=-\sqrt{1-u^2}$ on $\varOmega$. This entails (ii). $\square$

7 Convexity

Lemma 7.1

Let E be a bounded open set in $\mathbb {R}^2$ with $C^{1,1}$ boundary M and assume that $E{\setminus }\{0\}=E^{sc}$. Put $d:=\sup \{|x|:x\in M\}>0$ and $b:=(d,0)$. Let $\gamma _1:I\rightarrow M$ be a $C^{1,1}$ parametrisation of M near b with $\gamma _1(0)=b$. Then

$$\begin{aligned} \lim _{\delta \downarrow 0}\Big \{\mathrm {ess\,sup}_{[-\delta ,\delta ]}k_1\Big \}\ge 1/d. \end{aligned}$$

Proof

For $s\in I$,

$$\begin{aligned} \gamma _1(s)=de_1+se_2+\int _0^s\Big \{\dot{\gamma }_1(u)-\dot{\gamma }_1(0)\Big \}\,du \end{aligned}$$

and

$$\begin{aligned} \dot{\gamma }_1(u)-\dot{\gamma }_1(0)=\int _0^u k_1 n_1\,dv \end{aligned}$$

by (2.6). By the Fubini–Tonelli Theorem,

$$\begin{aligned} \gamma _1(s)=de_1+se_2+\int _0^s(s-u)k_1(u)n_1(u)\,du =de_1+se_2+R(s) \end{aligned}$$

for $s\in I$. Assume for a contradiction that

$$\begin{aligned} \lim _{\delta \downarrow 0}\Big \{\mathrm {ess\,sup}_{[-\delta ,\delta ]}k_1\Big \}<l< 1/d \end{aligned}$$

for some $l\in \mathbb {R}$. Then we can find $\delta >0$ such that $k_1<l$ a.e. on $[-\delta ,\delta ]$. So

$$\begin{aligned} \langle R(s),e_1\rangle&=\int _0^s(s-u)k_1(u)\langle n_1(u),e_1\rangle \,du >-(1/2)s^2l(1+o(1)) \end{aligned}$$

as $s\downarrow 0$ and

$$\begin{aligned} r_1(s)^2-d^2&=2d\langle R(s),e_1\rangle +s^2+o(s^2)\nonumber \\&>-dls^2(1+o(1))+s^2+o(s^2) \end{aligned}$$

as $s\downarrow 0$. Alternatively,

$$\begin{aligned} \frac{r_1(s)^2-d^2}{s^2}&>1-dl+o(1). \end{aligned}$$

As $1-dl>0$ we can find $s\in I$ with $r_1(s)>d$, contradicting the definition of d. $\square$

Lemma 7.2

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open with $C^{1,1}$ boundary M and that $E{\setminus }\{0\}=E^{sc}$. Suppose that $M{\setminus }\overline{\varLambda _1}\ne \emptyset$. Then $\lambda \le -1/d-\rho _-(d)<0$ with $\lambda$ as in Theorem 6.5.

Proof

We write M as the disjoint union $M=(M{\setminus }\overline{\varLambda _1})\cup \overline{\varLambda _1}$. Let b be as above. Suppose that $b\in \overline{\varLambda _1}$. Then $b\in \varLambda _1$; in fact, $b\in \varLambda _1^-$. By Theorem 6.5, $\lambda \le -\rho _--k$ at b. By Lemma 7.1, $\lambda \le -1/d-\rho _-(d)$ upon considering an appropriate sequence in M converging to b. Now suppose that b lies in the open set $M{\setminus }\overline{\varLambda _1}$ in M. Let $\gamma _1:I\rightarrow M$ be a $C^{1,1}$ parametrisation of M near b with $\gamma _1(I)\subset M{\setminus }\overline{\varLambda _1}$. By Theorem 6.5, $k_1+\rho (r_1)\sin \sigma _1+\lambda =0$ a.e. on I. Now $\sin \sigma _1(s)\rightarrow 1$ as $s\rightarrow 0$. In light of Lemma 7.1, $1/d+\rho (d-)+\lambda \le 0$ and $\lambda \le -1/d-\rho _-(d)$. $\square$

Theorem 7.3

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open with $C^{1,1}$ boundary M and that $E{\setminus }\{0\}=E^{sc}$. Suppose that $M{\setminus }\overline{\varLambda _1}\ne \emptyset$. Then E is convex.

Proof

The proof runs along similar lines as [22] Theorem 6.5. By Theorem 6.5, $k+\rho \sin \sigma +\lambda =0$ $\mathscr {H}^1$-a.e. on $M{\setminus }\overline{\varLambda _1}$. By Lemma 7.2,

$$\begin{aligned} 0\le k+\rho _-(d)+\lambda \le k-1/d \end{aligned}$$

and $k\ge 1/d$ $\mathscr {H}^1$-a.e. on $M{\setminus }\overline{\varLambda _1}$. On $\varLambda _1^+,k\ge \rho _--\lambda \ge \rho _-+\rho _-(d)+1/d>0$; on the other hand, $k<0$ on $\varLambda _1^+$. So in fact $\varLambda _1^+=\emptyset$. If $b\in \varLambda _1^-$ then $k=1/d$. On $\varLambda _1^-\cap B(0,d),k\ge -\rho _+-\lambda \ge -\rho _++\rho _-(d)+1/d\ge 1/d$. Therefore $k\ge 1/d>0$ $\mathscr {H}^1$-a.e. on M. The set E is then convex by a modification of [26] Theorem 1.8 and Proposition 1.4. It is sufficient that the function f (here $\alpha _1$) in the proof of the former theorem is non-decreasing. $\square$

8 A reverse Hermite–Hadamard inequality

Let $0\le a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let h be a primitive of $\rho$ on [a, b] so that $h\in C^{0,1}([a,b])$ and introduce the functions

$$\begin{aligned}&\mathtt {f}:[a,b]\rightarrow \mathbb {R};x\mapsto e^{h(x)}; \end{aligned}$$

(8.1)

$$\begin{aligned}&g:[a,b]\rightarrow \mathbb {R};x\mapsto x\mathtt {f}(x). \end{aligned}$$

(8.2)

Then

$$\begin{aligned} g^\prime =(1/x+\rho )g=\mathtt {f}+g\rho \end{aligned}$$

(8.3)

a.e. on (a, b). Define

$$\begin{aligned} m=m(\rho ,a,b):=\frac{g(b)-g(a)}{\int _a^b g\,dt}. \end{aligned}$$

(8.4)

If $\rho$ takes the constant value $\mathbb {R}\ni \lambda \ge 0$ on [a, b] we use the notation $m(\lambda ,a,b)$ and we write $m_0=m(0,a,b)$. A computation gives

$$\begin{aligned} m_0=m(0,a,b)=A(a,b)^{-1} \end{aligned}$$

(8.5)

where $A(a,b):=(a+b)/2$ stands for the arithmetic mean of a and b.

Lemma 8.1

Let $0\le a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Then $m_0\le m$.

Proof

Note that g is convex on [a, b] as can be seen from (8.3). By the Hermite-Hadamard inequality (cf. [15, 17]),

$$\begin{aligned} \frac{1}{b-a}\int _a^b g\,dt&\le \frac{g(a)+g(b)}{2}. \end{aligned}$$

(8.6)

The inequality $(b-a)(g(a)+g(b))\le (a+b)(g(b)-g(a))$ entails

$$\begin{aligned} \int _a^b g\,dt\le \frac{a+b}{2}(g(b)-g(a)) \end{aligned}$$

and the result follows on rearrangement. $\square$

Lemma 8.2

Let $0\le a<b<+\infty$ and $\lambda >0$. Then $m(\lambda ,a,b)<\lambda +A(a,b)^{-1}$.

Proof

First suppose that $\lambda =1$ and take $h:[a,b]\rightarrow \mathbb {R};t\mapsto t$. In this case,

$$\begin{aligned} \int _a^b g\,dt=\int _a^b te^t\,dt=(b-1)e^b-(a-1)e^a \end{aligned}$$

and

$$\begin{aligned} m(1,a,b)=\frac{be^b-ae^a}{(b-1)e^b-(a-1)e^a}. \end{aligned}$$

The inequality in the statement is equivalent to

$$\begin{aligned} (a+b)(be^b-ae^a)<((b-1)e^b-(a-1)e^a)(2+a+b) \end{aligned}$$

which in turn is equivalent to the statement $\tanh [(b-a)/2]<(b-a)/2$ which holds for any $b>a$.

For $\lambda >0$ take $h:[a,b]\rightarrow \mathbb {R};t\mapsto \lambda t$. Substitution gives

$$\begin{aligned} \int _a^b g\,dt= & {} (1/\lambda )^2[(\lambda b-1)e^{\lambda b}-(\lambda a-1)e^{\lambda a}] \text { and } \\ g(b)-g(a)= & {} (1/\lambda )[\lambda be^{\lambda b}-\lambda ae^{\lambda a}] \end{aligned}$$

so from above

$$\begin{aligned} m(\lambda ,a,b)=\lambda m(1,\lambda a,\lambda b) <\lambda \Big \{1+A(\lambda a,\lambda b)^{-1}\Big \} =\lambda +A(a,b)^{-1}. \end{aligned}$$

$\square$

Theorem 8.3

Let $0\le a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Then

• (i) $m(\rho ,a,b)\le \rho (b-)+A(a,b)^{-1}$;

• (ii) equality holds if and only if $\rho \equiv 0$ on [a, b).

Proof

(i) Define $h:=\int _a^\cdot \rho \,d\tau$ on [a, b] so that $h^\prime =\rho$ a.e. on (a, b). Define $h_1:[a,b]\rightarrow \mathbb {R};t\mapsto h(b)-\rho (b-)(b-t)$. Then $h_1(b)=h(b),h_1^\prime =\rho (b-)\ge \rho =h^\prime$ a.e. on (a, b) and hence $h\ge h_1$ on [a, b]. We derive

$$\begin{aligned} \int _a^b g\,dt=\int _a^b te^{h(t)}\,dt\ge \int _a^b te^{h_1(t)}\,dt=\int _a^b g_1\,dt \end{aligned}$$

and

$$\begin{aligned} g(b)-g(a)= & {} be^{h(b)}-ae^{h(a)}=be^{h_1(b)}-ae^{h(a)} \\\le & {} be^{h_1(b)}-ae^{h_1(a)}=g_1(b)-g_1(a) \end{aligned}$$

with obvious notation. This entails that $m(\rho ,a,b)\le m(\rho (b-),a,b)$ and the result follows with the help of Lemma 8.2.

(ii) Suppose that $\rho \not \equiv 0$ on [a, b). If $\rho$ is constant on [a, b] the assertion follows from Lemma 8.2. Assume then that $\rho$ is not constant on [a, b). Then $h\not \equiv h_1$ on [a, b] in the above notation and $\int _a^b te^{h(t)}\,dt>\int _a^b te^{h_1(t)}\,dt$ which entails strict inequality in (i). $\square$

With the above notation define

$$\begin{aligned} \hat{m}=\hat{m}(\rho ,a,b):=\frac{g(a)+g(b)}{\int _a^b g\,dt}. \end{aligned}$$

(8.7)

A computation gives

$$\begin{aligned} \hat{m}_0:=\hat{m}(0,a,b)=\frac{2}{b-a}. \end{aligned}$$

(8.8)

Lemma 8.4

Let $0\le a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Then $\hat{m}\ge \hat{m}_0$.

Proof

This follows by the Hermite-Hadamard inequality (8.6). $\square$

We prove a reverse Hermite-Hadamard inequality.

Theorem 8.5

Let $0\le a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Then

• (i) $(b-a)\hat{m}(\rho ,a,b)\le 2+a\rho (a+)+b\rho (b-)$;

• (ii) equality holds if and only if $\rho \equiv 0$ on [a, b).

This last inequality can be written in the form

$$\begin{aligned} \frac{g(a)+g(b)}{2+a\rho (a+)+b\rho (b-)}&\le \frac{1}{b-a}\int _a^b g\,dt;\nonumber \end{aligned}$$

comparing with (8.6) justifies naming this a reverse Hermite-Hadamard inequality.

Proof

(i) We assume in the first instance that $\rho \in C^1((a,b))$. We prove the above result in the form

$$\begin{aligned} \int _a^b g\,dt\ge (b-a)\frac{g(a)+g(b)}{2+a\rho (a)+b\rho (b)}. \end{aligned}$$

(8.9)

Put

$$\begin{aligned} w:=\frac{(t-a)(g(a)+g)}{2+a\rho (a)+t\rho } \end{aligned}$$

for $t\in [a,b]$ so that

$$\begin{aligned} \int _a^b w^\prime \,dt=(b-a)\frac{g(a)+g(b)}{2+a\rho (a)+b\rho (b)}. \end{aligned}$$

Then using (8.3),

$$\begin{aligned} w^\prime&=\frac{(g(a)+g+(t-a)g^\prime )(2+a\rho (a)+t\rho )-(t-a)(g(a)+g)(\rho +t\rho ^\prime )}{(2+a\rho (a)+t\rho )^2}\nonumber \\&=\frac{(g(a)-ag^\prime +(2+t\rho )g)(2+a\rho (a)+t\rho )-(t-a)(g(a)+g)(\rho +t\rho ^\prime )}{(2+a\rho (a)+t\rho )^2}\nonumber \\&=\frac{(2+t\rho )(2+a\rho (a)+t\rho )}{(2+a\rho (a)+t\rho )^2}g\nonumber \\&\quad +\,\frac{(g(a)-ag^\prime )(2+a\rho (a)+t\rho )-(t-a)(g(a)+g)(\rho +t\rho ^\prime )}{(2+a\rho (a)+t\rho )^2}\nonumber \\&\le g -\frac{2g(a)}{(2+a\rho (a)+b\rho (b))^2}(t-a)\rho \nonumber \\&\le g \end{aligned}$$

(8.10)

on (a, b) as

$$\begin{aligned} g(a)-ag^\prime =a(\mathtt {f}(a)-(1/t+\rho )g)=a(\mathtt {f}(a)-\mathtt {f}-\rho g)\le 0. \end{aligned}$$

An integration over [a, b] gives the result.

Let us now assume that $\rho \ge 0$ is a non-decreasing bounded function on [a, b]. Extend $\rho$ to $\mathbb {R}$ via

$$\begin{aligned} \widetilde{\rho }(t):= \left\{ \begin{array}{lcl} \rho (a+) &{} \text { for } &{} t\in (-\infty ,a];\\ \rho (t) &{} \text { for } &{} t\in (a,b];\\ \rho (b-) &{} \text { for } &{} t\in (b,+\infty );\\ \end{array} \right. \end{aligned}$$

for $t\in \mathbb {R}$. Let $(\psi _\varepsilon )_{\varepsilon >0}$ be a family of mollifiers (see e.g. [1] 2.1) and set $\widetilde{\rho }_\varepsilon :=\widetilde{\rho }\star \psi _\varepsilon$ on $\mathbb {R}$ for each $\varepsilon >0$. Then $\widetilde{\rho }_\varepsilon \in C^\infty (\mathbb {R})$ and is non-decreasing on $\mathbb {R}$ for each $\varepsilon >0$. Put $\rho _\varepsilon :=\widetilde{\rho }_\varepsilon \mid _{[a,b]}$ for each $\varepsilon >0$. Then $(\rho _\varepsilon )_{\varepsilon >0}$ converges to $\rho$ in $L^1((a,b))$ by [1] 2.1 for example. Note that $h_{\varepsilon }:=\int _a^\cdot \rho _\varepsilon \,dt\rightarrow h$ pointwise on [a, b] as $\varepsilon \downarrow 0$ and that $(h_\varepsilon )$ is uniformly bounded on [a, b]. Moreover, $\rho _\varepsilon (a)\rightarrow \rho (a+)$ and $\rho _\varepsilon (b)\rightarrow \rho (b-)$ as $\varepsilon \downarrow 0$. By the above result,

$$\begin{aligned} (b-a)\hat{m}(\rho _{\varepsilon },a,b)\le 2+a\rho _{\varepsilon }(a)+b\rho _{\varepsilon }(b) \end{aligned}$$

for each $\varepsilon >0$. The inequality follows on taking the limit $\varepsilon \downarrow 0$ with the help of the dominated convergence theorem.

(ii) We now consider the equality case. We claim that

$$\begin{aligned}&(b-a)\frac{g(a)+g(b)}{2+a\rho (a+)+b\rho (b-)}\le \int _a^b g\,dt\nonumber \\&\quad -\frac{2g(a)}{(2+a\rho (a+)+b\rho (b-))^2}\int _a^b(t-a)\rho \,dt; \end{aligned}$$

(8.11)

this entails the equality condition in (ii). First suppose that $\rho \in C^1((a,b))$. In this case the inequality in (8.10) implies (8.11) upon integration. Now suppose that $\rho \ge 0$ is a non-decreasing bounded function on [a, b]. Then (8.11) holds with $\rho _\varepsilon$ in place of $\rho$ for each $\varepsilon >0$. The inequality for $\rho$ follows by the dominated convergence theorem. $\square$

9 Comparison theorems for first-order differential equations

Let $\mathscr {L}$ stand for the collection of Lebesgue measurable sets in $[0,+\infty )$. Define a measure $\mu$ on $([0,+\infty ),\mathscr {L})$ by $\mu (dx):=(1/x)\,dx$. Let $0\le a<b<+\infty$. Suppose that $u:[a,b]\rightarrow \mathbb {R}$ is an $\mathscr {L}^1$-measurable function with the property that

$$\begin{aligned} \mu (\{u>t\})&<+\infty \text { for each }t>0. \end{aligned}$$

(9.1)

The distribution function $\mu _u:(0,+\infty )\rightarrow [0,+\infty )$ of u with respect to $\mu$ is given by

$$\begin{aligned} \mu _u(t):=\mu (\{u>t\})\text { for }t>0. \end{aligned}$$

Note that $\mu _u$ is right-continuous and non-increasing on $(0,\infty )$ and $\mu _u(t)\rightarrow 0$ as $t\rightarrow \infty$.

Let u be a Lipschitz function on [a, b]. Define

$$\begin{aligned} Z_1:=\{u\text { differentiable and }u^\prime =0\}, Z_2:=\{u\text { not differentiable}\}\text { and }Z:=Z_1\cup Z_2. \end{aligned}$$

By [1] Lemma 2.96, $Z\cap \{u=t\}=\emptyset$ for $\mathscr {L}^1$-a.e. $t\in \mathbb {R}$ and hence $N:=u(Z)\subset \mathbb {R}$ is $\mathscr {L}^1$-negligible. We make use of the coarea formula ( [1] Theorem 2.93 and (2.74)),

$$\begin{aligned} \int _{[a,b]}\phi |u^\prime |\,dx=\int _{-\infty }^\infty \int _{\{u=t\}}\phi \,d\mathscr {H}^{0}\,dt \end{aligned}$$

(9.2)

for any $\mathscr {L}^1$-measurable function $\phi :[a,b]\rightarrow [0,\infty ]$.

Lemma 9.1

Let $0\le a<b<+\infty$ and u a Lipschitz function on [a, b]. Then

• (i) $\mu _u\in \mathrm {BV}_{\mathrm {loc}}((0,+\infty ))$;

• (ii) $D\mu _u=-u_\sharp \mu$;

• (iii) $D\mu _u^a=D\mu _u|\!\_((0,+\infty ){\setminus } N)$;

• (iv) $D\mu _u^s=D\mu _u|\!\_N$;

• (v) $A:=\Big \{t\in (0,+\infty ):\mathscr {L}^1(Z\cap \{u=t\})>0\Big \}$ is the set of atoms of $D\mu _u$ and $D\mu _u^j=D\mu _u|\!\_A$;

• (vi) $\mu _u$ is differentiable $\mathscr {L}^1$-a.e. on $(0,+\infty )$ with derivative given by

  $$\begin{aligned} \mu _u^\prime (t)=-\int _{\{u=t\}{\setminus } Z}\frac{1}{|u^\prime |}\,\frac{d\mathscr {H}^{0}}{\tau } \end{aligned}$$

  for $\mathscr {L}^1$-a.e. $t\in (0,+\infty )$;

• (vii) $\mathrm {Ran}(u)\cap [0,+\infty )=\mathrm {supp}(D\mu _u)$.

The notation above $D\mu _u^a,D\mu _u^s,D\mu _u^j$ stands for the absolutely continuous resp. singular resp. jump part of the measure $D\mu _u$ (see [1] 3.2 for example).

Proof

For any $\varphi \in C^\infty _c((0,+\infty ))$ with $\mathrm {supp}[\varphi ]\subset (\tau ,+\infty )$ for some $\tau >0$,

$$\begin{aligned} \int _0^\infty \mu _u\varphi ^\prime \,dt&=\int _{[a,b]}\varphi \circ u\,d\mu \nonumber \\&=\int _{[a,b]}\chi _{\{u>\tau \}}\varphi \circ u\,d\mu \end{aligned}$$

(9.3)

by Fubini’s theorem; so $\mu _u\in \mathrm {BV}_{\mathrm {loc}}((0,+\infty ))$ and $D\mu _u$ is the push-forward of $\mu$ under $u,D\mu _u=-u_\sharp \mu$ (cf. [1] 1.70). By (9.2),

$$\begin{aligned} D\mu _u|\!\_((0,+\infty ){\setminus } N)(A)= & {} -\mu (\{u\in A\}{\setminus } Z)\\= & {} -\int _A\int _{\{u=t\}{\setminus } Z}\frac{1}{|u^\prime |}\,\frac{d\mathcal {H}^{0}}{\tau }\,dt \end{aligned}$$

for any $\mathscr {L}^1$-measurable set A in $(0,+\infty )$. In light of the above, we may identify $D\mu _u^a=D\mu _u|\!\_((0,+\infty ){\setminus } N)$ and $D\mu _u^s=D\mu _{u}|\!\_N$. The set of atoms of $D\mu _{u}$ is defined by $A:=\{t\in (0,+\infty ):D\mu _u(\{t\})\ne 0\}$. For $t>0$,

$$\begin{aligned} D\mu _u(\{t\})= & {} D\mu _u^s(\{t\})=(D\mu _u|\!\_N)((\{t\})\\= & {} -u_\sharp \mu (N\cap \{t\})=-\mu (Z\cap \{u=t\}) \end{aligned}$$

and this entails (v). The monotone function $\mu _u$ is a good representative within its equivalence class and is differentiable $\mathscr {L}^1$-a.e. on $(0,+\infty )$ with derivative given by the density of $D\mu _{u}$ with respect to $\mathscr {L}^1$ by [1] Theorem 3.28. Item (vi) follows from (9.2) and (iii). Item (vii) follows from (ii).$\square$

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $\eta \in \{\pm 1\}^2$. We study solutions to the first-order linear ordinary differential equation

$$\begin{aligned} u^\prime +(1/x+\rho )u+\lambda =0\text { a.e. on }(a,b)\text { with }u(a)=\eta _1\text { and }u(b)=\eta _2 \end{aligned}$$

(9.4)

where $u\in C^{0,1}([a,b])$ and $\lambda \in \mathbb {R}$. In case $\rho \equiv 0$ on [a, b] we use the notation $u_0$.

Lemma 9.2

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $\eta \in \{\pm 1\}^2$. Then

• (i) there exists a solution $(u,\lambda )$ of (9.4) with $u\in C^{0,1}([a,b])$ and $\lambda =\lambda _\eta \in \mathbb {R}$;

• (ii) the pair $(u,\lambda )$ in (i) is unique;

• (iii) $\lambda _\eta$ is given by

  $$\begin{aligned} -\lambda _{(1,1)}=\lambda _{(-1,-1)}=m;\,\lambda _{(1,-1)}=-\lambda _{(-1,1)}=\hat{m}; \end{aligned}$$

• (iv) if $\eta =(1,1)$ or $\eta =(-1,-1)$ then u is uniformly bounded away from zero on [a, b].

Proof

(i) For $\eta =(1,1)$ define $u:[a,b]\rightarrow \mathbb {R}$ by

$$\begin{aligned} u(t):=\frac{m\int _a^t g\,ds+g(a)}{g(t)}\text { for }t\in [a,b] \end{aligned}$$

(9.5)

with m as in (8.4). Then $u\in C^{0,1}([a,b])$ and satisfies (9.4) with $\lambda =-m$. For $\eta =(1,-1)$ set $u=(-\hat{m}\int _a^\cdot g\,ds+g(a))/g$ with $\lambda =\hat{m}$. The cases $\eta =(-1,-1)$ and $\eta =(-1,1)$ can be dealt with using linearity. (ii) We consider the case $\eta =(1,1)$. Suppose that $(u_1,\lambda _1)$ resp. $(u_2,\lambda _2)$ solve (9.4). By linearity $u:=u_1-u_2$ solves

$$\begin{aligned} u^\prime +(1/x+\rho )u+\lambda =0\text { a.e. on }(a,b) \text { with }u(a)=u(b)=0 \end{aligned}$$

where $\lambda =\lambda _1-\lambda _2$. An integration gives that $u=(-\lambda \int _a^\cdot g\,ds+c)/g$ for some constant $c\in \mathbb {R}$ and the boundary conditions entail that $\lambda =c=0$. The other cases are similar. (iii) follows as in (i). (iv) If $\eta =(1,1)$ then $u>0$ on [a, b] from (9.5) as $m>0$. $\square$

The boundary condition $\eta _1\eta _2=-1$.

Lemma 9.3

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $(u,\lambda )$ solve (9.4) with $\eta =(1,-1)$. Then

• (i) there exists a unique $c\in (a,b)$ with $u(c)=0$;

• (ii) $u^\prime <0$ a.e. on [a, c] and u is strictly decreasing on [a, c];

• (iii) $D\mu _u^s=0$.

Proof

(i) We first observe that $u^\prime \le -\hat{m}<0$ a.e. on $\{u\ge 0\}$ in view of (9.4). Suppose $u(c_1)=u(c_2)=0$ for some $c_1,c_2\in (a,b)$ with $c_1<c_2$. We may assume that $u\ge 0$ on $[c_1,c_2]$. This contradicts the above observation. Item (ii) is plain. For any $\mathscr {L}^1$-measurable set B in $(0,+\infty ),D\mu _u^s(B)=\mu (\{u\in B\}\cap Z)=0$ using Lemma 9.1 and (ii). $\square$

Lemma 9.4

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $(u,\lambda )$ solve (9.4) with $\eta =(1,-1)$. Assume that

• (a) u is differentiable at both a and b and that (9.4) holds there;

• (b) $u^\prime (a)<0$ and $u^\prime (b)<0$;

• (c) $\rho$ is differentiable at a and b.

Put $v:=-u$. Then

• (i) $\int _{\{v=1\}{\setminus } Z_v}\frac{1}{|v^\prime |}\frac{d\mathscr {H}^0}{\tau } \ge \int _{\{u=1\}{\setminus } Z_u}\frac{1}{|u^\prime |}\frac{d\mathscr {H}^0}{\tau }$;

• (ii) equality holds if and only if $\rho \equiv 0$ on [a, b).

Proof

First, $\{u=1\}=\{a\}$ by Lemma 9.3. Further $0<-au^\prime (a)=1+a[\hat{m}+\rho (a)]$ from (9.4). On the other hand $\{v=1\}\supset \{b\}$ and $0<bv^\prime (b)=-1+b[\hat{m}-\rho (b)]$. Thus

$$\begin{aligned}&\int _{\{v=1\}{\setminus } Z_v}\frac{1}{|v^\prime |}\frac{d\mathscr {H}^0}{\tau }- \int _{\{u=1\}{\setminus } Z_u}\frac{1}{|u^\prime |}\frac{d\mathscr {H}^0}{\tau }\nonumber \\&\quad \ge \frac{1}{-1+b[\hat{m}-\rho (b)]}-\frac{1}{1+a[\hat{m}+\rho (a)]}. \end{aligned}$$

By Theorem 8.5, $0\le 2+(a-b)\hat{m}+a\rho (a)+b\rho (b)$, noting that $\rho (a)=\rho (a+)$ in virtue of (c) and similarly at b. A rearrangement leads to the inequality. The equality assertion follows from Theorem 8.5. $\square$

Theorem 9.5

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Suppose that $(u,\lambda )$ solves (9.4) with $\eta =(1,-1)$ and set $v:=-u$. Assume that $u>-1$ on [a, b). Then

• (i) $-\mu _v^\prime \ge -\mu _u^\prime$ for $\mathscr {L}^1$-a.e. $t\in (0,1)$;

• (ii) if $\rho \not \equiv 0$ on [a, b) then there exists $t_0\in (0,1)$ such that $-\mu _v^\prime >-\mu _u^\prime$ for $\mathscr {L}^1$-a.e. $t\in (t_0,1)$;

• (iii) for $t\in [-1,1]$,

  $$\begin{aligned} \mu _{u_0}(t)=\log \Big \{\frac{-(b-a)t+\sqrt{(b-a)^2t^2+4ab}}{2a}\Big \} \end{aligned}$$

  and $\mu _{v_0}=\mu _{u_0}$ on $[-1,1]$;

in obvious notation.

Proof

(i) The set

$$\begin{aligned} Y_u:=Z_{2,u}\cup \Big (\{u^\prime +(1/x+\rho )u+\lambda \ne 0\}{\setminus } Z_{2,u}\Big )\cup \{\rho \text { not differentiable}\}\subset [a,b] \end{aligned}$$

(in obvious notation) is a null set in [a, b] and likewise for $Y_v$. By [1] Lemma 2.95 and Lemma 2.96, $\{u=t\}\cap (Y_u\cup Z_{1,u})=\emptyset$ for a.e. $t\in (0,1)$ and likewise for the function v. Let $t\in (0,1)$ and assume that $\{u=t\}\cap (Y_u\cup Z_{1,u})=\emptyset$ and $\{v=t\}\cap (Y_v\cup Z_{1,v})=\emptyset$. Put $c:=\max \{u\ge t\}$. Then $c\in (a,b),\{u>t\}=[a,c)$ by Lemma 9.3 and u is differentiable at c with $u^\prime (c)<0$. Put $d:=\max \{v\le t\}=\max \{u\ge -t\}$. As u is continuous on [a, b] it holds that $a<c<d<b$. Moreover, $u^\prime (d)<0$ as $v(d)=t$ and $d\not \in Z_v$. Put $\widetilde{u}:=u/t$ and $\widetilde{v}:=v/t$ on [c, d]. Then

$$\begin{aligned} \widetilde{u}^\prime +(1/\tau +\rho )\widetilde{u}+\hat{m}/t&=0\text { a.e. on }(c,d)\text { and }\widetilde{u}(c)=-\widetilde{u}(d)=1;\nonumber \\ \widetilde{v}^\prime +(1/\tau +\rho )\widetilde{v}-\hat{m}/t&=0\text { a.e. on }(c,d)\text { and }-\widetilde{v}(c)=\widetilde{v}(d)=1.\nonumber \end{aligned}$$

By Lemma 9.4,

$$\begin{aligned} \int _{\{v=t\}{\setminus } Z_v}\frac{1}{|v^\prime |}\frac{d\mathscr {H}^0}{\tau }&\ge \int _{[c,d]\cap \{v=t\}{\setminus } Z_v}\frac{1}{|v^\prime |}\frac{d\mathscr {H}^0}{\tau }\\&=(1/t)\int _{[c,d]\cap \{\widetilde{v}=1\}{\setminus } Z_v}\frac{1}{|\widetilde{v}^\prime |}\frac{d\mathscr {H}^0}{\tau }\nonumber \\&\ge (1/t)\int _{[c,d]\cap \{\widetilde{u}=1\}{\setminus } Z_u}\frac{1}{|\widetilde{u}^\prime |}\frac{d\mathscr {H}^0}{\tau }\nonumber \\&=\int _{\{u=t\}{\setminus } Z_u}\frac{1}{|u^\prime |}\frac{d\mathscr {H}^0}{\tau }.\nonumber \end{aligned}$$

By Lemma 9.1,

$$\begin{aligned} -\mu _u^\prime (t)=\int _{\{u=t\}{\setminus } Z_u}\frac{1}{|u^\prime |}\frac{d\mathscr {H}^0}{\tau } \end{aligned}$$

for $\mathscr {L}^1$-a.e. $t\in (0,1)$ and a similar formula holds for v. The assertion in (i) follows.

(ii) Assume that $\rho \not \equiv 0$ on [a, b). Put $\alpha :=\inf \{\rho >0\}\in [a,b)$. Note that $\max \{v\le t\}\rightarrow b$ as $t\uparrow 1$ as $v<1$ on [a, b) by assumption. Choose $t_0\in (0,1)$ such that $\max \{v\le t_0\}>\alpha$. Then for $t>t_0$,

$$\begin{aligned} a<\max \{u\ge t\}<\max \{u\ge -t_0\}=\max \{v\le t_0\}<\max \{v\le t\}<d; \end{aligned}$$

that is, the interval [c, d] with c, d as described above intersects $(\alpha ,b]$. So for $\mathscr {L}^1$-a.e. $t\in (t_0,1)$,

$$\begin{aligned} \int _{\{v=t\}{\setminus } Z_v}\frac{1}{|v^\prime |}\frac{d\mathscr {H}^0}{\tau }>\int _{\{u=t\}{\setminus } Z_u}\frac{1}{|u^\prime |}\frac{d\mathscr {H}^0}{\tau }. \end{aligned}$$

by the equality condition in Lemma 9.4. The conclusion follows from the representation of $\mu _u$ resp. $\mu _v$ in Lemma 9.1.

(iii) A direct computation gives

$$\begin{aligned} u_0(\tau )=\frac{1}{b-a}\Big \{-\tau +\frac{ab}{\tau }\Big \} \end{aligned}$$

for $\tau \in [a,b]$; $u_0$ is strictly decreasing on its domain. This leads to the formula in (iii). A similar computation gives

$$\begin{aligned} \mu _{v_0}(t)=\log \Big \{\frac{2b}{(b-a)t+\sqrt{(b-a)^2t^2+4ab}}\Big \} \end{aligned}$$

for $t\in [-1,1]$. Rationalising the denominator results in the stated equality. $\square$

Corollary 9.6

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Suppose that $(u,\lambda )$ solves (9.4) with $\eta =(1,-1)$ and set $v:=-u$. Assume that $u>-1$ on [a, b). Then

• (i) $\mu _u(t)\le \mu _v(t)$ for each $t\in (0,1)$;

• (ii) if $\rho \not \equiv 0$ on [a, b) then $\mu _u(t)<\mu _v(t)$ for each $t\in (0,1)$.

Proof

(i) By [1] Theorem 3.28 and Lemma 9.3,

$$\begin{aligned} \mu _u(t)= & {} \mu _u(t)-\mu _u(1)=-D\mu _u((t,1])\\= & {} -D\mu _u^a((t,1])-D\mu _u^s((t,1])\\= & {} -\int _{(t,1]}\mu _u^\prime \,ds \end{aligned}$$

for each $t\in (0,1)$ as $\mu _u(1)=0$. On the other hand,

$$\begin{aligned} \mu _v(t)= & {} \mu _v(1)+(\mu _v(t)-\mu _v(1)) =\mu _v(1)-D\mu _v((t,1])\\= & {} \mu _v(1)-\int _{(t,1]}\mu _v^\prime \,ds-D\mu _v^s((t,1]) \end{aligned}$$

for each $t\in (0,1)$. The claim follows from Theorem 9.5 noting that $D\mu _v^s((t,1])\le 0$ as can be seen from Lemma 9.1. Item (ii) follows from Theorem 9.5 (ii). $\square$

Corollary 9.7

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Suppose that $(u,\lambda )$ solves (9.4) with $\eta =(1,-1)$. Assume that $u>-1$ on [a, b). Let $\varphi \in C^1((-1,1))$ be an odd strictly increasing function with $\varphi \in L^1((-1,1))$. Then

• (i) $\int _{\{u>0\}}\varphi (u)\,d\mu <+\infty$;

• (ii) $\int _a^b\varphi (u)\,d\mu \le 0$;

• (iii) equality holds in (ii) if and only if $\rho \equiv 0$ on [a, b).

In particular,

• (iv) $\int _a^b\frac{u}{\sqrt{1-u^2}}\,d\mu \le 0$ with equality if and only if $\rho \equiv 0$ on [a, b).

Proof

(i) Put $I:=\{1>u>0\}$. The function $u:I\rightarrow (0,1)$ is $C^{0,1}$ and $u^\prime \le -\hat{m}$ a.e. on I by Lemma 9.3. It has $C^{0,1}$ inverse $v:(0,1)\rightarrow I,v^\prime =1/(u^\prime \circ v)$ and $|v^\prime |\le 1/\hat{m}$ a.e. on (0, 1). By a change of variables,

$$\begin{aligned} \int _{\{u>0\}}\varphi (u)\,d\mu&=\int _0^1\varphi (v^\prime /v)\,dt \end{aligned}$$

from which the claim is apparent. (ii) The integral is well-defined because $\varphi (u)^+=\varphi (u)\chi _{\{u>0\}}\in L^1((a,b),\mu )$ by (i). By Lemma 9.3 the set $\{u=0\}$ consists of a singleton and has $\mu$-measure zero. So

$$\begin{aligned} \int _a^b\varphi (u)\,d\mu&=\int _{\{u>0\}}\varphi (u)\,d\mu +\int _{\{u<0\}}\varphi (u)\,d\mu \nonumber \\&=\int _{\{u>0\}}\varphi (u)\,d\mu -\int _{\{v>0\}}\varphi (v)\,d\mu \nonumber \end{aligned}$$

where $v:=-u$ as $\varphi$ is an odd function. We remark that in a similar way to (9.3),

$$\begin{aligned} \int _0^1\varphi ^\prime \mu _u\,dt= & {} \int _{\{u>0\}}\Big \{\varphi (u)-\varphi (0)\Big \}\\ d\mu= & {} \int _{\{u>0\}}\varphi (u)\,d\mu \end{aligned}$$

using oddness of $\varphi$ and an analogous formula holds with v in place of u. Thus we may write

$$\begin{aligned} \int _a^b\varphi (u)\,d\mu&=\int _0^1\varphi ^\prime \mu _u\,dt-\int _0^1\varphi ^\prime \mu _v\,dt\\&=\int _0^1\varphi ^\prime \Big \{\mu _u-\mu _v\Big \}\,dt\le 0\nonumber \end{aligned}$$

by Corollary 9.6 as $\varphi ^\prime >0$ on (0, 1). (iii) Suppose that $\rho \not \equiv 0$ on [a, b). Then strict inequality holds in the above by Corollary 9.6. If $\rho \equiv 0$ on [a, b) the equality follows from Theorem 9.5. (iv) follows from (ii) and (iii) with the particular choice $\varphi :(-1,1)\rightarrow \mathbb {R};t\mapsto t/\sqrt{1-t^2}$. $\square$

The boundary condition $\eta _1\eta _2=1$. Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. We study solutions of the auxilliary Riccati equation

$$\begin{aligned} w^\prime +\lambda w^2=(1/x+\rho )w\text { a.e. on }(a,b) \text { with }w(a)=w(b)=1; \end{aligned}$$

(9.6)

with $w\in C^{0,1}([a,b])$ and $\lambda \in \mathbb {R}$. If $\rho \equiv 0$ on [a, b] then we write $w_0$ instead of w. Suppose $(u,\lambda )$ solves (9.4) with $\eta =(1,1)$. Then $u>0$ on [a, b] by Lemma 9.2 and we may set $w:=1/u$. Then $(w,-\lambda )$ satisfies (9.6).

Lemma 9.8

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Then

• (i) there exists a solution $(w,\lambda )$ of (9.6) with $w\in C^{0,1}([a,b])$ and $\lambda \in \mathbb {R}$;

• (ii) the pair $(w,\lambda )$ in (i) is unique;

• (iii) $\lambda =m$.

Proof

(i) Define $w:[a,b]\rightarrow \mathbb {R}$ by

$$\begin{aligned} w(t):=\frac{g(t)}{m\int _a^t g\,ds+g(a)}\text { for }t\in [a,b]. \end{aligned}$$

Then $w\in C^{0,1}([a,b])$ and (w, m) satisfies (9.6). (ii) We claim that $w>0$ on [a, b] for any solution $(w,\lambda )$ of (9.6). For otherwise, $c:=\min \{w=0\}\in (a,b)$. Then $u:=1/w$ on [a, c) satisfies

$$\begin{aligned} u^\prime +\left( \frac{1}{\tau }+\rho \right) u-\lambda =0\text { a.e. on }(a,c) \text { and }u(a)=1, u(c-)=+\infty . \end{aligned}$$

Integrating, we obtain

$$\begin{aligned} gu-g(a)-\lambda \int _a^\cdot g\,dt=0\text { on }[a,c) \end{aligned}$$

and this entails the contradiction that $u(c-)<+\infty$. We may now use the uniqueness statement in Lemma 9.2. (iii) follows from (ii) and the particular solution given in (i). $\square$

We introduce the mapping

$$\begin{aligned} \omega :(0,\infty )\times (0,\infty )\rightarrow \mathbb {R};(t,x)\mapsto -(2/t)\coth (x/2). \end{aligned}$$

For $\xi >0$,

$$\begin{aligned} |\omega (t,x)-\omega (t,y)|\le \mathrm {cosech}^2[\xi /2](1/t)|x-y| \end{aligned}$$

(9.7)

for $(t,x),(t,y)\in (0,\infty )\times (\xi ,\infty )$ and $\omega$ is locally Lipschitzian in x on $(0,\infty )\times (0,\infty )$ in the sense of [16] I.3. Let $0<a<b<+\infty$ and set $\lambda :=A/G>1$. Here, $A=A(a,b)$ stands for the arithmetic mean of a, b as introduced in the previous Section while $G=G(a,b):=\sqrt{|ab|}$ stands for their geometric mean. We refer to the inital value problem

$$\begin{aligned} z^\prime =\omega (t,z)\text { on }(0,\lambda ) \text { and }z(1)=\mu ((a,b)). \end{aligned}$$

(9.8)

Define

$$\begin{aligned} z_0:(0,\lambda )\rightarrow \mathbb {R};t\mapsto 2\log \Big \{\frac{\lambda +\sqrt{\lambda ^2-t^2}}{t}\Big \}. \end{aligned}$$

Lemma 9.9

Let $0<a<b<+\infty$. Then

• (i) $w_0(\tau )=\frac{2A\tau }{G^2+\tau ^2}$ for $\tau \in [a,b]$;

• (ii) $\Vert w_0\Vert _\infty =\lambda$;

• (iii) $\mu _{w_0}=z_0$ on $[1,\lambda )$;

• (iv) $z_0$ satisfies (9.8) and this solution is unique;

• (v) $\int _{\{w_0=1\}}\frac{1}{|w_0^\prime |}\,\frac{d\mathscr {H}^0}{\tau }=2\coth (\mu ((a,b))/2)$;

• (vi) $\int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{dx}{x}=\pi$.

Proof

(i) follows as in the proof of Lemma 9.8 with $g(t)=t$ while (ii) follows by calculus. (iii) follows by solving the quadratic equation $t\tau ^2-2A\tau +G^2t=0$ for $\tau$ with $t\in (0,\lambda )$. Uniqueness in (iv) follows from [16] Theorem 3.1 as $\omega$ is locally Lipschitzian with respect to x in $(0,\infty )\times (0,\infty )$. For (v) note that $|aw_0^\prime (a)|=1-a/A$ and $|bw_0^\prime (b)|=b/A-1$ and

$$\begin{aligned} 2\coth (\mu ((a,b))/2)=2(a+b)/(b-a). \end{aligned}$$

(vi) We may write

$$\begin{aligned} \int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{d\tau }{\tau }&=\int _a^b\frac{ab+\tau ^2}{\sqrt{(a+b)^2\tau ^2-(ab+\tau ^2)^2}} \frac{d\tau }{\tau }\\&=\int _a^b\frac{ab+\tau ^2}{\sqrt{(\tau ^2-a^2)(b^2-\tau ^2)}} \frac{d\tau }{\tau }.\nonumber \end{aligned}$$

The substitution $s=\tau ^2$ followed by the Euler substitution (cf. [14] 2.251)

$$\begin{aligned} \sqrt{(s-a^2)(b^2-s)}=t(s-a^2) \end{aligned}$$

gives

$$\begin{aligned} \int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{d\tau }{\tau } =\int _0^\infty \frac{1}{1+t^2}+\frac{ab}{b^2+a^2t^2}\,dt=\pi . \end{aligned}$$

$\square$

Lemma 9.10

Let $0<a<b<+\infty$. Then

• (i) for $y>a$ the function $x\mapsto \frac{by-ax}{(y-a)(b-x)}$ is strictly increasing on $(-\infty ,b]$;

• (ii) the function $y\mapsto \frac{(b-a)y}{(y-a)(b-y)}$ is strictly increasing on [G, b];

• (iii) for $x<b$ the function $y\mapsto \frac{by-ax}{(y-a)(b-x)}$ is strictly decreasing on $[a,+\infty )$

Proof

The proof is an exercise in calculus. $\square$

Lemma 9.11

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $(w,\lambda )$ solve (9.6). Assume

• (i) w is differentiable at both a and b and that (9.6) holds there;

• (ii) $w^\prime (a)>0$ and $w^\prime (b)<0$;

• (iii) $w>1$ on (a, b);

• (iv) $\rho$ is differentiable at a and b.

Then

$$\begin{aligned} \int _{\{w=1\}{\setminus } Z_w}\frac{1}{|w^\prime |}\frac{d\mathscr {H}^0}{\tau }\ge 2\coth (\mu ((a,b))/2) \end{aligned}$$

with equality if and only if $\rho \equiv 0$ on [a, b).

Proof

At the end-points $x=a,b$ the condition (i) entails that $w^\prime +m-\rho =1/x=w_0^\prime +m_0$ so that

$$\begin{aligned} w^\prime -w_0^\prime&=m_0-m+\rho \text { at }x=a,b. \end{aligned}$$

(9.9)

We consider the four cases

• (a) $w^\prime (a)\ge w_0^\prime (a)\text { and }w^\prime (b)\ge w_0^\prime (b)$;

• (b) $w^\prime (a)\ge w_0^\prime (a)\text { and }w^\prime (b)\le w_0^\prime (b)$;

• (c) $w^\prime (a)\le w_0^\prime (a)\text { and }w^\prime (b)\ge w_0^\prime (b)$;

• (d) $w^\prime (a)\le w_0^\prime (a)\text { and }w^\prime (b)\le w_0^\prime (b)$;

in turn.

• (a) Condition (a) together with (9.9) means that $m_0-m+\rho (a)\ge 0$; that is, $m-\rho (a)\le m_0$. By (i) and (ii), $bm-b\rho (b)-1=-bw^\prime (b)> 0$; or $m-\rho (b)>1/b$. Therefore,

  $$\begin{aligned} 0<1/b<m-\rho (b)\le m-\rho (a)\le 1/A \end{aligned}$$

  by (8.5). Put $x:=1/(m-\rho (b))$ and $y:=1/(m-\rho (a))$. Then

  $$\begin{aligned} a<A\le y\le x<b. \end{aligned}$$

  We write

  $$\begin{aligned} aw^\prime (a)&=-(m-\rho (a))a+1=-(1/y)a+1>0;\nonumber \\ bw^\prime (b)&=-(m-\rho (b))b+1=-(1/x)b+1<0.\nonumber \end{aligned}$$

  Making use of assumption (iii),

  $$\begin{aligned} \int _{\{w=1\}{\setminus } Z_w}\frac{1}{|w^\prime |}\frac{d\mathscr {H}^0}{x}&=\frac{1}{-(1/y)a+1}-\frac{1}{-(1/x)b+1}\\&=\frac{by-ax}{(y-a)(b-x)}. \end{aligned}$$

  By Lemma 9.10 (i) then (ii),

  $$\begin{aligned} \int _{\{w=1\}}\frac{1}{|w^\prime |}\frac{d\mathscr {H}^0}{x}&\ge \frac{(b-a)y}{(y-a)(b-y)} \ge \frac{(b-a)A}{(A-a)(b-A)}\\&=2\frac{a+b}{b-a} =2\coth (\mu ((a,b))/2). \end{aligned}$$

  If equality holds then $\rho (a)=\rho (b)$ and $\rho$ is constant on [a, b]. By Theorem 8.3 we conclude that $\rho \equiv 0$ on [a, b).

• (b) Condition (b) together with (9.9) entails that $0\le m_0-m+\rho (a)$ and $0\le -m_0+m-\rho (b)$ whence $0\le \rho (a)-\rho (b)$ upon adding; so $\rho$ is constant on the interval [a, b] by monotonicity. Define x and y as above. Then $x=y$ and $y\ge A$. The result now follows in a similar way to case (a).

• (c) In this case,

  $$\begin{aligned} \frac{1}{aw^\prime (a)}-\frac{1}{bw^\prime (b)}\ge & {} \frac{1}{aw_0^\prime (a)} -\frac{1}{bw_0^\prime (b)}\\= & {} 2\coth (\mu ((a,b))/2) \end{aligned}$$

  by Lemma 9.9. If equality holds then $w^\prime (b)=w_0^\prime (b)$ so that $m_0-m+\rho (b)=0$ and $\rho$ vanishes on [a, b] by Theorem 8.3.

• (d) Condition (d) together with (9.9) means that $m_0-m+\rho (b)\le 0$; that is, $m\ge \rho (b)+m_0$. On the other hand, by Theorem 8.3, $m\le \rho (b)+m_0$. In consequence, $m=\rho (b)+m_0$. It then follows that $\rho \equiv 0$ on [a, b] by Theorem 8.3. Now use Lemma 9.9.

$\square$

Lemma 9.12

Let $\phi :(0,+\infty )\rightarrow (0,+\infty )$ be a convex non-increasing function with $\inf _{(0,+\infty )}\phi >0$. Let $\varLambda$ be an at most countably infinite index set and $(x_h)_{h\in \varLambda }$ a sequence of points in $(0,+\infty )$ with $\sum _{h\in \varLambda }x_h<+\infty$. Then

$$\begin{aligned} \sum _{h\in \varLambda }\phi (x_h)\ge \phi \left( \sum _{h\in \varLambda } x_h\right) \end{aligned}$$

and the left-hand side takes the value $+\infty$ in case $\varLambda$ is countably infinite and is otherwise finite.

Proof

Suppose $0<x_1<x_2<+\infty$. By convexity $\phi (x_1)+\phi (x_2)\ge 2\phi (\frac{x_1+x_2}{2})\ge \phi (x_1+x_2)$ as $\phi$ is non-increasing. The result for finite $\varLambda$ follows by induction. $\square$

Theorem 9.13

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $(w,\lambda )$ solve (9.6). Assume that $w>1$ on (a, b). Then

• (i) for $\mathscr {L}^1$-a.e. $t\in (1,\Vert w\Vert _\infty )$,

  $$\begin{aligned} -\mu _w^\prime \ge (2/t)\coth ((1/2)\mu _w); \end{aligned}$$

  (9.10)

• (ii) if $\rho \not \equiv 0$ on [a, b) then there exists $t_0\in (1,\Vert w\Vert _\infty )$ such that strict inequality holds in (9.10) for $\mathscr {L}^1$-a.e. $t\in (1,t_0)$.

Proof

(i) The set

$$\begin{aligned} Y_w:= & {} Z_{2,w}\cup \Big (\{w^\prime +m w^2\ne (1/x+\rho )w\}{\setminus } Z_{2,w}\Big )\\&\cup \{\rho \text { not differentiable}\}\subset [a,b] \end{aligned}$$

is a null set in [a, b]. By [1] Lemma 2.95 and Lemma 2.96, $\{w=t\}\cap (Y_w\cap Z_{1,w})=\emptyset$ for a.e. $t>1$. Let $t\in (1,\Vert w\Vert _\infty )$ and assume that $\{w=t\}\cap (Y_w\cap Z_{1,w})=\emptyset$. We write $\{w>t\}=\bigcup _{h\in \varLambda }I_h$ where $\varLambda$ is an at most countably infinite index set and $(I_h)_{h\in \varLambda }$ are disjoint non-empty well-separated open intervals in (a, b). The term well-separated means that for each $h\in \varLambda ,\inf _{k\in \varLambda {\setminus }\{h\}}d(I_h,I_k)>0$. This follows from the fact that $w^\prime \ne 0$ on $\partial I_h$ for each $h\in \varLambda$. Put $\widetilde{w}:=w/t$ on $\overline{\{w>t\}}$ so

$$\begin{aligned} \widetilde{w}^\prime +(mt)\widetilde{w}^2=(1/x+\rho )\widetilde{w}\text { a.e. on }\{w>t\}\text { and }\widetilde{w}=1\text { on }\{w=t\}. \end{aligned}$$

We use the fact that the mapping $\phi :(0,+\infty )\rightarrow (0,+\infty );t\mapsto \coth t$ satisfies the hypotheses of Lemma 9.12. By Lemmas 9.11 and 9.12,

$$\begin{aligned} (0,+\infty ]\ni \int _{\{w=t\}{\setminus } Z_w}\frac{1}{|w^\prime |}\frac{d\mathscr {H}^0}{x}&=(1/t)\int _{\{\widetilde{w}=1\}}\frac{1}{|\widetilde{w}^\prime |}\frac{d\mathscr {H}^0}{\tau }\nonumber \\&=(1/t)\sum _{h\in \varLambda }\int _{\partial I_h}\frac{1}{|\widetilde{w}^\prime |}\frac{d\mathscr {H}^0}{\tau }\nonumber \\&\ge (2/t)\sum _{h\in \varLambda }\coth ((1/2)\mu (I_h))\nonumber \\&\ge (2/t)\coth \left( (1/2)\sum _{h\in \varLambda }\mu (I_h)\right) \nonumber \\&=(2/t)\coth ((1/2)\mu (\{w>t\})))\nonumber \\&=(2/t)\coth ((1/2)\mu _w(t)).\nonumber \end{aligned}$$

The statement now follows from Lemma 9.1.

(ii) Suppose that $\rho \not \equiv 0$ on [a, b). Put $\alpha :=\min \{\rho >0\}\in [a,b)$. Now that $\{w>t\}\uparrow (a,b)$ as $t\downarrow 1$ as $w>1$ on (a, b). Choose $t_0\in (1,\Vert w\Vert _\infty )$ such that $\{w>t_0\}\cap (\alpha ,b)\ne \emptyset$. Then for each $t\in (1,t_0)$ there exists $h\in \varLambda$ such that $\rho \not \equiv 0$ on $I_h$. The statement then follows by Lemma 9.11. $\square$

Lemma 9.14

Let $\emptyset \ne S\subset \mathbb {R}$ be bounded and suppose S has the property that for each $s\in S$ there exists $\delta >0$ such that $[s,s+\delta )\subset S$. Then S is $\mathscr {L}^1$-measurable and $|S|>0$.

Proof

For each $s\in S$ put $t_s:=\inf \{t>s:t\not \in S\}$. Then $s<t_s<+\infty ,[s,t_s)\subset S$ and $t_s\not \in S$. Define

$$\begin{aligned} \mathscr {C}:=\Big \{[s,t]:s\in S\text { and }t\in (s,t_s)\Big \}. \end{aligned}$$

Then $\mathscr {C}$ is a Vitali cover of S (see [6] Chapter 16 for example). By Vitali’s Covering Theorem (cf. [6] Theorem 16.27) there exists an at most countably infinite subset $\varLambda \subset \mathscr {C}$ consisting of pairwise disjoint intervals such that

$$\begin{aligned} \left| S{\setminus }\bigcup _{I\in \varLambda }I\right| =0. \end{aligned}$$

Note that $I\subset S$ for each $I\in \varLambda$. Consequently, $S=\bigcup _{I\in \varLambda }I\cup N$ where N is an $\mathscr {L}^1$-null set and hence S is $\mathscr {L}^1$-measurable. The positivity assertion is clear. $\square$

Theorem 9.15

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Let $(w,\lambda )$ solve (9.6). Assume that $w>1$ on (a, b). Put $T:=\min \{\Vert w_0\Vert _\infty ,\Vert w\Vert _\infty \}>1$. Then

• (i) $\mu _w(t)\le \mu _{w_0}(t)$ for each $t\in [1,T)$;

• (ii) $\Vert w\Vert _\infty \le \Vert w_0\Vert _\infty$;

• (iii) if $\rho \not \equiv 0$ on [a, b) then there exists $t_0\in (1,\Vert w\Vert _\infty )$ such that $\mu _w(t)<\mu _{w_0}(t)$ for each $t\in (1,t_0)$.

Proof

(i) We adapt the proof of [16] Theorem I.6.1. The assumption entails that $\mu _w(1)=\mu _{w_0}(1)=\mu ((a,b))$. Suppose for a contradiction that $\mu _w(t)>\mu _{w_0}(t)$ for some $t\in (1,T)$.

For $\varepsilon >0$ consider the initial value problem

$$\begin{aligned} z^\prime =\omega (t,z)+\varepsilon \text { and }z(1)=\mu ((a,b))+\varepsilon \end{aligned}$$

(9.11)

on (0, T). Choose $\upsilon \in (0,1)$ and $\tau \in (t,T)$. By [16] Lemma I.3.1 there exists $\varepsilon _0>0$ such that for each $0\le \varepsilon <\varepsilon _0$ (9.11) has a continuously differentiable solution $z_\varepsilon$ defined on $[\upsilon ,\tau ]$ and this solution is unique by [16] Theorem I.3.1. Moreover, the sequence $(z_\varepsilon )_{0<\varepsilon <\varepsilon _0}$ converges uniformly to $z_0$ on $[\upsilon ,\tau ]$.

Given $0<\varepsilon<\eta <\varepsilon _0$ it holds that $z_0\le z_\varepsilon \le z_\eta$ on $[1,\tau ]$ by [16] Theorem I.6.1. Note for example that $z_0^\prime \le \omega (\cdot ,z_0)+\varepsilon$ on $(1,\tau )$. In fact, $(z_\varepsilon )_{0<\varepsilon <\varepsilon _0}$ decreases strictly to $z_0$ on $(1,\tau )$. For if, say, $z_0(s)=z_\varepsilon (s)$ for some $s\in (1,\tau )$ then $z_\varepsilon ^\prime (s)=\omega (s,z_\varepsilon (s))+\varepsilon >\omega (s,z_0(s))=z_0^\prime (s)$ by (9.11); while on the other hand $z_\varepsilon ^\prime (s)\le z_0^\prime (s)$ by considering the left-derivative at s and using the fact that $z_\varepsilon \ge z_0$ on $[1,\tau ]$. This contradicts the strict inequality.

Choose $\varepsilon _1\in (0,\varepsilon _0)$ such that $z_\varepsilon (t)<\mu _w(t)$ for each $0<\varepsilon <\varepsilon _1$. Now $\mu _w$ is right-continuous and strictly decreasing as $\mu _w(t)-\mu _w(s)=-\mu (\{s<w\le t\})<0$ for $1\le s<t<\Vert w\Vert _\infty$ by continuity of w. So the set $\{z_\varepsilon <\mu _w\}\cap (1,t)$ is open and non-empty in $(0,+\infty )$ for each $\varepsilon \in (0,\varepsilon _1)$. Thus there exists a unique $s_\varepsilon \in [1,t)$ such that

$$\begin{aligned} \mu _w>z_\varepsilon \text { on }(s_\varepsilon ,t] \text { and }\mu _w(s_\varepsilon )=z_\varepsilon (s_\varepsilon ) \end{aligned}$$

for each $\varepsilon \in (0,\varepsilon _1)$. As $z_\varepsilon (1)>\mu ((a,b))$ it holds that each $s_\varepsilon >1$. Note that $1<s_\varepsilon <s_\eta$ whenever $0<\varepsilon <\eta$ as $(z_\varepsilon )_{_{0<\varepsilon <\varepsilon _0}}$ decreases strictly to $z_0$ as $\varepsilon \downarrow 0$.

Define

$$\begin{aligned} S:=\Big \{s_\varepsilon :0<\varepsilon <\varepsilon _1\Big \}\subset (1,t). \end{aligned}$$

We claim that for each $s\in S$ there exists $\delta >0$ such that $[s,s+\delta )\subset S$. This entails that S is $\mathscr {L}^1$-measurable with positive $\mathscr {L}^1$-measure by Lemma 9.14.

Suppose $s=s_\varepsilon \in S$ for some $\varepsilon \in (0,\varepsilon _1)$ and put $z:=z_\varepsilon (s)=\mu _w(s)$. Put $k:=\mathrm {cosech}^2(z_0(t)/2)$. For $0\le \zeta<\eta <\varepsilon _1$ define

$$\begin{aligned} \varOmega _{\zeta ,\eta }:=\Big \{(u,y)\in \mathbb {R}^2:u\in (0,t)\text { and }z_\zeta (u)<y<z_\eta (u)\Big \} \end{aligned}$$

and note that this is an open set in $\mathbb {R}^2$. We remark that for each $(u,y)\in \varOmega _{\zeta ,\eta }$ there exists a unique $\nu \in (\zeta ,\eta )$ such that $y=z_\nu (u)$. Given $r>0$ with $s+r<t$ set

$$\begin{aligned} Q=Q_r:=\Big \{(u,y)\in \mathbb {R}^2:s\le u<s+r\text { and }|y-z|<\Vert z_\varepsilon -z\Vert _{C([s,s+r])}\Big \}. \end{aligned}$$

Choose $r\in (0,t-s)$ and $\varepsilon _2\in (\varepsilon ,\varepsilon _1)$ such that

• (a) $Q_r\subset \varOmega _{0,\varepsilon _1}$;

• (b) $\Vert z_\varepsilon -z\Vert _{C([s,s+r])}<s\varepsilon /(2k)$;

• (c) $\sup _{\eta \in (\varepsilon ,\varepsilon _2)}\Vert z_\eta -z\Vert _{C([s,s+r])}\le \Vert z_\varepsilon -z\Vert _{C([s,s+r])}$;

• (d) $z_\eta <\mu _w$ on $[s+r,t]$ for each $\eta \in (\varepsilon ,\varepsilon _2)$.

We can find $\delta \in (0,r)$ such that $z_\varepsilon<\mu _w<z_{\varepsilon _2}$ on $(s,s+\delta )$ as $z_{\varepsilon _2}(s)>z$; in other words, the graph of $\mu _w$ restricted to $(s,s+\delta )$ is contained in $\varOmega _{\varepsilon ,\varepsilon _2}$.

Let $u\in (s,s+\delta )$. Then $\mu _w(u)=z_\eta (u)$ for some $\eta \in (\varepsilon ,\varepsilon _2)$ as above. We claim that $u=s_\eta$ so that $u\in S$. This implies in turn that $[s,s+\delta )\subset S$. Suppose for a contradiction that $z_\eta \not <\mu _w$ on (u, t]. Then there exists $v\in (u,t]$ such that $\mu _w(v)=z_\eta (v)$. In view of condition (d), $v\in (u,s+r)$. By [1] Theorem 3.28 and Theorem 9.13,

$$\begin{aligned} \mu _w(v)-\mu _w(u)&=D\mu _w((u,v]) =D\mu _w^a((u,v])+D\mu _w^s((u,v]) \nonumber \\&\le D\mu _w^a((u,v]) =\int _u^v\mu _w^\prime \,d\tau \le \int _u^v\omega (\cdot ,\mu _w)\,d\tau .\nonumber \end{aligned}$$

On the other hand,

$$\begin{aligned} z_\eta (v)-z_\eta (u)&=\int _u^v z_\eta ^\prime \,d\tau =\int _u^v\omega (\cdot ,z_\eta )\,d\tau +\eta (v-u).\nonumber \end{aligned}$$

We derive that

$$\begin{aligned} \varepsilon (v-u)&\le \eta (v-u) \le \int _u^v\Big \{\omega (\cdot ,\mu _w)-\omega (\cdot ,z_\eta )\Big \}\,d\tau \\&\le k\int _u^v|\mu _w-z_\eta |\,d\mu \nonumber \end{aligned}$$

using the estimate (9.7). Thus

$$\begin{aligned} \varepsilon&\le k\frac{1}{v-u}\int _u^v|\mu _w-z_\eta |\,d\mu \nonumber \\&\le (k/s)\Vert \mu _w-z_\eta \Vert _{C([u,v])}\nonumber \\&\le (k/s)\Big \{\Vert \mu _w-z\Vert _{C([s,s+r])}+\Vert z_\eta -z\Vert _{C([s,s+r])}\Big \}\nonumber \\&\le (2k/s)\Vert z_\varepsilon -z\Vert _{C([s,s+r])} <\varepsilon \nonumber \end{aligned}$$

by (b) and (c) giving rise to the desired contradiction.

By Theorem 9.13, $\mu _w^\prime \le \omega (\cdot ,\mu _w)$ for $\mathscr {L}^1$-a.e. $t\in S$. Choose $s\in S$ such that $\mu _w$ is differentiable at s and the latter inequality holds at s. Let $\varepsilon \in (0,\varepsilon _1)$ such that $s=s_\varepsilon$. For any $u\in (s,t)$,

$$\begin{aligned} \mu _w(u)-\mu _w(s)>z_\varepsilon (u)-z_\varepsilon (s). \end{aligned}$$

We deduce that $\mu _w^\prime (s)\ge z_\varepsilon ^\prime (s)$. But then

$$\begin{aligned} \mu _w^\prime (s)\ge z_\varepsilon ^\prime (s)=\omega (s,z_\epsilon (s))+\varepsilon >\omega (s,\mu _w(s)). \end{aligned}$$

This strict inequality holds on a set of full measure in S. This contradicts Theorem 9.13.

• (ii) Use the fact that $\Vert w\Vert _\infty =\sup \{t>0:\mu _w(t)>0\}$.

• (iii) Assume that $\rho \not \equiv 0$ on [a, b). Let $t_0\in (1,\Vert w\Vert _\infty )$ be as in Lemma 9.13. Then for $t\in (1,t_0)$,

  $$\begin{aligned} \mu _w(t)-\mu _w(1)&=D\mu _w((1,t])=D\mu _w^a((1,t])\nonumber \\&\quad +D\mu _w^s((1,t])\le D\mu _w^a((1,t])\nonumber \\&=\int _{(1,t]}\mu _w^\prime \,ds<\int _{(1,t]}\omega (s,\mu _w)\,ds\nonumber \\&\le \int _{(1,t]}\omega (s,\mu _{w_0})\,ds=\mu _{w_0}(t)-\mu _{w_0}(1)\nonumber \end{aligned}$$

  by Theorem 9.13, Lemma 9.9 and the inequality in (i).

$\square$

Corollary 9.16

Let $0<a<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [a, b]. Suppose that $(w,\lambda )$ solves (9.6). Assume that $w>1$ on (a, b). Let $0\le \varphi \in C^1((1,+\infty ))$ be strictly decreasing with $\int _a^b\varphi (w_0)\,d\mu <+\infty$. Then

• (i) $\int _a^b\varphi (w)\,d\mu \ge \int _a^b\varphi (w_0)\,d\mu$;

• (ii) equality holds in (i) if and only if $\rho \equiv 0$ on [a, b).

In particular,

• (iii) $\int _a^b\frac{1}{\sqrt{w^2-1}}\,d\mu \ge \pi$ with equality if and only if $\rho \equiv 0$ on [a, b).

Proof

(i) Let $\varphi \ge 0$ be a decreasing function on $(1,+\infty )$ which is piecewise $C^1$. Suppose that $\varphi (1+)<+\infty$. By Tonelli’s Theorem,

$$\begin{aligned} \int _{[1,+\infty )}\varphi ^\prime \mu _w\,ds&=\int _{[1,+\infty )}\varphi ^\prime \Big \{\int _{(a,b)}\chi _{\{w>s\}}\,d\mu \Big \}\,ds\nonumber \\&=\int _{(a,b)}\Big \{\int _{[1,+\infty )}\varphi ^\prime \chi _{\{w>s\}}\,ds\Big \}\,d\mu \nonumber \\&=\int _{(a,b)}\Big \{\varphi (w)-\varphi (1)\Big \}\,d\mu \\&=\int _{(a,b)}\varphi (w)\,d\mu -\varphi (1)\mu ((a,b))\nonumber \end{aligned}$$

and a similar identity holds for $\mu _{w_0}$. By Theorem 9.15, $\int _a^b\varphi (w)\,d\mu \ge \int _a^b\varphi (w_0)\,d\mu$. Now suppose that $0\le \varphi \in C^1((1,+\infty ))$ is strictly decreasing with $\int _a^b\varphi (w_0)\,d\mu <+\infty$. The inequality holds for the truncated function $\varphi \wedge n$ for each $n\in \mathbb {N}$. An application of the monotone convergence theorem establishes the result for $\varphi$.

(ii) Suppose that equality holds in (i). For $c\in (1,+\infty )$ put $\varphi _1:=\varphi \vee \varphi (c)-\varphi (c)$ and $\varphi _2:=\varphi \wedge \varphi (c)$. By (i) we deduce

$$\begin{aligned} \int _a^b\varphi _2(w)\,d\mu =\int _a^b\varphi _2(w_0)\,d\mu ; \end{aligned}$$

and hence by the above that

$$\begin{aligned} \int _{[c,+\infty )}\varphi ^\prime \Big \{\mu _w-\mu _{w_0}\Big \}\,ds=0. \end{aligned}$$

This means that $\mu _w=\mu _{w_0}$ on $(c,+\infty )$ and hence on $(1,+\infty )$. By Theorem 9.15 we conclude that $\rho \equiv 0$ on [a, b). (iii) flows from (i) and (ii) noting that the function $\varphi :(1,+\infty )\rightarrow \mathbb {R};t\mapsto 1/\sqrt{t^2-1}$ satisfies the integral condition by Lemma 9.9. $\square$

The case $a=0$. Let $0<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [0, b]. We study solutions to the first-order linear ordinary differential equation

$$\begin{aligned} u^\prime +(1/x+\rho )u+\lambda =0\text { a.e. on }(0,b)\text { with }u(0)=0\text { and }u(b)=1 \end{aligned}$$

(9.12)

where $u\in C^{0,1}([0,b])$ and $\lambda \in \mathbb {R}$. If $\rho \equiv 0$ on [0, b] then we write $u_0$ instead of u.

Lemma 9.17

Let $0<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [0, b]. Then

• (i) there exists a solution $(u,\lambda )$ of (9.12) with $u\in C^{0,1}([0,b])$ and $\lambda \in \mathbb {R}$;

• (ii) $\lambda$ is given by $\lambda =-g(b)/G(b)$ where $G:=\int _0^\cdot g\,ds$;

• (iii) the pair $(u,\lambda )$ in (i) is unique;

• (iv) $u>0$ on (0, b].

Proof

(i) The function $u:[a,b]\rightarrow \mathbb {R}$ given by

$$\begin{aligned} u=\frac{g(b)}{G(b)}\frac{G}{g} \end{aligned}$$

(9.13)

on [0, b] solves (9.12) with $\lambda$ as in (ii). (iii) Suppose that $(u_1,\lambda _1)$ resp. $(u_2,\lambda _2)$ solve (9.12). By linearity $u:=u_1-u_2$ solves

$$\begin{aligned} u^\prime +(1/x+\rho )u+\lambda =0\text { a.e. on }(0,b) \text { with }u(0)=u(b)=0 \end{aligned}$$

where $\lambda =\lambda _1-\lambda _2$. An integration gives that $u=(-\lambda G+c)/g$ for some constant $c\in \mathbb {R}$ and the boundary conditions entail that $\lambda =c=0$. (iv) follows from the formula (9.13) and unicity. $\square$

Lemma 9.18

Suppose $-\infty<a<b<+\infty$ and that $\phi :[a,b]\rightarrow \mathbb {R}$ is convex. Suppose that there exists $\xi \in (a,b)$ such that

$$\begin{aligned} \phi (\xi )=\frac{b-\xi }{b-a}\phi (a)+\frac{\xi -a}{b-a}\phi (b). \end{aligned}$$

Then

$$\begin{aligned} \phi (c)=\frac{b-c}{b-a}\phi (a)+\frac{c-a}{b-a}\phi (b) \end{aligned}$$

for each $c\in [a,b]$.

Proof

Let $c\in (\xi ,b)$. By monotonicity of chords,

$$\begin{aligned} \frac{\phi (\xi )-\phi (a)}{\xi -a}\le \frac{\phi (c)-\phi (\xi )}{c-\xi } \end{aligned}$$

so

$$\begin{aligned} \phi (c)&\ge \frac{c-a}{\xi -a}\phi (\xi )-\frac{c-\xi }{\xi -a}\phi (a)\nonumber \\&=\frac{c-a}{\xi -a}\Big \{\frac{b-\xi }{b-a}\phi (a)+\frac{\xi -a}{b-a}\phi (b)\Big \} -\frac{c-\xi }{\xi -a}\phi (a)\nonumber \\&=\frac{b-c}{b-a}\phi (a)+\frac{c-a}{b-a}\phi (b)\nonumber \end{aligned}$$

and equality follows. The case $c\in (a,\xi )$ is similar. $\square$

Lemma 9.19

Let $0<b<+\infty$ and $\rho \ge 0$ be a non-decreasing bounded function on [0, b]. Let $(u,\lambda )$ satisfy (9.12). Then

• (i) $u\ge u_0$ on [0, b];

• (ii) if $\rho \not \equiv 0$ on [0, b) then $u>u_0$ on (0, b).

Proof

(i) The mapping $G:[0,b]\rightarrow [0,G(b)]$ is a bijection with inverse $G^{-1}$. Define $\eta :[0,G(b)]\rightarrow \mathbb {R}$ via $\eta :=(tg)\circ G^{-1}$. Then

$$\begin{aligned} \eta ^\prime =\frac{(tg)^\prime }{g}\circ G^{-1} =(2+t\rho )\circ G^{-1} \end{aligned}$$

a.e. on (0, G(b)) so $\eta ^\prime$ is non-decreasing there. This means that $\eta$ is convex on [0, G(b)]. In particular, $\eta (s)\le [\eta (G(b))/G(b)]s$ for each $s\in [0,G(b)]$. For $t\in [0,b]$ put $s:=G(t)$ to obtain $tg(t)\le (bg(b)/G(b))G(t)$. A rearrangement gives $u\ge u_0$ on [0, b] noting that $u_0:[0,b]\rightarrow \mathbb {R};t\mapsto t/b$. (ii) Assume $\rho \not \equiv 0$ on [0, b). Suppose that $u(c)=u_0(c)$ for some $c\in (0,b)$. Then $\eta (G(c))=[\eta (G(b))/G(b)]G(c)$. By Lemma 9.18, $\eta ^\prime =0$ on (0, G(b)). This implies that $\rho \equiv 0$ on [0, b). $\square$

Lemma 9.20

Let $0<b<+\infty$. Then $\int _0^b\frac{u_0}{\sqrt{1-u_0^2}}\,d\mu =\pi /2$.

Proof

The integral is elementary as $u_0(t)=t/b$ for $t\in [0,b]$. $\square$

10 Proof of main results

Lemma 10.1

Let $x\in H$ and v be a unit vector in $\mathbb {R}^2$ such that the pair $\{x,v\}$ forms a positively oriented orthogonal basis for $\mathbb {R}^2$. Put $b:=(\tau ,0)$ where $|x|=\tau$ and $\gamma :=\theta (x)\in (0,\pi )$. Let $\alpha \in (0,\pi /2)$ such that

$$\begin{aligned} \frac{\langle v,x-b\rangle }{|x-b|}=\cos \alpha . \end{aligned}$$

Then

• (i) $C(x,v,\alpha )\cap H\cap \overline{C}(0,e_1,\gamma )=\emptyset$;

• (ii) for any $y\in C(x,v,\alpha )\cap H{\setminus }\overline{B}(0,\tau )$ the line segment [b, y] intersects $\mathbb {S}^1_\tau$ outside the closed cone $\overline{C}(0,e_1,\gamma )$.

We point out that $C(0,e_1,\gamma )$ is the open cone with vertex 0 and axis $e_1$ which contains the point x on its boundary. We note that $\cos \alpha \in (0,1)$ because

$$\begin{aligned} \langle v,x-b\rangle= & {} -\langle v,b\rangle =-\langle (1/\tau )Ox,b\rangle \nonumber \\= & {} -\langle Op,e_1\rangle =\langle x,O^\star e_1\rangle =\langle x,e_2\rangle >0 \end{aligned}$$

(10.1)

and if $|x-b|=\langle v,x-b\rangle$ then $b=x-\lambda v$ for some $\lambda \in \mathbb {R}$ and hence $x_1=\langle e_1,x\rangle =\tau$ and $x_2=0$.

Proof

(i) For $\omega \in \mathbb {S}^1$ define the open half-space

$$\begin{aligned} H_{\omega }:=\{y\in \mathbb {R}^2:\langle y,\omega \rangle >0\}. \end{aligned}$$

We claim that $C(x,v,\alpha )\subset H_v$. For given $y\in C(x,v,\alpha )$,

$$\begin{aligned} \langle y,v\rangle =\langle y-x,v\rangle>|y-x|\cos \alpha >0. \end{aligned}$$

On the other hand, it holds that $\overline{C}(0,e_1,\gamma )\cap H\subset \overline{H}_{-v}$. This establishes (i).

(ii) By some trigonometry $\gamma =2\alpha$. Suppose that $\omega$ is a unit vector in $C(b,-e_1,\pi /2-\alpha )$. Then $\lambda :=\langle \omega ,e_1\rangle <\cos \alpha$ since upon rewriting the membership condition for $C(b,-e_1,\pi /2-\alpha )$ we obtain the quadratic inequality

$$\begin{aligned} \lambda ^2-2\cos ^2\alpha \lambda +\cos \gamma >0. \end{aligned}$$

For $\omega$ a unit vector in $\overline{C}(0,e_1,\gamma )$ the opposite inequality $\langle \omega ,e_1\rangle \ge \cos \alpha$ holds. This shows that

$$\begin{aligned} C(b,-e_1,\pi /2-\alpha )\cap \overline{C}(0,e_1,\gamma )\cap \mathbb {S}^1_\tau =\emptyset . \end{aligned}$$

The set $C(x,v,\alpha )\cap H$ is contained in the open convex cone $C(b,-e_1,\pi /2-\alpha )$. Suppose $y\in C(x,v,\alpha )\cap H{\setminus }\overline{B}(0,\tau )$. Then the line segment [b, y] is contained in $C(b,-e_1,\pi /2-\alpha )\cup \{b\}$. Now the set $C(b,-e_1,\pi /2-\alpha )\cap \mathbb {S}^1_\tau$ disconnects $C(b,-e_1,\pi /2-\alpha )\cup \{b\}$. This entails that $(b,y]\cap C(b,-e_1,\pi /2-\alpha )\cap \mathbb {S}^1_\tau \ne \emptyset$. The foregoing paragraph entails that $(b,y]\cap \overline{C}(0,e_1,\gamma )\cap \mathbb {S}^1_\tau =\emptyset$. This establishes the result. $\square$

Lemma 10.2

Let E be an open set in $\mathbb {R}^2$ such that $M:=\partial E$ is a $C^{1,1}$ hypersurface in $\mathbb {R}^2$. Assume that $E{\setminus }\{0\}=E^{sc}$. Suppose

• (i) $x\in (M{\setminus }\{0\})\cap H$;

• (ii) $\sin (\sigma (x))=-1$.

Then E is not convex.

Proof

Let $\gamma _1:I\rightarrow M$ be a $C^{1,1}$ parametrisation of M in a neighbourhood of x with $\gamma _1(0)=x$ as above. As $\sin (\sigma (x))=-1,n(x)$ and hence $n_1(0)$ point in the direction of x. Put $v:=-t_1(0)=-t(x)$. We may write

$$\begin{aligned} \gamma _1(s)=\gamma _1(0)+st_1(0)+R_1(s)=x-sv+R_1(s) \end{aligned}$$

for $s\in I$ where $R_1(s)=s\int _0^1\dot{\gamma }_1(ts)-\dot{\gamma }_1(0)\,dt$ and we can find a finite positive constant K such that $|R_1(s)|\le Ks^2$ on a symmetric open interval $I_0$ about 0 with $I_0\subset \subset I$. Then

$$\begin{aligned} \frac{\langle \gamma _1(s)-x,v\rangle }{|\gamma _1(s)-x|}&=\frac{\langle -sv+R_1,v\rangle }{|-sv+R_1|}\\&=\frac{1-\langle (R_1/s),v\rangle }{|v-R_1/s|}\rightarrow 1 \end{aligned}$$

as $s\uparrow 0$. Let $\alpha$ be as in Lemma 10.1 with x and v as just mentioned. The above estimate entails that $\gamma _1(s)\in C(x,v,\alpha )$ for small $s<0$. By (2.9) and Lemma 5.4 the function $r_1$ is non-increasing on I. In particular, $r_1(s)\ge r_1(0)=|x|=:\tau$ for $I\ni s<0$ and $\gamma _1(s)\not \in B(0,\tau )$.

Choose $\delta _1>0$ such that $\gamma _1(s)\in C(x,v,\alpha )\cap H$ for each $s\in [-\delta _1,0)$. Put $\beta :=\inf \{s\in [-\delta _1,0]:r_1(s)=\tau \}$. Suppose first that $\beta \in [-\delta _1,0)$. Then E is not convex (see Lemma 5.2). Now suppose that $\beta =0$. Let $\gamma$ be as in Lemma 10.1. Then the open circular arc $\mathbb {S}^1_\tau {\setminus } \overline{C}(0,e_1,\gamma )$ does not intersect $\overline{E}$: for otherwise, M intersects $\mathbb {S}^1_\tau {\setminus } \overline{C}(0,e_1,\gamma )$ and $\beta <0$ bearing in mind Lemma 5.2. Choose $s\in [-\delta _1,0)$. Then the points b and $\gamma _1(s)$ lie in $\overline{E}$. But by Lemma 10.1 the line segment $[b,\gamma _1(s)]$ intersects $\mathbb {S}^1_\tau$ in $\mathbb {S}^1_\tau {\setminus } \overline{C}(0,e_1,\gamma )$. Let $c\in [b,\gamma _1(s)]\cap \mathbb {S}^1_\tau$. Then $c\not \in \overline{E}$. This shows that $\overline{E}$ is not convex. But if E is convex then $\overline{E}$ is convex. Therefore E is not convex. $\square$

Theorem 10.3

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open, $M:=\partial E$ is a $C^{1,1}$ hypersurface in $\mathbb {R}^2$ and $E{\setminus }\{0\}=E^{sc}$. Put

$$\begin{aligned} R:=\inf \{\rho >0\}\in [0,+\infty ). \end{aligned}$$

(10.2)

Then $\varOmega \cap (R,+\infty )=\emptyset$ with $\varOmega$ as in (5.2).

Proof

Suppose that $\varOmega \cap (R,+\infty )\ne \emptyset$. As $\varOmega$ is open in $(0,+\infty )$ by Lemma 5.6 we may write $\varOmega$ as a countable union of disjoint open intervals in $(0,+\infty )$. By a suitable choice of one of these intervals we may assume that $\varOmega =(a,b)$ for some $0\le a<b<+\infty$ and that $\varOmega \cap (R,+\infty )\ne \emptyset$. Let us assume for the time being that $a>0$. Note that $[a,b]\subset \pi (M)$ and $\cos \sigma$ vanishes on $M_a\cup M_b$.

Let $u:\varOmega \rightarrow [-1,1]$ be as in (6.6). Then u has a continuous extension to [a, b] and $u=\pm 1$ at $\tau =a,b$. This may be seen as follows. For $\tau \in (a,b)$ the set $M_\tau \cap \overline{H}$ consists of a singleton by Lemma 5.4. The limit $x:=\lim _{\tau \downarrow a}M_\tau \cap \overline{H}\in \mathbb {S}^1_a\cap \overline{H}$ exists as M is $C^1$. There exists a $C^{1,1}$ parametrisation $\gamma _1:I\rightarrow M$ with $\gamma _1(0)=x$ as above. By (2.9) and Lemma 5.4, $r_1$ is decreasing on I. So $r_1>a$ on $I\cap \{s<0\}$ for otherwise the $C^1$ property fails at x. It follows that $\gamma _1=\gamma \circ r_1$ and $\sigma _1=\sigma \circ \gamma \circ r_1$ on $I\cap \{s<0\}$. Thus $\sin (\sigma \circ \gamma )\circ r_1=\sin \sigma _1$ on $I\cap \{s<0\}$. Now the function $\sin \sigma _1$ is continuous on I. So $u\rightarrow \sin \sigma _1(0)\in \{\pm 1\}$ as $\tau \downarrow a$. Put $\eta _1:=u(a)$ and $\eta _2:=u(b)$.

Let us consider the case $\eta =(\eta _1,\eta _2)=(1,1)$. According to Theorem 6.5 the generalised (mean) curvature is constant $\mathscr {H}^1$-a.e. on M with value $-\lambda$, say. Note that $u<1$ on (a, b) for otherwise $\cos (\sigma \circ \gamma )$ vanishes at some point in (a, b) bearing in mind Lemma 5.4. By Theorem 6.6 the pair $(u,\lambda )$ satisfies (9.4) with $\eta =(1,1)$. By Lemma 9.2, $u>0$ on [a, b]. Put $w:=1/u$. Then $(w,-\lambda )$ satisfies (9.6) and $w>1$ on (a, b). By Lemma 6.7,

$$\begin{aligned} \theta _2(b)-\theta _2(a)= & {} \int _a^b\theta _2^\prime \,d\tau =-\int _a^b\frac{u}{\sqrt{1-u^2}}\,\frac{d\tau }{\tau }\\= & {} -\int _a^b\frac{1}{\sqrt{w^2-1}}\,\frac{d\tau }{\tau }. \end{aligned}$$

By Corollary 9.16, $|\theta _2(b)-\theta _2(a)|>\pi$. But this contradicts the definition of $\theta _2$ in (6.4) as $\theta _2$ takes values in $(0,\pi )$ on (a, b). If $\eta =(-1,-1)$ then $\lambda >0$ by Lemma 9.2; this contradicts Lemma 7.2.

Now let us consider the case $\eta =(-1,1)$. Using the same formula as above, $\theta _2(b)-\theta _2(a)<0$ by Corollary 9.7. This means that $\theta _2(a)\in (0,\pi ]$. As before the limit $x:=\lim _{\tau \downarrow a}M_\tau \cap \overline{H}\in \mathbb {S}^1_a\cap \overline{H}$ exists as M is $C^1$. Using a local parametrisation it can be seen that $\theta _2(a)=\theta (x)$ and $\sin (\sigma (x))=-1$. If $\theta _2(a)\in (0,\pi )$ then E is not convex by Lemma 10.2. This contradicts Theorem 7.3. Note that we may assume that $\theta _2(a)\in (0,\pi )$. For otherwise, $\langle \gamma ,e_2\rangle <0$ for $\tau >a$ near a, contradicting the definition of $\gamma$ (6.5). If $\eta =(1,-1)$ then $\lambda >0$ by Lemma 9.2 and this contradicts Lemma 7.2 as before.

Suppose finally that $a=0$. By Lemma 5.5, $u(0)=0$ and $u(b)=\pm 1$. Suppose $u(b)=1$. Again employing the formula above, $\theta _2(b)-\theta _2(0)<-\pi /2$ by Lemma 9.19, the fact that the function $\phi :(0,1)\rightarrow \mathbb {R};t\mapsto t/\sqrt{1-t^2}$ is strictly increasing and Lemma 9.20. This means that $\theta _2(0)>\pi /2$. This contradicts the $C^1$ property at $0\in M$. If $u(b)=-1$ then then $\lambda >0$ by Lemma 9.2 giving a contradiction. $\square$

Lemma 10.4

Let f be as in (1.3) where $h:[0,+\infty )\rightarrow \mathbb {R}$ is a non-decreasing convex function. Let $v>0$.

• (i) Let E be a bounded minimiser of (1.2). Assume that E is open, $M:=\partial E$ is a $C^{1,1}$ hypersurface in $\mathbb {R}^2$ and $E{\setminus }\{0\}=E^{sc}$. Then for any $r>0$ with $r\ge R,M{\setminus }\overline{B}(0,r)$ consists of a finite union of disjoint centred circles.

• (ii) There exists a minimiser E of (1.2) such that $\partial E$ consists of a finite union of disjoint centred circles.

Proof

(i) First observe that

$$\begin{aligned} \emptyset \ne \pi (M)&=\Big [\pi (M)\cap [0,r]\Big ]\cup \Big [\pi (M)\cap (r,+\infty )\Big ]{\setminus }\varOmega \end{aligned}$$

by Lemma 10.3. We assume that the latter member is non-empty. By definition of $\varOmega ,\cos \sigma =0$ on $M\cap A((r,+\infty ))$. Let $\tau \in \pi (M)\cap (r,+\infty )$. We claim that $M_\tau =\mathbb {S}^1_\tau$. Suppose for a contradiction that $M_\tau \ne \mathbb {S}^1_\tau$. By Lemma 5.2, $M_\tau$ is the union of two closed spherical arcs in $\mathbb {S}^1_\tau$. Let x be a point on the boundary of one of these spherical arcs relative to $\mathbb {S}^1_\tau$. There exists a $C^{1,1}$ parametrisation $\gamma _1:I\rightarrow M$ of M in a neighbourhood of x with $\gamma _1(0)=x$ as before. By shrinking I if necessary we may assume that $\gamma _1(I)\subset A((r,+\infty ))$ as $\tau >r$. By (2.9), $\dot{r}_1=0$ on I as $\cos \sigma _1=0$ on I because $\cos \sigma =0$ on $M\cap A((r,+\infty ))$; that is, $r_1$ is constant on I. This means that $\gamma _1(I)\subset \mathbb {S}^1_\tau$. As the function $\sin \sigma _1$ is continuous on I it takes the value $\pm 1$ there. By (2.10), $r_1\dot{\theta }_1=\sin \sigma _1=\pm 1$ on I. This means that $\theta _1$ is either strictly decreasing or strictly increasing on I. This entails that the point x is not a boundary point of $M_\tau$ in $\mathbb {S}^1_\tau$ and this proves the claim.

It follows from these considerations that $M{\setminus }\overline{B}(0,r)$ consists of a finite union of disjoint centred circles. Note that $f\ge e^{h(0)}=:c>0$ on $\mathbb {R}^2$. As a result, $+\infty >P_f(E)\ge cP(E)$ and in particular the relative perimeter $P(E,\mathbb {R}^2{\setminus }\overline{B}(0,r))<+\infty$. This explains why $M{\setminus }\overline{B}(0,r)$ comprises only finitely many circles.

(ii) Let E be a bounded minimiser of (1.2) such that E is open, $M:=\partial E$ is a $C^{1,1}$ hypersurface in $\mathbb {R}^2$ and $E{\setminus }\{0\}=E^{sc}$ as in Theorem 4.5. Assume that $R>0$. By (i), $M{\setminus }\overline{B}(0,R)$ consists of a finite union of disjoint centred circles. We claim that only one of the possibilities

$$\begin{aligned} M_R&=\emptyset ,\,M_R=\mathbb {S}^1_R,\,M_R=\{Re_1\}\text { or }M_R=\{-Re_1\} \end{aligned}$$

(10.3)

holds. To prove this suppose that $M_R\ne \emptyset$ and $M_R\ne \mathbb {S}^1_R$. Bearing in mind Lemma 5.2 we may choose $x\in M_R$ such that x lies on the boundary of $M_R$ relative to $\mathbb {S}^1_R$. Assume that $x\in H$. Let $\gamma _1:I\rightarrow M$ be a local parametrisation of M with $\gamma _1(0)=x$ with the usual conventions. We first notice that $\cos (\sigma (x))=0$ for otherwise we obtain a contradiction to Theorem 10.3. As $r_1$ is decreasing on I and x is a relative boundary point it holds that $r_1<R$ on $I^+:=I\cap \{s>0\}$. As $M{\setminus }\overline{\varLambda _1}$ is open in M we may suppose that $\gamma _1(I^+)\subset M{\setminus }\overline{\varLambda _1}$. According to Theorem 6.5 the curvature k of $\gamma _1(I^+)\cap B(0,R)$ is a.e. constant as $\rho$ vanishes on (0, R). Hence $\gamma _1(I^+)\cap B(0,R)$ consists of a line or circular arc. The fact that $\cos (\sigma (x))=0$ means that $\gamma _1(I^+)\cap B(0,R)$ cannot be a line. So $\gamma _1(I^+)\cap B(0,R)$ is an open arc of a circle C containing x in its closure with centre on the line-segment [0, x] and radius $r\in (0,R)$. By considering a local parametrisation, it can be seen that $C\cap B(0,R)\subset M$. But this contradicts the fact that $E{\setminus }\{0\}=E^{sc}$. In summary, $M_R\subset \{\pm Re_1\}$. Finally note that if $M_R=\{\pm Re_1\}$ then $M_R=\mathbb {S}^1_R$ by Lemma 5.2. This establishes (10.3).

Suppose that $M_R=\emptyset$. As both sets M and $\mathbb {S}^1_R$ are compact, $d(M,\mathbb {S}^1_R)>0$. Assume first that $\mathbb {S}^1_R\subset E$. Put $F:=B(0,R){\setminus } E$ and suppose $F\ne \emptyset$. Then F is a set of finite perimeter, $F\subset \subset B(0,R)$ and $P(F)=P(E,B(0,R))$. Let B be a centred ball with $|B|=|F|$. By the classical isoperimetric inequality, $P(B)\le P(F)$. Define $E_1:=(\mathbb {R}^2{\setminus } B)\cap (B(0,R)\cup E)$. Then $V_f(E_1)=V_f(E)$ and $P_f(E_1)\le P_f(E)$. That is, $E_1$ is a minimiser of (1.2) such that $\partial E_1$ consists of a finite union of disjoint centred circles. Now suppose that $\mathbb {S}^1_R\subset \mathbb {R}^2{\setminus }\overline{E}$. In like fashion we may redefine E via $E_1:=B\cup (E{\setminus }\overline{B}(0,R))$ with B a centred ball in B(0, R). The remaining cases in (10.3) can be dealt with in a similar way. The upshot of this argument is that there exists a m inimiser of (1.2) whose boundary M consists of a finite union of disjoint centred circles in case $R>0$.

Now suppose that $R=0$. By (i), $M{\setminus }\overline{B}(0,r)$ consists of a finite union of disjoint centred circles for any $r\in (0,1)$. If these accumulate at 0 then M fails to be $C^1$ at the origin. The assertion follows. $\square$

Lemma 10.5

Suppose that the function $J:[0,+\infty )\rightarrow [0,+\infty )$ is continuous non-decreasing and $J(0)=0$. Let $N\in \mathbb {N}\cup \{+\infty \}$ and $\{t_h:h=0,\ldots ,2N+1\}$ a sequence of points in $[0,+\infty )$ with

$$\begin{aligned} t_0>t_1>\cdots>t_{2h}>t_{2h+1}>\cdots \ge 0. \end{aligned}$$

Then

$$\begin{aligned} +\,\infty \ge \sum _{h=0}^{2N+1}J(t_h)\ge J\left( \sum _{h=0}^{2N+1}(-1)^{h}t_h\right) . \end{aligned}$$

Proof

We suppose that $N=+\infty$. The series $\sum _{h=0}^\infty (-1)^{h}t_h$ converges by the alternating series test. For each $n\in \mathbb {N}$,

$$\begin{aligned} \sum _{h=0}^{2n+1}(-1)^{h}t_h\le t_0 \end{aligned}$$

and the same inequality holds for the infinite sum. As in Step 2 in [5] Theorem 2.1,

$$\begin{aligned} +\,\infty \ge \sum _{h=0}^\infty J(t_h) \ge J(t_0) \ge J\left( \sum _{h=0}^\infty (-1)^{h}t_h\right) \end{aligned}$$

as J is non-decreasing. $\square$

Proof of Theorem 1.1

There exists a minimiser E of (1.2) with the property that $\partial E$ consists of a finite union of disjoint centred circles according to Lemma 10.4. As such we may write

$$\begin{aligned} E=\bigcup _{h=0}^NA((a_{2h+1},a_{2h})) \end{aligned}$$

where $N\in \mathbb {N}$ and $+\infty>a_0>a_1>\cdots>a_{2N}>a_{2N+1}>0$. Define

$$\begin{aligned}&\mathtt {f}:[0,+\infty )\rightarrow \mathbb {R};t\mapsto e^{h(t)};\nonumber \\&g:[0,+\infty )\rightarrow \mathbb {R};t\mapsto t\mathtt {f}(t);\nonumber \\&G:[0,+\infty )\rightarrow \mathbb {R};t\mapsto \int _0^t g\,d\tau .\nonumber \end{aligned}$$

Then $G:[0,+\infty )\rightarrow [0,+\infty )$ is a bijection with inverse $G^{-1}$. Define the strictly increasing function

$$\begin{aligned} J:[0,+\infty )\rightarrow \mathbb {R};t\mapsto g\circ G^{-1}. \end{aligned}$$

Put $t_h:=G(a_h)$ for $h=0,\ldots ,2N+1$. Then $+\infty>t_0>t_1>\cdots>t_{2N}>t_{2N+1}>> 0$. Put $B:=B(0,r)$ where $r:=G^{-1}(v/2\pi )$ so that $V_f(B)=v$. Note that

$$\begin{aligned} v= & {} V_f(E)=2\pi \sum _{h=0}^N\Big \{G(a_{2h})-G(a_{2h+1})\Big \}\\= & {} 2\pi \sum _{h=0}^{2N+1}(-1)^{h}t_h. \end{aligned}$$

By Lemma 10.5,

$$\begin{aligned} P_f(E)= & {} 2\pi \sum _{h=0}^{2N+1}g(a_h)=2\pi \sum _{h=0}^{2N+1}J(t_h) \\\ge & {} 2\pi J\left( \sum _{h=0}^{2N+1}(-1)^h t_h\right) \\= & {} 2\pi J(v/2\pi )=P_f(B). \end{aligned}$$

$\square$

Proof of Theorem 1.2

Let $v>0$ and E be a minimiser for (1.2). Then E is essentially bounded by Theorem 3.1. By Theorem 4.5 there exists an $\mathscr {L}^2$-measurable set $\widetilde{E}$ with the properties

• (a) $\widetilde{E}$ is a minimiser of (1.2);

• (b) $L_{\widetilde{E}}=L_E$ a.e. on $(0,+\infty )$;

• (c) $\widetilde{E}$ is open, bounded and has $C^{1,1}$ boundary;

• (d) $\widetilde{E}{\setminus }\{0\}=\widetilde{E}^{sc}$.

(i) Suppose that $0<v\le v_0$ so that $R>0$. Choose $r\in (0,R]$ such that $V(B(0,r))=V(E)=v$. Suppose that $\widetilde{E}{\setminus }\overline{B}(0,R)\ne \emptyset$. By Lemma 10.4 there exists $t>R$ such that $\mathbb {S}^1_t\subset M$. As g is strictly increasing, $g(t)>g(r)$. So $P_f(E)=P_f(\widetilde{E})\ge \pi g(t)>\pi g(r)=P_f(B(0,r))$. This contradicts the fact that E is a minimiser for (1.2). So $\widetilde{E}\subset \overline{B}(0,R)$ and $L_{\widetilde{E}}=0$ on $(R,+\infty )$. By property (b), $|E{\setminus }\overline{B}(0,R)|=0$. By the uniqueness property in the classical isoperimetric theorem (see for example [12] Theorem 4.11) the set E is equivalent to a ball B in $\overline{B}(0,R)$.

(ii) With $r>0$ as before, $V(B(0,r))=V(E)=v>v_0=V(B(0,R))$ so $r>R$. If $\widetilde{E}{\setminus }\overline{B}(0,r)\ne \emptyset$ we derive a contradiction in the same way as above. Consequently, $\widetilde{E}=B:=B(0,r)$. Thus, $L_E=L_B$ a.e. on $(0,+\infty )$; in particular, $|E{\setminus } B|=0$. This entails that E is equivalent to B. $\square$