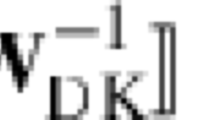Abstract
Let M be a smooth manifold and V a Euclidean space. Let \( \overline{{{\text{Emb}}}} \)(M,V) be the homotopy fiber of the map Emb(M,V) → Imm(M,V). This paper is about the rational homology of \( \overline{{{\text{Emb}}}} \)(M,V). We study it by applying embedding calculus and orthogonal calculus to the bifunctor (M,V)↦ HQ ∧ \( \overline{{{\text{Emb}}}} \)(M,V)+. Our main theorem states that if
(where ED(M) is the embedding dimension of M), the Taylor tower in the sense of orthogonal calculus (henceforward called “the orthogonal tower”) of this functor splits as a product of its layers. Equivalently, the rational homology spectral sequence associated with the tower collapses at E 1. In the case of knot embeddings, this spectral sequence coincides with the Vassiliev spectral sequence. The main ingredients in the proof are embedding calculus and Kontsevich's theorem on the formality of the little balls operad. We write explicit formulas for the layers in the orthogonal tower of the functor
The formulas show, in particular, that the (rational) homotopy type of the layers of the orthogonal tower is determined by the (rational) homotopy type of M. This, together with our rational splitting theorem, implies that, under the above assumption on codimension, rational homology equivalences of manifolds induce isomorphisms between the rational homology groups of \( \overline{{{\text{Emb}}}} \)(–,V).
Similar content being viewed by others
References
Arone, G., A note on the homology of ∑ n , the Schwartz genus, and solving polynomial equations, in An Alpine Anthology of Homotopy Theory, Contemp. Math., 399, pp. 1–10. Amer. Math. Soc., Providence, RI, 2006.
— The derivatives of embedding functors I: The stable case. Preprint. arXiv:0707.3489.
Arone, G., Lambrechts, P., Turchin, V. & Voliæ, I., Coformality and the rational homotopy groups of spaces of long knots. To appear in Math. Res. Lett. arXiv:math/0701350.
Borceux, F., Handbook of Categorical Algebra. 2. Encyclopedia of Mathematics and its Applications, 51. Cambridge University Press, Cambridge, 1994.
Ching, M., Bar constructions for topological operads and the Goodwillie derivatives of the identity. Geom. Topol., 9 (2005), 833–933.
Cohen, F. R. & Taylor, L. R., On the representation theory associated to the cohomology of configuration spaces, in Algebraic Topology (Oaxtepec, 1991), Contemp. Math., 146, pp. 91–109. Amer. Math. Soc., Providence, RI, 1993.
Deligne, P., Griffiths, P., Morgan, J. & Sullivan, D., Real homotopy theory of Kähler manifolds. Invent. Math., 29 (1975), 245–274.
Dwyer, W. G. & Spaliñski, J., Homotopy theories and model categories, in Handbook of Algebraic Topology, pp. 73–126. North-Holland, Amsterdam, 1995.
Goodwillie, T. G. & Klein, J. R., Excision statements for spaces of embeddings. In preparation.
Goodwillie, T. G., Klein, J. R. & Weiss, M. S., Spaces of smooth embeddings, disjunction and surgery, in Surveys on Surgery Theory, Vol. 2, Ann. of Math. Stud., 149, pp. 221–284. Princeton University Press, Princeton, NJ, 2001.
Goodwillie, T. G. & Weiss, M., Embeddings from the point of view of immersion theory. II. Geom. Topol., 3 (1999), 103–118.
Guillén Santos, F., Navarro, V., Pascual, P. & Roig, A., Moduli spaces and formal operads. Duke Math. J., 129 (2005), 291–335.
Hirschhorn, P. S., Model Categories and Their Localizations. Mathematical Surveys and Monographs, 99. Amer. Math. Soc., Providence, RI, 2003.
Kontsevich, M., Operads and motives in deformation quantization. Lett. Math. Phys., 48 (1999), 35–72.
Lambrechts, P., Turchin, V. & Voliæ, I., The rational homology of spaces of long knots in codimension >2. Preprint. arXiv:math/0703649.
Lambrechts, P. & Voliæ, I., Formality of the little balls operad. In preparation.
Orlik, P. & Terao, H., Arrangements of Hyperplanes. Grundlehren der Mathematischen Wissenschaften, 300. Springer, Berlin–Heidelberg, 1992.
Schwede, S., Stable homotopical algebra and Γ-spaces. Math. Proc. Cambridge Philos. Soc., 126 (1999), 329–356.
Schwede, S. & Shipley, B., Equivalences of monoidal model categories. Algebr. Geom. Topol., 3 (2003), 287–334.
Sullivan, D., Infinitesimal computations in topology. Inst. Hautes Études Sci. Publ. Math., (1977), 269–331.
Weibel, C. A., An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics, 38. Cambridge University Press, Cambridge, 1994.
Weiss, M. S., Orthogonal calculus. Trans. Amer. Math. Soc., 347:10 (1995), 3743–3796.
— Embeddings from the point of view of immersion theory. I. Geom. Topol., 3 (1999), 67–101.
— Homology of spaces of smooth embeddings. Q. J. Math., 55 (2004), 499–504.
Author information
Authors and Affiliations
Corresponding author
Additional information
The first and third authors were supported by the National Science Foundation, grants DMS 0605073 and DMS 0504390, respectively. The second author is chercheur qualifié au F.N.R.S. and he gratefully acknowledges support by the Institut Mittag–Leffler (Djursholm, Sweden).
Rights and permissions
About this article
Cite this article
Arone, G., Lambrechts, P. & Volić, I. Calculus of functors, operad formality, and rational homology of embedding spaces. Acta Math 199, 153–198 (2007). https://doi.org/10.1007/s11511-007-0019-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11511-007-0019-7