Introduction

Due to the growing need for integrated optical circuits and higher optical communication bandwidth, optical demultiplexers have a lot of potential in all-optical devices for the telecommunications industry [1]. The increasing need for data rate is what motivates the need for a multiplexing technique [2]. The following technological approaches can be used to create optical demultiplexers: Y-branch devices [3, 4], Mach–Zehnder interferometers (MZI) [5], blazed waveguide sidewall grating [6], and multimode interference (MMI) couplers [7, 8]. To boost the data transfer bitrate, wavelength division multiplexing (WDM) is one of the technologies that is widely employed [1]. By lessening the distance between peak wavelengths, more channels may be exploited for a single spectral band. A typical use for MMI coupler devices in photonic integrated circuits (PICs) is their high optical bandwidth, low losses, and small size. The self-imaging phenomenon, which is the basis for MMI waveguide functioning, repeats the electric field profile that enters the device into multiple images at frequent distances along the propagation axis of the device [9]. Back reflection, particularly the reflection of light into the laser source from the opposite direction, is one of the major issues that might degrade the performance of the transmitter system. The self-imaging trend and the mismatch in the refractive indices of silicon and silica can create reflections in silicon MMI couplers [10].

Plasmonic-based nanostructures have been suggested as a method to create these sorts of devices and get over the size and subwavelength light confinement problems [11]. Nevertheless, component downsizing is necessary for technological advancements, but because of the diffraction limit, it is difficult to access the nanoscale optical features; consequently, plasmonic has arisen as a possible substitute [12]. WDM optical systems increase the capacity of the optical network by combining several channels with different wavelengths and transmitting them collectively through an optical fiber. Plasmonic WDMs are therefore essential components of communication networks [13]. Plasmonic MIM waveguides are extensively studied for several eye-catching applications such as filters [14,15,16,17], sensors [18,19,20], all-optical logic gates [21], and switches [22], among others. In [23], a 1 × 2 plasmonic wavelength demultiplexer is proposed based on a rectangular MIM waveguide that offers low crosstalk of 11.06 dB. In [24], the multimode interference effect is utilized to make MIM waveguide-based demultiplexer and splitter with an extinction ratio of ~ 11.6 dB. Moreover, there are several other interesting works on plasmonic demultiplexers [25,26,27,28]; however, all of them failed to provide a mechanism for lighting coupling to the MIM waveguide. This is the reason, there is no experimental demonstration of the plasmonic device based on a MIM waveguide is yet available [29].

In this work, we proposed a 1 × 2 plasmonic demultiplexer for the telecommunication wavelengths such as 1310 nm and 1550 nm. The device design is composed of two circular cavities of different sizes side coupled to a metal–insulator-metal (MIM) waveguide. Eventually, the resonant wavelengths are collected from the output ports on both sides of the chip. The device design is simple and compact which offers low crosstalk between the output ports. Moreover, the light coupling mechanism to the MIM waveguide is also suggested via an efficient design of a mode converter.

1 × 2 Demultiplexer Design

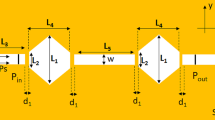
Absorption and scattering are the two factors that lead to fiber losses. Numerous wavelengths exhibit absorption. It happens because the light energy is absorbed by the water vapor in the glass. As a result, “water bands” are used to describe these specific wavelengths. Light energy bounces off molecules inside the fiber, which results in scattering. The wavelength influences how much scattering takes place. Higher degrees of scattering are seen at shorter wavelengths. Therefore, while choosing a wavelength, consider both the position of the water bands and the level of scattering. The wavelengths of 1310 nm and 1550 nm are now considered universal standards [30, 31]. In this paper, a 1 × 2 plasmonic demultiplexer is proposed which is comprised of a MIM waveguide and two hollow circular cavities side coupled to the bus waveguide as shown in Fig. 1.

Fig. 1
figure 1

Graphical illustration of a 1 × 2 plasmonic demultiplexer design established on a MIM waveguide and a Si mode converter

Full size image

When it comes to creating nanoscale integrated photonic circuits, MIM waveguide architectures are one of the most efficient methods, and they are largely favored in optical communication [32, 33] and the sensing domain [34,35,36]. A dielectric core, which may be made of air or another material with a low refractive index, is sandwiched between two metal claddings in this three-layer waveguide design. Gold (Au) is more oxidation-resistant and biocompatible than silver (Ag), which is why it is preferred as a metal. The oxidation in Ag can be controlled by depositing a thin layer of dielectric material; however, it can limit the sensitivity of the sensing devices. The Lorentz-Drude model, as shown in Eq. (1), is used to compute the permittivity of Au [37].

$$\varepsilon ={\varepsilon }_{\infty }-\frac{{\omega }_{p}^{2}}{{\omega }^{2}+j\omega \gamma }$$
(1)

where \({\varepsilon }_{\infty }=9.0685\), \({\omega }_{p}\)=135.44 × 1014 rad/s, and \(\gamma =1.15 \times 1014\mathrm{ rad}/\mathrm{s}\). These waveguides confine electromagnetic waves tightly near the interface, away from the diffraction limit of light [38]. The width of the MIM bus waveguide and output ports (P1 and P2) is denoted as W which is fixed at 80 nm to ensure the existence of only transverse magnetic (TM0) mode [39, 40]. Two hollow circular cavities of radius R1 and R2 are side coupled on both sides of the bus waveguide with a coupling distance of g. To collect the resonant wavelength of 1310 nm and 1550 nm, the output ports P1 and P2 are side coupled to the cavities, respectively. The gap between the P1(P2) and MIM bus waveguide is denoted as s which is around 120 nm. This separation should be greater than g to avoid direct coupling of light from the bus waveguide to the output port. Moreover, both cavities are 1500 nm apart to avoid crosstalk and minimize the footprint of the device. The crosstalk at P1 and P2 is calculated by utilizing (2) and (3), respectively. The geometric parameters of the device are presented in Table 1.

Table 1 Geometric variables of the 1 × 2 plasmonic demultiplexer
Full size table
$$Crosstalk\;\left(dB\right)at\;P1=10\times\log\;\left(\frac{P_{1550nm}}{P_{1310nm}}\right);$$
(2)
$$Crosstalk\;\left(dB\right)at\;P2=10\times\log\;\left(\frac{P_{1310nm}}{P_{1550nm}}\right);$$
(3)

We employed the finite element method (FEM) incorporated in the COMSOL Multiphysics program for numerical research. A mesh size of λ/150 is employed in the bus waveguide, output ports, and cavities, whereas a mesh size of λ/100 is utilized in the metallic part because the evanescent field in the dielectric is larger than the evanescent field in the metal. It is preferable to establish an open-bounded domain or limit of the computing domain while evaluating EM wave issues, where an EM wave passes without any reflection. Scattering boundary conditions (SBC) are introduced to the outer edges of the FEM simulation window to represent an open geometry. Most earlier investigations on plasmonic devices employed 2D numerical simulations, where one dimension is thought to be infinite [41,42,43]. As a result, assessing device performance may be done more quickly and with less loss, as was the case in this investigation. On the other hand, the loss of the system is significantly influenced by the height of the MIM waveguide, which should be considered in real-world processing [44].

Dielectric to Plasmonic Mode Converter

The MIM plasmonic waveguide devices have been thoroughly researched for several intriguing applications [11]. The coupling of the incident light to the nanosized MIM plasmonic waveguide, however, has not received any attention [29]. Since light can be dispersed at the interface, it is impossible to effectively couple light from the fiber to the metallic waveguide. Due to the physical proximity of the end facets of two different optical waveguides, end-fire coupling—also known as Butt coupling or edge coupling—is the easiest technique for connecting and transmitting optical signals between them [45]. In this work, a silicon-tapered waveguide mode converter is embedded in the circuit to efficiently convert the dielectric mode to the plasmonic mode. The total length of the converter (L1 + L2) is fixed at 1500 nm, where L1 = 1000 nm and L2 is 500 nm. The MIM waveguide is designed in such a way that the entrance of the waveguide (T) is 1500 nm wide and gradually tapered to 80 nm which is the actual width of the MIM waveguide. The gap between the metal and the tapered waveguide is around 70 to 76 nm labeled as d1 and d2, respectively. The tip of the mode converter is placed at the entrance of the MIM waveguide to allow the smooth transfer of optical power to the MIM waveguide.

The effective refractive index (neff) of the dielectric mode is calculated throughout the length of the mode converter to determine the efficient effective index matching of dielectric and plasmonic mode as shown in Fig. 2. At WSi = 400 nm, the neff is ~ 2.4668 and ~ 2.1132 for the working wavelength of 1310 nm and 1550 nm, respectively. The neff for the mode at the wavelength of 1310 nm is higher than the neff of the mode at 1550 nm because the mode is better confined. As WSi narrows down in the tapered region, the neff approaches to ~ 1.4606 and ~ 1.4454 which matches the neff of the plasmonic mode which is ~ 1.4589 and ~ 1.4425 for the operational wavelength of 1310 nm and 1550 nm, respectively. This provides an excellent effective index matching of ~ 99%.

Fig. 2
figure 2

Real part of the effective index (Re (neff)) of the dielectric mode and plasmonic mode matching

Full size image

The radius (R) of the hollow circular cavity differed between 400 and 800 nm to find the resonances for the operational wavelength of 1310 nm and 1550 nm, respectively. The remaining geometric parameters of the device such as g and W are kept at 20 nm and 80 nm, respectively. From Fig. 3a, it can be seen that the strongest resonance for the wavelength of 1310 nm and 1550 nm are obtained at R = 587 nm and R = 706 nm, respectively. This indicates that, for the 1 × 2 plasmonic demultiplexing system, R1 = 587 nm, and R2 = 706 nm should be embedded simultaneously to filter out the 1310 nm and 1550 nm from the broadband light source. The normalized transmission spectrum is mapped for the wavelength range of 1200 nm to 1650 nm at P1 and P2 as shown in Fig. 3b. The transmission wavelength of 1310 nm and 1550 nm is obtained at P1 and P2 and has got a full width at half maximum (FWHM) of ~ 40 nm, respectively.

Fig. 3
figure 3

a Transmission power of 1310 nm and 1550 nm wavelength versus radius (R) of the hollow circular cavity, b transmission at P1 and P2 versus wavelength

Full size image

The coupling gap (g) plays an important role in determining the optimum power of the resonant wavelength in the cavity. The geometric variables of the device for instance R1, R2, and W are kept at 587 nm, 706 nm, and 80 nm, respectively. The g is varied from 10 to 50 nm and examines the transmission at P1 and P2 for the working wavelength of 1310 nm and 1550 nm, respectively. Electron beam patterning is necessary to make air gaps in plasmonic waveguides that are in the sub-nm scale. The capability to write patterns with sub-10 nm precision is the major advantage of electron beam lithography. This kind of maskless lithography is only appropriate for R&D and small-scale semiconductor device manufacture due to its high resolution and poor throughput [46, 47]. From Fig. 4a, it can be seen that as g increases from 10 to 50 nm, the wavelength makes a blueshift from 1329 to 1303 nm. The resonant wavelength of 1310 nm having a power of 67% is obtained at P1 when g = 20 nm. The same assessment is carried out for the resonant wavelength of 1550 nm where the transmission power of 64% is obtained at P2 as shown in Fig. 4b. The transmission power can be enhanced by adjusting the radius (R1) and coupling gap (g).

Fig. 4
figure 4

Transmission power and wavelength dependence g for a P1 and b P2

Full size image

A broadband light source is used to excite the bus waveguide. The incoming light is coupled to the first cavity (on the left) at 1310 nm when the resonant condition is met, and later the light is transferred to the output port (P1) as shown by the normalized E-field mapping in Fig. 5a. Similarly, the normalized E-field mapping at 1550 nm concentrated in the second cavity (on the right) and output port (P2) is shown in Fig. 5b.

Fig. 5
figure 5

Normalized E-field distribution in a 1 × 2 plasmonic demultiplexer at a λ = 1310 nm and b λ = 1550 nm

Full size image

Limitations and Prospects of Plasmonic Demultiplexers

The 1 × 2 plasmonic demultiplexer is specifically optimized for 1310 nm and 1550 nm telecommunication wavelengths. The device is composed of a MIM waveguide where the refractive index in the hollow circular cavities is considered 1.0 (air). Any deviation in the refractive index of the ambient medium can bring a variation in the transmission wavelength due to the shift in neff of the resonant mode as shown in Fig. 6. The ambient index is varied between 1.0 and 1.02; as a result, the transmission wavelength shift of ∆λ = 27 nm (1310 to 1337 nm) at P1 and ∆λ = 32 nm (1550 to 1582 nm) at P2 is observed. Therefore, it is required to enclose the device in a chamber where environmental factors such as temperature, pressure, and refractive index should not interact with the device and deteriorate its performance. Dynamic spectral tunability is a key feature of plasmonic filters [48]. By introducing nonlinear material, such as electro-optical (EO) material having a high EO coefficient, into the cavities, wavelength tuning may be achieved [49]. In recent years, a few materials with EO coefficients over 150 pm/V have been discovered [49, 50]. The accessibility of such materials guarantees that the filter’s necessary index-modulation may be easily accomplished.

Fig. 6
figure 6

Transmission wavelength versus the ambient refractive index

Full size image

Conclusion

Herein, a compact 1 × 2 plasmonic demultiplexer based on a MIM waveguide is presented for the telecommunication wavelengths of 1310 nm and 1550 nm. Two hollow circular cavities are side coupled to the bus MIM waveguide on both sides of the chip, and the light is collected via output ports (P1 and P2) coupled to the cavities. The radius of the circular cavities is designed in such a way that a wavelength of 1310 nm is collected at P1 and 1550 nm is collected at P2. The mechanism of light coupling into the MIM waveguide is also suggested by embedding a silicon-based-mode converter which effectively transforms the dielectric mode into a plasmonic mode. The footprint of the device is around 6 μm × 6 μm, and the minimum crosstalk of the device is around 14.07 dB and 13.67 dB for the working wavelength of 1310 nm and 1550 nm, respectively.